Inverse Filtering of Magnetic Prospection Data—A Gateway to the Social Structure of Cucuteni–Tripolye Settlements?
Abstract
:1. Introduction
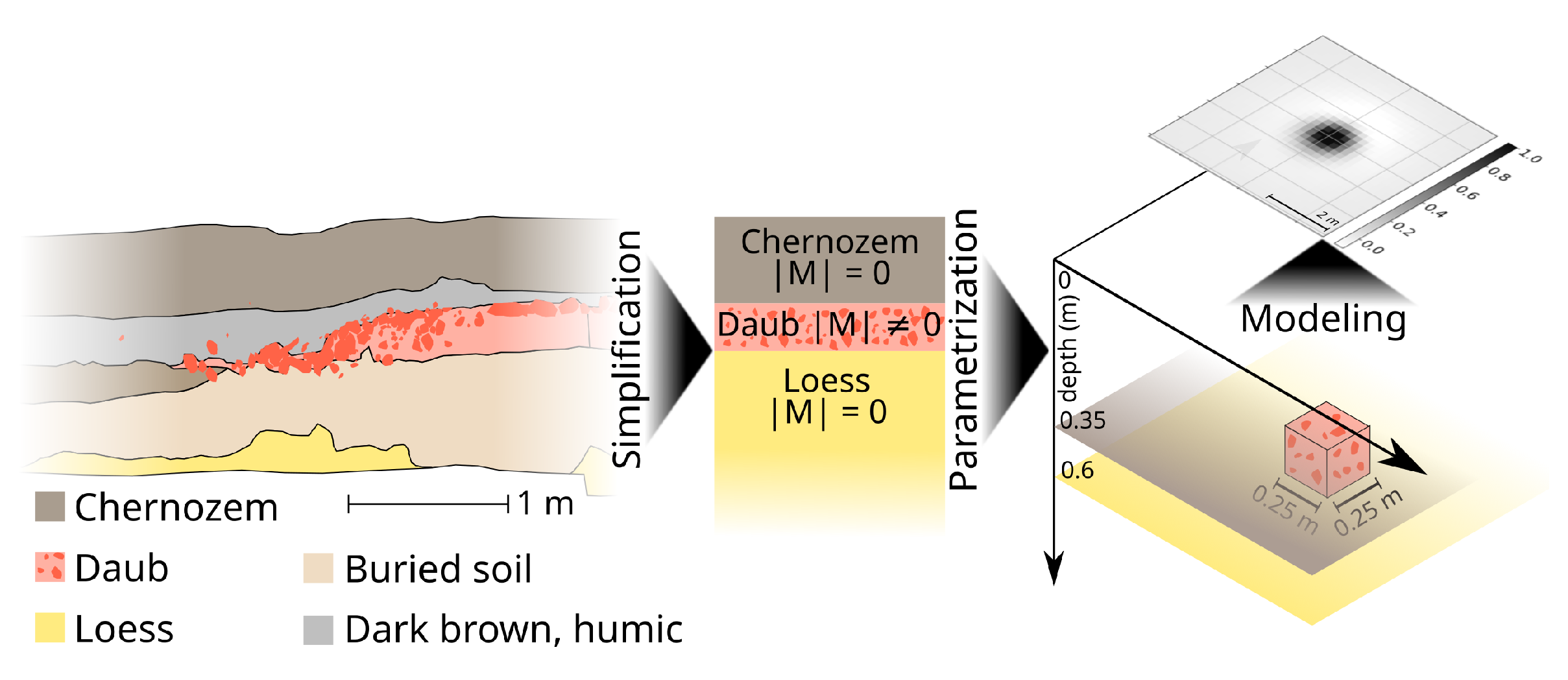
2. Materials and Methods
2.1. Magnetic Data
2.2. Inverse Filtering
2.3. Quantification of Building Remains
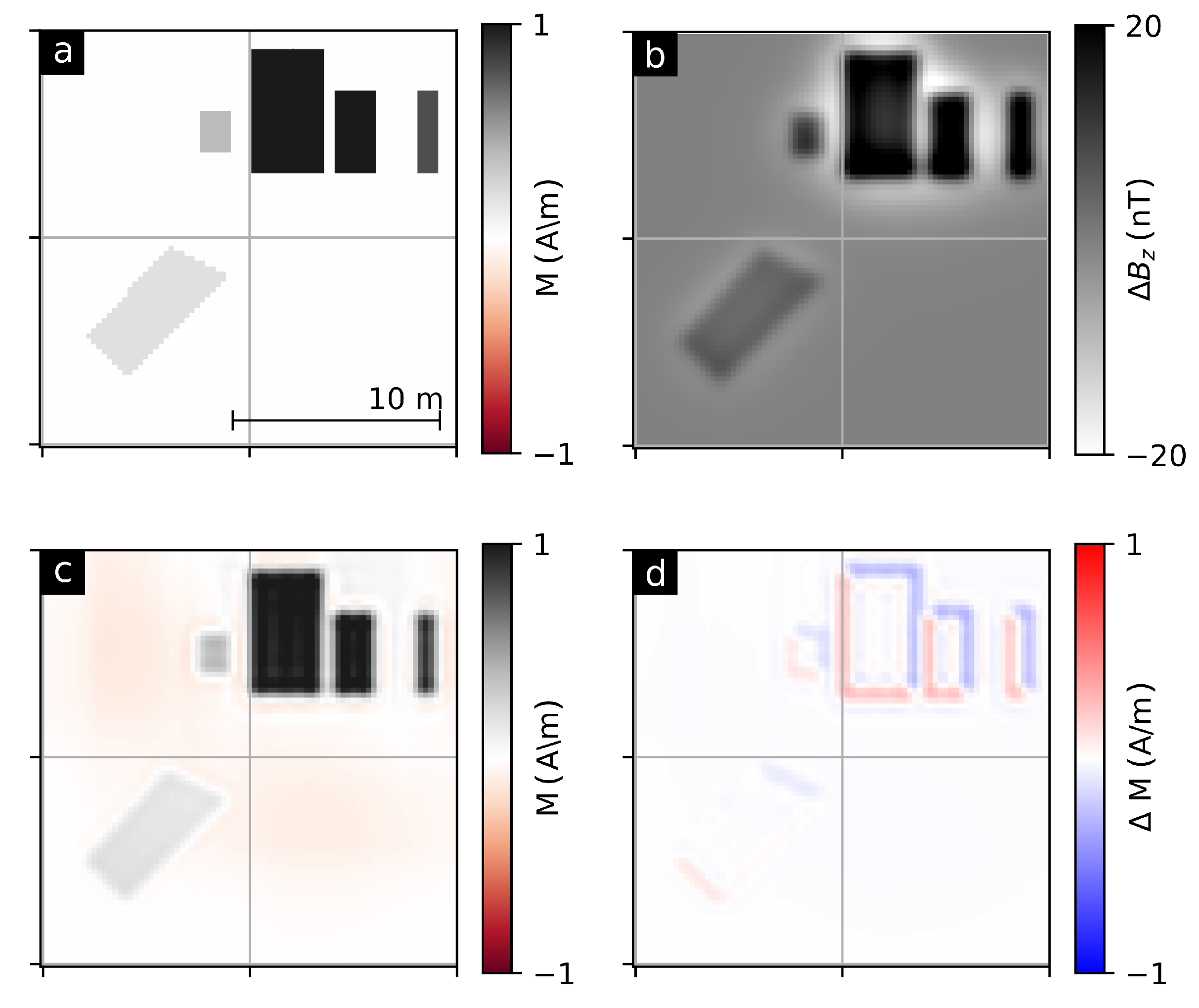
2.4. Synthetic Test
2.5. Comparison to Least-Squares Inversion
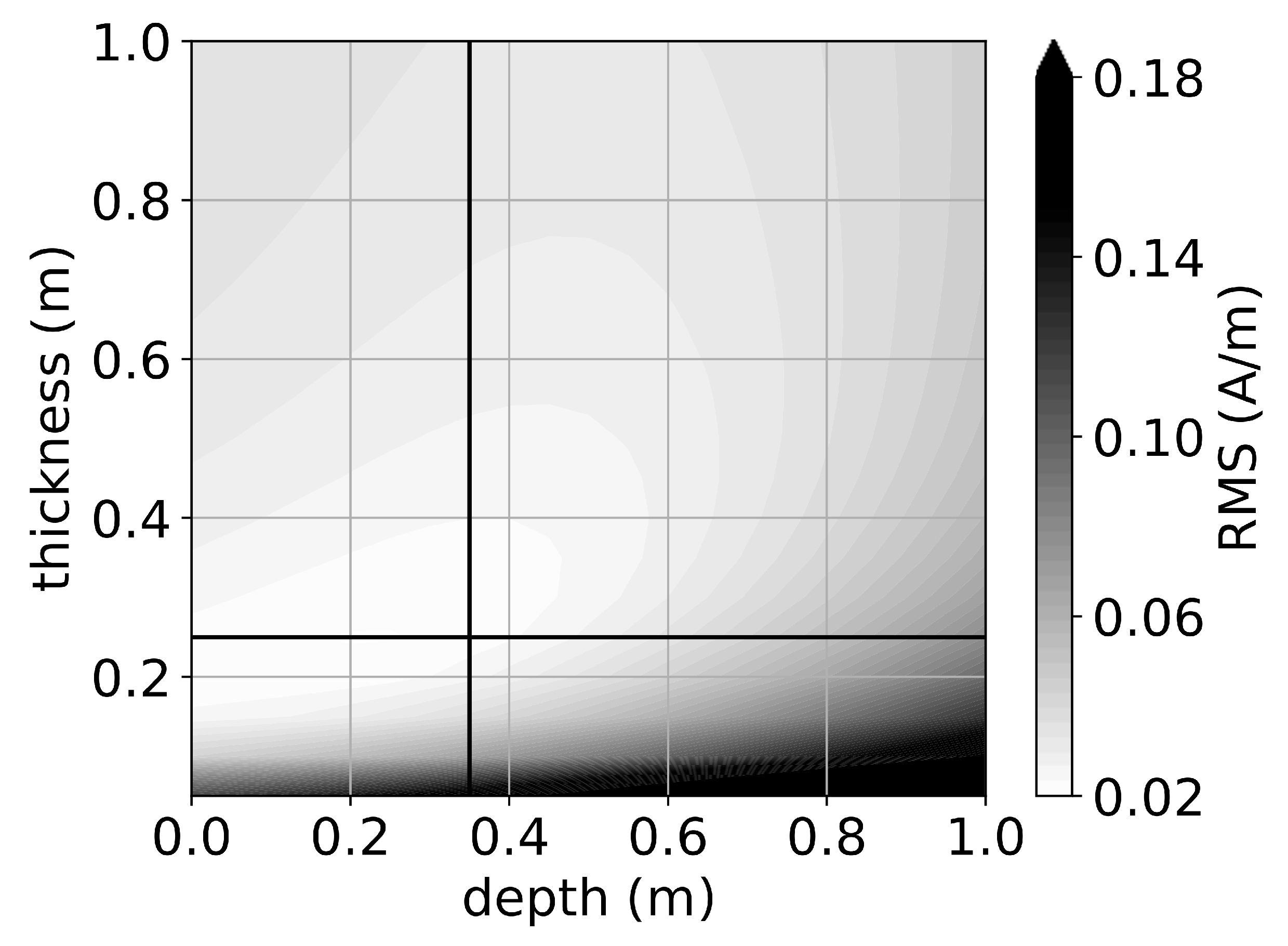
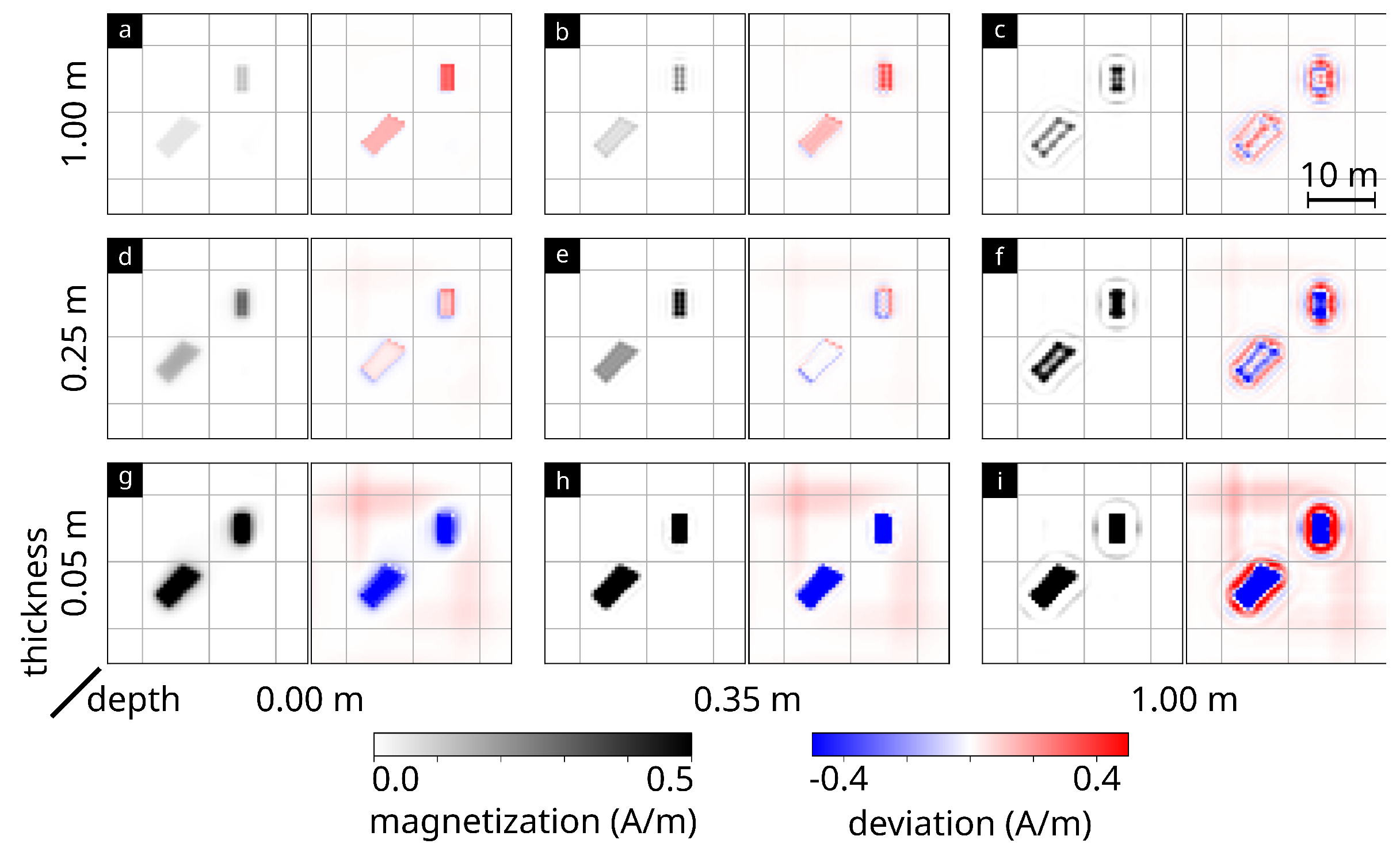
2.6. Influence of Depth and Thickness
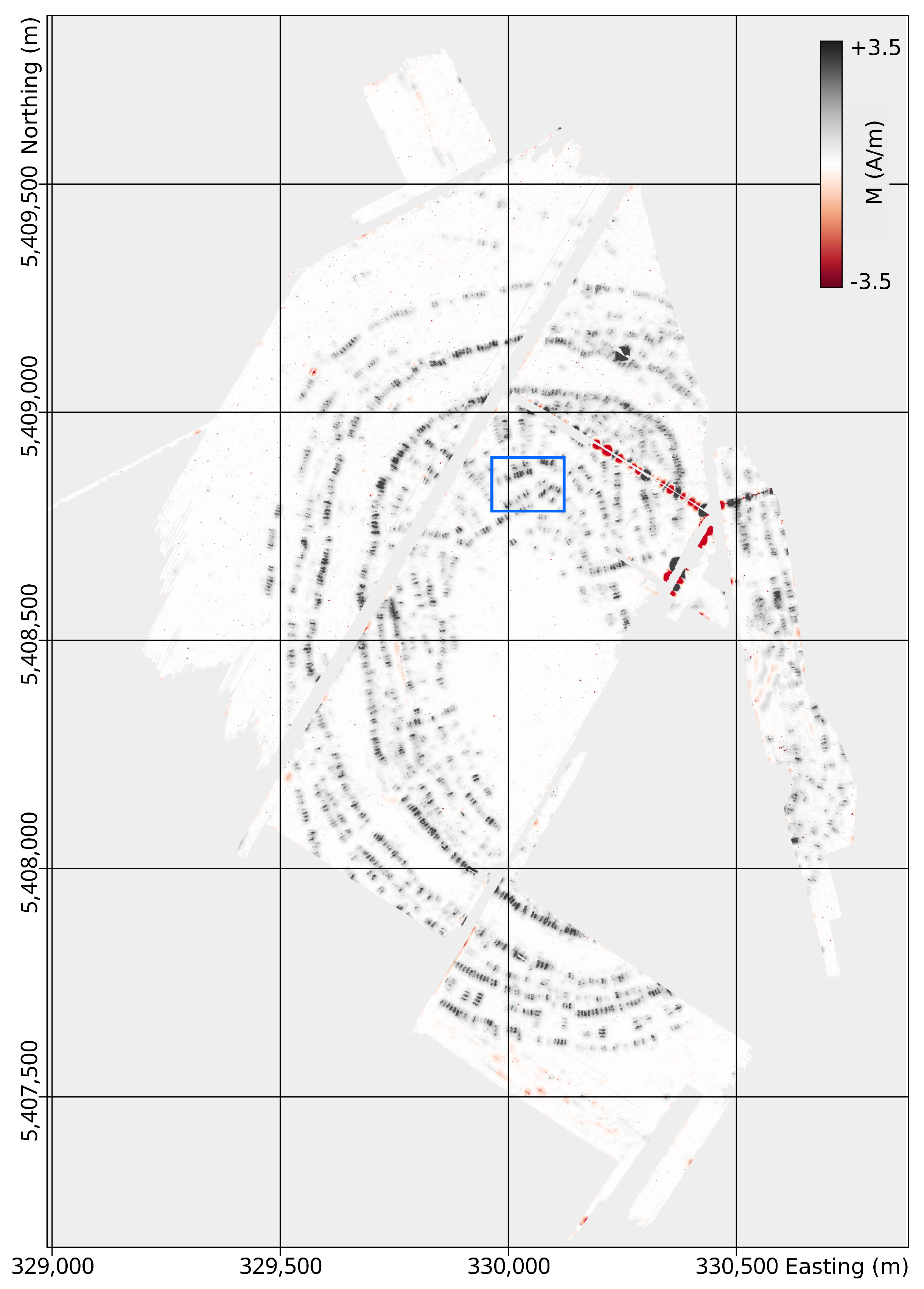
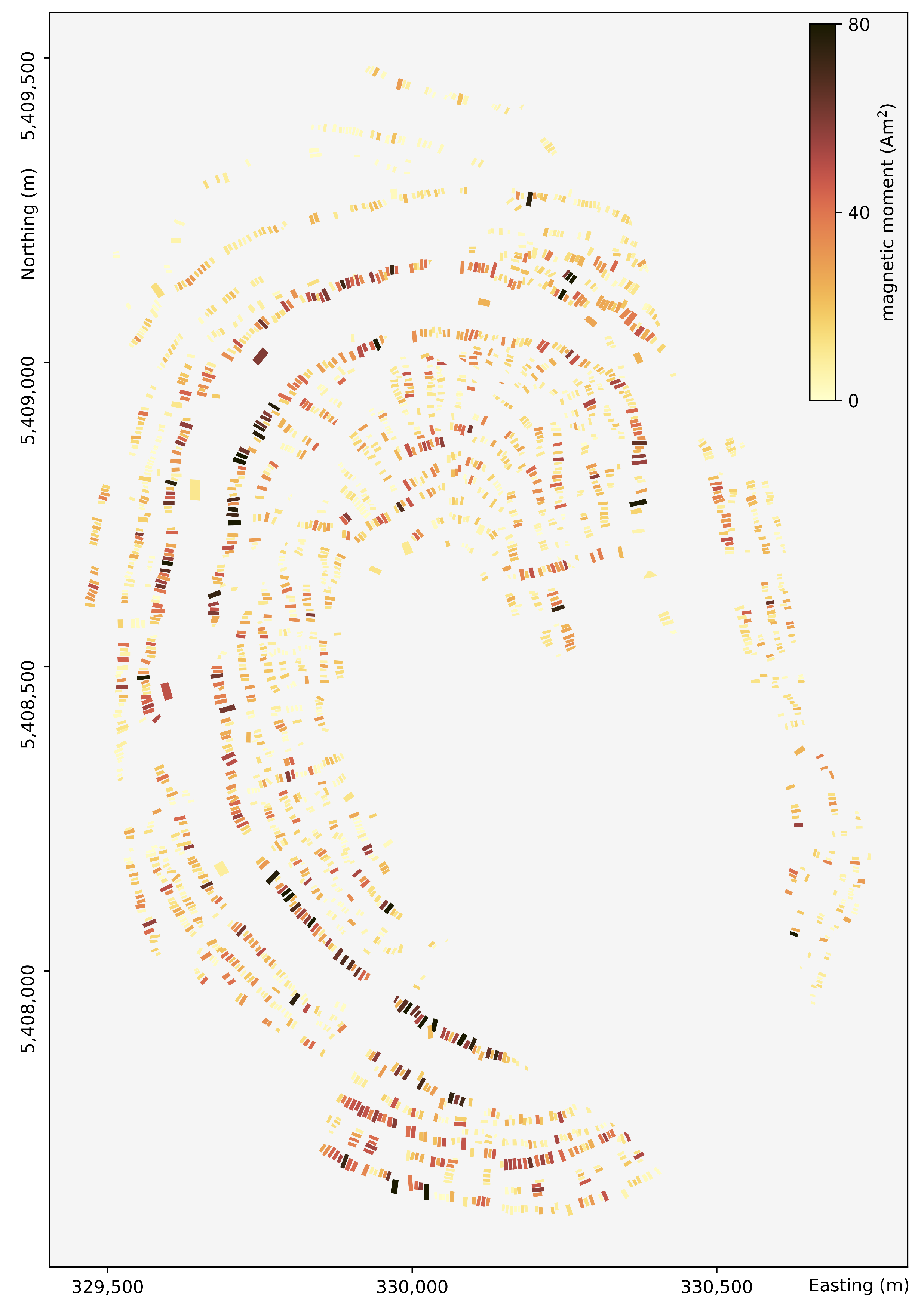
3. Results of Maidanetske
3.1. Magnetization Distribution
3.2. Quantification Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IGRF | International Geomagnetic Reference Field |
| RMS | Root mean square |
References
- Eder-Hinterleitner, A.; Neubauer, W.; Melichar, P. Restoring magnetic anomalies. Archaeol. Prospect. 1996, 3, 13. [Google Scholar] [CrossRef]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Eder-Hinterleitner, A.; Neubauer, W.; Melichar, P. Reconstruction of archaeological structures using magnetic prospection. Analecta Praehist. Leiden. 1996, 28, 131–137. [Google Scholar]
- Dittrich, G.; Koppelt, U. Quantitative interpretation of magnetic data over settlement structures by inverse modelling. Archaeol. Prospect. 1997, 4, 165–177. [Google Scholar] [CrossRef]
- Herwanger, J.; Maurer, H.; Green, A.G.; Leckebusch, J. 3-D inversions of magnetic gradiometer data in archeological prospecting: Possibilities and limitations. Geophysics 2000, 65, 849–860. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Bescoby, D.J.; Cawley, G.C.; Chroston, P.N. Enhanced interpretation of magnetic survey data from archaeological sites using artificial neural networks. Geophysics 2006, 71, H45–H53. [Google Scholar] [CrossRef]
- Schneider, M.; Stolz, R.; Linzen, S.; Schiffler, M.; Chwala, A.; Schulz, M.; Dunkel, S.; Meyer, H.G. Inversion of geo-magnetic full-tensor gradiometer data. J. Appl. Geophys. 2013, 92, 57–67. [Google Scholar] [CrossRef]
- Schneider, M.; Linzen, S.; Schiffler, M.; Pohl, E.; Ahrens, B.; Dunkel, S.; Stolz, R.; Bemmann, J.; Meyer, H.G.; Baumgarten, D. Inversion of Geo-Magnetic SQUID Gradiometer Prospection Data Using Polyhedral Model Interpretation of Elongated Anomalies. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Cheyney, S.; Fishwick, S.; Hill, I.; Linford, N. Successful adaptation of three-dimensional inversion methodologies for archaeological-scale, total-field magnetic data sets. Geophys. J. Int. 2015, 202, 1271–1288. [Google Scholar] [CrossRef] [Green Version]
- Tassis, G.; Hansen, R.; Tsokas, G.; Papazachos, C.; Tsourlos, P. Two-dimensional inverse filtering for the rectification of the magnetic gradiometry signal. Surf. Geophys. 2008, 6, 113–122. [Google Scholar] [CrossRef] [Green Version]
- Pickartz, N.; Hofmann, R.; Dreibrodt, S.; Rassmann, K.; Shatilo, L.; Ohlrau, R.; Wilken, D.; Rabbel, W. Deciphering archeological contexts from the magnetic map: Determination of daub distribution and mass of Chalcolithic house remains. Holocene 2019, 29, 1637–1652. [Google Scholar] [CrossRef]
- Chernovol, D. Houses of the Tomashovskaya local group. In The Tripolye Culture Giant-Settlements in Ukraine: Formation, Development and Decline; Menotti, F., Korvin-Piotrovskiy, A., Eds.; Oxbow Books: Oxford, UK, 2012. [Google Scholar]
- Kohler, T.A.; Smith, M.E.; Bogaard, A.; Feinman, G.M.; Peterson, C.E.; Betzenhauser, A.; Pailes, M.; Stone, E.C.; Marie Prentiss, A.; Dennehy, T.J.; et al. Greater post-Neolithic wealth disparities in Eurasia than in North America and Mesoamerica. Nature 2017, 551, 619–622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ohlrau, R. Maidanets’ke: Development and Decline of a Trypillia Mega-Site in Central Ukraine; Scales of Transformation in Prehistoric and Archaic Societies; Sidestone Press: Leiden, The Netherlands, 2020. [Google Scholar]
- Müller, J.; Hofmann, R.; Kirleis, W.; Dreibrodt, S.; Ohlrau, R.; Brandstätter, L.; Dal Corso, M.; Out, W.; Rassmann, K.; Burdo, N.; et al. Maidanetske 2013: New Excavations at a Trypilia Mega-Site; Dr. Rudolf Habelt GmbH: Bonn, Germany, 2017. [Google Scholar]
- Rassmann, K.; Ohlrau, R.; Hofmann, R.; Mischka, C.; Burdo, N.; Videjko, M.Y.; Müller, J. High precision Tripolye settlement plans, demographic estimations and settlement organization. J. Neolit. Archaeol. 2014, 96–134. [Google Scholar] [CrossRef]
- Sensys GmbH. FGM650 Gradiometer. Available online: https://sensysmagnetometer.com/products/fgm650-gradiometer/ (accessed on 26 December 2021).
- Papazachos, C.; Tsokas, G. A FORTRAN program for the computation of 2-dimensional inverse filters in magnetic prospecting. Comput. Geosci. 1993, 19, 705–715. [Google Scholar] [CrossRef]
- Tsokas, G.N.; Papazachos, C.B. The Applicability of Two-dimensional Inversion Filters in Magnetic Prospecting for Buried Antiquities. In Theory and Practice of Geophysical Data Inversion; Vogel, A., Sarwar, A.K.M., Gorenflo, R., Kounchev, O.I., Eds.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1992; pp. 121–144. [Google Scholar] [CrossRef]
- Tsokas, G.N.; Papazachos, C.B. Two-dimensional inversion filters in magnetic prospecting: Application to the exploration for buried antiquities. Geophysics 1992, 57, 1004–1013. [Google Scholar] [CrossRef] [Green Version]
- Tsokas, G.N.; Papazachos, C.B.; Loucoyannakis, M.Z.; Karousova, O. Geophysical data from archaeological sites: Inversion filters based on the vertical-sided finite prism model. Archaeometry 1991, 33, 215–230. [Google Scholar] [CrossRef]
- Uieda, L.; Oliveira, V.; Barbosa, V. Modeling the Earth with Fatiando a Terra. 2013. pp. 92–98. Available online: https://legacy.fatiando.org/cite.html#cite (accessed on 4 October 2021).
- Bhattacharyya, B.K. Magnetic anomalies due to prism-shaped bodies with arbitrary polarization. Geophysics 1964, 29, 517–531. [Google Scholar] [CrossRef]
- Shaffer, G.D. An Archaeomagnetic Study of a Wattle and Daub Building Collapse. J. Field Archaeol. 1993, 20, 59–75. [Google Scholar] [CrossRef]
- Wunderlich, T.; Kahn, R.; Nowaczyk, N.R.; Pickartz, N.; Schulte-Kortnack, D.; Hofmann, R.; Rabbel, W. On-site non-destructive determination of the remanent magnetization of archaeological finds using field magnetometers. Archaeol. Prospect. 2021, arp.1847. [Google Scholar] [CrossRef]
- Korte, M.; Constable, C.; Donadini, F.; Holme, R. Reconstructing the Holocene geomagnetic field. Earth Planet. Sci. Lett. 2011, 312, 497–505. [Google Scholar] [CrossRef] [Green Version]
- Magnetic Field Calculator. Available online: https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtm (accessed on 4 October 2021).





| Parameter | Filter A | Filter B |
|---|---|---|
| depth d of magnetized layer (m) | 0.35 | 0.5 |
| thickness t of magnetized layer (m) | 0.25 | 0.35 |
| grid discretization along east–west direction (m) | 0.25 | 0.3 |
| grid discretization along north–south direction (m) | 0.25 | 0.3 |
| height of lower sensor above ground (m) | 0.35 | 0.3 |
| height of upper sensor above ground (m) | 1.0 | 0.95 |
| magnetization M of block (A/m) | 1.0 | 1.0 |
| declination of magnetization in block (°) | 6.7 | 7.1 |
| inclination of magnetization in block (°) | 65.9 | 66.0 |
| truncation length l of filter from center to each edge (m) | 12.0 | 10.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pickartz, N.; Rabbel, W.; Rassmann, K.; Hofmann, R.; Ohlrau, R.; Thorwart, M.; Wilken, D.; Wunderlich, T.; Videiko, M.; Müller, J. Inverse Filtering of Magnetic Prospection Data—A Gateway to the Social Structure of Cucuteni–Tripolye Settlements? Remote Sens. 2022, 14, 484. https://doi.org/10.3390/rs14030484
Pickartz N, Rabbel W, Rassmann K, Hofmann R, Ohlrau R, Thorwart M, Wilken D, Wunderlich T, Videiko M, Müller J. Inverse Filtering of Magnetic Prospection Data—A Gateway to the Social Structure of Cucuteni–Tripolye Settlements? Remote Sensing. 2022; 14(3):484. https://doi.org/10.3390/rs14030484
Chicago/Turabian StylePickartz, Natalie, Wolfgang Rabbel, Knut Rassmann, Robert Hofmann, René Ohlrau, Martin Thorwart, Dennis Wilken, Tina Wunderlich, Mykhailo Videiko, and Johannes Müller. 2022. "Inverse Filtering of Magnetic Prospection Data—A Gateway to the Social Structure of Cucuteni–Tripolye Settlements?" Remote Sensing 14, no. 3: 484. https://doi.org/10.3390/rs14030484
APA StylePickartz, N., Rabbel, W., Rassmann, K., Hofmann, R., Ohlrau, R., Thorwart, M., Wilken, D., Wunderlich, T., Videiko, M., & Müller, J. (2022). Inverse Filtering of Magnetic Prospection Data—A Gateway to the Social Structure of Cucuteni–Tripolye Settlements? Remote Sensing, 14(3), 484. https://doi.org/10.3390/rs14030484







