Abstract
The Kofun period of the history of Japan—between the 3rd and the 7th century AD—bears its name from the construction of huge, earth mound tombs called Kofun. Among them, the largest have a keyhole shape and are attributed to the first, semi-legendary emperors. The study of the orientation of ancient tombs is usually a powerful tool to better understand the cognitive aspects of religion and power in ancient societies. This study has never been carried out in Japan due to the very large number of Kofun and to the fact that access to the perimeter is usually forbidden. For these reasons, to investigate Kofun orientations, simple tools of satellite imagery are used here. Our results strongly point to a connection of all Kofun entrance corridors with the arc of the sky where the Sun and the Moon are visible every day of the year; additionally, these show an orientation of the keyhole Kofun to the arc of the rising/shining Sun, the goddess that the Japanese emperors put at the mythical origin of their dynasty.
1. Introduction
In the present paper, we will be concerned with the Kofun (275–600 AD ca.) period of the history of Japan, which bears its name from the construction of thousands of earth mound tombs, some of which are among the largest monuments ever built on planet Earth [1]. There are no written sources about these tombs; excavations are rare and limited to the smaller ones, since the largest ones are considered the tombs of the first (semi-legendary) emperors and, as such, are strictly protected by law. Protection extends also to the exterior: many monuments are fenced and no permission to enter the perimeter is granted, so that it is impossible even to obtain precise measures of size or height. Furthermore, their astonishing number (a complete list is lacking, but those still visible today are many hundreds, and the total original number is estimated in the thousands) discourages every on-field investigation. It is thus natural to investigate them using simple but powerful tools of satellite imagery, in a manner similar to that recently followed for the Chinese imperial tombs complexes [2]. Our aim is to gain a better understanding of the cognitive aspects of the Kofun and, in particular, in the present paper, we investigate the possible relationships of these tombs with the sky, an aim also motivated by a recent work in which orientation along the winter solstice sunrise/summer solstice sunset line has been found to occur in the hugest Kofun ever built, the Daisen [3].
As far as we know, this is the first comprehensive attempt at analyzing the orientation of these fascinating monuments. To approach the problem in a reasonable but manageable way, we constructed two databases. One includes all the Kofun whose entrance corridor has been measured, the other includes virtually all the measurable keyhole Kofun, which, as we shall see, are the most characteristic and important from a historical point of view. In particular, the dimensions of these tombs have a large variability, but about 33% stand out for their length, which exceeds 150 m, and one of them is as large as 486 m in length. These are usually considered the tombs of the first emperors of Japan. The database (Appendix A) includes all these huge monuments. Furthermore, we measured all the recognizable elements of the five existing concentrations of Kofun (called clusters), among which are all the monuments recently included in the unique UNESCO site, the first ever to be devoted to the Kofun tombs (inscribed 2019)—the Mozu-Furuichi Kofun Group.
The locations of the sites under study are reported in the map of Figure 1.

Figure 1.
Locations of the sites considered in this study (image courtesy Google Earth Pro, edited by the authors).
2. A Brief Description of the Kofun Phenomenon
The reconstruction of the history of Japan before the 7th century AD is difficult due to the absence of Japanese records and the scarcity of information in other written records. The oldest known source is the Chinese Book of the Late Han, where Japan is mentioned as Wa. Subsequent chronicles of later Chinese dynasties occasionally record visits of envoys from the Japanese archipelago and give some information about customs and political situation of Wa, which appears to have been divided in many chieftains or kingships. As far as Japanese sources are concerned, the earliest are the chronicles called Kojiki and Nihon Shoki, dated to the beginning of the 8th century. Their content is a mixture of historical facts and legends; however, they are fundamental to show the conclusion of the slow process which led to the establishment of the centralized imperial power. In particular, Nihon Shoki was compiled with the scope of settling the imperial genealogy up to the mythical lineage from the supreme goddess of the sun, Amaterasu.
The Kofun period thus comprises the centuries of unification of Japan, and the Kofun tombs have to be interpreted as the burials of the chiefs and of their relatives and officers [4]. Their shape is sometimes circular or squared, but the largest ones have a keyhole form, which is peculiar to Japan (a few keyhole-shaped tombs do exist in the Korean Yŏngsan River Basin; however, the data collected from their excavation point to the late 5th–6th centuries, so the shape was probably imported from Japan) [5,6]. The keyhole Kofun are rarely isolated and even those we now identify as being isolated might be the only survivors of a cluster: a concentrated group of tombs of which one (or a few) are considerably bigger than the others [7]. The satellite Kofun of a cluster are usually burials of officers or member of the family of the chief interred in the main tomb, but in some cases contained only funeral equipment, in the form of offerings or of items belonging to the deceased [8,9]. From an examination of the grave goods present in satellite tombs and a careful study of the Haniwa (terracotta statues which were placed alongside the Kofun), a relatively good picture of the chronological evolution of the main chieftains and of the corresponding geographical areas has been achieved.
The early Kofun show a certain variety in detail, as a kind of experimentation was taking place. Thereafter, a transition from a local and varied funerary tradition settles to become a shared standard over much of the Japanese territory. Uniformization occurs also in the funerary chambers: in the first Kofun, the burial chamber is located at the end of a vertical pit excavated atop the circular part, while in those built later, a funerary corridor—usually constructed with megalithic blocks—leading to the chamber occurs; in almost all known examples, the access corridor of keyhole Kofun is parallel to the baseline of the trapezoidal part. It is important to stress that the Kofun are relatively complex architectures: to prevent erosion, they were built with layers of clay and sand, in many cases covered by pebbles and stones, preventing growth of plants (thus, the vegetation which covers most of them today is not representative of their original appearance). The stones were taken from riverbeds, and indeed many Kofun lie near rivers, which also provide waters for the ditches running along the entire perimeter of many of them. These moats still help today in making the tombs virtually inaccessible and sacred, assimilating them to microcosms composed of water and earth [8].
In the first and the last part of the Kofun period, the keyhole tombs were preferably built atop small hills (in isolated cases, a direct connection with a sacred mountain such, as Mount Fuji, has been shown to occur) [10]. In the middle Kofun period, especially in the 5th century AD, flat areas were preferred, not away from the coast, so that the mounds were visible from great distances, both from mainland and the sea. In these cases, huge quantities of earth were needed, taken from the moat’s excavations but also from distant areas, showing that the building of these large projects involved several villages [4,8,11]. In particular, the tomb attributed to the (semi-legendary) Emperor Nintoku, which is commonly called the Daisen Kofun, is about 480 m in length, and is the largest Kofun ever constructed (Figure 2). The Kofun era came to an end in the 7th century AD, when the practice of corpse burial gave way to cremation, which was introduced by Buddhism.

Figure 2.
The Daisen Kofun with some of its satellites in the Mozu cluster (image courtesy of Google Earth).
3. Materials and Methods
To study the orientations and other measurable characteristics of the Kofun, we used Google Earth Pro. There are several reasons for this choice. First, we do not need to explore the traces of buried monuments, or the monuments hidden by vegetation, since the vast majority of the surviving Kofun are embedded in the inhabited landscape and very clearly discernible, as well-delimited green areas on their own. This means that we need only standard satellite imagery, which already makes Google Earth Pro (GEP) the instrument of choice for many—technically simple but fruitful—remote sensing archaeological investigations [12]. As a matter of fact, GEP has been recently used in a variety of applications, such as to study activities that threaten archaeological sites [13,14], symmetry properties of the projects of the Angkor temples [15], and, recently, allowed our group to carry out a complete survey of cognitive aspects of Chinese imperial projects [16].
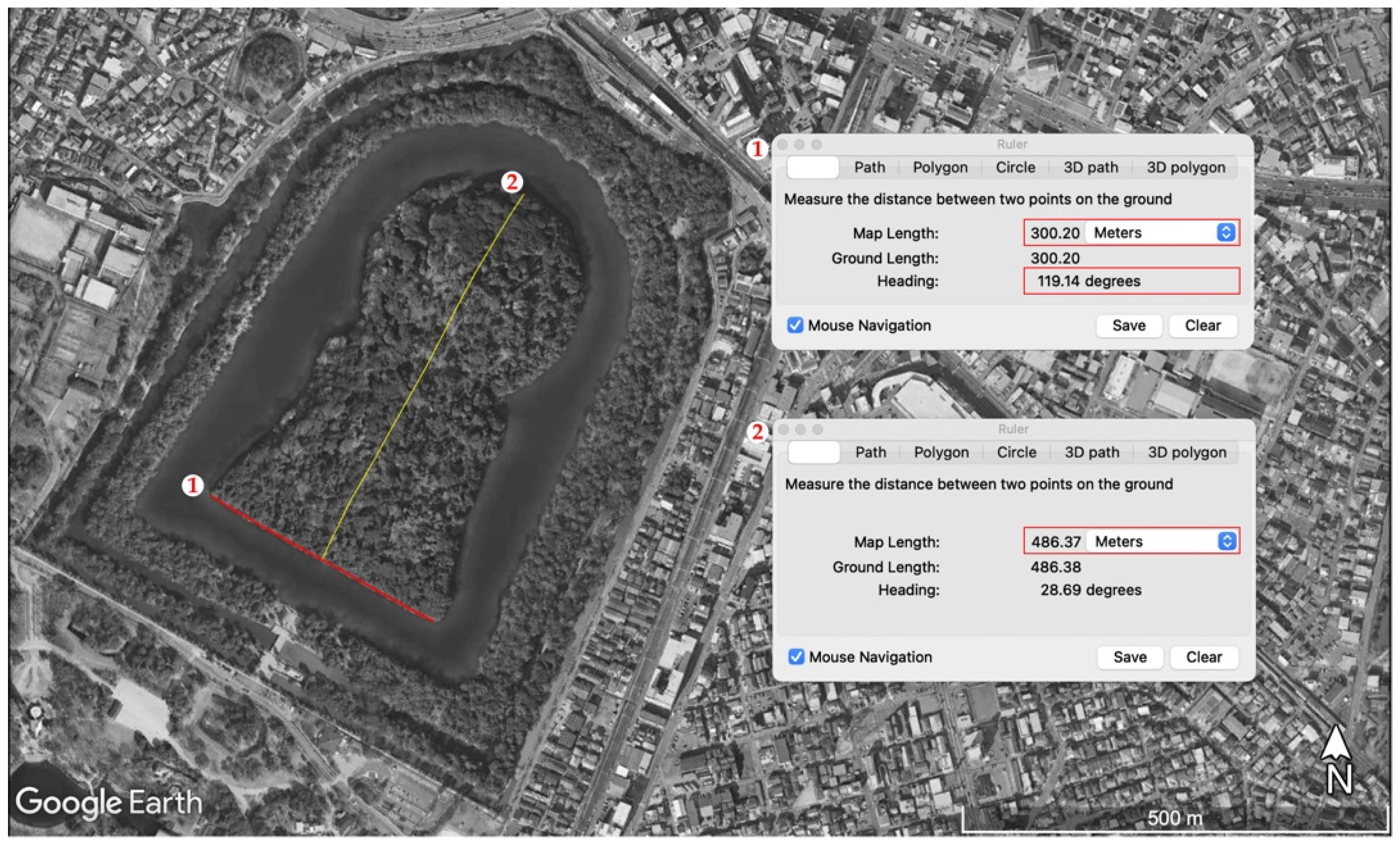
These applications in archaeology actually add to the impressively growing number of scientific applications of GEP and the Google Earth Engine (GEE) in several different fields [17]. There are also specific reasons for using GEP instead of GEE in the research context of the present paper—we needed to measure azimuths of the monuments with the best possible accuracy. This measure needed to be carried out for each monument and depended crucially on the accuracy of geographical north, which, in GEP, is referred to by the ruler instrument of the program (Figure 3). We have had, in the past, several occasions to verify on field (thus, with direct measures) the impressive precision of the program’s compass, while importing satellite images in processing programs (e.g., in AutoCAD) may introduce additional errors [18].
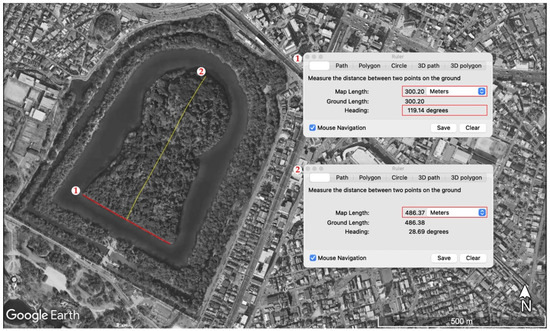
Figure 3.
Example of measurements: orientation with respect to north, length of the baseline, and transversal length of the Daisen Kofun. (Image courtesy of Google Earth, edited by the authors).
The list of the images that have been used is given in Appendix B. For each image, the resolution is also given. The image used for each monument is in turn referred to in the monuments list (Appendix A), in order to allow the reader to fully re-trace the data collection procedure. GEP does not provide the resolution directly, but it is possible to obtain it from the producer standard, knowing the provenience. It can be seen that the Google Earth coverage of the areas of Japan under study here is very good, with resolutions usually of 30 cm (see Appendix B for details). Thus, errors more likely may arise because of difficulties in precisely individuating the baseline of the mounds. Overall, we can prudentially estimate the azimuths data presented to have a maximal uncertainty of ±1°, a value which is by far sufficient for our purposes.
As explained below, in this way we obtained a complete data set for the keyhole Kofun as a well as a control test data set for the orientations of the Kofun access corridors, which were measured in the 19th century and are, in many cases, not measurable anymore. The results show clear patterns of astronomical orientation already looking at the orientation diagrams. However, the data have also been processed using standard statistical tools: kernel distribution and p-value. Again, the efficacy of these tools in analyzing orientations is well documented in the literature [19,20].
The Kernel density estimate is a simple method to highlight significant peaks in a set of discrete data. In this method, the (unknown) density distribution of the data is approximated by a sum of continuous distributions, f, placed on each point of the data set, as follows:
where h is a smoothing parameter. Here, we use, as smoothing parameter, h = 0.1, and, as f, the normal (Gaussian) distribution. Our Kernel estimates are thus obtained by adding normal distributions centred on each of the data points.
The p-value is a test of statistical significance with respect to the null hypothesis. Low p-values (usually of the order of 0.05 or less) indicate greater statistical significance. In our case, the null hypothesis is that the Kofun are oriented randomly, and the p-value is calculated by generating 100,000 random distributions (using the Python random.sample module) and comparing them with the observed distribution.
4. Results
4.1. The Orientation of the Kofun Access Corridors
In 1897, William Gowland made a thorough survey of many Kofun of different shapes, measuring the azimuths of their access corridors [21]. Today, the same measures would be impossible to obtain, due to the mentioned difficulties of access to the monuments and to the fact that many of them have been damaged; therefore, we decided to make use of Gowland’s data. Among these data, only a small number (around 10%) refer to keyhole Kofun, so we treat the keyhole phenomenon with a direct approach in the next section.
To check the reliability of the data set, we managed to identify the largest possible number of Kofun whose entrance (or entire corridor, in case the covering earthen mound is no longer extant) is visible on satellite images. Then, we compared our measures to Gowland’s ones. The comparison turned out to be always very good (within half a degree); therefore, we are confident that the data set is reliable. The data set contains Kofun of any shape; however, chronologically, the corridors (as opposed to the pit) started between the end of the 4th and the beginning of the 5th century, so the data mostly cover the middle and the late Kofun period. Comprehensively, we found reliable data for 127 mounds, a number which allows a reasonably clear analysis without resorting to sophisticated statistical tools.
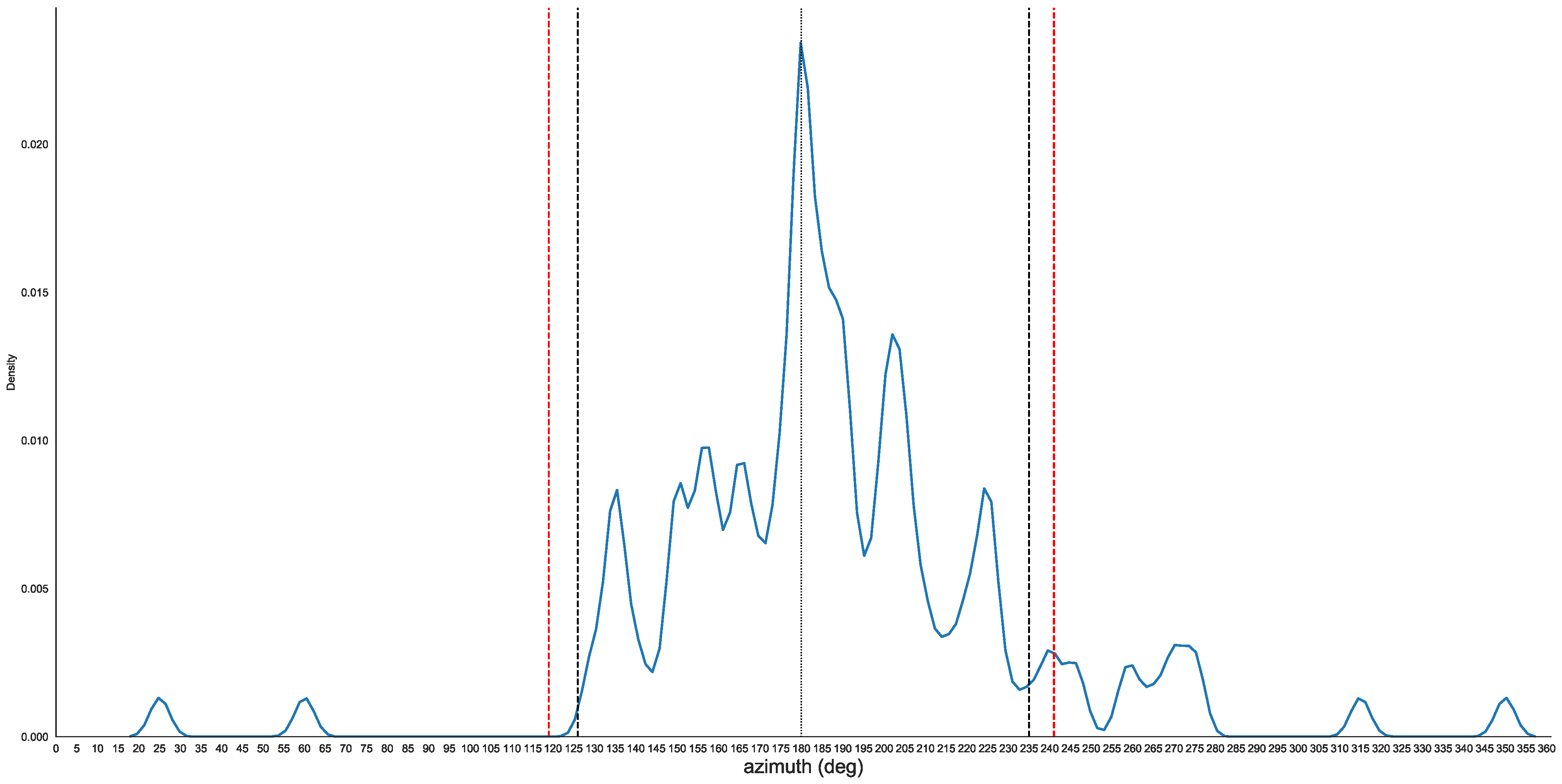
Actually, it is immediately clear that the distribution is not random (Figure 4 and Figure 5). The distribution is indeed peaked at due south, with 84% of the mounds presenting an alignment included between 125 and 235 degrees, to be compared with the 31% which would compete to a sector of less than 1/3 of a circle (110°) in a uniform distribution.
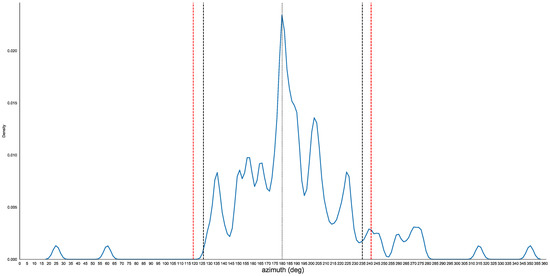
Figure 4.
Kernel distribution of the azimuths of Kofun access corridors. The dashed lines indicate the azimuths of the rising/setting of the Sun at the winter solstice (red lines) and of the Moon at the major southern standstill (black lines).
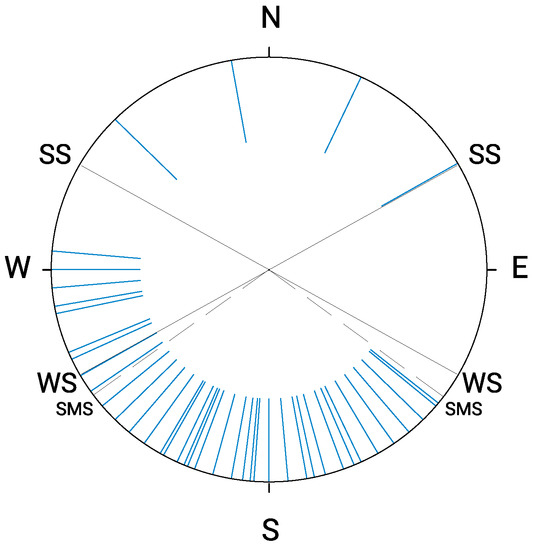
Figure 5.
Orientation diagram of Kofun access corridors. The azimuths of the Sun rising/setting at the winter solstice (WS) and those of the Moon at the southern major standstill (SMS) are marked.
Taking the latitude of Osaka as a reference (and a flat horizon), the azimuths of the rising/setting of the Sun at the winter solstice are about 118–242 degrees. Therefore, the vast majority of the Kofun access corridors are orientated to a sector of the sky in which the Sun shines every day (climbing or descending) with a marked preference for culmination at due south (comparable situations occur for instance for the megalithic tombs of Europe [22]).
According to these data, a willing orientation of the Kofun’s corridors to solar exposure is virtually certain. However, analyzing the data more carefully, a more intriguing scenario appears, which leads to a more complex interpretation. As is well known, due to the precessional cycle of the lunar nodes (the points where the lunar orbit intersects the ecliptic), the maximum (and minimum) declination of the Moon is reached every 18.6 years. These declinations are +/−28.5°, and, at fixed latitude, correspond to azimuths which are always smaller/greater to those of the Sun at the summer/winter solstice. This means that orienting a building within the arc of azimuths of the Moon at the southern standstill (the minimum possible declination) assures both illumination by the Sun every day and illumination by every full Moon (the full Moon nearest to the summer solstice, in particular, will always be the one rising closer to the maximum azimuth, although the true standstill can be reached by the Moon in any of its phases). The azimuths of the Moon at the southern standstill are, at the latitude of Osaka, 126–234° (we are neglecting here a small variation due to the slow change of the obliquity of the Ecliptic); therefore, the vast majority of the Kofun corridors’ entrances are illuminated by the Sun every day and by every full Moon.
As we will discuss in the final section, there are some hints coming from the Japanese traditions that combined solar–lunar exposure might be the correct interpretation for these orientations.
4.2. The Orientation of the Keyhole Kofun
We now concentrate on the keyhole Kofun which, as mentioned, enlist the largest royal tombs of Japan, and are poorly represented in the Gowland database. To define the orientation of a keyhole Kofun we could use the azimuth of its axis from the baseline to the round part. However, more suitable information is the azimuth of the baseline itself, since it is usually parallel to the direction of the entrance corridor, whenever present. We have thus measured the baseline azimuths of as many keyholes Kofun as possible; in order to define them uniquely, we used the following convention: we assigned a measure of 90° to a baseline which is oriented east–west, and the round part of the keyhole is located to the north of the baseline.
To study the orientations, a database has been collected through satellite imagery. To construct the database, using a list of the existing Kofun would have been optimal, but such a list has never been compiled. Therefore, we resorted to collecting information from different sources (articles, official websites of prefectures and local municipalities, UNESCO lists of protected sites). In this way, we have been able to list 158 localizable keyhole Kofun, among which, all the largest built Kofun (length of the axis greater than 200 m) are included. In compiling the database, we registered the geographic coordinates, the orientation, and short notes of information. These include length of the baseline, length of the symmetry axis, significant geo-morphological elements, such as presence of water, and position with respect to the mountain ranges (whether in the plains, by a slope, or on reliefs). These data might be useful for a deeper future analysis. Finally, we registered the membership to a cluster and the “role” of the Kofun in the cluster: certainly principal, probably principal, or satellite. The database is reported in the Appendix A.
To investigate orientations, it is preferable to use only the data of the keyholes, which are either isolated or (with good certainty) principal, because there are cases in which it was the orientation of the main Kofun of a cluster which governed those of the satellites (see also next section). However, since few satellites are measurable, this reduces our data slightly, to 151, a number which is still sufficient to see whether a custom of orientation is present (Figure 6 and Figure 7).
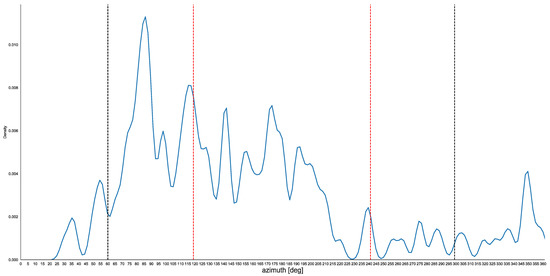
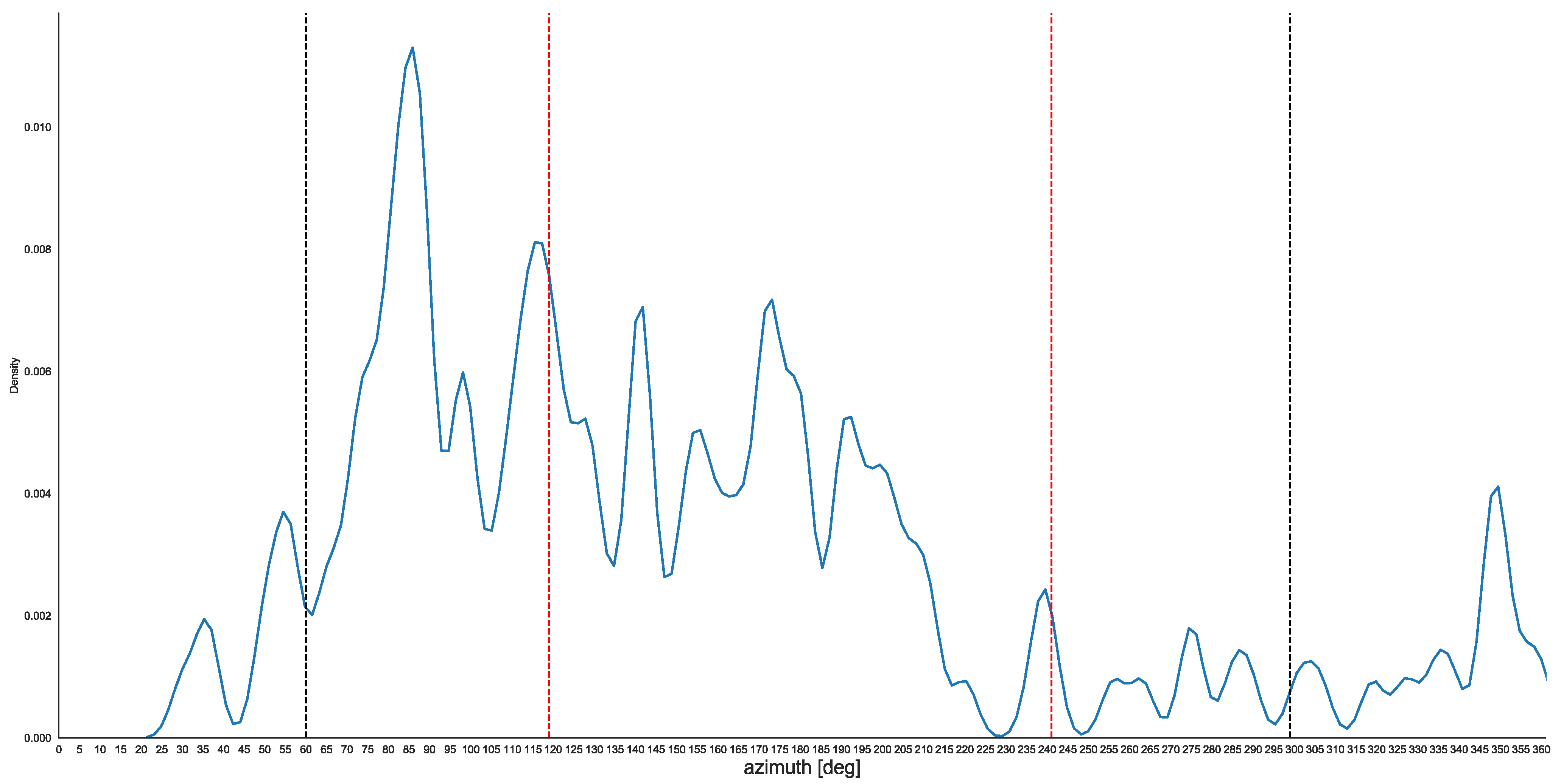
Figure 6.
Kernel distribution of the azimuths of keyhole Kofun baselines. The azimuths of the Sun rising/setting at the summer (black lines)/winter (red lines) solstice (SS, WS) are reported.
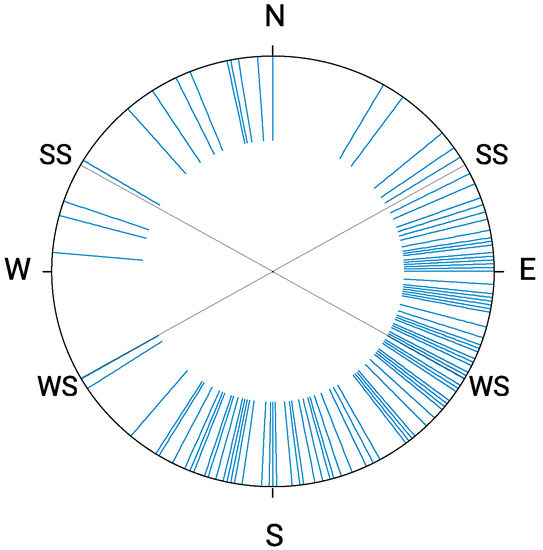
Figure 7.
Orientation diagram of the azimuths of keyhole Kofun baselines. The azimuths of the Sun rising/setting at the summer/winter solstice (SS, WS) are reported.
The majority of the orientations of these Kofun (82% or 130 Kofun) is located in an arc of about half of a circle. Comparing our distribution with 100,000 random distributions (generated in Python with random.sample), we confirmed that the alignments of the Kofun are not random.
It should be noted that distributions in azimuths on a circle, like the one studied here, can be compared with simple uniform distributions—that is, the null hypothesis in which each azimuth value is equally likely to be picked, since each azimuth value is an independent “box”—this would not be true in case of declination data, which, in the null hypothesis, would accumulate at the extreme and directional (circular) statistics would be needed [19,20].
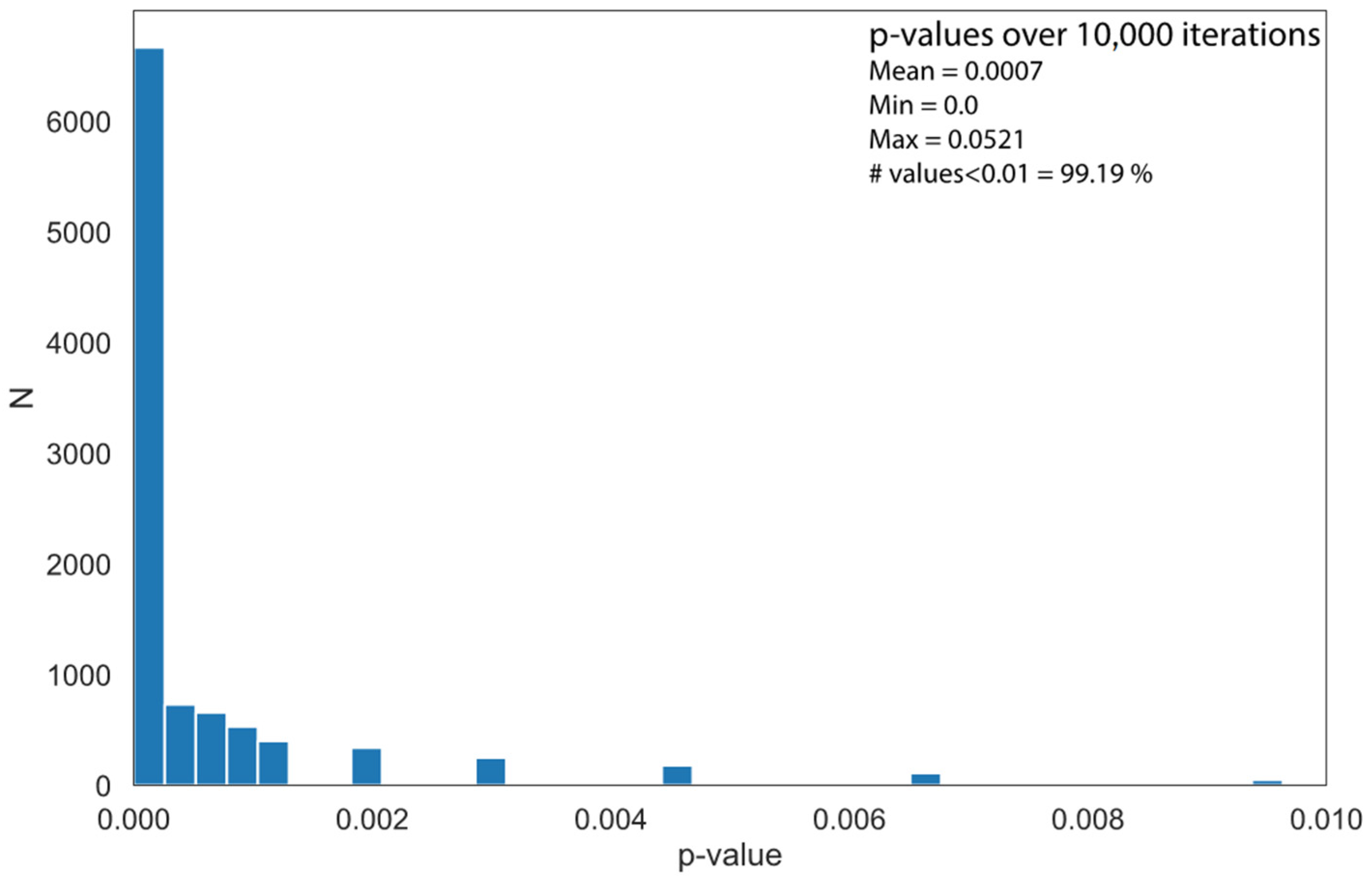
The resulting p-value (mean 7 × 10−4) is far below the usually accepted significance value of 0.05; therefore, the test fully refutes the null hypothesis of random orientation, confirming that the orientation was intentional (Figure 8).
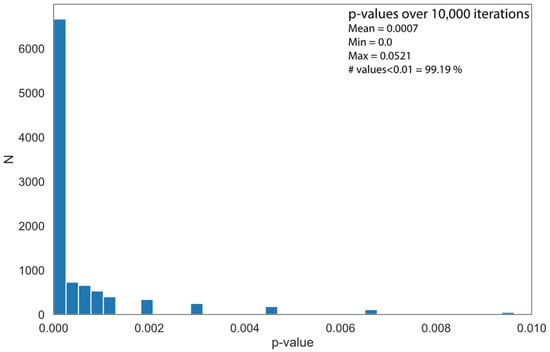
Figure 8.
p-value test results over 10,000 random distributions.
Proving that the orientation was intentional of course does not necessarily imply that it was astronomical. However, the arc comprising the vast majority of the azimuths is located roughly between summer solstice sunrise (az. 62) and winter solstice sunset (az. 242). This arc thus includes the arc of orientation we have found before for the Kofun corridors independently from the shape, but in a sense “adds” to it the arc of the Sun rising in the whole year. Interestingly, a clear peak occurs near due east—another in correspondence of the winter solstice sunrise (the peak close to due east might a priori also correspond to orientation of the orthogonal axis to true north, if a systematic error to the west of north was present in the orientation method, for instance, if it were related to the western elongation of a circumpolar star).
The above discussion was based on azimuths only. Of course, a more detailed examination would require a study in terms of declinations; therefore, a measure of the horizon heights associated with each azimuth would be required. We can, however, perform a qualitative analysis of the possible effects of non-negligible horizon altitudes (for instance, nearby hills). For this aim, the effects at rising and at setting must be distinguished. At setting, the effect for the vast majority of the azimuths (see Figure 4 and Figure 6) is an increase in (negative) declination with respect to the declination corresponding to the same azimuth and zero height. We see from the orientation diagrams that, for the vast majority of the azimuths, the only sensible result may be to spread the distribution from true south towards the winter solstice sunset a bit; therefore, no qualitative change to our results would occur. At rising, the effect is again an increase in declination with respect to the declination corresponding to the same azimuth and zero height. Again, Figure 4 and Figure 6 show that the eventual effect is negligible for the corridors, since, “at worst”, a few declinations might spread towards winter solstice. In the keyhole case, the vast majority of the data would remain into the solar range of declinations, with only some azimuths close to summer solstice sunrise, which may eventually lead to a little spread of the data out of the solar range (i.e., towards declinations greater than 23.5°).
We are, therefore, fully confident in the robustness of the solar (or luni-solar) interpretation.
4.3. The Clusters
As far as satellite Kofun are concerned, it is interesting to analyze the data referring to each cluster, although the small number of items makes any discussion purely qualitative. In the literature there are five well-documented clusters (Figure 9).

Figure 9.
Location of the clusters (image courtesy of Google Earth).
These are (in rough chronological order) Oyamato and Saki in the first half of the Kofun period, and Furuichi, Mozu, and Sakitama in the second half. We have found clear patterns of orientation in three of them, as follows:
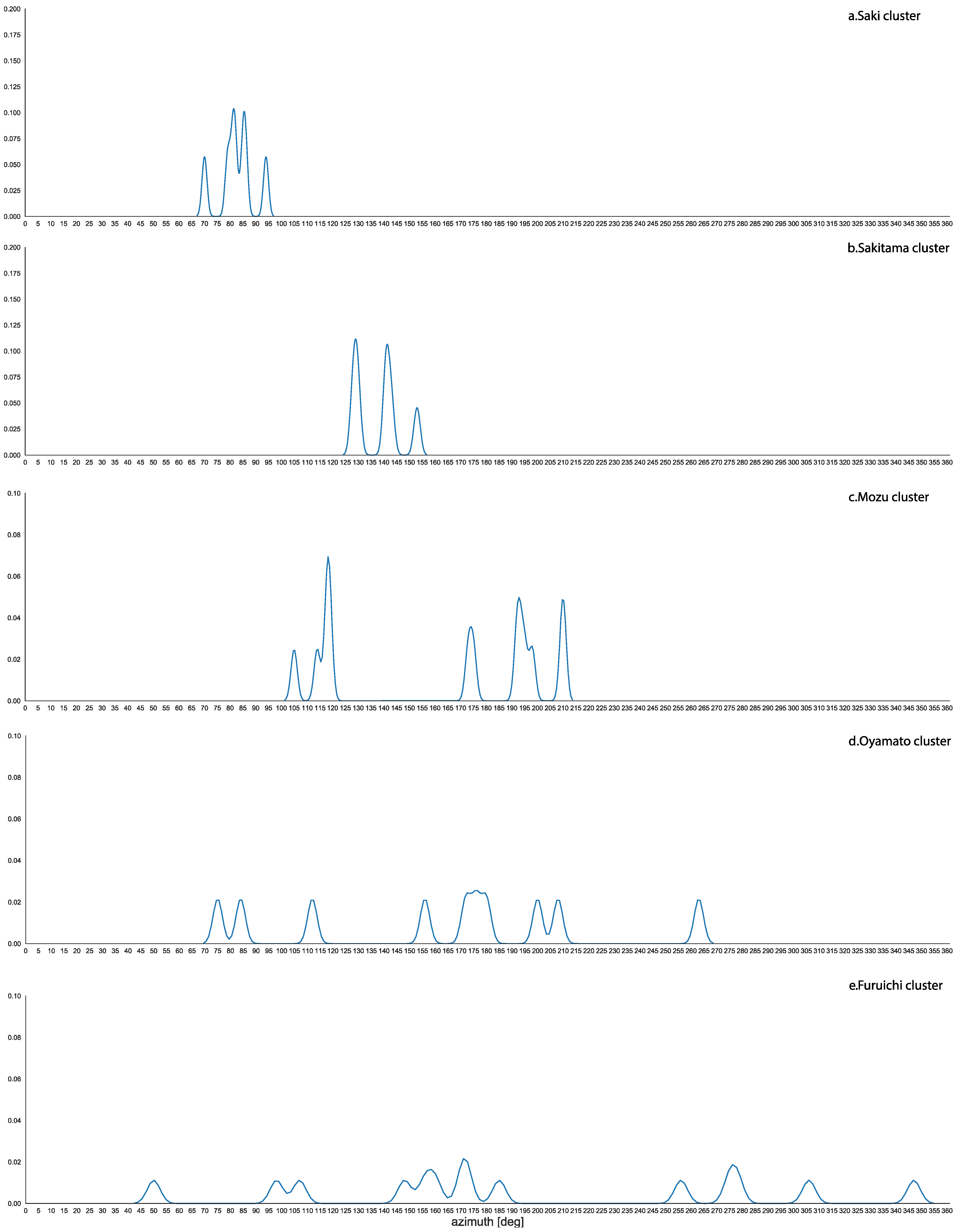
- In the Saki and Sakitama clusters, the orientation of the principal tomb directly governed the orientation of the others (Figure 10a,b).
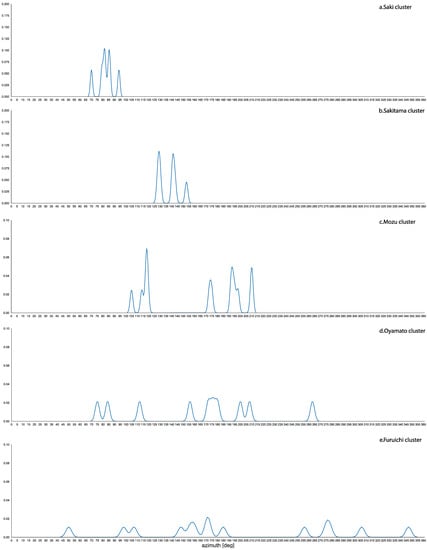 Figure 10. Kernel distribution of the orientations of keyhole Kofun in the Saki (a), Sakitama (b), Mozu (c), Oyamato (d), and Furuichi (e) clusters.
Figure 10. Kernel distribution of the orientations of keyhole Kofun in the Saki (a), Sakitama (b), Mozu (c), Oyamato (d), and Furuichi (e) clusters. - In the Mozu cluster, the orientation of the principal tomb (the Daisen Kofun, oriented to summer solstice sunset) governed that of the others in the sense that a part is orientated in the same way and another part are orientated (almost) orthogonally (azimuths greater of about 90°) (Figure 10c).
- No pattern is discernible in the orientations of the Oyamato and Furuichi clusters; although, at least in the first case, topographical reasons connected to the mountain range of Mount Miwa may have played a role (Figure 10d,e).
At the level of observation, we notice that these patterns may correspond to political–religious patterns, which differentiate the corresponding periods/areas and might be enlightened by future historical research.
5. Discussion
The Japanese Kofun correspond to a funerary religion, of which, little is known. However, there is seldom any doubt that ancestral cults formed an animistic religion aimed at propitiating the favor of nature. Shintoism originated from this religion and identified all natural elements as sacred (mountains, rivers, forests, etc.). In this context, the cult of Amaterasu emerged, which at some point of the Kofun period (perhaps the 5th century AD) was placed at the foundation of imperial power [23,24]. This is described explicitly in the two, already mentioned, most ancient works that have come down to us, which were drawn up by imperial order with the aim of legitimizing divine descent and political power of the ruling dynasty. The two works describe—albeit, at times, in a divergent way—the myths of creation and the birth of the first divinities, until the appearance of a couple of gods, brother and sister, Izanagi and Izanami. The two gods shaped the Japanese islands from drops of water that they let run down the blade of a sword. They generated many kami, like those of the sea, rivers, woods, and mountains. One of these was Amaterasu; she was the direct ancestor of the Yamato clan, as it was her nephew to receive the order to rule the earth, together with the three symbols of royal power: a sword, a mirror, and a jewel [25,26].
Interest in the celestial cycles should have been contemporary with the development of astronomical knowledge. Unfortunately, the history of astronomy in Japan in the Kofun period suffers from the same problems existing in the whole approach to its history: the lack of written sources. Furthermore, clear archaeological evidence exists of influences from Korean and Chinese astronomy (in particular, it is certain that the Chinese–Korean tradition of depicting the celestial vault on the ceiling of the funerary chambers was imported in Japan at least in the 7 century AD, if not before) [27]. So, it is difficult to ascertain to what extant the Japanese people developed their own astronomical “worldview” [28,29]. We can, however, again rely on the Shinto tradition and texts, which show us that Amaterasu was in some sense placed at the head of the gods’ hierarchy. Actually, the identification of Japan as the land of the rising Sun (the last land to the east) covers a central part of the Japanese consciousness; the celebration of the New Year’s Day is still seen as a renewal of the Sun’s lightness. In turn, all this points very naturally to the idea that the tombs of the rulers were to be associated with the sun, a thing which we have found both in the orientation of the Kofun access corridors—which are, for the vast majority, illuminated by the Sun every day of the year—and in the orientations of the keyhole Kofun, which add to the arc of the shining Sun that of the Sun rising in the course of the year.
In our results on the corridors, we have, however, presented evidence of a possible, coupled role of the Moon’s illumination. The origin of this role may perhaps be found in Shinto belief as well. The Moon is the brother of Amaterasu, born from the right eye of Izanagi. After climbing a celestial ladder, Tsukuyomi lived in “Paradise” with his sister, until one day he killed Uke-Mochi, the goddess of food. Consequently, Amaterasu exiled her brother in a separate part of the sky. However, the two together contribute to light the earth: in Japanese traditional celebrations of the new year, for instance, the Moon is also involved. In the traditional wishes, darkness gives way to new light, and this new light entails the Sun and the Moon getting together and becoming brighter.
6. Conclusions
The Kofun are silent, spectacular signposts, speaking to the era of the grand unification of Japan as an empire. Their importance in understanding the formative period of the imperial power is fundamental, given the complete absence of Japanese written sources. This importance has been recently recognized by UNESCO with the inscription of the Mozu-Furuichi Kofun Group in the World Heritage List.
In spite of their recognized importance, not much is known about the Kofun. In particular, their large number, together with the difficulties in taking direct measures, has discouraged any cognitive approach to their placement and orientation. Very few have been excavated, but scattered information about the interiors shows a likely derivation of the ceiling’s decoration from Korean and Chinese astronomy, at least in the late Kofun period.
Thus motivated, we presented here a systematic study aimed at identifying possible patterns of astronomical orientation and based on simple but effective tools of satellite imagery and statistical analysis. Our results establish a very likely connection of these buildings with Amaterasu, the Sun Goddess, as well as possible local patterns of orientation related to specific clusters. These astronomical references have been present since the beginning of the Kofun era and have to be considered as directly related to the Japanese culture of the epoch, rather than being imported. In particular, the emperors entombed in the largest keyhole Kofun were considered the direct descendants of Amaterasu. Perhaps then, the curious and seemingly inexplicable keyhole shape is nothing more (and nothing less) then a simple representation of the rising Sun behind a sacred mountain, as a tribute to the name of the land which was under the emperors’ rule.
Author Contributions
The whole paper benefited of the contribution of all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Orientation data of 158 Keyhole Kofun.
Table A1.
Orientation data of 158 Keyhole Kofun.
| n° | Prefecture | Nameor (Cluster) | Lat (N) | Long (E) | Baseline Orientation (°) | Baseline Length (m) | Symmetry Axis Length (m) | Hill Plain Slopes | Principal Prob Principal Satellite |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Aichi | Aotsuka | 35°19′36″ | 136°55′45″ | 123 | 66 | 117 | P/S | P |
| 2 | Danpusan | 35°07′51″ | 136°54′12″ | 55 | 119 | 144 | P | ||
| 3 | Shidami | 35°15′11″ | 137°02′29″ | 128 | 15 | 46 | S | PP | |
| 4 | Chiba | (Dairizuka) | 35°19′11″ | 139°51′30″ | 87 | 65 | 105 | P | PP |
| 5 | (Dairizuka) | 35°19′01″ | 139°51′30″ | 72 | 48 | 77 | P | PP | |
| 6 | (Dairizuka) | 35°19′11″ | 139°50′47″ | 127 | 77 | 106 | P | PP | |
| 7 | Dairizuka (Dairizuka) | 35°19′34″ | 139°51′26″ | 118 | 74 | 133 | P | PP | |
| 8 | Sanjozuka (Dairizuka) | 35°19′18″ | 139°51′43″ | 114 | 122 | P | PP | ||
| 9 | Ehime | Myokenyama | 34°03′31″ | 132°55′51″ | 349 | 30 | 58 | H | P |
| 10 | Fukui | Jonozuka | 35°28′04″ | 135°52′29″ | 82 | 40 | 85 | S | PP |
| 11 | Fukuoka | Hiwazuka | 33°31′24″ | 130°26′19″ | 179 | 12 | 34 | P | P |
| 12 | Otsuka | 33°34′24″ | 130°16′14″ | 66 | 40 | 55 | S | P | |
| 13 | Ozuka | 33°35′20″ | 130°39′50″ | 112 | 58 | 86 | P/S | P | |
| 14 | Fukushima | Kamegamori | 37°35′35″ | 139°49′45″ | 190 | 50 | 117 | P | P |
| 15 | Kamegamori Chinjumori | 37°35′32″ | 139°49′40″ | 190 | 26 | 56 | P | PP | |
| 16 | Oyasuba | 37°21′21″ | 140°24′14″ | 285 | 30 | 70 | P | P | |
| 17 | Ryugatsuka | 37°15′06″ | 140°15′ 13″ | 197 | 15 | 33 | P | P | |
| 18 | Gifu | 35°28′57″ | 136°37′19″ | 83 | 39 | 74 | S | P | |
| 19 | 35°28′57″ | 136°37′19″ | 122 | 24 | 67 | S | PP | ||
| 20 | 35°28′57″ | 136°37′19″ | 155 | 24 | 74 | S | PP | ||
| 21 | Hirui Otsuka | 35°23′15″ | 136°34′17″ | 141 | 64 | 140 | S | P | |
| 22 | Kotozuka | 35°25′06″ | 136°48′53″ | 108 | 84 | 124 | S | P | |
| 23 | Gunma | 36°17′56″ | 139°02′02″ | 55 | 78 | 168 | P | PP | |
| 24 | Futako Ideyama (Hodota) | 36°22′43″ | 138°59′02″ | 151 | 60 | 97 | P | ||
| 25 | Hachimantsuka (Hodota) | 36°22′52″ | 138°59′09″ | 74 | 61 | 101 | P | ||
| 26 | Hachiman Kannonzuka | 36°20′30″ | 138°56′28″ | 202 | 75 | P | |||
| 27 | Maebashi Hachimanyama | 36°22′35″ | 139°05′20″ | 212 | 48 | 75 | P | P | |
| 28 | 36°23′11″ | 139°11′47″ | 162 | 30 | 72 | P | |||
| 29 | Nanakoshiyama | 36°15′42″ | 139°02′24″ | 191 | 92 | 140 | P | P | |
| 30 | Sho-Futago | 36°23′22″ | 139°11′38″ | 203.5 | 33 | P | |||
| 31 | 36°23′28″ | 139°11′41″ | 211 | P | |||||
| 32 | Tenjinyama | 36°17′32″ | 139°23′29″ | 133 | 127 | 196 | P | PP | |
| 33 | Tsukamaki | 36°17′07″ | 139°25′26″ | 172 | 5 | 19 | P | ||
| 34 | Ushirofutago | 36°23′15″ | 139°11′44″ | 169 | 128 | P | |||
| 35 | Watanuki Kannonyama | 36°18′26″ | 139°04′39″ | 240 | 97 | P | |||
| 36 | Hiroshima | Mitsujo | 34°25′02″ | 132°44′00″ | 327 | 48 | 83 | P | |
| 37 | Hyogo | Goshikizuka | 34°37′48″ | 135°02′46″ | 116 | 52 | 176 | P | |
| 38 | Yoro Hisagotsuka | 34°49′03″ | 134°36′ | 110 | 40 | 103 | P | ||
| 39 | Otomezuka | 34°42′41″ | 135°14′51″ | 89 | 14 | 55 | P | PP | |
| 40 | Ibaraki | Chokushizuka | 36°22′53″ | 140°36′57″ | 140 | 32 | 74 | P | PP |
| 41 | Funatsukayama | 36°10′04″ | 140°17′24″ | 167 | 87 | 180 | P | P | |
| 42 | Sarashii | 36°23′48″ | 140°27′06″ | 55 | 130 | P | PP | ||
| 43 | Ishikawa | Akitsuneyama | 36°26′59″ | 136°31′09″ | 115 | 30 | 100 | P | PP |
| 44 | Ame-no Miya A | 36°58′33″ | 136°52′18″ | 349 | 29 | 59 | H | PP | |
| 45 | Ame-no Miya B | 36°58′36″ | 136°52′22″ | 142 | 25 | 65 | H | PP | |
| 46 | Iwate | Tsunokuza | 39°08′29″ | 141°05′38″ | 85 | 22 | 40 | P | PP |
| 47 | Kumamoto | Eta/Eda Funayama | 32°58′16″ | 130°35′58″ | 142 | 38 | 63 | S/P | P |
| 48 | Iwabaru Futagozuka (Iwabaru) | 32°59′46″ | 130°40′10″ | 220 | 47 | 100 | S | P | |
| 49 | Kokuku Kurazuka | 32°58′13″ | 130°35′54″ | 173 | 56 | S/P | PP | ||
| 50 | Yokoyama (Iwabaru) | 32°59′42″ | 130°40′16″ | 250 | 16 | 36 | S | S | |
| 51 | Kyoto | Amatsuka | 35°00′26″ | 135°42′44″ | 63 | 40 | 66 | P | P |
| 52 | Igenoyama | 34°54′52″ | 135°41′52″ | 58 | 80 | 128 | P | P | |
| 53 | Kutsukawa A (Kutsukawa) | 34°52′04″ | 135°46′41″ | 96 | 50 | 100 | P | P | |
| 54 | Kutsukawa B (Kutsukawa) | 34°51′55″ | 135°46′45″ | 99 | 143 | P | P | ||
| 55 | Miyazaki | Saitobaru #1 | 32°06′39″ | 131°23′40″ | 183 | 12 | 45 | PP | |
| 56 | Saitobaru #13 | 32°06′42″ | 131°23′41″ | 98 | 27 | 81 | P | ||
| 57 | Saitobaru #202 | 32°06′49″ | 131°23′30″ | 76 | 38 | 55 | PP | ||
| 58 | Saitobaru #46 | 32°06′47″ | 131°23′38″ | 360 | 38 | 89 | PP | ||
| 59 | Saitobaru A | 32°06′46″ | 131°23′42″ | 111 | 18 | 65 | PP | ||
| 60 | Saitobaru B | 32°06′49″ | 131°23′42″ | 188 | 9 | 31 | PP | ||
| 61 | Saitobaru C | 32°06′54″ | 131°23′41″ | 79 | 27 | 76 | PP | ||
| 62 | Miyagi | Raijinyama | 38°09′04″ | 140°52′47″ | 120 | 90 | 162 | P | |
| 63 | Tomizuka | 38°14′17″ | 140°54′53″ | 89 | 61 | 119 | P | PP | |
| 64 | Nagano | Koboyama | 36°12′45″ | 137°59′02″ | 36 | 63 | S | PP | |
| 65 | Mori Shogunzuka | 36°31′53″ | 138°08′14″ | 140 | 28 | 94 | H | P | |
| 66 | Nagasaki | Soroku | 33°47′55″ | 129°42′14″ | 207 | 26 | H | P | |
| 67 | Nara | Maruyama (G121) | 34°28′33″ | 135°47′54″ | 180 | 260 | P | P | |
| 68 | Nenbutsuji yama | 34°41′00″ | 135°49′26″ | 72 | 64 | 104 | P | P | |
| 69 | Kawai Otsukayama (Umami) | 34°35′10″ | 135°44′35″ | 79 | 109 | 194 | P | P | |
| 70 | Masuyama Chongjin | 34°28′34″ | 135°46′45″ | 319 | 83 | 205 | S | PP | |
| 71 | Mesuriyama | 34°29′56″ | 135°50′52″ | 179 | 72 | 209 | S | P | |
| 72 | Muro Miyayama | 34°26′35″ | 135°44′02″ | 165 | 104 | 198 | S | P | |
| 73 | Nishiyama | 34°35′33″ | 135°50′36″ | 159 | 73 | 178 | S | P | |
| 74 | (Oyamato) | 34°34′12″ | 135°50′55″ | 263 | 40 | 105 | S | PP | |
| 75 | Sujinryo (Oyamato) | 34°33′26″ | 135°50′59″ | 208.5 | 103 | 242 | S | P | |
| 76 | (Oyamato) | 34°33′36″ | 135°50′36″ | 176 | 44 | 126 | S | PP | |
| 77 | Hashinakayama (Oyamato) | 34°32′22″ | 135°50′28″ | 156 | 109 | 262 | S | PP | |
| 78 | Hatagozuka (Oyamato) | 34°34′19″ | 135°50′53″ | 180 | 140 | S | P | ||
| 79 | Kushiyama (Oyamato) | 34°33′25″ | 135°51′08″ | 200 | 60 | 123 | S | P | |
| 80 | Nakayama Otsuka (Oyamato) | 34°33′58″ | 135°50′54″ | 112 | 58 | 130 | S | PP | |
| 81 | Nishi Tonozuka (Oyamato) | 34°34′07″ | 135°51′04″ | 84 | 107 | 200 | S | P | |
| 82 | Shibutani-Mukouyama (Oyamato) | 34°33′03″ | 135°50′58″ | 171.5 | 161 | 286 | S | P | |
| 83 | Shimoikeyama (Oyamato) | 34°34′08″ | 135°50′47″ | 75 | 120 | S | PP | ||
| 84 | Jingu Kogoroyo (Saki) | 34°42′23″ | 135°47′07″ | 79 | 172 | 273 | P | PP | |
| 85 | Iwanohime Kogoroyo (Saki) | 34°42′06″ | 135°48′10″ | 93.5 | 136 | 218 | P | P | |
| 86 | Seimuryo (Saki) | 34°42′01″ | 135°47′15″ | 85 | 111 | 207 | P | P | |
| 87 | Konabe (Saki) | 34°41′53″ | 135°48′17″ | 82 | 125 | 200 | P | P | |
| 88 | Hibasuhimeryo (Saki) | 34°41′59″ | 135°47′21″ | 81 | 89 | 209 | P | P | |
| 89 | Uwanabe (Saki) | 34°41′52″ | 135°48′33″ | 86 | 123 | 251 | P | P | |
| 90 | Senka Empire | 34°28′41″ | 135°46′48″ | 301 | 72 | 150 | S | PP | |
| 91 | Shima no yama (Umami) | 34°35′02″ | 135°45′57″ | 66 | 86 | 185 | P | PP | |
| 92 | Shiro yama (Umami) | 34°35′21″ | 135°44′45″ | 100 | 68 | 102 | P | PP | |
| 93 | Suininryo (Saki) | 34°40′49″ | 135°46′52″ | 70 | 116 | 229 | P | P | |
| 94 | Sakurai Chausuyama | 34°30′42″ | 135°51′25″ | 88 | 55 | 173 | S | PP | |
| 95 | Tsukiyama (Umami) | 34°31′23″ | 135°43′51″ | 348 | 108 | 212 | P | P | |
| 96 | Udo Tsuka | 34°37′04″ | 135°42′09″ | 275 | 30 | 60 | P | PP | |
| 97 | Nagareyama (Umami) | 34°33′37″ | 135°44′10″ | 87 | 62 | 103 | P | PP | |
| 98 | Nikiyama (Umami) | 34°33′02″ | 135°44′13″ | 351 | 110 | 193 | P | P | |
| 99 | Suyama (Umami) | 34°33′23″ | 135°44′27″ | 289 | 102 | 203 | P | P | |
| 100 | Oita | Kamezuka | 33°14′06″ | 131°44′23″ | 85 | 40 | 112 | H | P |
| 101 | Okayama | Ryoguzan | 34°44′24″ | 134°00′09″ | 50 | 117 | 188 | P | P |
| 102 | Sakuzan | 34°39′55″ | 133°46′11″ | 124 | 131 | 254 | P | P | |
| 103 | 34°41′52″ | 133°45′20″ | 356 | 21 | 28 | P | PP | ||
| 104 | 34°41′52″ | 133°45′20″ | 181 | 18 | 27 | P | PP | ||
| 105 | Zozan | 34°40′26″ | 133°48′14″ | 120 | 167 | 313 | P/S | P | |
| 106 | Osaka | Tsudo-shiroyama | 34°34′55″ | 135°35′37″ | 50.2 | 168 | 272 | P | P |
| 107 | Hazamiyama | 34°33′42″ | 135°36′07″ | 347 | 59 | 98 | P | PP | |
| 108 | Hakayama | 34°33′28″ | 135°36′17″ | 171 | 148 | 226 | P | PP | |
| 109 | Minegazuka | 34°33′08″ | 135°35′51″ | 159.5 | 42 | 89 | P | PP | |
| 110 | Hakuchoryo | 34°33′05″ | 135°36′16″ | 172.5 | 154 | 195 | P | PP | |
| 111 | Chuai-tenno-ryo | 34°33′57″ | 135°35′39″ | 107 | 174 | 240 | P | P | |
| 112 | Hachizuka | 34°34′05″ | 135°35′44″ | 185 | 46 | 58 | P | S | |
| 113 | Ingyo-tenno-ryo | 34°34′23″ | 135°37′00″ | 274.9 | 164 | 227 | P | P | |
| 114 | Nakatsuhime-no-mikoto-ryo | 34°34′13″ | 135°36′47″ | 148 | 192 | 296 | P | P | |
| 115 | Komuroyama | 34°34′05″ | 135°36′34″ | 306 | 94 | 153 | P | PP | |
| 116 | Otorizuka | 34°34′00″ | 135°36′32″ | 97.5 | 45 | 104 | P | PP | |
| 117 | Konda-maruyana Ojin tenno | 34°33′43″ | 135°36′35″ | 256 | 300 | 413 | P | P | |
| 118 | Higashiumazuka | 34°33′49″ | 135°36′41″ | 278 | 71 | 122 | P | S | |
| 119 | Imashirozuka | 34°51′00″ | 135°35′42″ | 201 | 157 | 180 | P/S | P | |
| 120 | Kawachi Otsukayana | 34°34′20″ | 135°34′05″ | 74 | 215 | 335 | P | P | |
| 121 | Mayuyama | 34°27′47″ | 135°25′57″ | 36 | 97 | 177 | P | P | |
| 122 | Richu-tenno-ryo | 34°33′17″ | 135°28′41″ | 118 | 239 | 376 | P | P | |
| 123 | Itasuke | 34°33′12″ | 135°29′09″ | 198 | 89 | 150 | P | PP | |
| 124 | Gobyoyama | 34°33′17″ | 135°29′28″ | 192 | 118 | 195 | P | PP | |
| 125 | Haji Nisanzai | 34°32′48″ | 135°29′58″ | 195 | 215 | 280 | P | P | |
| 126 | Nagayama | 34°34′06″ | 135°29′13″ | 114 | 59 | 92 | P | S | |
| 127 | Magodayuyama | 34°33′37″ | 135°29′06″ | 210 | 25 | 63 | P | S | |
| 128 | Tatsusayama | 34°33′40″ | 135°29′00″ | 210 | 32 | 63 | P | S | |
| 129 | Maruhoyama | 34°34′02″ | 135°29′08″ | 118 | 34 | 84 | P | S | |
| 130 | Nagatsuka | 34°33′28″ | 135°29′16″ | 193 | 64 | 95 | P | PP | |
| 131 | Hatazuka | 34°33′24″ | 135°28′58″ | 175 | 24 | 60 | P | PP | |
| 132 | Zenizuka | 34°33′19″ | 135°29′04″ | 173 | 42 | 72 | P | PP | |
| 133 | Nintoku-tenno-ryo -Daisen- | 34°33′54″ | 135°29′17″ | 119 | 300 | 486 | P | P | |
| 134 | Hanzei-tenno-ryo | 34°34′34″ | 135°29′19″ | 105 | 111 | 158 | P | P | |
| 135 | Sairyo | 34°19′36″ | 135°10′08″ | 115 | 132 | 209 | S | P | |
| 136 | (Furuichi) | 34°32′56″ | 135°36′02″ | 156 | 122 | 118 | P | P | |
| 137 | Shionjiyama | 34°38′22″ | 135°38′27″ | 89 | 41 | 131 | P | P | |
| 138 | Taninowa Goryo | 34°19′50″ | 135°10′45″ | 153 | 97 | 172 | S | P | |
| 139 | Saga | Funatsuka | 36°07′39″ | 139°28′40″ | 130 | 84 | 131 | P | |
| 140 | Saitama | Futakoyama (Sakitama) | 36°07′39″ | 139°28′40″ | 130 | 84 | 131 | P | |
| 141 | Gunzan (Sakitama) | 36°07′39″ | 139°28′40″ | 129 | 71 | 110 | P | ||
| 142 | Inariyama (Sakitama) | 36°07′39″ | 139°28′40″ | 128 | 80 | 115 | P | ||
| 143 | Nakayama (Sakitama) | 36°07′39″ | 139°28′40″ | 153 | 35 | 75 | P | ||
| 144 | Shogunyama (Sakitama) | 36°07′39″ | 139°28′40″ | 141 | 68 | 97 | P | ||
| 145 | Taruzuka (Sakitama) | 36°07′39″ | 139°28′40″ | 141 | 48 | 71 | P | ||
| 146 | Yamako (Sakitama) | 36°07′39″ | 139°28′40″ | 143 | 44 | 69 | P | ||
| 147 | Shimane | Imaichi Kofun (G36) | 35°21′47″ | 132°45′53″ | 240 | 100 | P | ||
| 148 | Okadayama | 35°25′40″ | 133°05′29″ | 88 | 14 | 26 | PP | ||
| 149 | Shizuoka | Miikedaira | 35°03′12″ | 138°28′52″ | 30 | 30 | 68 | S | P |
| 150 | Tochigi | (Machizuka) | 36°48′54″ | 140°07′25″ | 90 | 10 | 28 | P | PP |
| 151 | Shimo Samurai tsuka (Machizuka) | 36°48′48″ | 140°07′23″ | 97 | 33 | 87 | P | PP | |
| 152 | Tsukayama | 36°30′22″ | 139°51′37.2″ | 164 | 60 | 90 | P | P | |
| 153 | Tokyo | Noge Otsuka | 35°36′18″ | 139°38′35″ | 136 | 27 | 72 | P | |
| 154 | Toyama | Sakuraya | 36°48′59″ | 137°01′52″ | 334 | 25 | 55 | P/S | PP |
| 155 | Yanaidanu-no-oyama | 36°49′23″ | 136°59′30″ | 237 | 43 | 105 | P | ||
| 156 | Yamaguchi | Wakamiya | 34°00′46″ | 130°55′28″ | 101 | 25 | 48 | P | P |
| 157 | Yamanashi | Kai Saikozuka | 35°35′32″ | 138°34′41″ | 338 | 65 | 168 | S | P |
| 158 | Yamagata | Inarimori | 38°02′23″ | 140°09′26″ | 116 | 30 | 96 | P/S | PP |
Appendix B

Table A2.
List of the images used for the study.
Table A2.
List of the images used for the study.
| n° | Satellite | Resolution | mm/dd/yyyy |
|---|---|---|---|
| 1 | Airbus | 50 cm | 1/11/2020 |
| 2 | Airbus | 50 cm | 3/7/2019 |
| 3 | Maxar Technologies | 30 cm | 4/18/2019 |
| 4 | Maxar Technologies | 30 cm | 4/13/2019 |
| 5 | Maxar Technologies | 30 cm | 12/18/2020 |
| 6 | Maxar Technologies | 30 cm | 4/13/2019 |
| 7–8 | Maxar Technologies | 30 cm | 12/17/2020 |
| 9 | Maxar Technologies | 30 cm | 05/04/2021 |
| 10 | Maxar Technologies | 30 cm | 04/15/2021 |
| 11 | Maxar Technologies | 30 cm | 04/17/2021 |
| 12 | Maxar Technologies | 30 cm | 01/04/2021 |
| 13 | Maxar Technologies | 30 cm | 06/14/2017 |
| 14–15 | Maxar Technologies | 30 cm | 08/03/2018 |
| 16 | Maxar Technologies | 30 cm | 04/30/2020 |
| 17 | Maxar Technologies | 30 cm | 04/02/2014 |
| 18–21 | Maxar Technologies | 30 cm | 01/23/2012 |
| 22 | Maxar Technologies | 30 cm | 10/08/2018 |
| 23 | Maxar Technologies | 30 cm | 05/16/2018 |
| 24–25 | PlanetScope | 3.7 m | 12/18/2020 |
| 26 | Maxar Technologies | 30 cm | 04/29/2018 |
| 27 | Maxar Technologies | 30 cm | 03/15/2013 |
| 28–31 | Maxar Technologies | 30 cm | 04/29/2018 |
| 32 | Maxar Technologies | 30 cm | 01/30/2019 |
| 33 | Maxar Technologies | 30 cm | 05/05/2018 |
| 34 | Maxar Technologies | 30 cm | 04/29/2018 |
| 35 | Maxar Technologies | 30 cm | 05/16/2018 |
| 36 | Maxar Technologies | 30 cm | 07/10/2018 |
| 37 | Maxar Technologies | 30 cm | 02/22/2019 |
| 38 | Maxar Technologies | 30 cm | 11/02/2019 |
| 39 | Maxar Technologies | 30 cm | 05/24/2020 |
| 40 | Maxar Technologies | 30 cm | 02/20/2021 |
| 41 | PlanetScope | 3.7 m | 11/10/2019 |
| 42 | Maxar Technologies | 30 cm | 02/20/2021 |
| 43 | Maxar Technologies | 30 cm | 03/13/2017 |
| 44–45 | Maxar Technologies | 30 cm | 09/27/2012 |
| 46 | Maxar Technologies | 30 cm | 10/05/2017 |
| 47 | Maxar Technologies | 30 cm | 05/07/2019 |
| 48 | PlanetScope | 3.7 m | 11/13/2020 |
| 49 | Maxar Technologies | 30 cm | 05/07/2019 |
| 50 | PlanetScope | 3.7 m | 11/13/2020 |
| 51–54 | Maxar Technologies | 30 cm | 01/30/2019 |
| 55–61 | Maxar Technologies | 30 cm | 12/01/2020 |
| 62 | Maxar Technologies | 30 cm | 04/05/2016 |
| 63 | Maxar Technologies | 30 cm | 11/17/2020 |
| 64–65 | Maxar Technologies | 30 cm | 12/15/2017 |
| 66 | Maxar Technologies | 30 cm | 11/12/2020 |
| 67 | Maxar Technologies | 30 cm | 03/11/2021 |
| 68 | PlanetScope | 3.7 m | 09/07/2019 |
| 69 | Maxar Technologies | 30 cm | 05/08/2019 |
| 70 | Maxar Technologies | 30 cm | 03/11/2021 |
| 71 | Maxar Technologies | 30 cm | 03/11/2021 |
| 72 | Maxar Technologies | 30 cm | 03/11/2021 |
| 73–83 | Maxar Technologies | 30 cm | 03/11/2021 |
| 84 | Maxar Technologies | 30 cm | 01/30/2019 |
| 90 | Maxar Technologies | 30 cm | 03/11/2021 |
| 91–92 | Maxar Technologies | 30 cm | 03/11/2021 |
| 93 | Maxar Technologies | 30 cm | 01/30/2019 |
| 94 | Maxar Technologies | 30 cm | 03/18/2021 |
| 95 | Maxar Technologies | 30 cm | 03/11/2021 |
| 96 | PlanetScope | 3.7 m | 03/09/2020 |
| 97–99 | Maxar Technologies | 30 cm | 03/11/2021 |
| 100 | Maxar Technologies | 30 cm | 12/06/2020 |
| 101–105 | Maxar Technologies | 30 cm | 03/26/2021 |
| 106–138 | Maxar Technologies | 30 cm | 11/24/2020 |
| 139 | Maxar Technologies | 30 cm | 05/01/2016 |
| 140–146 | Maxar Technologies | 30 cm | 05/05/2018 |
| 147 | Maxar Technologies | 30 cm | 06/17/2017 |
| 148 | Maxar Technologies | 30 cm | 02/04/2017 |
| 149 | Maxar Technologies | 30 cm | 08/25/2020 |
| 150–151 | Maxar Technologies | 30 cm | 09/29/2014 |
| 152 | Maxar Technologies | 30 cm | 07/02/2018 |
| 153 | Maxar Technologies | 30 cm | 05/24/2019 |
| 154–155 | Maxar Technologies | 30 cm | 05/28/2014 |
| 156 | Maxar Technologies | 30 cm | 02/18/2019 |
| 157 | Maxar Technologies | 30 cm | 03/24/2021 |
| 158 | Maxar Technologies | 30 cm | 11/04/2015 |
References
- Mizoguchi, K. An Archaeological History of Japan; University of Pennsylvania Press: Philadelphia, PA, USA, 2002. [Google Scholar]
- Magli, G. Astronomy and Feng Shui in the projects of the Tang, Ming and Qing royal mausoleums: A satellite imagery approach. Archaeol. Res. Asia 2018, 17, 98–108. [Google Scholar] [CrossRef]
- Magli, G. The Orientation of the Daisen Kofun. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3604011 (accessed on 18 May 2020).
- Mizoguchi, K. Yayoi-shakai no soshiki to kategori (The organization and categories of the Yayoi society). In Yayoi-jidai no kokogaku, Volume 8. Shuraku kara yomu Yayoishakai (The Archaeology of the Yayoi Period, Volume 8. The Yayoi Society as Seen from the Settlement); Matsugi, T., Fujio, S., Shitara, H., Eds.; Doseisha: Tokyo, Japan, 2008; pp. 74–95. [Google Scholar]
- Kang, I. Che-5-jang Hanbando ŭi chŏnbang huwŏnbun [Chapter 5 Keyhole tombs of the Korean peninsula]. In Minjok Munhwa Yŏn’gu ch’ongsŏ; Hagyon Munhwasa: Seoul, Korea, 1983; Volume 10, pp. 257–312. [Google Scholar]
- Lee, D.H.S. Keyhole-Shaped Tombs and Unspoken Frontiers: Exploring the Borderlands of Early Korean-Japanese Relations in the 5th–6th Centuries; University of California: Los Angeles, CA, USA, 2014. [Google Scholar]
- Kidder, J.E. The Fujinoki Tomb and Its Grave-Goods. Monum. Nippon. 1987, 42, 57. [Google Scholar] [CrossRef]
- Mizoguchi, K. The Archaeology of Japan; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ishino, H. Rites and rituals of the Kofun period. Jpn. J. Relig. Stud. 1992, 19, 191–216. [Google Scholar] [CrossRef]
- Yoshitaka, H. Burial mounds, volcanoes, and the sun. Quat. Res. 2017, 56, 97–110. [Google Scholar]
- Mizoguchi, K. The emergence of anthropomorphic representation. In Image and Imagination: A Global Prehistory of Figurative Representation; Renfrew, C., Morley, I., Eds.; McDonald Institute for Archaeological Research: Cambridge, UK, 2007; pp. 185–195. [Google Scholar]
- Parcak, S.H. Satellite Remote Sensing for Archaeology; Routledge: London, UK; New York, NY, USA, 2009. [Google Scholar]
- Parcak, S.; Gathings, D.; Childs, C.; Cline, G.M.E. Satellite Evidence of Archaeological Site Looting in Egypt: 2002–2013. Antiquity 2016, 90, 188–205. [Google Scholar] [CrossRef] [Green Version]
- Rayne, L.; Gatto, M.; Abdulaati, L.; Al-Haddad, M.; Sterry, M.; Sheldrick, N.; Mattingly, D. Detecting Change at Archaeo-logical Sites in North Africa Using Open-Source Satellite Imagery. Remote Sens. 2020, 12, 3694. [Google Scholar] [CrossRef]
- Romain, W.F. Solstice Alignments at Angkor Wat and Nearby Temples: Connecting to the Cycles of Time. J. Skyscape Archaeol. 2018, 4, 176–200. [Google Scholar] [CrossRef]
- Baratta, N.C.; Magli, G. The Role of Astronomy and Feng Shui in the Planning of Ming Beijing. Nexus Netw. J. 2021, 23, 1–21. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, L.; Li, X.; Peng, D.; Zhang, Y.; Gong, P. Progress and Trends in the Application of Google Earth and Google Earth Engine. Remote. Sens. 2021, 13, 3778. [Google Scholar] [CrossRef]
- Potere, D. Horizontal Positional Accuracy of Google Earth’s High-Resolution Imagery Archive. Sensors 2008, 8, 7973–7981. [Google Scholar] [CrossRef] [PubMed]
- González-García, C.; Šprajc, I. Astronomical significance of architectural orientations in the Maya Lowlands: A statistical approach. J. Archaeol. Sci. Rep. 2016, 9, 191–202. [Google Scholar] [CrossRef]
- Silva, F. A probabilistic framework and significance test for the analysis of structural orientations in skyscape archaeology. J. Archaeol. Sci. 2020, 118, 105138. [Google Scholar] [CrossRef]
- Gowland, W. XX.—The Dolmens and Burial Mounds in Japan. Archaeologia 1897, 55, 439–524. [Google Scholar] [CrossRef]
- Hoskin, M. Tombs, Temples, and Their Orientations. A New Perspective on Mediterranean Prehistory; Ocarina Books: Bognor Regis, UK, 2001. [Google Scholar]
- Barnes, G.L. A hypothesis for early Kofun rulership. Jpn. Rev. 2014, 27, 3–29. [Google Scholar]
- Kishimoto, N. Dual Kingship in the Kofun Period as Seen from the Keyhole Tombs. UrbanScope (Electron. J.) 2013, 4, 1–21. [Google Scholar]
- Tsude, H. Chiefly lineages in Kofun-period Japan: Political relations between centre and region. Antiquity 1990, 64, 923–929. [Google Scholar] [CrossRef]
- Edwards, W. Mirrors on Ancient Yamato: The Kurozuka Kofun Discovery and the Question of Yamatai. Monum. Nippon. 1999, 54, 75. [Google Scholar] [CrossRef]
- Comina, C.; Sotiropoulos, P.; Maroulakis, S.; Vacha, D.; Mandrone, G.; Masturzo, N.; Matsumoto, N.; Seike, A.A. Geophysical surveys over and inside the Tobiotsuka Kofun–Okayama prefecture. J. Archaeol. Sci. 2020, 30, 102256. [Google Scholar] [CrossRef]
- Renshaw, S.L.; Ihara, S. Archaeoastronomy and Astronomy in Culture in Japan: Paving the Way to Interdisciplinary Study. Archaeoastronomy 1999, 14, 59–88. [Google Scholar]
- Renshaw, S.L.; Ihara, S. A Cultural History of Astronomy in Japan. In Astronomy across Cultures. Science across Cultures: The History of Non-Western Science; Selin, H., Xiaochun, S., Eds.; Springer: Dordrecht, The Netherlands, 2000; Volume 1, pp. 385–407. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).