1. Introduction
Considering the growing frequency of disasters recently, many studies have been conducted on disaster monitoring using satellite images, which can periodically provide information on a large area [
1,
2,
3]. Satellite images are effectively used for detecting areas damaged by disasters and analyzing the scope and level of damage. To validate the reliability of the analysis in detecting disaster-stricken areas using satellite images, it is important to (1) ensure satellite images at a suitable time [
4] and (2) acquire fine-scale (i.e., high spatial resolution) satellite images that allow the detailed damage analysis [
5,
6]. However, compared to coarse-scale (i.e., low spatial resolution) satellite images, fine-scale satellite images have a lower temporal resolution. With the recent development of remote sensing, it is possible to acquire satellite images at high temporal and spatial resolutions by constellation of several satellites such as RapidEye and PlanetScope. Nevertheless, there is a limitation to acquiring an optical satellite image at a suitable time for disaster monitoring. This is because the optical satellite images may have limitations in direct use due to the influence of clouds or climate factors.
To compensate for the missing information in these fine-scale satellite images, spatiotemporal data fusion integrating coarse-scale satellite images with high temporal resolution and fine-scale satellite images with high spatial resolution, can be applied [
7,
8,
9]. Here, the spatiotemporal data fusion combines the complementary characteristics of the spatial resolution of sparse time series data with a fine-scale (i.e., SF data) and the temporal resolution of dense time series data with a coarse-scale (i.e., DC data). For example, MODIS satellite images, provided daily at a spatial resolution of 250 m, and Landsat satellite images, provided at a spatial resolution of 30 m every 16 days, are considered as DC and SF data, respectively. A synthetic dense time series data with a fine-scale (i.e., SDF data) is generated from the spatiotemporal data fusion.
In detail, the spatiotemporal data fusion input DC data acquired at the time when SF data is missing (i.e., prediction date) and both DC and SF data acquired at the same time (i.e., pair date) to generate SDF data at the prediction date. Since the missing SF data can be generated as SDF data by spatiotemporal data fusion, it can be effectively applied to disaster monitoring that requires a satellite image with fine spatial resolution in a suitable time. To enhance the applicability of spatiotemporal data fusion in disaster monitoring, reflectance changes due to disasters should be indicated well in the fusion results. Since the occurrence of disasters such as wildfires, landslides, and floods cause changes in land cover because of the loss of forests and flooding [
10,
11,
12,
13]. Such changes are observed as abrupt reflectance changes in time series satellite images [
14,
15,
16,
17]. To explain the reflectance changes, the developed fusion models apply the assumptions for the reflectance changes or the modeling for the reflectance changes using time series DC data.
In relation to the models applying the assumptions, there is a representative fusion model, a Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM) [
18]. STARFM applies an assumption that temporal changes of the reflectance observed in SF data are the same as those in DC data regardless of difference of spatial resolution. However, since the landscape included in the satellite image differs depending on the spatial resolution, the reflectance changes may vary depending on the spatial resolution in DC and SF data. Regarding this, to account for the difference in spatial resolution of DC and SF data, Zhu et al. [
19] proposed an Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model (ESTARFM). ESTARFM applies spectral unmixing to consider the difference in spatial resolution. Specifically, the reflectance changes observed in DC data are reflected in SDF data through the spectral unmixing which is constructed by using DC and SF data acquired at the pair dates. Here, ESTARFM applies an assumption that the reflectance changes linearly. Such an assumption may be suitable, however, when there is no significant difference in the reflectance changes between the pair dates and the prediction date. In particular, there is a limit to assuming the linear changes because disasters cause abrupt changes in reflectance.
In contrast, the spatiotemporal data fusion models that model the reflectance changes from DC data with relatively high temporal resolution have been proposed. As one of these models, Xue et al. [
20] proposed a Spatio-Temporal Bayesian Fusion Model (STBFM). STBFM incorporates the temporal correlation extracted from multi-temporal DC data by applying the joint distribution and generates the fusion result by applying the maximum posterior estimator. There is a limit to the temporal correlation extraction that DC data with high temporal resolution can provide, however, since it only uses DC data acquired at the prediction date and the pair dates. In addition, STBFM assumes that DC data have Gaussian distribution to extract the temporal correlation using the joint distribution, though it is difficult to assure that the real satellite images have a Gaussian distribution. Recently, Zhou and Zhong [
21] proposed a Kalman Filter Reflectance Fusion Model (KFRFM) which models the temporal trends using a Kalman filter algorithm and time series DC data. KFRFM assumes that the land-cover types are identical in DC and SF data. However, the land-cover type of a pixel may vary depending on the spatial resolution of DC and SF data. Since the temporal trend may present differently depending on the land-cover type, the assumption applied by KFRFM may not always be valid.
Regarding these limitations, Kim et al. [
9] proposed a new geostatistics-based spatiotemporal data fusion model, which is a Spatial Time series Geostatistical/Deconvolution Fusion Model (STGDFM). STGDFM performs spatiotemporal data fusion by using the spatial time series modeling and deconvolution matrix. The spatial time series modeling is a geostatistical framework for spatiotemporal modeling, which can be applied regardless of the periodicity, tendency, and seasonality of time series data [
22]. Additionally, the deconvolution matrix is constructed for each pair date using DC and SF data acquired at each pair date, and the deconvolution matrix at the prediction date is estimated considering the change between the prediction date and the pair dates. The estimated deconvolution matrix is applied to the temporal trends extracted from time series DC data to convert it’s the spatial resolution to that of SF data. Moreover, STGDFM decomposes the prediction property into trend and residual components. The residual component indicates the reflectance changes that cannot be explained by the temporal trends. STGDFM generates the fusion result combining the trend and residual components to capture both the temporal trends and the abrupt reflectance changes.
Using these developed spatiotemporal fusion models, the applicability assessments have been conducted. Zhang et al. [
14] conducted the fusion of MODIS and Landsat images for urban flood mapping using STARFM and ESTARFM. They concluded that the fusion results of STARFM and ESTARFM showed similar prediction performance for urban flood mapping. Dao et al. [
23] applied ESTARFM to analyze flood inundation, which was applied for MODIS and Landsat data to generate synthetic Landsat data. The result of this study presented that ESTARFM captured surface reflectances of true Landsat data with highly correlation. For disaster monitoring, the previous studies applying spatiotemporal data fusion have been conducted, but most of these studies have applied only STARFM and ESTARFM, which adopt the assumptions of temporal changes in reflectance. As mentioned above, when a disaster occurs, the reflectance does not change periodically but abruptly changes. Therefore, the assumption of reflectance change applied by STARFM or ESATRFM may not be valid in the disaster monitoring. For this, spatiotemporal data fusion modeling temporal changes from time series DC data can be applied to explain the abrupt changes in reflectance due to disasters.
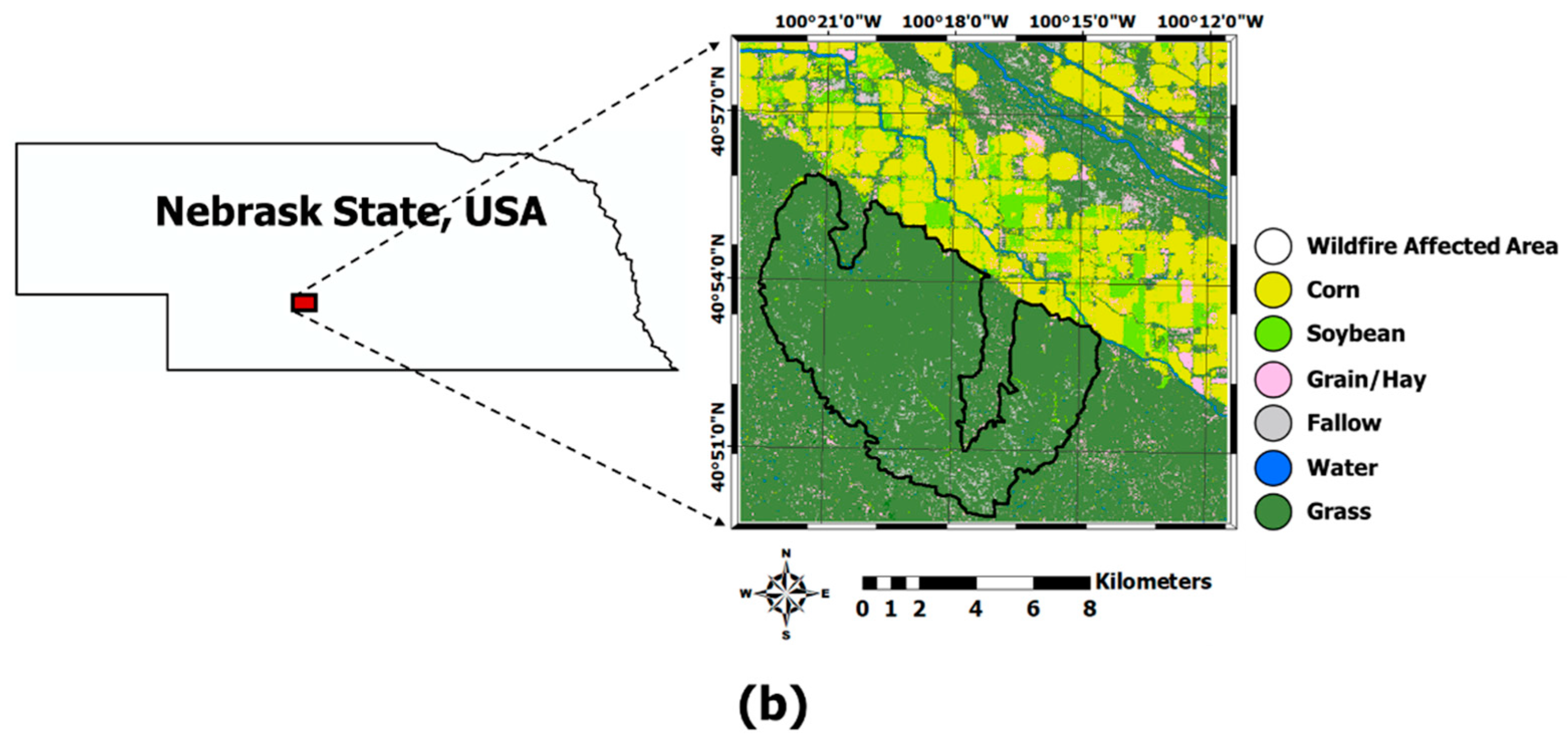
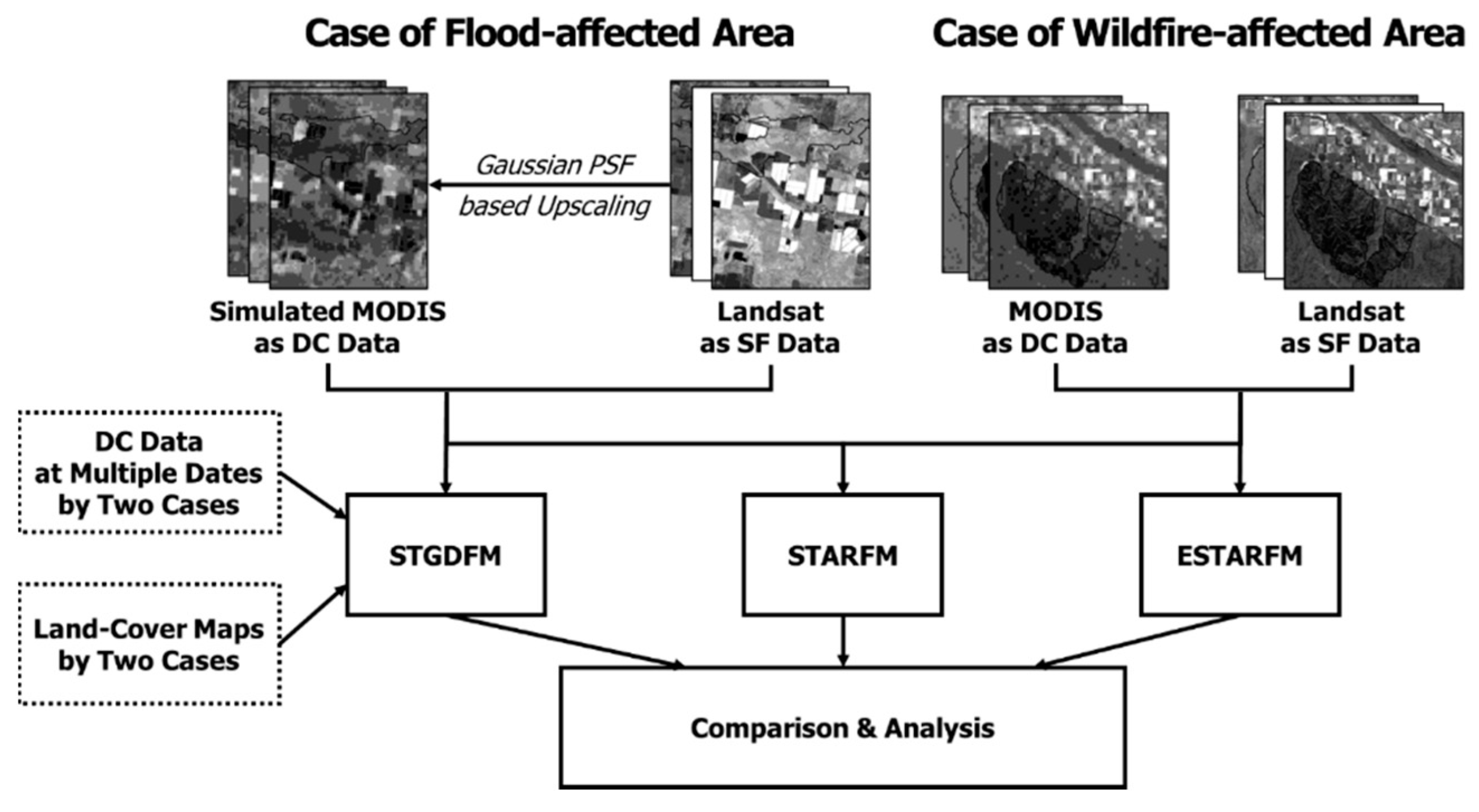
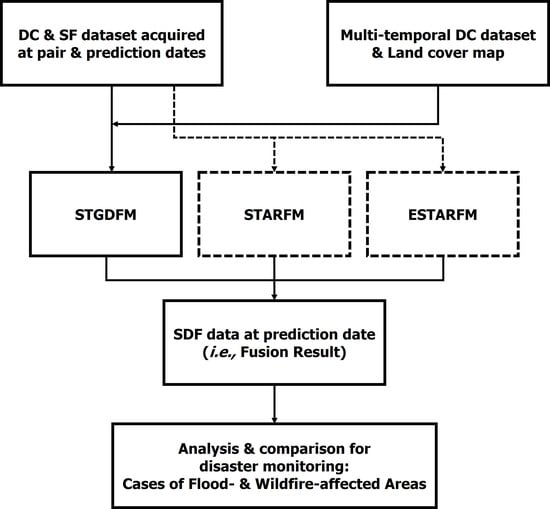
Based on this, this study assessed the applicability of STGDFM in disaster monitoring. To assess its explanatory capacity on the abrupt reflectance changes due to disasters, the study compared STGDFM and two other popular spatiotemporal data fusion models, STARFM and ESTARFM, and evaluated the results. The applicability assessment was conducted two case study areas affected by flood and wildfire. The near the Gwydir River Catchment located in Australia was selected as the study area of the Case of Flood-affected Area. In the Case of Flood-affected Area, the applicability assessment used simulation data using Landsat satellite images. The part of Nebraska state in the U.S. was selected as the study area of the Case of Wildfire-affected Area. Landsat and MODIS satellite images were used for the applicability assessment in the Case of Wildfire-affected Area.
2. Spatial Time Series Geostatistical/Deconvolution Fusion Model
This study supposes that the reflectances in the DC and SF data are and , respectively. Here, the superscripts and refer to coarse-scale and fine-scale, and and are the th and th coarse-scale and fine-scale in the th and th coarse-scale and fine-scale pixels, respectively. Additionally, and refer to the acquisition date of the DC and SF data, respectively, and are because the DC data is more frequently acquired than the SF data. Furthermore, is the pair date considering the composition of the input data in the spatiotemporal data fusion. Accordingly, STGDFM predicts , the DFS data, at the prediction date.
STGDFM first decomposes the predictive properties into trend and residual components [
9]. Therefore, the DC data at the prediction date can be defined as follows:
where
and
refer to the trend component and the residual component in
, respectively. In the same context,
, the spatiotemporal data fusion result, is expressed as the sum of the trend and residual components estimated in the fine-scale location
.
where
and
refer to the trend and residual components estimated at the fine-scale location at
, respectively.
To estimate from , STGDFM implements the spatial time series modelling and deconvolution matrix. Additionally, to estimate from , it applies a geostatistics-based downscaling technique: area-to-point kriging (ATPK).
First, STGDFM applies a spatial time series modeling to quantify the temporal trend components from the multi-temporal DC data [
22]. These temporal trend components refer to the quantification of the trend of the change of predictive properties over time. The multi-temporal DC data can be considered spatial time series that have time series values per pixel unit. Based on this, the temporal trend components are calculated at all coarse-scale pixel locations
through spatial time series modeling. Spatial time series modeling calculates temporal trend components by estimating the relationship between the time series value at each coarse-scale pixel and the basis time series elements [
9].
To consider the characteristics of land cover types, STGDFM defines the basis time series elements as the time series value per key land cover types of the target areas. For example, this time series value per land cover type means the calculation of the average value of all pixels in DC data corresponding to Class 1 by the acquisition date of the DC data. Further, STGDFM uses random forest, a non-parametric model, to define the relationship between the calculated basis time series elements and the time series value of each coarse-scale pixel [
24]. Through the result of random forest, the temporal trend components based on the DC data are quantified.
The previously estimated temporal trend components are quantified in the spatial resolution of the DC data. Therefore, to estimate the trend components in the fine-scale resolution, STGDFM uses a deconvolution matrix. The deconvolution matrix defines the linear relation of the DC and SF data acquired from the pair date in matrix form [
20]. Based on this, if there are DC and SF data acquired from
number of pair dates,
number of deconvolution matrices can be constructed. Because there are no true values of the SF data, the deconvolution matrix at
is estimated by the weighted coupling of the deconvolution matrix constructed in the pair dates.
Here, the weighted value is calculated by the relationship between the temporal trend components quantified at the prediction date and the pair date. That is, the relationship between the quantified temporal trend components at the prediction date and in each pair date is calculated, and a higher weighted value is assigned to the deconvolution matrix constructed in the highly correlated pair date. Although correlation can be generally calculated in the whole research region, the global relationship assumes that the local variability is not considered, and a linear relationship appears constantly in the whole research region [
25]. However, because the linear relationship can differ by region, STGDFM uses a regional linear relationship coefficient to calculate the weighting value, which is assigned to the deconvolution matrix. Thus, the weighted value assigned to the deconvolution matrix at each pair date is calculated, and the deconvolution matrix at the prediction date is estimated by the weighted coupling of the deconvolution matrix per pair date. Further, STGDFM estimates fine-scale trend components
by applying the estimated deconvolution matrix to the temporal trend components at the prediction date.
According to Equation (2), the predictive properties are not included in the trend component modeling, whereas the residual properties—that is, the residual components—are included. Therefore, to predict the spatiotemporal fusion result
, both the trend components and the residual components should be estimated simultaneously. To this end, STGDFM first calculates the coarse-scale residual components
at the prediction date. The coarse-scale residual components use the previously estimated fine-scale trend components
. First, Gaussian kernel-based point spread function (PSF) is applied to the final-scale trend components to upscale the components to the coarse-scale resolution. Then, through the difference between the trend components upscaled by Equation (1) and the DC data acquired at
, the coarse-scale residual components are calculated. Next, to estimate the fine-scale residual components in Equation (2), STGDFM uses ATPK, a geostatistics-based downscaling technique [
26]. The ATPK estimates the fine-scale residual components by the weighted linear coupling of the coarse-scale residual components, as shown in Equation (3):
where
refers to the weighting value of ordinary kriging assigned to the
th coarse-scale residual components (
close to the predicted location (
). This weighting value can be calculated by the concept of block kriging [
27].
Finally, STGDFM produces the spatiotemporal fusion result
by summing the fine-scale residual components estimated by Equation (3) and the fine-scale trend components estimated through the spatial time series modeling and deconvolution matrix [
9].
5. Discussion
The summary of the key results of this study are as follows: (1) The ESTARFM fusion result showed poor prediction performance in the reflectance changes in the damaged region and the period, as opposed to the Landsat data from the prediction date. (2) The STARFM fusion result showed a locally smoothed pattern in contrast to the application results of the other two models. (3) When compared to the fusion results of STARFM and ESTARFM, the fusion result of STGDFM showed a higher prediction performance. This section presents the analysis of the results.
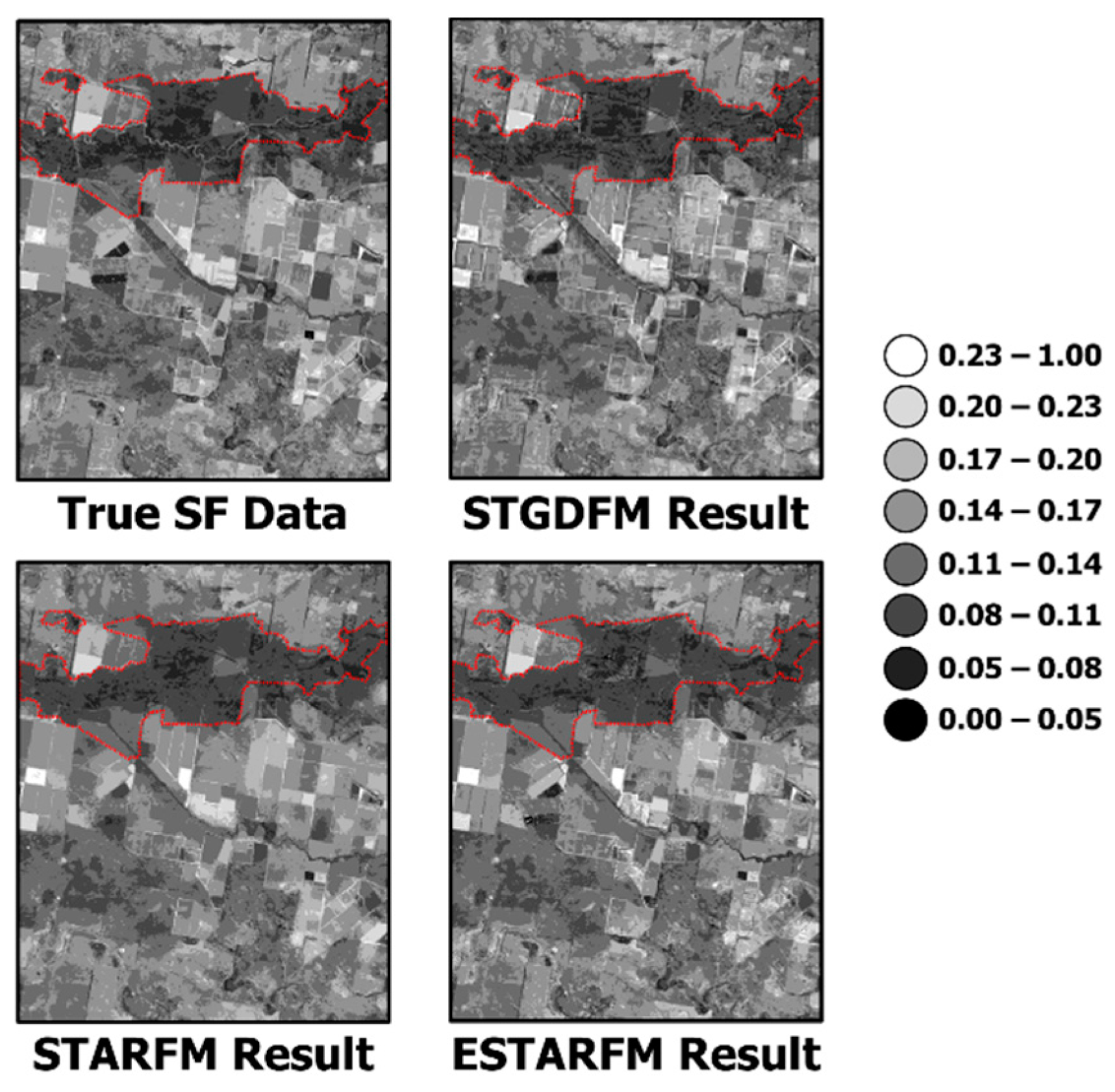
This study constructed the DC and SF data acquired before and after disaster as pair data and used them as input data to detect the region damaged by disaster (
Figure 2 and
Figure 3). The NIR channel data that showed a significant amount of the reflectance changes due to disaster (
Figure 2b and
Figure 3b) showed that there were huge reflectance changes between the pair dates and the prediction date. In particular, such reflectance changes were considerable in the first pair date, the time before the disaster, and the prediction date. However, ESTARFM assumes that reflectance changes linearly between the pair dates and the prediction date [
19]. Therefore, if there is a considerable change of reflectance between the prediction date and the pair dates due to disaster, it is difficult to assume that reflectance changes linearly. As such, the prediction performance of ESTARFM was the poorest among the three models. The previous studies also reported this interpretation in Xue et al. [
20].
As opposed to ESTARFM, STARFM assumes that the changes observed in the DC data are maintained in the fine-scale data [
18]. Therefore, if damage by disaster was observed in the DC data acquired in the prediction date, as shown in
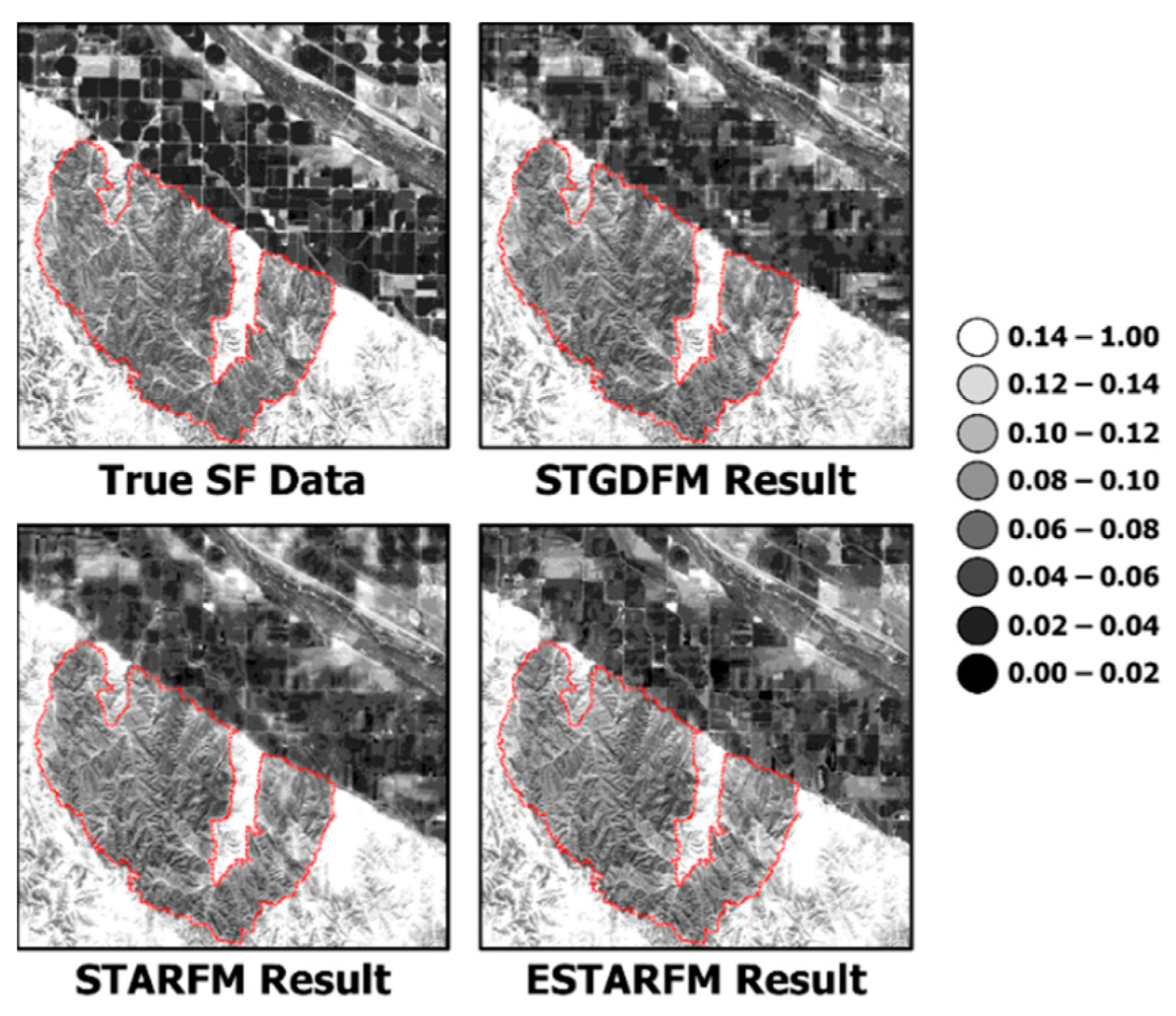
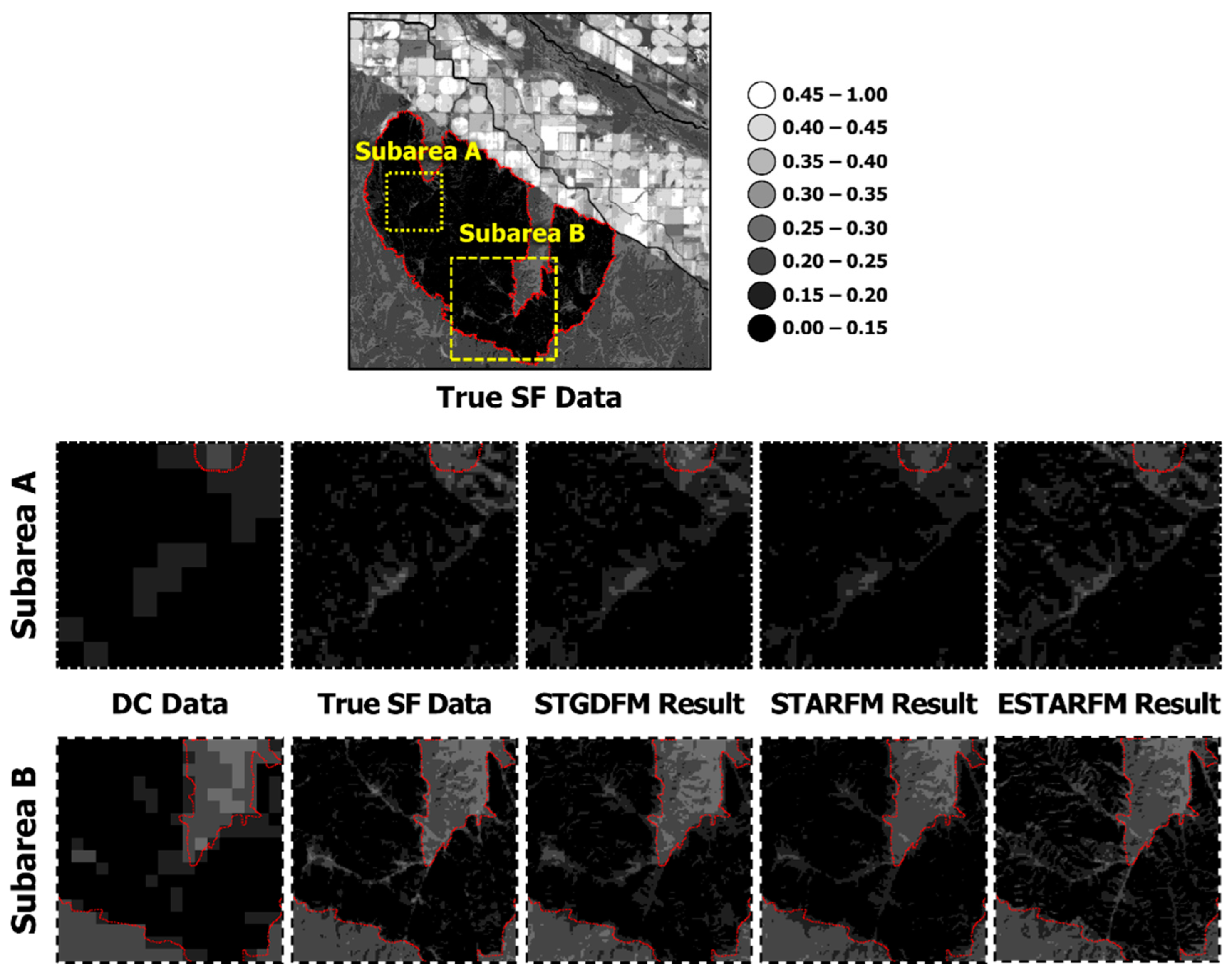
Figure 3, such data can be reflected onto the fusion result to explain the reflectance changes due to a disaster. As such, it is determined that STARFM showed a relatively more improved prediction performance, compared to ESTARFM. However, the fusion result of STARFM showed a smoothed pattern; in particular, the region with marked damage by wildfire, as shown in
Figure 12, did not reflect the local variations observed in the true SF data.
This is because such a result does not reflect the difference in the spatial resolution between the DC and SF data in the process of coupling the reflectance changes observed in the DC data according to STARFM’s assumption. Further, STARFM uses DC data converted into the spatial resolution of SF data as input data by applying bilinear interpolation. The DC data with the converted spatial resolution presents a smoothed pattern. Here, to explain the reflectance changes due to disaster, STARFM assigns a high weighting value to the DC data with the converted spatial resolution acquired on the prediction date. As a result, the effect of the DC data with smoothed patterns is largely reflected in the fusion result of STARFM, which showed limitations in explaining local variations. These results are conspicuous in
Figure 12, which enlarges the wildfire-affected areas. This means that to couple the reflectance changes observed in the DC data to the fusion result, the difference in the spatial resolution between the DC and SF data should be considered.
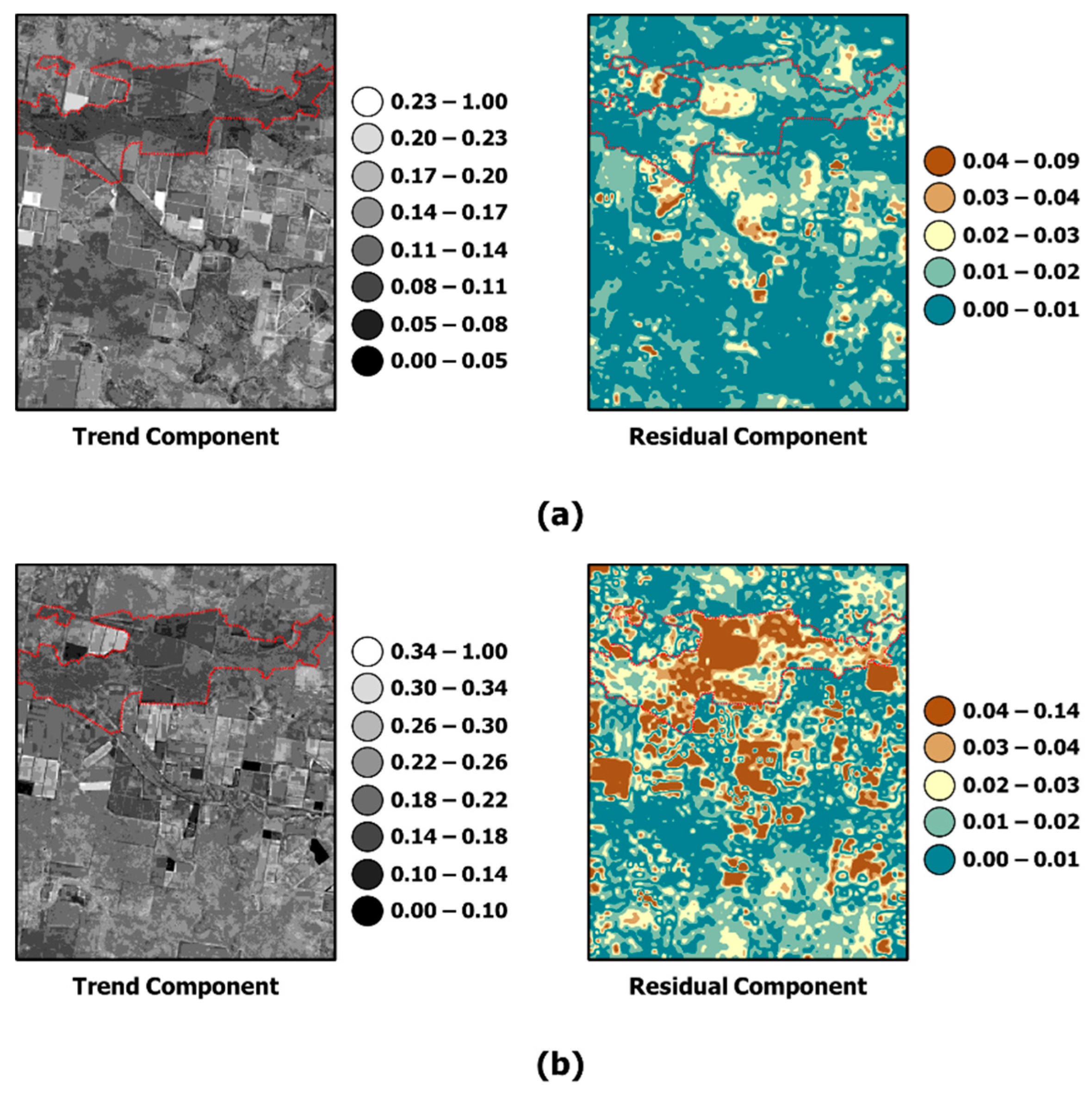
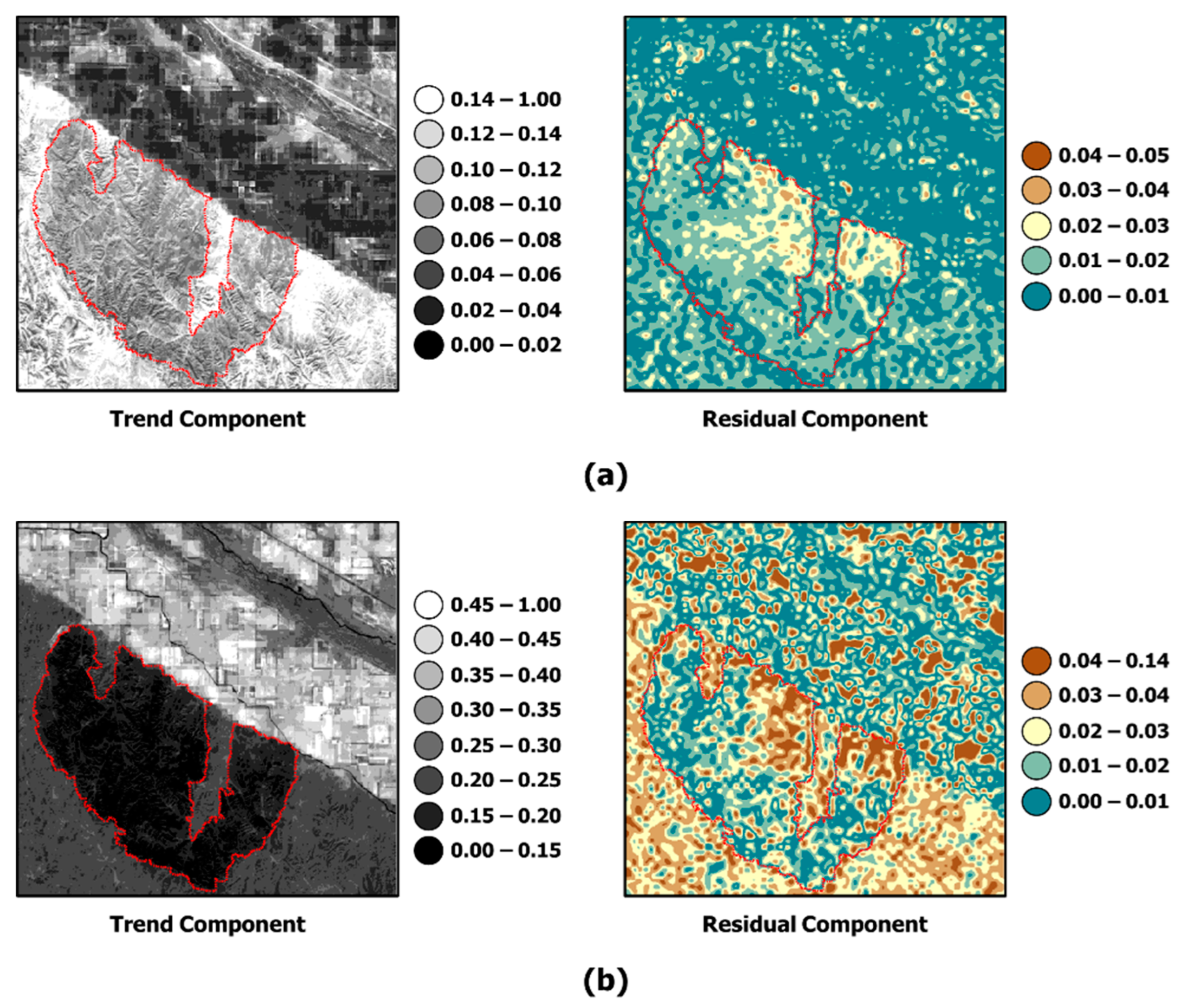
Next, the study analyzed the result of STGDFM, which showed a relatively higher predictive performance with its fusion result. As STGDFM is based on the decomposition of the components into the trend and residual components [
9], the study examined the trend and residual components, the intermediate result of STGDFM by each case (
Figure 13 and
Figure 14). To analyze the effect of the residual components on the fusion result of STGDFM, this study compared the absolute value of the residual components, where the larger the absolute value of the residual components, the greater the effect of the residual.
As show in
Figure 13 and
Figure 14, the effect of the residual components was higher in the red channel than in the NIR channel. Here, the large influence of the residual component means that the effect of the DC data acquired on the prediction date was highly reflected in the STGDFM fusion result explaining the reflectance changes due to the disaster. The reason for a large effect of the residual components in the NIR channel is that the main land coverage in two cases was vegetation (
Figure 1). Further, with flooding and wildfire, there was a change in the proportion of vegetation coverage, a key land coverage type in the two regions. Vegetation shows sensitive responses to reflectance changes in the NIR channel; as a result, the effect of the residual components increased in STGDFM to explain the reflectance changes due to disaster in vegetation coverage. In particular, the effect of the residual components was higher in the Case of Flood-affected Area, whereas no reflectance change resulting from disaster is observed in a date different from the prediction date (
Figure 2b and
Figure 13b).
The case of Wildfire-affected Area explains the reflectance changes due to wildfire not only with the residual components but also with the trend components (
Figure 14). Specifically, the effect of the trend components was shown to be considerably applied in the lower right corner of the wildfire-damaged region. As in
Figure 3, this is because damage by wildfire was also observed in the DC and SF data acquired after the wildfire. In other words, damage by wildfire was observed in dates other than the prediction date, and the changes in reflectance observed here could be explained in the fusion result with the trend components.
Meanwhile, the large effect of the residual components in STGDFM mean that the influence of DC data acquired on the prediction date was greatly reflected in the fusion result. While this is similar to STARFM where a high-weighing value is assigned to the DC data acquired on the prediction date, the smoothing pattern observed in the fusion result of STARFM did not occur in that of STGDFM. Thus, STGDFM explained the local variations of the SF data in the trend components by using the deconvolution matrix, which was then coupled with residual components to produce the fusion result in the spatial pattern similar to the true SF data.
In summary, STGDFM explained the reflectance changes due to disaster through the trend components and the residual components. In particular, its explanatory power for the abrupt reflectance changes due to disaster could be improved by reflecting the large effect of the residual components for the prediction date. Furthermore, STGDFM combines with the trend components the local variations of the SF data acquired in the pair dates based on the deconvolution matrix. In this way, STGDFM could produce fusion results with the true SF data and fine-scale spatial similarity (i.e., higher SSIM values) compared to STARFM and ESTARFM.
6. Conclusions
This study assessed the applicability of the spatiotemporal data fusion for the detection of regions damaged by disaster. To this end, the performance of detecting regions damaged by disaster was analyzed using spatiotemporal fusion results. In particular, the study applied three spatiotemporal data fusion models to detect the region damaged by disaster and compared and analyzed their performance. The summary of the analysis is as follows: (1) ESTARFM assumes that the reflectance changes linearly between the pair date and the prediction date; thus, its explanatory power for the reflectance changes due to disaster was relatively poor. (2) STARFM assumes that the reflectance changes observed in the DC data are maintained in the SF data; thus, it was limited in explaining the detailed variations of the reflectance changes. (3) STGDFM was able to show the highest prediction performance among the three models as it explained the reflectance change due to disaster with the residual components and the detailed variations of the reflectance changes with the trend components. Based on these results, STGDFM is expected to be useful only if DC data is acquired in the detection of regions damaged due to disaster.
The experimental results showed that the spatiotemporal data fusion can effectively produce synthetic satellite images with high spatial and temporal resolutions. For monitoring of disasters such as flood, wildfire, and forest landslide, fine-scale time series satellite images should be constructed quickly. The government or local governments can use these data to yield the scale and damage of disasters and to establish prevention measures in advance. In this respect, spatiotemporal data fusion methods need to be continuously enhanced. Even if this study compared and analyzed the performance of the three spatiotemporal data fusion models in disaster monitoring, there are still issues to be discussed or improved. For example, unlike the reflectance changes due to disasters, in order to predict the changes in reflectance due to climate change, the long time series satellite images should be used. Consequently, the geostatistical spatial time series modeling applied in STGDFM can capture the temporal trends from the long time series satellite images. However, since reflectance changes due to climate change generally appear in large areas, the difference in spatial resolution of DC and SF data may increase depending on the coverage area. As the difference in spatial resolution between DC and SF data increases, the noise patterns such as block artifacts can become more pronounced in the result of STGDFM. To reduce these noise patterns, stepwise STGDFM can be applied. That is, instead of directly converting DC data into spatial resolution of SF data, the spatial resolution is converted stepwise to finally generate SDF data. Therefore, in the future study, the prediction performance of STGDFM for reflectance changes due to climate change will be evaluated, and STGDFM will be improved to be applicable on a large scale.