The Suitability of UAV-Derived DSMs and the Impact of DEM Resolutions on Rockfall Numerical Simulations: A Case Study of the Bouanane Active Scarp, Tétouan, Northern Morocco
Abstract
1. Introduction
2. Study Area
2.1. Geological and Geomorphological Setting
2.2. Rockfall Occurences in the Bouanane Site
3. Materials and Methods
3.1. Stability of the Bouanane Cliff
3.2. Detachment Mechanisms
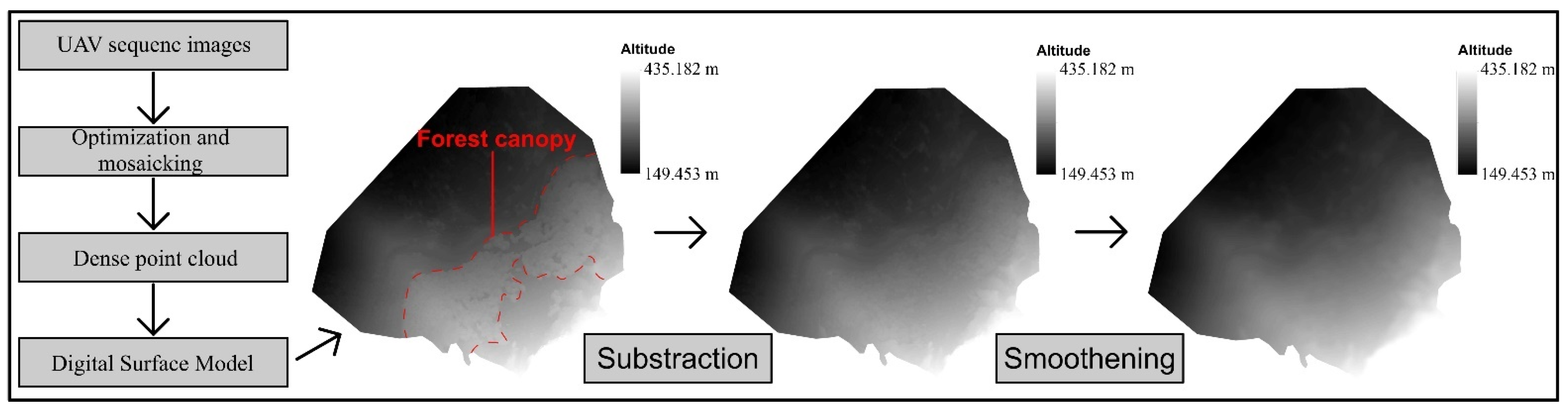
3.3. Preparation of Topographic Data
3.4. D trajectory Simulation
3.5. Statistical Analyses
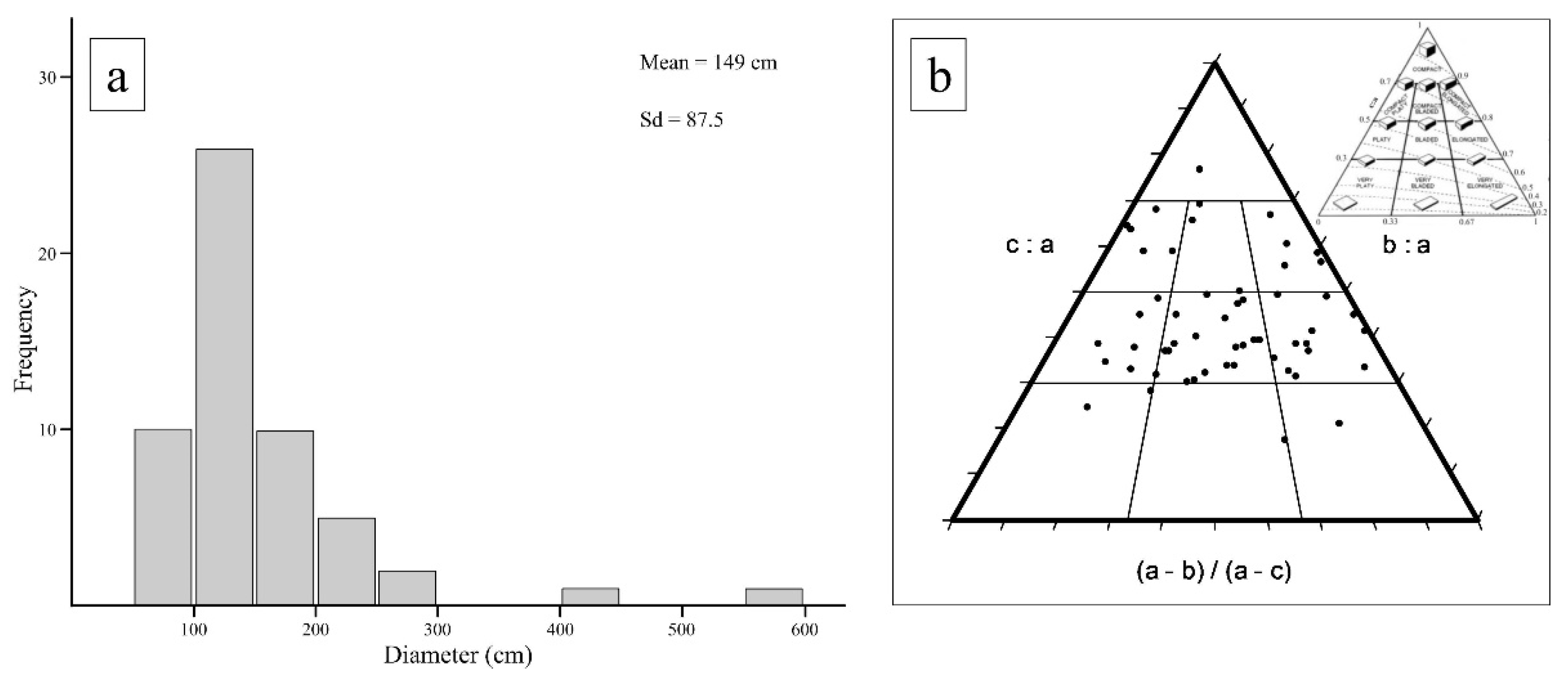
3.6. Morphometry of Scree Pebbles and Boulders
4. Results
4.1. Stability of the Bouanane Cliff and Detachment Mechanisms
4.2. Investigation of the December 2018 Event
4.3. Significance of the 2018 Event
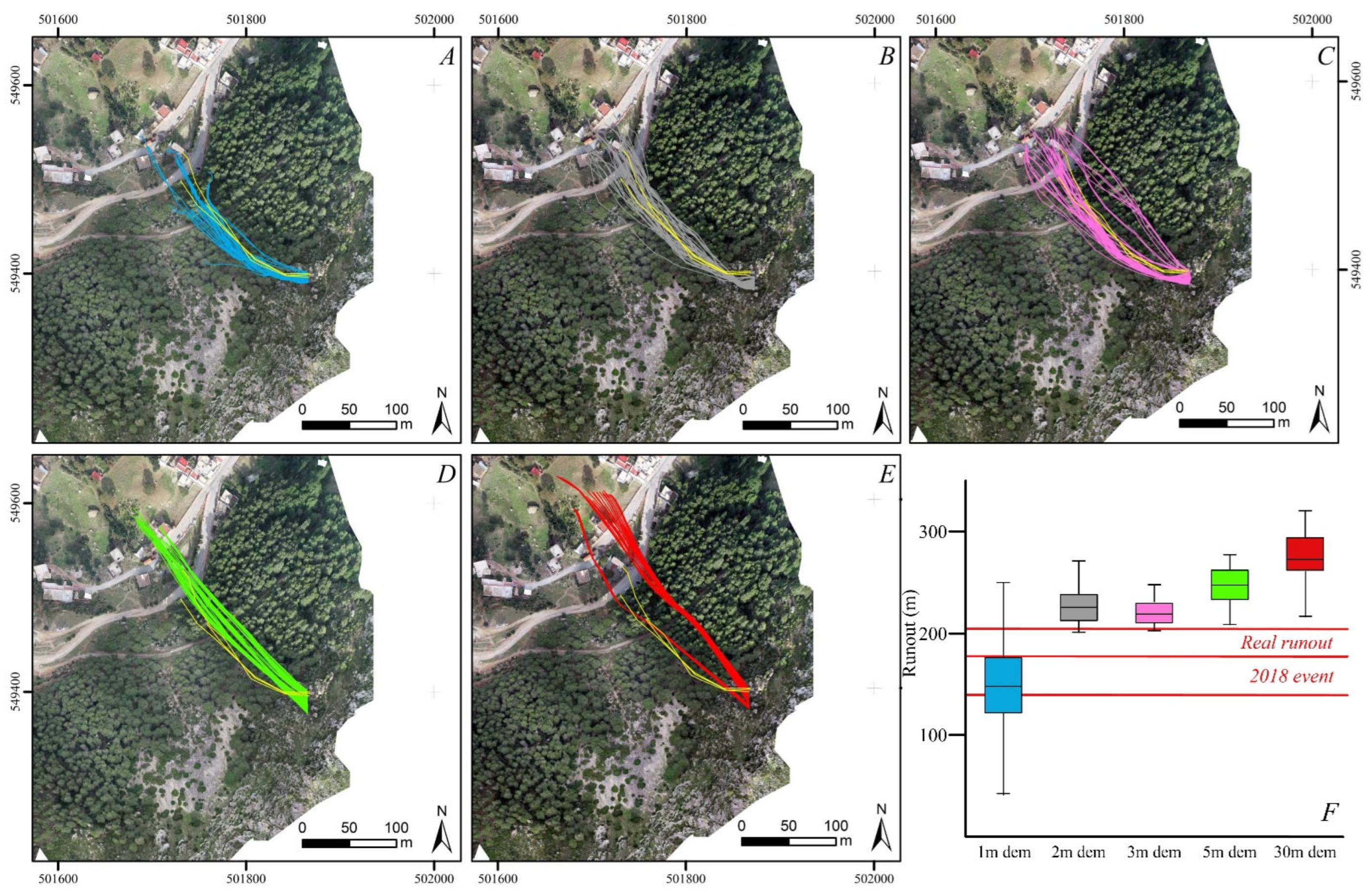
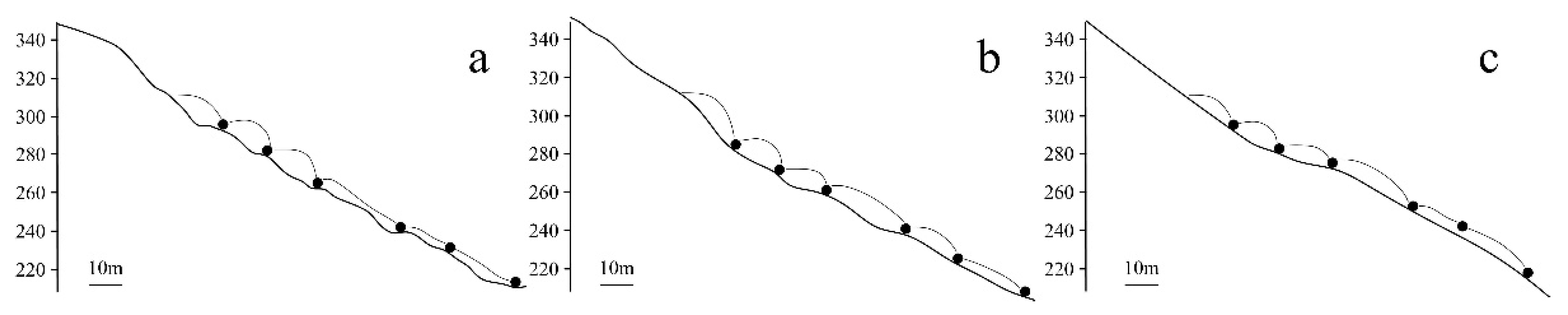
4.4. Rockfall Trajectory Simulation and Back-Analysis
4.5. Energy and Velocity Simulation
5. Discussion
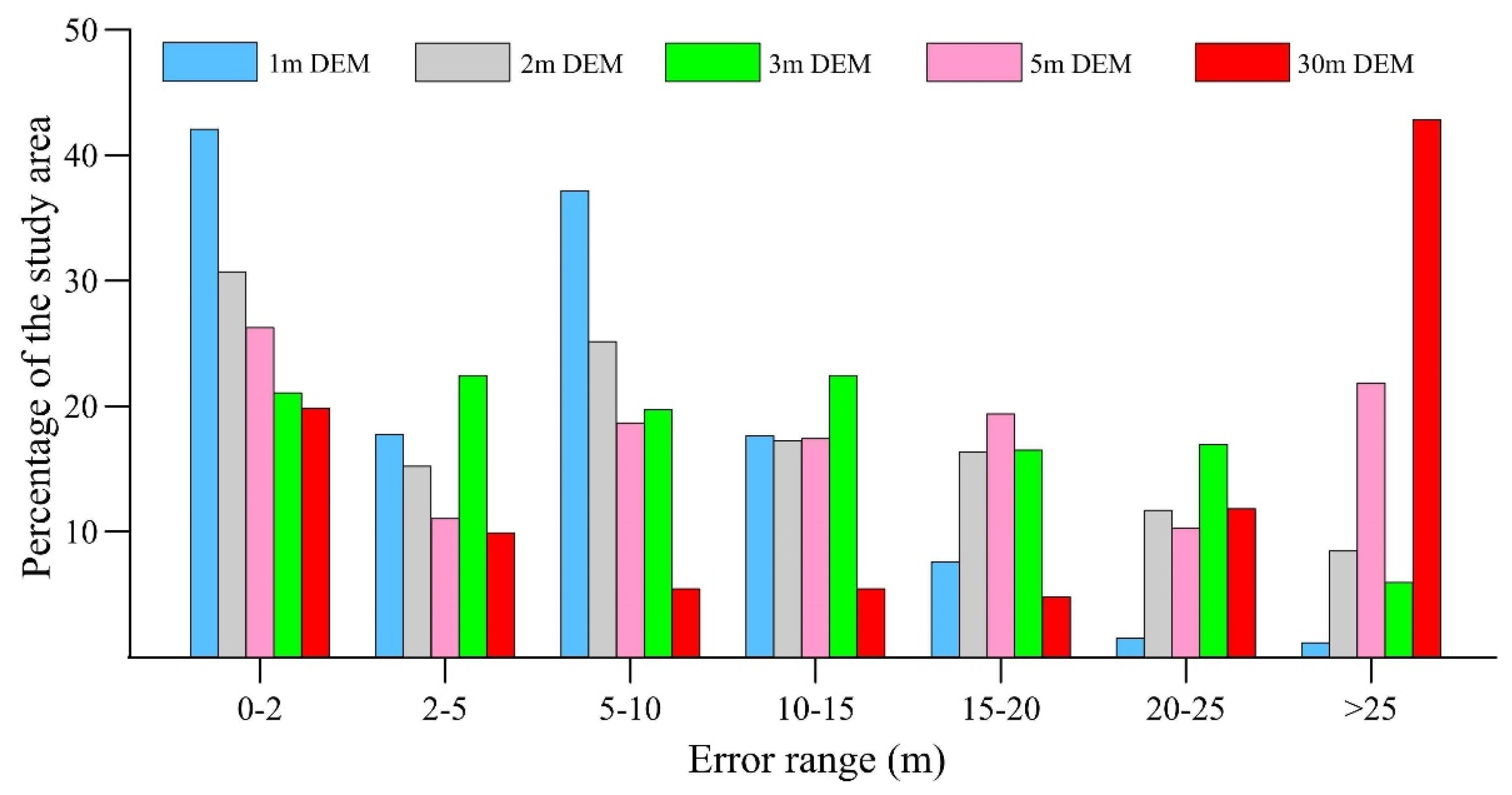
5.1. How the DSM Resolution Impacts the Rockfall Numerical Simulations
5.2. Impact of the Simulation Results on the Hazard Assessment and Prevention Efforts
5.3. How the DEM Resolution Improve the Results
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cruden, D.M.; Varnes, D.J. Landslide Types and Processes, Special Report, Transportation Research Board, National Academy of Sciences. U. S. Geol. Surv. 1996, 247, 36–75. [Google Scholar]
- Guzzetti, F.; Reichenbach, P.; Ghigi, S. Rockfall Hazard and Risk Assessment Along a Transportation Corridor in the Nera Valley, Central Italy. Environ. Manag. 2004, 34, 191–208. [Google Scholar] [CrossRef]
- Schweigl, J.; Ferretti, C.; Nössing, L. Geotechnical Characterization and Rockfall Simulation of a Slope: A Practical Case Study from South Tyrol (Italy). Eng. Geol. 2003, 67, 281–296. [Google Scholar] [CrossRef]
- Gunzburger, Y.; Merrien-Soukatchoff, V.; Guglielmi, Y. Influence of Daily Surface Temperature Fluctuations on Rock Slope Stability: Case Study of the Rochers de Valabres Slope (France). Int. J. Rock Mech. Min. Sci. 2005, 42, 331–349. [Google Scholar] [CrossRef]
- Abellán, A.; Vilaplana, J.M.; Calvet, J.; García-Sellés, D.; Asensio, E. Rockfall Monitoring by Terrestrial Laser Scanning-Case Study of the Basaltic Rock Face at Castellfollit de La Roca (Catalonia, Spain). Nat. Hazards Earth Syst. Sci. 2011, 11, 829–841. [Google Scholar] [CrossRef]
- Sarro, R.; Mateos, R.M.; García-Moreno, I.; Herrera, G.; Reichenbach, P.; Laín, L.; Paredes, C. The Son Poc Rockfall (Mallorca, Spain) on the 6th of March 2013: 3D Simulation. Landslides 2014, 11, 493–503. [Google Scholar] [CrossRef]
- Mateos, R.M.; Azañón, J.M.; Roldán, F.J.; Notti, D.; Pérez-Peña, V.; Galve, J.P.; Pérez-García, J.L.; Colomo, C.M.; Gómez-López, J.M.; Montserrat, O.; et al. The Combined Use of PSInSAR and UAV Photogrammetry Techniques for the Analysis of the Kinematics of a Coastal Landslide Affecting an Urban Area (SE Spain). Landslides 2017, 14, 743–754. [Google Scholar] [CrossRef]
- Dellero, H.; El Kharim, Y. Rockfall Hazard in an Old Abandoned Aggregate Quarry in the City of Tetouan, Morocco. Int. J. Geosci. 2013, 4, 1228–1232. [Google Scholar] [CrossRef]
- Asteriou, P.; Tsiambaos, G. Empirical Model for Predicting Rockfall Trajectory Direction. Rock Mech. Rock Eng. 2016, 49, 927–941. [Google Scholar] [CrossRef]
- Chen, G.; Zheng, L.; Zhang, Y.; Wu, J. Numerical Simulation in Rockfall Analysis: A Close Comparison of 2-D and 3-D DDA. Rock Mech. Rock Eng. 2013, 46, 527–541. [Google Scholar] [CrossRef]
- Glover, J.; Schweizer, A.; Christen, M.; Gerber, W.; Leine, R.; Bartelt, P. Numerical Investigation of the Influence of Rock Shape on Rockfall Trajectory. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; p. 11022. [Google Scholar]
- Tarquini, S.; Vinci, S.; Favalli, M.; Doumaz, F.; Fornaciai, A.; Nannipieri, L. Release of a 10-m-Resolution DEM for the Italian Territory: Comparison with Global-Coverage DEMs and Anaglyph-Mode Exploration via the Web. Comput. Geosci. 2012, 38, 168–170. [Google Scholar] [CrossRef]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and Digital Aerial Photogrammetry Point Clouds for Estimating Forest Structural Attributes in Subtropical Planted Forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; White, J.C. Digital Aerial Photogrammetry for Updating Area-Based Forest Inventories: A Review of Opportunities, Challenges, and Future Directions. Curr. For. Rep. 2019, 5, 55–75. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, C.; Jiang, W. Efficient Structure from Motion for Large-Scale UAV Images: A Review and a Comparison of SfM Tools. ISPRS J. Photogramm. Remote Sens. 2020, 167, 230–251. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Žabota, B.; Repe, B.; Kobal, M. Influence of Digital Elevation Model Resolution on Rockfall Modelling. Geomorphology 2019, 328, 183–195. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B. High Resolution Three-Dimensional Numerical Modelling of Rockfalls. Int. J. Rock Mech. Min. Sci. 2003, 40, 455–471. [Google Scholar] [CrossRef]
- Lan, H.; Martin, C.D.; Zhou, C.; Lim, C.H. Rockfall Hazard Analysis Using LiDAR and Spatial Modeling. Geomorphology 2010, 118, 213–223. [Google Scholar] [CrossRef]
- Bühler, Y.; Christen, M.; Glover, J.; Christen, M.; Bartelt, P. Significance of Digital Elevation Model Resolution for Numerical Rockfall Simulations. In Proceedings of the 3rd International Symposium Rock Slope Stability C2ROP RSS 2016, Lyon, France, 15–17 November 2016; pp. 15–17. [Google Scholar]
- PFEIFFER, T.J.; BOWEN, T.D. Computer Simulation of Rockfalls. Bull. Assoc. Eng. Geol. 1989, 26, 135–146. [Google Scholar] [CrossRef]
- Fisher, R.A. The Correlation between Relatives on the Supposition of Mendelian Inheritance. Earth Environ. Sci. Trans. R. Soc. Edinburgh 1919, 52, 399–433. [Google Scholar] [CrossRef]
- Rammer, W.; Brauner, M.; Dorren, L.K.A.; Berger, F.; Lexer, M.J. Evaluation of a 3-D Rockfall Module within a Forest Patch Model. Nat. Hazards Earth Syst. Sci. 2010, 10, 699–711. [Google Scholar] [CrossRef]
- Žabota, B.; Kobal, M. A New Methodology for Mapping Past Rockfall Events: From Mobile Crowdsourcing to Rockfall Simulation Validation. ISPRS Int. J. Geo-Inf. 2020, 9, 514. [Google Scholar] [CrossRef]
- Lambert, S.; Bourrier, F. Design of Rockfall Protection Embankments: A Review. Eng. Geol. 2013, 154, 77–88. [Google Scholar] [CrossRef]
- Schober, A.; Bannwart, C.; Keuschnig, M. Rockfall Modelling in High Alpine Terrain—Validation and Limitations/Steinschlagsimulation in Hochalpinem Raum—Validierung Und Limitationen. Geomech. Tunn. 2012, 5, 368–378. [Google Scholar] [CrossRef]
- Pellicani, R.; Spilotro, G.; Van Westen, C.J. Rockfall Trajectory Modeling Combined with Heuristic Analysis for Assessing the Rockfall Hazard along the Maratea SS18 Coastal Road (Basilicata, Southern Italy). Landslides 2016, 13, 985–1003. [Google Scholar] [CrossRef]
- Bonneau, D.A.; Hutchinson, D.J.; DiFrancesco, P.-M.; Coombs, M.; Sala, Z. Three-Dimensional Rockfall Shape Back Analysis: Methods and Implications. Nat. Hazards Earth Syst. Sci. 2019, 19, 2745–2765. [Google Scholar] [CrossRef]
- Saroglou, C.; Asteriou, P.; Zekkos, D.; Tsiambaos, G.; Clark, M.; Manousakis, J. UAV-Based Mapping, Back Analysis and Trajectory Modeling of a Coseismic Rockfall in Lefkada Island, Greece. Nat. Hazards Earth Syst. Sci. 2018, 18, 321–333. [Google Scholar] [CrossRef]
- Fallot, P. Essai Sur La Géologie Du Rif Septentrional; Imprimerie officielle: Rabat, Morocco, 1937; 553p.
- Durand-Delga, M.; Hottinger, L.; Marcais, J.; Mattauer, M.; Milliard, Y.; Suter, C. Données Actuelles sur la Structure du Rif. Livre a la Mémoire du Professeur Paul Fallot; Société Géologique de France: Paris, France, 1961; pp. 339–422. [Google Scholar]
- Didon, J.; Durand-Delga, M.; Kornprobst, J. Homologies Géologiques Entre Les Deux Rives Du Détroit de Gibraltar. Bull. Soc. Géologique Fr. 1973, 7, 77–105. [Google Scholar] [CrossRef]
- Nold, M.; Uttinger, J.; Wildi, W. Géologie de La Dorsale Calcaire Entre Tétouan et Assifane (Rif Interne, Maroc). Notes Mémoires Serv. Géologique Maroc 1981, 233, 1–233. [Google Scholar]
- El Gharbaoui, A. Note Preliminaire Sur l’evolution Geomorphologique de La Peninsule de Tanger. Bull. Société Géologique Fr. 1977, 7, 615–622. [Google Scholar] [CrossRef]
- Romagny, A. Evolution des Mouvements Verticaux Néogènes de La Chaîne du Rif (Nord-Maroc): Apports d’une Analyse Structurale et Thermochronologique. Doctoral Dissertation, Université Nice Sophia Antipolis, Nice, France, 2014. [Google Scholar]
- Benmakhlouf, M. Genèse et Évolution de l’accident de Tétouan et Son Rôle Transformant Au Niveau Du Rif Septentrional (Maroc) (Depuis l’oligocène Jusqu’à l’actuel). Ph.D. Thesis, Université Mohammed V, Faculté des Sciences, Rabat, Morocco, 1990. [Google Scholar]
- Mastere, M. La Susceptibilité Aux Mouvements de Terrain Dans La Province de Chefchaouen: Analyse Spatiale, Modélisation Probabiliste Multi-Échelle et Impacts Sur l’aménagement & l’urbanisme. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2011. [Google Scholar]
- El Kharim, Y.; Darraz, C.; Hlila, R.; El Hajjaji, K. Écroulements et Mouvements de Versants Associés Au Niveau Du Col de Onsar (Rif, Maroc) Dans Un Contexte Géologique de Décrochement. Rev. Française Géotechnique 2003, 103, 3–11. [Google Scholar] [CrossRef]
- Romana, M.R. A Geomechanical Classification for Slopes: Slope Mass Rating. In Rock Testing and Site Characterization; Elsevier: Amsterdam, The Netherlands, 1993; pp. 575–600. [Google Scholar] [CrossRef]
- Riquelme, A.; Tomás, R.; Abellán, A. SMRTool Beta. A Calculator for Determining Slope Mass Rating (SMR). Universidad de Alicante. License: Creative Commons BY-NC-SA. 2014. Available online: http://personal.ua.es/es/ariquelme/smrtool.html (accessed on 2 May 2022).
- Romana, M.; Tomás, R.; Serón, J.B. Slope Mass Rating (SMR) Geomechanics Classification: Thirty Years Review. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015; Volume 2015-MAY. [Google Scholar]
- Chen, Z. Recent Developments in Slope Stability Analysis. In Proceedings of the 8th ISRM Congress, Tokyo, Japan, 25–29 September 1995. [Google Scholar]
- Beniawski, Z.T. Rock Mass Classification in Rock Engineering Applications. In Proceedings of the a Symposium on Exploration for Rock Engineering 12, Johannesburg, South Africa, 1–5 November 1976; pp. 97–106. [Google Scholar]
- Goodman, R.E. Introduction to Rock Mechanics; Wiley: New York, NY, USA, 1980; pp. 254–287. [Google Scholar]
- Meng, X.; Shang, N.; Zhang, X.; Li, C.; Zhao, K.; Qiu, X.; Weeks, E. Photogrammetric UAV Mapping of Terrain under Dense Coastal Vegetation: An Object-Oriented Classification Ensemble Algorithm for Classification and Terrain Correction. Remote Sens. 2017, 9, 1187. [Google Scholar] [CrossRef]
- Skarlatos, D.; Vlachos, M. Vegetation Removal from UAV Derived DSMS, Using Combination of RGB and NIR IMAGERY. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Riva del Garda, Italy, 4–7 June 2018; Volume 4. [Google Scholar]
- Prokop, A.; Panholzer, H. Assessing the Capability of Terrestrial Laser Scanning for Monitoring Slow Moving Landslides. Nat. Hazards Earth Syst. Sci. 2009, 9, 1921–1928. [Google Scholar] [CrossRef]
- Blanca Mena, M.J.; Alarcón Postigo, R.; Arnau Gras, J.; Bono Cabré, R.; Bendayan, R. Non-Normal Data: Is ANOVA Still a Valid Option? Psicothema 2017, 29, 552–557. [Google Scholar]
- Dunn, O.J. Multiple Comparisons Using Rank Sums. Technometrics 1964, 6, 241–252. [Google Scholar] [CrossRef]
- Sneed, E.D.; Folk, R.L. Pebbles in the Lower Colorado River, Texas a Study in Particle Morphogenesis. J. Geol. 1958, 66, 114–150. [Google Scholar] [CrossRef]
- Hockey, B. An Improved Co_Ordinate System for Particle Shape Representation: NOTES. J. Sediment. Res. 1970, 40, 1054–1056. [Google Scholar] [CrossRef]
- Perret, S.; Baumgartner, M.; Kienholz, H. Inventory and Analysis of Tree Injuries in a Rockfall-Damaged Forest Stand. Eur. J. For. Res. 2006, 125, 101–110. [Google Scholar] [CrossRef]
- Blair, T.C.; McPherson, J.G. Grain-Size and Textural Classification of Coarse Sedimentary Particles. J. Sediment. Res. 1999, 69, 6–19. [Google Scholar] [CrossRef]
- Wang, I.-T.; Lee, C.-Y. Influence of Slope Shape and Surface Roughness on the Moving Paths of a Single Rockfall. Int. J. Civ. Environ. Eng. 2010, 4, 122–128. [Google Scholar]
- Abramson, L.W.; Lee, T.S.; Sharma, S.; Boyce, G.M. Slope Stability and Stabilization Methods; John Wiley & Sons, INC.: Hoboken, NJ, USA, 2001; Volume 706. [Google Scholar]
- Rosenberg, D.; Shtober-Zisu, N. The Stone Components of the Pits and Pavements. In An Early Pottery Neolithic Occurrence at Beisamoun, the Hula Valley, Northern Israel; BAR International Series: Oxford, UK, 2007; pp. 19–34. [Google Scholar]







| Joints Family * | RMR | α (j) | β (j) | α (s) | β (s) | H (m) | L | E | F1 | F2 | F3 | F1*F2*F3 | CSMR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 40.12 | 225 | 55 | 315 | 50 | 65 | 0.85 | 2.23 | 0.15 | 1 | 0.65 | 0 | 89.5 |
| F2 | 27.32 | 270 | 66 | 315 | 50 | 65 | 1 | 2.23 | 0.22 | 0.98 | 1.19 | −0.25 | 61 |
| F2’ | 27.32 | 90 | 66 | 315 | 50 | 65 | 1 | 2.23 | 0.22 | 1 | −2.15 | −0.47 | 60 |
| F3 | 34.6 | 315 | 54 | 315 | 50 | 65 | 1 | 2.23 | 1 | 0.96 | −4.68 | −4 | 73 |
| F4 | 39.4 | 180 | 65 | 315 | 50 | 65 | 0.9 | 2.23 | 1 | 0.96 | −1.76 | −0.39 | 88 |
| F5’ | 27.1 | 135 | 80 | 315 | 50 | 65 | 1 | 2.23 | 1 | 1 | −25 | -25 | 35 |
| F5 | 27.1 | 315 | 80 | 315 | 50 | 65 | 1 | 2.23 | 1 | 0.99 | −0.64 | −0.63 | 60 |
| F6 | 39.33 | 225 | 85 | 315 | 50 | 65 | 0.8 | 2.23 | 0.15 | 1 | −25.31 | −4 | 85 |
| F7 | 39.3 | 0 | 63 | 315 | 50 | 65 | 1 | 2.23 | 0.22 | 0.97 | −1.47 | −0.31 | 87 |
| Average = | 70 |
| Dependent Variable | Kruskal–Wallis Test | |
|---|---|---|
| H | p-Value | |
| Velocity | 470.035 | <0.001 |
| Energy | 1387.988 | <0.001 |
| Bouncing height | 498.55 | <0.001 |
| Dependent Variable | DEMs | p-Value | Dependent Variable | DEMs | p-Value |
|---|---|---|---|---|---|
| Velocity | 1–2 m | <0.001 | Bouncing height | 1–2 m | <0.001 |
| 1–3 m | <0.001 | 1–3 m | <0.001 | ||
| 1–5 m | <0.001 | 1–5 m | <0.001 | ||
| 1–30 m | 0.002 | 1–30 m | <0.001 | ||
| 2–30 m | <0.001 | 2–3 m | <0.001 | ||
| 2–3 m | 0.237 | 2–5 m | <0.001 | ||
| 2–5 m | <0.001 | 2–30 m | <0.001 | ||
| 3–5 m | <0.001 | 3–5 m | <0.001 | ||
| 3–30 m | <0.001 | 3–30 m | <0.001 | ||
| 5–30 m | <0.001 | 5–30 m | <0.001 | ||
| Energy | 1–2 m | <0.001 | |||
| 1–3 m | <0.001 | ||||
| 1–5 m | <0.001 | ||||
| 1–30 m | <0.001 | ||||
| 2–3 m | <0.001 | ||||
| 2–5 m | <0.001 | ||||
| 2–30 m | <0.001 | ||||
| 3–5 m | <0.001 | ||||
| 3–30 m | <0.001 | ||||
| 5–30 m | <0.001 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bounab, A.; El Kharim, Y.; El Hamdouni, R. The Suitability of UAV-Derived DSMs and the Impact of DEM Resolutions on Rockfall Numerical Simulations: A Case Study of the Bouanane Active Scarp, Tétouan, Northern Morocco. Remote Sens. 2022, 14, 6205. https://doi.org/10.3390/rs14246205
Bounab A, El Kharim Y, El Hamdouni R. The Suitability of UAV-Derived DSMs and the Impact of DEM Resolutions on Rockfall Numerical Simulations: A Case Study of the Bouanane Active Scarp, Tétouan, Northern Morocco. Remote Sensing. 2022; 14(24):6205. https://doi.org/10.3390/rs14246205
Chicago/Turabian StyleBounab, Ali, Younes El Kharim, and Rachid El Hamdouni. 2022. "The Suitability of UAV-Derived DSMs and the Impact of DEM Resolutions on Rockfall Numerical Simulations: A Case Study of the Bouanane Active Scarp, Tétouan, Northern Morocco" Remote Sensing 14, no. 24: 6205. https://doi.org/10.3390/rs14246205
APA StyleBounab, A., El Kharim, Y., & El Hamdouni, R. (2022). The Suitability of UAV-Derived DSMs and the Impact of DEM Resolutions on Rockfall Numerical Simulations: A Case Study of the Bouanane Active Scarp, Tétouan, Northern Morocco. Remote Sensing, 14(24), 6205. https://doi.org/10.3390/rs14246205







