Correcting Underestimation and Overestimation in PolInSAR Forest Canopy Height Estimation Using Microwave Penetration Depth
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. RVoG Coherence Scattering Model
2.3. Baseline Selection Method
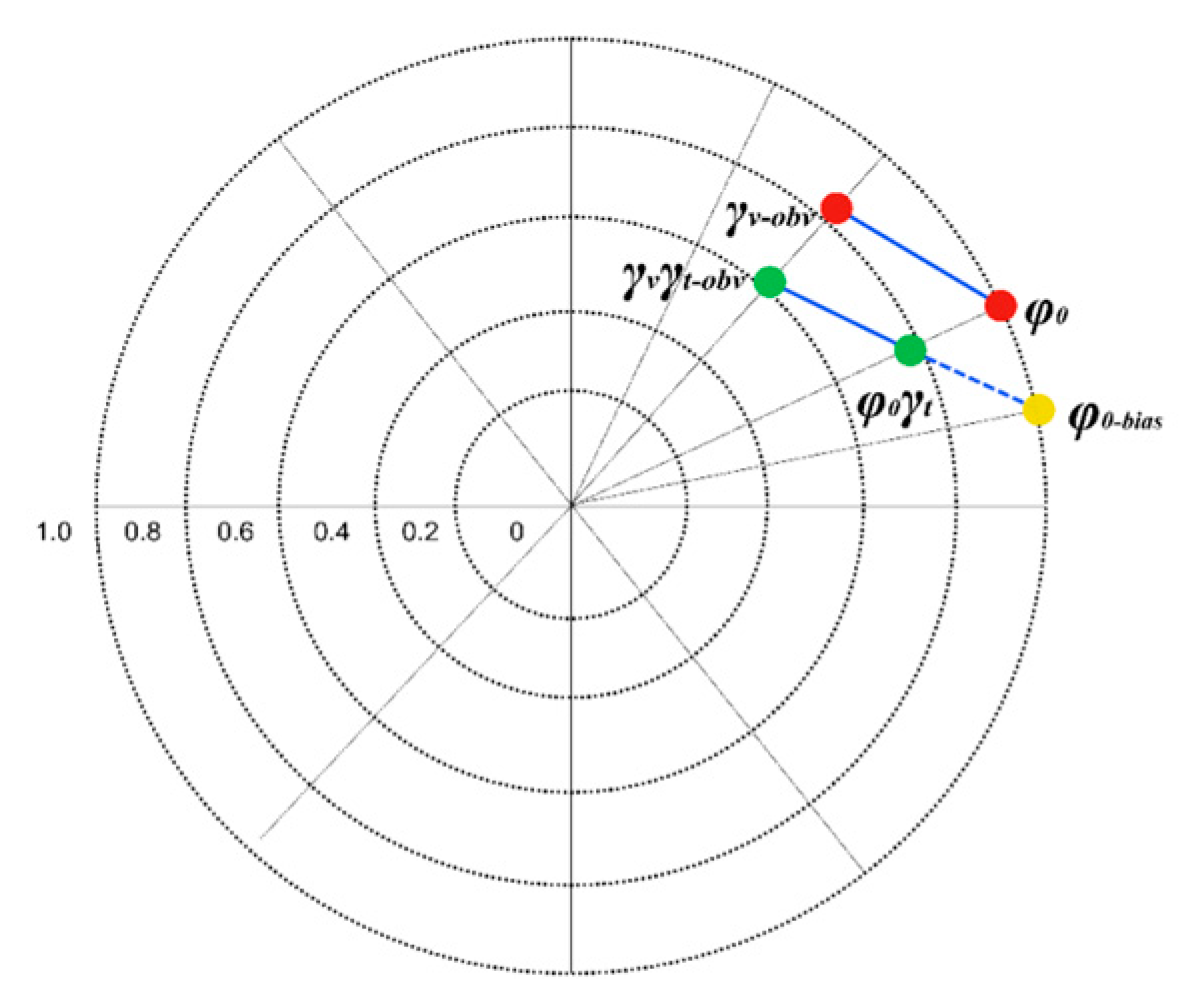
2.4. Error Source Analysis of Underestimation and Overestimation in the RVoG Model
2.4.1. Analysis of the Error Sources of Overestimation for Low Canopy
2.4.2. Analysis of the Error Sources of Underestimation for Tall Canopy
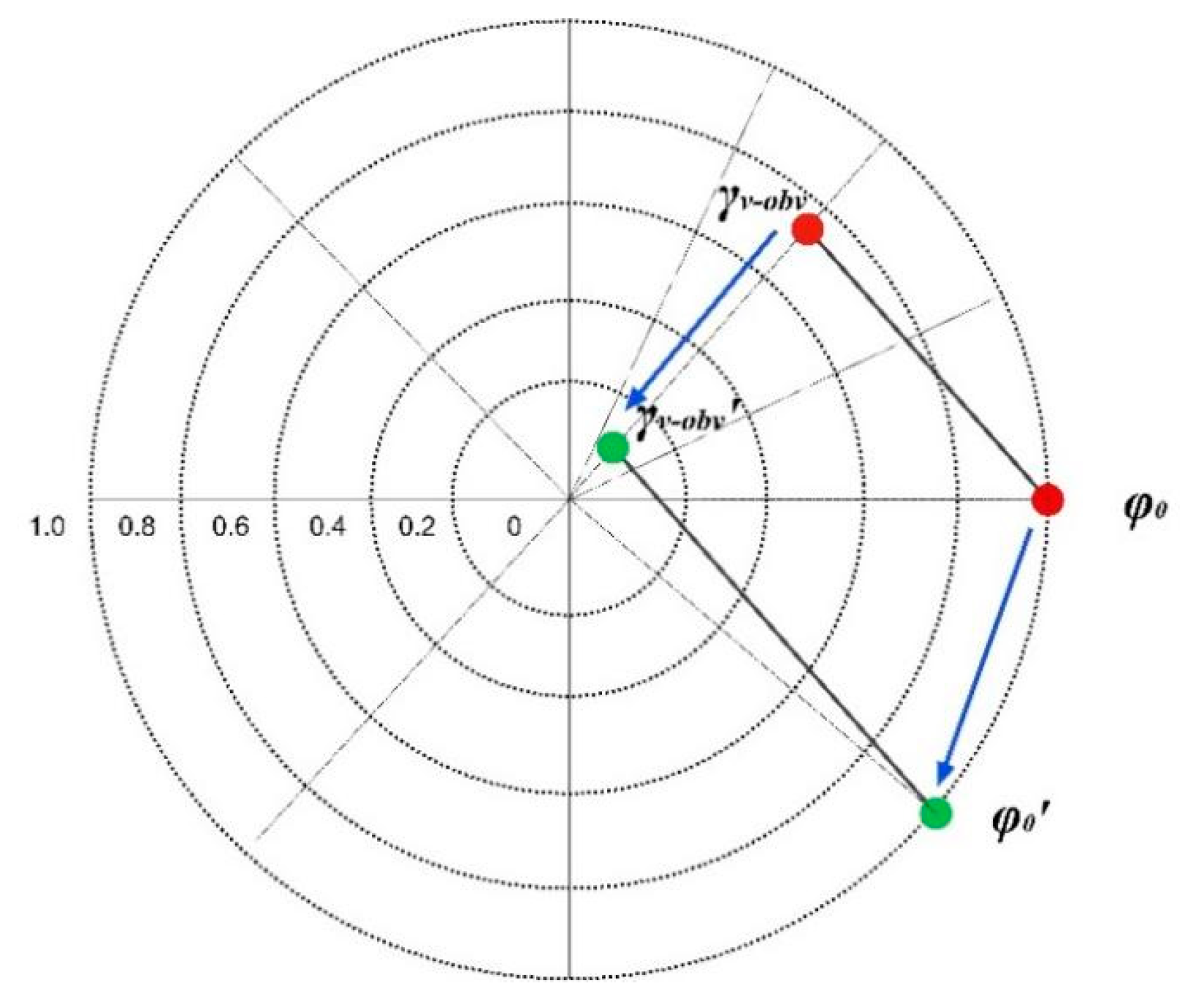
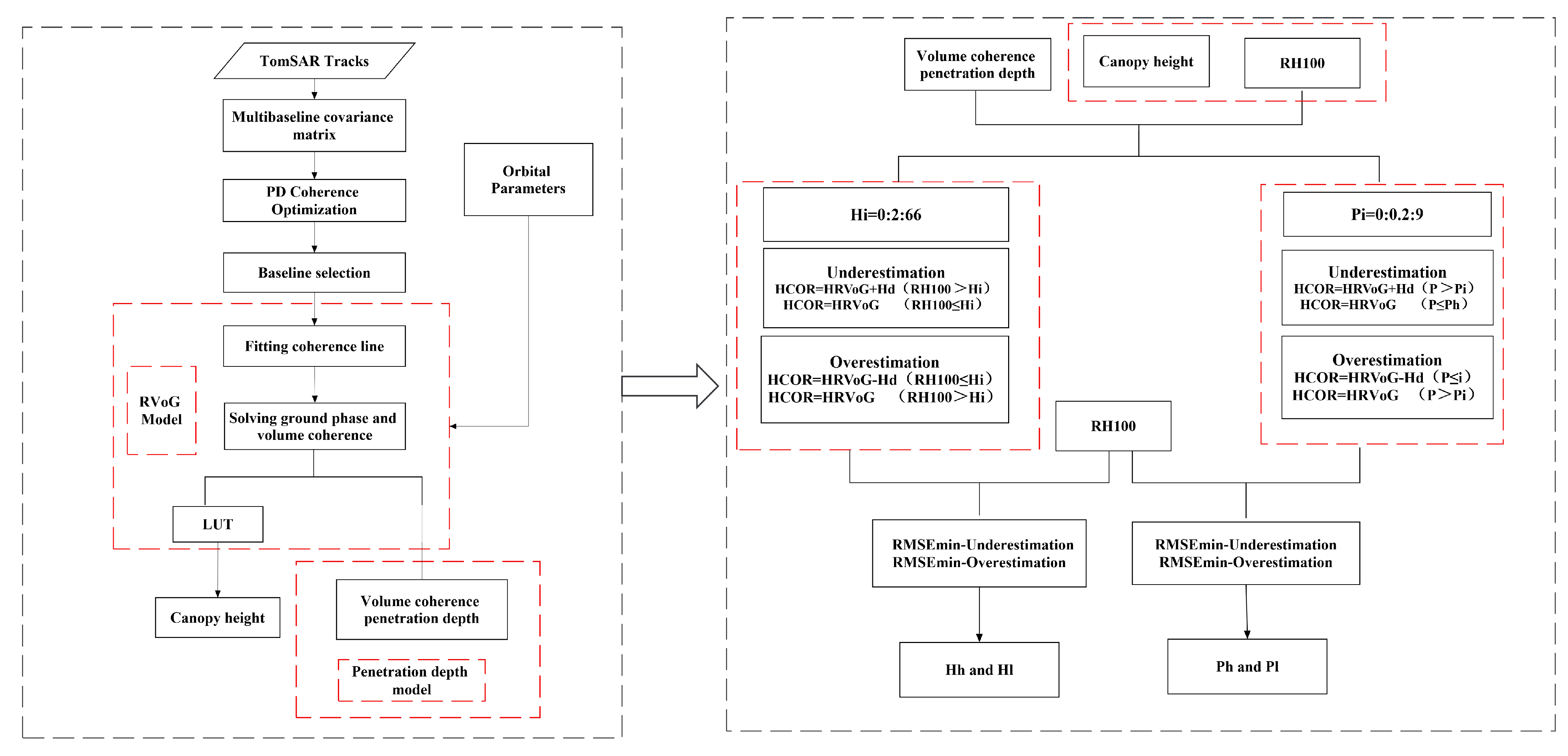
2.5. Error Correction of the RVoG Model Based on Penetration Depth
2.5.1. Method of Underestimation Correction for Tall Canopy Height
2.5.2. Method of Overestimation Correction for Low Canopy Height
2.5.3. Simulation Experiments
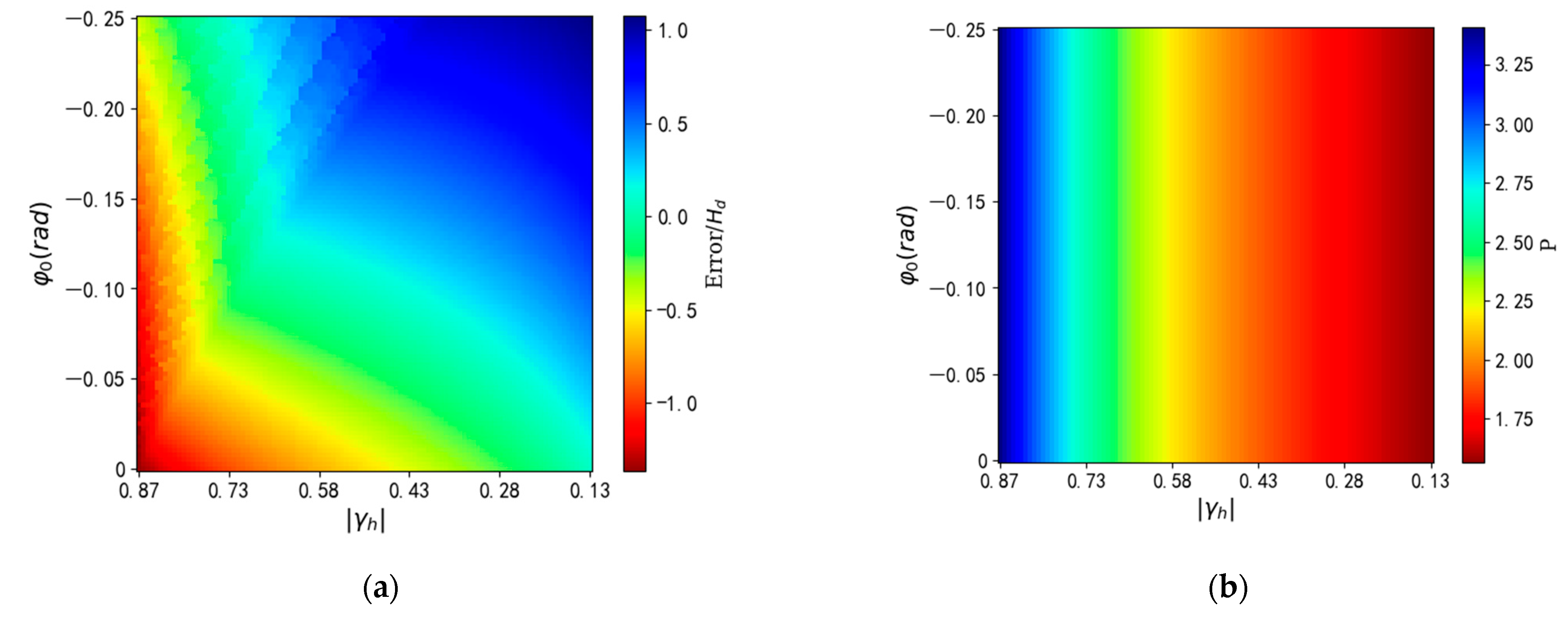
2.6. Determination of Correction Thresholds
2.6.1. Correction Threshold Determination Based on Reference Height (RH100)
2.6.2. Correction Threshold Determination Based on p-Value
2.7. Model Evaluation Indicators
3. Results
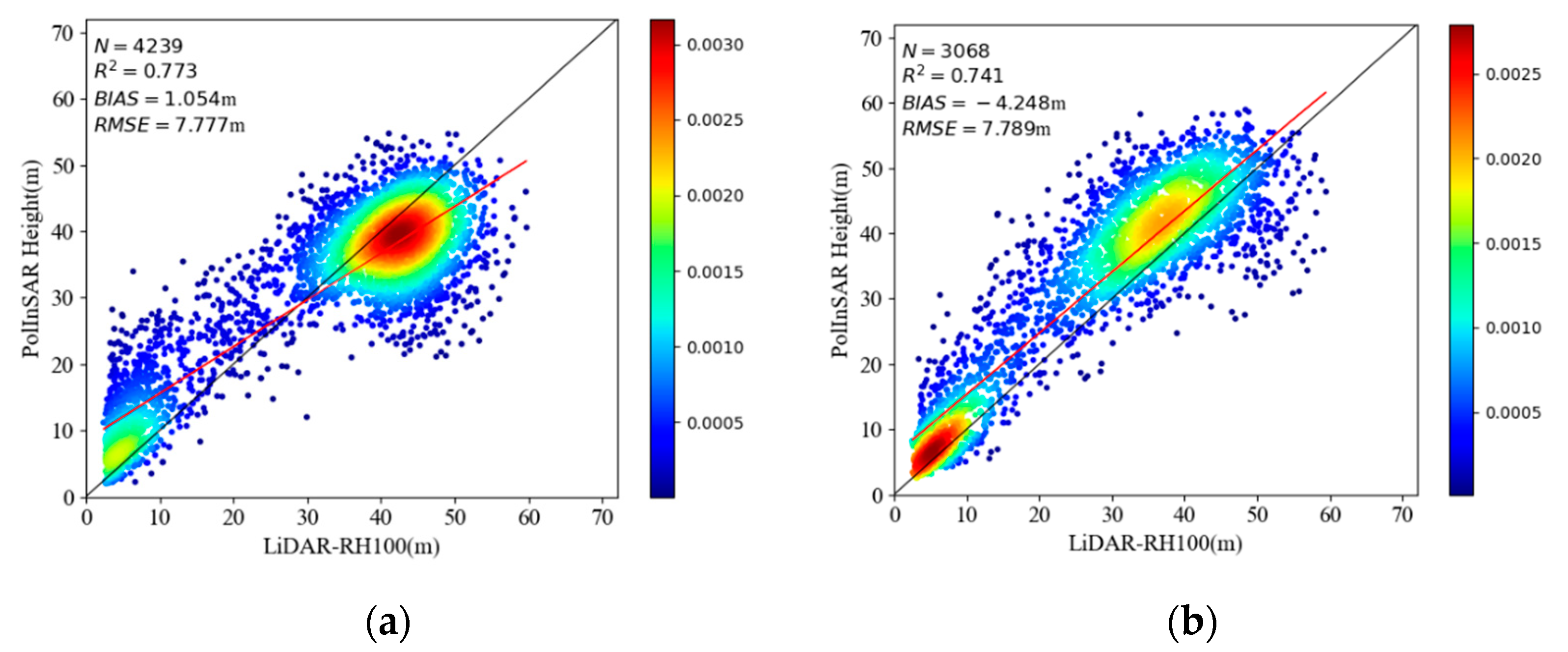
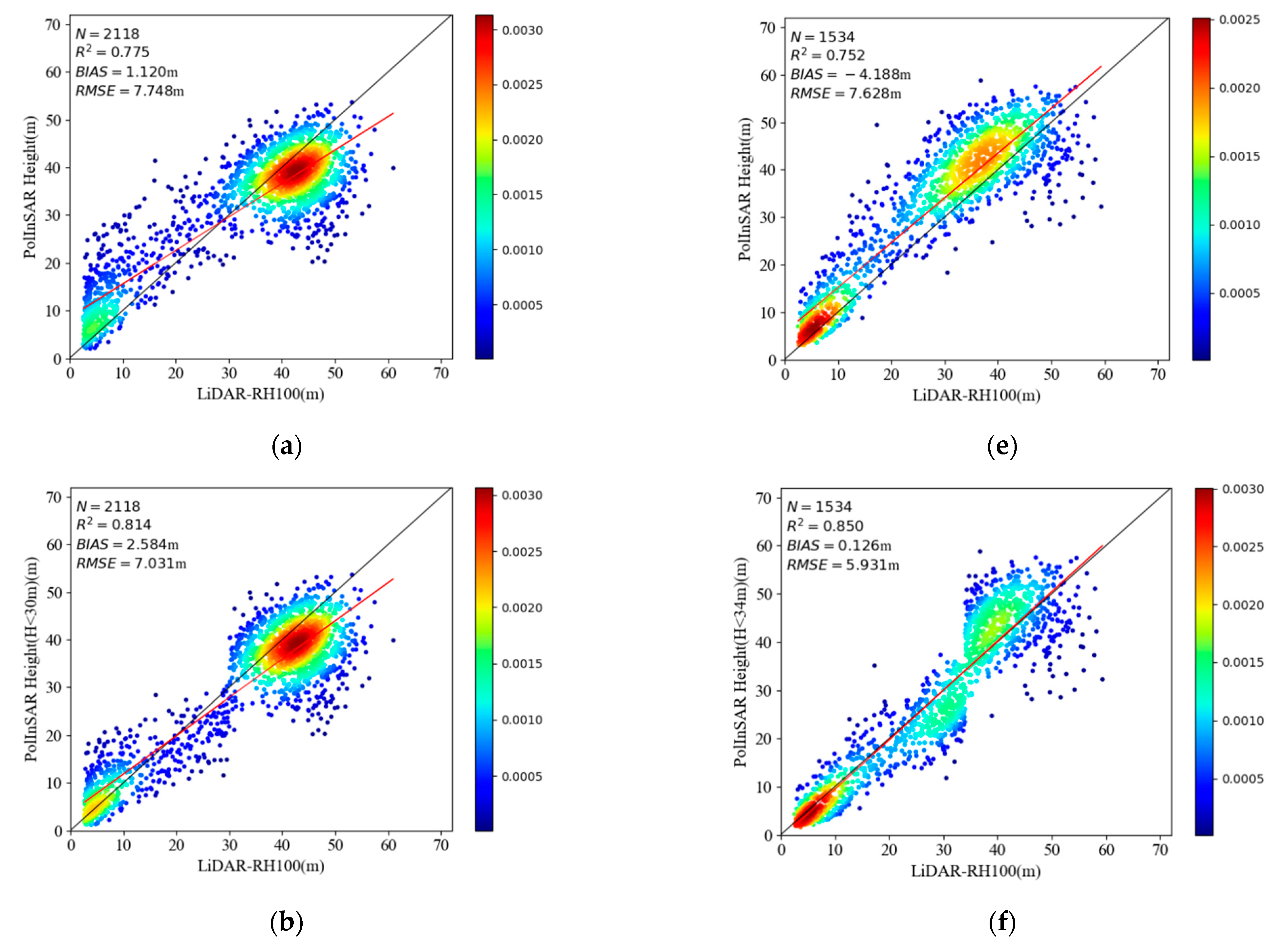
3.1. Error Correction Based on Reference Height (RH100)
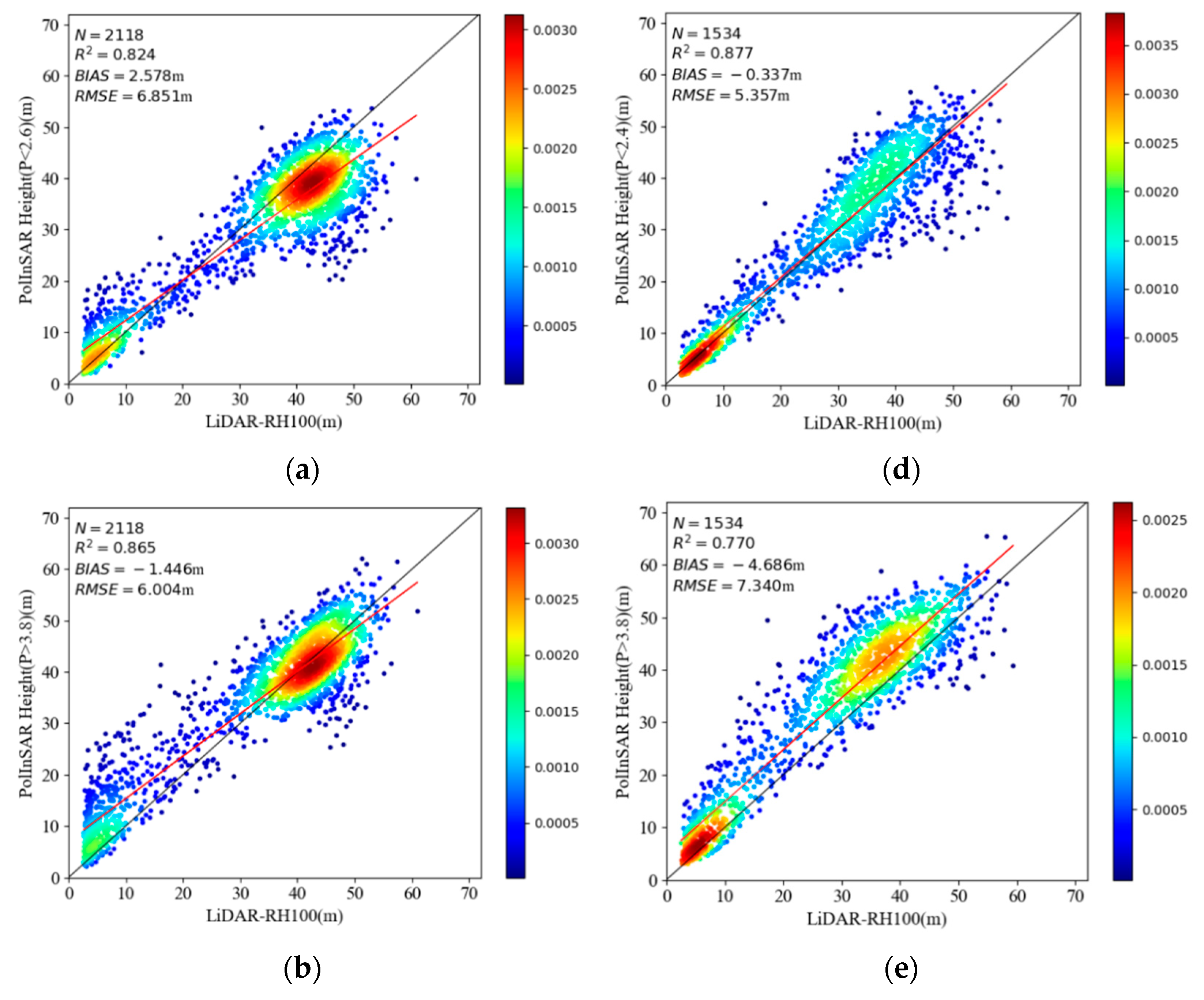
3.2. Error Correction Based on the p-Value
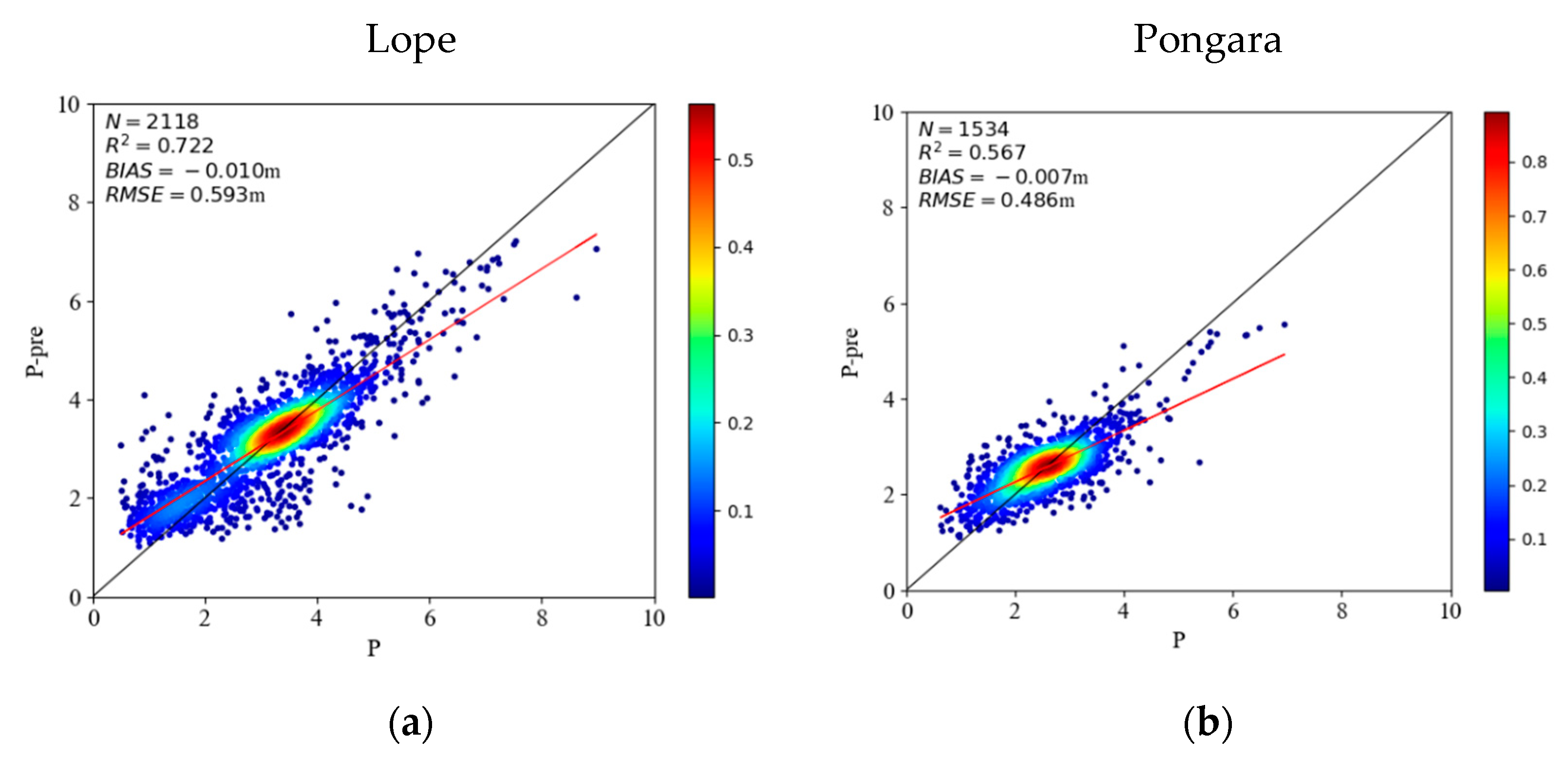
3.3. p-Value Prediction Based on Machine Learning
3.4. Error Correction Based on PRF
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Izzawati, I.H.W.; Wallington, E.D.; Woodhouse, I.H. Forest height retrieval from commercial X-band SAR products. IEEE Trans. Geosci. Remote Sens. 2006, 44, 863–870. [Google Scholar] [CrossRef]
- Laurin, G.V.; Ding, J.; Disney, M.; Bartholomeus, H.; Valentini, R. Tree height in tropical forest as measured by different ground, proximal, and remote sensing instruments, and impacts on above ground biomass estimates. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101899. [Google Scholar]
- Chen, W.; Zhao, J.; Cao, C.X.; Tian, H.J. Shrub biomass estimation in semi-arid sandland ecosystem based on remote sensing technology. Glob. Ecol. Conserv. 2018, 16, e00479. [Google Scholar]
- Ghulam, A.; Porton, I.; Freeman, K. Detecting subcanopy invasive plant species in tropical rainforest by integrating optical and microwave (InSAR/PolInSAR) remote sensing data, and a decision tree algorithm. ISPRS J. Photogramm. Remote Sens. 2014, 88, 174–192. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, Q.; Xiang, H.; Chen, X.; Sakai, T. Forest Canopy Height Estimation Using Polarimetric Interferometric Synthetic Aperture Radar (PolInSAR) Technology Based on Full-Polarized ALOS/PALSAR Data. Remote Sens. 2021, 13, 174. [Google Scholar] [CrossRef]
- Zhang, L.; Duan, B.; Zou, B. Research on Inversion Models for Forest Height Estimation Using Polarimetric SAR Interferometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 659–663. [Google Scholar] [CrossRef] [Green Version]
- Garestier, F.; Le Toan, T. Forest modeling for height inversion using single-baseline InSAR/Pol-InSAR data. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1528–1539. [Google Scholar]
- Kumar, S.; Govil, H.; Srivastava, P.K.; Thakur, P.K.; Kushwaha, S.P. Spaceborne multifrequency PolInSAR-based inversion modelling for forest height retrieval. Remote Sens. 2020, 12, 4042. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Fu, H.; Xie, Q.; Zhu, J. The impact of forest density on forest height inversion modeling from polarimetric InSAR data. Remote Sens. 2019, 8, 291. [Google Scholar] [CrossRef] [Green Version]
- Schlund, M.; Baron, D.; Magdon, P.; Erasmi, S. Canopy penetration depth estimation with TanDEM-X and its compensation in temperate forests. ISPRS J. Photogramm. Remote Sens. 2019, 147, 232–241. [Google Scholar] [CrossRef]
- Qi, W.; Lee, S.K.; Hancock, S.; Luthcke, S.; Tang, H.; Armston, J.; Dubayah, R. Improved forest height estimation by fusion of simulated GEDI Lidar data and TanDEM-X InSAR data. Remote Sens. Environ. 2019, 221, 621–634. [Google Scholar] [CrossRef] [Green Version]
- Hajnsek, I.; Kugler, F.; Lee, S.K. Tropical-forest-parameter estimation by means of Pol-InSAR: The INDREX-II campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar]
- Praks, J.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I.; Hallikainen, M. Height estimation of boreal forest: Interferometric model-based inversion at L-and X-band versus HUTSCAT profiling scatterometer. IEEE Geosci. Remote Sens. 2007, 4, 466–470. [Google Scholar] [CrossRef]
- Liao, Z.; He, B.; Quan, X.; van Dijk, A.I.; Qiu, S.; Yin, C. Biomass estimation in dense tropical forest using multiple information from single-baseline P-band PolInSAR data. Remote Sens. Environ. 2018, 221, 489–507. [Google Scholar]
- Treuhaft, R.N.; Moghaddam, M.; van Zyl, J.J. Vegetation characteristics and underlying topography from interferometric radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Liao, Z.; He, B.; van Dijk, A.I.; Bai, X.; Quan, X. The impacts of spatial baseline on forest canopy height model and digital terrain model retrieval using P-band PolInSAR data. Remote Sens. Environ. 2018, 210, 403–421. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for polarimetric SAR interferometry. IEE Proc.-Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Mette, T.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Forest and the random volume over ground—Nature and effect of 3 possible error types. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), VDE Verlag GmbH, Dresden, Germany, 16–18 May 2006. [Google Scholar]
- Lee, S.-K.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I. Quantifying temporal decorrelation over boreal forest at L-and P-band. In Proceedings of the 7th European Conference on. VDE, Friedrichshafen, Germany, 2–5 June 2008. [Google Scholar]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.; Moreira, A. Forest height estimation by means of Pol-InSAR limitations posed by temporal decorrelation. In Proceedings of the 11th ALOS Kyoto & Carbon Initiative, Tsukuba, Japan, 28 December 2009. [Google Scholar]
- Lee, S.K.; Kugler, F.; Hajnsek, I.; Papathanassiou, K. The impact of temporal decorrelation over forest terrain in polarimetric SAR interferometry. In Proceedings of the International Workshop on Applications of Polarimetry and Polarimetric Interferometry (Pol-InSAR). ESA, Frascati, Italy, 26–30 January 2009. [Google Scholar]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Multibaseline polarimetric SAR interferometry forest height inversion approaches. In Proceedings of the ESA POLinSAR Workshop, Frascati, Italy, 24–28 January 2011. [Google Scholar]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Quantification and compensation of temporal decorrelation effects in polarimetric SAR interferometry. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Solberg, S.; Astrup, R.; Weydahl, D.J. Detection of forest clear-cuts with shuttle radar topography mission (SRTM) and TanDEM-X InSAR data. Remote Sens. 2013, 5, 5449–5462. [Google Scholar] [CrossRef] [Green Version]
- Tanase, M.A.; Ismail, I.; Lowell, K.; Karyanto, O.; Santoro, M. Detecting and quantifying forest change: The potential of existing C- and X-band radar datasets. PLoS ONE 2015, 10, e0131079. [Google Scholar]
- Schlund, M.; von Poncet, F.; Hoekman, D.H.; Kuntz, S.; Schmullius, C. Importance of bistatic SAR features from TanDEM-X for forest mapping and monitoring. Remote Sens. Environ. 2014, 151, 16–26. [Google Scholar] [CrossRef]
- Weydahl, D.J.; Sagstuen, J.; Dick, O.B.; Ronning, H. SRTM DEM accuracy assessment over vegetated areas in Norway. Int. J. Remote Sens. 2007, 28, 3513–3527. [Google Scholar] [CrossRef]
- Treuhaft, R.; Goncalves, F.; dos Santos, J.; Keller, M.; Palace, M.; Madsen, S.; Sullivan, F.; Graca, P. Tropical-forest biomass estimation at X-band from the spaceborne TanDEM-X interferometer. IEEE Geosci. Remote Sens. Lett. 2015, 12, 239–243. [Google Scholar] [CrossRef] [Green Version]
- Kugler, F.; Schulze, D.; Hajnsek, I.; Pretzsch, H.; Papathanassiou, K. TanDEM-X Pol-InSAR performance for forest height estimation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6404–6422. [Google Scholar] [CrossRef]
- Varekamp, C.; Hoekman, D.H. High-resolution InSAR image simulation for forest canopies. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1648–1655. [Google Scholar]
- Dall, J. InSAR elevation bias caused by penetration into uniform volumes. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2319–2324. [Google Scholar] [CrossRef] [Green Version]
- Fore, A.G.; Chapman, B.D.; Hawkins, B.P.; Hensley, S.; Jones, C.E.; Michel, T.R.; Muellerschoen, R.J. UAVSAR polarimetric calibration. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3481–3491. [Google Scholar] [CrossRef]
- Armston, J.; Tang, H.; Hancock, S.; Marselis, S.; Duncanson, L.; Kellner, J.; Hofton, M.; Blair, J.B.; Fatoyinbo, T.; Dubayah, R.O. AfriSAR: Gridded Forest Biomass and Canopy Metrics Derived from LVIS, Gabon, 2016; ORNL DAAC: Oak Ridge, TN, USA, 2020. [Google Scholar] [CrossRef]
- Papathanassiou, K.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens 2001, 39, 2352–2363. [Google Scholar] [CrossRef] [Green Version]
- Kugler, F.; Lee, S.K.; Hajnsek, I.; Papathanassiou, K.P. Forest height estimation by means of Pol-InSAR data inversion: The role of the vertical wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Denbina, M.; Simard, M. Kapok: An open source Python library for PolInSAR forest height estimation using UAVSAR data. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017.
- Luo, H.B.; Zhu, B.D.; Yue, C.R.; Wang, N. Forest Canopy Height Inversion Based On Airborne Multi-Baseline PolInSAR. J. Geomat. 2022, 48, 1–7. [Google Scholar]
- Papathanassiou, K.P.; Cloude, S.R. The effect of temporal decorrelation on the inversion of forest parameters from Pol-InSAR data. In Proceedings of the International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003. [Google Scholar]
- Lavalle, M.; Simard, M.; Hensley, S. A temporal decorrelation model for polarimetric radar interferometers. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2880–2888. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Purohit, S.; Aggarwal, S.P.; Patel, N.R. Estimation of forest aboveground biomass using combination of Landsat 8 and Sentinel-1A data with random forest regression algorithm in Himalayan Foothills. Trop. Ecol. 2021, 62, 288–300. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X. Constructing a Finer-Resolution Forest Height in China Using ICESat/GLAS, Landsat and ALOS PALSAR Data and Height Patterns of Natural Forests and Plantations. Remote Sens. 2019, 11, 1740. [Google Scholar]
- Simard, M.; Denbina, M. An assessment of temporal decorrelation compensation methods for forest canopy height estimation using airborne L-band same-day repeat-pass polarimetric SAR interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 95–111. [Google Scholar] [CrossRef]
- Zhang, B.; Fu, H.; Zhu, J.; Peng, X.; Lin, D.; Xie, Q.; Hu, J. Forest Height Estimation Using Multi Baseline Low-Frequency PolInSAR Data Affected by Temporal Decorrelation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4009405. [Google Scholar]
- Fatoyinbo, T.; Armston, J.; Simard, M.; Saatchi, S.; Denbina, M.; Lavalle, M.; Hofton, M.; Tang, H.; Marselis, S.; Pinto, N.; et al. The NASA AfriSAR Campaign: Airborne SAR and Lidar Measurements of Tropical Forest Structure and Biomass in Support of Current and Future Space Missions. Remote Sens. Environ. 2021, 264, 112533. [Google Scholar]
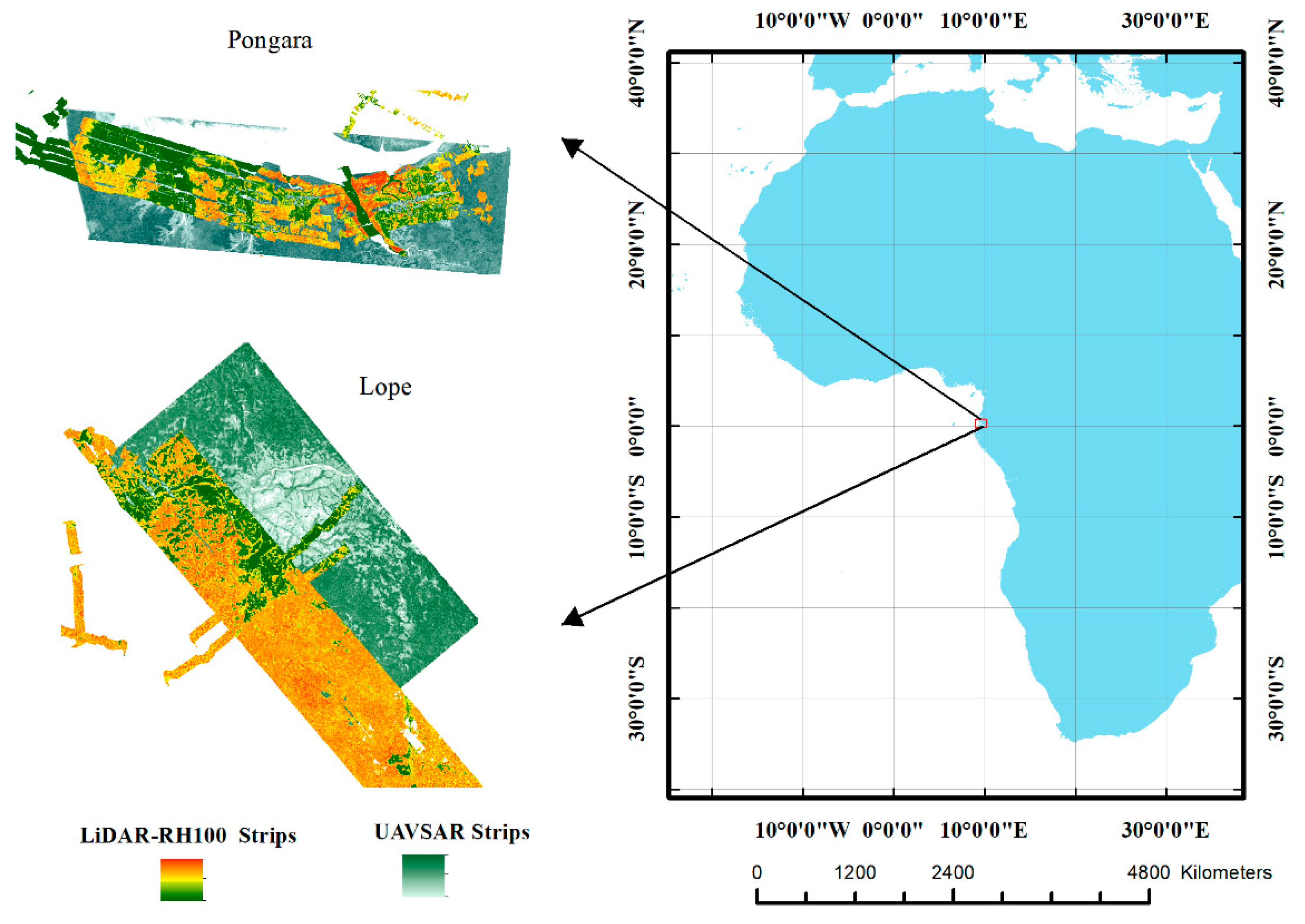





| Test Area | Type of Forest | Forest Height Information (m) | ||
|---|---|---|---|---|
| Max Height | Min Height | Average Height | ||
| Lope | Inland tropical forest | 84.28 | 1.94 | 36.94 |
| Pongara | Mangrove forest | 65.11 | 1.80 | 20.71 |
| Test Area | Number of Tracks | Vertical Baseline (m) | Range Resolution (m) | Azimuth Resolution (m) |
|---|---|---|---|---|
| Lope | 8 | 0, 20, 45, 105 | 3.33 | 4.8 |
| Pongara | 5 | 0, 20, 40, 60, 80, 100, 120 | 3.33 | 4.8 |
| Lope | Pongara | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hi (m) | RMSE (m) | R2 | RMSE (m) | R2 | Hi (m) | RMSE (m) | R2 | RMSE (m) | R2 |
| 0.000 | 11.763 | 0.481 | 7.777 | 0.773 | 0.000 | 17.519 | −0.310 | 7.789 | 0.741 |
| 2.000 | 11.763 | 0.481 | 7.777 | 0.773 | 2.000 | 17.519 | −0.310 | 7.789 | 0.741 |
| 4.000 | 11.632 | 0.493 | 7.658 | 0.780 | 4.000 | 17.482 | −0.304 | 7.749 | 0.744 |
| 6.000 | 11.465 | 0.507 | 7.511 | 0.788 | 6.000 | 17.406 | −0.293 | 7.681 | 0.748 |
| 8.000 | 11.330 | 0.519 | 7.399 | 0.795 | 8.000 | 17.321 | −0.280 | 7.602 | 0.753 |
| 10.000 | 11.207 | 0.529 | 7.299 | 0.800 | 10.000 | 17.248 | −0.270 | 7.552 | 0.757 |
| 12.000 | 11.131 | 0.535 | 7.247 | 0.803 | 12.000 | 17.184 | −0.260 | 7.501 | 0.760 |
| 14.000 | 11.081 | 0.540 | 7.216 | 0.805 | 14.000 | 17.091 | −0.247 | 7.422 | 0.765 |
| 16.000 | 11.032 | 0.544 | 7.193 | 0.806 | 16.000 | 16.969 | −0.229 | 7.303 | 0.772 |
| 18.000 | 10.953 | 0.550 | 7.151 | 0.808 | 18.000 | 16.852 | −0.212 | 7.212 | 0.778 |
| 20.000 | 10.879 | 0.556 | 7.123 | 0.810 | 20.000 | 16.731 | −0.195 | 7.102 | 0.785 |
| 22.000 | 10.814 | 0.561 | 7.107 | 0.811 | 22.000 | 16.576 | −0.173 | 6.977 | 0.792 |
| 24.000 | 10.737 | 0.568 | 7.088 | 0.812 | 24.000 | 16.408 | −0.149 | 6.878 | 0.798 |
| 26.000 | 10.659 | 0.574 | 7.077 | 0.812 | 26.000 | 16.130 | −0.110 | 6.695 | 0.809 |
| 28.000 | 10.564 | 0.582 | 7.063 | 0.813 | 28.000 | 15.763 | −0.061 | 6.481 | 0.821 |
| 30.000 | 10.378 | 0.596 | 7.056 | 0.813 | 30.000 | 15.338 | −0.004 | 6.289 | 0.831 |
| 32.000 | 10.121 | 0.616 | 7.066 | 0.813 | 32.000 | 14.522 | 0.100 | 5.986 | 0.847 |
| 34.000 | 9.824 | 0.638 | 7.114 | 0.810 | 34.000 | 13.709 | 0.198 | 5.839 | 0.854 |
| 36.000 | 9.427 | 0.667 | 7.239 | 0.804 | 36.000 | 12.866 | 0.293 | 5.909 | 0.851 |
| 38.000 | 8.957 | 0.699 | 7.590 | 0.784 | 38.000 | 11.912 | 0.394 | 6.061 | 0.843 |
| 40.000 | 8.380 | 0.737 | 8.255 | 0.744 | 40.000 | 10.841 | 0.498 | 6.386 | 0.826 |
| 42.000 | 7.691 | 0.778 | 9.332 | 0.673 | 42.000 | 9.991 | 0.574 | 6.746 | 0.806 |
| 44.000 | 7.121 | 0.810 | 10.669 | 0.573 | 44.000 | 9.181 | 0.640 | 7.203 | 0.779 |
| 46.000 | 6.995 | 0.817 | 11.873 | 0.471 | 46.000 | 8.613 | 0.683 | 7.613 | 0.753 |
| 48.000 | 7.225 | 0.804 | 13.009 | 0.365 | 48.000 | 8.236 | 0.710 | 8.049 | 0.723 |
| 50.000 | 7.420 | 0.794 | 13.625 | 0.304 | 50.000 | 7.843 | 0.737 | 8.495 | 0.692 |
| 52.000 | 7.562 | 0.786 | 13.954 | 0.270 | 52.000 | 7.760 | 0.743 | 8.910 | 0.661 |
| 54.000 | 7.667 | 0.780 | 14.118 | 0.253 | 54.000 | 7.743 | 0.744 | 9.102 | 0.646 |
| 56.000 | 7.729 | 0.776 | 14.196 | 0.244 | 56.000 | 7.748 | 0.744 | 9.265 | 0.634 |
| 58.000 | 7.763 | 0.774 | 14.233 | 0.240 | 58.000 | 7.773 | 0.742 | 9.339 | 0.628 |
| 60.000 | 7.777 | 0.773 | 14.252 | 0.238 | 60.000 | 7.789 | 0.741 | 9.385 | 0.624 |
| 62.000 | 7.777 | 0.773 | 14.252 | 0.238 | 62.000 | 7.789 | 0.741 | 9.385 | 0.624 |
| 64.000 | 7.777 | 0.773 | 14.252 | 0.238 | 64.000 | 7.789 | 0.741 | 9.385 | 0.624 |
| 66.000 | 7.777 | 0.773 | 14.252 | 0.238 | 66.000 | 7.789 | 0.741 | 9.385 | 0.624 |
| Lope | Pongara | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Pi | RMSE (m) | R2 | RMSE (m) | R2 | P | RMSE (m) | R2 | RMSE (m) | R2 |
| 0.000 | 11.763 | 0.481 | 7.777 | 0.773 | 0.000 | 17.519 | −0.310 | 7.789 | 0.741 |
| 0.200 | 11.763 | 0.481 | 7.777 | 0.773 | 0.200 | 17.519 | −0.310 | 7.789 | 0.741 |
| 0.400 | 11.763 | 0.481 | 7.777 | 0.773 | 0.400 | 17.519 | −0.310 | 7.789 | 0.741 |
| 0.600 | 11.726 | 0.484 | 7.741 | 0.775 | 0.600 | 17.516 | −0.309 | 7.785 | 0.741 |
| 0.800 | 11.670 | 0.489 | 7.683 | 0.779 | 0.800 | 17.477 | −0.304 | 7.733 | 0.745 |
| 1.000 | 11.584 | 0.497 | 7.600 | 0.783 | 1.000 | 17.440 | −0.298 | 7.684 | 0.748 |
| 1.200 | 11.465 | 0.507 | 7.491 | 0.790 | 1.200 | 17.313 | −0.279 | 7.541 | 0.757 |
| 1.400 | 11.320 | 0.520 | 7.365 | 0.797 | 1.400 | 17.091 | −0.247 | 7.305 | 0.772 |
| 1.600 | 11.191 | 0.530 | 7.260 | 0.802 | 1.600 | 16.767 | −0.200 | 6.991 | 0.791 |
| 1.800 | 11.097 | 0.538 | 7.191 | 0.806 | 1.800 | 16.258 | −0.128 | 6.627 | 0.813 |
| 2.000 | 10.979 | 0.548 | 7.123 | 0.810 | 2.000 | 15.463 | −0.020 | 6.134 | 0.839 |
| 2.200 | 10.736 | 0.568 | 7.010 | 0.816 | 2.200 | 14.381 | 0.117 | 5.631 | 0.865 |
| 2.400 | 10.442 | 0.591 | 6.914 | 0.821 | 2.400 | 13.024 | 0.276 | 5.308 | 0.880 |
| 2.600 | 9.955 | 0.628 | 6.877 | 0.823 | 2.600 | 11.718 | 0.414 | 5.339 | 0.878 |
| 2.800 | 9.305 | 0.675 | 7.040 | 0.814 | 2.800 | 10.042 | 0.570 | 5.750 | 0.859 |
| 3.000 | 8.423 | 0.734 | 7.438 | 0.793 | 3.000 | 8.852 | 0.666 | 6.504 | 0.819 |
| 3.200 | 7.481 | 0.790 | 8.116 | 0.753 | 3.200 | 8.048 | 0.724 | 7.306 | 0.772 |
| 3.400 | 6.623 | 0.836 | 9.152 | 0.686 | 3.400 | 7.693 | 0.747 | 7.838 | 0.738 |
| 3.600 | 6.126 | 0.859 | 10.268 | 0.605 | 3.600 | 7.562 | 0.756 | 8.302 | 0.706 |
| 3.800 | 5.996 | 0.865 | 11.257 | 0.525 | 3.800 | 7.531 | 0.758 | 8.598 | 0.684 |
| 4.000 | 6.128 | 0.859 | 12.031 | 0.457 | 4.000 | 7.539 | 0.757 | 8.842 | 0.666 |
| 4.200 | 6.378 | 0.847 | 12.603 | 0.404 | 4.200 | 7.572 | 0.755 | 8.983 | 0.656 |
| 4.400 | 6.625 | 0.835 | 13.011 | 0.365 | 4.400 | 7.598 | 0.754 | 9.064 | 0.649 |
| 4.600 | 6.837 | 0.825 | 13.306 | 0.336 | 4.600 | 7.638 | 0.751 | 9.156 | 0.642 |
| 4.800 | 7.055 | 0.813 | 13.572 | 0.309 | 4.800 | 7.653 | 0.750 | 9.185 | 0.640 |
| 5.000 | 7.188 | 0.806 | 13.730 | 0.293 | 5.000 | 7.675 | 0.749 | 9.225 | 0.637 |
| 5.200 | 7.304 | 0.800 | 13.854 | 0.280 | 5.200 | 7.695 | 0.747 | 9.257 | 0.634 |
| 5.400 | 7.403 | 0.794 | 13.947 | 0.271 | 5.400 | 7.724 | 0.745 | 9.298 | 0.631 |
| 5.600 | 7.489 | 0.790 | 14.023 | 0.263 | 5.600 | 7.743 | 0.744 | 9.326 | 0.629 |
| 5.800 | 7.541 | 0.787 | 14.069 | 0.258 | 5.800 | 7.757 | 0.743 | 9.346 | 0.627 |
| 6.000 | 7.575 | 0.785 | 14.099 | 0.255 | 6.000 | 7.763 | 0.743 | 9.353 | 0.627 |
| 6.200 | 7.602 | 0.783 | 14.121 | 0.252 | 6.200 | 7.776 | 0.742 | 9.369 | 0.625 |
| 6.400 | 7.633 | 0.782 | 14.145 | 0.250 | 6.400 | 7.783 | 0.741 | 9.377 | 0.625 |
| 6.600 | 7.658 | 0.780 | 14.164 | 0.248 | 6.600 | 7.783 | 0.741 | 9.377 | 0.625 |
| 6.800 | 7.685 | 0.779 | 14.185 | 0.246 | 6.800 | 7.789 | 0.741 | 9.385 | 0.624 |
| 7.000 | 7.718 | 0.777 | 14.210 | 0.243 | 7.000 | 7.789 | 0.741 | 9.385 | 0.624 |
| 7.200 | 7.727 | 0.776 | 14.217 | 0.242 | 7.200 | 7.789 | 0.741 | 9.385 | 0.624 |
| 7.400 | 7.727 | 0.776 | 14.217 | 0.242 | 7.400 | 7.789 | 0.741 | 9.385 | 0.624 |
| 7.600 | 7.735 | 0.776 | 14.223 | 0.242 | 7.600 | 7.789 | 0.741 | 9.385 | 0.624 |
| 7.800 | 7.754 | 0.775 | 14.236 | 0.240 | 7.800 | 7.789 | 0.741 | 9.385 | 0.624 |
| 8.000 | 7.765 | 0.774 | 14.243 | 0.239 | 8.000 | 7.789 | 0.741 | 9.385 | 0.624 |
| 8.200 | 7.773 | 0.773 | 14.249 | 0.239 | |||||
| 8.400 | 7.777 | 0.773 | 14.252 | 0.238 | |||||
| 8.600 | 7.777 | 0.773 | 14.252 | 0.238 | |||||
| 8.800 | 7.777 | 0.773 | 14.252 | 0.238 | |||||
| 9.000 | 7.777 | 0.773 | 14.252 | 0.238 | |||||
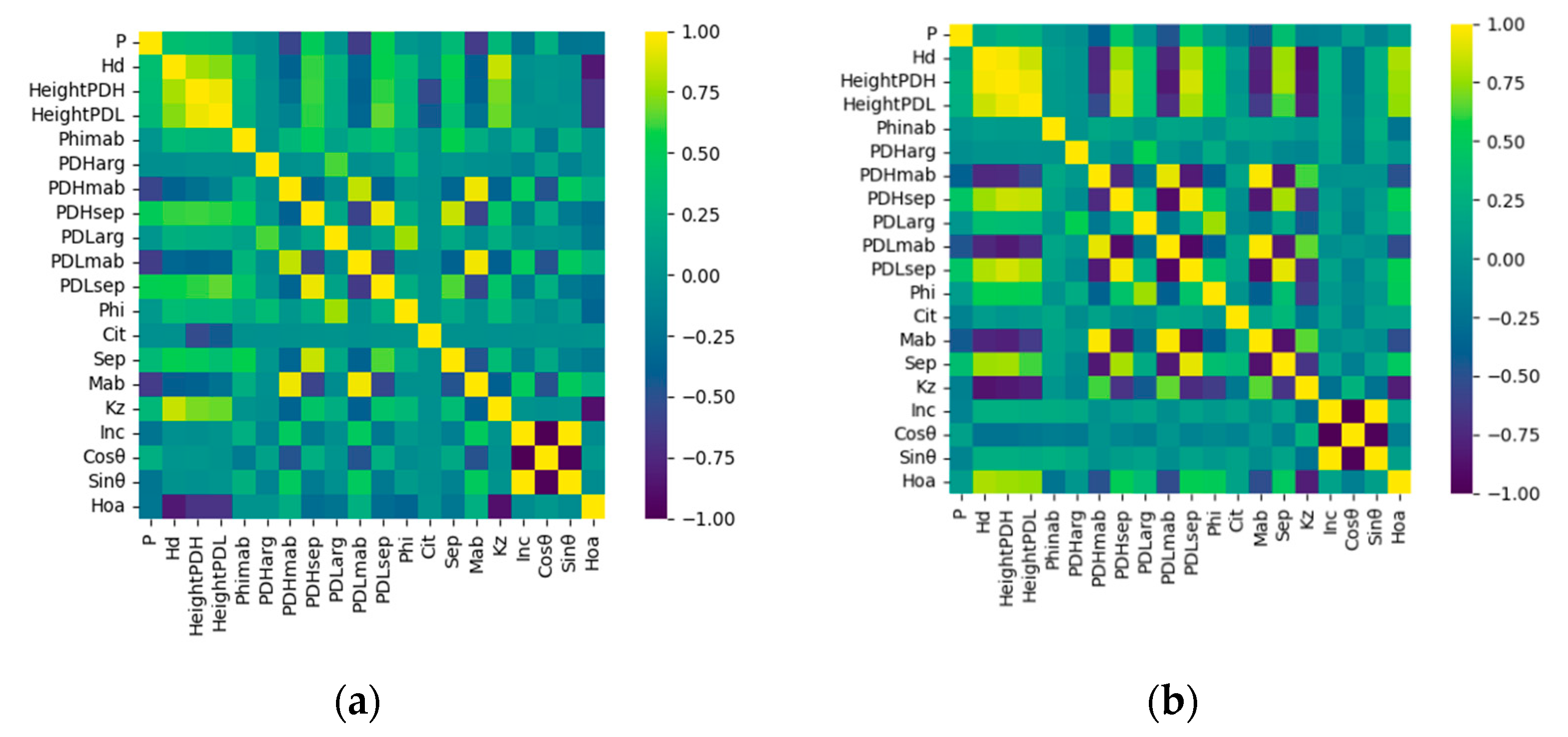
| Variable Type | Name | Description | Expressions |
|---|---|---|---|
| Geometric parameters | Cos θ | Incident angle cosine | None |
| Sin θ | Incident angle sine | None | |
| Inc | Incident angle | None | |
| Kz | Vertical wave number | / | |
| HoA | Height of ambiguity | ||
| Penetration depth | Hd | Penetration depth | / |
| Coherence phase center height and coherence separation | PDHsep | High-coherence separation | |
| PDLsep | Low-coherence separation | ||
| PDHmab | High-coherence magnitude | ||
| PDLmab | Low-coherence amplitude | ||
| PDHarg | High-coherence phases | ||
| PDLarg | Low-coherence phases | ||
| Phi | Ground phase | / | |
| Phimab | Surface coherence amplitude | ||
| HeightPDH | High-coherence phase center height | ||
| HeightPDL | Low-coherence phase center height | ||
| Baseline selection parameters | Sep | Coherence separation | |
| Mab | Coherence amplitude | ||
| Cit | Product of coherence separation and coherence amplitude |
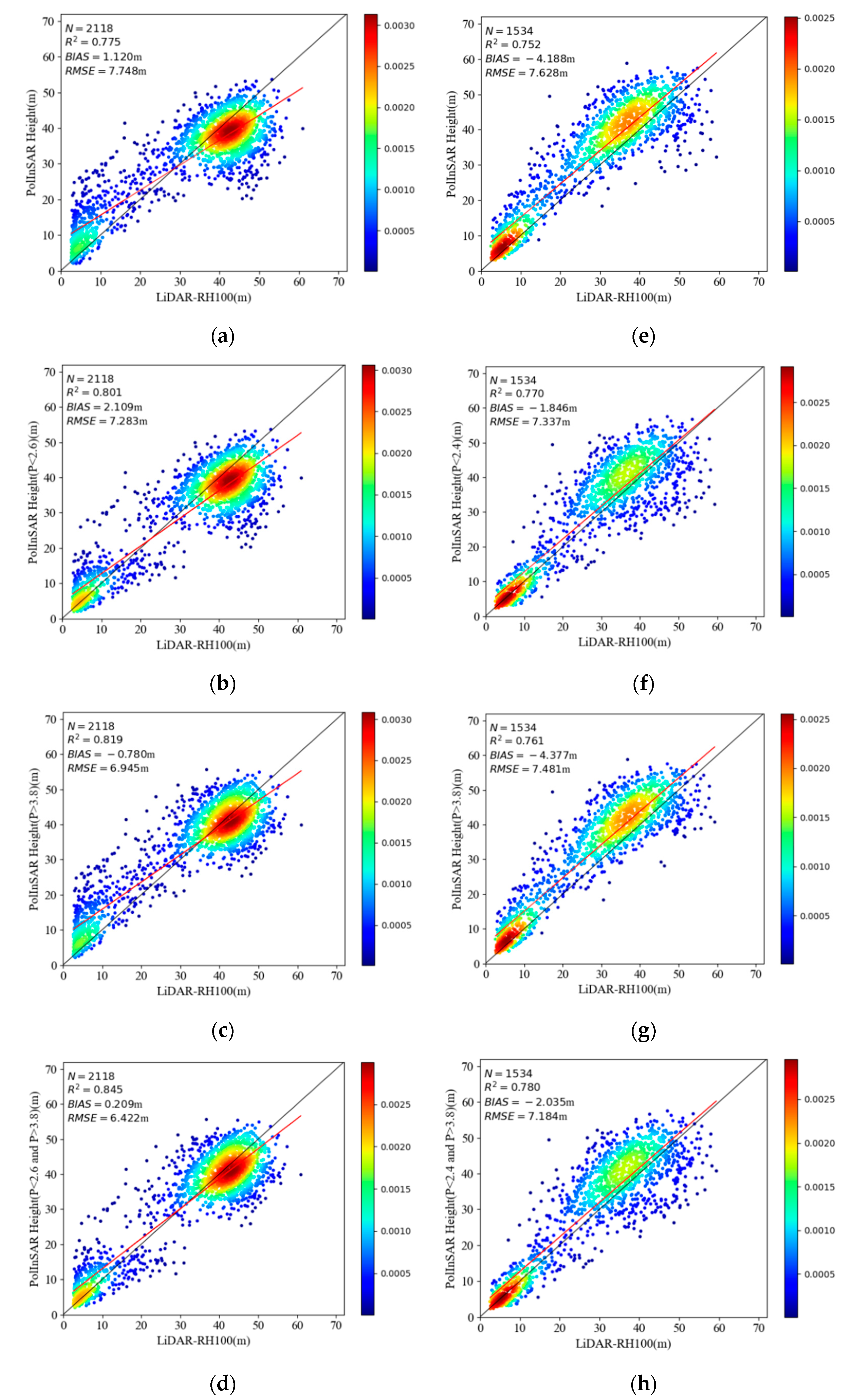
| Correction Scheme | Test Area | R2 | RMSE (m) | BIAS (m) |
|---|---|---|---|---|
| Uncorrected | Lope | 0.775 | 7.748 | 1.120 |
| Pongara | 0.752 | 7.628 | −4.188 | |
| Correction based on RH100 | Lope | 0.856 | 6.204 | 0.536 |
| Pongara | 0.854 | 5.856 | −0.024 | |
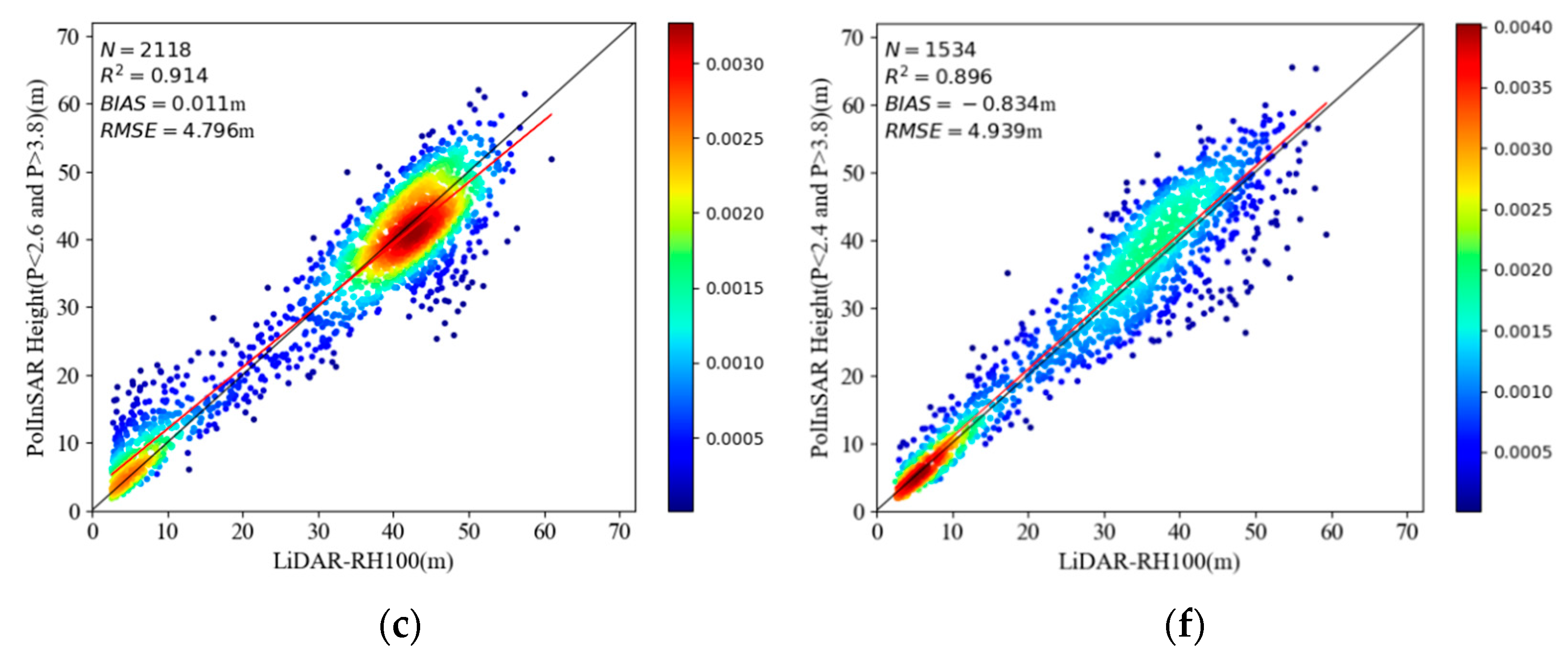
| Correction based on P | Lope | 0.914 | 4.796 | 0.011 |
| Pongara | 0.896 | 4.939 | −0.834 | |
| Correction based on PRF | Lope | 0.845 | 6.422 | 0.209 |
| Pongara | 0.780 | 7.184 | −2.035 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Yue, C.; Wang, N.; Luo, G.; Chen, S. Correcting Underestimation and Overestimation in PolInSAR Forest Canopy Height Estimation Using Microwave Penetration Depth. Remote Sens. 2022, 14, 6145. https://doi.org/10.3390/rs14236145
Luo H, Yue C, Wang N, Luo G, Chen S. Correcting Underestimation and Overestimation in PolInSAR Forest Canopy Height Estimation Using Microwave Penetration Depth. Remote Sensing. 2022; 14(23):6145. https://doi.org/10.3390/rs14236145
Chicago/Turabian StyleLuo, Hongbin, Cairong Yue, Ning Wang, Guangfei Luo, and Si Chen. 2022. "Correcting Underestimation and Overestimation in PolInSAR Forest Canopy Height Estimation Using Microwave Penetration Depth" Remote Sensing 14, no. 23: 6145. https://doi.org/10.3390/rs14236145
APA StyleLuo, H., Yue, C., Wang, N., Luo, G., & Chen, S. (2022). Correcting Underestimation and Overestimation in PolInSAR Forest Canopy Height Estimation Using Microwave Penetration Depth. Remote Sensing, 14(23), 6145. https://doi.org/10.3390/rs14236145









