Relative Pose Estimation of Non-Cooperative Space Targets Using a TOF Camera
Abstract
1. Introduction
2. Architecture of the Proposed Method
2.1. TOF Camera Projection Model
2.2. TOF Data Preprocessing Module
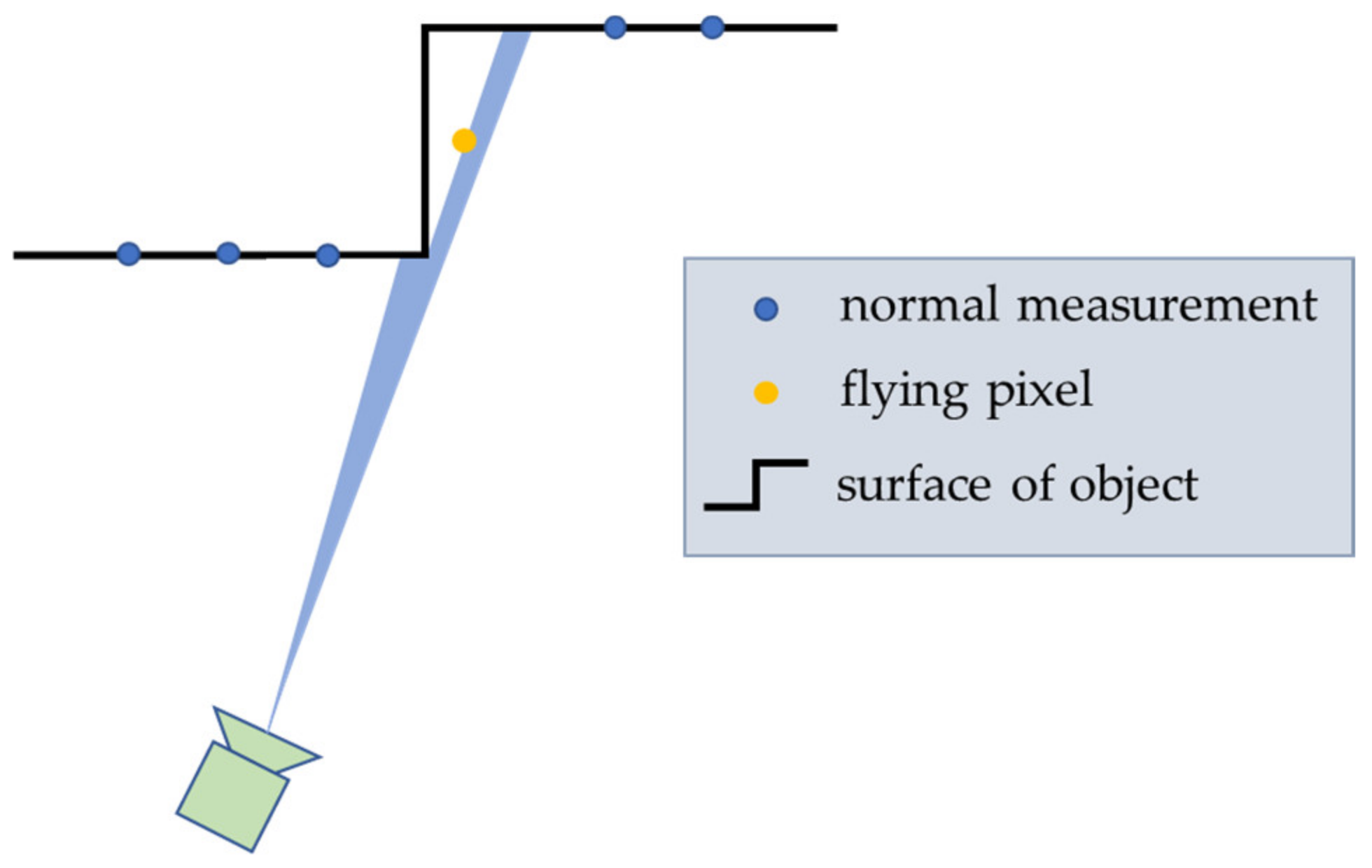
2.2.1. Noise Reduction
2.2.2. Edge Preserving Filter
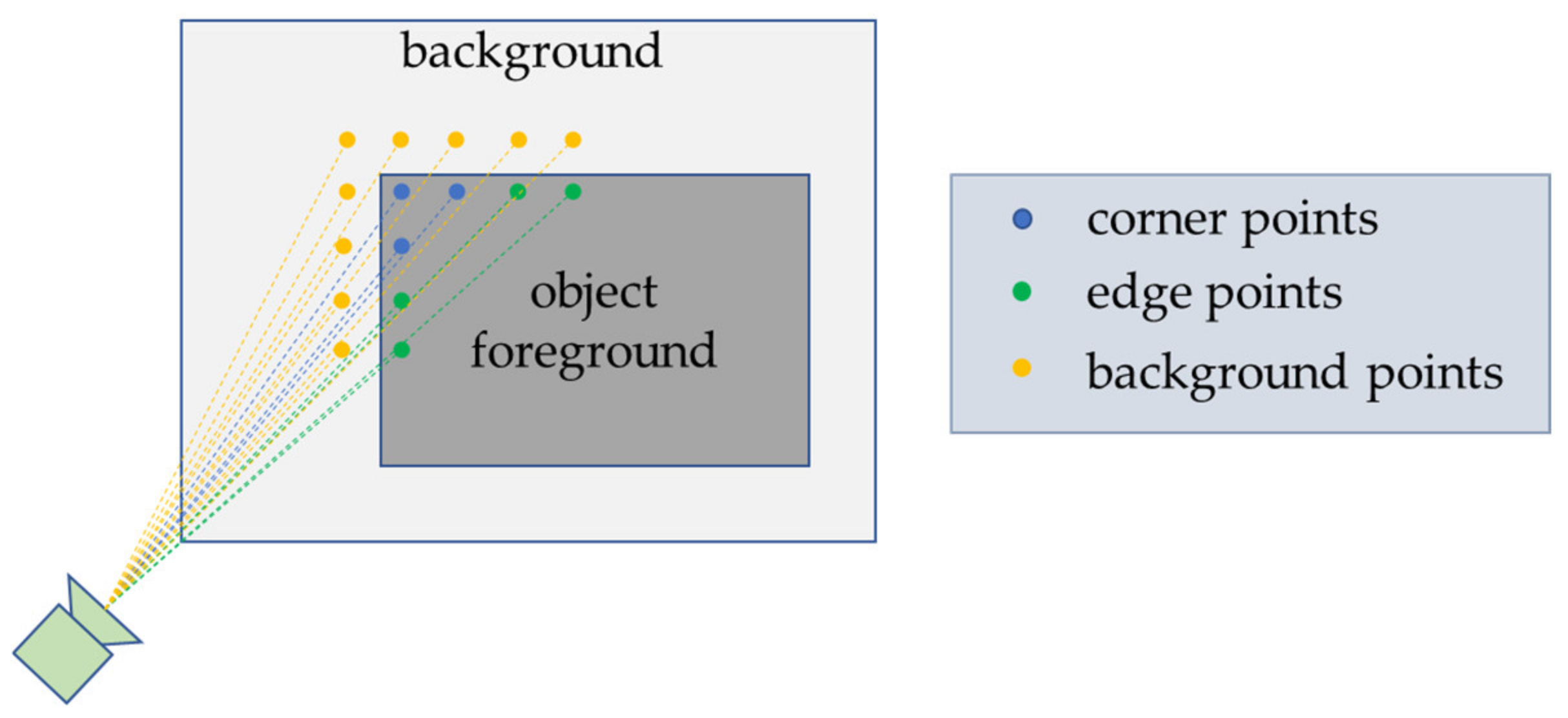
2.2.3. Salient Point Selection
2.3. Registration Module by Frame-to-Frame
- Selecting the source points from the source point cloud;
- Matching the corresponding points set or line in the target point cloud, for which the minimized Euclidean metric or , is the two-norm operator;
- Rejecting the “corner-edge” point pairs by types of salient points;
- Weighting the correspondence as , where and represent the intensity value of the i-th point in the source and target point cloud, respectively;
- Estimating the increment transformation from the corresponding point set which minimizes the error metric , where n is the number of corresponding point pairs;
- Updating the transformation matrix ;
- If the error is less than a given threshold or greater than the preset maximum number of iterations, the iterative calculation is stopped. Otherwise, repeat from step 2 until achieving convergence conditions.
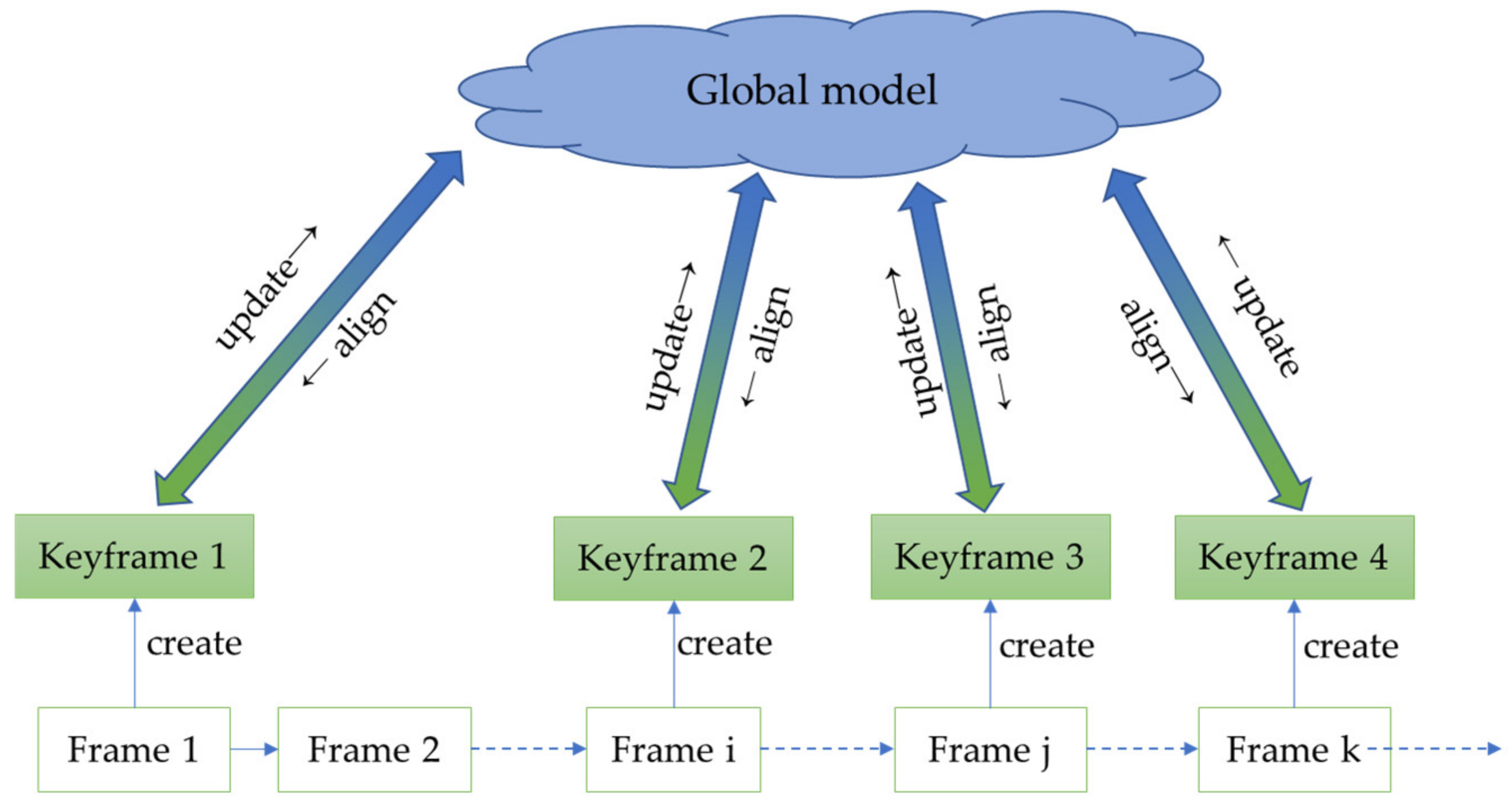
2.4. Model Mapping Module by Model-to-Frame
2.4.1. Keyframe Selection
- 20 frames have passed from the previous key frame;
- The Euclidean distance between the current frame position and the previous key frame position is greater than a certain threshold T1;
- The difference of Euler angles between current frame and the previous key frame is greater than a certain threshold T2.
2.4.2. Model Updating
3. Semi-Physical Experiment and Analysis
3.1. Experimental Environment Setup
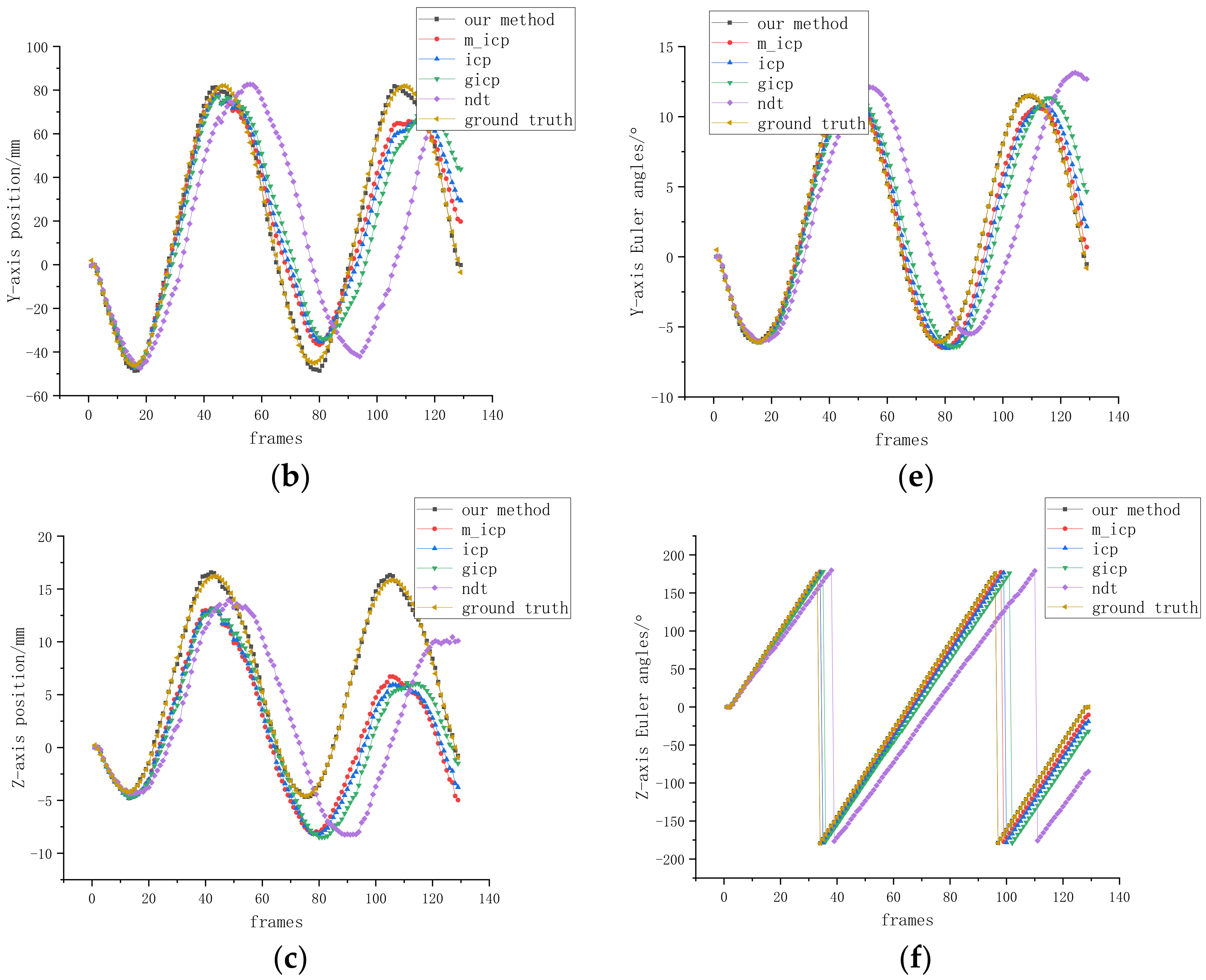
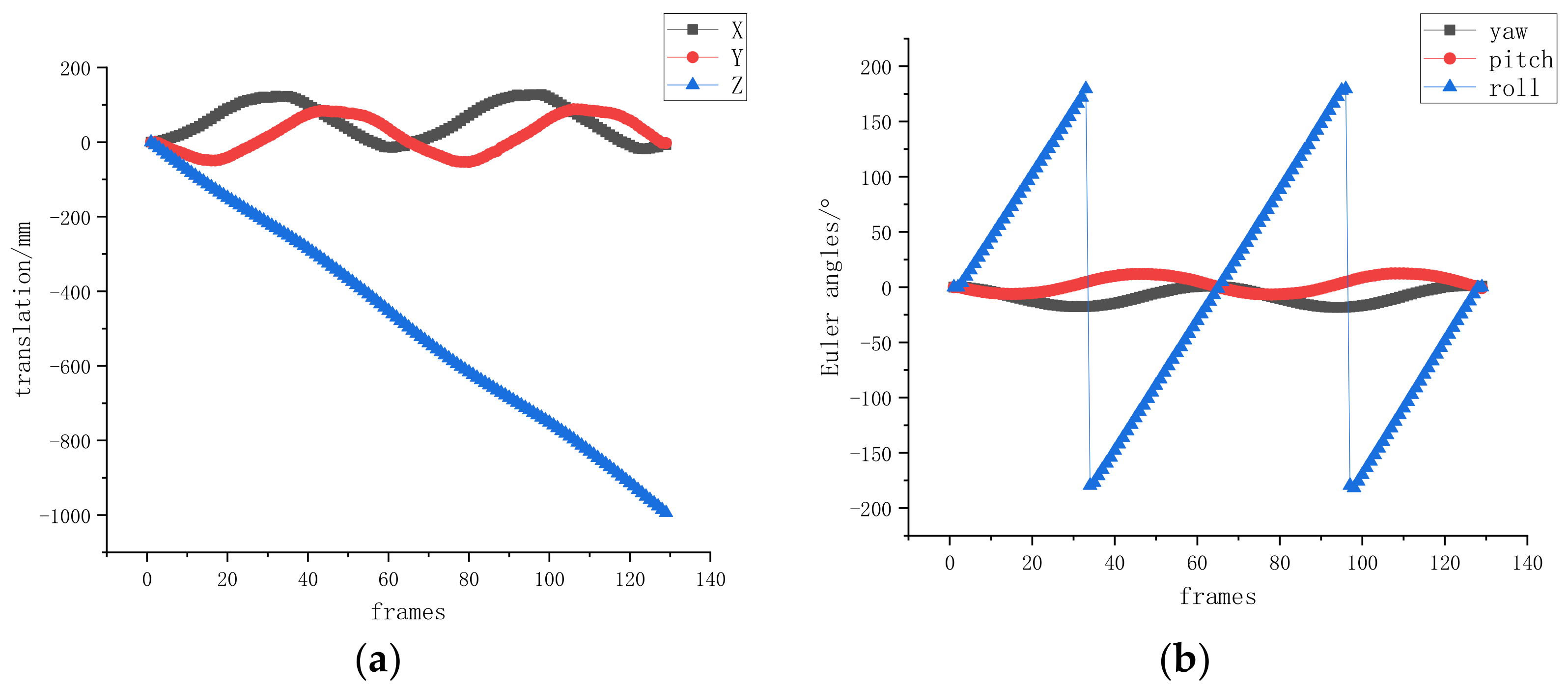
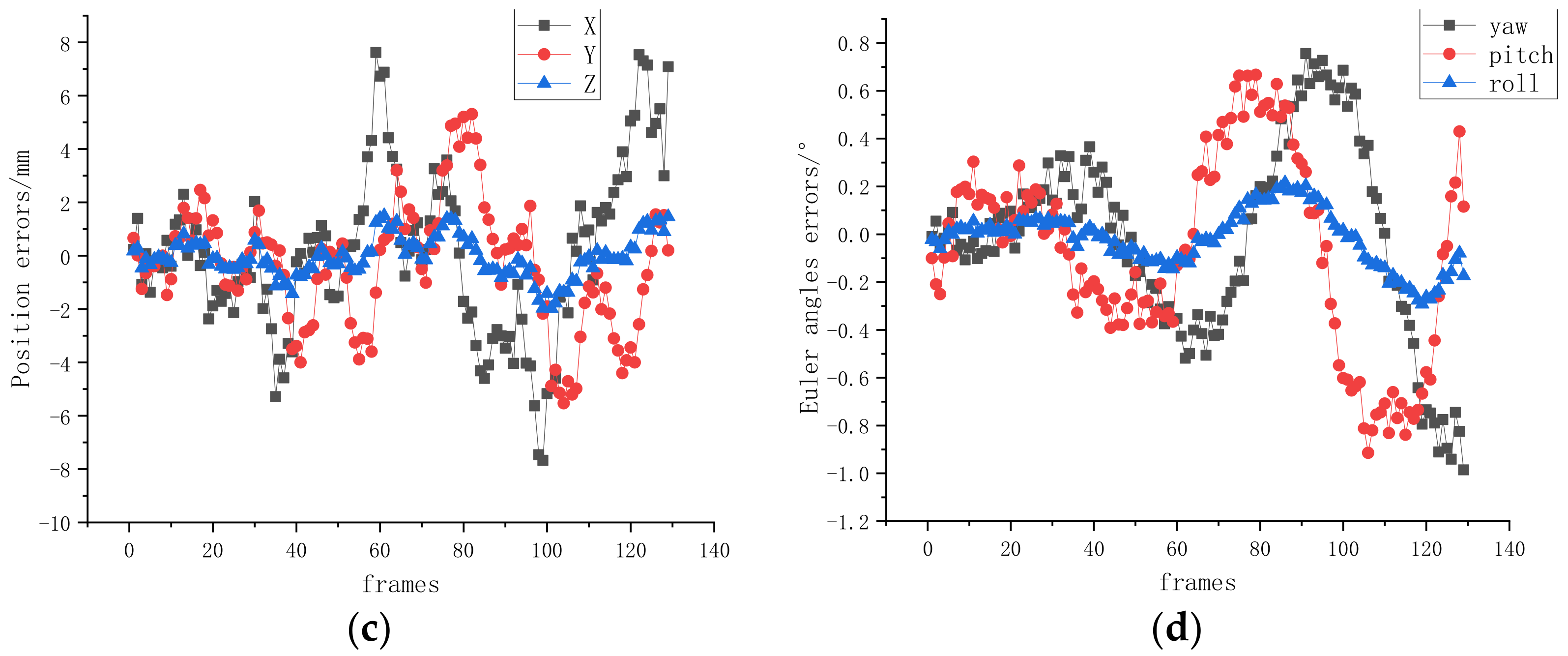
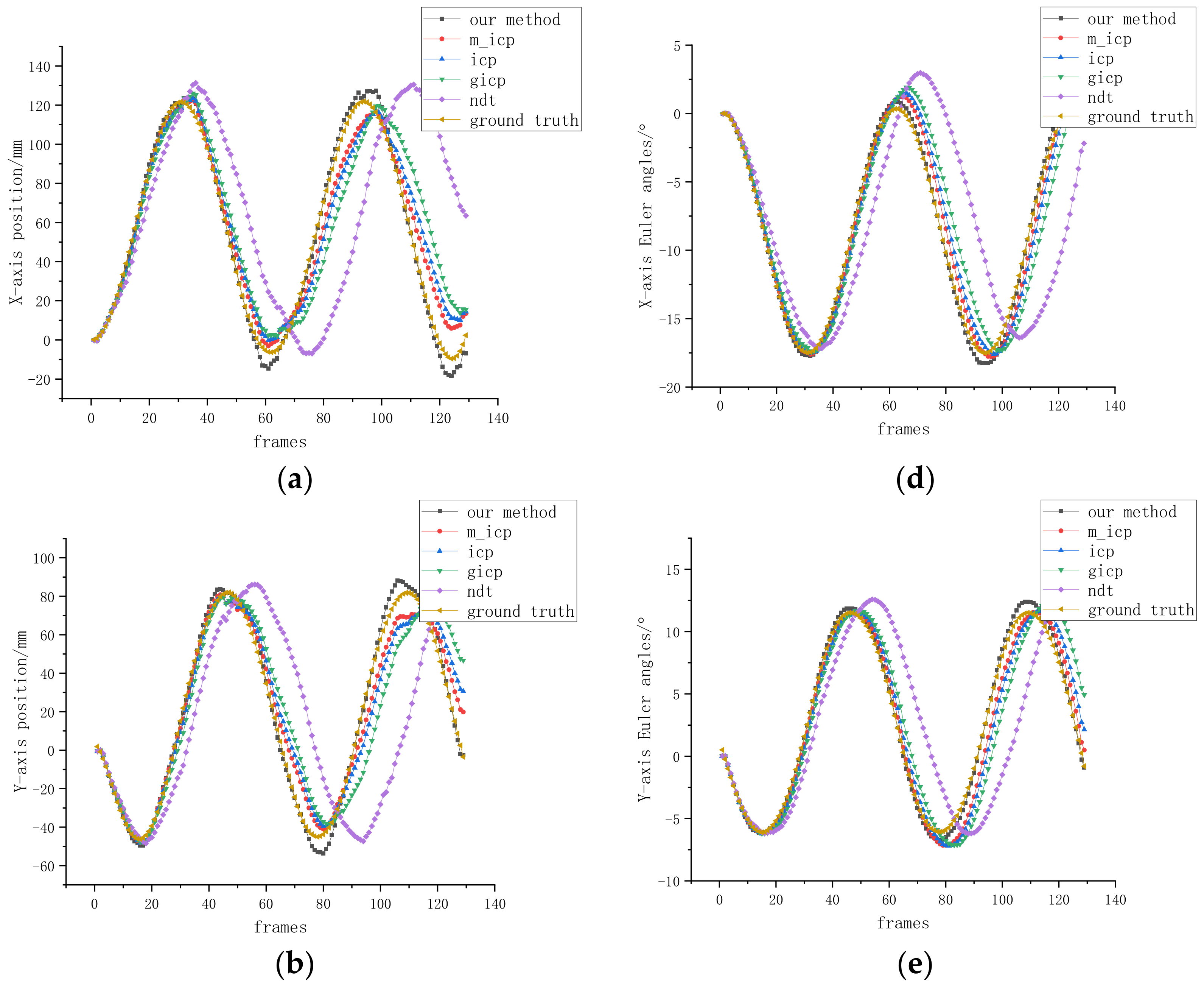
3.2. Results of Semi-Physical Experiments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Forshaw, J.L.; Aglietti, G.S.; Navarathinam, N.; Kadhem, H.; Salmon, T.; Pisseloup, A.; Joffre, E.; Chabot, T.; Retat, I.; Axthelm, R.; et al. RemoveDEBRIS: An in-orbit active debris removal demonstration mission. Acta Astronaut. 2016, 127, 448–463. [Google Scholar] [CrossRef]
- Zhao, P.Y.; Liu, J.G.; Wu, C.C. Survey on research and development of on-orbit active debris removal methods. Sci. China Technol. Sci. 2020, 63, 2188–2210. [Google Scholar] [CrossRef]
- Li, W.J.; Cheng, D.Y.; Liu, X.G.; Wang, Y.; Shi, W.; Tang, Z.; Gao, F.; Zeng, F.; Chai, H.; Luo, W.; et al. On-orbit service (OOS) of spacecraft: A review of engineering developments. Prog. Aerosp. Sci. 2019, 108, 32–120. [Google Scholar] [CrossRef]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Long, A.M.; Richards, M.G.; Hastings, D.E. On-orbit servicing: A new value proposition for satellite design and operation. J. Spacecr. Rocket. 2007, 44, 964–976. [Google Scholar] [CrossRef]
- Hirzinger, G.; Landzettel, K.; Brunner, B.; Fischer, M.; Preusche, C.; Reintsema, D.; Albu-Schäffer, A.; Schreiber, G.; Steinmetz, B. DLR’s robotics technologies for on-orbit servicing. Adv. Robot. 2004, 18, 139–174. [Google Scholar] [CrossRef]
- De Carvalho, T.H.M.; Kingston, J. Establishing a framework to explore the Servicer-Client relationship in On-Orbit Servicing. Acta Astronaut. 2018, 153, 109–121. [Google Scholar] [CrossRef]
- Zou, T.; Wang, L.; Zhu, T.; Zhai, X. Non-cooperative Target Relative Navigation Method Based on Vortex Light, Vision and IMU Information. In Proceedings of the 2021 6th International Conference on Systems, Control and Communications (ICSCC), Chongqing, China, 15–17 October 2021; pp. 48–53. [Google Scholar]
- Du, X.; Liang, B.; Xu, W.; Qiu, Y. Pose measurement of large non-cooperative satellite based on collaborative cameras. Acta Astronaut. 2011, 68, 2047–2065. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.; Mu, J.; Hao, X.; Zhu, W.; Hu, J. Research Advancements in Key Technologies for Space-Based Situational Awareness. Space: Sci. Technol. 2022, 2022, 9802793. [Google Scholar] [CrossRef]
- Min, J.; Yi, J.; Ma, Y.; Chen, S.; Zhang, H.; Wu, H.; Cao, S.; Mu, J. Recognizing and Measuring Satellite based on Monocular Vision under Complex Light Environment. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 464–468. [Google Scholar]
- Volpe, R.; Palmerini, G.B.; Sabatini, M. A passive camera-based determination of a non-cooperative and unknown satellite’s pose and shape. Acta Astronaut. 2018, 151, 805–817. [Google Scholar] [CrossRef]
- Cassinis, L.P.; Fonod, R.; Gill, E. Review of the robustness and applicability of monocular pose estimation systems for relative navigation with an uncooperative spacecraft. Prog. Aerosp. Sci. 2019, 110, 100548. [Google Scholar]
- Perfetto, D.M.; Opromolla, R.; Grassi, M.; Schmitt, C. LIDAR-based model reconstruction for spacecraft pose determination. In Proceedings of the 2019 IEEE 5th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Turin, Italy, 19–21 June 2019; pp. 1–6. [Google Scholar]
- Zhu, W.; She, Y.; Hu, J.; Wang, B.; Mu, J.; Li, S. A hybrid relative navigation algorithm for a large–scale free tumbling non–cooperative target. Acta Astronaut. 2022, 194, 114–125. [Google Scholar] [CrossRef]
- May, S.; Droeschel, D.; Holz, D.; Wiesen, C.; Fuchs, S. 3D pose estimation and mapping with time-of-flight cameras. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), 3D Mapping Workshop, Nice, France, 22–26 September 2008. [Google Scholar]
- Zhu, W.; Mu, J.; Shao, C.; Hu, J.; Wang, B.; Wen, Z.; Han, F.; Li, S. System Design for Pose Determination of Spacecraft Using Time-of-Flight Sensors. Space: Sci. Technol. 2022, 2022, 9763198. [Google Scholar] [CrossRef]
- Tzschichholz, T.; Boge, T.; Schilling, K. Relative pose estimation of satellites using PMD-/CCD-sensor data fusion. Acta Astronaut. 2015, 109, 25–33. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Zhao, X. Relative Pose Determination of Uncooperative Spacecraft Based on Circle Feature. Sensors 2021, 21, 8495. [Google Scholar] [CrossRef]
- Kawahito, S.; Halin, I.A.; Ushinaga, T.; Sawada, T.; Homma, M.; Maeda, Y. A CMOS time-of-flight range image sensor with gates-on-field-oxide structure. IEEE Sens. J. 2007, 7, 1578–1586. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A model-based 3D template matching technique for pose acquisition of an uncooperative space object. Sensors 2015, 15, 6360–6382. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. Pose estimation for spacecraft relative navigation using model-based algorithms. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 431–447. [Google Scholar] [CrossRef]
- Martínez, H.G.; Giorgi, G.; Eissfeller, B. Pose estimation and tracking of non-cooperative rocket bodies using time-of-flight cameras. Acta Astronaut. 2017, 139, 165–175. [Google Scholar] [CrossRef]
- Zeng-yu, S.U.; Yue, G.A. Relative position and attitude measurement for non-cooperative spacecraft based on binocular vision. J. Astronaut. Metrol. Meas. 2017, 37, 1. [Google Scholar]
- Zhang, S.; Li, J.; Zhang, W.; Zhou, W. Research on docking ring pose estimation method based on point cloud grayscale image. Adv. Space Res. 2022, 70, 3466–3477. [Google Scholar] [CrossRef]
- Zhao, G.; Xu, S.; Bo, Y. LiDAR-based non-cooperative tumbling spacecraft pose tracking by fusing depth maps and point clouds. Sensors 2018, 18, 3432. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Lei, T.; Liu, X.; Cai, G.; Yang, Y.; Jiang, L.; Yu, Z. Pose estimation of non-cooperative target coated with MLI. IEEE Access 2019, 7, 153958–153968. [Google Scholar] [CrossRef]
- Kang, G.; Zhang, Q.; Wu, J.; Zhang, H. Pose estimation of a non-cooperative spacecraft without the detection and recognition of point cloud features. Acta Astronaut. 2021, 179, 569–580. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Chen, X.; Chen, W.; Xie, Z. Position Awareness Network for Non-Cooperative Spacecraft Pose Estimation Based on Point Cloud. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Sensor Fusion IV: Control Paradigms and Data Structures; SPIE: Bellingham, DC, USA, 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-icp. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2009; Volume 2, p. 435. [Google Scholar]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Las Vegas, NV, USA, 27–31 October 2003; Volume 3, pp. 2743–2748. [Google Scholar]
- Sabov, A.; Krüger, J. Identification and correction of flying pixels in range camera data. In Proceedings of the 24th Spring Conference on Computer Graphics, Budmerice Castle, Slovakia, 21–23 April 2008; pp. 135–142. [Google Scholar]
- Xiao, J.; Zhang, J.; Adler, B.; Zhang, H.; Zhang, J. Three-dimensional point cloud plane segmentation in both structured and unstructured environments. Robot. Auton. Syst. 2013, 61, 1641–1652. [Google Scholar] [CrossRef]
- Holzer, S.; Rusu, R.B.; Dixon, M.; Gedikli, S.; Navab, N. Adaptive neighborhood selection for real-time surface normal estimation from organized point cloud data using integral images. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2684–2689. [Google Scholar]
- Borgefors, G. Distance transformations in digital images. Comput. Vis. Graph. Image Process. 1986, 34, 344–371. [Google Scholar] [CrossRef]
- Foix, S.; Alenya, G.; Torras, C. Lock-in time-of-flight (ToF) cameras: A survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef]
- Chen, S.; Chang, C.W.; Wen, C.Y. Perception in the dark; development of a tof visual inertial odometry system. Sensors 2020, 20, 1263. [Google Scholar] [CrossRef]


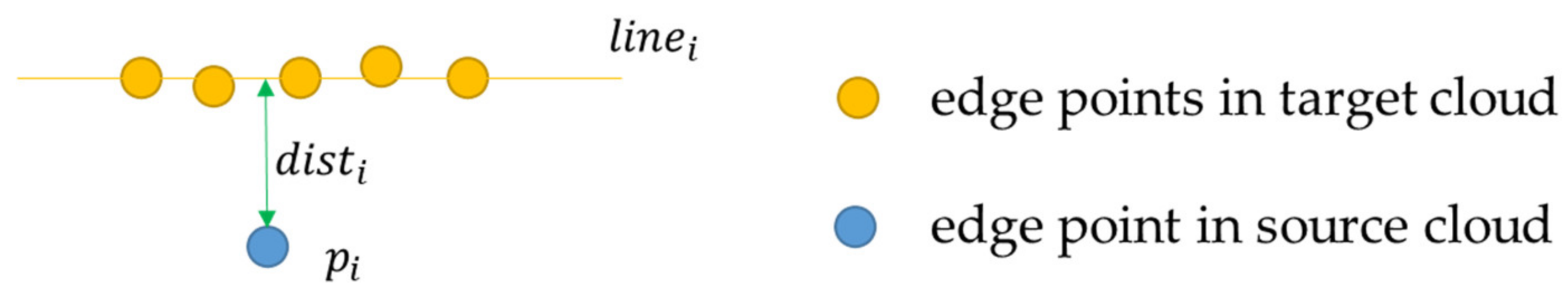





| Parameter | Value |
|---|---|
| (525.89, 525.89) | |
| (319.10, 232.67) |
| Method | Our Method | Bilateral Filter | Fast Bilateral Filter | Guided Filter | Fast Guided Filter |
|---|---|---|---|---|---|
| Time Consumption (ms) | 17 | 865 | 102 | 317 | 79 |
| Parameter | Value |
|---|---|
| Resolution | 640 × 480 px, 0.3 MP |
| Pixel Size | 10.0 µm (H) × 10.0 µm (V) |
| Illumination | 4 × VCSEL laser diodes, Class1, @ 850 nm |
| Lens Field of View | 69° × 51° (nominal) |
| Method | Our Method | ICP | GICP | NDT | |||
|---|---|---|---|---|---|---|---|
| Time Consumption (ms) | Preprocessing | Salient Point Selection | Modified ICP | ||||
| Mean | 20 | 36 | 49 | 946 | 788 | 1145 | |
| Std. Dev | 3 | 4 | 6 | 87 | 64 | 95 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Hu, L.; Duan, H.; Pei, H. Relative Pose Estimation of Non-Cooperative Space Targets Using a TOF Camera. Remote Sens. 2022, 14, 6100. https://doi.org/10.3390/rs14236100
Sun D, Hu L, Duan H, Pei H. Relative Pose Estimation of Non-Cooperative Space Targets Using a TOF Camera. Remote Sensing. 2022; 14(23):6100. https://doi.org/10.3390/rs14236100
Chicago/Turabian StyleSun, Dianqi, Liang Hu, Huixian Duan, and Haodong Pei. 2022. "Relative Pose Estimation of Non-Cooperative Space Targets Using a TOF Camera" Remote Sensing 14, no. 23: 6100. https://doi.org/10.3390/rs14236100
APA StyleSun, D., Hu, L., Duan, H., & Pei, H. (2022). Relative Pose Estimation of Non-Cooperative Space Targets Using a TOF Camera. Remote Sensing, 14(23), 6100. https://doi.org/10.3390/rs14236100






