Application of 3D Error Diagram in Thermal Infrared Earthquake Prediction: Qinghai–Tibet Plateau
Abstract
1. Introduction
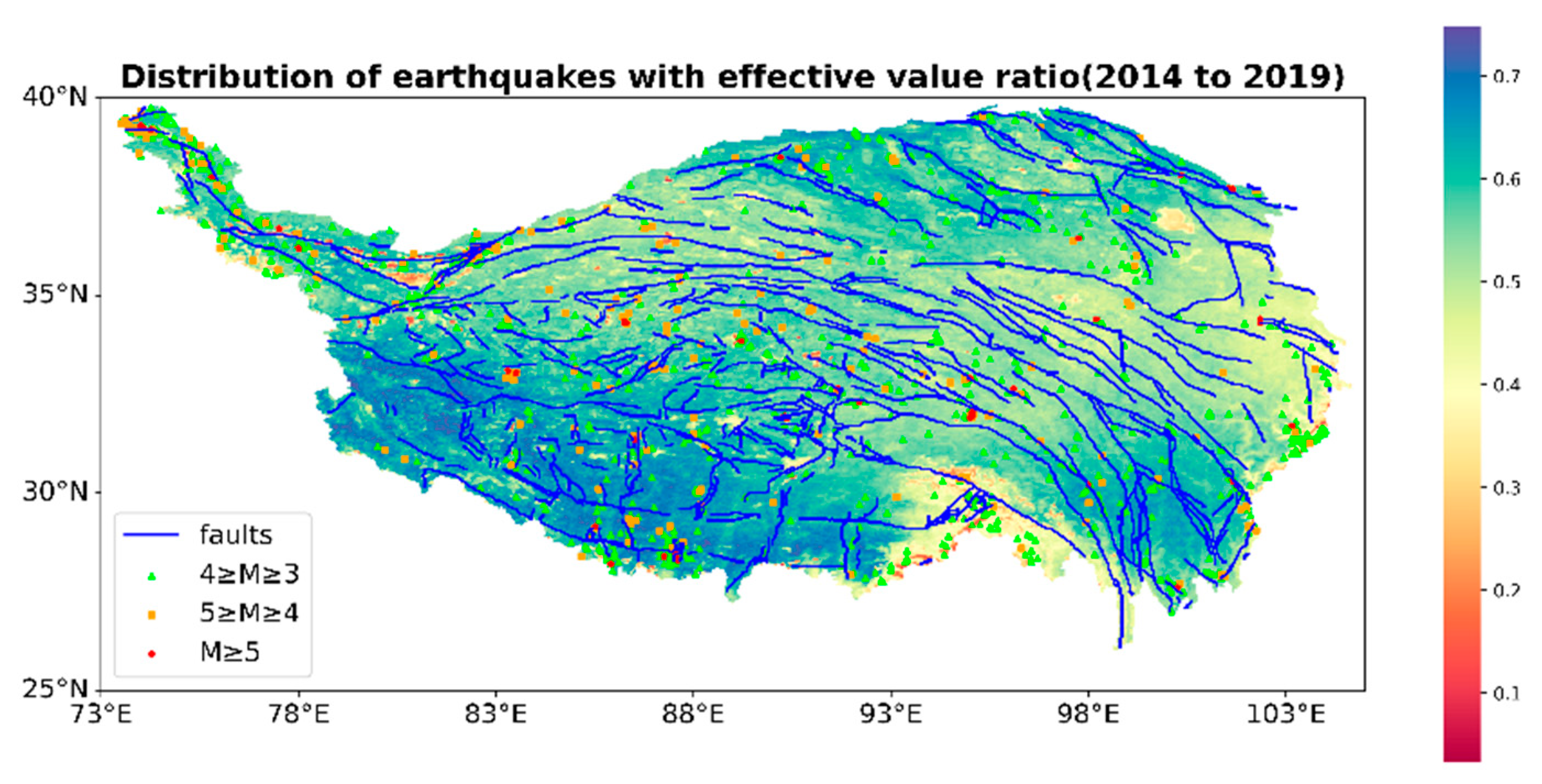
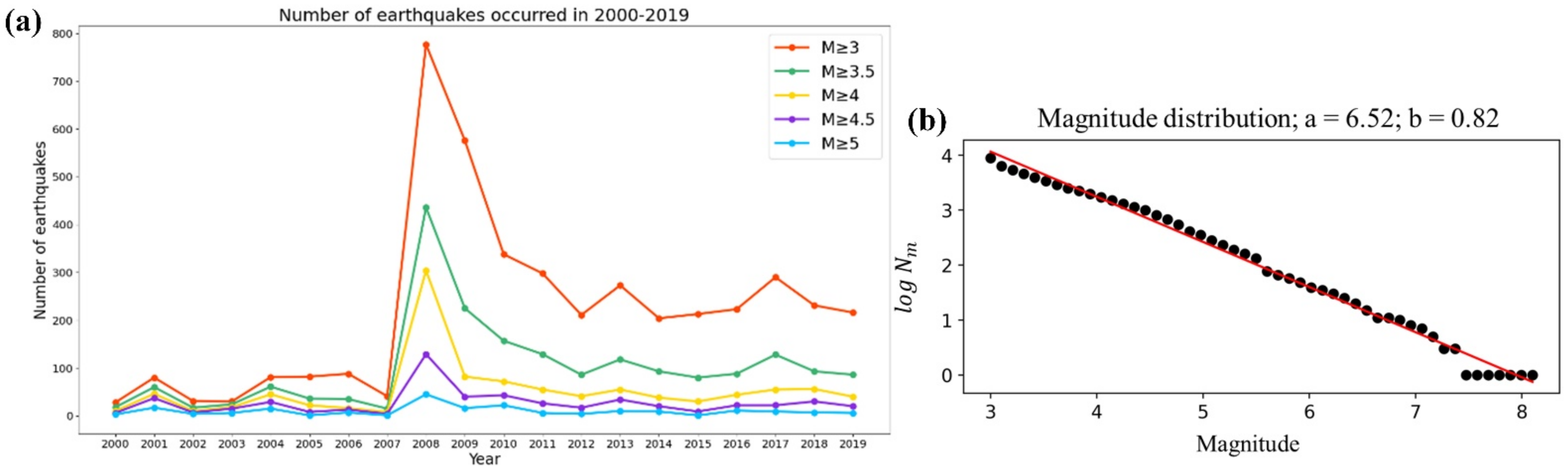
2. Dataset and Study Area
3. Methodology
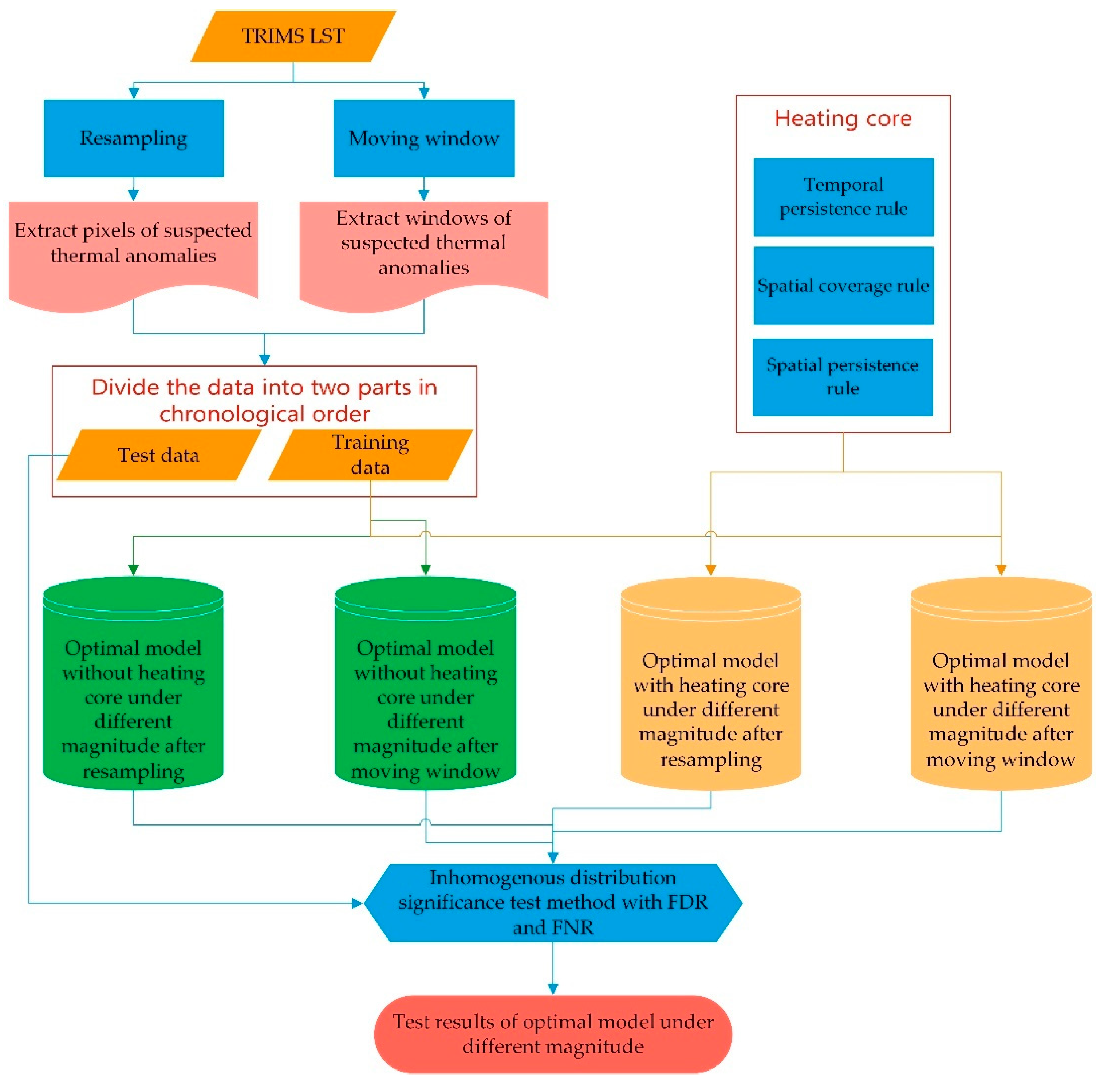
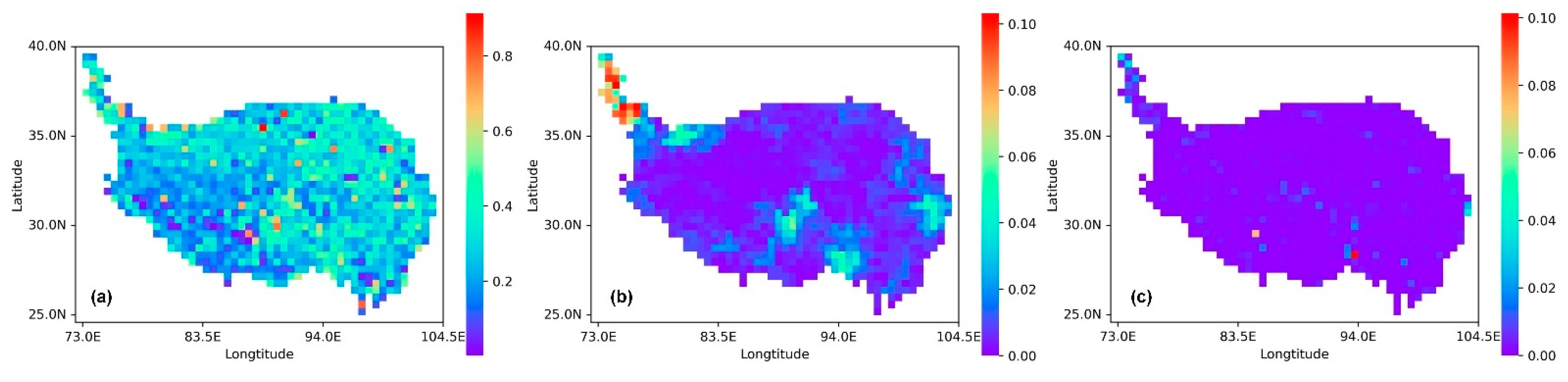
3.1. Thermal Anomaly Extraction Based on Resampling and Moving Windows
3.2. Thermal Anomaly Filtering
3.3. Correspondence between Earthquakes and Thermal Anomalies
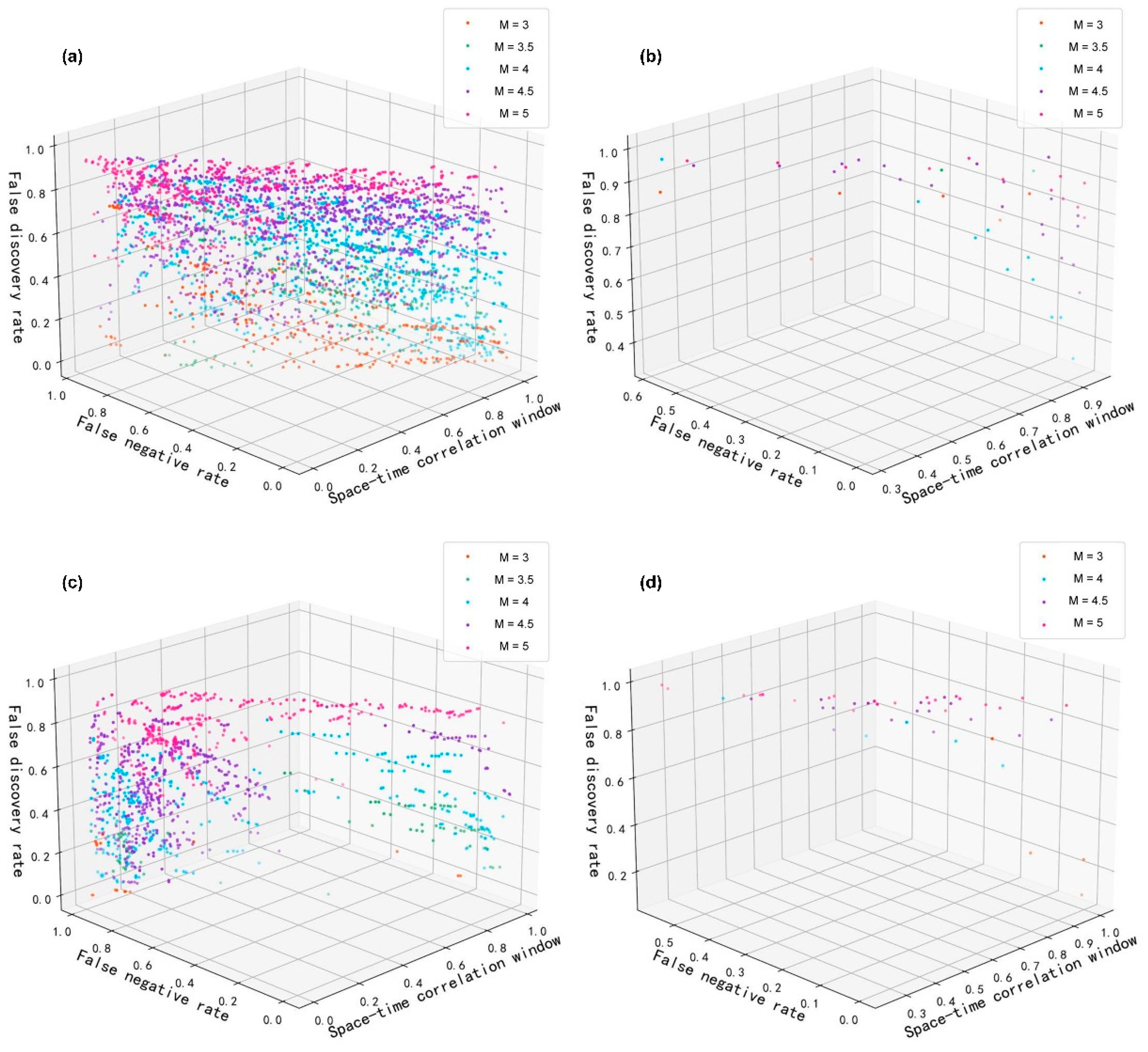
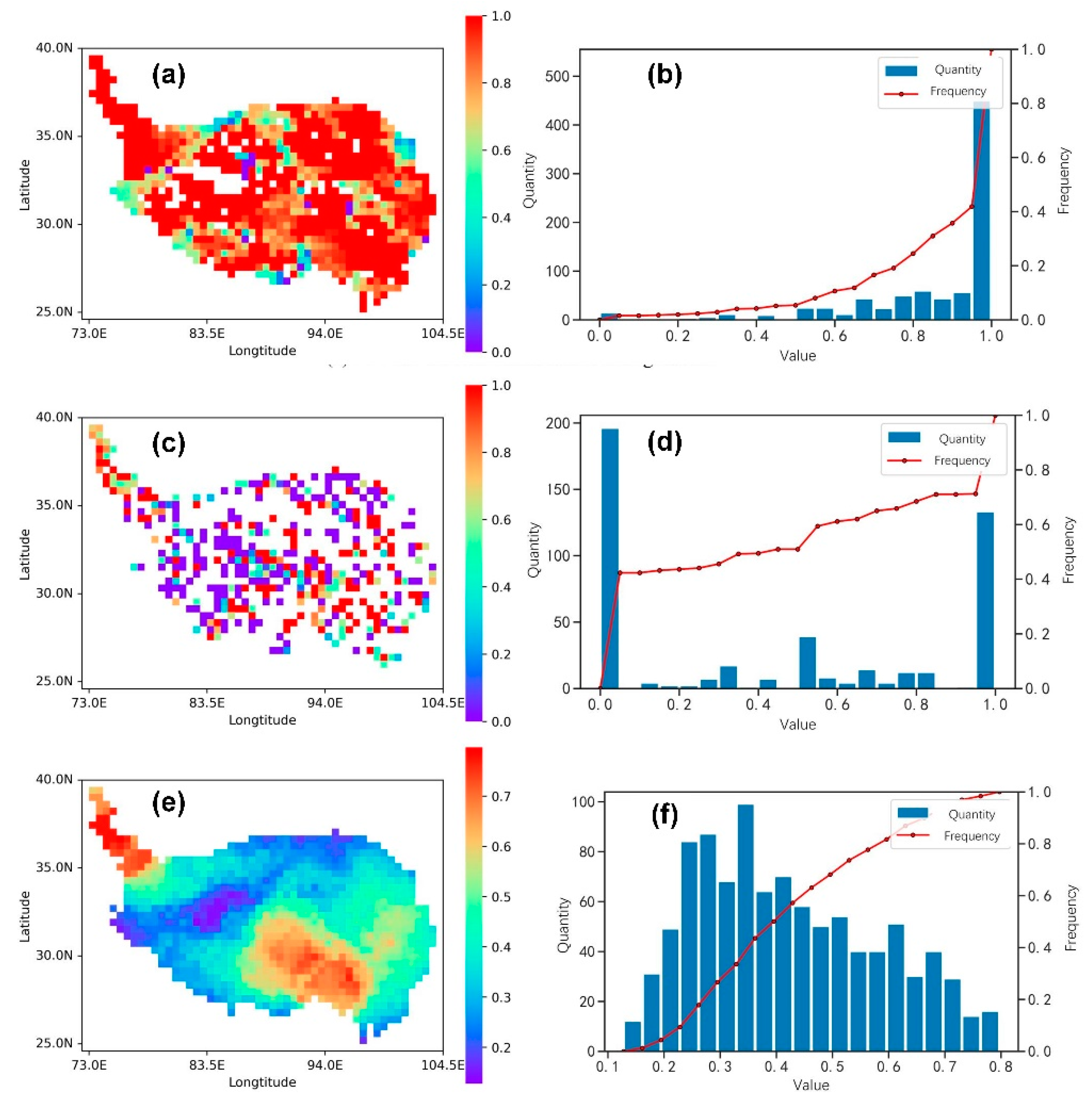
3.4. D-Molchan Diagram
- TP1 (true positive 1): the number of alarms that correspond to earthquakes;
- FP (false positive): the number of alarms that do not correspond to earthquakes;
- TP2 (true positive 2): the number of earthquakes that correspond to alarms;
- FN (false negative): the number of earthquakes that do not correspond to alarms;
- FDR (false discovery rate): the ratio of the number of alarms that do not correspond to earthquakes to the total number of alarms;
- FNR (false negative rate): the ratio of the number of earthquakes that do not correspond to alarms to the total number of earthquakes;
- STCW (space–time correlation window): the ratio of the spatiotemporal range of the warning to the total spatiotemporal range of the study area.
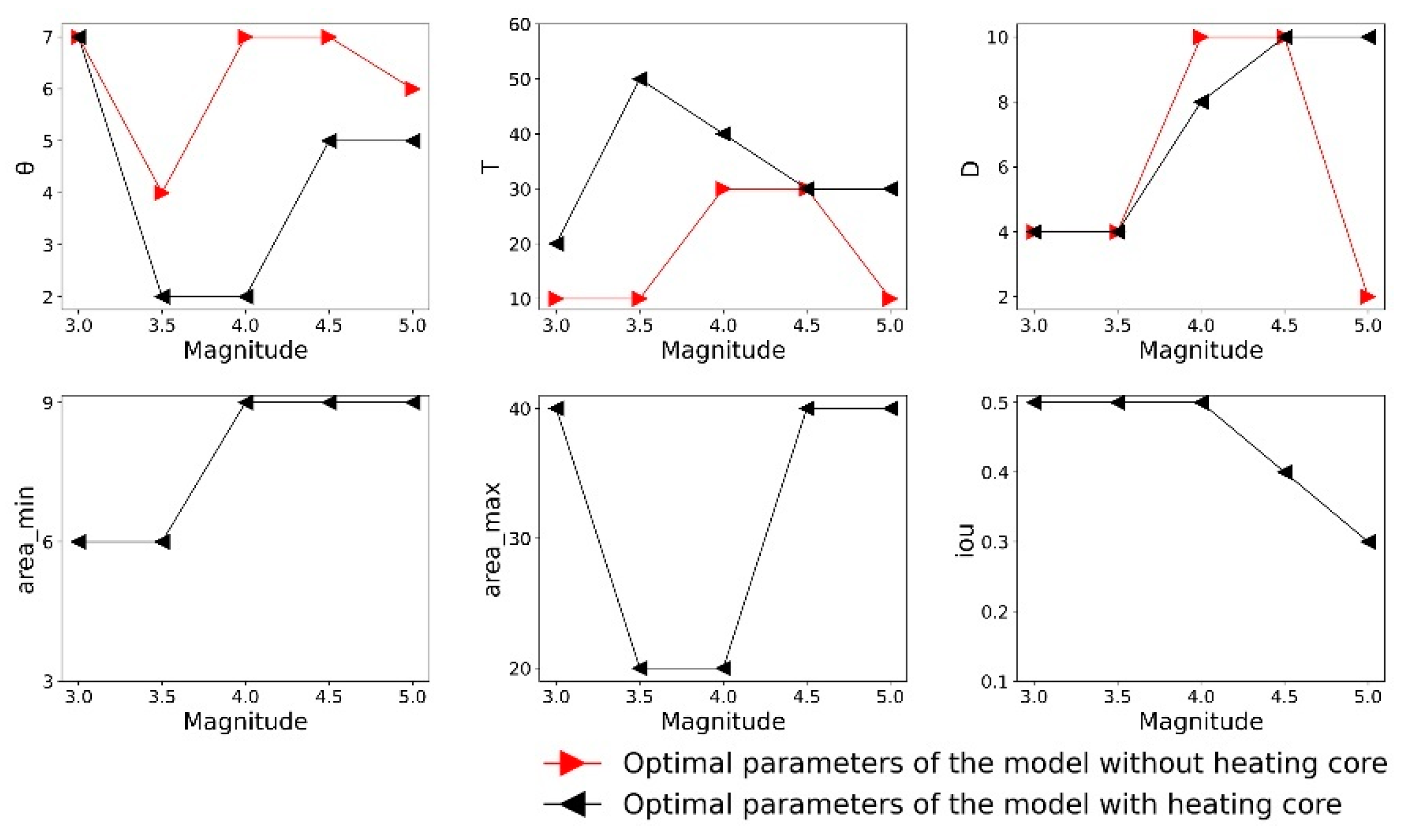
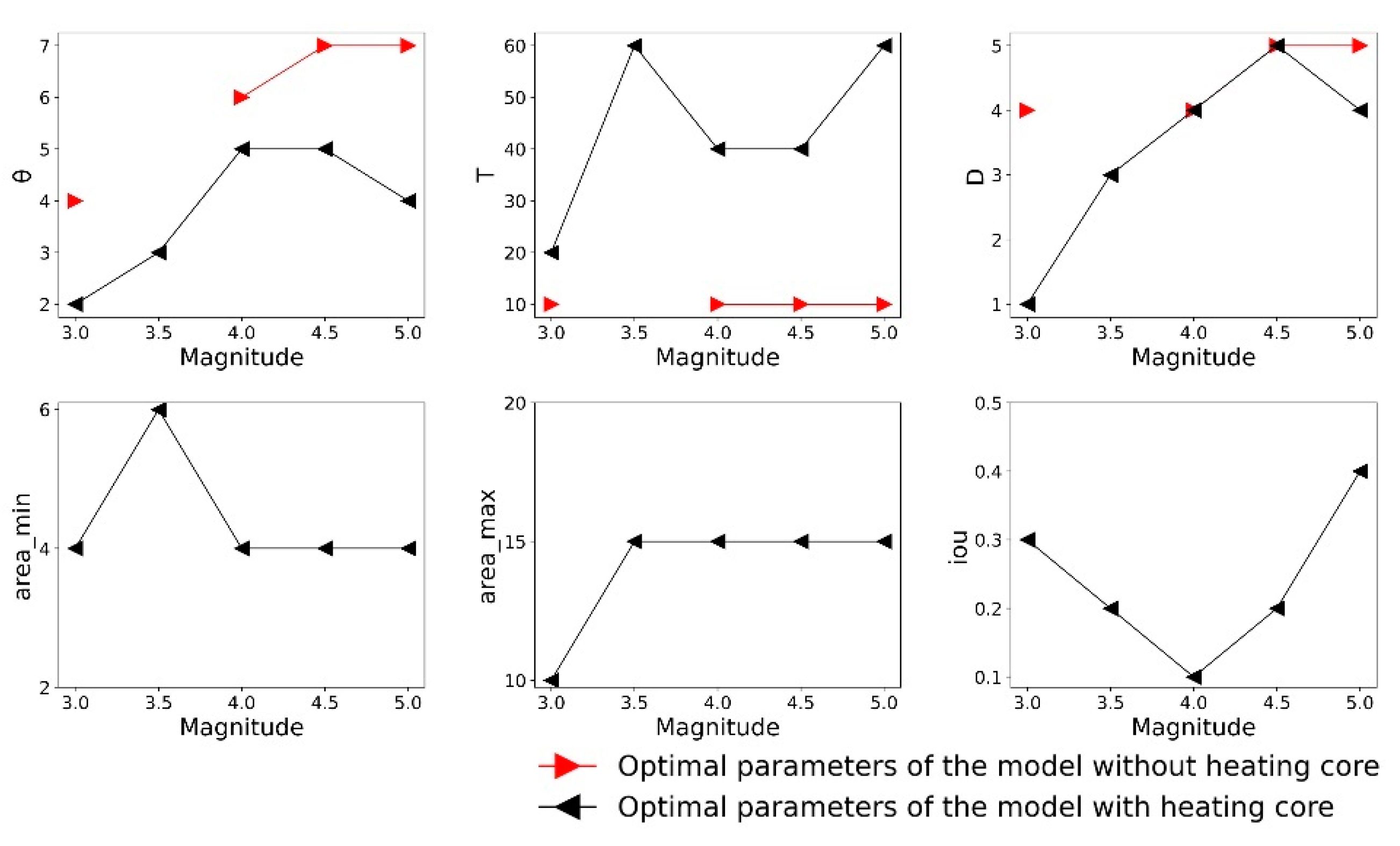
3.5. Minimum Magnitude and Optional Parameters
4. Results and Analysis
4.1. Resampling
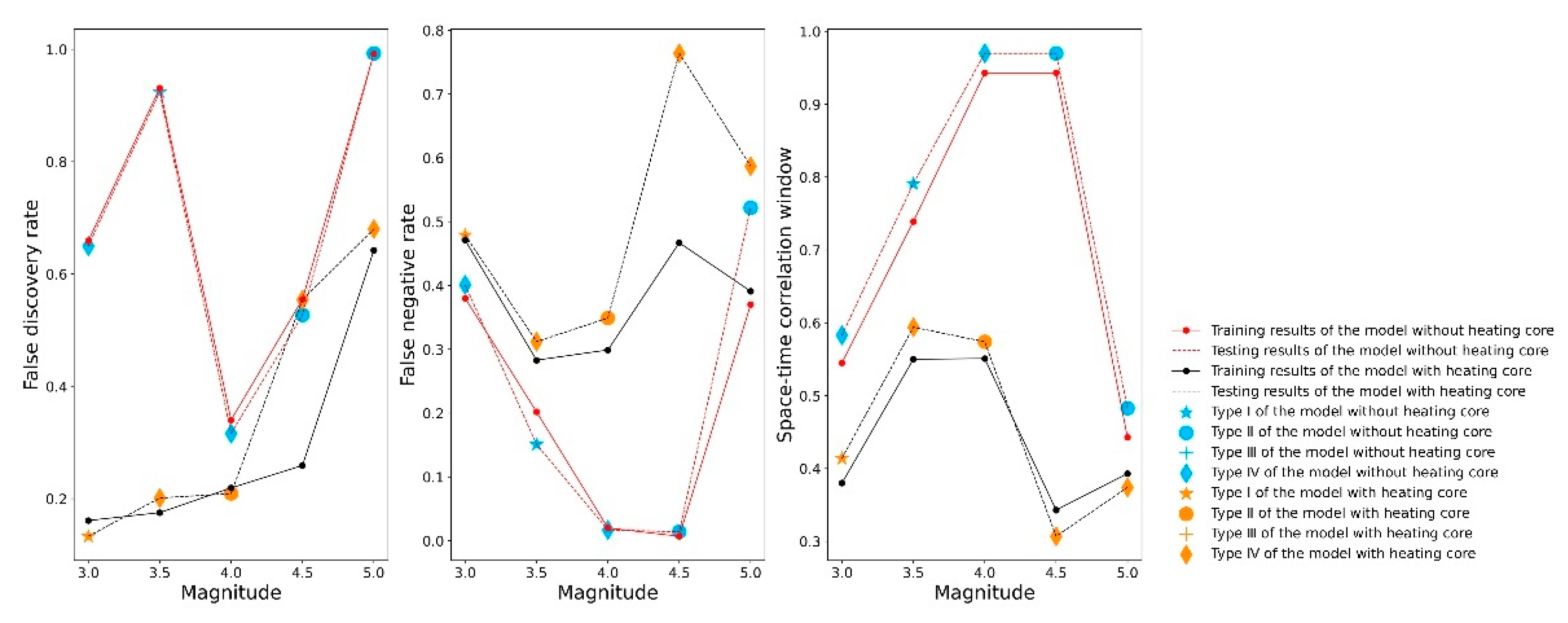
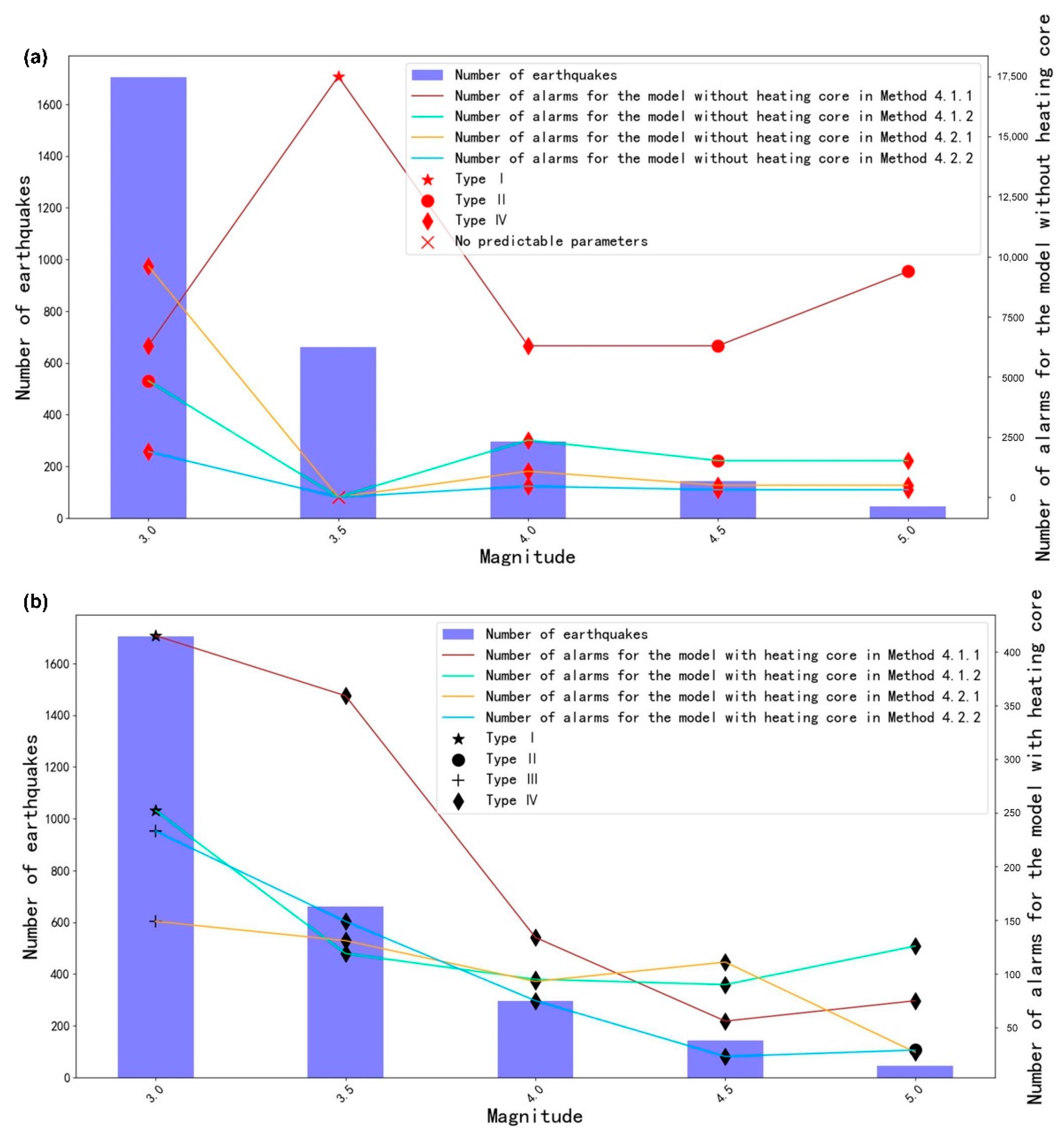
4.1.1. Comparison with or without a “Heating Core” When the Resampling Scale Is 50
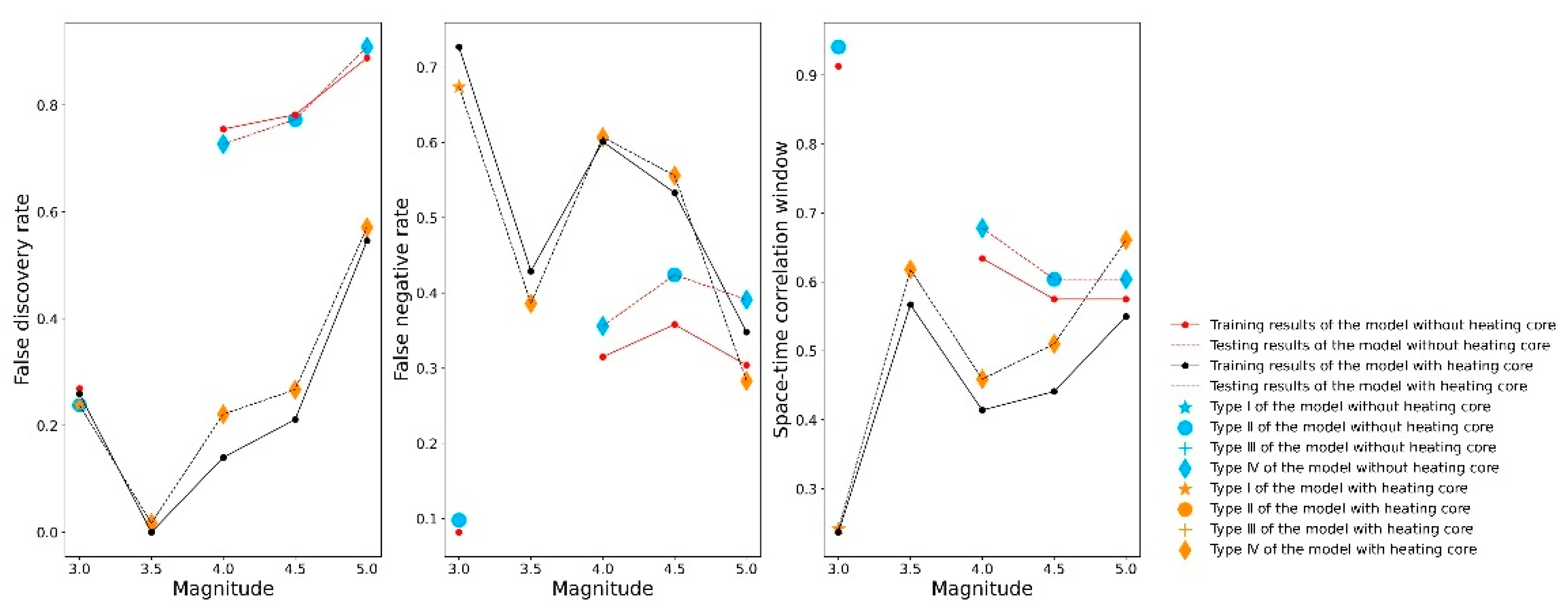
4.1.2. Comparison with or without a “Heating Core” When the Resampling Scale Is 100
4.2. Moving Window
4.2.1. Comparison with or without a “Heating Core” When the Moving Window Size Is 50
4.2.2. Comparison with or without a “Heating Core” When the Moving Window Size Is 100
5. Discussion
6. Conclusions
- (1)
- The downscaled spatial resolution method of resampling is superior to the moving-window method, the downscaled spatial resolution scale of 50 km is superior to 100 km, and the “heating core” model with the resampling scale of 50 has the best prediction performance.
- (2)
- The model with a “heating core” has superior performance compared to the model without a “heating core”, and the “heating core” filter greatly improves the S/N ratio of seismic thermal anomalies. However, the “heating core” is only valid for earthquakes of magnitude 3 and above, and it cannot distinguish the thermal anomalies produced by earthquakes of different magnitudes under this condition.
- (3)
- For earthquakes of magnitude 3 and above, the test results of the resampling method for the model with the “heating core” under the two scales are all Type I. This model is superior to random guessing from the FNR and FDR perspectives, and the losses are 0.647 (FDR = 13.3%, FNR = 47.9%, STCW = 41.4%) and 0.755 based on the 3D error diagram, respectively; the best model can predict earthquakes effectively within 200 km and within 20 days of a thermal anomaly’s appearance, which can provide a reference for earthquake prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Gornyy, V.; Sal’Man, A.G.; Tronin, A.; Shlin, B.V. The Earth’s Outgoing IR Radiation as an Indicator of Seismic Activity. Proc. Acad. Sci. USSR 1988, 301, 67–69. [Google Scholar]
- Freund, F.; Takeuchi, A.; Lau, B.; Hall, C. Positive Holes and Their Role during the Build-up of Stress Prior to the Chi-Chi Earthquake. In Proceedings of the International Conference in Commemoration of 5th Anniversary of the 1999 Chi-Chi Earthquake, Taipei, Taiwan, 8–12 September 2004. [Google Scholar]
- Zhu, C.; Jiao, Z.; Shan, X.; Zhang, G.; Li, Y. Land Surface Temperature Variation Following the 2017 Mw 7.3 Iran Earthquake. Remote Sens. 2019, 11, 2411. [Google Scholar] [CrossRef]
- Lu, X.; Meng, Q.Y.; Gu, X.F.; Zhang, X.D.; Xie, T.; Geng, F. Thermal Infrared Anomalies Associated with Multi-Year Earthquakes in the Tibet Region Based on China’s FY-2E Satellite Data. Adv. Space Res. 2016, 58, 989–1001. [Google Scholar] [CrossRef]
- Zhong, M.; Shan, X.; Zhang, X.; Qu, C.; Guo, X.; Jiao, Z. Thermal Infrared and Ionospheric Anomalies of the 2017 Mw6.5 Jiuzhaigou Earthquake. Remote Sens. 2020, 12, 2843. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, L.; Mao, W.; Ding, Y.; He, M. Discriminating Possible Causes of Microwave Brightness Temperature Positive Anomalies Related with May 2008 Wenchuan Earthquake Sequence. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1903–1916. [Google Scholar] [CrossRef]
- Pergola, N.; Aliano, C.; Coviello, I.; Filizzola, C.; Genzano, N.; Lacava, T.; Lisi, M.; Mazzeo, G.; Tramutoli, V. Using RST Approach and EOS-MODIS Radiances for Monitoring Seismically Active Regions: A Study on the 6 April 2009 Abruzzo Earthquake. Nat. Hazards Earth Syst. Sci. 2010, 10, 239–249. [Google Scholar] [CrossRef]
- Ouzounov, D.; Liu, D.; Chunli, K.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing Long Wave Radiation Variability from IR Satellite Data Prior to Major Earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Kong, X.; Bi, Y.; Glass, D.H. Detecting Seismic Anomalies in Outgoing Long-Wave Radiation Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 649–660. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Q.; Wang, Z.; Lu, X.; Hu, D. Temperature Variations in Multiple Air Layers before the Mw 6.2 2014 Ludian Earthquake, Yunnan, China. Remote Sens. 2021, 13, 884. [Google Scholar] [CrossRef]
- Khalili, M.; Eskandar, S.S.A.; Panah, S.K.A. Thermal Anomalies Detection before Saravan Earthquake (April 16th, 2013, MW = 7.8) Using Time Series Method, Satellite, and Meteorological Data. J. Earth Syst. Sci. 2020, 129, 5. [Google Scholar] [CrossRef]
- Jing, F.; Singh, R.P.; Cui, Y.; Sun, K. Microwave Brightness Temperature Characteristics of Three Strong Earthquakes in Sichuan Province, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 513–522. [Google Scholar] [CrossRef]
- Peleli, S.; Kouli, M.; Vallianatos, F. Satellite-Observed Thermal Anomalies and Deformation Patterns Associated to the 2021, Central Crete Seismic Sequence. Remote Sens. 2022, 14, 3413. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Q. A Statistical Analysis of TIR Anomalies Extracted by RSTs in Relation to an Earthquake in the Sichuan Area Using MODIS LST Data. Nat. Hazards Earth Syst. Sci. 2019, 19, 535–549. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Q.; Ouillon, G.; Sornette, D.; Ma, W.; Zhang, L.; Zhao, J.; Qi, Y.; Geng, F. Spatially Variable Model for Extracting TIR Anomalies before Earthquakes: Application to Chinese Mainland. Remote Sens. Environ. 2021, 267, 112720. [Google Scholar] [CrossRef]
- Fu, C.C.; Lee, L.C.; Ouzounov, D.; Jan, J.C. Earth’s Outgoing Longwave Radiation Variability Prior to M $\geq$6.0 Earthquakes in the Taiwan Area During 2009–2019. Front. Earth Sci. 2020, 8, 364. [Google Scholar] [CrossRef]
- Genzano, N.; Filizzola, C.; Hattori, K.; Pergola, N.; Tramutoli, V. Statistical Correlation Analysis Between Thermal Infrared Anomalies Observed from MTSATs and Large Earthquakes Occurred in Japan (2005–2015). J. Geophys. Res. Solid Earth 2021, 126, e2020JB020108. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Q.; Ouillon, G.; Zhang, L.; Hu, D.; Ma, W.; Sornette, D. Long-Term Statistical Evidence Proving the Correspondence between Tir Anomalies and Earthquakes Is Still Absent. Eur. Phys. J. Spec. Top. 2021, 230, 133–150. [Google Scholar] [CrossRef]
- Eleftheriou, A.; Filizzola, C.; Genzano, N.; Lacava, T.; Lisi, M.; Paciello, R.; Pergola, N.; Vallianatos, F.; Tramutoli, V. Long-Term RST Analysis of Anomalous TIR Sequences in Relation with Earthquakes Occurred in Greece in the Period 2004–2013. Pure Appl. Geophys. 2015, 173, 285–303. [Google Scholar] [CrossRef]
- Filizzola, C.; Corrado, A.; Genzano, N.; Lisi, M.; Pergola, N.; Colonna, R.; Tramutoli, V. RST Analysis of Anomalous TIR Sequences in Relation with Earthquakes Occurred in Turkey in the Period 2004–2015. Remote Sens. 2022, 14, 381. [Google Scholar] [CrossRef]
- Molchan, G.M. Strategies in Strong Earthquake Prediction. Phys. Earth Planet. Inter. 1990, 61, 84–98. [Google Scholar] [CrossRef]
- Molchan, G.M. Structure of Optimal Strategies in Earthquake Prediction. Tectonophysics 1991, 193, 267–276. [Google Scholar] [CrossRef]
- Swets, J.A. The Relative Operating Characteristic in Psychology. Science 1973, 182, 990–1000. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guy, O.; Shyam, N.; Didier, S.; Meng, Q. A New 3-D Error Diagram: An Effective and Better Tool for Finding TIR Anomalies Related to Earthquakes. IEEE Trans. Geosci. Remote Sens. under review.
- Zechar, J.D.; Jordan, T.H. Testing Alarm-Based Earthquake Predictions. Geophys. J. Int. 2008, 172, 715–724. [Google Scholar] [CrossRef]
- Tiampo, K.F.; Rundle, J.B.; McGinnis, S.; Gross, S.J.; Klein, W. Mean-Field Threshold Systems and Phase Dynamics: An Application to Earthquake Fault Systems. Europhys. Lett. EPL 2002, 60, 481–488. [Google Scholar] [CrossRef]
- DeVries, P.M.R.; Viégas, F.; Wattenberg, M.; Meade, B.J. Deep Learning of Aftershock Patterns Following Large Earthquakes. Nature 2018, 560, 632–634. [Google Scholar] [CrossRef]
- Mignan, A.; Broccardo, M. One Neuron versus Deep Learning in Aftershock Prediction. Nature 2019, 574, E1–E3. [Google Scholar] [CrossRef]
- Yousefzadeh, M. Spatiotemporally Explicit Earthquake Prediction Using Deep Neural Network. Soil Dyn. Earthq. Eng. 2021, 11, 106663. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Y.; Yu, L.; Li, P. Earthquake Prediction Based on Spatio-Temporal Data Mining: An LSTM Network Approach. IEEE Trans. Emerg. Top. Comput. 2020, 8, 148–158. [Google Scholar] [CrossRef]
- Berhich, A.; Belouadha, F.Z.; Kabbaj, M.I. LSTM-Based Models for Earthquake Prediction. In Proceedings of the 3rd International Conference on Networking, Information Systems & Security, Marrakech, Morocco, 31 March–2 April 2020; ACM: Marrakech, Morocco, 2020; pp. 1–7. [Google Scholar]
- Banna, M.d.H.A.; Ghosh, T.; Nahian, M.d.J.A.; Taher, K.A.; Kaiser, M.S.; Mahmud, M.; Hossain, M.S.; Andersson, K. Attention-Based Bi-Directional Long-Short Term Memory Network for Earthquake Prediction. IEEE Access 2021, 9, 56589–56603. [Google Scholar] [CrossRef]
- Shodiq, M.N.; Kusuma, D.H.; Rifqi, M.G.; Barakbah, A.R.; Harsono, T. Adaptive Neural Fuzzy Inference System and Automatic Clustering for Earthquake Prediction in Indonesia. JOIV Int. J. Inform. Vis. 2019, 3, 47–53. [Google Scholar] [CrossRef]
- Jiang, C.; Wei, X.; Cui, X.; You, D. Application of Support Vector Machine to Synthetic Earthquake Prediction. Earthq. Sci. 2009, 22, 315–320. [Google Scholar] [CrossRef]
- Parsons, T. On the Use of Receiver Operating Characteristic Tests for Evaluating Spatial Earthquake Forecasts. Geophys. Res. Lett. 2020, 47, e2020GL088570. [Google Scholar] [CrossRef]
- Blackett, M.; Wooster, M.J.; Malamud, B.D. Exploring Land Surface Temperature Earthquake Precursors: A Focus on the Gujarat (India) Earthquake of 2001. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, Y. Discovery of Spatial-Temporal Causal Interactions between Thermal and Methane Anomalies Associated with the Wenchuan Earthquake. Eur. Phys. J. Spec. Top. 2021, 230, 247–261. [Google Scholar] [CrossRef]
- Weiyu, M.; Xuedong, Z.; Liu, J.; Yao, Q.; Zhou, B.; Yue, C.; Kang, C.; Lu, X. Influences of Multiple Layers of Air Temperature Differences on Tidal Forces and Tectonic Stress before, during and after the Jiujiang Earthquake. Remote Sens. Environ. 2018, 210, 159–165. [Google Scholar] [CrossRef]
- Genzano, N.; Filizzola, C.; Paciello, R.; Pergola, N.; Tramutoli, V. Robust Satellite Techniques (RST) for Monitoring Earthquake Prone Areas by Satellite TIR Observations: The Case of 1999 Chi-Chi Earthquake (Taiwan). J. Asian Earth Sci. 2015, 114, 289–298. [Google Scholar] [CrossRef]
- Genzano, N.; Filizzola, C.; Lisi, M.; Pergola, N.; Tramutoli, V. Toward the Development of a Multi Parametric System for a Short-Term Assessment of the Seismic Hazard in Italy. Ann. Geophys. 2020, 63, PA550. [Google Scholar] [CrossRef]
- Blum, M.; Lensky, I.M.; Nestel, D. Estimation of Olive Grove Canopy Temperature from MODIS Thermal Imagery Is More Accurate than Interpolation from Meteorological Stations. Agric. For. Meteorol. 2013, 176, 90–93. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.L. Quality Assessment and Validation of the MODIS Global Land Surface Temperature. Int. J. Remote Sens. 2004, 25, 261–274. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, L.; Zheng, D.; Tao, J. Cloudiness Variations over the Qinghai-Tibet Plateau during 1971–2004. J. Geogr. Sci. 2008, 18, 142–154. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X.; Zhan, W.; Gottsche, F.M.; Liu, S.; Olesen, F.S.; Hu, W.; Dai, F. A Thermal Sampling Depth Correction Method for Land Surface Temperature Estimation from Satellite Passive Microwave Observation Over Barren Land. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4743–4756. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Gottsche, F.M.; Zhan, W.; Liu, S.; Cao, R. A Method Based on Temporal Component Decomposition for Estimating 1-Km All-Weather Land Surface Temperature by Merging Satellite Thermal Infrared and Passive Microwave Observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4670–4691. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A Practical Reanalysis Data and Thermal Infrared Remote Sensing Data Merging (RTM) Method for Reconstruction of a 1-Km All-Weather Land Surface Temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, J.; Zhang, X.; Zhang, X.; Ma, J.; Ding, L. Daily 1-Km All-Weather Land Surface Temperature Dataset for the Chinese Landmass and Its Surrounding Areas (TRIMS LST.; 2000–2020); National Tibetan Plateau Data Center: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Žalohar, J. Gutenberg-Richter’s Law. In Developments in Structural Geology and Tectonics; Elsevier: Amsterdam, The Netherlands, 2018; pp. 173–178. [Google Scholar]
- Ellsworth, W.L.; Fatih, B. Nucleation of the 1999 Izmit Earthquake by a Triggered Cascade of Foreshocks. Nat. Geosci. 2018, 11, 531–535. [Google Scholar] [CrossRef]
- Helmstetter, A.; Sornette, D.; Grasso, J.R. Mainshocks Are Aftershocks of Conditional Foreshocks: How Do Foreshock Statistical Properties Emerge from Aftershock Laws: Mainshocks are Aftershocks of Conditional Foreshocks. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Bouchon, M.; Durand, V.; Marsan, D.; Karabulut, H.; Schmittbuhl, J. The Long Precursory Phase of Most Large Interplate Earthquakes. Nat. Geosci. 2013, 6, 299–302. [Google Scholar] [CrossRef]
- Carl, T.; Stephen, H.; Vipul, S.; Jessica, H.; Yoshihiro, K.; Paul, A.J.; Chen, J.; Natalia, R.; Kyle, S.; West, M.E. Earthquake Nucleation and Fault Slip Complexity in the Lower Crust of Central Alaska. Nat. Geosci. 2018, 11, 536–541. [Google Scholar]
- Tormann, T.; Enescu, B.; Woessner, J.; Wiemer, S. Randomness of Megathrust Earthquakes Impliedby Rapid Stress Recovery after the Japanearthquake. Nat. Geosci. 2015, 8, 152–158. [Google Scholar] [CrossRef]
- Zhang, Y. Earthquake Forecasting Model Based on the Thermal Infrared Anomalies for Chinese Mainland. Ph.D. Thesis, University of Chinese Academy of Sciences, Huairou District, China, 2021. [Google Scholar]
- Gardner, J.K.; Knopoff, L. Is the Sequence of Earthquakes in Southern California, with Aftershocks Removed, Poissonian? Bull. Seismol. Soc. Am. 1974, 64, 1363–1367. [Google Scholar] [CrossRef]
- Knopoff, L. The Statistics of Earthquakes in Southern California. Seismol. Soc. Am. 1964, 54, 1871–1873. [Google Scholar] [CrossRef]
- Knopoff, L.; Gardner, J.K. Higher Seismic Activity During Local Night on the Raw Worldwide Earthquake Catalogue. Geophys. J. R. Astron. Soc. 2010, 28, 311–313. [Google Scholar] [CrossRef]
- Reasenberg, P. Second-Order Moment of Central California Seismicity, 1969–1982. J. Geophys. Res. 1985, 90, 5479–5495. [Google Scholar] [CrossRef]
- Frohlich, C.; Davis, S.D. Single-Link Cluster Analysis as A Method to Evaluate Spatial and Temporal Properties of Earthquake Catalogues. Geophys. J. Int. 1990, 100, 19–32. [Google Scholar] [CrossRef]
- Zaliapin, I.; Gabrielov, A.; Keilis-Borok, V.; Wong, H. Clustering Analysis of Seismicity and Aftershock Identification. Phys. Rev. Lett 2008, 101, 018501. [Google Scholar] [CrossRef]
- Baiesi, M.; Paczuski, M. Scale Free Networks of Earthquakes and Aftershocks. Phys. Rev. E 2004, 69, 066106. [Google Scholar] [CrossRef]
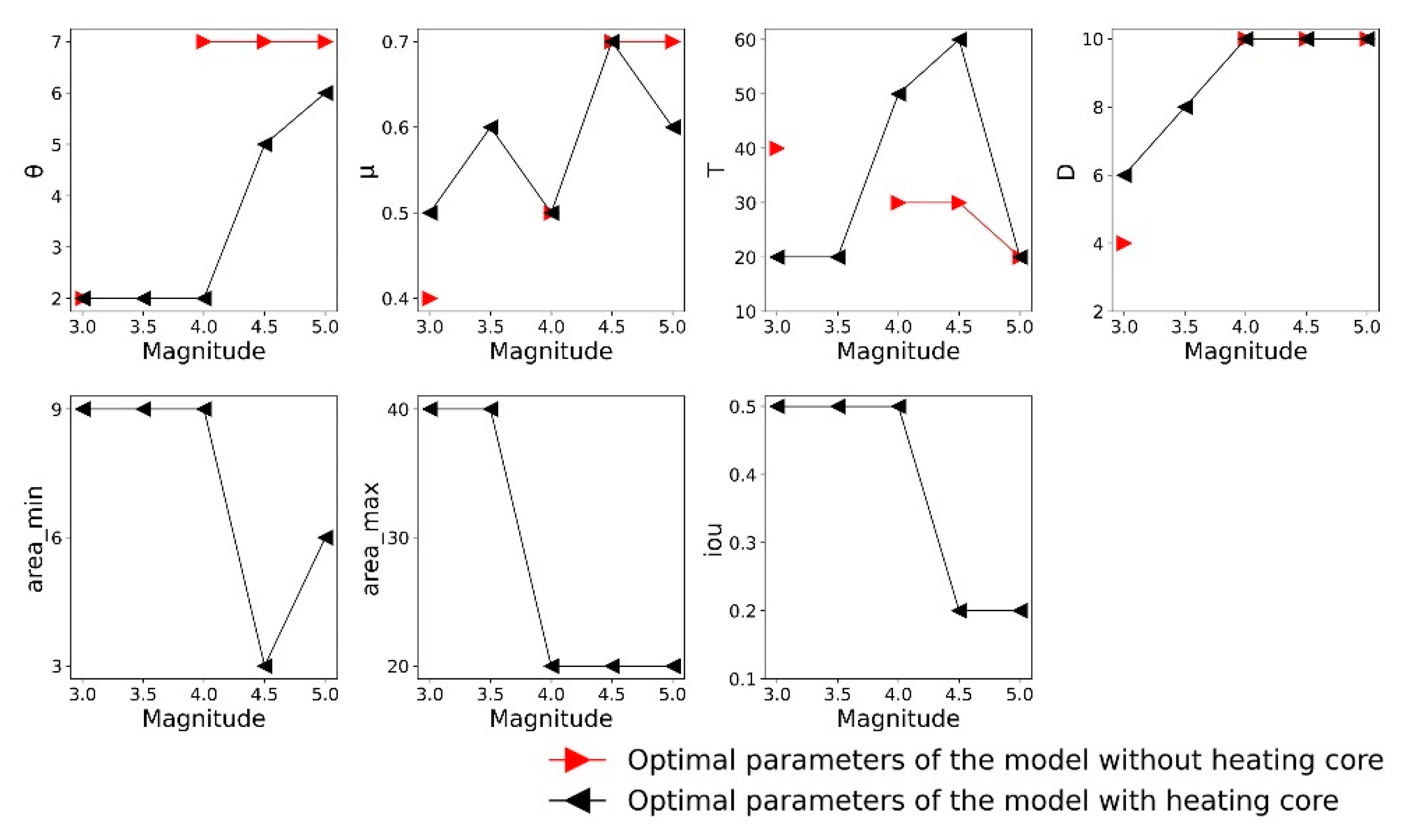

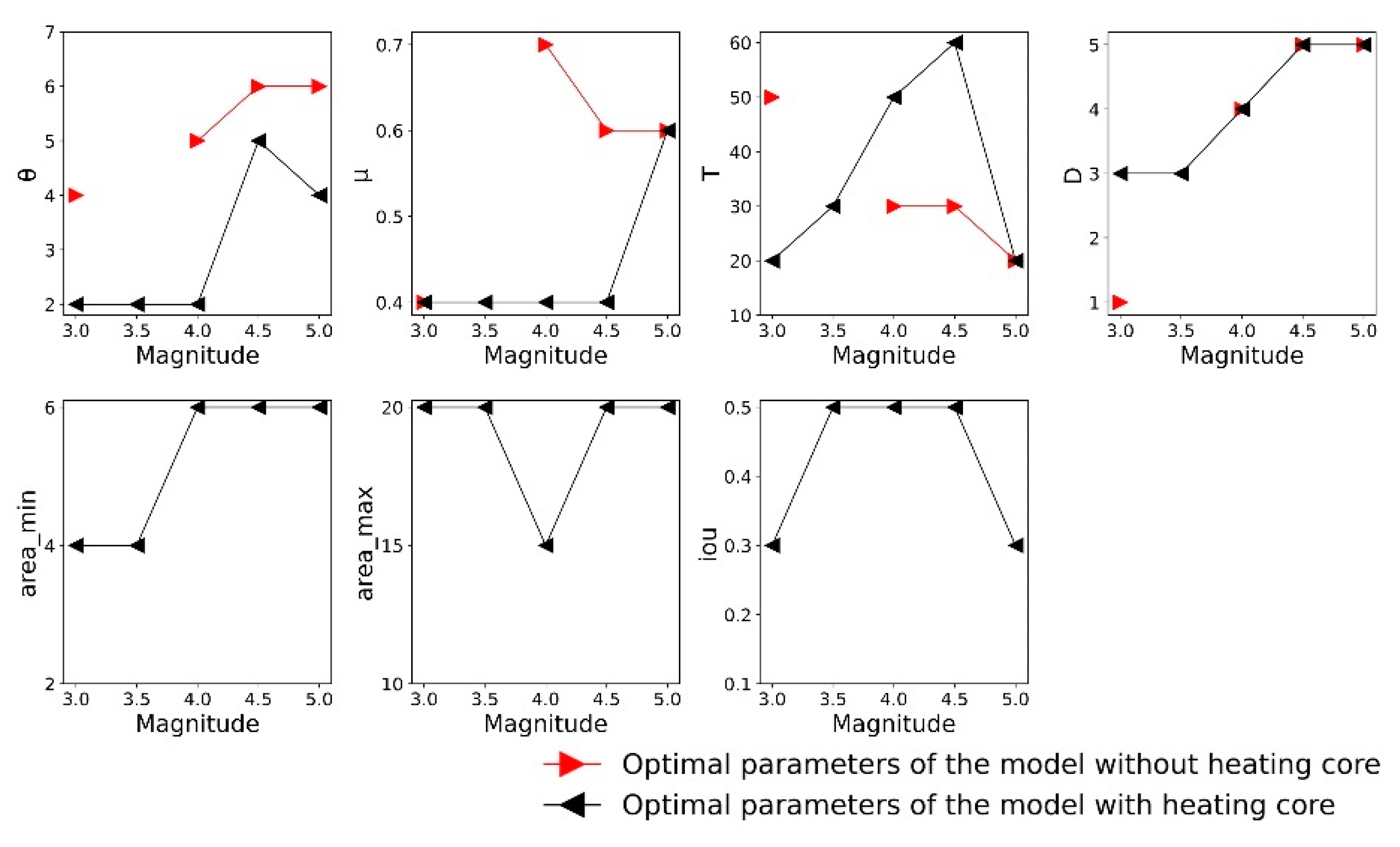
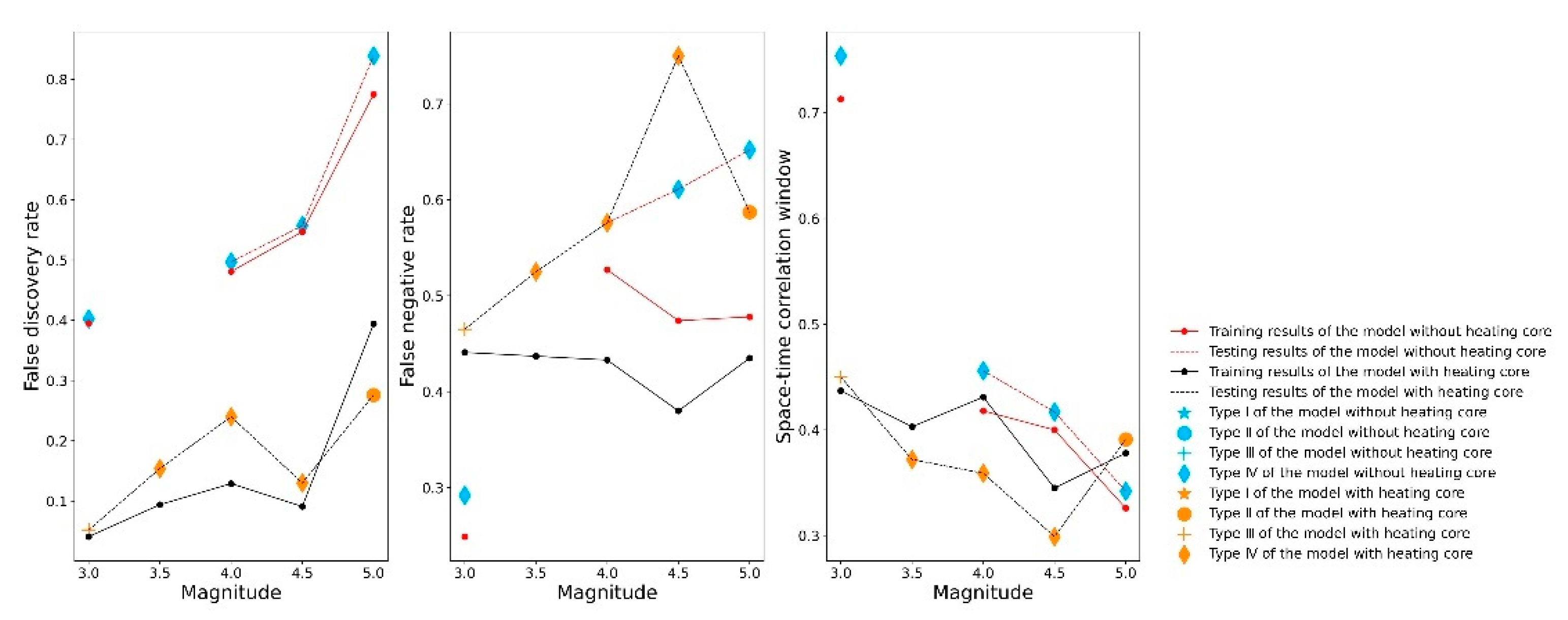
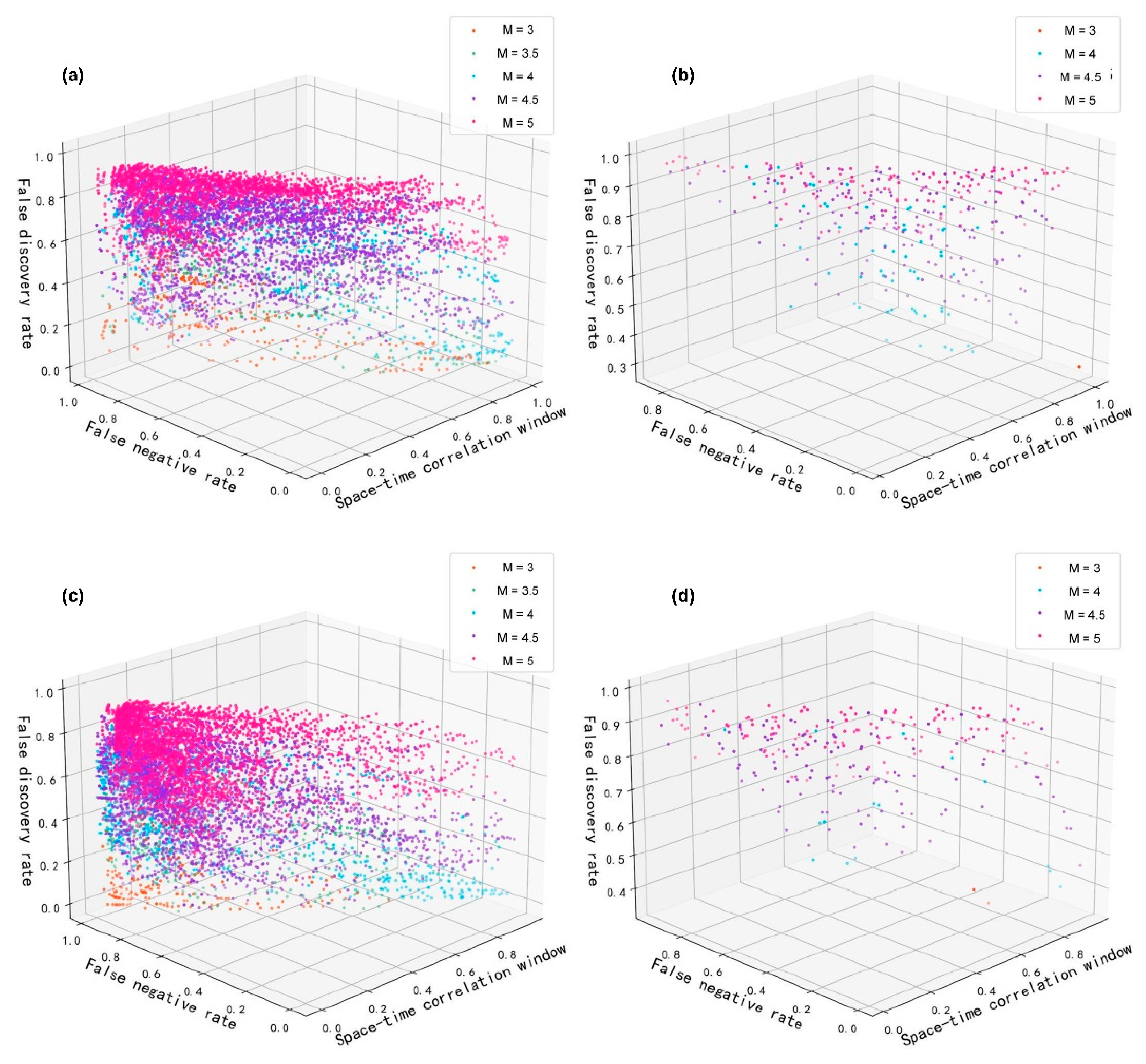

| Type | Condition |
|---|---|
| I | P1 ≤ 0.05 and P2 ≤ 0.05 |
| II | P1 ≥ 0.05 and P2 ≤ 0.05 |
| III | P1 ≤ 0.05 and P2 ≥ 0.05 |
| IV | P1 ≥ 0.05 and P2 ≥ 0.05 |
| Parameter | Heating Core | Value |
|---|---|---|
| Yes/No | 50 (km) | |
| Yes/No | 2, 3, 4, 5, 6, 7 (K) | |
| Yes | 3, 6, 9 (50 km × 50 km) | |
| Yes | 20, 30, 40 (50 km × 50 km) | |
| Yes | 0.1, 0.2, 0.3, 0.4, 0.5 | |
| Yes/No | 10, 20, 30, 40, 50, 60 (days) | |
| Yes/No | 2, 4, 6, 8, 10 (50 km) | |
| Yes/No | 3, 3.5, 4, 4.5, 5 |
| Parameter | Heating Core | Value |
|---|---|---|
| Yes/No | 100 (km) | |
| Yes/No | 2, 3, 4, 5, 6, 7 (K) | |
| Yes | 2, 4, 6 (100 km × 100 km) | |
| Yes | 10, 15, 20 (100 km × 100 km) | |
| Yes | 0.1, 0.2, 0.3, 0.4, 0.5 | |
| Yes/No | 10, 20, 30, 40, 50, 60 (day) | |
| Yes/No | 1, 2, 3, 4, 5 (100 km) | |
| Yes/No | 3, 3.5, 4, 4.5, 5 |
| Parameter | Heating Core | Value |
|---|---|---|
| Yes/No | 50 (km) | |
| Yes/No | 0.4, 0.5, 0.6, 0.7 | |
| Yes/No | 2, 3, 4, 5, 6, 7 (K) | |
| Yes | 3, 6, 9 (50 km × 50 km) | |
| Yes | 20, 30, 40 (50 km × 50 km) | |
| Yes | 0.1, 0.2, 0.3, 0.4, 0.5 | |
| Yes/No | 10, 20, 30, 40, 50, 60 (day) | |
| Yes/No | 2, 4, 6, 8, 10 (50 km) | |
| Yes/No | 3, 3.5, 4, 4.5, 5 |
| Parameter | Heating Core | Value |
|---|---|---|
| Yes/No | 100 (km) | |
| Yes/No | 0.4, 0.5, 0.6, 0.7 | |
| Yes/No | 2, 3, 4, 5, 6, 7 (K) | |
| Yes | 2, 4, 6 (100 km × 100 km) | |
| Yes | 10, 15, 20 (100 km × 100 km) | |
| Yes | 0.1, 0.2, 0.3, 0.4, 0.5 | |
| Yes/No | 10, 20, 30, 40, 50, 60 (day) | |
| Yes/No | 1, 2, 3, 4, 5 (100 km) | |
| Yes/No | 3, 3.5, 4, 4.5, 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, C.; Meng, Q.; Zhang, Y.; Allam, M.; Wu, P.; Zhang, L.; Lu, X. Application of 3D Error Diagram in Thermal Infrared Earthquake Prediction: Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 5925. https://doi.org/10.3390/rs14235925
Zhan C, Meng Q, Zhang Y, Allam M, Wu P, Zhang L, Lu X. Application of 3D Error Diagram in Thermal Infrared Earthquake Prediction: Qinghai–Tibet Plateau. Remote Sensing. 2022; 14(23):5925. https://doi.org/10.3390/rs14235925
Chicago/Turabian StyleZhan, Chengxiang, Qingyan Meng, Ying Zhang, Mona Allam, Pengcheng Wu, Linlin Zhang, and Xian Lu. 2022. "Application of 3D Error Diagram in Thermal Infrared Earthquake Prediction: Qinghai–Tibet Plateau" Remote Sensing 14, no. 23: 5925. https://doi.org/10.3390/rs14235925
APA StyleZhan, C., Meng, Q., Zhang, Y., Allam, M., Wu, P., Zhang, L., & Lu, X. (2022). Application of 3D Error Diagram in Thermal Infrared Earthquake Prediction: Qinghai–Tibet Plateau. Remote Sensing, 14(23), 5925. https://doi.org/10.3390/rs14235925










