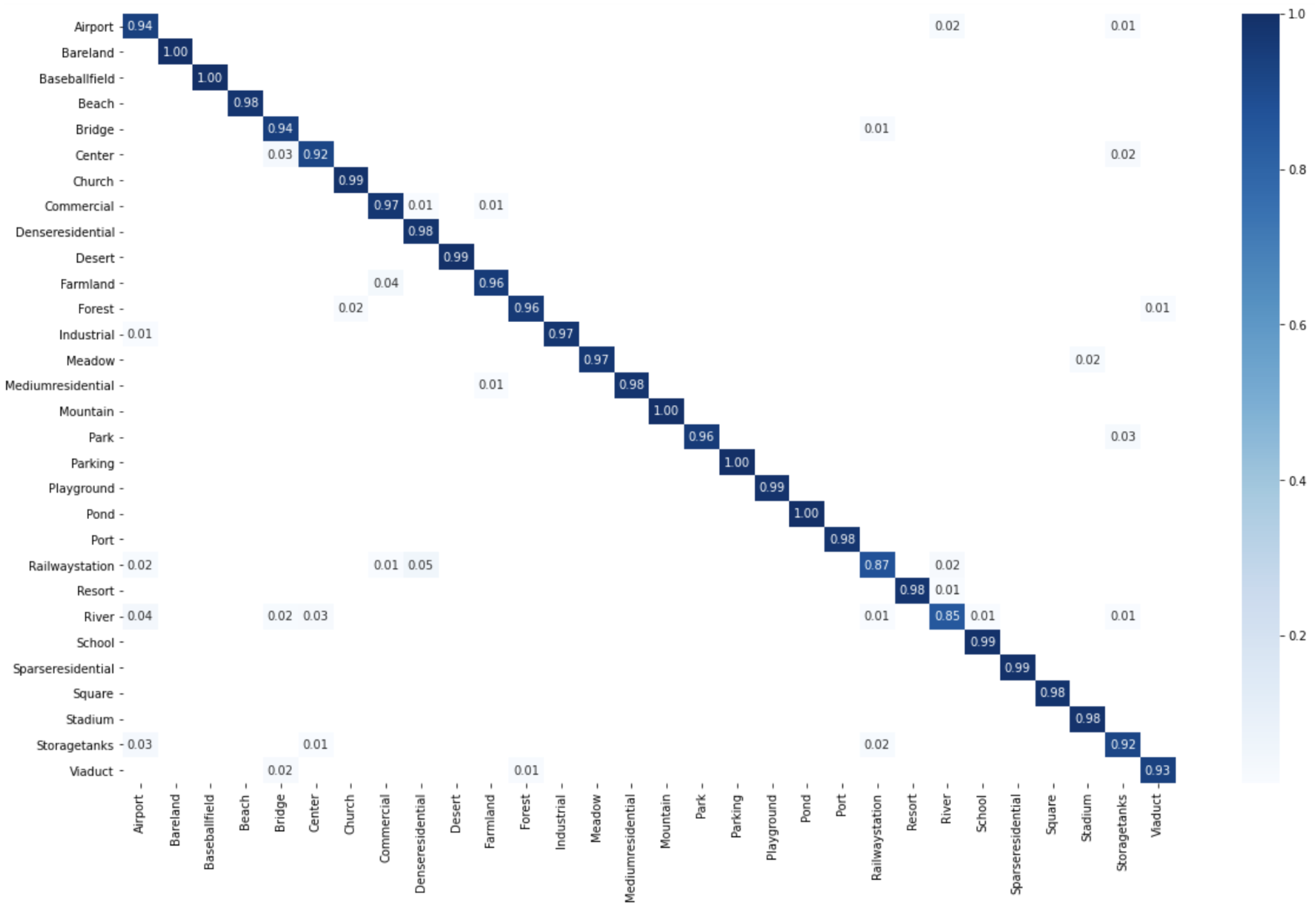
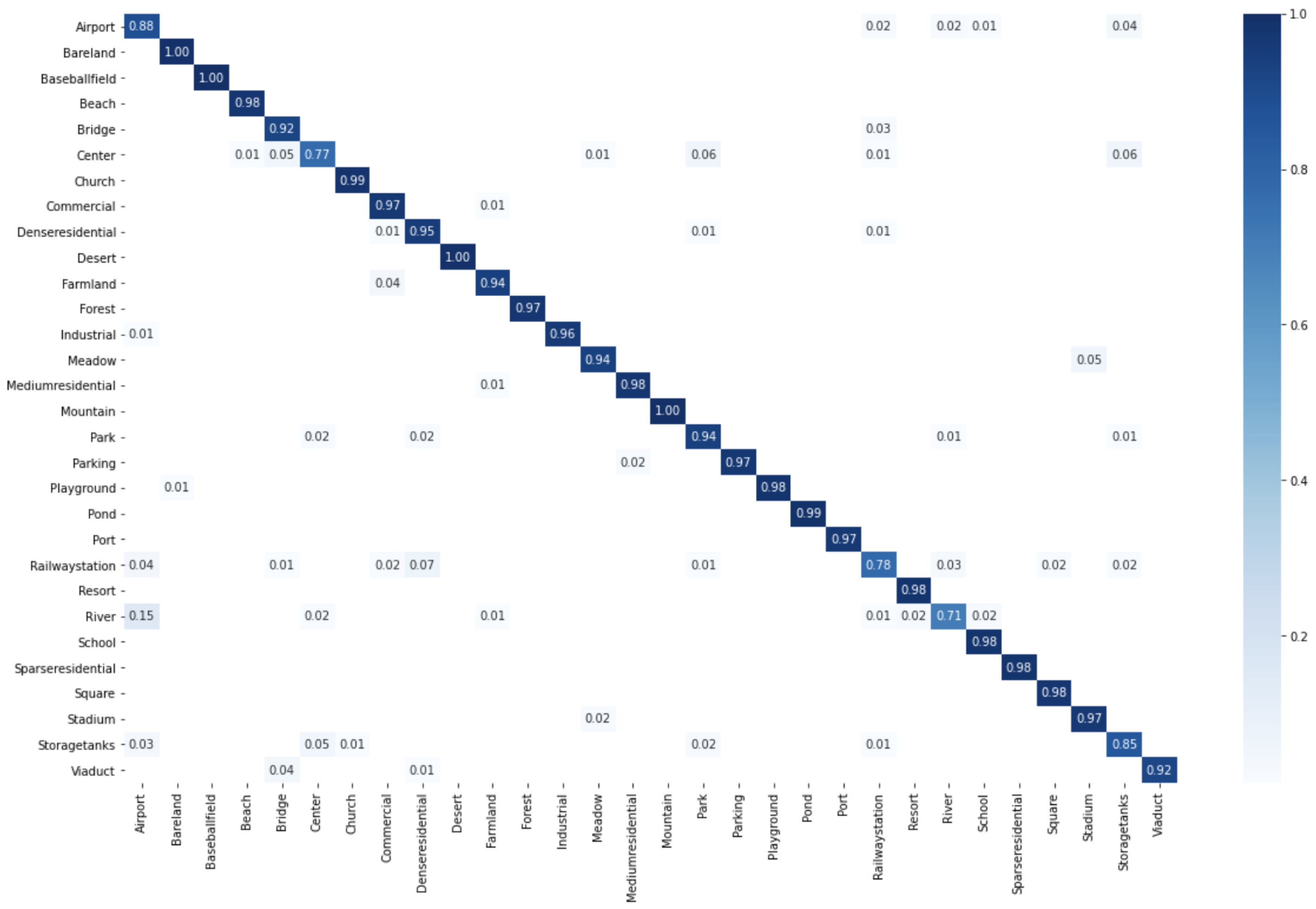
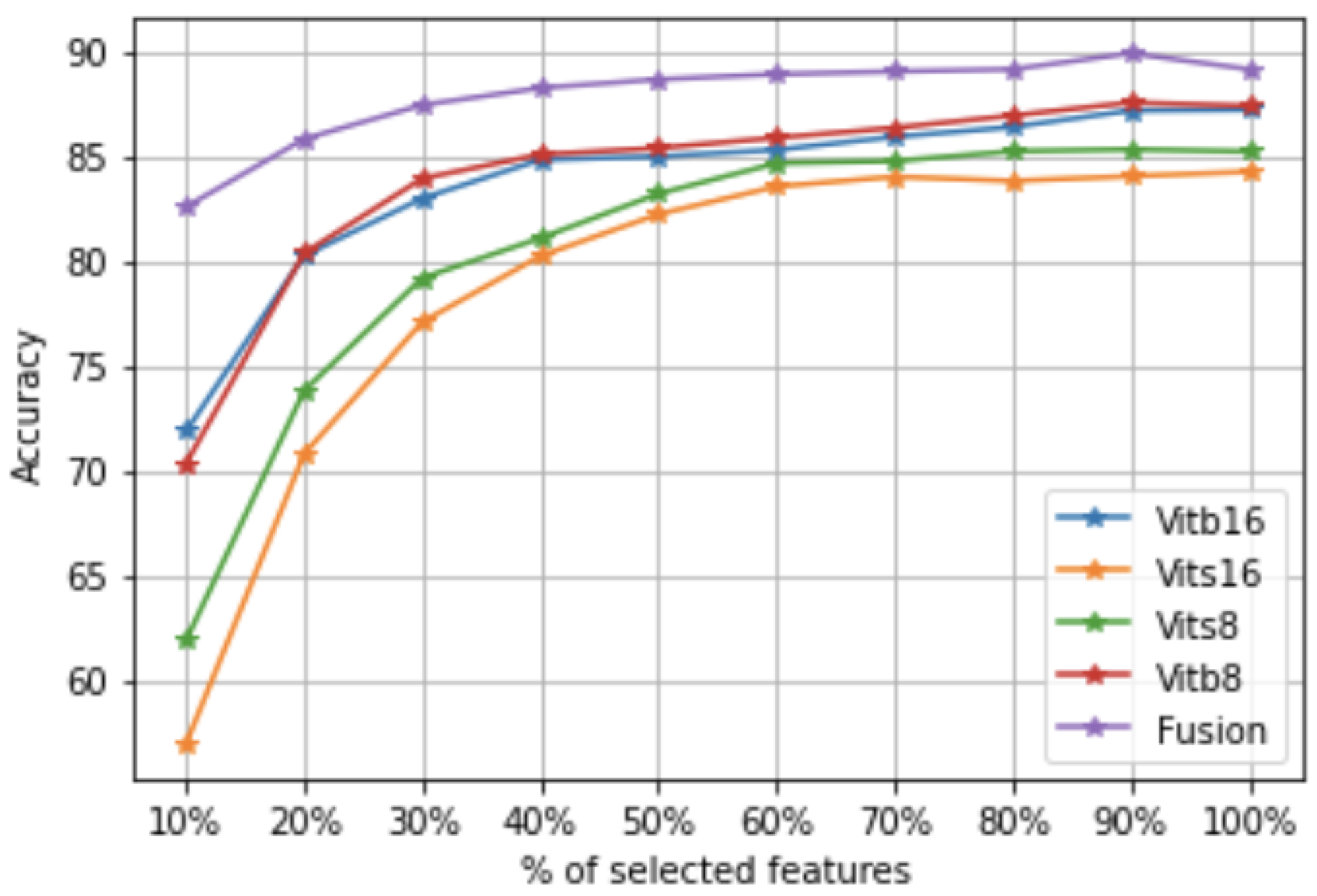
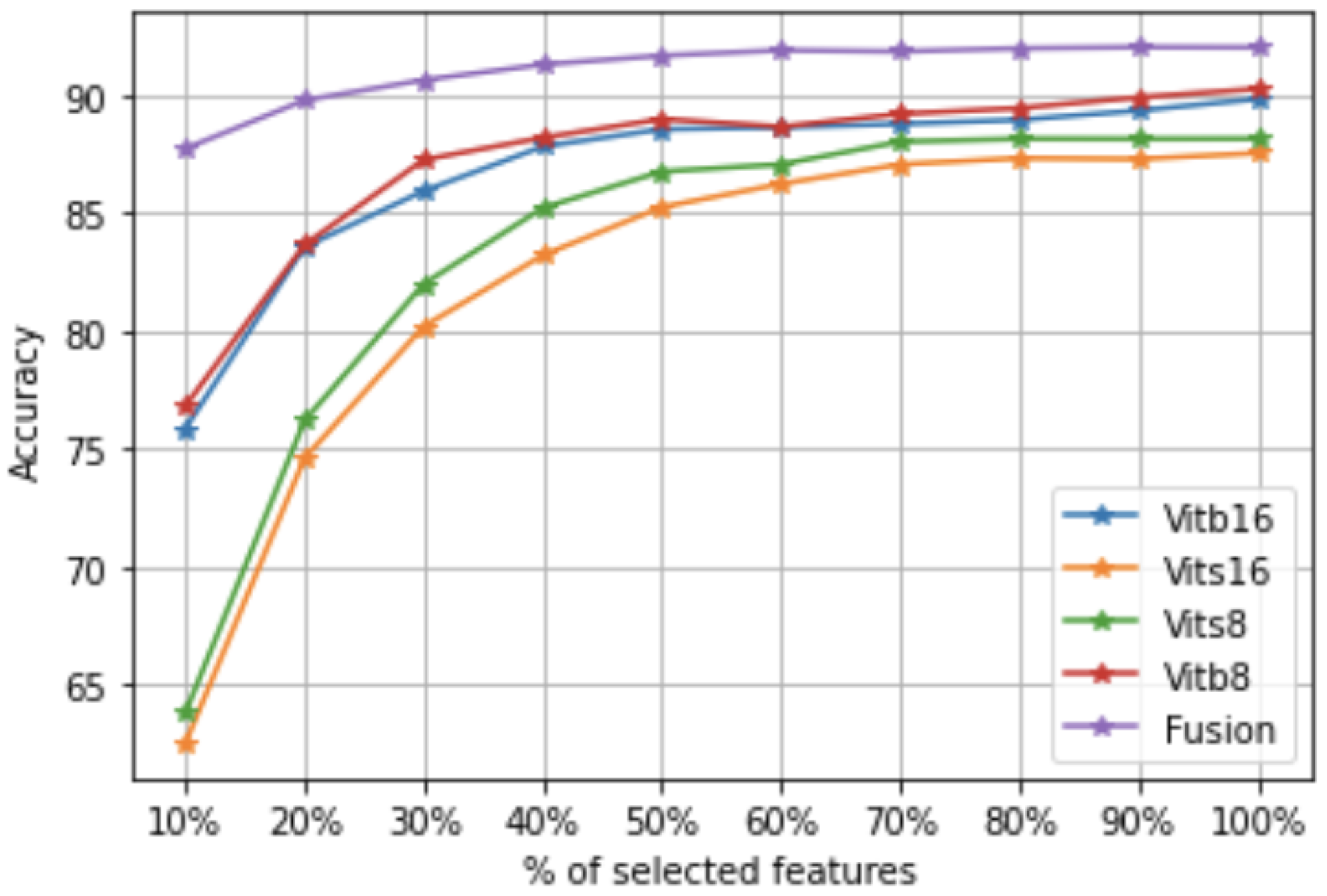
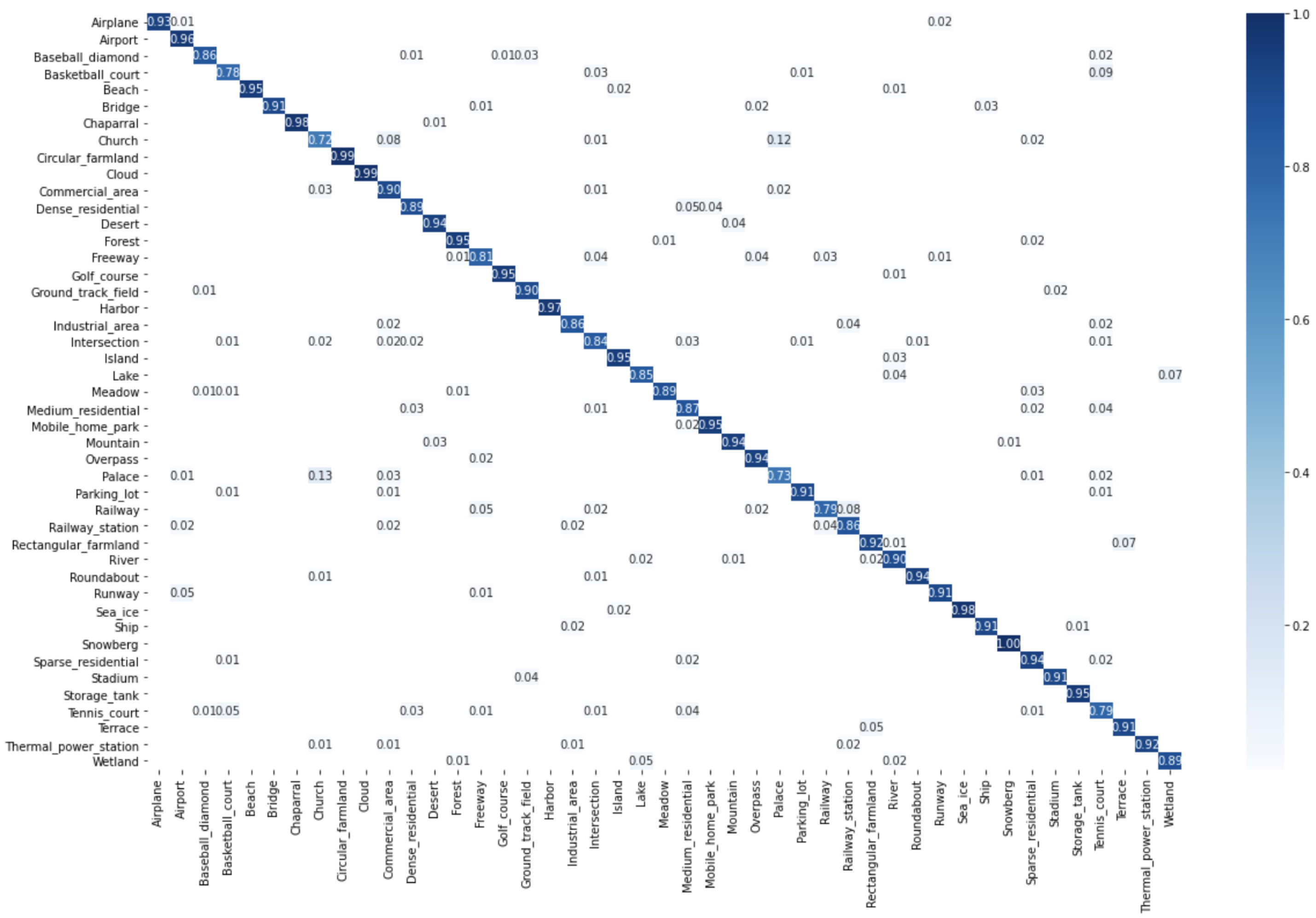
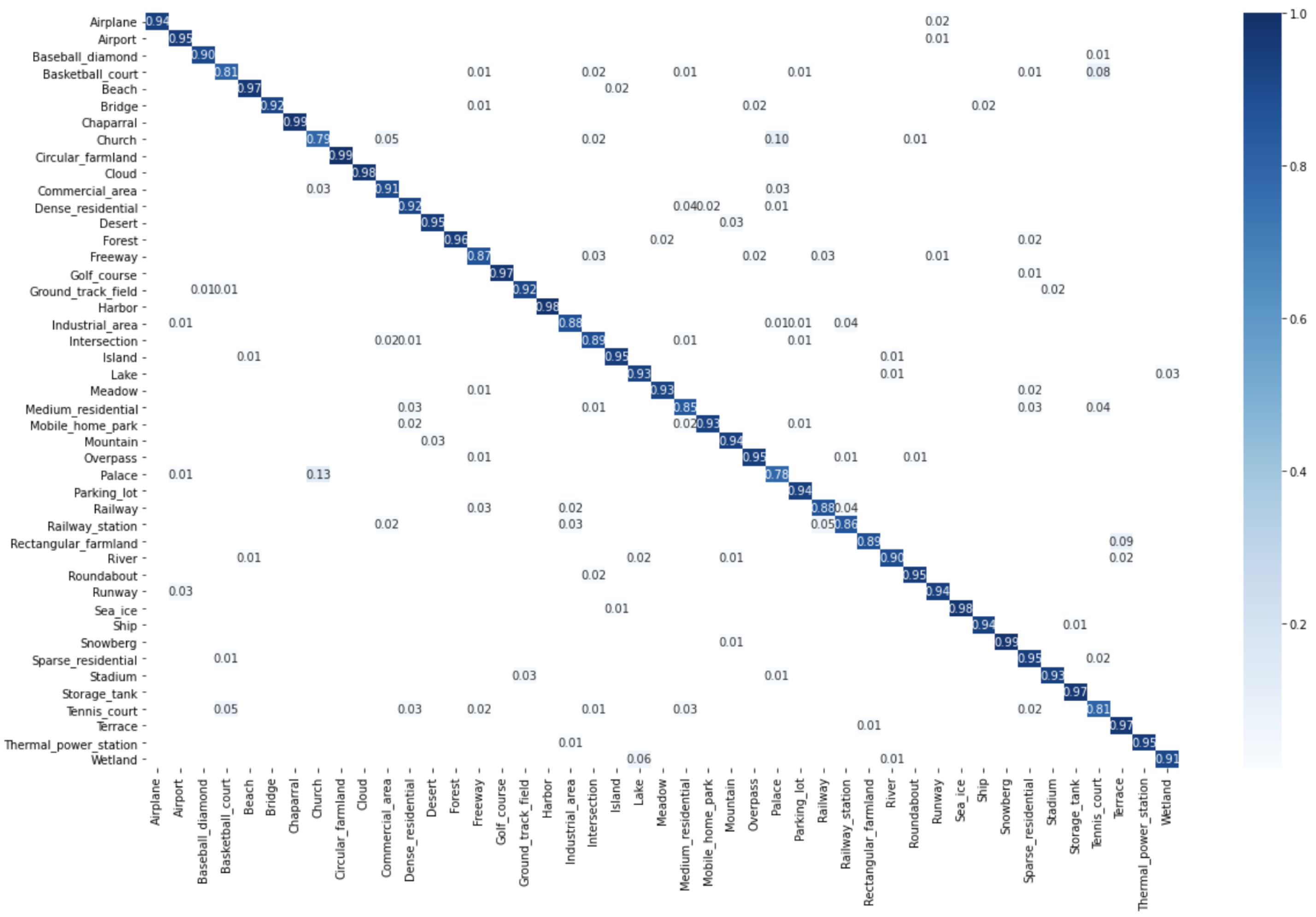
1. Introduction
The high-speed development of remote sensing instruments and technologies has provided us with the ability to capture high and very high-resolution (VHR) images. This raises challenging problems concerning appropriate and efficient methods for image scene understanding and classification. The classification of VHR images into the corresponding and adequate classes of the same semantics (according to the image scene) is critical. In the last decade, several methods have been proposed for VHR image scene understanding. The existing scene classification methods are distinguished by three categories, which depend on the pixel-/object-level image representation, in which the VHR image scene classification techniques directly depend on the holistic representation of the image scene as demonstrated in [
1]. These kinds of methods represent the VHR image scenes with handcrafted features, which are also called low-level features, such as texture descriptors [
2], color histogram (CH) [
3], the scale-invariant feature transform (SIFT) [
4], and the histogram of the oriented gradient (HOG) [
5].
Several works based on low-level features have been developed for VHR image scene classification. Yang and Newsam [
6] compared Gabor texture features and SIFT features for the IKONOS remote sensing image classification, and Dos-Santos et al. [
2] evaluated the CH descriptor and local binary patterns (LBP) for remote sensing image retrieval and classification [
7]. As demonstrated in [
6,
7,
8], image scene classification based on a single kind of low-level feature achieved high accuracy.
Unfortunately, in real applications, one single feature is not able to well represent the entire information of the image scene, so scene information is usually described by a set of descriptors, which better improves the results than singular features [
9,
10]. Lou et al. [
11] combined the Gabor filters, SIFT features, simple radiometric features, Gaussian wavelet features [
12], gray level co-occurrence matrix (GLCM), and shape features [
13], with the aim to form a global features representation for remote sensing image indexing. Avramovic and Risojevic [
14] proposed combining SIFT with GIST features for aerial scene classification. In addition, other approaches were developed to select a subset of low-level features for aerial image classification [
15]. Although the combination of low-level features can often improve the results, how to effectively combine different types of features is a challenging problem. Moreover, handcrafted features are not capable of accurately representing the entire content of the image scene, especially when the scene images become more challenging. To alleviate this concern, other techniques have been developed for image scene descriptions based on mid-level features.
Mid-level approaches [
16,
17,
18] often represent the image scene by coding low-level feature descriptors. To describe the entire image scene, they build blocks to construct the global image features, such as the bag of visual words (BOVW) [
19], which is the most popular encoding model for remote sensing image scene descriptions [
20,
21,
22,
23], and the HOG feature-based models [
24].
Approaches based on low-level and mid-level features require a considerable amount of engineering skills and domain expertise for the VHR image scene understanding. To overcome this limit, deep learning-based methods were introduced to classify remote sensing images, which learned features from input data using a general-purpose learning procedure via the deep architecture of neural networks. The main advantage of deep learning methods is the ability to learn more informative and powerful features to describe the input data with several levels of abstraction [
25].
Convolutional neural networks (CNNs) and their variants are popular deep learning models that have proven their effectiveness for image scene classifications as demonstrated with ImageNet large-scale visual recognition competition (ILSVRC) [
26]. CNNs can learn the image scene by leveraging a hierarchical representation that describes the content of an image. Recently, CNNs have become widely applied in remote sensing image analyses, thus becoming more suitable for scene classification and retrieval from VHR images [
25].
Based on the combination of various deep neural networks for VHR image scene interpretations, Zhang et al. [
27] introduced a novel framework that achieved specifiable results when applied to the UC Merced data set [
28]. The small sizes of remote sensing data sets make it extremely hard to train new a CNN model [
29]. However, pre-trained CNN models have achieved acceptable results for VHR remote sensing image scene classification [
30]. In this context, Othman et al. [
30] leveraged pre-trained CNN models to generate the preliminary representation features from an image scene; they applied a sparse autoencoder that learned the final feature description of the target image. In the same vein, Hu et al. [
25] employed pre-trained CNNs for scene classification in two different ways. In the fist way, they used two fully connected layers as final feature descriptors of the target images. In the second step, they applied convolutional layers as initial feature descriptors of the target image scenes with different scale sizes, then they took advantage of popular coding approaches, such as BOVW, to encode the dense convolutional features into a global features descriptor.
In recent years, transformers have revolutionized the field of deep learning. Transformers have achieved extraordinary results in different challenges of natural language processing (NLP) [
31,
32]. Encouraged by the success of transformer models in the NLP area, there have been important advances in transformers in computer vision tasks. ViT models achieved great results in various challenges of computer vision, such as image classification [
33]. As mentioned in [
34], deep feature fusion is an efficient technique for understanding remote sensing images. In this study, we explored the use of the vision transformer for VHR image scene classification. We focused on using pre-trained ViT models to extract feature descriptors from VHR images in order to generate global image description vectors for image scene representation. In summary, the contributions of this paper are three-fold:
- 1.
We explore the performance of the vision transformer method based on the pre-trained ViT model. The transformer–encoder layer is considered a feature descriptor, where a discriminative image scene representation is generated from the transformer–encoder layer.
- 2.
Second, we present a new approach that consists of selecting the most important features and images and detecting unwanted and noisy images. Indeed, these images can have negative impacts on the accuracy of the final model. By doing so, we obtained a good data set without noise, which allowed us to have good accuracy and, consequently, reduce the learning time.
- 3.
Another challenging problem in understanding a VHR image scene involves the classification strategy. To this end, we used the support vector machine (SVM) to classify the extracted ViT features corresponding to the selected encoder layers.
The rest of the paper is organized as follows.
Section 2 introduces the proposed framework and the processing pipelines to extract the feature descriptor for VHR image scene classification. Firstly, we introduce the pre-trained ViT model to automatically extract features from the VHR images. Second, we present the proposed approach, which consists of selecting the most important features and images. The sub-selection allows for achieving good accuracy and reduces the learning time. Finally, we present the last block of our framework in which we learn a classification model from the data set obtained by the co-selection step. The experimental results from various databases are presented in
Section 3. Finally, we conclude the paper in
Section 4.
2. Proposed Framework
In this section, we describe the three blocks that are the bases of our VHR Image classification framework.
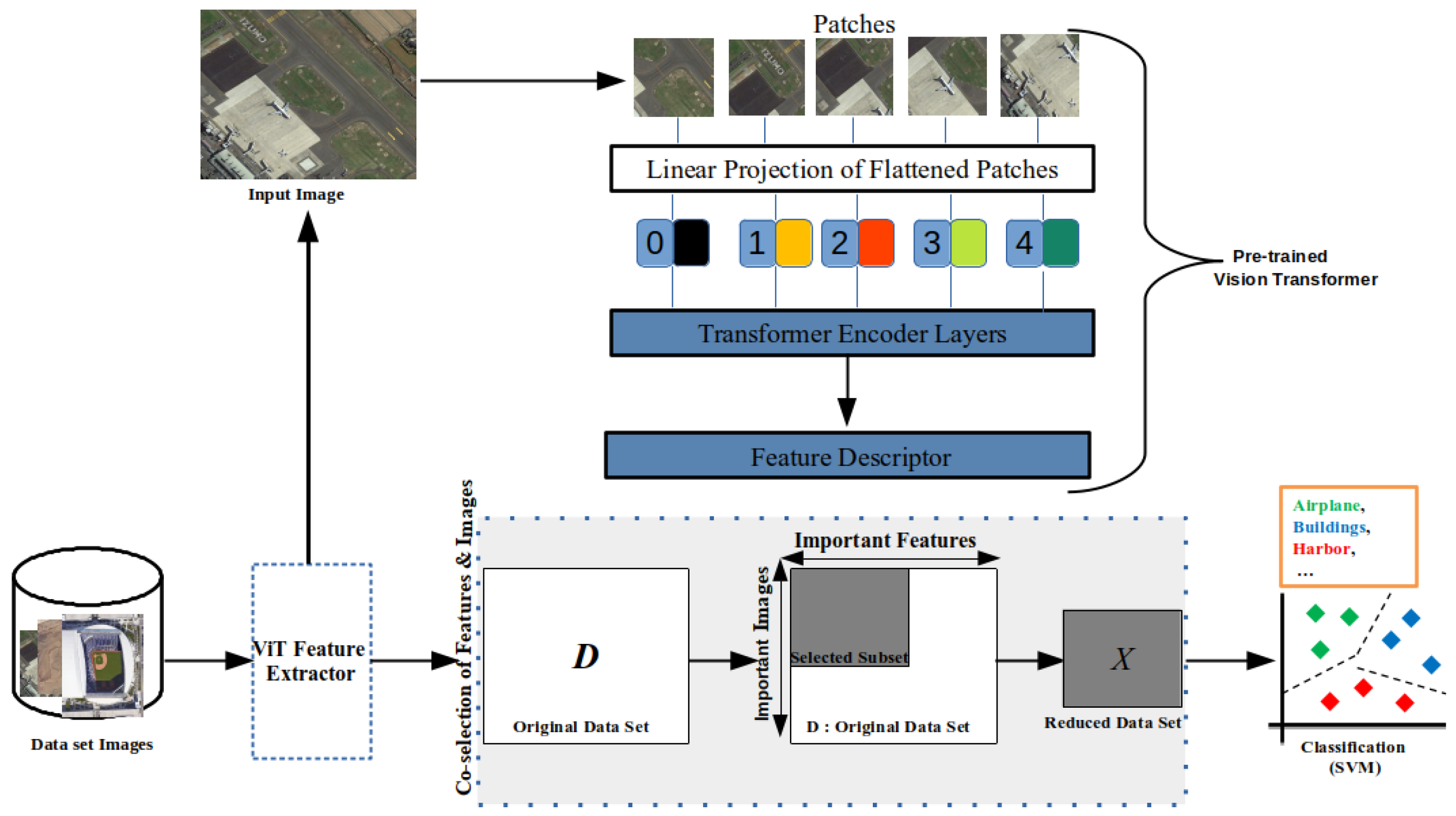
The idea of the framework is to transform the input images with four ViT models and merge the features obtained to obtain a single raw data set containing all features (
Figure 1). However, such a data set can have redundant and highly correlated features. Therefore, a feature selection step is required. In addition, some images in VHR data sets may be abnormal, which can degrade the quality of the classifier during the training phase. That is why we propose selecting both features and images in order to have the best data set for the learning step (unlike other frameworks that focus only on feature selection or reduction). Then, we create a classification model on top of the obtained data set.
2.1. ViT Model and Feature Fusion
In order to represent the image scene, we put the VHR images into four different models, i.e.,
,
,
, and
, where the transformer–encoder layer is considered a final feature descriptor of the image scene. The four models encode the input image scenes with different dimensions as shown in the following
Table 1:
Let X be the set of n input images, and the map function that transforms each image to a feature vector according to the model m, such that m is one of the four ViT models, .
We denote by
the matrix that contains all vectors
generated from the images
X by the model
m:
where
is the number of features extracted by model
m.
We represent by
the concatenation of all features generated by the four models:
where
is the number of all features.
2.2. Co-Selection of Features and Images
We select the most important ViT features based on the similarity-preservation of the input images; we also select the most important images and drop the irrelevant ones. In fact, these anomalous images can degrade the quality of the classifier. Unlike other approaches that focus only on feature selection or reduction, we select the most important images (instances) and drop anomalous images that can degrade the quality of the classifier. We will describe how we perform this co-selection before describing the different components of our proposed framework.
First, in order to select the most important features, we rely on the similarity preserving technique that consists of finding a projection matrix
Q, which transforms the data set
to a low-dimensional one
in order to preserve the similarity of
with
Q by minimizing the difference between the similar structure in the original space and the low-dimensional one:
where
Q is a projection matrix to be estimated. It is of dimension () where and h denote the sizes of the new feature set.
A is a binary matrix, which is derived from the label information
as follows:
is a regularization hyperparameter used to control the sparsity of the projection matrix Q.
is the
-norm. If
is
matrix, then its
-norm is defined by:
is the Frobenius norm (
) defined by:
However, the above optimization problem is NP-hard and cannot be solved as shown in [
35]. This leads to a reformulation of the problem as follows:
where
can be obtained by an eigendecomposition of the binary matrix
A, such that:
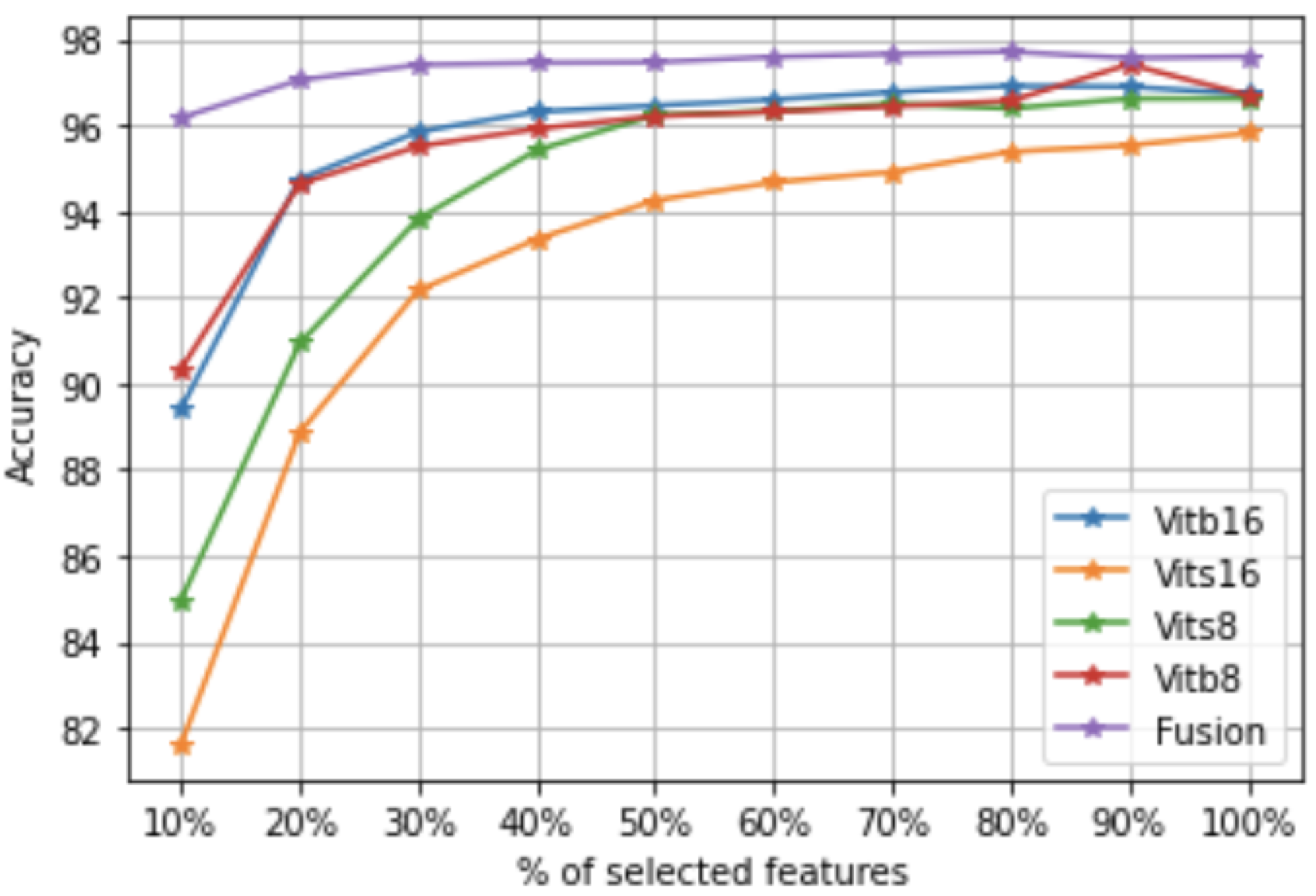
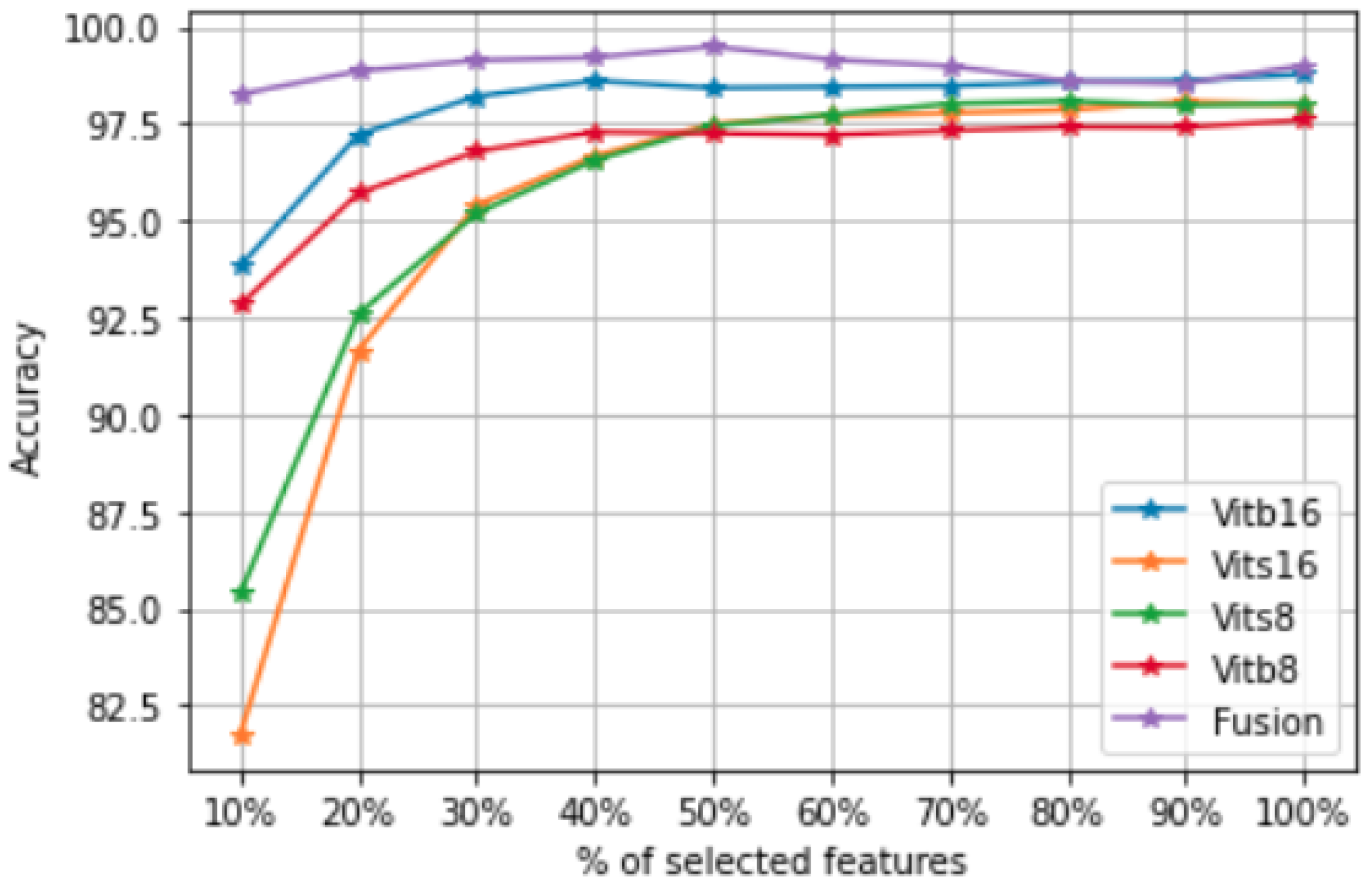
Once the projection matrix is fitted, the features can be ranked according to the -norms of the rows of the matrix . In fact, each row in corresponds to a feature importance and a large -norm of the ith row of indicates that the ith feature of is important.
Second, in order to drop the irrelevant images and select the most representative ones for the classification task, we propose modifying the objective function in (
6) by adding a residual matrix
to weigh the images [
36]. We define this matrix by
, where
is a random matrix, usually assumed to be a multi-dimensional normal distribution [
37]. Exploiting the
R matrix is a good way to detect and identify anomalies in a data set. Each column of
R corresponds to an image and a large norm of
shows a significant deviation of the
ith image, which is more likely to be an irrelevant image. Thus, we propose detecting both irrelevant features and images by solving the following problem:
where:
The first term in Equation (
7) exploits the data structure by preserving the pairwise sample similarities of the images. The second and third terms are used to perform feature selection and image selection, respectively.
2.3. Optimization
To solve the problem in Equation (
7), we adopt an alternating optimization over
Q and
R by solving two reduced minimization problems:
Problem 1:
Minimizing Equation (
7) by fixing
R to find the solution for
Q (for the feature selection). To solve this problem, we consider the Lagrangian of Equation (
7):
Then, we calculate the derivative of
w.r.t Q:
where
is a (
) diagonal matrix with the
ith element equal to
.
Subsequently, we set the derivative to zero to update
Q by the following formula:
Problem 2: Minimizing Equation (
7) by fixing
Q to find the solution for
R (for image selection). To solve this problem, we consider the Lagrangian of Equation (
7):
Then, we calculate the derivative of
w.r.t R:
where
is a (
) diagonal matrix with the
ith element equal to
.
Subsequently, we set the derivative to zero to update
R by the following formula:
where
I is an (
) identity matrix. We summarize all of the above mathematical developments on Algorithm 1.
| Algorithm 1 The Proposed Framework |
Input: Data set X of n images and the label information ; the map function of the deep model m; the hyperparameters: .
Output: the fitted Q and R.
- 1:
Transform the images X by the four ViT models according to Equation ( 1) to obtain . - 2:
Randomly split the data set into train and test sets (, , , ). - 3:
Calculate A according to Equation ( 3) over . - 4:
Eigen-decompose A such as . - 5:
Set and as identity matrices and R to zero-matrix. - 6:
repeat - 7:
Update Q according to Equation ( 10) over . - 8:
Update R according to Equation ( 13) over . - 9:
Update and . - 10:
untilConvergence - 11:
Rank the features according to in descending order () and the images according to in ascending order (). - 12:
Remove the irrelevant features and images from over and over . - 13:
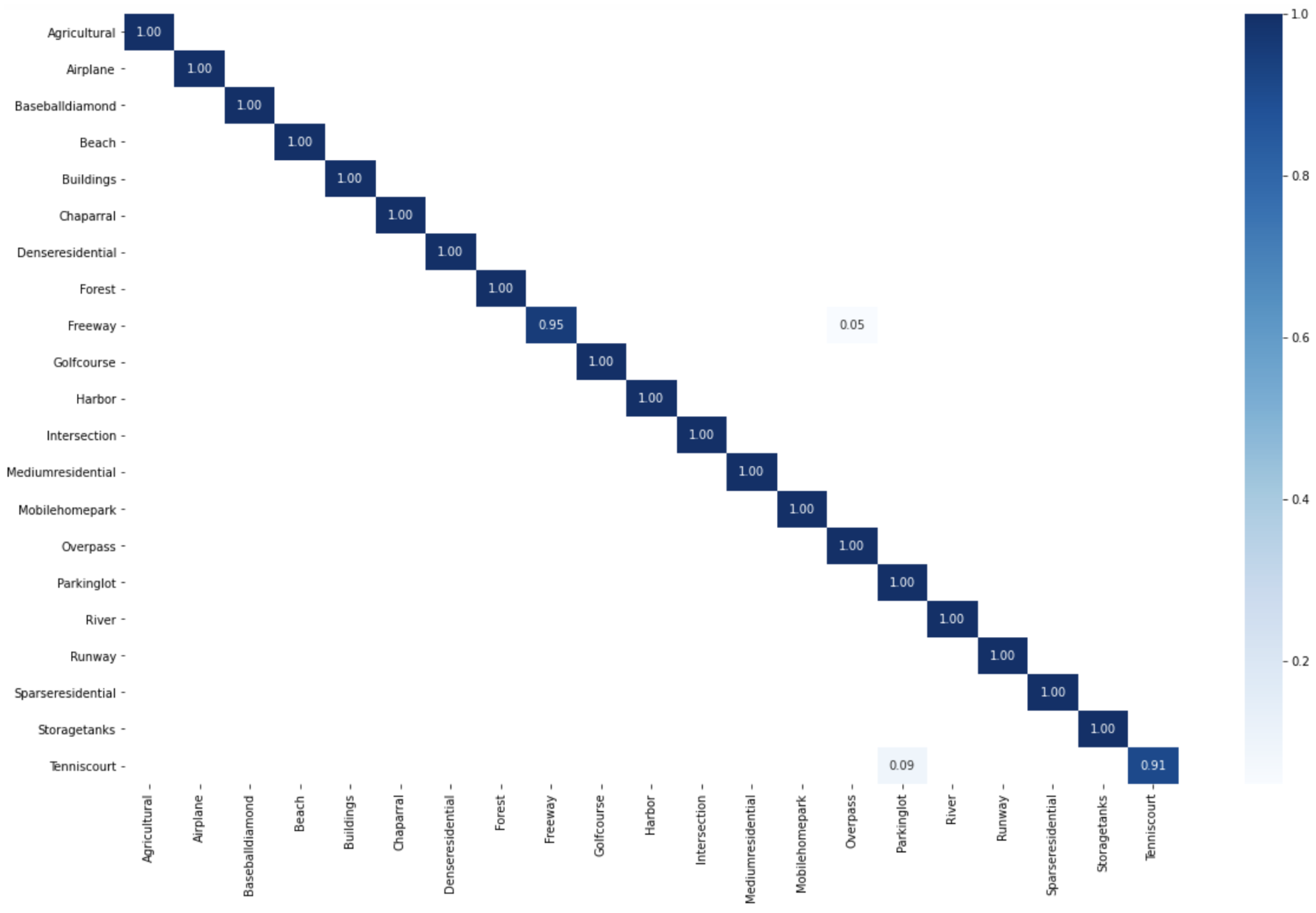
Learn a classification model by SVM on the new data set (, , , ).
|