The Temporal Evolution of Coastlines in the Bohai Sea and Its Impact on Hydrodynamics
Abstract
1. Introduction
2. Materials and Methods
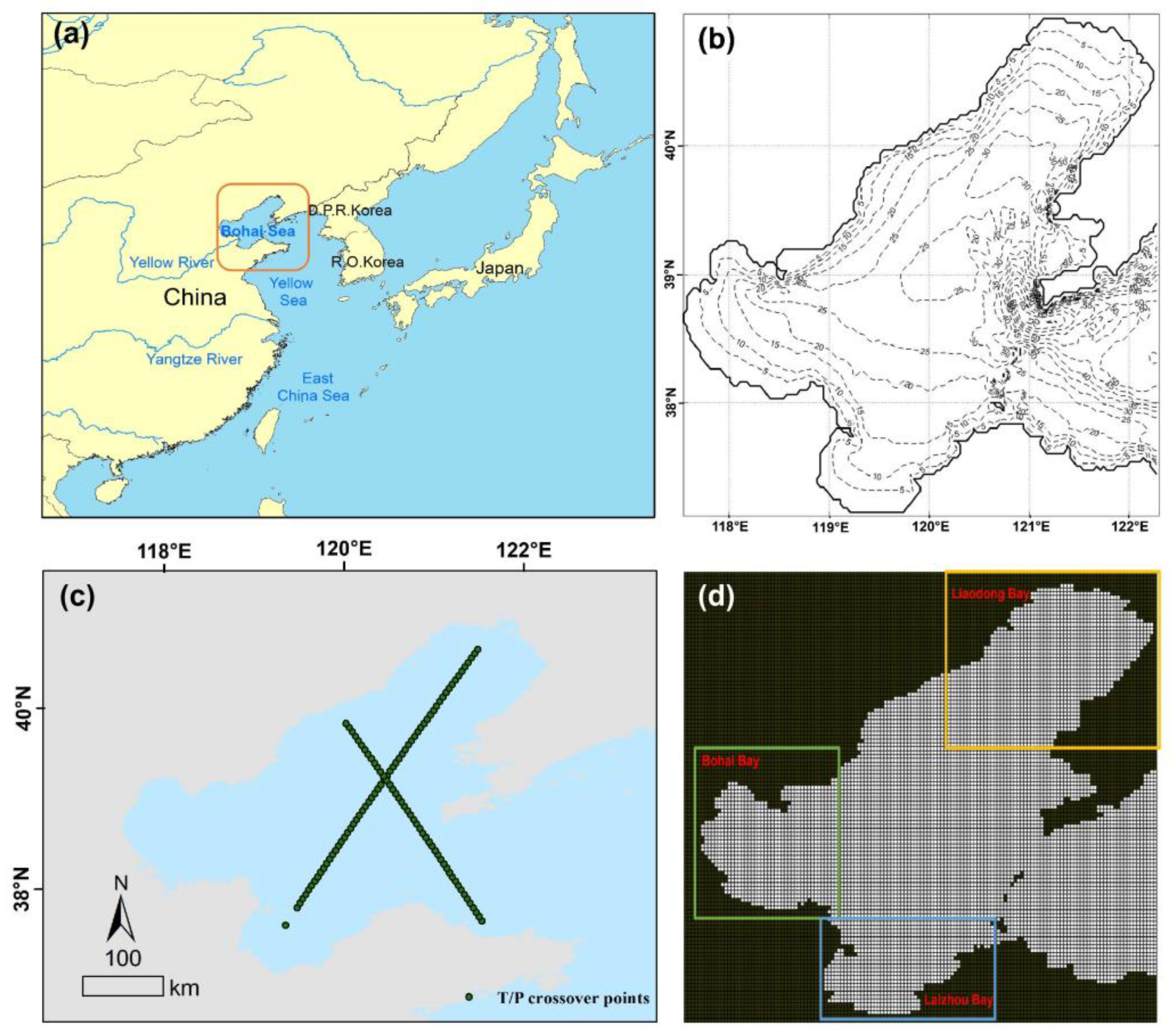
2.1. Study Area
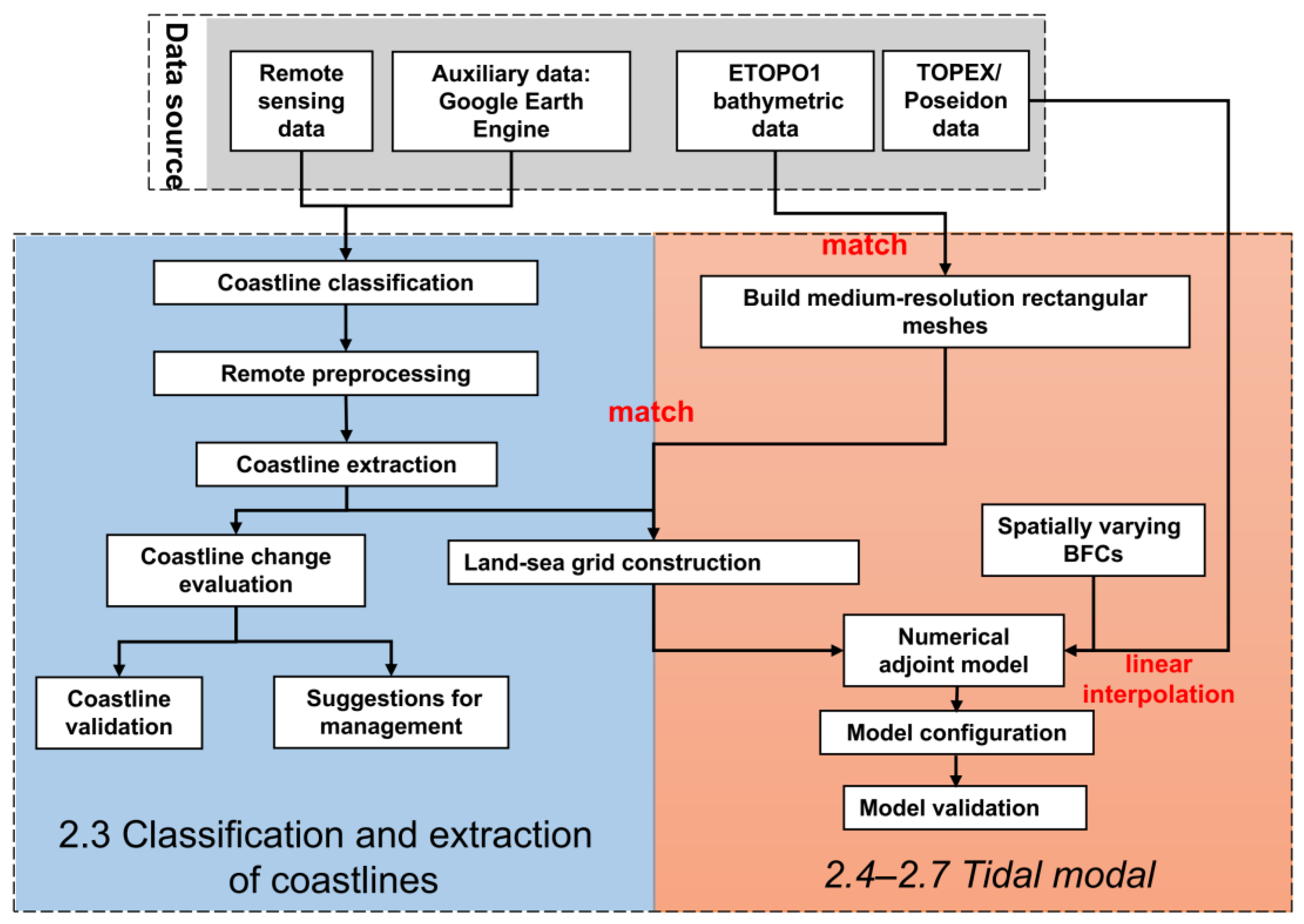
2.2. Data Source and Technological Route
2.3. Classification and Extraction of Coastlines
2.3.1. Coastline Classification
2.3.2. Coastline Extraction
2.3.3. Coastline Change Evaluation
2.3.4. Coastline Validation
2.4. Land–Sea Grid Construction
2.5. Numerical Adjoint Model
- Governing equations of forward model
- Adjoint equations
- Correction equations
2.6. Estimation Algorithm of Spatially Varying BFCs
2.7. Model Configuration
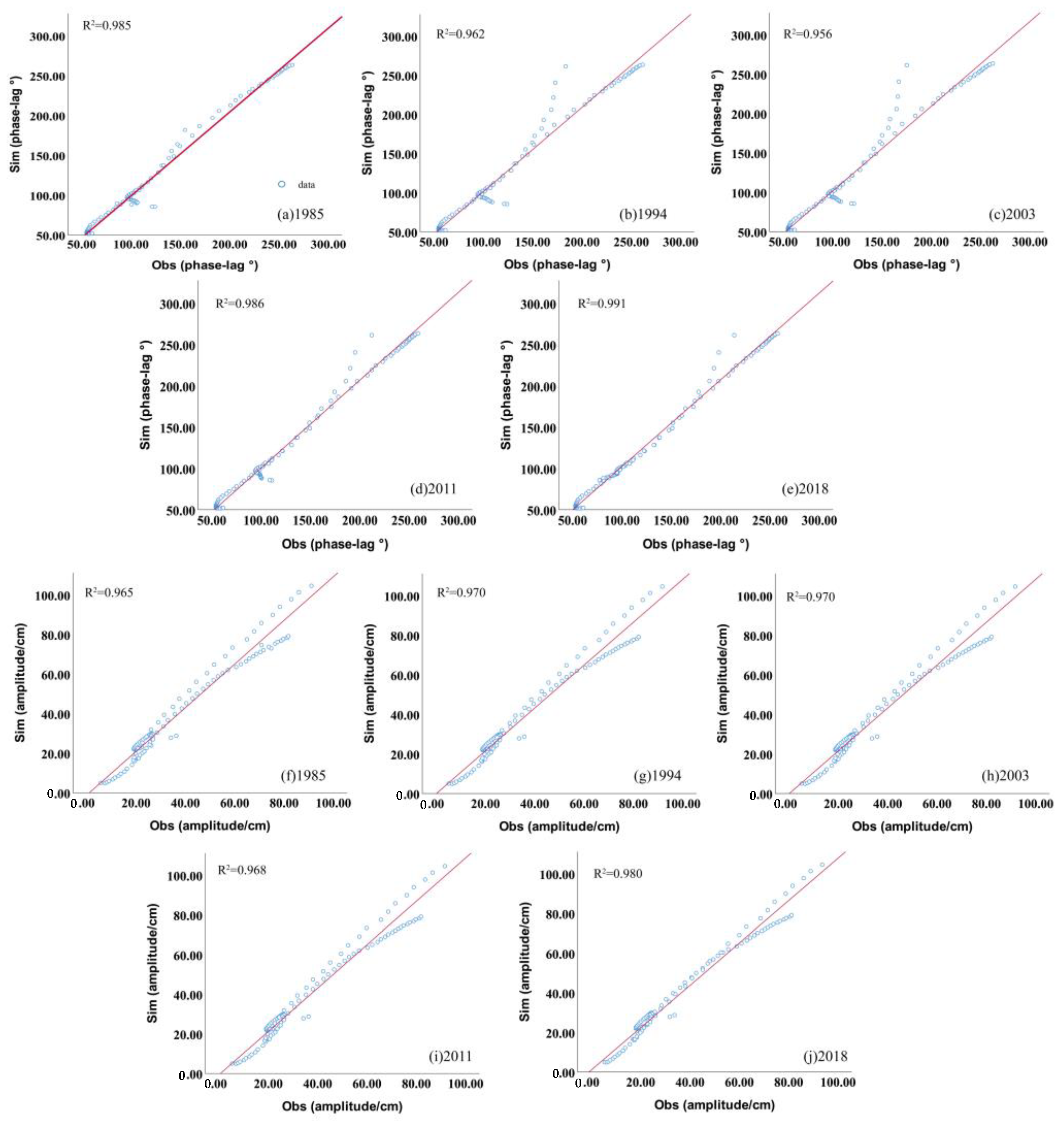
2.8. Model Validation
3. Results
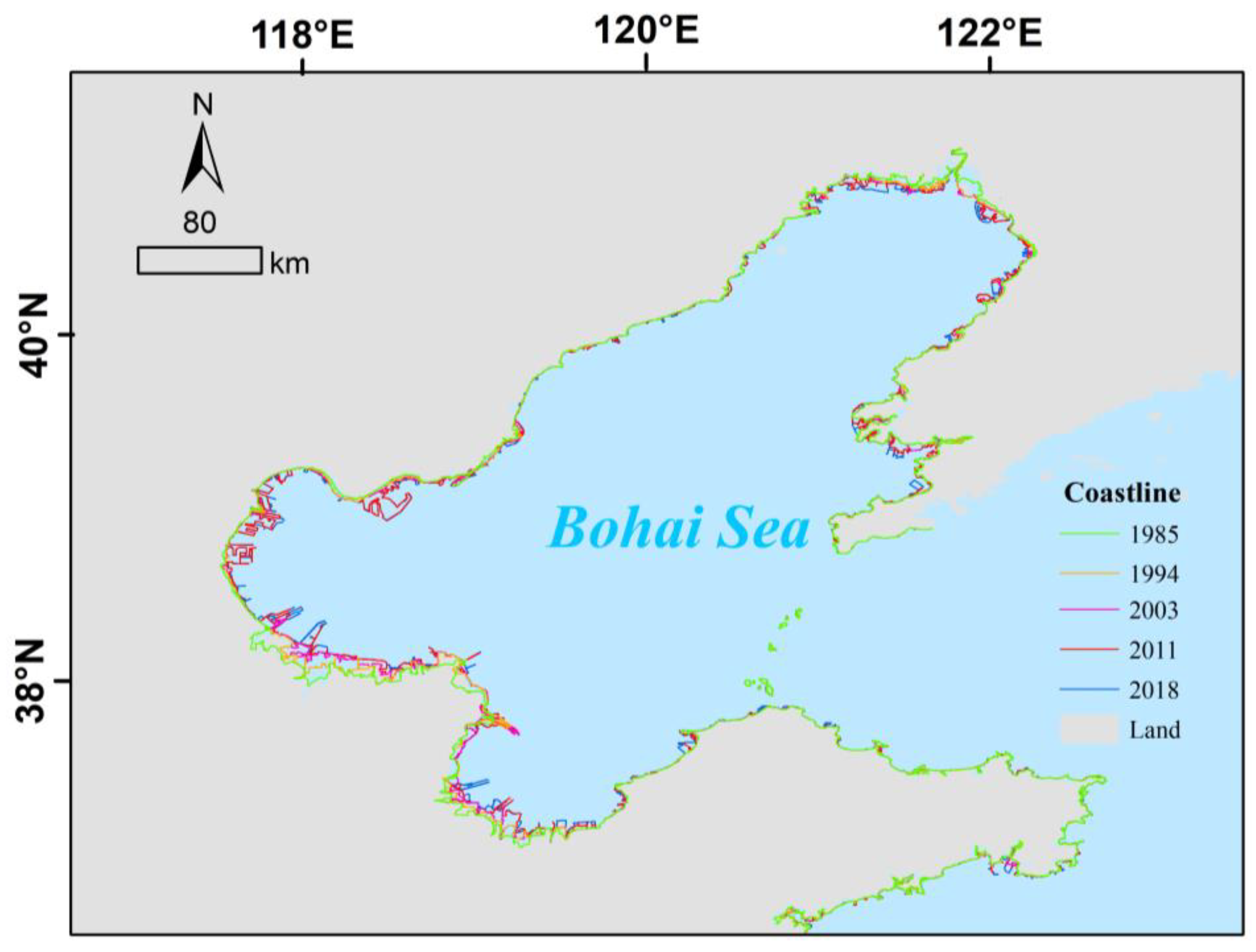
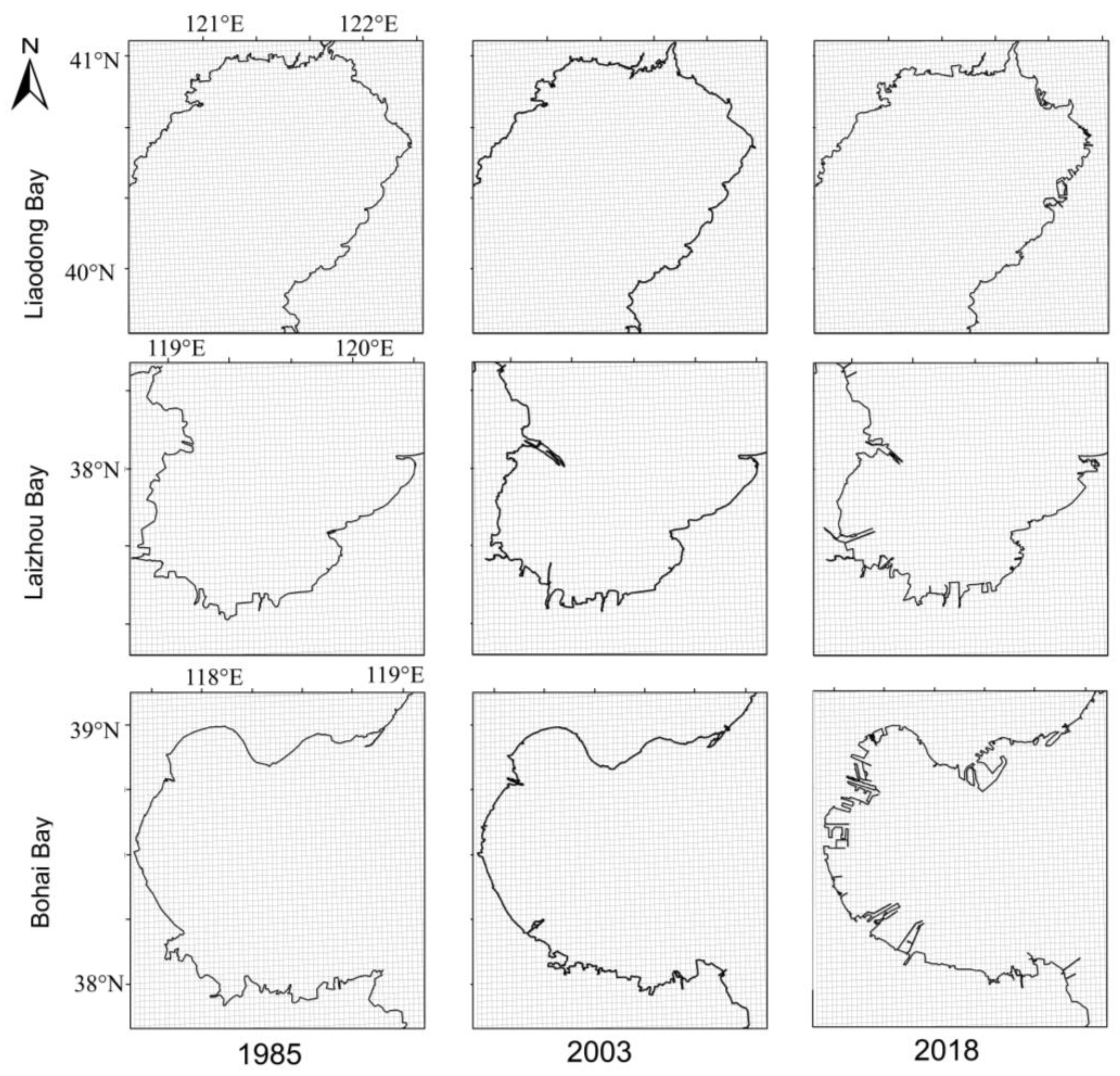
3.1. The Changing BHS Coast
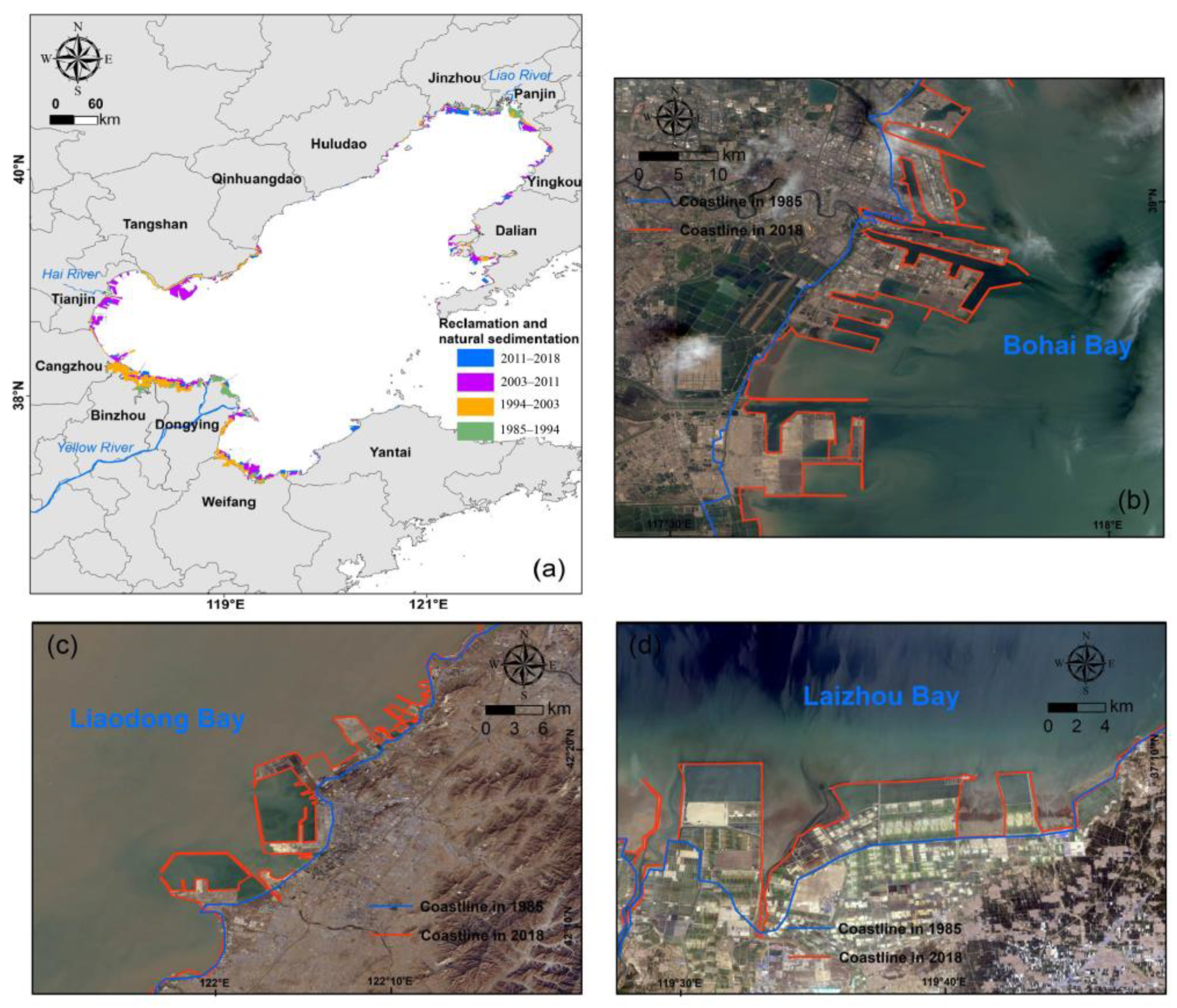
3.1.1. Reclamation and Sedimentation
3.1.2. Change in Coastline
3.1.3. Analysis of Coastline Movement
3.2. Responses of Hydrodynamics to Changes in Coastline
3.2.1. Sea Surface Area, Kinetic Energy, and Sea Water Volume
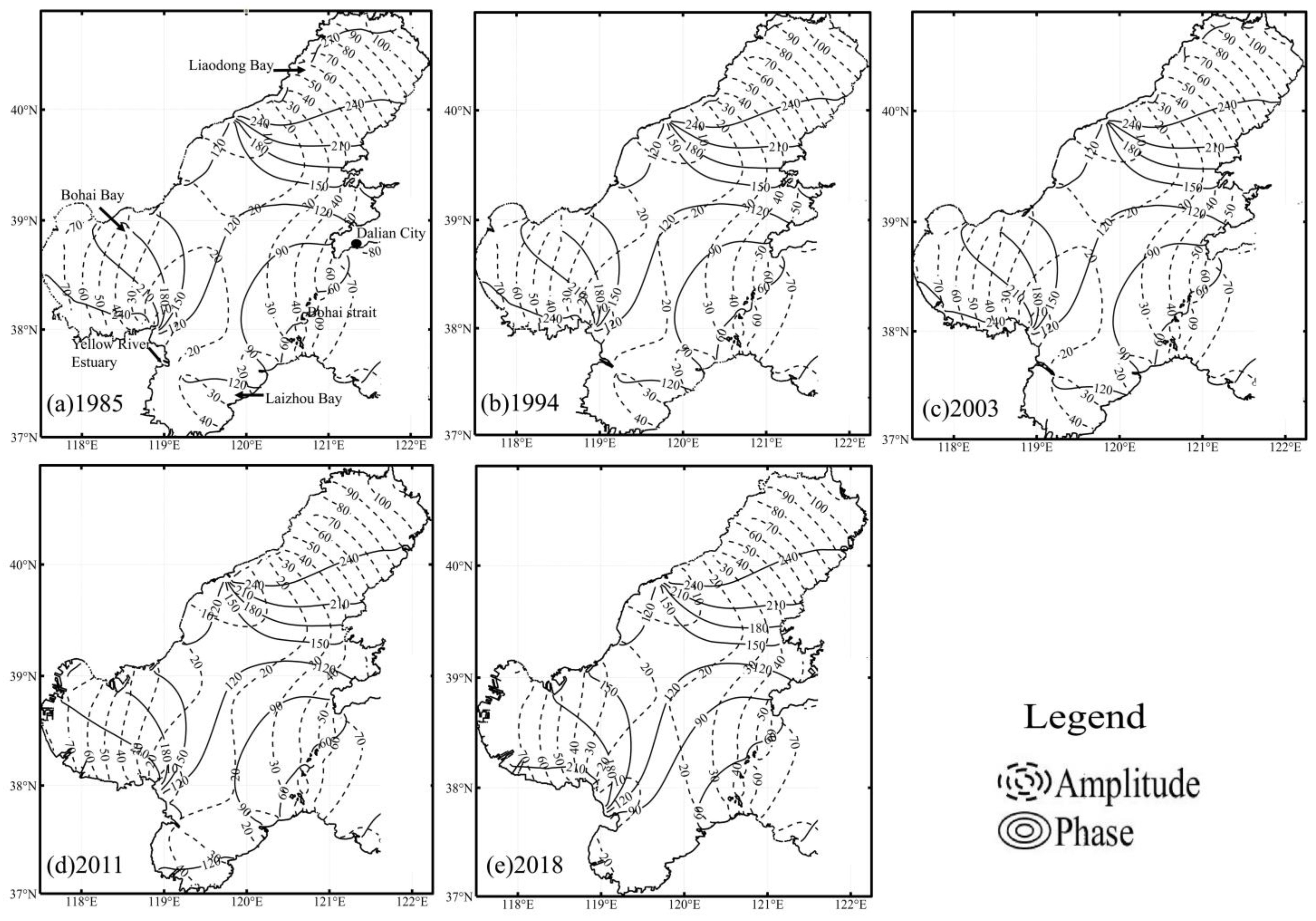
3.2.2. Effect on the M2 Tidal Constituent
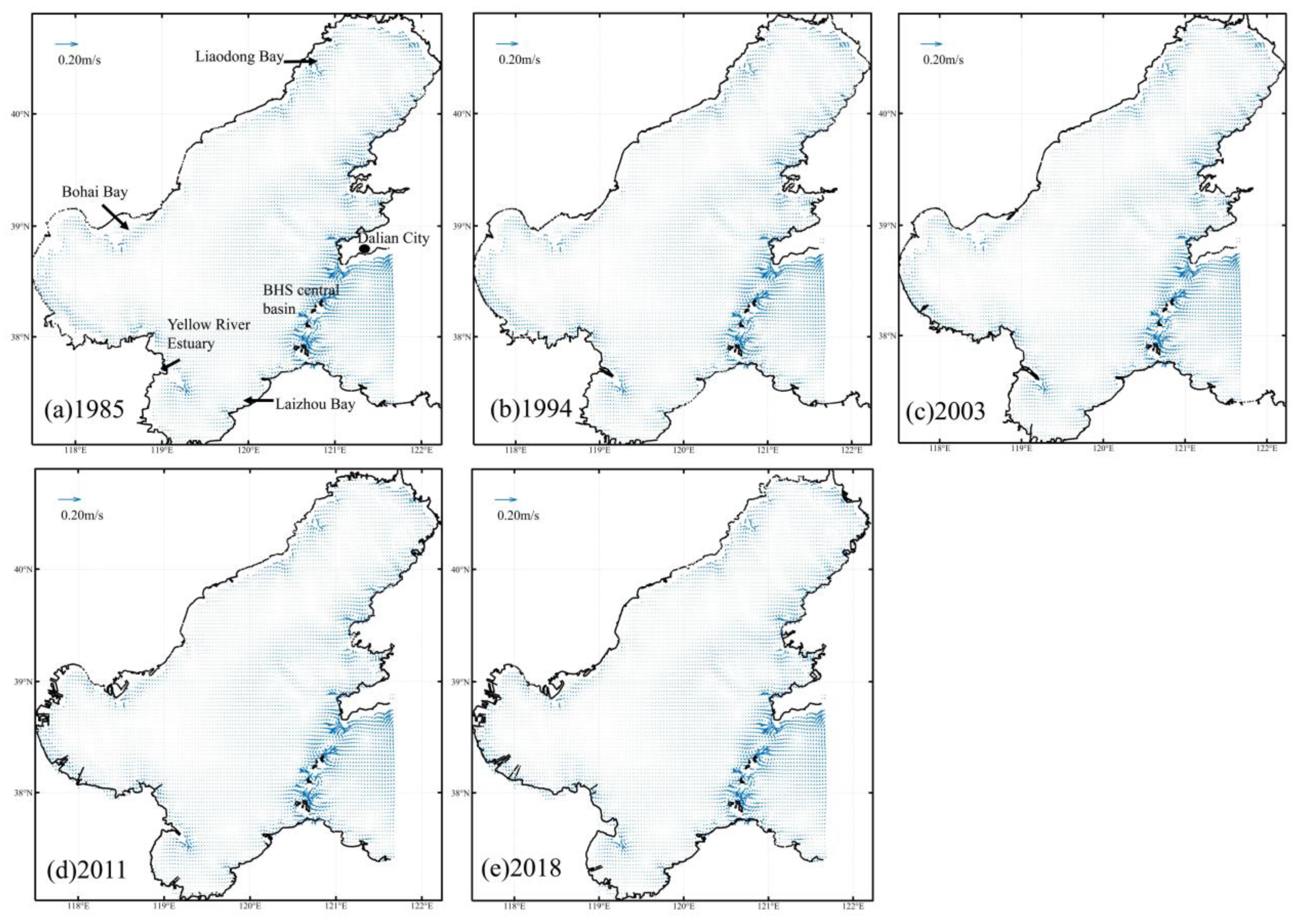
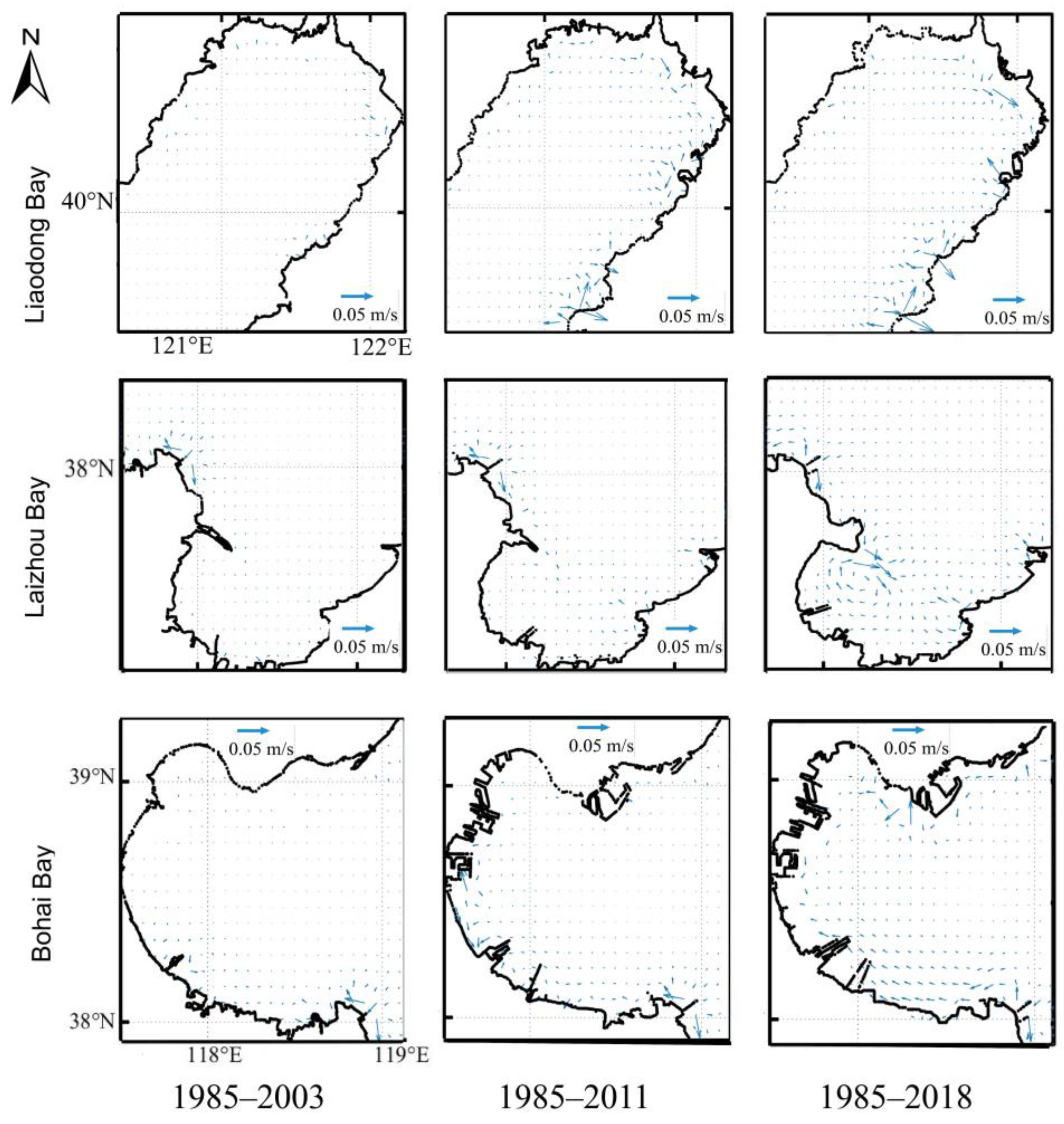
3.2.3. Effect on Residual Current (RC)
4. Discussion
4.1. Evaluation of Coastline Change
4.2. Evaluation of Hydrodynamics Change
4.3. Suggestions for Management of Coastal Reclamation
5. Conclusions
- The coastline showed an overall advancing trend over the 34-year period from 1985 to 2018, which was particularly obvious on the south coast of Laizhou Bay and Bohai Bay. According to the statistics, the average net coastline movement was 996 m (29.3 m/yr), and the maximum reclamation distance into the sea was 492 m/yr. Around 72.9% of the coastline of the BHS mapped in 2018 moved compared with its position in 1985, and more than 30% of the coastline expanded more than 1 km into the sea.
- During the simulation, reclamation projects have had a great influence on the tidal velocity and direction across the coastline extension. However, the influence is limited, and the inner bay area receives a greater impact, especially in Bohai Bay and Liaodong Bay. The model results show that the change in the coastline increased the amplitude of the M2 tidal constituent in the Bohai Bay by 6–14 cm and increased the RC on the eastern coast of the Liaodong Bay by up to 0.07 (0.01) m/s.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pucino, N.; Kennedy, D.M.; Young, M.; Ierodiaconou, D. Assessing the accuracy of Sentinel-2 instantaneous subpixel shorelines using synchronous UAV ground truth surveys. Remote Sens. Environ. 2022, 282, 113293. [Google Scholar] [CrossRef]
- Konlechner, T.M.; Kennedy, D.M.; O’Grady, J.J.; Leach, C.; Ierodiaconou, D. Mapping spatial variability in shoreline change hotspots from satellite data; a case study in southeast Australia. Estuar. Coast. Shelf Sci. 2020, 246, 107018. [Google Scholar] [CrossRef]
- Anthony, E.J.; Kestenare, E.; Reyns, J.; Jouanno, J.; Anthony, E.J.; Laibi, R.; Hemer, M.; Penhoat, Y.D.; Ranasinghe, R. Response of the Bight of Benin (Gulf of Guinea, West Africa) coastline to anthropogenic and natural forcing, Part 2: Sources and patterns of sediment supply, sediment cells, and recent shoreline change. Cont. Shelf Res. 2019, 173, 93–103. [Google Scholar] [CrossRef]
- Arkema, K.K.; Guannel, G.; Verutes, S.; Wood, A.; Silver, J.M. Coastal habitats shield people and property from sea-level rise and storms. Nat. Clim. Chang. 2013, 3, 913–918. [Google Scholar] [CrossRef]
- Paz-Delgado, M.V.; Payo, A.; Gómez-Pazo, A.; Beck, A.-L.; Savastano, S. Shoreline Change from Optical and Sar Satellite Imagery at Macro-Tidal Estuarine, Cliffed Open-Coast and Gravel Pocket-Beach Environments. J. Mar. Sci. Eng. 2022, 10, 561. [Google Scholar] [CrossRef]
- Bugnot, A.B.; Mayer-Pinto, M.; Airoldi, L.; Heery, E.C.; Johnston, E.L.; Critchley, L.P.; Strain, E.M.A.; Morris, R.L.; Loke, L.H.L.; Bishop, M.J.; et al. Current and projected global extent of marine built structures. Nat. Sustain. 2020, 4, 33–41. [Google Scholar] [CrossRef]
- Pianca, C.; Holman, R.; Siegle, E. Shoreline variability from days to decades: Results of long-term video imaging. J. Geophys. Res. Ocean. 2015, 120, 2159–2178. [Google Scholar] [CrossRef]
- Li, P.; Li, G.; Qiao, L.; Chen, X.; Shi, J.; Gao, F.; Wang, N.; Yue, S. Modeling the tidal dynamic changes induced by the bridge in Jiaozhou Bay, Qingdao, China. Cont. Shelf Res. 2014, 84, 43–53. [Google Scholar] [CrossRef]
- Lin, S.; Liu, G.; Niu, J.; Wei, X.; Cai, S. Responses of hydrodynamics to changes in shoreline and bathymetry in the Pearl River Estuary, China. Cont. Shelf Res. 2021, 229, 104556. [Google Scholar] [CrossRef]
- Zhang, P.C.; Sun, L.Y.; Zhu, Y.L. Reclamation-induced influence on hydrodynamics and suspended sediment concentration at three estuary areas in Bohai Bay. China Harb. Eng. 2015, 35, 6–12. [Google Scholar]
- Wang, X.Z.; Zhang, H.G.; Fu, B.; Shi, A. Analysis on the coastline change and erosion-accretion evolution of the Pearl River Estuary, China, based on remote sensing images and nautical charts. J. Appl. Remote Sens. 2013, 7, 073519. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Z.; Xie, L.; Gao, H.; Cai, Z.; Chen, Z.; Zhao, J. Dynamics governing the response of tidal current along the mouth of Jiaozhou Bay to land reclamation. J. Geophys. Res.-Ocean. 2015, 120, 2958–2972. [Google Scholar] [CrossRef]
- Chu, N.; Yao, P.; Ou, S.; Wang, H.; Yang, H.; Yang, Q. Response of tidal dynamics to successive land reclamation in the Lingding Bay over the last century. Coast. Eng. 2022, 173, 104095. [Google Scholar] [CrossRef]
- Byun, D.S.; Wang, X.H.; Holloway, P.E. Tidal characteristic adjustment due to dyke and seawall construction in the Mokpo Coastal Zone, Korea. Estuar. Coast. Shelf Sci. 2004, 59, 185–196. [Google Scholar] [CrossRef]
- Pelling, H.E.; Uehara, K.; Green JA, M. The impact of rapid coastline changes and sea level rise on the tides in the Bohai Sea, China. J. Geophys. Res. Ocean. 2013, 118, 3462–3472. [Google Scholar] [CrossRef]
- Fu, Y.; Guo, Q.Z.; Wu, X.; Feng, H.; Pan, Y.Y. Prediction of Changes in Coastline Morphology in the Bohai Sea, C.U.R.S. Sustainability 2017, 9, 900. [Google Scholar] [CrossRef]
- Ding, Z.; Su, F.; Zhang, J.; Zhang, Y.; Luo, S.; Tang, X. Clustering Coastal Land Use Sequence Patterns along the Sea–Land Direction: A Case Study in the Coastal Zone of Bohai Bay and the Yellow River Delta, China. Remote Sens. 2019, 11, 2024. [Google Scholar] [CrossRef]
- Tang, S.; Song, L.; Wan, S.; Wang, Y.; Jiang, Y.; Liao, J. Long-Time-Series Evolution and Ecological Effects of Coastline Length in Coastal Zone: A Case Study of the Circum-Bohai Coastal Zone, China. Land 2022, 11, 1291. [Google Scholar] [CrossRef]
- Pantusa, D.; D’Alessandro, F.; Riefolo, L.; Principato, F.; Tomasicchio, G.R. Application of a coastal vulnerability index. A case study along the Apulian Coastline, Italy. Water 2018, 10, 1218. [Google Scholar] [CrossRef]
- Vittal Hegde, A.; Radhakrishnan Reju, V. Development of coastal vulnerability index for Mangalore coast, India. J. Coast. Res. 2007, 23, 1106–1111. [Google Scholar] [CrossRef]
- Ding, X.; Shan, X.; Chen, Y.; Jin, X.; Muhammed, F.R. Dynamics of shoreline and land reclamation from 1985 to 2015 in the Bohai Sea, China. J. Geogr. Sci. 2020, 29, 2031–2046. [Google Scholar] [CrossRef]
- Feng, L.; He, J.; Ai, J.; Sun, X.; Bian, F.; Zhu, X. Evaluation for coastal reclamation feasibility using a comprehensive hydrodynamic framework: A case study in Haizhou Bay. Mar. Pollut. Bull. 2015, 100, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.W. Changes in tidal characteristics as a result of the construction of sea-dike/sea-walls in the Mokpo coastal zone in Korea. Estuar. Coast. Shelf Sci. 1999, 48, 429–438. [Google Scholar] [CrossRef]
- Wang, K.; Fang, G.; Feng, S. A 3-D numerical simulation of M2 tides and tidal currents in the Bohai Sea, the Huanghai Sea and the East China Sea. Acta Oceanol. Sin. 1999, 21, 1–13. [Google Scholar]
- Liu, Z.; Wei, H.; Jiang, S. Characteristics of seasonal variation of monthly mean temperature and salinity fields in the Bohai Sea and analysis of the related dynamics. J. Ocean Univ. China 2003, 33, 007–014. [Google Scholar]
- Qian, S.; Wang, D.; Zhang, J.; Li, C. Adjoint estimation and interpretation of spatially varying bottom friction coefficients of the M2 tide for a tidal model in the Bohai, Yellow and East China Seas with multi-mission satellite observations. Ocean Model. 2021, 161, 101783. [Google Scholar] [CrossRef]
- Zhu, L.; Hu, R.; Zhu, H.; Jiang, S.; Xu, Y.; Wang, N. Modeling studies of tidal dynamics and the associated responses to coastline changes in the Bohai Sea, China. Ocean Dynam. 2018, 68, 1625–1648. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, X.Q.; Wang, P.; Wang, Y.P. Study on linear and nonlinear bottom friction parameterizations for regional tidal models using data assimilation. Cont. Shelf Res. 2011, 31, 555–57325. [Google Scholar] [CrossRef]
- Guo, W.J.; Wu, G.X.; Liang, B.C.; Xu, T.J.; Chen, X.B.; Yang, Z.W. The influence of surface wave on water exchange in the Bohai Sea. Cont. Shelf Res. 2016, 118, 128–142. [Google Scholar] [CrossRef]
- Nerem, R.S.; Chambers, D.P.; Choe, C.; Mitchum, G.T. Estimating mean sea level change from the TOPEX and Jason altimeter missions. Mar. Geod. 2010, 33, 435–446. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Zhang, J.S. Study on Bohai sea tidal dynamics under extratropical storm surge. In Proceedings of the 9th International Conference on Hydrodynamics, Shanghai, China, 11–15 October 2010. [Google Scholar]
- Liang, S.; Li, X.; Wang, J.; Liang, S.; Li, X.; Wang, J.A. Systematic view of remote sensing. In Advanced Remote Sensing, 1st ed.; Academic Press: Cambridge, MA, USA, 2012; pp. 1–31. [Google Scholar]
- Tang, M.; Zhao, Q.; Pepe, A.; Devlin, A.T.; Falabella, F.; Yao, C.; Li, Z. Changes of Chinese Coastal Regions Induced by Land Reclamation as Revealed through TanDEM-X DEM and InSAR Analyses. Remote Sens. 2022, 14, 637. [Google Scholar] [CrossRef]
- Thieler, E.R.; Himmelstoss, E.A.; Zichichi, J.L.; Ergul, A. The Digital Shoreline Analysis System (DSAS) Version 4.0-an ArcGIS Extension for Calculating Shoreline Change. 2009. Available online: http://woodshole.er.usgs.gov/projectpages/DSAS/version4/index.html (accessed on 22 June 2021).
- Thakur, S.; IMondal, S.; Bar, S.; Nandi, P.B.; Ghosh, P.; Das, T.K. Shoreline changes and its impact on the mangrove ecosystems of some islands of Indian Sundarbans, North-East coast of India. J. Clean. Prod. 2021, 284, 124764. [Google Scholar] [CrossRef]
- Thieler, E.R.; Himmelstoss, E.A.; Zichichi, J.L.; Ayhan, E. Geological Survey Open-File Report, 2008–1278; USGS: Reston, VA, USA, 2017.
- Lu, X.Q.; Zhang, J.C. Numerical study on spatially varying bottom friction coefficient of a 2D tidal model with adjoint method. Cont. Shelf Res. 2006, 26, 1905–1923. [Google Scholar] [CrossRef]
- Ullman, D.S.; Robert, E.W. Model parameter estimation from data assimilation modelling: Temporal and spatial variability of the bottom drag coefficient. J. Geophys. Res. 1998, 103, 5531–5549. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Suo, A.N.; Yang, Z.X. Evaluation and Early-Warning Technical Methouds for Marine Resources & Environmental Carrying Capacity and Its Application; China Ocean Press: Beijing, China, 2019; pp. 101–106. [Google Scholar]
- Tian, B.; Wu, W.T.; Yang, Z.Q. Drivers, trends, and potential impacts of long-term coastal reclamation in China from 1985 to 2010. Estuar. Coast. Shelf. Sci. 2016, 170, 83–90. [Google Scholar] [CrossRef]
- Zavala-Garay, J.; Rogowski, P.; Wilkin, J.; Terrill, E.; Shearman, R.K.; Tran, L.H. An Integral View of the Gulf of Tonkin Seasonal Dynamics. J. Geophys. Res. Ocean. 2022, 127, e2021JC018125. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J.; Mu, L. A feature point scheme for improving estimation of the temporally varying bottom friction coefficient in tidal models using adjoint method. Ocean Eng. 2021, 220, 108481. [Google Scholar] [CrossRef]
- Zhuang, Z.Y.; Yang, Y.X.; Liu, H.X. Sandy beach erosion and beach nourishment in circum Bohai Sea. Mar. Geol. Front. 2013, 29, 1–9. [Google Scholar]
- Li, J.; Cheng, J.; Liu, S. An experimental study on the hydrodynamic performance of the twin vertical baffles underflow breakwater. Ocean Eng. 2022, 256, 111566. [Google Scholar] [CrossRef]
- Saitis, G.; Karkani, A.; Koutsopoulou, E.; Tsanakas, K.; Kawasaki, S.; Evelpidou, N. Beachrock Formation Mechanism Using Multiproxy Experimental Data from Natural and Artificial Beachrocks: Insights for a Potential Soft Engineering Method. J. Mar. Sci. Eng. 2022, 10, 87. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.J.; Ysebaert, T.; DeVriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef] [PubMed]



| Region | Year | Image Sensor | Path/Row |
|---|---|---|---|
| BHS | 1985, 1994 | Landsat5 TM, | 120/034, 121/034, 122/033, |
| 2003, 2011, | Landsat7 ETM, | 121/033, 121/032, 120/032, | |
| 2018 | Landsat8 OLI. | 120/033, 119/033 |
| Coastline Types | Spatial Location | Description of Interpretation Identifier (543 Band) |
|---|---|---|
| Bedrock coastline | Trace line of direct meeting of land and water | The widths of the headland angle and the upright cliff (base rock) are small, generally within 20 m. High-reflectivity white tone and vegetation coverage near them. |
| Sandy coastline | Trace line at the high-tide level on a sandy beach or gravel beach | High reflectivity of sandy gravel bank and beach, which were formed through a long-term process, and their textures are white and uniform. |
| Estuary coastline | The first water gate, dam, connection line of turning points on both sides of an estuary, or first bridge near the sea | Located at the mouth of a river, usually forming a silty beach, which can be easily identified on remote sensing images. The presence of estuary dams along the coast resulted in a relatively high sediment suspension in the estuary area. Subsequently, the water is relatively cloudy and gray, while the water around the lagoon dams is blue. |
| Lagoon coastline | The extracted contour line of a physical dam or physical gate when there is a physical dam or gate in the tidal channel | A clear internal texture with a flake or strip shape in the sea water area, separated from the open sea by a gray strip of sand spouts and dams. |
| Protective dam coastline and pond coastline | Contour line of the dam on the sea side | An aquaculture pond is dark blue with a uniform color, clear texture, flaky or striped distribution, and without vegetation coverage. A protective dam has clear and gray textures with generally small widths, and industrial/urban development is located around the protective dam. |
| Marine construction coastline | Seaward edge of construction if there is a port wharf or an impervious offshore structure. | Near urban and industrial areas, the textures of offshore structures are blurred, gray, mostly in strips, and perpendicular to the land. |
| YR | AD (cm) | PD (°) | VD (cm) | |||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| 1985 | 2.9 | 3.5 | 5.4 | 8.1 | 4.0 | 4.8 |
| 1994 | 2.8 | 3.2 | 5.2 | 7.2 | 3.9 | 4.6 |
| 2003 | 2.8 | 3.4 | 5.3 | 7.7 | 3.9 | 4.7 |
| 2011 | 2.8 | 3.2 | 4.4 | 5.8 | 4.0 | 4.5 |
| 2018 | 3.1 | 3.6 | 4.5 | 5.7 | 4.4 | 5.0 |
| Yr/Indexes | Area (1012 m3) | Volume (1010 m2) | Kinetic Energy (1014 J) |
|---|---|---|---|
| 1985 | 2.0710 | 8.4294 | 1.4957 |
| 1994 | 2.0703 | 8.3911 | 1.4937 |
| 2003 | 2.0706 | 8.3778 | 1.4910 |
| 2011 | 2.0679 | 8.2147 | 1.5248 |
| 2018 | 2.0674 | 8.0564 | 1.5343 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Zhang, Y.; Lv, X.; Shi, H. The Temporal Evolution of Coastlines in the Bohai Sea and Its Impact on Hydrodynamics. Remote Sens. 2022, 14, 5549. https://doi.org/10.3390/rs14215549
Lu J, Zhang Y, Lv X, Shi H. The Temporal Evolution of Coastlines in the Bohai Sea and Its Impact on Hydrodynamics. Remote Sensing. 2022; 14(21):5549. https://doi.org/10.3390/rs14215549
Chicago/Turabian StyleLu, Jingfang, Yibo Zhang, Xianqing Lv, and Honghua Shi. 2022. "The Temporal Evolution of Coastlines in the Bohai Sea and Its Impact on Hydrodynamics" Remote Sensing 14, no. 21: 5549. https://doi.org/10.3390/rs14215549
APA StyleLu, J., Zhang, Y., Lv, X., & Shi, H. (2022). The Temporal Evolution of Coastlines in the Bohai Sea and Its Impact on Hydrodynamics. Remote Sensing, 14(21), 5549. https://doi.org/10.3390/rs14215549







