Abstract
Understanding nodal tidal characteristics is essential for accurate long-term tidal prediction. Observational nodal evolution of tides is mainly based on tide gauge records in coastal areas which are limited in time and space, thus impeding coherent determinations of basin-wide patterns of tidal variability. In this paper, we indicate the potential of satellite altimeter data to investigate 18.61-year nodal modulations of main constituents in the Gulf of Tonkin. Three tide gauges and multi-source satellite altimeter observations (TOPEX/Poseidon, Jason1, Jason2, and Jason3) revealed that 18.61-year nodal cycles in tidal amplitudes have noticeable deviations from the equilibrium tidal theory in the Gulf of Tonkin. In general, M2 and N2 nodal modulations are anomalously larger than theoretical values while K2, K1, and O1 nodal modulations are noticeably smaller than theoretical values. Compared to point-based tide gauges, satellite altimeter records can provide basin-wide features of nodal modulations of main constituents. Although overlapping geographical blocks are applied to eliminate the effect of tidal alias originated from long-period sampling intervals, the estimation of nodal cycles of minor constituents are still questionable. Nevertheless, the methods described here provide a strong foundation for future research on time-varying tidal dynamics using the combination of tide gauges and satellite altimeter data.
1. Introduction
The 18.61-year lunar nodal cycle is due to the retrograde precession of the lunar ascending and descending nodes along the orbital plane of the Moon and can modulate both lunar and lunisolar tides [1]. Tidal equilibrium theory suggests that the M2 tidal amplitude should be modified by about 3.7% due to the nodal variations, while the amplitude of the K1, O1, and K2 tides should be modified by about 11.6%, 18.7%, and 28.6%, respectively, over a full nodal cycle [2,3]. However, deviations from theoretical values have been observed in numerous regions around the world such as the Gulf of Tonkin and the Gulf of Maine, typically with real nodal modulations smaller than theoretical values, mainly due to the effects of bottom friction and resonance [1,4,5].
The nodal modulation of the semi-diurnal tides and diurnal tides are notable because they can significantly affect extreme sea levels [6,7,8]. Recently, Peng et al. (2019) [9] calculated the contribution of the lunar nodal modulation to monthly high-water levels (HWLs) globally using long-term hourly tide gauge observations from 574 stations distributed worldwide and found that the nodal modulation had a large influence on the monthly HWLs in the Gulf of Tonkin, the Bristol Channel, and the English Channel; changes in tidal range over the nodal cycle are often observed to be up to 30 cm. An accurate assessment of the influence of these long-period tidal modulations is of critical importance since it may allow the better prediction of coastal flood risk over long periods [10]. It is widely recognized that nodal cycles can also exert strong effects on tidal currents as well as vertical mixing, and therefore influence local sea surface temperature (SST), sea surface salinity (SSS), air temperature, and possibly large-scale climate patterns [11,12,13].
To date, nearly all studies on nodal modulations of major tidal constituents employ hourly long-term point-based tide gauge observations which impede the determination of coherent basin-wide patterns of nodal variability of the major tidal constituents. Although satellite altimetry observations provide a consistent and nearly global coverage of oceanic water levels, few studies have used them. Cherniawsky et al. (2010) [13] carried out harmonic analyses on 16-years of TOPEX/Poseidon (T/P) and Jason-1 data in the Pacific and western Atlantic Oceans. They found that the amplitude ratios between the nodal satellites and their parent constituents are often larger than the theoretical values. Though their work is significant, there are a few major limitations to their approach. First, 16 years of satellite records are barely sufficient to adequately separate the nodal satellite constituents (such as M2n and K1n) from their parent constituents (such as M2 and K1); since the amplitudes of these nodal satellites are relatively small, they are easily contaminated by low-frequency aliased signals and other potential background noise, especially when the length of records (LORs) is short. Furthermore, compared to coastal areas, satellite altimeter observations are better determined in the open ocean. In shallow water regions (especially coastal zones), altimeter data often cannot provide reliable sea level observations due to various factors such as the interference of land topography on the radar signal [14]. Therefore, the results of Cherniawsky et al. (2010) [13] may be questionable in the marginal seas (e.g., Gulf of Tonkin) and they did not compare the altimeter-based nodal cycles with those of nearby tide gauges.
In the last decade, the spatial coverage and accuracy of satellite altimeter observations in the coastal areas have been significantly improved mainly due to new optimized waveform retracking algorithms, improved radar technology, and geophysical corrections [15]. Numerous coastal altimetry products providing a wide variety of processing level are now available to the scientific community. Among these products is the X-TRACK regional dataset, which is developed by the Center of Topography of the Ocean and Hydrosphere in Toulouse and provides freely available and highly accurate along-track water levels that cover all of the coastal ocean [14]. In this paper, we aim to reveal anomalous 18.61-year nodal cycles of main constituents in the Gulf of Tonkin from a combination of three tide gauges and 27 years of T/P-Jason sea level records processed by X-TRACK. The reminder of this paper is structured as follows. The study area and datasets are described in Section 2. Section 3 details the methodology, followed by the results, discussions, and conclusions in Section 4, Section 5, and Section 6, respectively. In Appendix A, the generation of the nodal factor for K1 tide is detailed.
2. Study Domain and Data
2.1. Study Domain
The Gulf of Tonkin is a semi-enclosed gulf located in the northwest of the South China Sea (SCS). The average water depth of the Gulf of Tonkin is ~42 m while the deepest part can reach ~100 m. Due to resonance, the Gulf of Tonkin has the strongest diurnal tides in the SCS [16]. As shown in Figure 1, the largest amplitudes of K1 and O1 tides can reach 90 cm and 100 cm in the Gulf of Tonkin based on the EOT20 ocean tidal model which is one of the most accurate tidal models [17]. The EOT20 model is derived based on residual tidal analysis of multi-satellite altimeter records, including T/P-Jason, ERS, Envisat, and T/P-Jason interleaved. Compared to diurnal tides, semi-diurnal tides are much smaller, the largest amplitudes of M2 and S2 tides are near 45 cm and 10 cm in the Gulf of Tonkin.
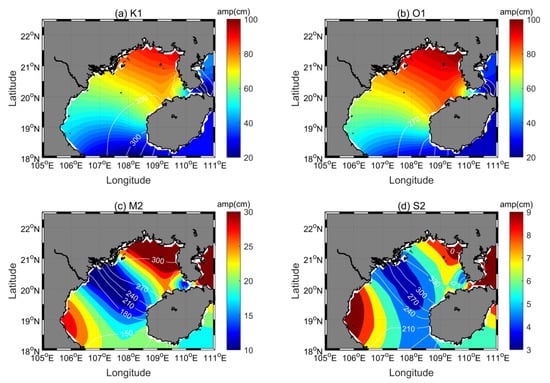
Figure 1.
Cotidal charts for (a) K1, (b) O1, (c) M2, and (d) S2 constituents in the Gulf of Tonkin calculated from EOT20 model. The amplitudes are indicated by color. The white lines are Greenwich phases spaced at intervals of 30°.
2.2. Water Level Observations
The X-TRACK sea level anomaly (SLA) records are obtained from AVISO (https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/coastal-tide-xtrack.html) (accessed on 10 January 2022) over a 27-year period (from March 1993 to May 2020), including T/P data (March 1993–January 2002), Jason-1 data (January 2002–July 2008), Jason-2 data (July 2008–February 2016), and Jason-3 data (February 2016–May 2020). These satellites share the same orbit with a sampling period of 9.915642 days. Compared to other altimeter missions, T/P-Jason satellite observations have a shorter sampling period and longer LOR. Thus, T/P-Jason altimeter data are widely used in the research of tidal dynamics. Other satellites, such as Envisat which has a sampling interval of 35 days and relatively short LOR (8 years), cannot resolve nodal satellite constituents. Figure 2 displays the ground tracks of T/P-Jason satellite altimetry in the Gulf of Tonkin. There are 126 observation points in the Gulf of Tonkin, but to ensure the reliability of the results, we use 114 points which are selected based on the LOR (more than 18.61 years) and data completeness (more than 75%). Hourly water level records from three tide gauges in the Gulf of Tonkin (Figure 2) are downloaded from the University of Hawaii Sea Level Center (https://uhslc.soest.hawaii.edu/data/?fd) (accessed on 21 June 2020). These tide gauges are also selected according to the same criteria as satellite data. The missing values of three tide gauges are all smaller than 0.17%. Although water level observations at Beihai, Haikou, and Dongfang are outdated (~1975 to 1997), they are still analyzed considering the scarcity of long-term tide gauges in the Gulf of Tonkin.
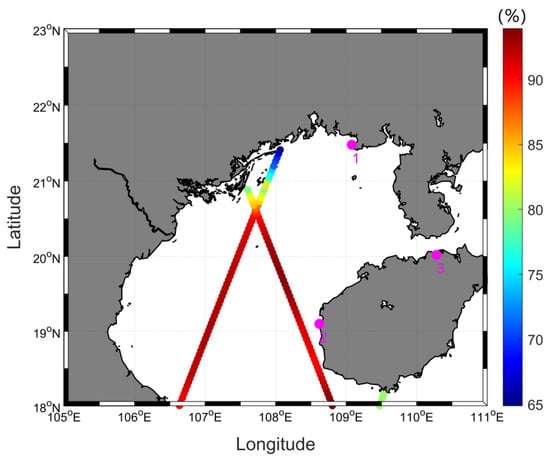
Figure 2.
The completeness (%) of T/P-Jason observations in the Gulf of Tonkin. Pink dots represent the location of tide gauges (1 Beihai, 2 Dongfang, 3 Haikou).
3. Methodology
3.1. Processing Tide Gauge Data
Hourly tide gauge observations were harmonically analyzed without nodal corrections in yearly windows of 8767 h, using the S_TIDE MATLAB toolbox (Qingdao, China) [18] at monthly (720 h) time steps. The S_TIDE toolbox is used to realize classical harmonic analysis as based on the T_TIDE software package [19,20]. We used 8767 h used because this is the minimum length which can resolve MA2 and MB2 tides which represent the seasonal variation of M2 tide. Yearly windows are long enough for resolving P1 (K2) from K1 (S2). A total of 67 tidal constituents (including 6 long-period constituents and 22 shallow water constituents) can be resolved according to LOR and Rayleigh criterion. Traditionally, the actual nodal cycle of tidal amplitudes as well as the linear trend are estimated by the least square model [3,4,5,21,22,23], which can be expressed as:
where A(t) is the estimated value of tidal amplitudes or phases at time t. C0 is a constant, C1 is the linear trend. HN and GN are the amplitude and phase of the nodal cycle, respectively. To decrease the potential effects of background noise on tidal estimation and increase the signal-to-noise ratio (SNR), we use an iteratively reweighted least squares (IRLS) regression [23,24] in the harmonic analysis model instead of ordinary least squares (OLS) regression [20]. The ratio of the calculated nodal amplitude HN over the mean value of tidal amplitude is estimated as the actual nodal modulation and compared with the theoretical nodal factor f in Table 1, showing that major tidal constituents have significant 18.61-year cycles as well as weak 9.3-year cycles and 6.2-year cycles [19].

Table 1.
Nodal factor f for the four major tidal constituents as derived from equilibrium tidal theory. N is the longitude of the lunar ascending node, which was 0° in November 1987 and June 2006, and was 180° in March 1997 and October 2015 [1,19].
3.2. Processing Satellite Altimeter Data
The analysis of altimeter data requires consideration of the aliasing effect. The periods of the diurnal and semi-diurnal constituents are shorter than twice the T/P repeat period; thus, aliasing is induced according to the Nyquist sampling theorem. Table 2 displays the tidal periods and T/P alias periods of major tidal constituents. Note that for the long-period constituents Ssa and Sa, no aliasing is involved. To fully separate two constituents of alias periods Ti and Tj, the LOR must satisfy Equation (2) (the Rayleigh criterion):

Table 2.
Major tidal constituents resolved in classical harmonic analysis, showing frequency, Doodson numbers, and alias periods. The first Doodson number represents tidal species (2 means semidiurnal tide, 1 means diurnal tide, 0 means long-period tide).
As displayed in Table 3 (derived from Equation (2) and Table 2), full resolution of the M2 and S2 tide from T/P-Jason satellite altimeter data requires at least 2.97 years of observations. To fully separate K2 from P1, and K1 from Ssa, at least 9.18 years of data are needed (Table 3). The data we use are long enough (27-year) to sufficiently separate aliased pairs, such as Ssa-K1 and P1-K2, and to fully resolve the 18.61-year nodal satellites (such as M2n and K1n) and their parent constituents (such as M2 and K1). The nodal satellites such as M2n and K1n are denoted with subscript n to represent the nodal modulations of major constituents (e.g., M2 and K1). Mn is the long-period constituent with a period of 18.61-years. Shallow water constituents such as SK3, 2MK6, and MKS2 should resolved because their alias periods are close to the alias period of O1n tide (Table 2). The ratios of the amplitudes of the nodal satellites over their parent constituents are calculated as the actual nodal modulation and compared with the theoretical values derived from the equilibrium tidal theory. The theoretical values for M2n/M2, K1n/K1, O1n/O1, and Q1n/Q1 are 0.0373, 0.1356, 0.1885, and 0.1884, respectively [13]. There is an obvious difference between the K1n/K1 ratio of 0.1356 while the K1 amplitude is nodally modified by about 11.6%; a detailed explanation of this phenomenon is provided in Appendix A.

Table 3.
Minimum length (years) for resolving each pair of constituents from T/P-Jason altimetry observations [30].
Note that the SCS is known to exhibit significant mesoscale eddy activity [25]. The presence of such strong mesoscale activity can influence the accuracy of tidal estimation from altimetry time series [26]. Ray and Byrne (2010) [27] used multi-satellite mapped sea level anomaly (SLA) fields as a prior correction for the mesoscale ocean variability before tidal harmonic analysis and found that this method can significantly improve the along track altimeter tidal estimates. To ensure obtained tidal amplitudes are purely tidal, we compiled satellite data into small overlapping geographical blocks and the sea levels in each circular block with radius of 0.25° were independently subjected to harmonic analysis [28]. To account for the distinct behavior of sea levels, collected sea level data were weighted using a Gaussian function based on the distance to the analyzed point [16,29]. We selected 0.25° because it can effectively decrease the errors of tidal amplitudes.
We mainly focused on nodal variability of M2, O1, K1, and Q1 constituents because they are strongest constituents in the Gulf of Tonkin. To ensure the reliability of the results of harmonic analysis and minimize the potential effects of aliasing and non-tidal signals, two editing criteria are adopted: (1) Only satellite altimeter records which are at least 75% complete are used for harmonic analysis to extract tidal amplitudes. (2) The SNR (defined as the square of the ratio of the estimated amplitude to its error) should be larger than two. Applying both of these criteria can eliminate most spurious results.
4. Results
4.1. 18.61-Year Nodal Variability from Tide Gauges
Table 4 displays the actual nodal modulations of the tidal amplitudes of the six major constituents in the Gulf of Tonkin. At all tide gauges in the SCS, M2 and N2 nodal modulations are anomalously larger than theoretical values while K2, K1, and O1 nodal modulations are noticeably smaller than theoretical values. Q1 nodal modulations are only slightly smaller than the theoretical value. The temporal variations of M2, K1, O1, and Q1 amplitudes at Haikou are highly consistent with theory in terms of phase: they all reach extreme values in November 1987 and M2 amplitudes vary reversely to K1, O1, and Q1 amplitudes (Figure 3 and Table 1). The results at Dongfang and Beihai stations (not shown) are consistent with those of Haikou. In fact, extreme nodal modulations at Beihai, Dongfang, and Haikou have been observed by Feng et al. (2015) [1]. A possible factor that may affect M2 nodal variability involves resonant triads, also known as three-wave resonances [31], which are nonlinear interactions between the M2 and K1/O1 tides which may transfer energy to each other, and in cases may decrease the K1/O1 nodal modulations and increase the M2 nodal modulation [1]. Similarly, nonlinear interactions between the N2 and K1/Q1 tides may decrease the K1/Q1 nodal modulations and increase the N2 nodal modulation. The K2 tide can be generated by the nonlinear interaction of K1 tide with itself which should increase K2 nodal modulation; however, actual K2 nodal modulations are anomalously small in the Gulf of Tonkin (Table 4) which needs further study. It is obvious that only three coastal tide gauges cannot represent the whole gulf. There are 114 valid T/P-Jason observation points in the Gulf of Tonkin, which can provide an opportunity to explore whether the whole gulf shows similar characteristics.

Table 4.
Actual 18.61-year nodal modulations and their errors of tidal amplitudes of main constituents at three tide gauges in the Gulf of Tonkin. Errors are calculated using 95% confidence intervals.
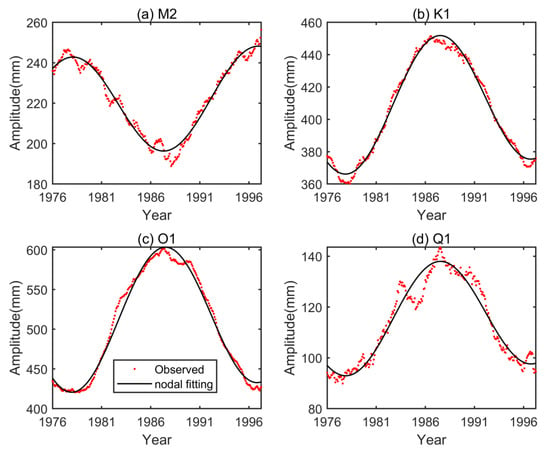
Figure 3.
Tidal amplitudes (red dots) and their nodal fitting results (black lines) at Haikou. (a) M2 (b) K1 (c) O1 (d) Q1.
4.2. Main Constituents Extracted from Satellite Altimeter
Figure 4 shows the amplitudes of M2, S2, K1, and O1 tides in the Gulf of Tonkin from T/P-Jason observations, which are generally consistent with Figure 1. The results from satellite altimeter data indicate that the largest amplitude of M2, S2, K1, and O1 tides can reach 25.10 cm, 8.05 cm, 81.22 cm, and 90.12 cm, respectively. For diurnal tides, extreme small amplitudes occur in the southern boundary of the gulf because the effect of diurnal resonance is negligible. The theoretical ratio for P1 to K1 amplitude is 0.3309 based on the equilibrium tidal theory [30] and after considering the nearby diurnal free wobble resonance, the P1/K1 ratio reduces to ~0.3180 [32]. As displayed in Figure 5a, satellite-derived P1/K1 ratios are basically consistent with the theory and the spatially averaged P1/K1 ratio is 0.3237. The theoretical ratio for O1 to K1 amplitude is 0.711 while actual O1 amplitudes are slightly larger than K1 amplitudes in the Gulf of Tonkin (Figure 5b). It is believed that the O1 period is closer to the resonance period of the gulf, thus, the amplification of O1 amplitude is more significant than K1 [33].
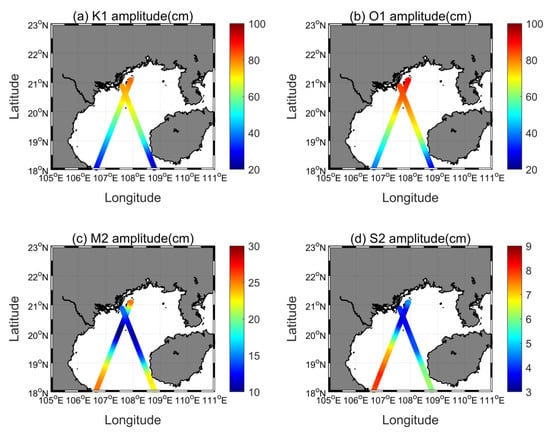
Figure 4.
Tidal amplitudes of (a) K1, (b) O1, (c) M2, and (d) S2 constituents extracted from T/P-Jason observations in the Gulf of Tonkin.
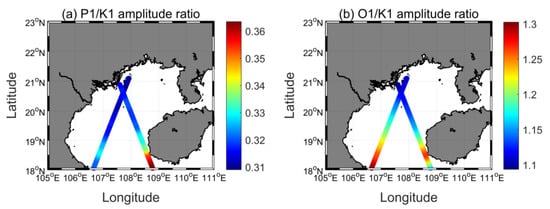
Figure 5.
Amplitude ratios from T/P-Jason observations in the Gulf of Tonkin: (a) P1/K1, (b) O1/K1.
4.3. 18.61-Year Nodal Variability from Satellite Altimeter
As displayed in Figure 6a, M2n amplitudes in the Gulf of Tonkin range from 0.6 cm (in the central part of the Gulf of Tonkin) to 1.8 cm (in the northern part of the Gulf of Tonkin). In the central of the Guf of Tonkin, M2n tides are very weak and their amplitudes are insignificant. The results from satellite data indicate that the M2 nodal modulation (namely, M2n/M2) in the Gulf of Tonkin ranges from 3.59% to 8.01% while the spatially averaged value is 5.90%, which is significantly larger than the theoretical value (3.73%). There are indeed extremely large M2 nodal modulations in the northeast of the Gulf of Tonkin (Figure 6b). However, in the southwest of the Gulf of Tonkin, M2 nodal modulations are generally consistent with the theoretical value. Thus, the findings on M2 nodal modulations from three tide gauges (Beihai, Haikou and Dongfang) are not universal in the Gulf of Tonkin.
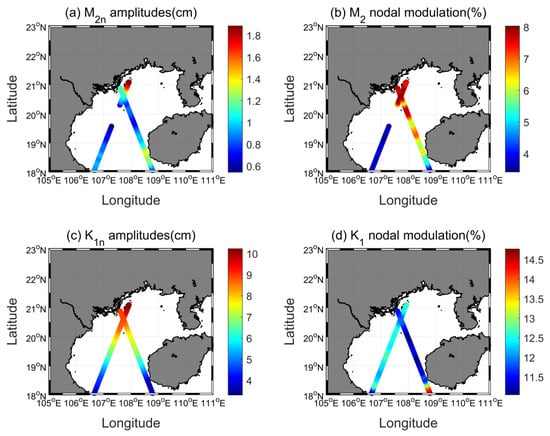
Figure 6.
Estimated nodal amplitudes and nodal modulations from T/P-Jason observations in the Gulf of Tonkin: (a) M2n amplitudes, (b) M2 nodal modulations, (c) K1n amplitudes, and (d) K1 nodal modulations.
K1n amplitudes in the Gulf of Tonkin (Figure 6c), ranging from 3.31 cm (in the southern part of the Gulf of Tonkin) to 10.20 cm (in the northern part of the Gulf of Tonkin), are much larger than M2n amplitudes. Satellite results indicate that the K1 nodal modulation in the Gulf of Tonkin ranges from 11.05% to 14.76% while the spatially averaged value is 12.07% which is clearly smaller than theoretical value (13.56%). Note that large K1 nodal modulations only occur near the southeastern boundary of the Gulf of Tonkin (Figure 6d). In general, the findings of small K1 nodal modulation from tide gauges are universal in the Gulf of Tonkin.
O1n amplitudes are largest among nodal tides in the Gulf of Tonkin (Figure 7a), ranging from 4.59 cm (in the southeastern part of the Gulf of Tonkin) to 16.60 cm (in the northern part of the Gulf of Tonkin). Satellite results indicate that the O1 nodal modulation in the Gulf of Tonkin ranges from 15.30% to 18.42% while the spatially averaged value is 17.38% which is clearly smaller than the theoretical value (18.85%). Extremely small O1 nodal modulations occur near the southeastern boundary of the Gulf of Tonkin (Figure 7b). At all T/P-Jason observation points, O1 nodal modulations are smaller than the theoretical value, which is generally consistent with tide gauges.
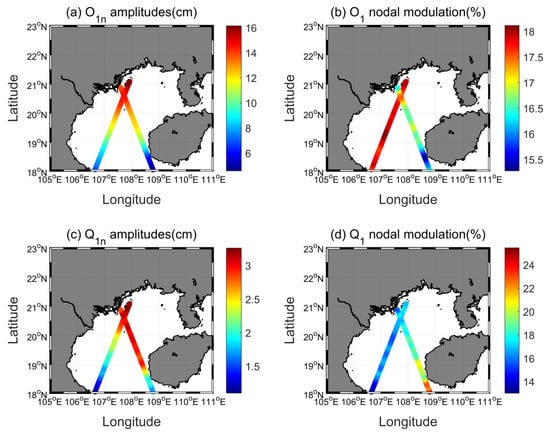
Figure 7.
Estimated nodal amplitudes and nodal modulations from T/P-Jason observations in the Gulf of Tonkin: (a) O1n amplitudes, (b) O1 nodal modulations, (c) Q1n amplitudes, (d) Q1 nodal modulations.
Q1n amplitudes in the Gulf of Tonkin are much smaller than O1n and K1n amplitudes, but noticeably larger than M2n amplitudes (Figure 7c), ranging from 1.10 cm (in the southwestern part of the Gulf of Tonkin) to 3.28 cm (in the northern part of the Gulf of Tonkin). Satellite results indicate that the Q1 nodal modulation in the Gulf of Tonkin ranges from 13.02% to 25.58% while the spatially averaged value is 17.66%, which is slightly smaller than the theoretical value (18.84%). Extremely large Q1 nodal modulations occur in the southeastern part of the Gulf of Tonkin while extremely small Q1 nodal modulations occur near the southwestern boundary of the Gulf of Tonkin (Figure 7d). Except for 27 observation points located in the southeastern part of the Gulf of Tonkin, the findings on Q1 nodal modulations from satellite data are consistent with tide gauges.
The maximum amplitude of N2 tide in the Gulf of Tonkin is 4.9 cm (Figure 8a), thus, the maximum amplitude of N2n tide should be 0.184 cm based on the equilibrium tidal theory. However, satellite-derived N2n amplitudes significantly exceed 0.184 cm (Figure 8b). In the central part of the Gulf of Tonkin, N2 tides are very weak while N2 nodal modulations are abnormally large (more than 80%). Such large N2n amplitudes should not be real, but induced by background noise (e.g., mesoscale ocean variability). Although overlapping geographical blocks are used to eliminate the effect of tidal alias originating from long-period sampling intervals, the estimation of nodal cycles of minor constituents are still questionable (Figure 8). K2n shows similar problematic features as N2n (not displayed).
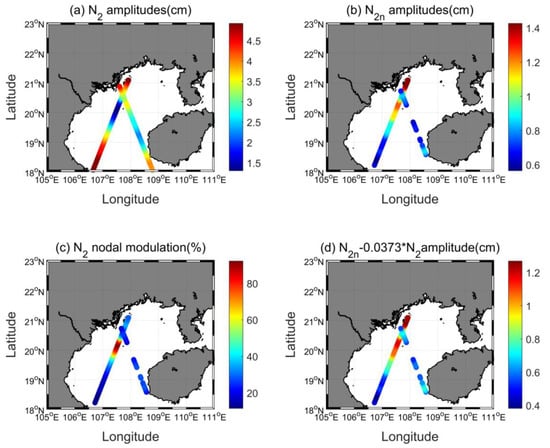
Figure 8.
Estimated nodal amplitudes and nodal modulations from T/P-Jason observations in the Gulf of Tonkin: (a) N2 amplitudes, (b) N2n amplitudes, (c) N2 nodal modulations, (d) the difference of theoretical and estimated N2n amplitudes in the Gulf of Tonkin.
5. Discussion
5.1. Systematic Nomenclature of Nodal Satellite Tides
As displayed in Appendix A, the nodal cycle of K1 tide is the resultant of two nodal satellite constituents whose frequencies are wK1 − wMn and wK1 + wMn, where wK1 and wMn represent the frequencies of K1 and Mn constituents. The constituent whose frequency is wK1 + wMn, has been named as K1n (Table 2) while the other can be named as K−1n. K−1n tides are very small in theory (Table A1), thus, they are not analyzed in this paper. Like K1, the nodal cycle of M2 tide is derived from M2n and M−2n tides, but the frequency of M2n is wM2 − wMn, not wM2 + wMn. The present nomenclature of nodal satellite tides may cause potential confusion on their frequencies. In addition, except for the 18.61-year nodal cycle, main constituents are also modulated by 9.3-year and 6.2-year cycles (Table 1). The constituents that generate 9.3-year and 6.2-year cycles are not named yet. Here, we systematically name these nodal satellite tides. Taking K1 for example, constituents whose frequencies are wK1 − wMn, wK1 – 2 × wMn, and wK1 – 3 × wMn are named as , , and where N is the longitude of the lunar ascending node (Table A1). Using this naming rule, K1n, O1n, K2n, and M2n tides can be renamed as , , , and which are more intuitive in terms of frequencies.
5.2. The Advantages and Disadvantages of X-TRACK Data
Although there are thousands of tide gauges around the world, many of them have only been established in recent decades and some are poorly maintained. Nearly all available long-term (more than 50 years) tide gauges are located on the coasts of Japan, North America, Australia, and Europe. For the tide gauges analyzed in this paper, both the location, number, and time span are highly limited which hinder us from determining basin-wide patterns of tidal variability in the Gulf of Tonkin. There are almost no continuous long-term (more than 18.61 years) tide gauges in the coasts of Vietnam although they have very long coastlines. Recent high-frequency (daily or hourly) water level observations are often not publicly available because of concerns of security and propriety, and only limited monthly or yearly averaged data are accessible for scientific research. Compared to this sparse distribution of tide gauges, T/P-Jason observations processed by X-TRACK software are abundant both in number and location, as well as freely available, which give us a unique opportunity to verify whether the findings from limited tide gauges are universal in the study area.
However, satellite altimeter observations also have their disadvantages. The satellite records mainly start in 1993, and long-period sampling intervals make the results of harmonic analysis more influenced by background noise such as mesoscale ocean variability, especially for minor constituents (e.g., N2n and K2n in this study). When tides are weak, especially near the amphidromic points, the ratios of nodal satellite constituents and their parent constituents may be abnormally large or small. Therefore, it is not recommended to use satellite altimeter observations to explore nodal modulations of weak tidal constituents.
6. Conclusions
Careful analysis of time-varying tidal characteristics is helpful and necessary for many practical purposes, such as navigation, coastal engineering, the utilization of tidal energy, and flood prevention. It is common knowledge that the actual nodal modulations of tidal amplitudes and phases have often been observed to be different from equilibrium theory in many coastal regions around the world based on long-term tide gauge observations. Less known, and less studied, is the nodal variability in the open sea where few tide gauges exist. In this paper, we analyzed the 18.61-year tidal variability in the Gulf of Tonkin using the combination of 27-year T/P-Jason satellite altimeter records and three coastal tide gauges. The main findings are summarized as follows:
- 1.
- Both tide gauges and satellite altimeter observations indicate that 18.61-year nodal cycles in tidal amplitudes significantly deviate from the equilibrium theory in the Gulf of Tonkin. In general, M2 and N2 nodal modulations significantly exceed theoretical values while K2, K1, and O1 nodal modulations are significantly lower than theoretical values.
- 2.
- Compared to point-based tide gauges, satellite altimeter records can provide basin-wide features of nodal modulations of main constituents. It is found that M2 nodal modulations are generally consistent with the theoretical value in the southwest of the Gulf of Tonkin. Furthermore, Q1 nodal modulations are noticeably larger than the theoretical value in the southeastern part of the Gulf of Tonkin. Although overlapping geographical blocks are applied to eliminate the potential effect of tidal alias, the estimated N2 and K2 nodal modulations are still questionable.
Partial results obtained from satellite data are disturbed by tidal aliasing due to long-period sampling intervals. However, the methods presented here provide an important supplement to the observed variability seen at coastal tide gauges, which are limited in time and space in the study area. In the future, the accuracy of satellite altimeter records will be improved, and their length or record will increase, which will improve estimates. Additionally, next-generation altimetry missions, such as the recently launched Sentinel-6 mission from ESA (http://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-6, (accessed on 21 June 2020)), and the upcoming Surface Water Ocean Topography (SWOT) platform from NASA (https://eospso.nasa.gov/missions/surface-water-ocean-topography, (accessed on 21 June 2020)) will bring new and improved observations of the coastal ocean, which will further help to resolve decadal variability behavior of sea level and tides and close the gap between coastal tide gauge observations and open-ocean altimetry observations.
Author Contributions
Conceptualization, H.P. and Z.W.; methodology, H.P.; software, H.P.; validation, H.P.; formal analysis, H.P.; investigation, H.P.; data curation, H.P.; writing—original draft preparation, H.P.; writing—review and editing, H.P, A.T.D., T.X., X.L., Z.W.; visualization, H.P.; supervision, Z.W.; project administration, Z.W.; funding acquisition, Z.W. and H.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (42076024, 41821004), the Qingdao postdoctoral application research project (QDBSH202108), and China Postdoctoral Science Foundation (2022M713677).
Data Availability Statement
The X-TRACK sea level anomaly (SLA) records are obtained from AVISO (https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/coastal-tide-xtrack.html) (accessed on 10 January 2022). The tide gauge data used in our study are obtained from University of Hawaii Sea Level Center (https://uhslc.soest.hawaii.edu/data/?fd) (accessed on 21 June 2020).
Acknowledgments
Harmonic analysis is performed via s_tide_m55 function in S_TIDE v1.23 toolbox which can be downloaded from https://www.researchgate.net/project/A-non-stationary-tidal-analysis-toolbox-S-TIDE (accessed on 11 January 2022). Alias periods in Table 2 are calculated by s_alias function in S_TIDE. Cotidal charts in the Gulf of Tonkin are drawn using s_draw_tidalchart function in S_TIDE toolbox.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Generation of the Nodal Factor of K1 Tide
and with frequencies at 1/18.61 cpy (cycle per year) at sidelines around K1 represent the 18.61-year nodal variation of K1 tide (see Table A1). The sum of the , K1, and tides can be expressed as:
where N is the longitude of lunar ascending node, w is the frequency of K1 tide. The amplitude of K1 is set to 1, thus, the amplitude of and are 0.1356 and 0.0198, respectively (see Table A1). Then, Equation (A1) can be rewritten as:
Equation (A2) can be rewritten as Equation (A3):
where
Therefore, the standard nodal factor for K1 tide can be calculated as:
Equation (A4) can be further simplified using Taylor expansion:
Note that Equation (A5) is derived from without consideration of and .

Table A1.
Constituents near K1 tide. Their frequency, Doodson numbers, and theoretical amplitude ratios are listed. The theoretical values for /K1 and /K1 are 0.1356 and 0.0198, respectively [32].
Table A1.
Constituents near K1 tide. Their frequency, Doodson numbers, and theoretical amplitude ratios are listed. The theoretical values for /K1 and /K1 are 0.1356 and 0.0198, respectively [32].
| Tidal Constituent | Doodson Numbers | Frequency (h−1) | Amplitude Ratio |
|---|---|---|---|
| 1 1 0 0-2 0 | 0.041768488 | 0.0001 | |
| 1 1 0 0-1 0 | 0.041774617 | 0.0198 | |
| K1 | 1 1 0 0 0 0 | 0.041780746 | 1 |
| 1 1 0 0 1 0 | 0.041786875 | 0.1356 | |
| 1 1 0 0 2 0 | 0.041793004 | 0.0029 |
References
- Feng, X.; Tsimplis, M.; Woodworth, P. Nodal variations and long-term changes in the main tides on the coasts of China. J. Geophys. Res. Oceans. 2015, 120, 1215–1232. [Google Scholar] [CrossRef] [Green Version]
- Müller, M. Rapid change in semi-diurnal tides in the North Atlantic since 1980. Geophys. Res. Lett. 2011, 38, L11602. [Google Scholar] [CrossRef]
- Pan, H.; Zheng, Q.; Lv, X. Temporal changes in the response of the nodal modulation of the M2 tide in the Gulf of Maine. Cont. Shelf Res. 2019, 186, 13–20. [Google Scholar] [CrossRef]
- Ku, L.; Greenberg, D.; Garrett, C.; Dobson, F. Nodal Modulation of the Lunar Semidiurnal Tide in the Bay of Fundy and Gulf of Maine. Science 1985, 230, 69–71. [Google Scholar] [CrossRef]
- Ray, R.D. Secular Changes of the M2 Tide in the Gulf of Maine. Cont. Shelf Res. 2006, 26, 422–427. [Google Scholar] [CrossRef] [Green Version]
- Eliot, M. Influence of interannual tidal modulation on coastal flooding along the Western Australian coast. J. Geophys. Res. 2010, 115, C11013. [Google Scholar] [CrossRef] [Green Version]
- Haigh, I.; Nicholls, R.; Wells, N. Assessing changes in extreme sea levels: Application to the English Channel, 1900–2006. Cont. Shelf Res. 2010, 30, 1042–1055. [Google Scholar] [CrossRef]
- Shaw, A.; Tsimplis, M. The 18.6-yr nodal modulation in the tides of southern European coasts. Cont. Shelf Res. 2010, 30, 138–151. [Google Scholar] [CrossRef]
- Peng, D.; Hill, E.; Meltzner, A.; Switzer, A. Tide gauge records show that the 18.61-year nodal tidal cycle can change high water levels by up to 30 cm. J. Geophys. Res. Ocean. 2019, 124, 736–749. [Google Scholar] [CrossRef] [Green Version]
- Haigh, I.; Eliot, M.; Pattiaratchi, C. Global influences of the 18.61 year nodal cycle and 8.85 year cycle of lunar perigee on high tidal levels. J. Geophys. Res. 2011, 116, C06025. [Google Scholar] [CrossRef] [Green Version]
- Royer, T. High-latitude oceanic variability associated with the 18.6-year nodal tide. J. Geophys. Res. 1993, 98, 4639–4644. [Google Scholar] [CrossRef]
- Yasuda, I.; Osafune, S.; Tatebe, H. Possible explanation linking 18.6-year period nodal tidal cycle with bi-decadal variations of ocean and climate in the North Pacific. Geophys. Res. Lett. 2006, 33, L08606. [Google Scholar] [CrossRef]
- Cherniawsky, J.; Foreman, M.; Kang, S.; Scharroo, R.; Eert, A. 18.6-year lunar nodal tides from altimeter data. Cont. Shelf Res. 2010, 30, 575–587. [Google Scholar] [CrossRef]
- Birol, F.; Fuller, N.; Lyard, F.; Cancet, M.; Niño, F.; Delebecque, C.; Fleury, S.; Toublanc, F.; Melet, A.; Saraceno, M.; et al. Coastal Applications from Nadir Altimetry: Example of the X-TRACK Regional Products. Adv. Space Res. 2017, 59, 936–953. [Google Scholar] [CrossRef]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Fu, L.-L.; Picot, N.; Raynal, M.; Roinard, M. Satellite Altimetry Measurements of Sea Level in the Coastal Zone. Rev. Geophys. 2019, 40, 1319–1349. [Google Scholar] [CrossRef]
- Fang, G.; Kwok, Y.; Yu, K.; Zhu, Y. Numerical Simulation of Principal Tidal Constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand. Cont. Shelf Res. 1999, 19, 845–869. [Google Scholar] [CrossRef]
- Hart-Davis, M.; Piccioni, G.; Dettmering, D.; Schwatke, C.; Passaro, M.; Seitz, F. EOT20: A global ocean tide model from multi-mission satellite altimetry. Earth Syst. Sci. Data. 2021, 13, 3869–3884. [Google Scholar] [CrossRef]
- Pan, H.; Lv, X.; Wang, Y.; Matte, P.; Chen, H.; Jin, G. Exploration of Tidal-Fluvial Interaction in the Columbia River Estuary Using S_TIDE. J. Geophys. Res. 2018, 123, 6598–6619. [Google Scholar] [CrossRef]
- Pugh, D.; Woodworth, P. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes; Cambridge University Press: Cambridge, UK, 2012; p. 395. [Google Scholar]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical Tidal Harmonic Analysis with Error Analysis in MATLAB Using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Ray, R.D. Secular changes in the solar semidiurnal tide of the western North Atlantic Ocean. Geophys. Res. Lett. 2009, 36, L19601. [Google Scholar] [CrossRef] [Green Version]
- Jay, D.A. Evolution of tidal amplitudes in the eastern Pacific Ocean. Geophys. Res. Lett. 2009, 36, L04603. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.; Lv, X. Is there a quasi 60-year oscillation in global tides? Cont. Shelf Res. 2021, 222, 104433. [Google Scholar] [CrossRef]
- Leffler, K.; Jay, D. Enhancing Tidal Harmonic Analysis: Robust (Hybrid L1/L2) Solutions. Cont. Shelf Res. 2009, 29, 78–88. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, W.; Tian, J.; Liang, X. A mesoscale eddy pair southwest of Taiwan and its influence on deep circulation. J. Geophys. Res. Atmos. 2013, 118, 6479–6494. [Google Scholar] [CrossRef]
- Ray, R.; Zaron, E. Internal tides and their observed wavenumber spectra from satellite altimetry. J. Phys. Oceanogr. 2016, 46, 3–22. [Google Scholar] [CrossRef]
- Ray, R.; Byrne, D. Bottom Pressure Tides along a Line in the Southeast Atlantic Ocean and Comparisons with Satellite Altimetry. Ocean. Dyn. 2010, 60, 1167–1176. [Google Scholar] [CrossRef] [Green Version]
- Ray, R.D. Propagation of the overtide M4 through the deep Atlantic Ocean. Geophys. Res. Lett. 2007, 34, L21602. [Google Scholar] [CrossRef]
- Piccioni, G.; Dettmering, D.; Schwatke, C.; Passaro, M.; Seitz, F. Design and regional assessment of an empirical tidal model based on FES2014 and coastal altimetry. Adv. Space Res. 2021, 68, 1013–1022. [Google Scholar] [CrossRef]
- Yu, Q.; Pan, H.; Gao, Y.; Lv, X. The Impact of the Mesoscale Ocean Variability on the Estimation of Tidal Harmonic Constants Based on Satellite Altimeter Data in the South China Sea. Remote Sens. 2021, 13, 2736. [Google Scholar] [CrossRef]
- Devlin, A.; Jay, D.; Talke, S.; Zaron, E. Can tidal perturbations associated with sea level variations in the western Pacific Ocean be used to understand future effects of tidal evolution? Ocean Dyn. 2014, 64, 1093–1120. [Google Scholar] [CrossRef] [Green Version]
- Ray, R.D. On Tidal Inference in the Diurnal Band. J. Atmos. Ocean. Technol. 2017, 34, 437–446. [Google Scholar] [CrossRef]
- Nguyen, N.M.; Marchesiello, P.; Lyard, F.; Ouillon, S.; Cambon, G.; Allain, D.; Dinh, U.V. Tidal characteristics of the Gulf of Tonkin. Cont. Shelf Res. 2014, 91, 37–56. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).