Evaluation of Urban Spatial Structure from the Perspective of Socioeconomic Benefits Based on 3D Urban Landscape Measurements: A Case Study of Beijing, China
Abstract
1. Introduction
2. Materials and Methods
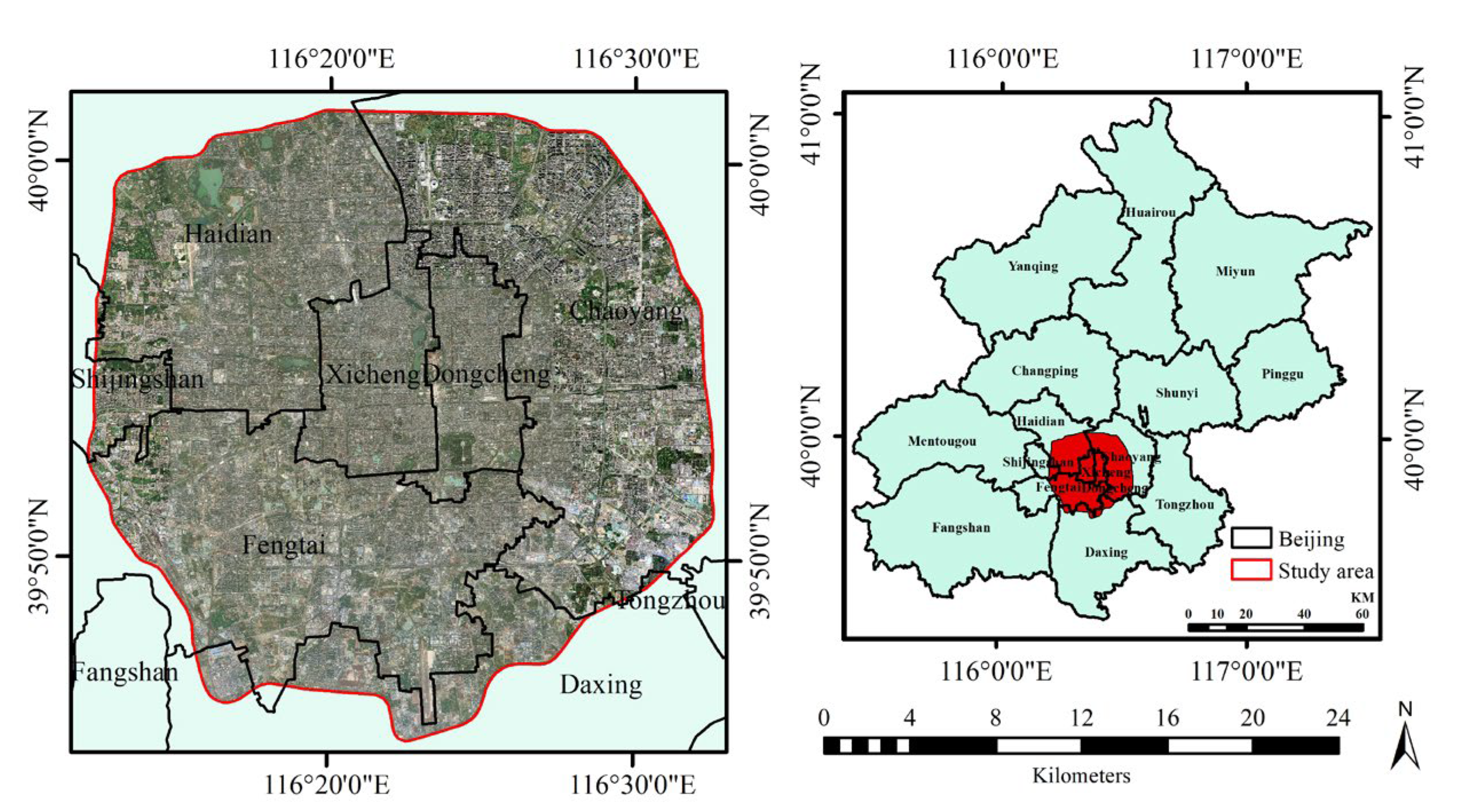
2.1. Study Area
2.2. Used Data
- Satellite images. We obtained a satellite image from the ESRI image product, which was generated by splicing images from different sensors. It was produced in 2021 with three bands (red, green, and blue) with a spatial resolution of 4.11 m. The original image has been corrected and stitched, and projection conversion and cropping are required to provide accurate image feature information before use.
- POI data. We collected 359,659 POI in 2021 from Amap (https://www.amap.com/ (accessed on 22 November 2021)), a leading digital mapping, navigation, and location service company in China, whose data are updated frequently so that accurate and reliable information on the location and function of POIs is available. In this paper, Arcgis10.7 software is first used to preprocess POI data, including vector transformation, coordinate transformation, removal of duplication, and missing information points. Then, these POIs were reclassified into 11 categories: government institutions, medical service facilities, sports facilities, educational and cultural service facilities, commercial service facilities, business service facilities, business residences, residential areas, transportation facilities, industrial facilities, and scenic and recreational service facilities. POI is closely related to the activities of residents and the configuration of urban facilities and thus contributes to the analysis of the urban spatial structure.
- Road network data. OpenStreetMap (https://www.openstreetmap.org/ (accessed on 8 September 2021)) is a free, open-source, editable nonprofit mapping service data. This study selected primary, secondary, tertiary, trunk, and residential road network line data from the 2021 OSM data. Arcgis10.7 software was used for clipping, topology checking, line turning polygon, and buffer processing, and then constructed the urban block unit data based on road network data to assist the functional area classification labeling samples.
- Buildings data. In May 2021, we collected information on 402,927 buildings from AMap, which are presented as vector polygons. This can provide the bottom profile and height of buildings for urban studies. As shown in Figure 2, overlaying the buildings with satellite images shows that almost all the buildings in the study area are included.
- Nighttime light data. Nighttime light intensity (NTLI) has been widely used to estimate socioeconomic metrics, such as gross domestic product (GDP), population, total freight, housing vacancy rate, poverty, and CO2 emissions [41,42,43,44,45]. Numerous investigations have confirmed the ability of the NTLI to reflect human socioeconomic activities, which can be a better alternative for urban socioeconomic activity intensity [46,47,48]. In this study, we used nighttime light remote sensing data from the Luojia1-01 star from the high-resolution Earth observation system (EOS), technology, and application (https://www.hbeos.org.cn/ (accessed on 6 November 2021)). The image was acquired in November 2018 with a spatial resolution of 130 m, which can be used to characterize socioeconomic activities at a fine scale within urban areas. To obtain valid light values, ENVI 5.3 software was used for pre-processing, including coordinate system conversion, radiance conversion, data clipping, partition statistics, and data connection.
2.3. Methods
2.3.1. Land-Use Function Classification Method
2.3.2. Multi-Scale Feature Statistical Method
2.3.3. Geographical Detector Method
2.3.4. Random Forest Regression (RFR) Method
2.3.5. Analytic Hierarchy Process (AHP) Method
3. Results
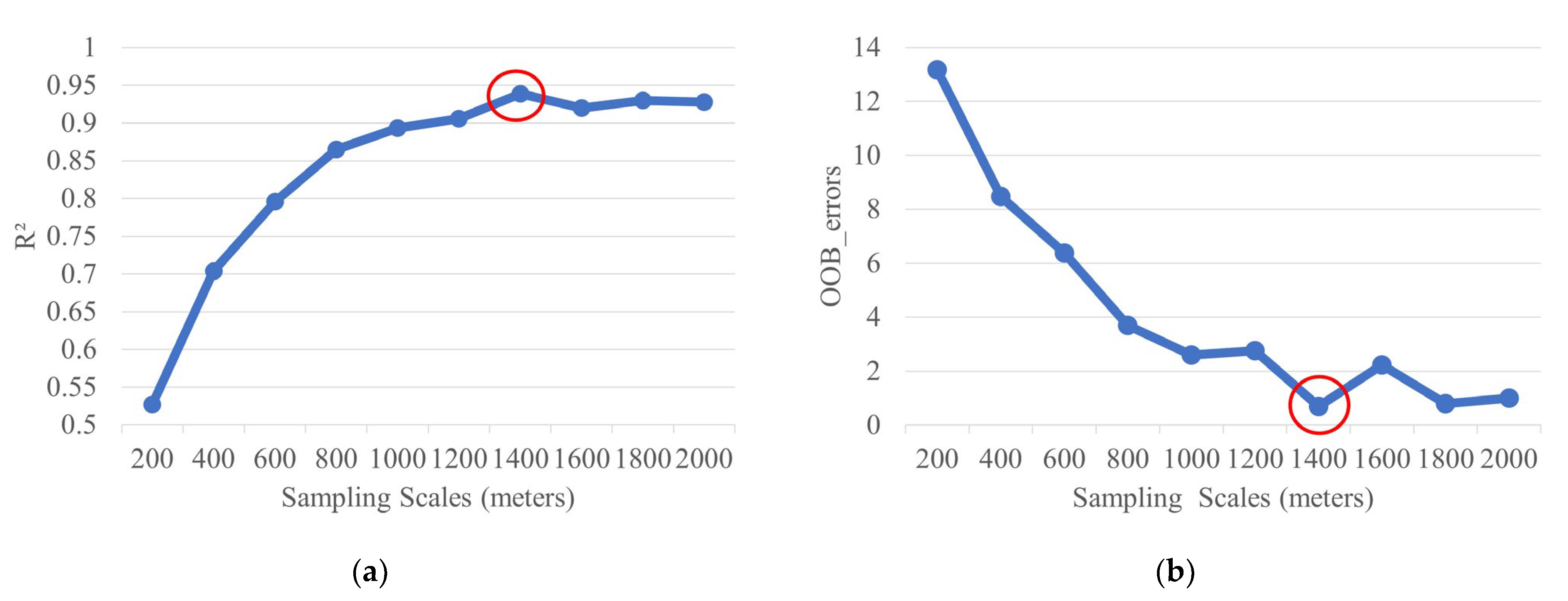
3.1. Optimal Scale for USS Analysis
3.2. Analysis of the Relationship between USS Features and NTLI
3.2.1. Correlation of Diverse USS Features on NTLI
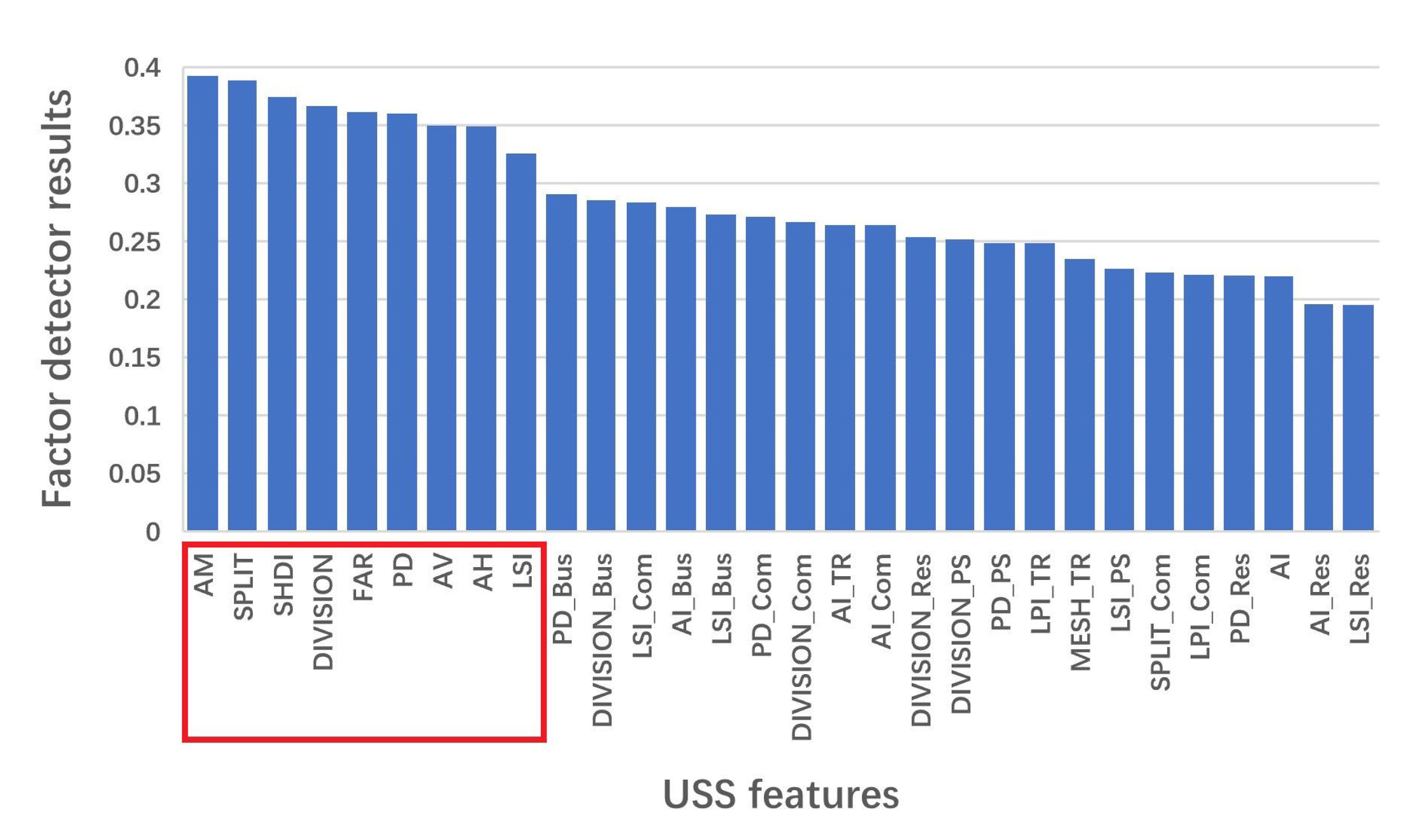
3.2.2. Driving Effects of Diverse USS Features on NTLI
3.2.3. Interaction Detection of Diverse USS Factors on NTLI
3.3. Socioeconomic Benefits Evaluation of the Urban Spatial Structure
3.3.1. Model Construction
+ 0.0967 × DIVISION + 0.1184 × SHDI + 0.2367 × SPLIT
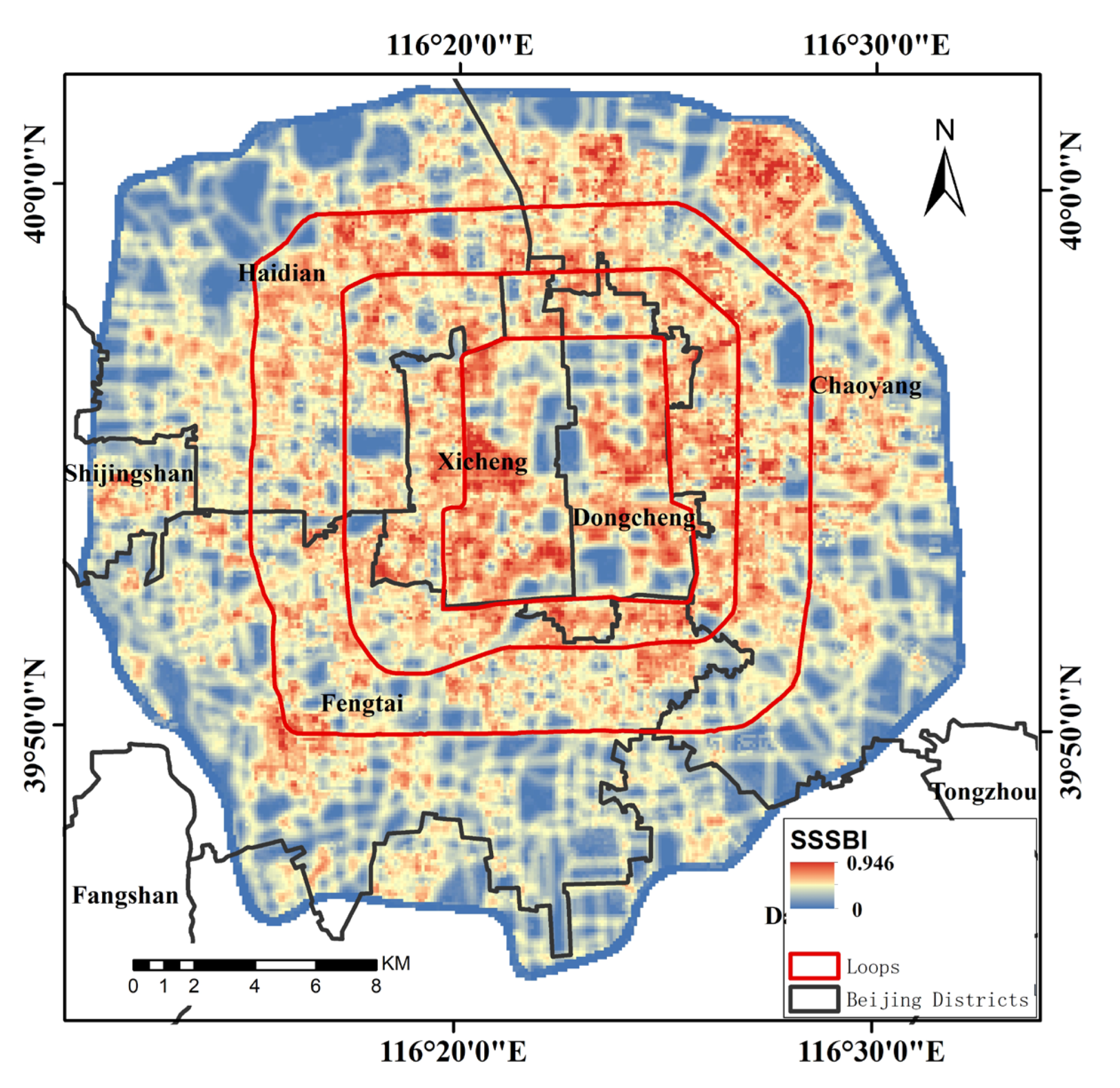
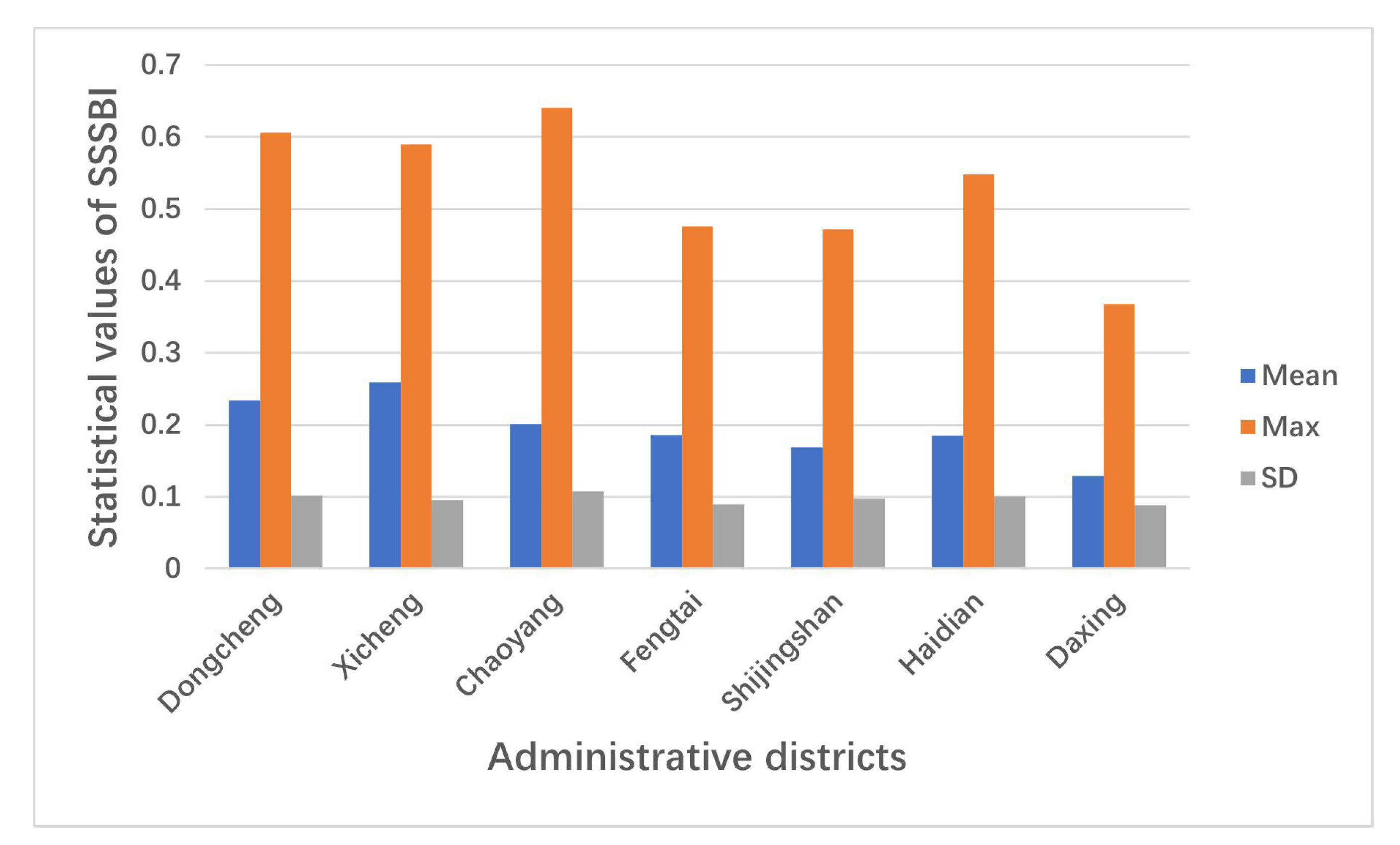
3.3.2. SSSBI Distribution and Its Hot/Cold spots
4. Discussion
4.1. Methodological Contributions
4.2. Strategies for Optimizing Urban Spatial Structure Patterns
4.2.1. Correlation between USS and NTLI
4.2.2. Optimize the Spatial Structure at the Indicator Level
4.2.3. USS Quality Improvement in the SSSBI Cold Spots Region
- (1)
- Enrichment of the hierarchical structure of green spaces. Integrated planning of different types and scales of parks to build a hierarchical and comprehensive green space system. Large landscape parks could meet the needs of public excursions, and small green spaces could improve the accessibility of urban open spaces.
- (2)
- Strengthen night tour programs. Adding night tour projects can not only extend the tour time of visitors and increase the park’s capacity for same-day visitors but also attract visitors to shop and stay near the park. Gradually improve the night tour product system and promote the development of the tourism industry.
- (3)
- Introduce more urban public activities. Based on the open space and pleasant park environment, the internal site design was adjusted to transform the simple green garden into a green urban square with composite functions. Form a new model of diversified park tours combined with cultural experience, fitness and leisure, industrial sightseeing, and other themes.
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoekstra, A.Y.; Wiedmann, T.O. Humanity’s Unsustainable Environmental Footprint. Science 2014, 344, 1114–1117. [Google Scholar] [CrossRef] [PubMed]
- Bhatta, B. Analysis of Urban Growth and Sprawl from Remote Sensing Data; Advances in Geographic Information Science; Springer: Heidelberg, Germany; New York, NY, USA, 2010; ISBN 978-3-642-05298-9. [Google Scholar]
- Al-Mulali, U.; Ozturk, I.; Lean, H.H. The Influence of Economic Growth, Urbanization, Trade Openness, Financial Development, and Renewable Energy on Pollution in Europe. Nat. Hazards 2015, 79, 621–644. [Google Scholar] [CrossRef]
- Bai, X.; Chen, J.; Shi, P. Landscape Urbanization and Economic Growth in China: Positive Feedbacks and Sustainability Dilemmas. Environ. Sci. Technol. 2012, 46, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Clark, D. Book Review: Internal Structure of the City: Readings on Urban Growth, form and Policy. Prog. Hum. Geogr. 1984, 8, 453–455. [Google Scholar] [CrossRef]
- Bourne, L.S. Internal Structure of the City: Readings on Urban Form, Growth, and Policy; Oxford University Press: New York, NY, USA, 1982. [Google Scholar]
- Angel, S.; Parent, J.; Civco, D.L.; Blei, A.; Potere, D. The Dimensions of Global Urban Expansion: Estimates and Projections for All Countries, 2000–2050. Prog. Plan. 2011, 75, 53–107. [Google Scholar] [CrossRef]
- Chong, Z.; Qin, C.; Ye, X. Environmental Regulation and Industrial Structure Change in China: Integrating Spatial and Social Network Analysis. Sustainability 2017, 9, 1465. [Google Scholar] [CrossRef]
- Deng, X.; Huang, J.; Rozelle, S.; Uchida, E. Economic Growth and the Expansion of Urban Land in China. Urban Stud. 2010, 47, 813–843. [Google Scholar] [CrossRef]
- De Espindola, G.M.; da Costa Carneiro, E.L.N.; Façanha, A.C. Four Decades of Urban Sprawl and Population Growth in Teresina, Brazil. Appl. Geogr. 2017, 79, 73–83. [Google Scholar] [CrossRef]
- Buhaug, H.; Urdal, H. An Urbanization Bomb? Population Growth and Social Disorder in Cities. Glob. Environ. Chang. 2013, 23, 1–10. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y. Investigating the Effects of 3D Urban Morphology on the Surface Urban Heat Island Effect in Urban Functional Zones by Using High-Resolution Remote Sensing Data: A Case Study of Wuhan, Central China. ISPRS J. Photogramm. Remote Sens. 2019, 152, 119–131. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Song, W.; Liu, H.; Wu, Q.; Shi, K.; Wu, J. A New Approach for Detecting Urban Centers and Their Spatial Structure With Nighttime Light Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6305–6319. [Google Scholar] [CrossRef]
- Zhang, Q.; Seto, K.C. Mapping Urbanization Dynamics at Regional and Global Scales Using Multi-Temporal DMSP/OLS Nighttime Light Data. Remote Sens. Environ. 2011, 115, 2320–2329. [Google Scholar] [CrossRef]
- Li, Q.; Zheng, H.; Zhang, G.; Guo, X.; Liu, W. Analysis of luojia1-01 index based on nighttime light imagery. J. Geomat. 2020, 45, 8–15. [Google Scholar] [CrossRef]
- Yu, B.; Lian, T.; Huang, Y.; Yao, S.; Ye, X.; Chen, Z.; Yang, C.; Wu, J. Integration of Nighttime Light Remote Sensing Images and Taxi GPS Tracking Data for Population Surface Enhancement. Int. J. Geogr. Inf. Sci. 2019, 33, 687–706. [Google Scholar] [CrossRef]
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining Satellite Imagery and Machine Learning to Predict Poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef]
- Tan, Z.; Wei, D.; Yin, Z. Housing Vacancy Rate in Major Cities in China: Perspectives from Nighttime Light Data. Complexity 2020, 2020, 5104578. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R.; Davis, C.W. Relation between Satellite Observed Visible-near Infrared Emissions, Population, Economic Activity and Electric Power Consumption. Int. J. Remote Sens. 1997, 18, 1373–1379. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Gao, S.; Gong, L.; Kang, C.; Zhi, Y.; Chi, G.; Shi, L. Social Sensing: A New Approach to Understanding Our Socioeconomic Environments. Ann. Assoc. Am. Geogr. 2015, 105, 512–530. [Google Scholar] [CrossRef]
- Li, D.R. Towards geo-spatial information science in big data era. Acta Geod. Cartogr. Sin. 2016, 45, 379–384. [Google Scholar] [CrossRef]
- Shan, J.; Qin, K.; Huang, C.Q.; Hu, X.Y.; Yu, Y.; Hu, Q.W.; Lin, Z.Y.; Chen, J.P.; Jia, T. Methods of Crowd Sourcing Geographic Data Processing and Analysis. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 390–396. [Google Scholar] [CrossRef]
- Wang, X.; Meng, Q.; Zhang, L.; Hu, D. Evaluation of urban green space in terms of thermal environmental benefits using geographical detector analysis. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102610. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Mei, Y.; Li, W. Assessment of Ecosystem Service Quality and Its Correlation with Landscape Patterns in Haidian District, Beijing. Int. J. Environ. Res. Public Health 2019, 16, 1248. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Shu, S.; Liu, H.; Song, W.; Wu, J.; Wang, L.; Chen, Z. Object-Based Spatial Cluster Analysis of Urban Landscape Pattern Using Nighttime Light Satellite Images: A Case Study of China. Int. J. Geogr. Inf. Sci. 2014, 28, 2328–2355. [Google Scholar] [CrossRef]
- Huang, X.; Hu, T.; Li, J.; Wang, Q.; Benediktsson, J.A. Mapping Urban Areas in China Using Multisource Data With a Novel Ensemble SVM Method. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4258–4273. [Google Scholar] [CrossRef]
- Liu, X. Mapping Urban Extent at Large Spatial Scales Using Machine Learning Methods with VIIRS Nighttime Light and MODIS Daytime NDVI Data. Remote Sens. 2019, 11, 1247. [Google Scholar] [CrossRef]
- Yu, L.; Wang, J.; Gong, P. Improving 30 m Global Land-Cover Map FROM-GLC with Time Series MODIS and Auxiliary Data Sets: A Segmentation-Based Approach. Int. J. Remote Sens. 2013, 34, 5851–5867. [Google Scholar] [CrossRef]
- Tian, Y. The Effect of Urban 2D and 3D Morphology on Air Temperature in Residential Neighborhoods. Landsc. Ecol. 2019, 34, 1161–1178. [Google Scholar] [CrossRef]
- Small, C. Multisensor Characterization of Urban Morphology and Network Structure. Remote Sens. 2019, 11, 2162. [Google Scholar] [CrossRef]
- Chen, K.; Zou, Z.; Shi, Z. Building Extraction from Remote Sensing Images with Sparse Token Transformers. Remote Sens. 2021, 13, 4441. [Google Scholar] [CrossRef]
- Chen, M.; Wu, J.; Liu, L.; Zhao, W.; Tian, F.; Shen, Q.; Zhao, B.; Du, R. DR-Net: An Improved Network for Building Extraction from High Resolution Remote Sensing Image. Remote Sens. 2021, 13, 294. [Google Scholar] [CrossRef]
- Lv, N.; Zhang, Z.; Li, C.; Deng, J.X.; Su, T.; Chen, C. A hybrid-attention semantic segmentation network for remote sensing interpretation in land-use surveillance. Int. J. Mach. Learn. Cyber. 2022. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Meng, Q.; Zhang, L.; Wang, C.; Liu, X.; Zhao, M. Developing a Method to Extract Building 3D Information from GF-7 Data. Remote Sens. 2021, 13, 4532. [Google Scholar] [CrossRef]
- Bullinger, S.; Bodensteiner, C.; Arens, M. 3D Surface Reconstruction From Multi-Date Satellite Images. arXiv 2021, arXiv:2102.02502. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Chen, Z.; Yao, S.; Huang, Y.; Wu, J. An Extended Minimum Spanning Tree Method for Characterizing Local Urban Patterns. Int. J. Geogr. Inf. Sci. 2018, 32, 450–475. [Google Scholar] [CrossRef]
- Xie, J.; Feng, C.-C. An Integrated Simplification Approach for 3D Buildings with Sloped and Flat Roofs. IJGI 2016, 5, 128. [Google Scholar] [CrossRef]
- Zhang, P.F.; Hu, Y.M.; Xiong, Z.P. Variation pattern and its affecting factors of three-dimensional landscape in urban residential community of Shenyang. Chin. J. Appl. Ecol. 2011, 2011, 453–459. [Google Scholar] [CrossRef]
- Wu, Q.; Guo, F.X.; Li, H.Q.; Kang, J.Y. Measuring landscape pattern in three dimensional space. Landsc. Urban Plan. 2017, 167, 49–59. [Google Scholar] [CrossRef]
- Long, Y.; Li, P.; Hou, J.X. Three-dimensional Urban Form at the Street Block Level for Major Cities in China. Shanghai Urban Plan. Rev. 2019, 3, 1673–8985. [Google Scholar] [CrossRef]
- Bennett, M.M.; Smith, L.C. Advances in Using Multitemporal Night-Time Lights Satellite Imagery to Detect, Estimate, and Monitor Socioeconomic Dynamics. Remote Sens. Environ. 2017, 192, 176–197. [Google Scholar] [CrossRef]
- Wang, L.; Fan, H.; Wang, Y. Improving Population Mapping Using Luojia 1-01 Nighttime Light Image and Location-Based Social Media Data. Sci. Total Environ. 2020, 730, 139148. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Hu, Y.; Huang, C.; Shi, K.; Wu, J. Estimating House Vacancy Rate in Metropolitan Areas Using NPP-VIIRS Nighttime Light Composite Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2188–2197. [Google Scholar] [CrossRef]
- Venkatalaxmi, A.; Padmavathi, B.S.; Amaranath, T. A General Solution of Unsteady Stokes Equations. Fluid Dyn. Res. 2004, 35, 229–236. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, B.; Liu, Y.; Chen, Z.; Li, Q.; Wang, C.; Wu, J. Estimation of Poverty Using Random Forest Regression with Multi-Source Data: A Case Study in Bangladesh. Remote Sens. 2019, 11, 375. [Google Scholar] [CrossRef]
- Shi, K.; Chen, Y.; Yu, B.; Xu, T.; Yang, C.; Li, L.; Huang, C.; Chen, Z.; Liu, R.; Wu, J. Detecting Spatiotemporal Dynamics of Global Electric Power Consumption Using DMSP-OLS Nighttime Stable Light Data. Appl. Energy 2016, 184, 450–463. [Google Scholar] [CrossRef]
- Shi, K.; Chen, Y.; Yu, B.; Xu, T.; Chen, Z.; Liu, R.; Li, L.; Wu, J. Modeling Spatiotemporal CO2 (Carbon Dioxide) Emission Dynamics in China from DMSP-OLS Nighttime Stable Light Data Using Panel Data Analysis. Appl. Energy 2016, 168, 523–533. [Google Scholar] [CrossRef]
- Zhang, X.; Du, S.; Du, S.; Liu, B. How Do Land-Use Patterns Influence Residential Environment Quality? A Multiscale Geographic Survey in Beijing. Remote Sens. Environ. 2020, 249, 112014. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W.D. Using Luminosity Data as a Proxy for Economic Statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar] [CrossRef]
- Chen, C.; Fushing, H. Multiscale Community Geometry in a Network and Its Application. Phys. Rev. E 2012, 86, 041120. [Google Scholar] [CrossRef]
- Mcgarigal, K.S.; Cushman, S.A.; Neel, M.C. Spatial Pattern Analysis Program for Categorical Maps. Fragstats. 2002. Available online: www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 3 March 2021).
- Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Zhang, T.; Gu, X.; Zheng, X. Geographical Detectors-Based Health Risk Assessment and Its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Hao, H.; Yang, Y. Quantifying the Spatial Heterogeneity and Driving Factors of Aboveground Forest Biomass in the Urban Area of Xi’an, China. ISPRS Int. J. Geo-Inf. 2020, 9, 744. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Bu, Y. Quantitative Analysis of Spatial Heterogeneity and Driving Forces of the Thermal Environment in Urban Built-up Areas: A Case Study in Xi’an, China. Sustainability 2021, 13, 1870. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Statistics, L.B.; Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kordi, M.; Brandt, S.A. Effects of Increasing Fuzziness on Analytic Hierarchy Process for Spatial Multicriteria Decision Analysis. Comput. Environ. Urban Syst. 2012, 36, 43–53. [Google Scholar] [CrossRef]
- Parsian, S.; Amani, M.; Moghimi, A.; Ghorbanian, A.; Mahdavi, S. Flood Hazard Mapping Using Fuzzy Logic, Analytical Hierarchy Process, and Multi-Source Geospatial Datasets. Remote Sens. 2021, 13, 4761. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making—The Analytic Hierarchy and Network Processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Fan, P.; Xu, L.; Yue, W.; Chen, J. Accessibility of Public Urban Green Space in an Urban Periphery: The Case of Shanghai. Landsc. Urban Plan. 2017, 165, 177–192. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Q.; Zhang, Y. Vertical decentralization and horizontal competition: How administrative governance models affect the coordinated development of urbanization and industrialization in prefecture-level cities. Financ. Trade Econ. 2022, 43, 112–127. [Google Scholar] [CrossRef]
- Zheng, L.; Li, Z.; Li, P.; Gao, H.; Xu, G.; Ke, H. Simulation of landscape pattern and socio-economic response relationship in the Danjiang Tusk Mountains. Soil Water Conserv. Res. 2019, 26, 338–343. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Z.; Yang, C.; Li, Q.; Wu, Q.; Wu, J.; Zhang, G.; Yu, B. Analyzing Parcel-Level Relationships between Luojia 1-01 Nighttime Light Intensity and Artificial Surface Features across Shanghai, China: A Comparison with NPP-VIIRS Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101989. [Google Scholar] [CrossRef]
- Zhang, P.; Song, Y.; Liu, J.; Gao, Y.; Li, X. Analysis of influencing factors of urban three-dimensional architectural landscape. Urban Archit. 2019, 16, 135–139. [Google Scholar] [CrossRef]







| Categories | Samples | Producer’s Accuracies (%) | User’s Accuracies (%) | F1-Score (%) |
|---|---|---|---|---|
| Transport | 138 | 88.49 | 89.13 | 88.81 |
| Public service | 1439 | 90.06 | 91.31 | 90.68 |
| Residential | 1148 | 82.55 | 91.46 | 86.78 |
| Parkland | 509 | 85.06 | 91.75 | 88.28 |
| Business | 498 | 90.55 | 73.09 | 80.89 |
| Commercial | 338 | 97.14 | 60.36 | 74.45 |
| Industrial | 317 | 86.24 | 96.85 | 91.23 |
| total | 4387 | 86.43 | ||
| Category | Indicator Name | Abbreviation | Range/Expression | Description |
|---|---|---|---|---|
| Urban functional landscape patterns | Largest Patch Index | LPI | 0% < LPI ≤ 100% | Indicates the percentage of the landscape occupied by the largest patch area |
| Effective Mesh Size | MESH | 0% < MESH ≤ 100% | Indicates the proportion of different land-use area to the total area | |
| Patch Density | PD | PD > 0 | Indicates the number of patches of a certain landscape type per unit area | |
| Landscape Shape Index | LSI | LSI ≥ 1 | Indicates the degree of regularity of the shape of the landscape patches; the higher the value, the more irregular the shape of the patch | |
| Landscape Division Index | DIVISION | 0% < DIVISION ≤ 100% | Indicates the degree of fragmentation of the landscape; the higher the value, the smaller the patches and the more dispersed the distribution | |
| Splitting Index | SPLIT | 0% < SPLIT ≤ 100% | Indicates the degree of landscape fragmentation; the values increase as the landscape is subdivided into smaller patches | |
| Aggregation Index | AI | 0% ≤ AI ≤ 100% | Indicates the degree of aggregation and dispersion of certain patches in the landscape; a higher value indicates a more aggregated distribution of patches | |
| Shannon Diversity Index | SHDI | SHDI ≥ 1 | Measures the diversity of patch types in the landscape, with higher values indicating a richer patch type | |
| Building forms | Average Number | AN | Reflects the average level of the number of buildings in the area | |
| Average Area | AA | Reflects the average level of building space in the area | ||
| Average Height | AH | Reflects the average level of building height in the area | ||
| Building Height Fluctuation | BF | Reflects the degree of ebb and flow of building heights in the area; the higher the value, the greater the fluctuation of building heights in the area | ||
| Average Volume | AV | Reflects the average level of building volume in the area | ||
| Floor Area Ratio | FAR | Measures the intensity of use of a building site and is a dimensionless ratio. The lower the volume ratio, the higher the comfort level of the inhabitants and vice-versa | ||
| Socioeconomic vitality | Nighttime Light Intensity | NTLI | Reflects the activity level in economic activities such as production, services, and consumer spending |
| Level | Correlation Coefficient | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Class-level | PD | LPI | MESH | LSI | DIVISION | SPLIT | AI | ||
| Transport | 0.334 | 0.479 | 0.417 | 0.407 | 0.385 | −0.371 | 0.577 | ||
| *** | *** | *** | *** | *** | *** | *** | |||
| Institution | 0.56 | 0.299 | 0.216 | 0.547 | 0.57 | 0.061 | 0.53 | ||
| *** | *** | *** | *** | *** | / | *** | |||
| Residential | 0.525 | 0.141 | 0.027 | 0.49 | 0.564 | 0.129 | 0.455 | ||
| *** | *** | / | *** | *** | ** | *** | |||
| Parkland | 0.242 | −0.012 | −0.078 | 0.228 | 0.413 | 0.276 | 0.208 | ||
| *** | / | / | *** | *** | *** | *** | |||
| Business | 0.574 | 0.449 | 0.406 | 0.553 | 0.57 | 0.371 | 0.599 | ||
| *** | *** | *** | *** | *** | *** | *** | |||
| Commercial | 0.584 | 0.495 | 0.413 | 0.578 | 0.582 | 0.48 | 0.574 | ||
| *** | *** | *** | *** | *** | *** | *** | |||
| Industrial | −0.029 | −0.124 | −0.153 | −0.024 | −0.041 | −0.029 | −0.026 | ||
| / | ** | *** | / | / | / | / | |||
| Landscape- | NP | LPI | MESH | LSI | DIVISION | SPLIT | AI | SHDI | |
| level | 0.666 | −0.283 | −0.346 | 0.65 | 0.682 | 0.702 | 0.156 | 0.692 | |
| *** | *** | *** | *** | *** | *** | *** | *** | ||
| Building form | AN | AA | AH | AM | FAR | AV | |||
| 0.252 | 0.106 | 0.692 | 0.703 | 0.625 | 0.58 | ||||
| *** | *** | *** | *** | *** | *** | ||||
| Variable1 | Variable2 | qV1 | qV2 | q(V1 ∩ V2) | Interaction |
|---|---|---|---|---|---|
| SPLIT | AV | 0.389071 | 0.349941 | 0.595315 | Bi-Enhance |
| PD | AV | 0.360324 | 0.349941 | 0.577724 | Bi-Enhance |
| AM | AV | 0.392863 | 0.349941 | 0.552989 | Bi-Enhance |
| DIVISION | AV | 0.366888 | 0.349941 | 0.552392 | Bi-Enhance |
| SHDI | AV | 0.374618 | 0.349941 | 0.548748 | Bi-Enhance |
| LSI | AV | 0.326183 | 0.349941 | 0.546908 | Bi-Enhance |
| LPI_TR | AV | 0.248607 | 0.349941 | 0.515834 | Bi-Enhance |
| PD_PS | AV | 0.248839 | 0.349941 | 0.512589 | Bi-Enhance |
| AH | AV | 0.349102 | 0.349941 | 0.512571 | Bi-Enhance |
| SPLIT_Com | AV | 0.22315 | 0.349941 | 0.51012 | Bi-Enhance |
| Objective Level | Criterion Level | Solution Level | Weight |
|---|---|---|---|
| Spatial Structure Socioeconomic Benefit Index, SSSBI(A), weight = 1 | Evaluation of Spatial Structure at 3D_Buildings Structures(B1), weight = 0.5 | AH(C1) | 0.0659 |
| AV(C2) | 0.0697 | ||
| FAR(C3) | 0.0697 | ||
| AM(C4) | 0.2948 | ||
| Evaluation of Spatial Structure at land-use function patterns(B2), weight = 0.5 | PD(C5) | 0.0483 | |
| DIVISION(C6) | 0.0967 | ||
| SHDI(C7) | 0.1184 | ||
| SPLIT(C8) | 0.2367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Meng, Q.; Zhang, J.; Zhang, L.; Allam, M.; Hu, X.; Zhan, C. Evaluation of Urban Spatial Structure from the Perspective of Socioeconomic Benefits Based on 3D Urban Landscape Measurements: A Case Study of Beijing, China. Remote Sens. 2022, 14, 5511. https://doi.org/10.3390/rs14215511
Liu Y, Meng Q, Zhang J, Zhang L, Allam M, Hu X, Zhan C. Evaluation of Urban Spatial Structure from the Perspective of Socioeconomic Benefits Based on 3D Urban Landscape Measurements: A Case Study of Beijing, China. Remote Sensing. 2022; 14(21):5511. https://doi.org/10.3390/rs14215511
Chicago/Turabian StyleLiu, Yujia, Qingyan Meng, Jichao Zhang, Linlin Zhang, Mona Allam, Xinli Hu, and Chengxiang Zhan. 2022. "Evaluation of Urban Spatial Structure from the Perspective of Socioeconomic Benefits Based on 3D Urban Landscape Measurements: A Case Study of Beijing, China" Remote Sensing 14, no. 21: 5511. https://doi.org/10.3390/rs14215511
APA StyleLiu, Y., Meng, Q., Zhang, J., Zhang, L., Allam, M., Hu, X., & Zhan, C. (2022). Evaluation of Urban Spatial Structure from the Perspective of Socioeconomic Benefits Based on 3D Urban Landscape Measurements: A Case Study of Beijing, China. Remote Sensing, 14(21), 5511. https://doi.org/10.3390/rs14215511










