Exploring the Environmental Conditions of Snow Particles Using Spaceborne Triple-Frequency Radar Measurements over Ocean

Abstract

The environmental conditions of snow particles with different particle sizes and bulk effective densities over the ocean are explored using a coincidence dataset of National Aeronautics and Space Administration (NASA) CloudSat Cloud Profiling Radar (CPR) and Global Precipitation Mission (GPM) Dual-frequency Precipitation Radar (DPR). Observed triple-frequency radar signatures for snow particles over the ocean are firstly derived. Based on modeled triple-frequency signatures for various snow particles, DFR Ku/Ka and the ratio of DFR Ku/Ka to DFR Ku/W from observations are selected to indicate the snow particle size and bulk effective density, respectively. The dependences of two indicators on temperature, relative humidity and cloud liquid water content are presented. The snow particle size range becomes wider at warmer temperatures, higher relative humidities or lower cloud liquid water contents. At cold temperatures, low relative humidities or high cloud liquid water contents, large snow particles are prevalent. At high cloud liquid water contents, the riming process mainly contributes to the increase in snow particle bulk effective density. When supersaturation occurs, a large portion of snow particles have large sizes and low bulk effective densities at cold temperatures. This study can improve the understanding of snow microphysics and demonstrate the potential of spaceborne radar measurements in global snowfall retrievals.

1. Introduction

Snow forms a large portion of precipitation at mid and high latitudes during winter. It plays an important role in the global hydrological cycle. With the development of passive and active remote sensors, the global falling snow observation has been improved consistently over the decades. Nevertheless, the retrieval of snowfall rate remains a large uncertainty due the lack of understanding of snow microphysics. In recent years, several studies have found that combining the use of triple-frequency radar measurements may provide crucial information about snow microphysical properties. Kneifel et al. [1] employed snow particle models to show that different snow particle types occupy distinct areas of the triple-frequency plane enclosed by two dual-frequency ratios (DFRs) at Ku, Ka and W bands. Leinonen et al. [2] and Kulie et al. [3] both examined triple-frequency signatures from Wakasa Bay aircraft radar measurements. Their results indicated that complex snow aggregate models can fit well for most observed triple-frequency radar signatures rather than spheroidal models. Kneifel et al. [4], for the first time, investigated the relation between observed triple-frequency radar signatures and snow microphysics from in situ measurements at ground level. A hook signature is evident on the triple-frequency plane when large snow aggregates exist. When the bulk effective density of snow particles increases, a rotation of DFR curves on the triple-frequency plane is observed. The modeling experiments conducted by Leinonen and Moisseev [5], Leinonen and Szyrmer [6], Yin et al. [7] as well as Gergely et al. [8] further verified this finding. Their results revealed that triple-frequency radar signatures are closely related to snow particle size and bulk effective density. From unrimed snow particle models with low density to heavily rimed snow particle models with high density, DFR Ku/Ka values decrease, while DFR Ka/W values increase, resulting in a rotation of DFR curves on the triple-frequency plane.

Following early studies on triple-frequency radar signatures, more recent studies have been focused on the retrieval of snow particle properties, the validation of snow particle scattering models and weather forecast models as well as the understanding of snow microphysics using triple-frequency approaches. Chase et al. [9] evaluated coincident airborne radar triple-frequency and snow microphysical measurements. They demonstrated that triple-frequency observations support the retrieval of snow particle size and bulk effective density, but independent measurements for deriving a reliable mass-size relation are required to reduce the retrieval uncertainty. Leinonen et al. [10] used a Bayesian algorithm to retrieve the snow particle size, number concentration and density from airborne triple-frequency radar observations. Their results suggested that triple-frequency measurements can provide better estimates of snow particle density compared to dual-frequency measurements. In addition, they found that the retrieval of snow particle number concentration and density is strongly affected by a priori assumptions in the algorithm. Mroz et al. [11] also designed a Bayesian algorithm to retrieve the size, ice water content and degree of riming of ice clouds from aircraft triple-frequency radar observations. Using in situ measurements of snow microphysics as validation, their results indicated that the estimates of ice water content and mean mass-related diameter are generally accurate, while the accurate retrieval of the degree of riming needs extra information of Doppler mean velocity.

Tyynelä and vonLerber [12] evaluated nine different snow particle models, including single crystals, rimed/unrimed aggregates and graupels, using in situ and triple-frequency dual-polarization radar measurements. It was shown that denser snow particle models generally fit in situ measurements better due to the prevalent existence of rimed snow particles. By comparing modeled and observed triple-frequency radar signatures at X, Ka and W bands, they also found that the physical aggregate models that incorporate physics into the modeling perform better than the empirical ones that incorporate the information of snowflake measurements into the modeling. Ori et al. [13] employed triple-frequency Doppler radar measurements to evaluate the snow particle growth process in the Icosahedral Nonhydrostatic (ICON) forecast model. The statistical comparison indicated that the ICON model increasingly overestimates the mean particle size at temperatures higher than –7 °C. The terminal velocities of snow particles are also overestimated by the ICON model at large particle sizes.

Dias Neto et al. [14] presented a dataset of triple-frequency Doppler radar measurements for improving the understanding of winter precipitations. The joint use of DFRs and Doppler mean velocities allows for the distinction of rimed and melting snow particles. The extremely large DFRs (up to 20 dB) are found for melting particles mainly due to the strong aggregation. Tridon el at. [15] derived unusual signatures from triple-frequency radar observations in the West Antarctic. The extremely high DFR Ka/W values are frequently observed with relatively low DFR X/Ka values at unexpected low temperatures of –20 °C. Throughout a case study, the results indicated that these unusual triple-frequency signatures can only be explained by rimed aggregates and a narrow particle size distribution. Nguyen et al. [16] explored the potential use of a coincident dataset of in situ and triple-frequency radar airborne measurements in the Arctic. The observed triple-frequency radar signatures are grouped based on the degree of snow aggregation and riming. The results are generally consistent with previous studies, implying that triple-frequency signatures contain the information of snow particle size and bulk effective density. Nevertheless, they pointed out that the triple-frequency retrieval algorithm remains challenging since different combinations of snow particles may produce similar triple-frequency radar signatures.

While several triple-frequency radar experiments for snow particles have been conducted over land, similar experiments over ocean are still rare. It is important to derive oceanic triple-frequency radar signatures for snow particles from satellite measurements. In this study, a coincidence dataset of CloudSat Cloud Profiling Radar (CPR, 94 GHz) [17] and Global Precipitation Mission (GPM) Dual-frequency Precipitation Radar (DPR, 13.6 and 35.5 GHz) [18] is employed to provide spaceborne triple-frequency radar measurements over the ocean, where ground-based in situ and radar measurements are sparse. By linking various atmospheric state variables from CloudSat and GPM precipitation products with observed triple-frequency radar signatures, the environmental conditions of snow particles with different microphysical properties over the ocean are explored for a period of more than three years. It is worth noting that the data processing method is partly adopted from Yin et al. [7], with some adjustments and refinements. Yin et al. [7] mainly focused on interpreting theoretical and observed triple-frequency radar signatures rather than snow microphysics. The main goal of this study is to improve the understanding of snow microphysics and demonstrate the potential use of spaceborne triple-frequency radar measurements for reliable global snowfall retrievals. The information obtained from this study is beneficial for the upcoming Aerosol Cloud Convection and Precipitation (ACCP) mission [19,20] with triple-frequency Doppler radars at Ku, Ka and W bands onboard the mission satellites, aiming to promote global precipitation estimations.

The remainder of this paper is organized as follows. Section 2 provides the description of data sources and processing steps. Section 3 describes the details of the employed triple-frequency approach. Section 4 presents the statistical results of the environmental conditions of snow particles with different microphysical properties over the ocean. The conclusions are given in Section 5.

2. Data Sources and Processing Steps

The coincidence dataset between CloudSat and GPM [21] is primarily used for this study. It mainly includes collocated CloudSat CPR radar reflectivity profiles, GPM DPR radar reflectivity profiles and European Centre for Medium-range Weather Forecasts (ECMWF) ancillary state variables for CloudSat CPR. In this dataset, each CPR radar reflectivity profile is matched with a nearest DPR radar reflectivity profile when two satellite tracks coincide within 15 min. Since this dataset provides the along-track and cross-track collocation indices for CPR and DPR, it is easy to implement other variables from GPM and CloudSat precipitation products.

The CloudSat CPR is a 94 GHz (W band) nadir-looking radar with global coverage, designed for monitoring global cloud and precipitation systems. It has a footprint size of about 2.3 km along the track and 1.4 km across the track. A single CPR profile has a total of 150 vertical bins, with a bin size of about 240 m. The GPM DPR is a dual-frequency radar operating at 13.6 GHz (Ku band) and 35.5 GHz (Ka band). The spatial coverage of DPR is from 65°S to 65°N. The DPR Ku band operates in normal scan, while the DPR Ka band operates in match scan (MS) and high-sensitivity scan (HS). The Ku NS has 49 beams for each scan. The Ka MS has 25 beams for each scan. The beams of Ka MS correspond to the central beams of Ku NS from 13 to 37. The footprint size of DPR is about 5.2 km at nadir. A single DPR profile has a total of 176 vertical bins, with a bin size of about 125 m for Ku NS and Ka MS.

In this study, the triple-frequency signatures of snow particles over the ocean are explored, so all radar bins above freezing level heights with CPR surface type classified as ocean are selected. As mentioned by Yin et al. [7], strong updrafts may lift raindrops above freezing levels in deep convective clouds. To minimize this possible contamination, only radar bins with freezing level heights lower than 3 km remain. This approach can effectively remove those deep convective clouds at low latitudes where their freezing level heights are about 5 km [22]. The strong updrafts are less likely to occur in the remaining radar bins, so the contamination of raindrops is negligible. To remove the surface contamination, the radar bins of the lowest 1 km were excluded for this study. Due to the difference in scanning geometry between DPR and CPR, only radar bins within DPR scan angles of $\pm {2.8}^{\circ }$ are selected.

It is seen that there is an obvious discrepancy in horizontal and vertical resolutions between DPR and CPR. Since the horizontal resolution of CPR (about 2 km) is smaller than that of DPR (about 5 km at nadir), the beam averaging is applied to CPR measurements. All CPR profiles within a searching radius of 4 km around the location of a single DPR profile are averaged to produce a matched CPR profile. The averaged CPR radar reflectivity (Z_e,avg) of each vertical bin can be expressed as

$$Z_{\mathrm{e},\mathrm{avg}}=\frac{1}{\mathrm{k}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{k}}{\mathrm{w}}_{\mathrm{i}}{\mathrm{Z}}_{\mathrm{e},\mathrm{i}}}$$

(1)

$${\mathrm{w}}_{\mathrm{i}}=\frac{{\mathrm{d}}_{\mathrm{i}}^{-2}}{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{k}}{\mathrm{d}}_{\mathrm{i}}^{-2}}}$$

(2)

where Z_e,i is the linear-scale radar reflectivity of each bin for the ith CPR profile matched to a DPR profile, d_i is the distance between the location of the DPR profile and that of the ith CPR profile and k is the total number of matched CPR profiles within the searching radius. w_i is the weighting factor for the ith CPR profile, inversely proportional to the square of d_i. The vertical bin size of CPR is about 240 m, while the vertical bin size of DPR Ku NS and Ka MS is about 125 m. In this coincidence dataset, for each CPR bin, the matched DPR profile will be searched from the bottom until the first DPR bin above this CPR bin is determined, implying that approximately every other DPR Ku NS and Ka MS bin is matched to a CPR bin. Other vertical matching methods are also examined, including searching the last DPR bin below this CPR bin or averaging two nearest DPR bins above and below this CPR bin, both producing very similar results to the original dataset. Therefore, we do not alter the vertical matching method for this coincidence dataset. It is worth mentioning that even after those processing steps, the mismatching errors sill remain between DPR and CPR due to their different platforms and instrument characteristics.

The correction of attenuation is also applied to this triple-frequency radar dataset. The attenuation due to snow can be ignored at Ku and Ka bands but can be substantial at the W band. The study of Matrosov [23] has shown that the attenuation at W band can reach above 1 dB for heavy snowfall, while the attenuation at the Ka band is about one order of magnitude lower than that at the W band. Hence, a correction method from Kulie et al. [3] is employed to calculate the W band attenuation due to snow. We select two snow particle models, dendrite [24] and oblate aggregate [25] and then derive an averaged linear relationship between radar reflectivity at the Ku band (mm⁶ m⁻³) and specific attenuation at W band (dB km⁻¹). It is assumed that the particle size distribution follows an exponential form

$${\mathrm{N}\left(\mathrm{D}\right)=\mathrm{N}}_0\exp (-\mathsf{\Lambda }\mathrm{D})$$

(3)

where N₀ is the intercept parameter, L is the slope parameter and D represents the maximum diameter of snow particle. Based on in situ measurements [26], N₀ usually varies from 10⁵ to 10⁷ m⁻⁴ and L usually varies from 5 to 40 cm⁻¹. In simple crystals, D is generally smaller than 5 mm, while in complex aggregates, D can be as large as 20 mm [4,26]. Previous studies have found that the exponential particle size distribution describes the snow particle size spectra well [23,26,27]. It has also been widely used in the studies of triple-frequency radar signatures [5,8,10]. Further, 49 pairs of N₀ and Λ are adopted from in situ snow particle size measurements of Braham [26] to calculate specific attenuation at the W band and radar reflectivity at the Ku band. D can be obtained from selected snow particle models. For each CPR bin, the sum of linear-scale radar reflectivity at the Ku band of all DPR bins above this CPR bin is converted to the total attenuation due to snow for this CPR bin. Cloud liquid water also contributes significantly to the attenuation at the Ka and W bands. Assuming that cloud liquid water content is up to 0.5 g m⁻³, the specific attenuation at the Ku band is negligible, with values less than 0.2 dB km⁻¹, while the specific attenuation at the Ka and W bands can extend to 1 dB km⁻¹ and 4 dB km⁻¹, respectively [28]. In this study, cloud liquid water profiles come from the GPM-combined radar-radiometer product [29]. In this product, precipitation profiles and environmental parameters are firstly derived from DPR Ku band radar reflectivity profiles and then employed to simulate GPM Microwave Imager (GMI) brightness temperatures and DPR Ka band radar reflectivity profiles. Initial precipitation profiles and environmental parameters are updated to generate simulations more consistent with observed GMI brightness temperatures and DPR Ka band radar reflectivities. The retrieved cloud liquid water profiles are good enough for correcting the attenuation of spaceborne radar measurements even though they may contain some retrieved errors. The cloud liquid water content, frequency and complex dielectric permittivity can be used to calculate the Ka and W band attenuation due to cloud liquid water [30,31]. A double-Debye model is employed to calculate the complex dielectric permittivity as a function of frequency and temperature [32]. In addition, the gaseous attenuation at the W band is also corrected directly using estimates from CloudSat product 2B-GEOPROF.

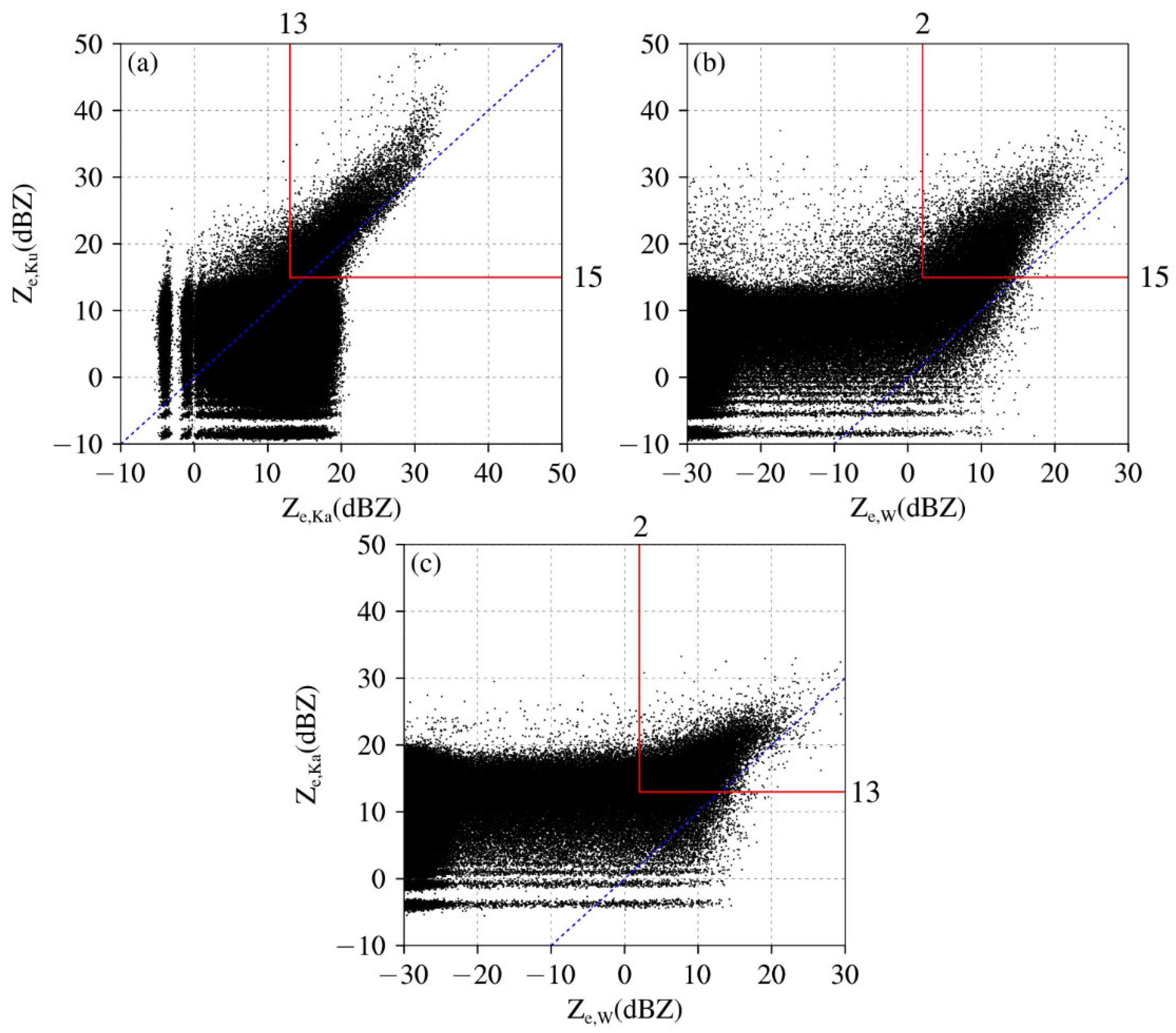
The scatterplots of radar reflectivities between Ku and Ka, Ku and W and Ka and W bands for all qualified radar bins are shown in Figure 1. It is seen that radar reflectivities at the Ka and W bands generally increase with increasing radar reflectivities at the Ku band in the red boxes. Accordingly, only radar bins with radar reflectivities larger than 15, 13 and 2 dBZ for the Ku, Ka and W bands remain. The minimum thresholds of triple-frequency radar reflectivities are generally consistent with the evaluation results of DPR precipitation detectability from Hamada and Takayasu [33]. Their results suggested that DPR Ku NS and Ka MS signals ranging from 12 to 18 dBZ are meaningful meteorological echoes.

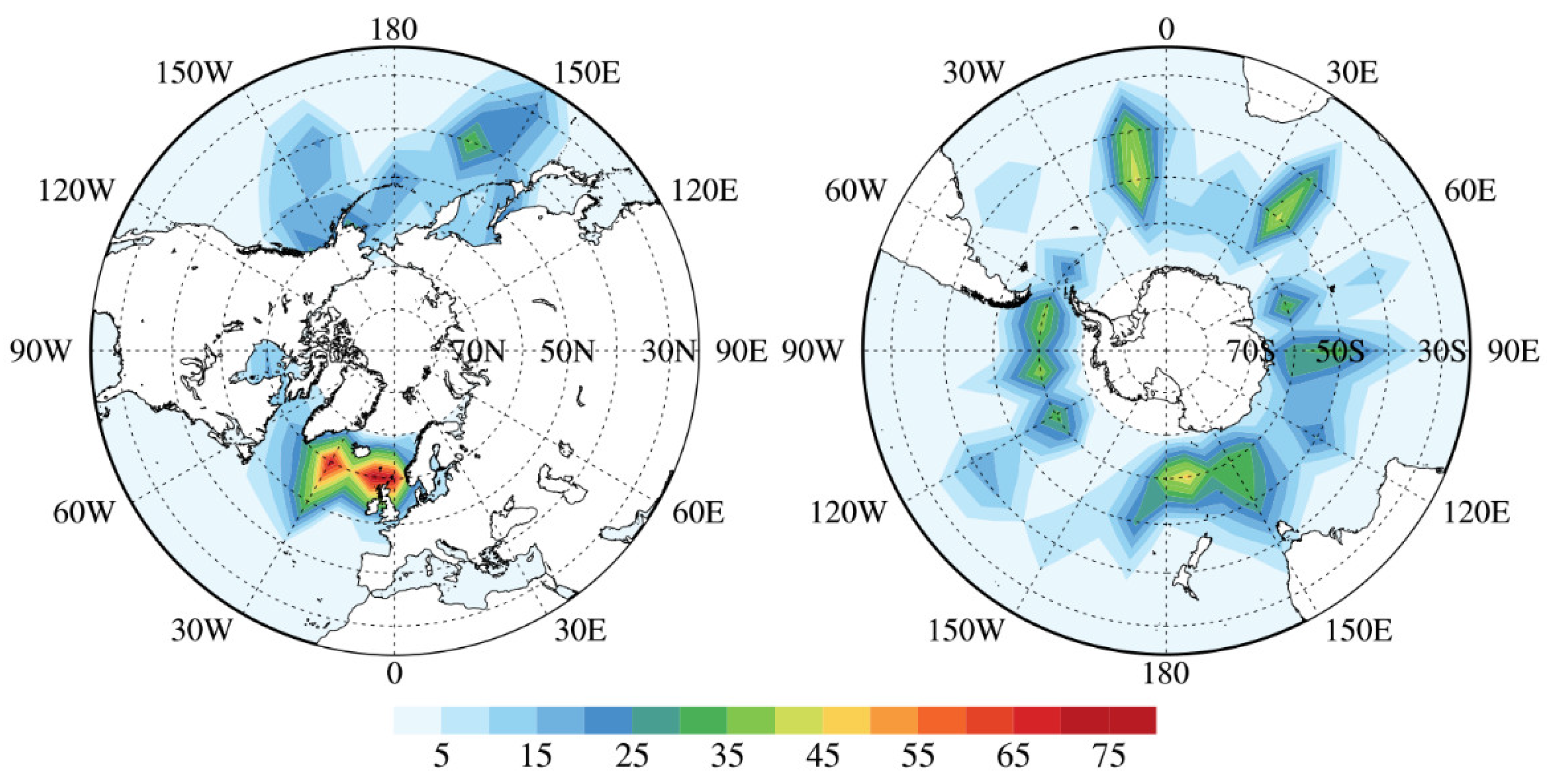
The geolocations of selected radar profiles are shown in Figure 2. It is seen that the longitudinal distribution of radar profiles is more homogeneous in the southern hemisphere. Most selected radar profiles are located at latitudes higher than 50°. We finally have about 10,500 qualified radar bins with latitudes higher than 25°. The time duration of selected radar bins is from March 2014 to October 2017.

3. Triple-frequency Approach

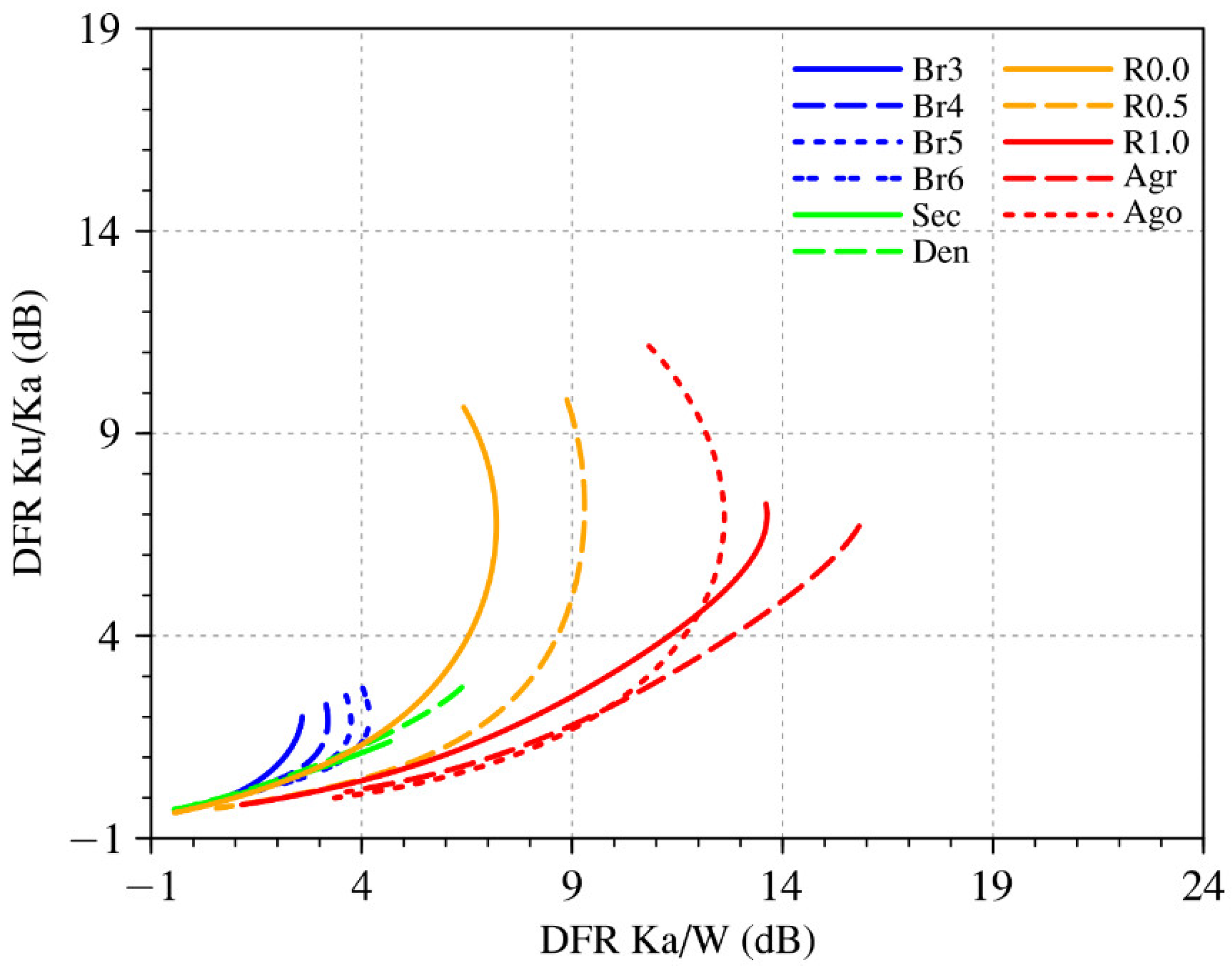
Triple-frequency signatures for various snow particle models are firstly calculated and presented in Figure 3. Simple crystals include 3-, 4-, 5- and 6-bullet rosettes (Br3–Br6), sectors (Sec) and dendrites (Den) from Liu [24]. Unrimed and rimed dendrite aggregates from Leinonen and Szyrmer [6] are selected to represent snow aggregates. They used effective liquid water path (ELWP) to control the riming degrees of aggregates. The unrimed aggregate corresponds to ELWP of 0.0 kg m⁻². In scenarios A and B (different riming and aggregation process), there are five aggregates with ELWPs of 0.1, 0.2, 0.5, 1.0 and 2.0 kg m⁻². For simplicity, we only show the results for dendrite aggregates with ELWPs of 0.0, 0.5 and 1.0 kg m⁻² (R0.0, R0.5 and R1.0) from scenario B in the figure. One rounded and one oblate rosette aggregate (Agr and Ago) are also included from Nowell et al. [34] and Honeyager et al. [25]. The exponential particle size distribution (2.3) is employed for theoretical calculations. The DFR is independent of N₀. The slope parameter L varies from 1 to 45 cm⁻¹. The maximum diameters of simple crystals are truncated at 5 mm [4]. The maximum diameters of unrimed and rimed dendrite aggregates can extend to 22 mm. Rosette aggregates have the maximum diameters up to 12 mm. DFRs can be calculated as

$$\mathrm{DFR}\mathrm{Ku}/\mathrm{Ka}=10{\log }_{10}{Z}_{\mathrm{e},\mathrm{Ku}}-10{\log }_{10}{Z}_{\mathrm{e},\mathrm{Ka}}$$

(4)

$$\mathrm{DFR}\mathrm{Ku}/\mathrm{W}=10{\log }_{10}{Z}_{\mathrm{e},\mathrm{Ku}}-10{\log }_{10}{Z}_{\mathrm{e},\mathrm{W}}$$

(5)

$${\mathrm{Z}}_{\mathrm{e}}=\frac{{\mathsf{\lambda }}^4}{{\mathsf{\pi }}^5{\left|\mathrm{K}\right|}^2}{\displaystyle \underset{{\mathrm{D}}_{\min }}{\overset{{\mathrm{D}}_{\max }}{\int }}{\mathrm{N}\left(\mathrm{D}\right)\mathsf{\sigma }}_{\mathrm{bsc}}\left(\mathrm{D}\right)\mathrm{dD}}$$

(6)

where Z_e is the effective radar reflectivity factor, D_min and D_max are lower and upper limits of the snowflake maximum diameter, N(D) is the particle size distribution, m(D) is the mass of the particle, λ is the wavelength, K is a function of the dielectric constant of water and ${\mathsf{\sigma }}_{\mathrm{bsc}}\left(\mathrm{D}\right)$ is the backscatter cross section of the snowflake. It is seen that when the particle size increases, the DFR Ku/Ka value monotonically increases, while the DFR Ka/W value increases at the beginning and then gradually decreases, especially for rosettes (Br) and dendrite aggregates. From unrimed snow particles (Br, Sec, Den and R0.0) to heavily rimed or aggregated snow particles (R1.0, Agr and Ago), there is a rotation of DFR curves on the triple-frequency plane, corresponding to the increase in particle bulk effective density.

Yin et al. [7] grouped snow particle models based on their triple-frequency signatures. Accordingly, we classified snow particles into three groups and calculated their averaged triple-frequency signatures, respectively. Modeled triple-frequency signatures overlaid on the normalized occurrence frequencies of observed triple-frequency signatures are shown in Figure 4. It is worth noting that DFR Ku/W is also used as x-axis (right panel of Figure 4) since DFR Ku/W, the sum of DFR Ku/Ka and Ka/W, also contains the information of particle bulk effective density. Type A particles include bullets rosettes (R3 to R6), sectors (Sec) and dendrites (Den). Type B particles include unrimed and lightly rimed particles with ELWPs of 0.0, 0.1, 0.2 and 0.5 kg m⁻² from both scenarios A and B. Type C particles include heavily rimed (ELWPs of 1.0 and 2.0 kg m⁻² from scenarios A and B) and aggregated (Agr and Ago) particles. It is found that type B and C particles can explain most observed triple-frequency signatures, while type A particles only occupy a specific region of the triple-frequency plane where DFR values are both small. A hook feature of observed triple-frequency signatures is evident when using DFR Ka/W as x-axis, which can only be explained by type B particles. In other words, pristine crystals (type A) are not abundant, while unrimed or rimed aggregates (type B and C) are prevalent in ice clouds. A hook feature of observed triple-frequency signatures is associated with large unrimed or lightly rimed aggregates with low density. Large DFR Ka/W values with relatively small DFR Ku/Ka values are closely related to small heavily rimed or aggregated particles with high density.

Based on our results, two simple indicators are employed to infer the snow particle size and bulk effective density qualitatively. DFR Ku/Ka is a good indicator of snow particle size since its values monotonically increases when the particle size increases. The slope of the DFR curve is used to indicate the snow particle bulk effective density since there is a clockwise rotation of DFR curves on the triple-frequency plane when the particle bulk effective density increases. From modeled triple-frequency signatures, it is seen that the DFR curves are not linear when using DFR Ka/W as x-axis, while the DFR curves are approximately linear when using DFR Ku/W as x-axis. Therefore, the ratio of DFR Ku/Ka to DFR Ku/W is chosen to represent the slope of the DFR curve and denoted as R_density in the remaining part. R_density for type A particles is about 0.5, while that for type C particles is about 0.25, inversely proportional to the snow particle bulk effective density. It is worth mentioning that there is no intention to retrieve the snow particle size or bulk effective density using any triple-frequency approach [10,11]. Due to the lack of extra Doppler radar measurements and the existing mismatching errors between DPR and CPR, it is highly possible that the spaceborne retrievals of snow microphysical properties contain large uncertainty [11,35]. Two chosen indicators are only used for exploring the environmental conditions of snow particles with different particle sizes and bulk effective densities qualitatively.

4. Statistics of Environmental Conditions of Snow Particles

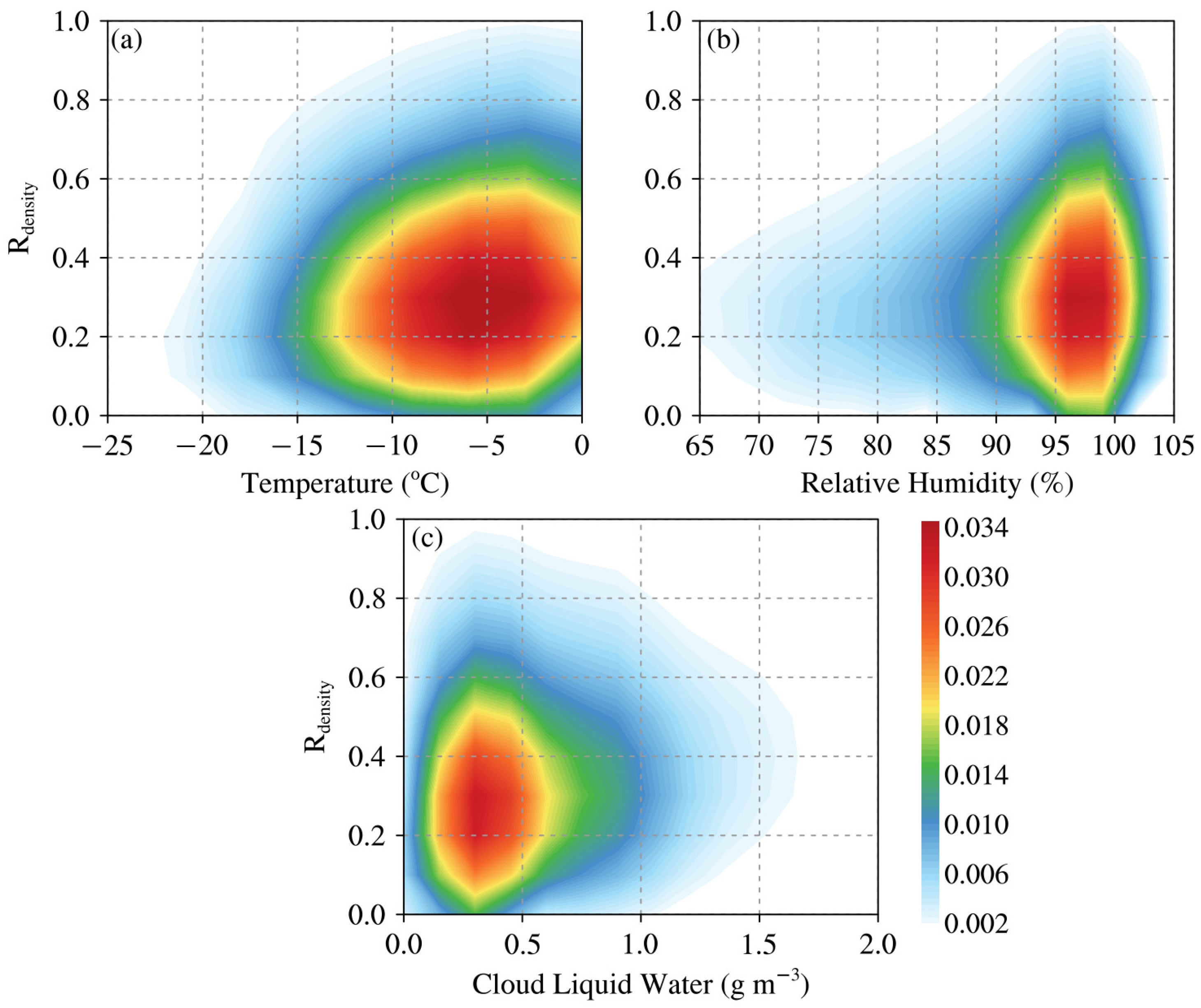
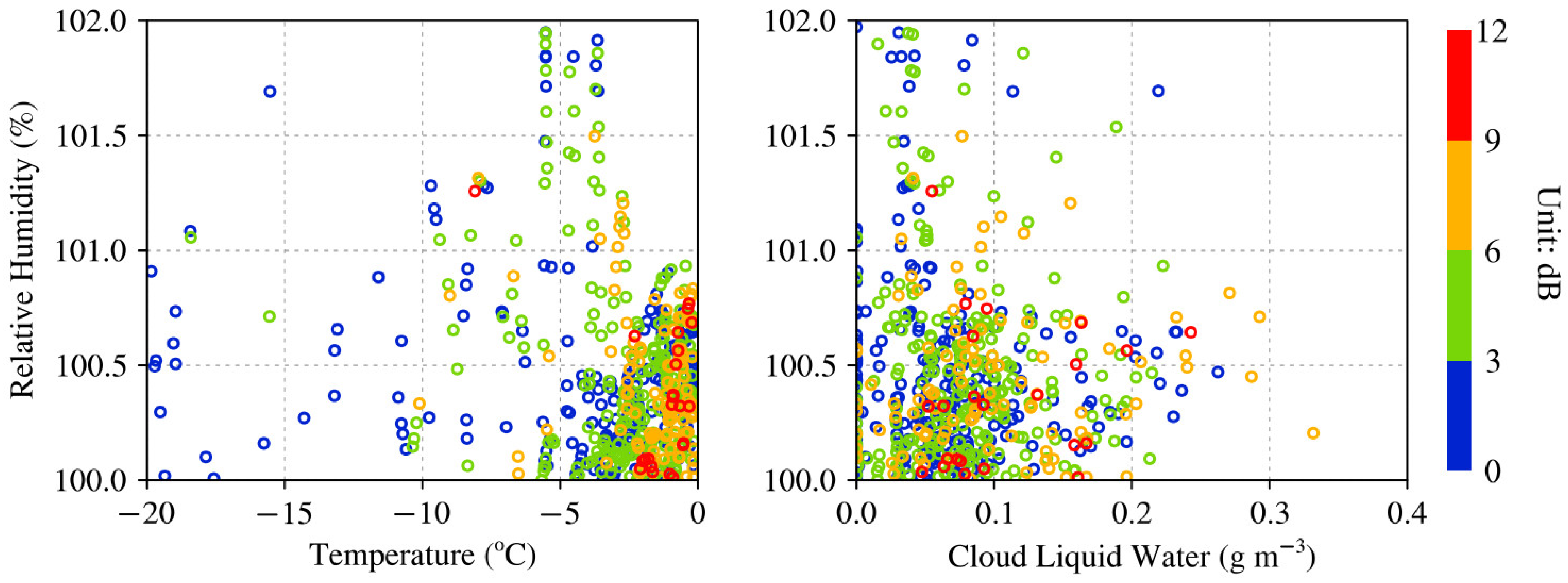
The dependence of DFR Ku/Ka for all qualified radar bins on temperature, relative humidity and cloud liquid water is shown in Figure 5. Temperature and specific humidity profiles come from the ECMWF ancillary dataset for CloudSat CPR, while cloud liquid water profiles are adopted from the GPM-combined radar-radiometer precipitation product. Relative humidity profiles are simply derived from specific humidity profiles. It is seen that a large portion of radar bins are associated with temperatures around –5 °C. At temperatures lower than –10 °C, radar bins are relatively sparse. DFR Ku/Ka values cover a wide range up to 10 dB near 0 °C. When temperatures decrease, there is a tendency for DFR Ku/Ka values to decrease. At temperatures lower than –15 °C, DFR Ku/Ka values are mainly constrained by 4 dB. It suggests that a large percentage of snow particles is associated with relatively warm temperatures around –5 °C. At warm temperatures near 0 °C, the snow particle size range is wide, consisting of small pristine crystals and large aggregates. When temperatures are colder than –15 °C, a large percentage of snow particles have relatively small particle sizes. The results are generally consistent with the studies of Dias Neto et al. [14] and Tridon et al. [15]. They both found that the snow particle size range is wider at warmer temperatures towards 0 °C. It is worth mentioning that their datasets include many radar bins associated with temperatures colder than –20 °C and very small DFR X/Ka values. Those radar bins usually represent tiny ice particles at high altitudes, which are ignored in this study, since the minimum threshold of radar reflectivity at the W band is selected as 2 dBZ.

It is seen that a large percentage of radar bins lies in a range of relative humidities between 95 and 100%. When relative humidities are lower than 90% or higher than 100%, the number of radar bins is small. At relative humidities above 95%, DFR Ku/Ka values can reach above 8 dB. At relative humidities below 90%, DFR Ku/Ka values are mainly concentrated below 4 dB. Additionally, when relative humidities exceed 100%, there is a sharp decrease in DFR Ku/Ka values. In other words, snow particles are abundant at relative humidities between 95 and 100%. At relative humidities lower than 90%, small snow particles are prevalent. It is worth mentioning that radar bins with low relative humidities usually locate at high altitudes, since there is less water vapor at higher altitudes. Duran et al. [36] reported similar results that relative humidities of snow particles tend to decrease at higher altitudes. The snow particle size range becomes wider towards saturation conditions. When the supersaturation occurs, the snow particle size decreases rapidly. It is worth mentioning that at polar regions, specific humidity can be low, while relative humidity can be high.

The dependence of DFR Ku/Ka on cloud liquid water content has shown that most radar bins have small cloud liquid water contents around 0.3 g m⁻³. Only a small portion of radar bins have cloud liquid water contents larger than 0.8 g m⁻³. When cloud liquid water contents increase, there is a tendency for DFR Ku/Ka values to decrease gradually. DFR Ku/Ka values are mainly below 4 dB at cloud liquid water contents near 1.0 g m⁻³. The results imply that snow particles tend to have small cloud liquid water contents around 0.3 g m⁻³. At large cloud liquid water contents near 1.0 g m⁻³, relatively small snow particles are present. In contrast, the percentage of large snow particles is considerable at low cloud liquid water contents.

The dependence of R_density on temperature, relative humidity and cloud liquid water is presented in Figure 6. Basically, the dependence of R_density on environmental parameters is very similar to that of DFR Ku/Ka. It is seen that R_density has a wide range up to 1.0 at warm temperatures near 0 °C. When temperatures decrease, the range of R_density becomes narrower. At temperatures lower than –15 °C, R_density values are mainly constrained by 0.4. The results imply that at warm temperatures near 0 °C, snow particles have a wide range of bulk effective density. At temperatures colder than –15 °C, snow particles with high densities are prevalent. At high relative humidities between 95 and 100%, R_density can extend to 1.0. When relative humidities decrease, the percentage of small R_density values becomes larger. At relative humidities lower than 90%, R_density values are mainly concentrated below 0.4. At relative humidities higher than 100%, R_density values decrease dramatically. It suggests that the bulk effective density range of snow particles is wider at higher relative humidities. When relative humidities are lower than 90%, a large portion of snow particles has high densities. When supersaturation occurs, the bulk effective densities of snow particles increase significantly. At low cloud liquid water contents around 0.3 g m⁻³, the range of R_density values is wide. When cloud liquid water contents increase, R_density values gradually decrease and are mainly constrained by 0.4 near 1.0 g m⁻³. It is seen that at low cloud liquid water contents, around 0.3 g m⁻³, the range of snow particle bulk effective density is wide. At high cloud liquid water contents above 0.8 g m⁻³, a large percentage of snow particles has high densities. It seems that there is a correlation between cloud liquid water content and snow particle bulk effective density. Mason et al. [35] also found that the liquid water path is strongly correlated to the retrieved snow particle density factor. Since previous studies [37,38] demonstrated that the cloud liquid water content is a good indicator of the snow riming, the results suggest that the riming process is mainly responsible for the increase in snow particle bulk effective density at high cloud liquid water contents.

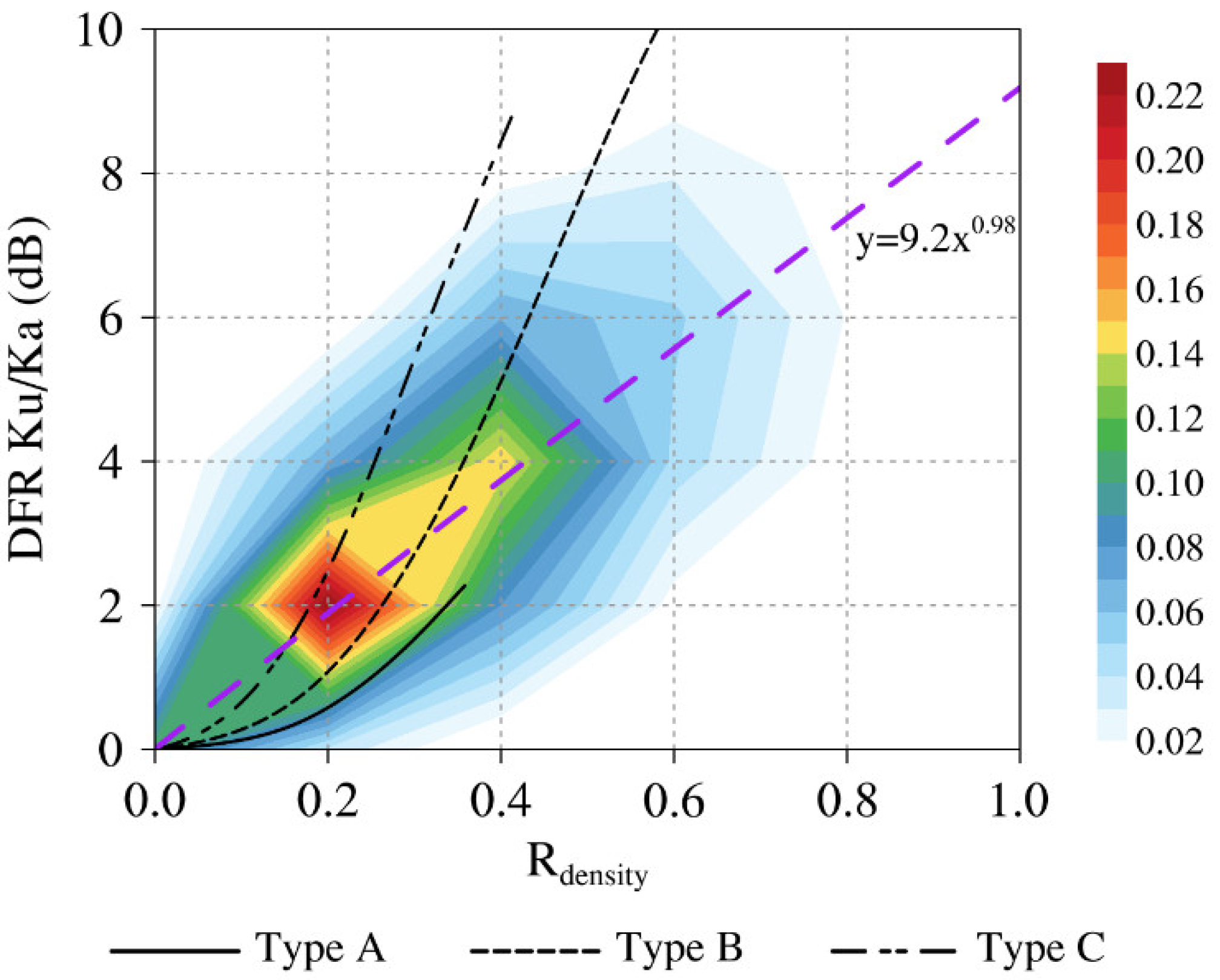
The similar dependence on environmental parameters between DFR Ku/Ka and R_density has implied that DFR Ku/Ka values are correlated to R_density values. The relation between DFR Ku/Ka and R_density for modeled and observed results is shown in Figure 7. It is worth mentioning that the modeled lines are generated by varying the slope parameter L in the exponential particle size distribution. For modeled results, it is seen that R_density increases with DFR Ku/Ka but more slowly at larger DFR Ku/Ka values. In other words, the snow particle bulk effective density is inversely proportional to the snow particle size with a power law relationship. Several studies using disdrometers derived similar density-size relationships for snow particles [39,40,41]. Basically, type B and C particles can explain most data points (red and yellow areas), except a small portion of data points with DFR Ku/Ka values larger than 4 dB and R_density larger than 0.5. Those data points represent large aggregates with bulk effective densities as low as pristine crystals and correspond to observed triple-frequency signatures with large DFR Ku/Ka and small DFR Ka/W values (see Figure 4). Similar observed triple-frequency signatures have been found from recent ground-based experiments, including Chase et al. [9], Nguyen et al. [16] and Mason et al. [35]. As shown by Chase et al. [9], a dendrite aggregate from Petty and Huang [42] can generally fit this area on the triple-frequency plane where snow particles are large aggregates with extremely low bulk effective densities (see Figure 4).

Since the supersaturation is important for snow particle growth [43,44], the environmental conditions of snow particles under supersaturations are further investigated. Figure 8 shows the scatterplots between relative humidity and temperature as well as relative humidity and cloud liquid water for supersaturation measurements. It is seen that a large portion of snow particles are constrained by relative humidities of 101%. Under relative humidities of 101%, most snow particles are associated with temperatures warmer than –5 °C and cloud liquid water contents lower than 0.1 g m⁻³. At warm temperatures, the range of DFR Ku/Ka values is wide. At temperatures colder than –10 °C, DFR Ku/Ka values are mainly under 3 dB. In contrast, the range of DFR Ku/Ka values is generally wide, even at high cloud liquid water contents. When relative humidities increase, there is a tendency for DFR Ku/Ka values to decrease. It seems that a large percentage of snow particles exist at warm temperatures and low cloud liquid water contents under relative humidities of 101%. At temperatures colder than –10 °C, large snow particles with low densities are prevalent. When relative humidities increase, snow particles tend to have smaller sizes and higher densities under supersaturations.

5. Conclusions

Unlike airborne triple-frequency radar measurements that have been widely collected and utilized, only a coincident dataset between CloudSat and GPM can provide global spaceborne triple-frequency radar measurements. The coincident dataset collocates CloudSat CPR radar reflectivity profiles, GPM DPR radar reflectivity profiles and ECMWF ancillary state variables for CloudSat CPR. The environmental conditions of snow particles with different microphysical properties are investigated over the ocean for a time span of about 3.5 years using this coincident dataset. By overcoming the discrepancy in spatial resolutions and minimum detectable echoes between CPR and DPR, observed triple-frequency signatures are derived for snow particles over the ocean. Based on modeling results for various snow particles, including pristine crystals and aggregates, two indicators are simply adopted to infer the particle size and bulk effective density. DFR Ku/Ka is selected to indicate the snow particle size, while the ratio of DFR Ku/Ka to DFR Ku/W (R_density) is selected to indicate the snow particle bulk effective density. Three environmental parameters, including temperature, relative humidity and cloud liquid water content, are linked to observed triple-frequency signatures.

The statistical results show that the size range of snow particles becomes wider at warmer temperatures, higher relative humidities or lower cloud liquid water contents. It is also seen that the snow particle size is inversely proportional to the snow particle bulk effective density. At high cloud liquid water contents, the riming process plays an important role in increasing the snow particle density. When the supersaturation occurs, most snow particles are associated with warm temperatures and low cloud liquid water contents. The findings are generally consistent with previous snowfall studies [37,38,39,40,41]. It is worth mentioning that no empirical model is developed for DFR Ku/Ka (snow particle size indicator) or R_density (snow particle density indicator) among three environmental parameters in this study. At warm temperatures, high relative humidities or low cloud liquid water contents, the snow particle size range is wide. For example, at a temperature of –5 °C, DFR Ku/Ka values can range from 1 to 6 dB, with relatively large occurrence frequencies. In other words, at warm temperatures, high relative humidities or low cloud liquid water contents, the dependences of DFR Ku/Ka or R_density on these parameters are relatively weak. The DFR Ku/Ka or R_density values derived from environmental parameters using an empirical model may remain a large uncertainty. Only three parameters are not enough to determine snow particle size or density physically. On the other hand, the environmental parameters can be useful for providing physical constraints on snow particle size or bulk effective density retrieved from triple-frequency radar measurements in the future.

The results presented in this study are valuable for better understanding snow microphysics and demonstrate that spaceborne triple-frequency measurements are potentially beneficial for global snowfall retrievals. Nevertheless, it is seen that the current configuration of spaceborne triple-frequency radars from CloudSat CPR and GPM DPR is not able to obtain the information of tiny ice particles due to the low sensitivity of DPR. New technologies mentioned by Kummerow et al. [19] are demanded to increase the sensitivity of future spaceborne radars at Ku and Ka bands. Utilizing spaceborne radar measurements at the G band is another approach to improve the detection of tiny ice particles [20]. On the other hand, the availability of spaceborne Doppler radar measurements is necessary to reduce the retrieval uncertainty [11,35,45].