Self-Calibrated Multi-Floor Localization Based on Wi-Fi Ranging/Crowdsourced Fingerprinting and Low-Cost Sensors

Abstract

Crowdsourced localization using geo-spatial big data has become an effective approach for constructing smart-city-based location services with the fast growing number of Internet of Things terminals. This paper presents a self-calibrated multi-floor indoor positioning framework using a combination of Wi-Fi ranging, crowdsourced fingerprinting and low-cost sensors (SM-WRFS). The localization parameters, such as heading and altitude biases, step-length scale factor, and Wi-Fi ranging bias are autonomously calibrated to provide a more accurate forward 3D localization performance. In addition, the backward smoothing algorithm and a novel deep-learning model are applied in order to construct an autonomous and efficient crowdsourced Wi-Fi fingerprinting database using the detected quick response (QR) code-based landmarks. Finally, the adaptive extended Kalman filter is adopted to combine the corresponding location sources using different integration models to provide a precise multi-source fusion based multi-floor indoor localization performance. The real-world experiments demonstrate that the presented SM-WRFS is proven to realize precise 3D indoor positioning under different environments, and the meter-level positioning accuracy can be acquired in Wi-Fi ranging supported indoor areas.

1. Introduction

Indoor positioning ability has become an essential requirement towards smart city and Internet-of-Things (IoT)-based applications as people spend more time indoors. Due to the variability of indoor scenes, it is still challenging to provide universal and precise pedestrian navigation services under Global Navigation Satellite Systems (GNSS) denied indoor environments. The wireless navigation system has attracted the attention of researchers due to its low-cost and wide distribution characteristics [1]. A variety of features acquired from wireless signals could be adopted for indoor navigation purposes, for example, received signal strength indication (RSSI) [2], channel impulse response (CIR) [3], time of arrival (TOA) [4], time difference of arrival (TDOA) [5], angle of arrival (AOA) [6], and channel state information (CSI) [7].

Based on IoT-terminal-supported indoor positioning technology, part of the acquired wireless features cannot be applied because of hardware constraints or time synchronization problems. Compared with other wireless features, Wireless Fidelity (Wi-Fi) RSSI is supported by almost all types of IoT terminals and can be acquired in real-time, and the Wi-Fi-RSSI-based positioning system usually contains two approaches: triangulation and fingerprinting [8,9]. Zhuang et al. [10] enhanced the traditional Wi-Fi RSSI ranging model by taking the RSSI measurement bias into consideration, and adopted the extended Kalman filter (EKF) to combine the Wi-Fi RSSI aimed distance measurement results and mobile self-contained sensors. The realized average root mean square error (RMSE) using the compensated RSSI observations was less than 3.47 m. Li et al. [11] proposed a novel fusion structure which combines the inertial, Wi-Fi and magnetic location sources. A multi-level quality-control (QC) strategy was applied to increase the efficiency and precision of the final localization phase, and the RMSE of the proposed structure was within 4.3 m among different environments. Chen et al. [12] proposed a deep long short-term memory (DLSTM) network to improve the accuracy of the traditional Wi-Fi fingerprinting approach, by decreasing the influence of environmental effects on the collected RSSI vectors and extracting more characteristics of continuous RSSI signals under time domains.

The existing research indicates that the traditional Wi-Fi RSSI based localization system cannot fulfil the requirement of meter-level indoor localization accuracy because of the instability of RSSI signal propagation in complex indoor scenes and artificial interference. To enhance the ability of an existing Wi-Fi positioning system (WPS), IEEE 802.11-2016 proposed the 802.11mc protocol, which provides round-trip-time (RTT)-based distance measurement results among different mobile terminals and Wi-Fi access points (APs) [13]. However, because of the hardware deviations between smartphones and Wi-Fi APs, the raw measured RTT value normally contains initial bias which leads to the overall drift of distance information received at terminals. Ibrahim M et al. [14] used the Intel provided open-source software and hardware to evaluate the performance of Wi-Fi RTT ranging, and tested the effects of initial bias and environmental factors in different indoor and outdoor scenes and provided the basic method for bias calibration. Subsequently, ref. [15] provided the systematic analysis of influencing factors of initial bias of Wi-Fi RTT and drew the conclusion that both hardware platform and methods of signal processing would affect the value of initial bias, and also indicated that the initial bias of Wi-Fi RTT follows the environment-related Gaussian distribution duo to its measurement mechanism. Sun et al. [16] proposed the geomagnetism and improved genetic approach to realize accurate Wi-Fi ranging based localization and ranging bias compensation at the same time. The distribution of ranging error under the NLOS scene is collected on the off-line phase, which is further applied to the on-line phase for ranging bias compensation, and effectively improves the accuracy of final positioning.

During the actual positioning procedure, the precision of Wi-Fi Fine Time Measurement (FTM) may also be affected by the multipath propagation and non-line-of-sight (NLOS) that may lead to the influences in real-time ranging observations [17]. In addition, Micro-Electromechanical-System (MEMS)-sensor-based localization solutions, such as pedestrian dead reckoning (PDR) or inertial navigation system (INS) can only maintain positioning accuracy in a short-use period, which can further be integrated with Wi-Fi ranging to compensate for signal fluctuation and provide possible solutions for the real-time calibration of Wi-Fi ranging. Choi et al. [18] proposed a self-calibrated multi-source fusion system using the combination of Wi-Fi RTT, RSSI and MEMS sensors, in which the RTT ranging and RSSI ranging are adopted as the observations to compensate for the cumulative error of PDR, and also the initial bias, heading, and step-length parameters are calibrated simultaneously. The experimental performance realizes the localization precision within 1.28 m in 75% under 40-MHz bandwidth. Zhou et al. [19] developed a device-to-device cooperative localization system, which is assisted by matrix completion and anchor selection, and can further be applied in rare ranging results received within indoor scenes using a limited number of anchors.

The crowdsourcing-based localization algorithm is achieved based on the analysis of geo-spatial big data, which can be regarded as an effective way for the realization of autonomous positioning in smart-city-based indoor scenarios. To self-construct a precise crowdsourced Wi-Fi fingerprinting database, the following challenges are required to be tackled: the low accuracy of collected daily-life MEMS sensors data which is seriously influenced by cumulative error and local artificial interference [20], the autonomous evaluation and accurate combination of crowdsourced trajectories [21], and the efficient deployment and the fast detection of reference points (RPs) [22]. Zhang et al. [23] proposed a novel crowdsourced navigation database generation method using the optimized pedestrians’ daily-life inertial data, and established a robust quality evaluation criteria towards crowdsourced trajectories, which takes the sensor’s biases, navigation time, and handheld modes into consideration. The final experiments showed comparable results with the traditional map-aided localization method. Zhuang et al. [24] tested the positioning accuracy of two crowdsourcing-based Wi-Fi positioning systems (WPS) including fingerprinting and trilateration methods, which are not depend on the requirements of accurate indoor map and outdoor GNSS reference. The final estimated average positioning error under different indoor scenes are lower than 5.75 m.

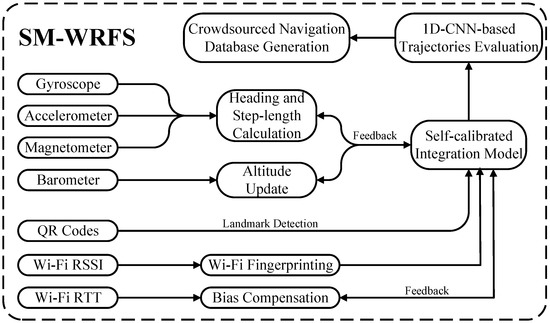
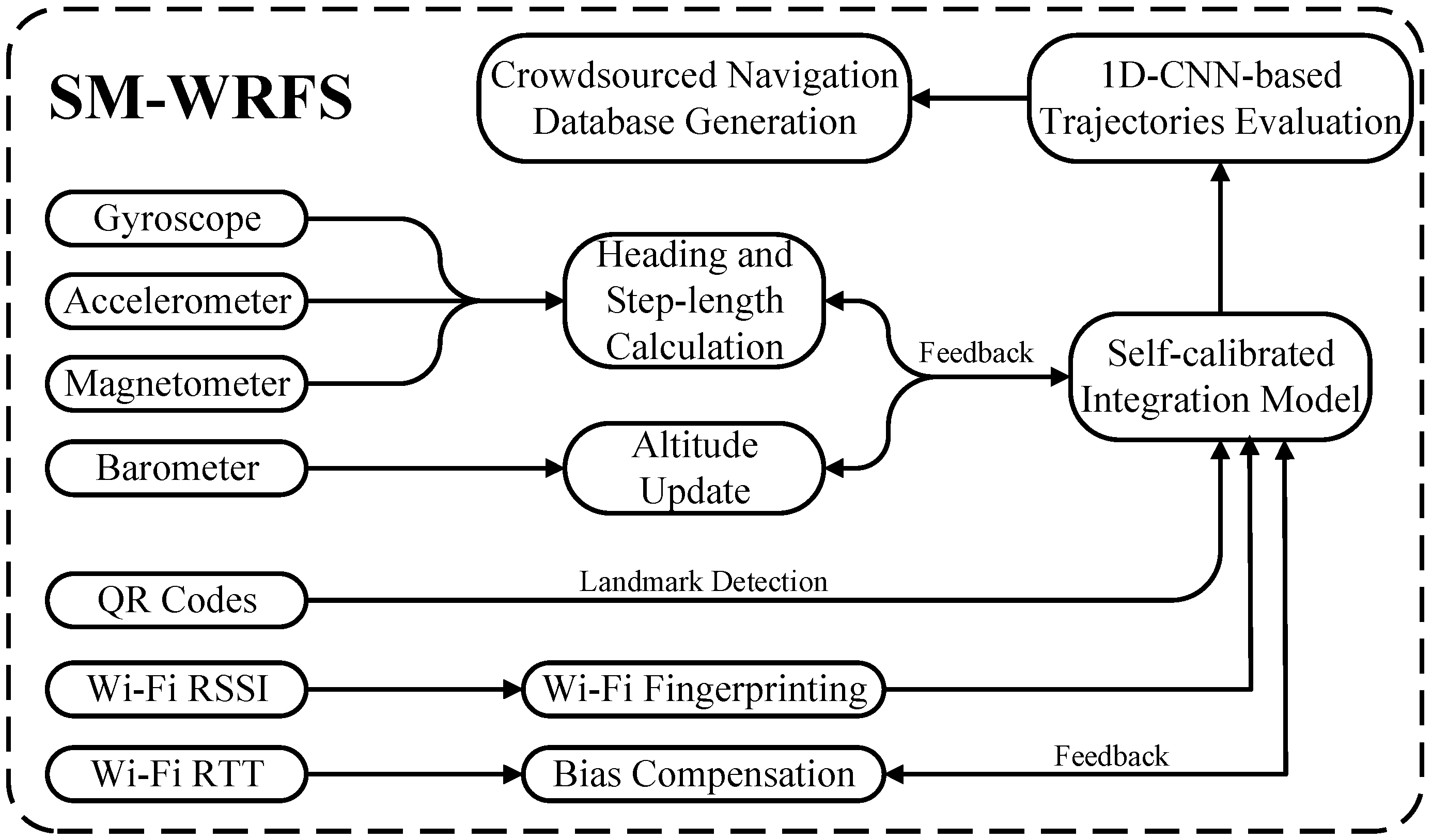
In order to provide an autonomous localization performance and realize meter-level precision in selected areas, this paper presents a self-calibrated multi-floor aimed indoor localization structure using the combination of Wi-Fi ranging, crowdsourced Wi-Fi fingerprinting and low-cost sensors (SM-WRFS). The innovations of this article are described as follows:

(1)

This paper proposes a low-cost-sensor-based forward 3D localization and backward smoothing framework towards the crowdsourced trajectories collection and optimization with a combination of quick-response (QR)-code-based landmark detection, which significantly reduces the divergence error and magnetic interference of raw trajectories.

(2)

This paper presents a novel crowdsourcing-based Wi-Fi fingerprinting database generation algorithm using the 1D-Convolutional-Neural-Network (1D-CNN)-based crowdsourced trajectories evaluation framework to autonomously estimate the positioning error of each step period among the collected trajectory and generate the merged navigation database based on the error evaluation results.

(3)

This paper designs the self-calibrated localization model which takes the heading bias, altitude bias, step-length scale factor, and Wi-Fi ranging bias into consideration, and all the related parameters are predicted and optimized simultaneously to increase the robustness of the final multi-source fusion.

(4)

This paper realizes two different types of self-calibrated integration structures: the tightly coupled positioning method using Wi-Fi ranging and low-cost sensors and the loosely coupled positioning method using a crowdsourced Wi-Fi database and low-cost sensors. The integration of different location sources significantly improves the accuracy and universality of multi-source multi-floor indoor positioning.

The main structure of this work is arranged as follows. Section 2 details the low-cost-sensor-based 3D indoor localization and deep-learning based Wi-Fi navigation database construction. Section 3 introduces the self-calibrated indoor localization models and multi-source integration structures. Section 4 describes the experimental results of the proposed SM-WRFS. Section 5 concludes this paper.

2. Low-Cost-Sensor-Based 3D Indoor Localization and Navigation Database Generation

Pedestrians’ daily-life data acquired from massive smart terminals provide an effective approach for crowdsourced Wi-Fi-based navigation database construction and updating. The accuracy of the constructed navigation database is subject to the poor performance of crowdsourced trajectories. In order to effectively improve the performance of daily-life trajectories, the different types of sensors data are fused using the self-calibrated integration model and it provides feedback of the corresponding error parameters in real-time. In addition, the 1D-CNN-based trajectories evaluation model is developed for autonomously predicting the positioning error of generated crowdsourced trajectories. Finally, the absolute location sources, including Wi-Fi RSSI fingerprinting and RTT ranging are adaptively combined by the self-integration model and correct the Wi-Fi ranging bias at the same time. The overall flow of proposed SM-WRFS structure is described in Figure 1.

Figure 1. Overall flow of proposed SM-WRFS structure.

In this section, a low-cost-sensor-based forward positioning and backward smoothing framework is introduced in order to provide a more robust reference trajectory during the off-line phase of Wi-Fi database generation. In addition, a novel deep-learning-based trajectory error prediction model is proposed to autonomously generate the final navigation database using the error evaluation results of crowdsourced trajectories.

2.1. Low-Cost-Sensor-Based Localization and Optimization

In this work, the low-cost sensors are applied as the autonomous location source during the off-line phase of crowdsourced fingerprinting database generation. In this case, the pedestrian’s 3D location, the real-time heading information, and the heading bias are modeled as the state vector [25]:

$$\begin{array}{c}{\mathit{X}}_t={\left[r_x^t,r_y^t,r_z^t,{\theta }_t,b_t\right]}^{\mathrm{T}}\end{array}$$

(1)

where $r_x^t$, $r_y^t$, $r_z^t$ indicate the updated 3D position of the pedestrian at the current moment t, ${\theta }_t$ represents the calculated real-time heading, and $b_t$ is the corresponding heading bias.

The current state vector is updated by the detected step-length and calculated heading information, and the dynamic model of the proposed state update equation is described as:

$${\mathit{X}}_{t+1}=f({\mathit{X}}_t)+{\mathit{G}}_t{\mathbf{\omega }}_t$$

(2)

where $f({\mathit{X}}_t)$ indicates the system relationship, ${\mathit{G}}_t$ indicates the noise distribution matrix, and ${\mathbf{\omega }}_t$ indicates the state noise with Gaussian distribution. The detailed description of $f({\mathit{X}}_t)$ is shown as:

$$f({\mathit{X}}_t)=\{\begin{array}{l}{r}_x^{t-1}+\cos {\theta }_t\cdot L_t\\ r_y^{t-1}+\sin {\theta }_t\cdot L_t\\ r_z^{t-1}+\Delta h_t\\ {\theta }_{t-1}+\Delta T\cdot b_t\\ \exp (-\Delta T/T_c)\cdot b_{t-1}\end{array}$$

(3)

where the heading bias b_t is presented as a first-order Markov process, which is updated and provides feedback in real-time to compensate for the drift error of the calculated heading ${\theta }_t$, $\Delta T$ represents the update time period, T_c is the correlation time, $L_t$ represents the calculated step-length information, and is provided by [26]:

$$L_t=\alpha \cdot [0.7+\beta (H-1.75)+\varsigma \cdot \frac{(F_t-1.79)H}{1.75}]$$

(4)

in which $\alpha$, $\beta$, $\varsigma$ represent the scale related parameters, $F_t$ represents the gait frequency, and H is the pedestrian’s height. To realize 3D localization, the barometer data is collected for the altitude update [27]:

$$\Delta h_t=\mathrm{44,330}\cdot (1.0-{(\frac{100p_t}{p_0})}^{\frac{1.0}{5.255}})$$

(5)

where $\Delta h_t$ indicates the estimated relative altitude indoors, p_t and p₀ are the acquired pressure data during current time period t and the reference pressure level.

The EKF linearizes the proposed state model through the first-order Taylor series, the Jacobian matrix of the state equation $f({\mathit{X}}_t)$ is linearized as:

$${\mathit{F}}_t=\left[\begin{array}{ccccc}1& 0& 0& -\sin {\theta }_t\cdot L_t& 0\\ 0& 1& 0& \cos {\theta }_t\cdot L_t& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& \Delta T\\ 0& 0& 0& 0& \exp (-\Delta T/T_c)\end{array}\right]$$

(6)

Among the forward localization procedure, to improve the heading estimation performance, the measured magnetic vector is firstly calibrated by the ellipsoid fitting method in order to provide more robust initial heading information [28]. When the pedestrian is walking in indoor environments, the magnetic data during detected quasi-static magnetic field (QSMF) periods [29] is applied as the observation for real-time heading bias calibration:

$${\tilde{\psi }}_t-{\widehat{\psi }}_0=\delta {\psi }_t+n_{\psi }$$

(7)

where ${\widehat{\psi }}_0$ represents the calculated magnetic heading under the first epoch of the detected QSMF period, and the magnetic measurement ${\tilde{\psi }}_t$ under other QSMF epochs is applied as the real-time observations, and $n_{\psi }$ indicates the measurement noise.

In this paper, the QR code is developed to acquire the reference 3D location for the low-cost-sensor-based method. The QR codes and the corresponding location information can be generated from the on-line website [30], which are deployed in indoor scenes and can be scanned by Android-supported smartphones as shown in Figure 2.

Figure 2. Acquirement of QR-Code-Based Reference Points.

In the off-line phase of crowdsourced database generation procedure, the 3D reference location provided by the scanned QR code and the calculated relative heading change information under recognized QSMF periods is applied as the observation vector:

$${\mathit{Z}}_t=h({\mathit{X}}_t)+{\mathbf{\nu }}_t=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1\end{array}\right]{\mathit{X}}_t+{\mathbf{\nu }}_t$$

(8)

where ${\mathit{Z}}_t=[p_x^t,p_y^t,p_z^t,\delta {\psi }_t]$ represents the acquired QR code based 3D location reference, and ${\mathbf{\nu }}_t$ indicates the measured error of reference location and heading deviation, which is assumed to be zero-mean Gaussian white noise.

The raw crowdsourced trajectories between two recognized QR reference points can be optimized by the EKF-based backward smoothing algorithm; the whole procedure of low-cost-sensor-based forward localization and back smoothing is described as follows:

(1)

State vector update using the real-time calculated gait and heading values:

$${\mathit{x}}_t^{-}=f({\mathit{x}}_{t-1})$$

(9)

(2)

Linearization procedure using the first-order Taylor series:

$${\mathit{F}}_t=\frac{\partial f({\mathit{x}}_t)}{\partial {\mathit{x}}_t}|{}_{x_t=x_t^{-}}$$

(10)

(3)

Covariance matrix prediction:

$${\mathit{P}}_t^{-}={\mathit{F}}_{t,t-1}{\mathit{P}}_{t-1}{\mathit{F}}_{t,t-1}^T+{\mathit{Q}}_t$$

(11)

(4)

Kalman gain matrix update:

$${\mathit{K}}_t={\mathit{P}}_t^{-}{\mathit{H}}_t{}^{\mathrm{T}}{\left[{\mathit{H}}_t{\mathit{P}}_t^{-}{\mathit{H}}_t{}^{\mathrm{T}}+{\mathit{R}}_t\right]}^{-1}$$

(12)

(5)

State vector update:

$${\mathit{x}}_t={\mathit{x}}_t^{-}+{\mathit{K}}_t\left[{\mathit{z}}_t-{\mathit{H}}_t{\mathit{x}}_t^{-}\right]$$

(13)

(6)

Covariance matrix update:

$${\mathit{P}}_t={\mathit{P}}_t^{-}-{\mathit{K}}_t{\mathit{H}}_t{\mathit{P}}_t^{-}$$

(14)

(7)

Backward Smoothing:

$${\widehat{\mathit{x}}}_{t-1,t}={\widehat{\mathit{x}}}_{t-1}+{\mathit{P}}_{t-1}{\mathit{F}}_t^{\mathrm{T}}{({\mathit{P}}_{{}_{t-1}}^{-})}^{-1}({\widehat{\mathit{x}}}_t-{\widehat{\mathit{x}}}_t{}^{-})$$

(15)

$${\mathit{P}}_{t-1|t}={\mathit{P}}_{t-1}-({\mathit{P}}_{t-1}{\mathit{F}}_t^{\mathrm{T}}{({\mathit{P}}_t{}^{-})}^{-1})({\mathit{P}}_t-{\mathit{P}}_t{}^{-})\cdot {({\mathit{P}}_{t-1}{\mathit{F}}_t^{\mathrm{T}}{({\mathit{P}}_t{}^{-})}^{-1})}^{\mathrm{T}}$$

(16)

where ${\mathit{x}}_t$ and ${\mathit{z}}_t$ indicate the state vector and observation vector provided by the low-cost sensors update and QR code. Equations (9) to (14) define the low-cost-sensor-based forward localization, and Equations (15) and (16) describe the backward-smoothing procedure using the forward result.

2.2. Crowdsourced Fingerprinting Database Generation

In order to generate an autonomous and efficient crowdsourcing-based Wi-Fi RSSI fingerprinting database, the crowdsourced trajectories should be evaluated and weighted based on the positioning error prediction result. The challenge is that the ground-truth dataset is missing in the real-world procedure of the crowdsourced trajectories collection; the only ground-truth information that can be acquired is the detected QR-code-based landmark points. To realize the autonomous prediction of positioning error, an effective evaluation and selection of crowdsourced trajectories plays an important role in the final procedure of Wi-Fi fingerprinting database construction. The quality of a pedestrian’s daily-life trajectory is affected by the navigation time, walking distance, handheld modes, motion modes, and so on. In this section, 1D-CNN-based error prediction model is proposed for autonomously evaluating the quality of each collected trajectory. The following features are extracted from each trajectory, which are applied as the input vector in the procedure of 1D-CNN training phase, which include:

(1)

Collected gait-length information ${\varpi }_t$ during each recognized gait period.

(2)

Estimated heading value ${\theta }_t$ during each recognized gait period.

(3)

Ratio between current itinerary and total itinerary:

$$p_d(t)=\frac{{\displaystyle \sum _{t=1}^k{\varpi }_t}}{{\displaystyle \sum _{t=1}^n{\varpi }_t}}$$

(17)

where n represents the collected gait number during each trained trajectory, k indicates the steps taken.

(4)

Ratio between the current used time and total used time:

$$p_t(t)=T(t)/T_{total}$$

(18)

where $T_{total}$ represents the overall time duration of the counted trajectory, and $T(t)$ indicates the used time period at the current moment.

(5)

Ratio between current counted step quantity and the overall step quantity:

$$p_s(t)=step(t)/ste{p}_{total}$$

(19)

where $ste{p}_{total}$ represents the overall step quantity of estimated trajectory, and $step(t)$ indicates the current counted step quantity.

(6)

The estimated product of trajectory distance and time period between two detected reference points:

$$S_1=d_i\cdot t_i,d_i={\displaystyle \sum _{k=1}^N{L}_k}$$

(20)

where S₁ indicates the estimated time and distance index of selected trajectory, d_i and t_i represent the recorded distance and time period of the selected trajectory, and L_k indicates the recorded gait-length vector during the selected trajectory.

(7)

The similarity among raw walking track and optimized walking track: In this work, the dynamic time warping (DTW) index is applied to calculate the similarity among raw walking track and optimized walking track. The location vector of raw walking track can be described as ${\varsigma }_k=\{{\tau }_1,{\tau }_2,\dots ,{\tau }_m\}$, and the optimized walking track can be modelled as ${\varsigma }_{refer}=\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}$, the DTW index is calculated as [31]:

$$\begin{array}{l}DTW({\varsigma }_{\mathrm{refer}},{\varsigma }_k)\\ =Dist({\gamma }_n,{\tau }_m)+\min [D({\gamma }_n{}_{-1},{\tau }_m),D({\gamma }_n,{\tau }_{m-1}),D({\gamma }_{n-1},{\tau }_{m-1})]\end{array}$$

(21)

where $DTW({\varsigma }_{\mathrm{refer}},{\varsigma }_k)$ indicates the cumulated distance provided by the raw walking track and the optimized walking track, and $D({\gamma }_n,{\tau }_m)$ indicates the distance between two location vectors.

(8)

Trajectory offset angle: Assuming that two reference points can be acquired in each collected trajectory, and the trajectory offset angle can be calculated by constructing the reference vector and raw vector:

$$\vartheta =\arccos \left(\frac{\overrightarrow{AB}\cdot \overrightarrow{AC}}{\left|\overrightarrow{AB}\right|\cdot \left|\overrightarrow{AC}\right|}\right)$$

(22)

where $\overrightarrow{AB}$ indicates the reference vector which is constructed by the first reference point and the second reference point, and $\overrightarrow{AC}$ is the raw vector which is constructed by the first reference point and the end point of the raw trajectory.

The above extracted features are modeled as the input vector of 1D-CNN for training purposes, the positioning error under each step period of optimized trajectories by Equations (15) and (16) is modeled as the output vector.

The main description of 1D-CNN model is presented as [32].

Figure 3 describes the main description of the proposed 1D-CNN error prediction model, in which the input vector is provided by the calculated characteristics of crowdsourced trajectories and the overall error evaluation results of crowdsourced trajectories are further considered for navigation database generation after removing the trajectory data with the larger error.

Figure 3. The description of 1D-CNN Network.

In the training phase of the 1D-CNN model, the ground-truth trajectory is provided in order to obtain the optimal model parameters. In the prediction phase, the positioning error of crowdsourced trajectories is autonomously predicted without ground-truth data. After the 1D-CNN-based evaluation of each collected trajectory, the localization error of each point in the trajectory can be acquired, and the optimized crowdsourced Wi-Fi navigation database is generated using weighted results acquired from the raw dataset:

$$\mathit{R}\mathit{S}{\mathit{S}}_{weighted}^m={\displaystyle \sum _{j=1}^n(\frac{{\varpi }_{CNN}^j}{{\displaystyle \sum _{j=1}^n{\varpi }_{CNN}^j}})\cdot \mathit{R}\mathit{S}{\mathit{S}}_{collected}^j}$$

(23)

where $\mathit{R}\mathit{S}{\mathit{S}}_{weighted}^m$ indicates the weighted RSSI values at the m^st position among navigation database, ${\varpi }_{CNN}^j$ indicates the 1D-CNN reported positioning error of each trajectory at the adjacent reported locations, and n is the number of collected trajectories. $\mathit{R}\mathit{S}{\mathit{S}}_{collected}^j$ indicates the collected RSSI vector provided for crowdsourced trajectories at the same reported location. The proposed crowdsourced Wi-Fi database generation structure can significantly increase the generation efficiency and decrease the dimension and complexity.

3. Self-Calibrated Integration Model and Multi-Source Fusion Framework

In the proposed self-calibrated localization framework, all the related parameters are modeled and calibrated simultaneously in order to obtain the optimal positioning result, including the heading bias, step-length scale factor, Wi-Fi ranging bias, and altitude bias. This section will introduce the detailed self-calibration multi-floor indoor localization model using the different fusion models which contain Wi-Fi FTM, RSSI fingerprinting, and low-cost-sensor-based positioning methods.

3.1. Self-Calibration Model of Step-Length and Altitude

The pedestrian’s step-length in this work is estimated according to the relationship between height and step frequency, while the scale parameter $\alpha$ affects the precision of step-length calculation due to the different motion features of pedestrians. To enhance the adaptability of step-length model, the scale parameter $\alpha$ is modeled as the random walk process:

$${\alpha }_{step}={\alpha }_0+{\displaystyle \underset{t=0}{\overset{\Delta T_{step}}{\int }}{\epsilon }_{{\alpha }_{Step}}dt}$$

(24)

where ${\alpha }_{step}$ indicates the step-length parameter, ${\alpha }_0$ represents the initial value, ${\epsilon }_{{\alpha }_{Step}}$ indicates the white noise, and $\Delta T_{step}$ represents the step interval.

The initial bias of the low-cost barometer is influenced by the cumulative error and environmental factors, such as temperature and humidity. In proposed SM-WRFS, a novel height-related zero-velocity update technology (H-ZUPT) is proposed to enhance the performance of the speed estimation error in the z-axis. Instead of detecting the quasi-static (QS) period by the acceleration or gyroscope angular rate data, the pressure change information and radio-frequency (RF)-based observations are adopted to detect the height-related QS period:

$$\frac{1}{N}{\displaystyle \sum _{k=1}^N(\frac{{\Vert p_k^b-p_{average}^b\Vert }^2}{{\zeta }_p^2}+\frac{{\Vert u_k^b-u_{k-1}^b\Vert }^2}{{\zeta }_u^2})}<\xi$$

(25)

where $p_{average}^b$ indicates the mean value of real-time measured pressure data in a slide window of length N, ${\zeta }_p^2$ is the measured noise, $u_k^b$ indicates the RF reported floor, and ${\zeta }_u^2$ is RF-based measured noise. When the height-related QS period is detected, the state update model of altitude and related bias information can be modeled as [27]:

$$\left[\begin{array}{l}\dot{h}\\ {\dot{b}}_h\end{array}\right]=\left[\begin{array}{c}{w}_h\\ -\frac{1}{{\tau }_{b_h}}{b}_h+{\upsilon }_{b_h}\end{array}\right]$$

(26)

where $w_h$ indicates the state noise for the altitude update, ${\tau }_{b_h}$ and ${\upsilon }_{b_h}$ represent the correlation time and the driving noise of the random walk process.

During the detected height-related QS periods, the measured model for the H-ZUPT based altitude update is described as:

$${\tilde{h}}_b-{\widehat{h}}_0=\delta h+b_h+n_{h_b}$$

(27)

where ${\tilde{h}}_b$ is the barometer measured altitude and ${\widehat{h}}_0$ is extracted from the first epoch of each detected height-related QS period. In these detected QS periods, the ideal observed value is always regarded as zero when the pedestrian remains static or moves among the same floor, and the change of altitude at the detected height-related QS period is caused by the bias of barometer. By using the above equation, the bias of barometer originated altitude estimation is estimated in real-time, and provides feedback to the original altitude estimation result ${\tilde{h}}_b{}^{calibrated}={\tilde{h}}_b-b_h$, thus the barometer-calculated altitude information can autonomously be calibrated by the proposed model.

3.2. Self-Calibration Model of Wi-Fi Ranging

The deviation of different intelligent terminals and Wi-Fi APs leads to various ranging biases. In this work, the bias of Wi-Fi ranging is calibrated to constrain the influences of mobile terminals deviations. We divide the calibration cases into dynamic and static scenes, during the static periods in the pedestrian’s initial walking procedure, the Gradient-Descent (GD)-based ranging bias calibration algorithm is proposed to estimate high-precision initial ranging bias. The QS periods are recognized using the collected inertial sensors data [29]:

$$\frac{1}{N}{\displaystyle \sum _{k=1}^N(\frac{{\Vert {\mathit{f}}_k^b-{\mathit{g}}^n\Vert }^2}{{\zeta }_f^2}+\frac{{\Vert {\mathbf{\omega }}_g^k\Vert }^2}{{\zeta }_w^2})}<\mathsf{\Omega }$$

(28)

where N represents the length of sliding window, ${\mathit{f}}_k^b$ and ${\mathbf{\omega }}_g^k$ indicate the measured acceleration and angular velocity data at epoch k, ${\zeta }_f^2$ and ${\zeta }_f^2$ represent the measured noises of accelerometer and gyroscope, and $\mathsf{\Omega }$ is the set threshold.

Once the QS periods are recognized, the least square (LS) algorithm is applied to acquire the location of the pedestrian based on the real-time RTT measurements [17]:

$${\mathit{P}}_{RTT}={({\mathit{A}}^{\mathrm{T}}\mathit{A})}^{-1}{\mathit{A}}^{\mathrm{T}}\mathit{B}$$

(29)

where P_RTT is the optimal position of the users, and the matrix A and B are described as:

$$\mathit{A}=2\cdot \left[\begin{array}{c}{({\mathit{P}}_{AP(2)}-{\mathit{P}}_{AP(1)})}^{\mathrm{T}}\\ ⋮\\ {({\mathit{P}}_{AP(N)}-{\mathit{P}}_{AP(1)})}^{\mathrm{T}}\end{array}\right]$$

(30)

$$\mathit{B}=\left[\begin{array}{c}{\Vert {\mathit{P}}_{AP(2)}\Vert }^2-{\Vert {\mathit{P}}_{AP(1)}\Vert }^2-{(L_{raw(2)}-d_{bias})}^2+{(L_{raw(1)}-d_{bias})}^2\\ ⋮\\ {\Vert {\mathit{P}}_{AP(N)}\Vert }^2-{\Vert {\mathit{P}}_{AP(1)}\Vert }^2-{(L_{raw(N)}-d_{bias})}^2+{(L_{raw(1)}-d_{bias})}^2\end{array}\right]$$

(31)

where P_AP(N) indicates the position of the selected Wi-Fi AP, L_raw(N) represents the measured RTT value, d_bias is the RTT bias that exists among the smartphone and Wi-Fi AP.

Under ideal circumstances, the position of the pedestrian remains theoretically unchanged in the detected QS periods. Thus, the differences between the estimated positions during each detected QS period approximately equals zero, and the GD-based RTT bias optimization model is presented as:

$$h(\mathit{x})={{\displaystyle \sum _{i=1}^{M-1}{\displaystyle \sum _{j=i}^{M-1}\Vert {\mathit{P}}_{\mathrm{RTT}}^{j+1}-{\mathit{P}}_{\mathrm{RTT}}^i\Vert }}}^2$$

(32)

where x represents the RTT bias, and M indicates the collected Wi-Fi-FTM-based positioning results during the detected QS period using the LS algorithm, the difference between each estimated location is cumulated to obtain the optimal bias value. The loss function is presented as:

$$L(\widehat{\mathit{x}})={(\varpi -h(\widehat{\mathit{x}}))}^{\mathrm{T}}{R}^{-1}(\varpi -h(\widehat{\mathit{x}}))$$

(33)

Because the optimization model is not linear, Taylor series are applied to linearize the proposed model:

$$\begin{array}{c}\varpi =h(\mathit{x})+\mathbf{\omega }\hfill \\ =h(\widehat{\mathit{x}})+{\frac{dh(\mathit{x})}{d\mathit{x}}|}_{x=\widehat{x}}(\mathit{x}-\widehat{\mathit{x}})+\frac{1}{2!}{\frac{d^{2}h(\mathit{x})}{d{\mathit{x}}^2}|}_{x=\widehat{x}}{(\mathit{x}-\widehat{\mathit{x}})}^2+\cdots +\mathbf{\omega }\hfill \\ \approx h(\widehat{\mathit{x}})+{\frac{dh(\mathit{x})}{d\mathit{x}}|}_{x=\widehat{x}}(\mathit{x}-\widehat{\mathit{x}})+\mathbf{\omega }\hfill \\ =h(\widehat{\mathit{x}})+\mathit{H}\delta \mathit{x}+\mathbf{\omega }\hfill \end{array}$$

(34)

where $\delta \mathit{x}$ is the deviation of state value and observed value, and H indicates the Jacobian matrix. The relationship between observation and prediction vectors is shown as:

$$\varpi -h(\widehat{\mathit{x}})=\mathit{H}\delta \mathit{x}+\mathbf{\omega }$$

(35)

The final expression of $\delta \mathit{x}$ can be obtained as:

$$\delta \mathit{x}={({\mathit{H}}^{\mathrm{T}}{\mathit{R}}^{-1}\mathit{H})}^{-1}{\mathit{H}}^{\mathrm{T}}{\mathit{R}}^{-1}\delta \varpi$$

(36)

Non-linear least squares need to iterate the above process until the state estimation error is lower than the threshold. In general, the nonlinear least squares update is described as:

$${\widehat{\mathit{x}}}_{\gamma }={\widehat{\mathit{x}}}_{\gamma -1}+\delta {\widehat{\mathit{x}}}_{\gamma -1}$$

(37)

where $\gamma$ represents the number of iterations, and the optimal bias value can be obtained if $L(\widehat{\mathit{x}})$ reaches the specified value.

In a dynamic scene, the result provided by the GD algorithm can be served as the initial ranging bias if the initial QS period is detected, and the Wi-Fi ranging bias in a dynamic case is modeled as the random walk process, which can feedback in real-time to obtain better calibration and integration performance:

$${\dot{b}}_{RTT}=-(1/{\tau }_{b_{RTT}})b_{RTT}+{\epsilon }_{b_{RTT}}$$

(38)

where $b_{RTT}$ indicates the Wi-Fi ranging bias, and ${\epsilon }_{b_{RTT}}$ is the white noise. The RTT-bias-based error model is described as:

$$\delta {\dot{\mathit{X}}}_W={\mathit{F}}_W\delta {\mathit{X}}_W+{\mathit{G}}_W{\epsilon }_W$$

(39)

where $\delta {\mathit{X}}_W=b_{\mathrm{RTT}}$, ${\mathit{F}}_W=0$, ${\mathit{G}}_W=1$, and ${\epsilon }_W={\epsilon }_{b_{\mathrm{RTT}}}$.

3.3. Self-Calibrated Integration Model Based on AEKF

In this section, the AEKF is adopted to realize a concrete and accuracy framework for multi-source integration. The system model in AEKF uses the MEMS-sensor-based method which is proposed in Section 2. In this section, a universal and self-calibrated integration structure using Wi-Fi FTM, RSSI fingerprinting, and low-cost sensors is proposed.

The state vector of multi-source integration and calibration model is described as:

$${\mathit{X}}_{total}^t={[r_x^t,r_y^t,r_z^t,{\theta }^t,{\alpha }_{step}^t,b_{\theta }^t,b_h^t,b_{RTT}^t]}^{\mathrm{T}}$$

(40)

where $r_x^t$, $r_y^t$, and $r_z^t$$r_z^t$ indicate the updated 3D position of the pedestrian at the current moment t, ${\theta }_t$ represents the calculated real-time heading, $b_{\theta }^t$, $b_h^t$, and $b_{RTT}^t$ indicate the heading bias, altitude bias, and Wi-Fi ranging bias, and ${\alpha }_{step}^t$ is the step-length parameter.

The total self-calibrated state update model $f({\mathit{X}}_{total}^{t+1})$ can be described as:

$$f({\mathit{X}}_{total}^{t+1})=\{\begin{array}{l}{r}_x^t+\cos {\theta }_t\cdot L({\alpha }_{step}^t)\\ r_y^t+\sin {\theta }_t\cdot L({\alpha }_{step}^t)\\ r_z^t+\Delta h_t-b_h^t\\ {\theta }^t+\Delta T_{gyro}\cdot b_{\theta }^t\\ {\alpha }_0+\exp (-\Delta T_{step}/{\tau }_{\alpha })\cdot {\alpha }_{step}^t\\ \exp (-\Delta T_{\mathrm{gyro}}/{\tau }_{b_{\theta }})\cdot b_{\theta }^t\\ \exp (-\Delta T_{baro}/{\tau }_{b_h})\cdot b_h^t\\ b_{RTT}^0+\exp (-\Delta T_{RTT}/{\tau }_{b_{RTT}})\cdot b_{RTT}^t\end{array}$$

(41)

where $b_{\theta }^t$, $b_h^t$, and $b_{RTT}^t$ indicate the heading bias, altitude bias and Wi-Fi ranging bias, $\Delta T_{step}$ is the step interval, $\Delta T_{\mathrm{gyro}}$, $\Delta T_{baro}$, and $\Delta T_{RTT}$ represent the sampling interval of gyroscope, barometer, and Wi-Fi RTT. ${\tau }_{\alpha }$, ${\tau }_{b_{\theta }}$, ${\tau }_{b_h}$, ${\tau }_{b_{RTT}}$ are the correlation times of step, heading, altitude, and RTT. $L({\alpha }_{step}^t)$ indicates the calibrated step-length.

The integration structure in this work includes two types: the tightly coupled positioning method and the loosely coupled positioning method. Under the Wi-Fi FTM covered indoor scenes, the observed Wi-Fi ranging is presented as:

$$\delta {\mathit{Z}}_{RTT}=\left[\begin{array}{c}\delta {\mathit{z}}_{1,range}\\ \delta {\mathit{z}}_{2,range}\\ ⋮\\ \delta {\mathit{z}}_{m,range}\end{array}\right]=\left[\begin{array}{c}{d}_{MEMS,1}-d_{FTM,1}\\ d_{MEMS,2}-d_{FTM,2}\\ ⋮\\ d_{MEMS,m}-d_{FTM,m}\end{array}\right]$$

(42)

where $\delta {\mathit{z}}_{m,range}$ represents the observation residuals among Wi-Fi RTT and MEMS sensors-provided distance measurements; The MEMS-sensor-based distance observation $d_{MEMS,m}$ is described as follow:

$$d_{MEMS,m}=\sqrt{{(E_{{}_{MEMS}}^k-P_m^E)}^2+{(N_{{}_{MEMS}}^k-P_m^N)}^2}$$

(43)

where (E^k_MEMS, N^k_MEMS) represents the MEMS-sensors-originated location information, and (P_m^E, P_m^N) represents the position of the m^st Wi-Fi AP.

The overall measured distance using Wi-Fi RTT protocol can be modeled as:

$$d_{FTM,m}=L_{raw}-b_{RTT}-v_{RTT}$$

(44)

For the Wi-Fi FTM ranging bias self-calibration, the real-time estimated ranging bias $b_{RTT}$ is provided feedback by the above equation and the final calibrated ranging result $d_{FTM,m}$ is further served as the observation in Equation (38) to obtain the optimal estimation results of the state vector.

For normal indoor scenes that do not cover the Wi-Fi ranging protocol supported APs, the crowdsourced Wi-Fi-RSSI-fingerprinting-based loosely coupled positioning method is adopted to provide a universal positioning solution by integrating with MEMS sensors. The observed model of RSSI fingerprinting is presented as:

$$\{\begin{array}{l}\delta {\mathit{z}}_p^n=p_{rssi}^n-p_{{}_{MEMS}}^n\\ \delta {\mathit{z}}_v^n=v_{rssi}^n-v_{{}_{MEMS}}^n\end{array}$$

(45)

where $p_{rssi}^n$ and $v_{GNSS}^n$ indicate the acquired Wi-Fi RSSI fingerprint provided location and velocity results under the navigation system, $p_{{}_{MEMS}}^n$ and $v_{{}_{MEMS}}^n$ are the MEMS-sensor-based results by which $p_{{}_{MEMS}}^n=\left[r_x^t,r_y^t,r_z^t\right]$ is calculated in Equation (37), and $v_{rssi}^n$ and $v_{{}_{MEMS}}^n$ are calculated as follows:

$$\{\begin{array}{l}{v}_{rssi}^n=\frac{p_{{}_{rssi}}^n(t)-p_{rssi}^n(t-1)}{\Delta T_{rssi}}\\ v_{{}_{MEMS}}^n=\frac{p_{{}_{MEMS}}^n(t)-p_{{}_{MEMS}}^n(t-1)}{\Delta T_L}\end{array}$$

(46)

where $v_{rssi}^n$ and $v_{{}_{MEMS}}^n$ are calculated using the time difference of locations changes provided by the Wi-Fi fingerprinting and MEMS sensors, respectively. $\Delta T_{rssi}$ and $\Delta T_L$ indicate the update rates of Wi-Fi fingerprinting and MEMS-sensor-based step detection.

4. Experimental Results of SM-WRFS

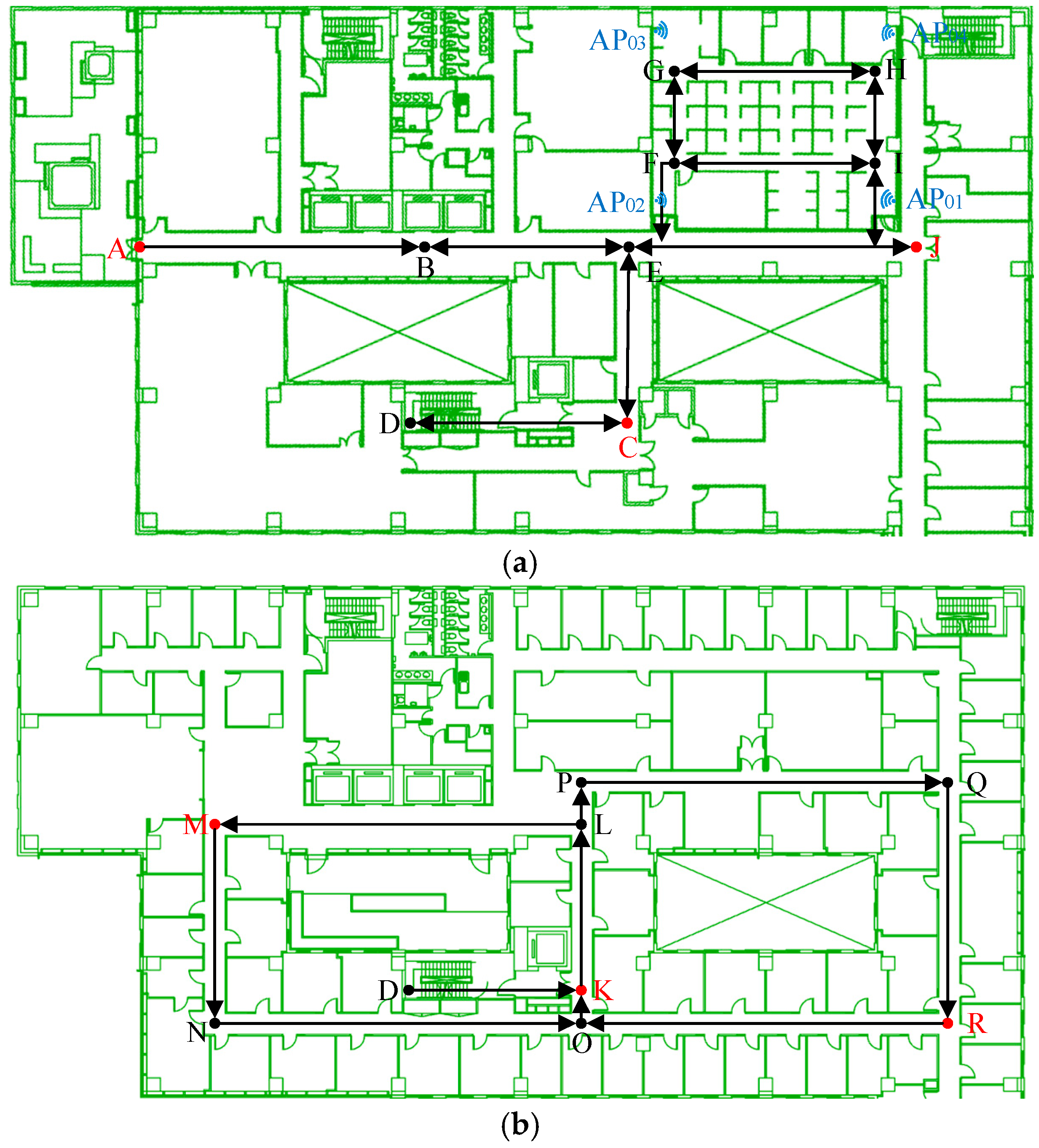
To estimate the precision of proposed SM-WRFS, comprehensive experiments are presented in this work. The results also aim to estimate the precision of crowdsourced trajectory optimization and the navigation database generation algorithm, and the self-calibrated integration framework. A complex office building which contains multiple floors was adopted as the experimental site, as described in Figure 4. Several QR codes were deployed at points A, C, J, K, M, and R. The Intel 8260AC integrated Wi-Fi APs were applied to provide FTM function. Google Pixel 3 and Pixel 4 were adopted as the tracking terminals, which support the Wi-Fi FTM protocol and integrate rich sensors. The sampling rates of Wi-Fi FTM, RSSI fingerprinting and low-cost sensors were 5 Hz, 0.3 Hz and 50 Hz, respectively.

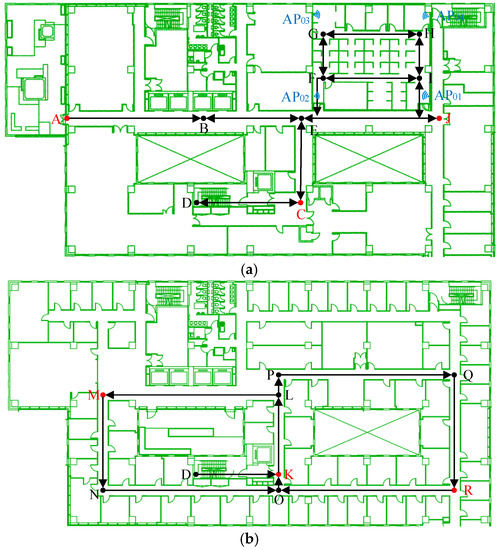
Figure 4. (a)The 10th Floor of an Office Building; (b) The 9th Floor of an Office Building.

4.1. Performance Estimation of the Forward Localization and Trajectory Optimization

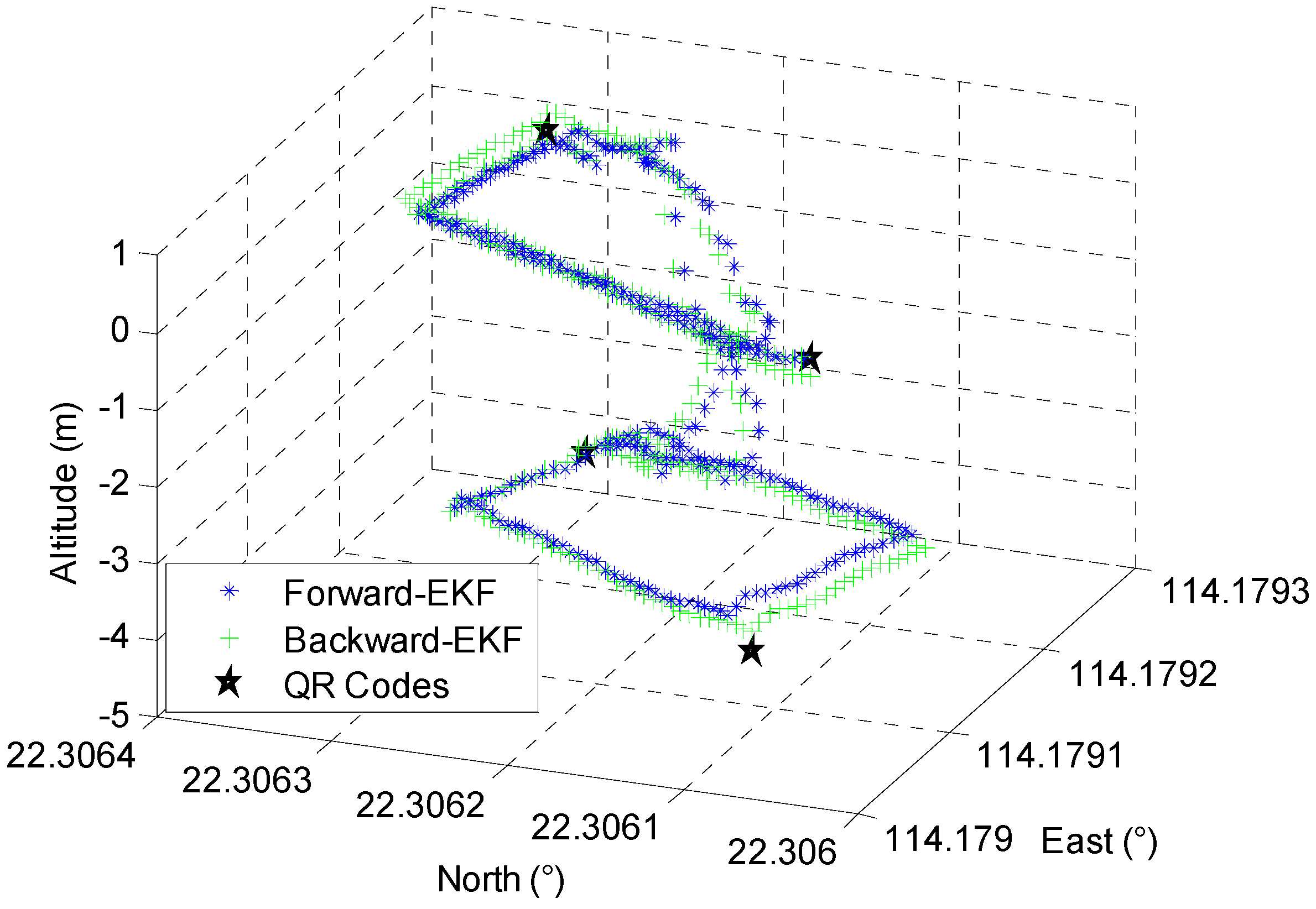
The accuracy of crowdsourced trajectories proved to have significant effects during the on-line phase of Wi-Fi fingerprinting. To estimate the accuracy of EKF-based forward localization and backward smoothing, the pedestrian began at point A, passed point B, C, D, K, L, M, N, O, K, D, C, E, B, and finally walked back to point A. The QR codes deployed at A, C, K and M were applied in this case. The performance comparison between EKF-based 3D forward localization and backward smoothing is shown in Figure 5.

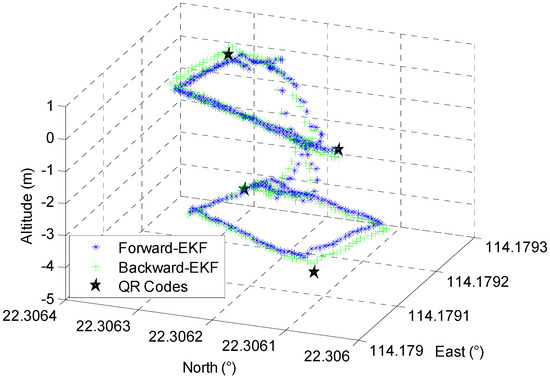
Figure 5. Comparison of Forward and Backward EKF.

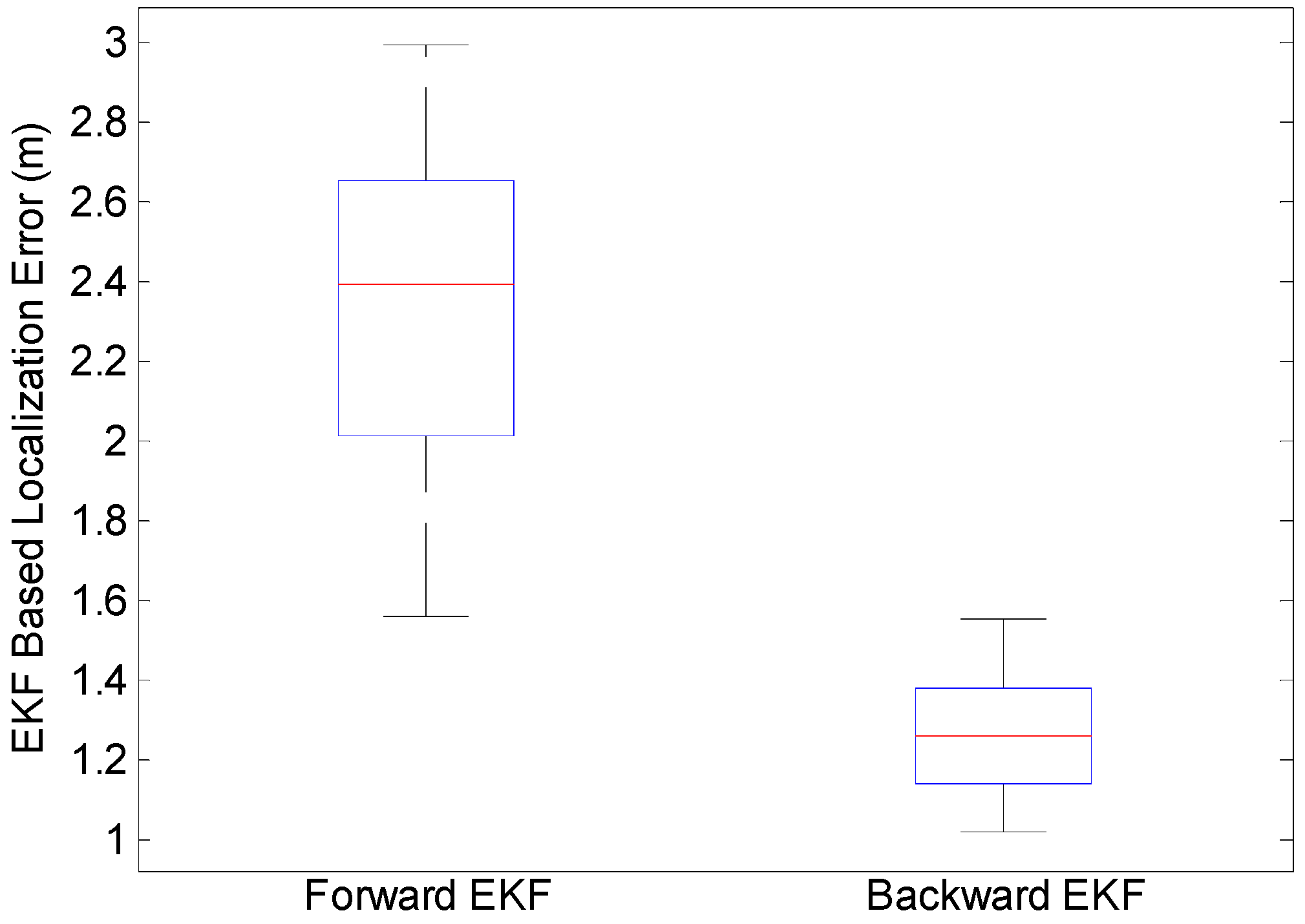
Figure 5 demonstrates that the proposed EKF-based backward smoothing algorithm further improves the accuracy of the proposed crowdsourced forward trajectory; the comparison of estimated accuracy on the reference points is described in Figure 6.

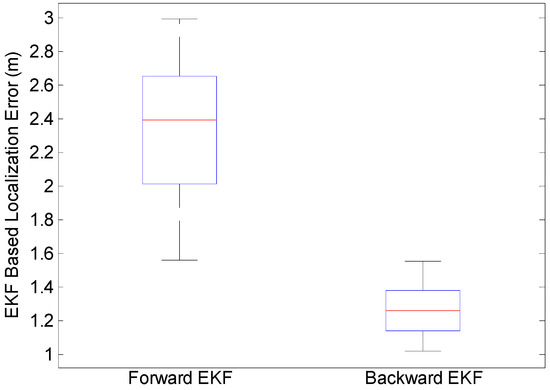
Figure 6. Accuracy Comparison of Forward and Backward EKF.

It can be seen in Figure 6 that the proposed backward EKF effectively improves the performance of forward trajectories, and the average positioning error decreased from 2.4 m to 1.2 m.

4.2. Performance Estimation of the Crowdsourced Navigation Database Generation

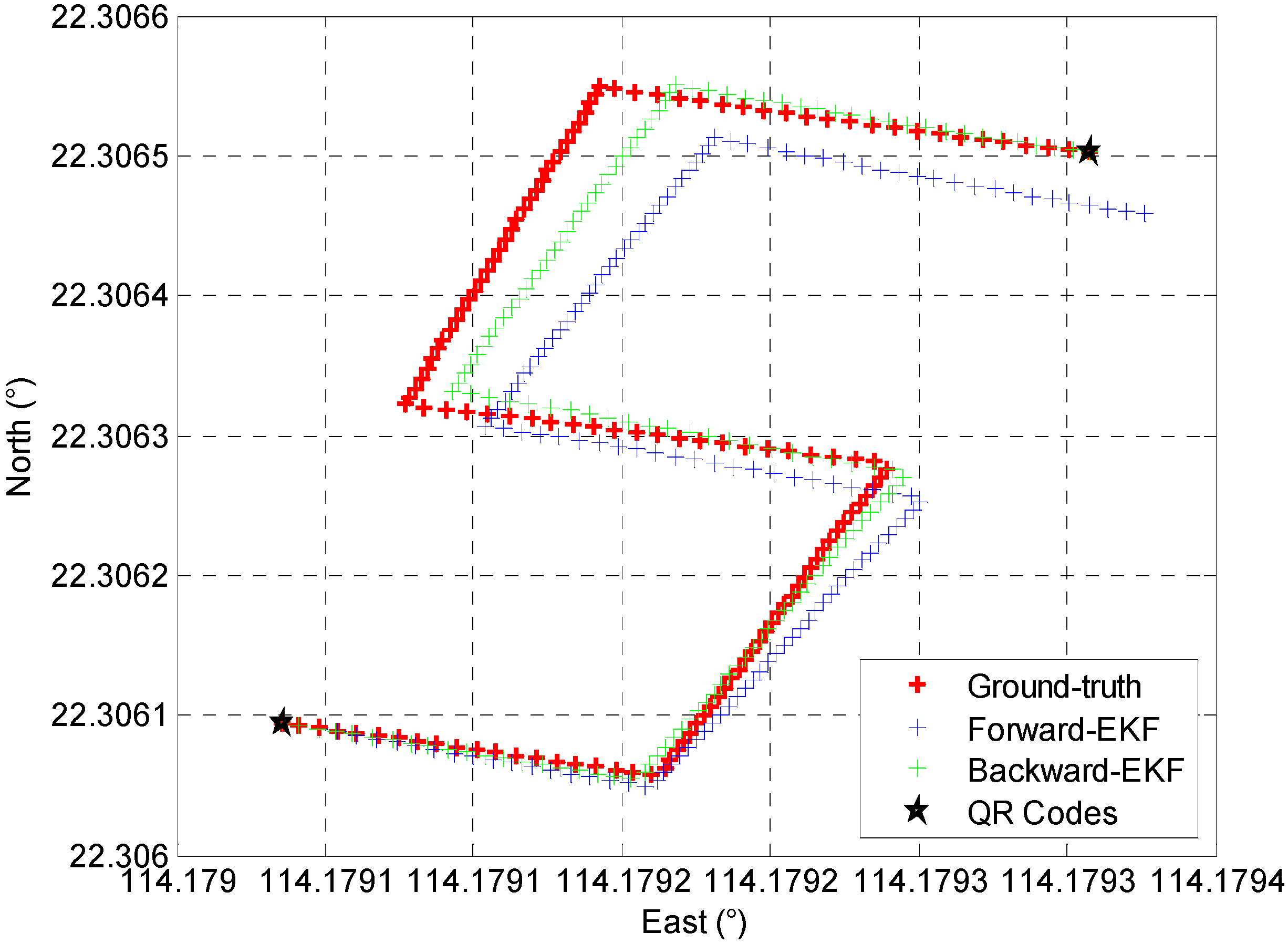
In our paper, a deep-learning based model is developed to independently estimate the positioning error of crowdsourced trajectories. The training dataset is collected in different indoor environments, and the ground-truth trajectory is provided by the total station with centimeter-level accuracy. The performance comparison between forward-EKF trajectory, backward-EKF trajectory, and ground-truth trajectory is described in Figure 7.

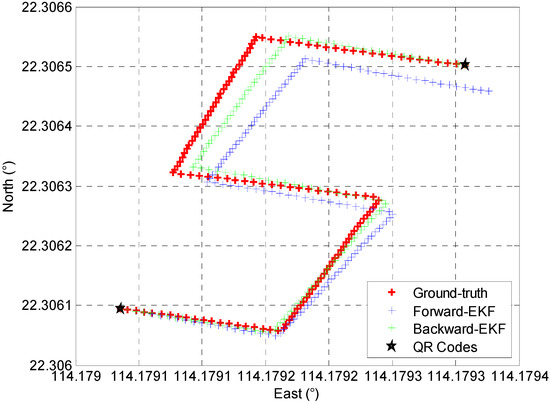
Figure 7. Comparison of Collected Trajectories.

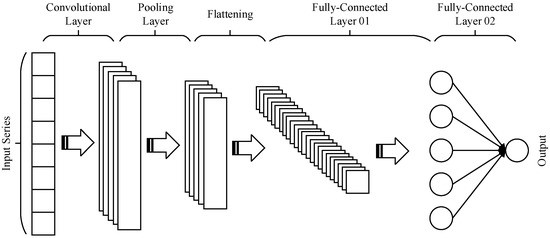
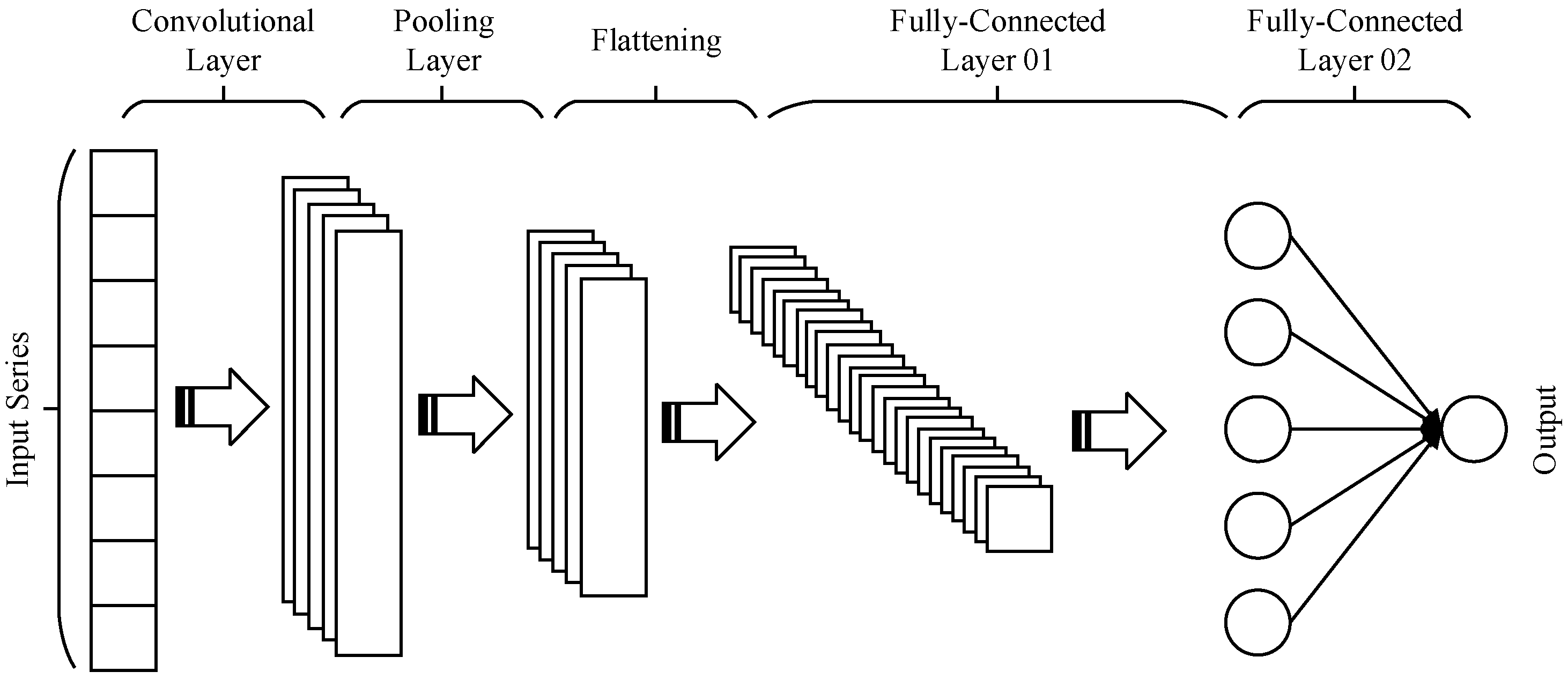
In this work, the 1D-CNN-based crowdsourced trajectory evaluation algorithm is proposed for the positioning error evaluation during each step. The proposed 1D-CNN model contains two phases; in the training phase, the extracted feature from optimized crowdsourced trajectories is modeled as the input vector and the ground-truth positioning error during each step period is modeled as the output vector. After the training phase, the optimal parameter of 1D-CNN can be acquired. During the prediction phase, the ground-truth positioning error is not required, only the input vector provided by the extracted feature from optimized crowdsourced trajectories is needed for trained 1D-CNN, and the positioning error under each step period can be autonomously predicted by the trained 1D-CNN model. In this case, the open-source dataset provided by IPIN-2020 Track 3 [33] is generated for the training purposes of the proposed 1D-CNN-based crowdsourced trajectories error prediction model, then the trained model is applied to autonomously predict the positioning error during each step period of collected crowdsourced trajectories; the comparison between the predicted positioning error and ground-truth positioning error at each step is presented in Figure 8.

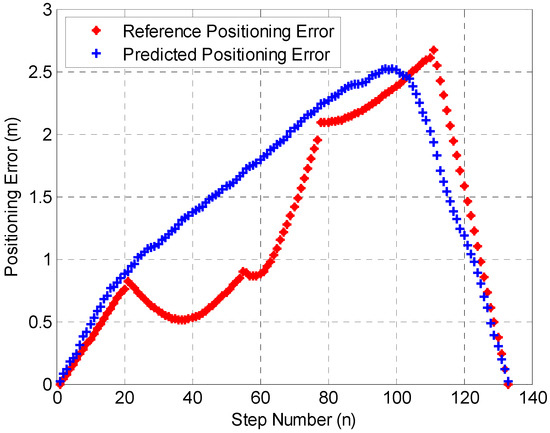
Figure 8. Performance of Error Prediction.

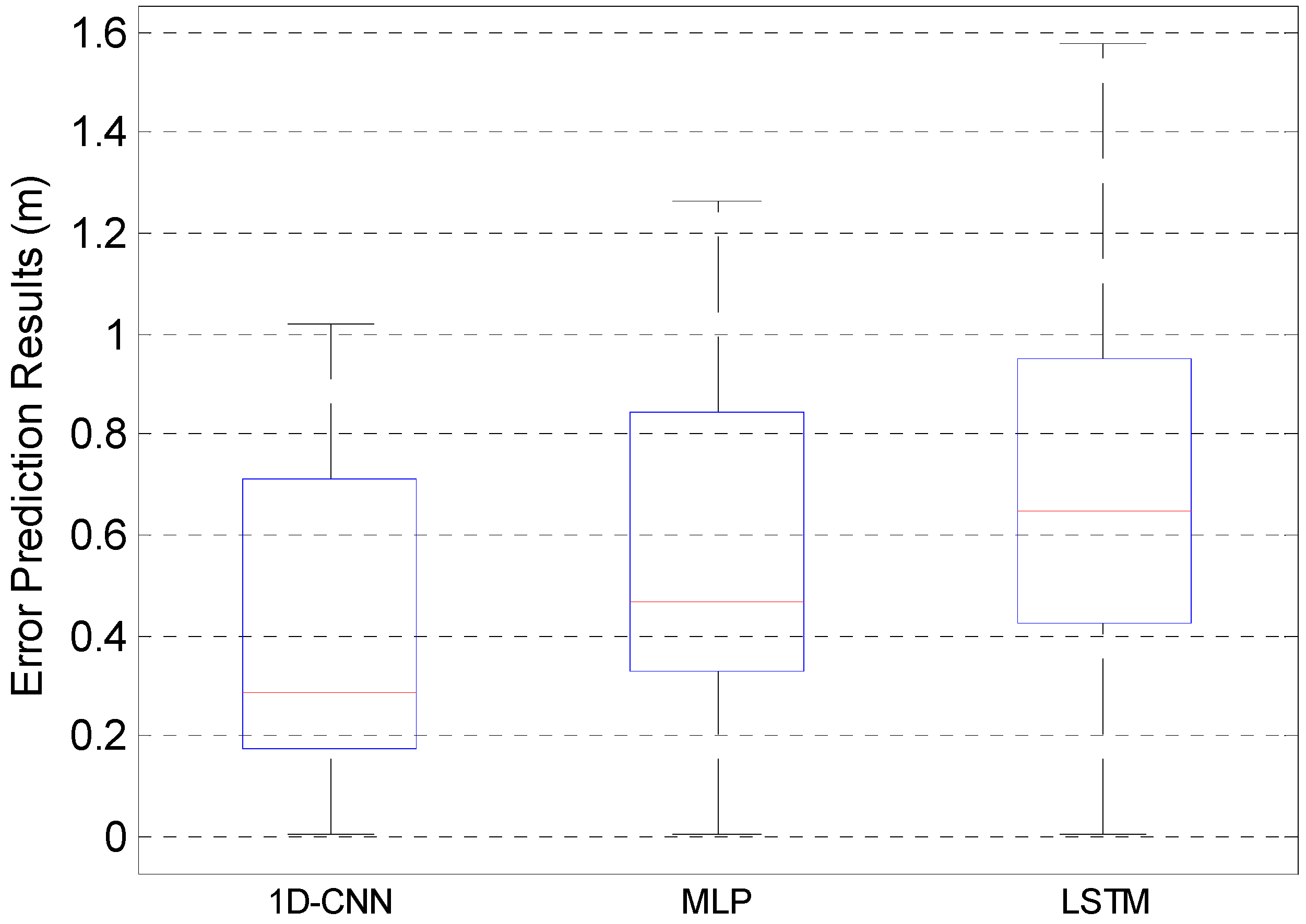
Figure 8 shows that the proposed deep-learning based trajectory evaluation algorithm achieved meter-level error prediction accuracy, and the proposed 1D-CNN structure is compared with state-of-art long short-term memory (LSTM) [34] and multilayer perceptron (MLP) network [35], and the error prediction comparison results are described in Figure 9.

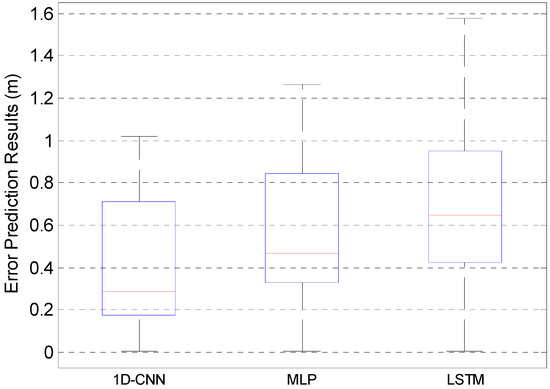
Figure 9. Accuracy Comparison of Different Models.

Figure 9 indicates that the proposed 1D-CNN model proves to have a much better performance compared with the MLP and LSTM networks, and the error prediction accuracies of the three algorithms were 0.71 m, 0.84 m, and 0.95 m in case of 75%, respectively.

In this work, the crowdsourced Wi-Fi fingerprinting database was generated by collecting the daily-life trajectories provided by 25 different users and the overall number of 56 trajectories were collected and the raw RSSI vector was further weighted according to the 1D-CNN-based trajectory error prediction results in order to generate the final crowdsourced database. To evaluate the performance of crowdsourced Wi-Fi fingerprinting and calculation efficiency of the final generated crowdsourced navigation database, the proposed deep-learning approach was compared with the state-of-art database establishment (DE) method proposed in [23]. Four Indexes are compared, including k-nearest-neighbor-based positioning precision in 75% (KNN-P), the capacity of generated crowdsourced fingerprinting database (C-CFD), the calculation time of KNN (KNN-T), and the crowdsourced trajectory optimization error in 75% (CT-OPE); the comparison results are described in Table 1.

Table 1. Comparison of Database Generation Methods.

	Index	KNN-P	C-CFD	KNN-T	CT-OPE
Model
SL-WRFS		5.2 m	150	14.89 ms	1.375 m
DE [20]		6.1 m	200	20.11 ms	1.369 m

Table 1 describes the main indexes of two database generation methods. The proposed SL-WRFS proves to have a higher localization accuracy within 5.2 m in 75%, and smaller database capacity and calculation time, and the two algorithms show the similar trajectory optimization error within 1.375 m and 1.369 m in 75%, respectively. Thus, the proposed deep-learning-based navigation database generation algorithm presents a better performance compared with the quality assessment criteria proposed in [23].

4.3. Performance Estimation of SM-WRFS

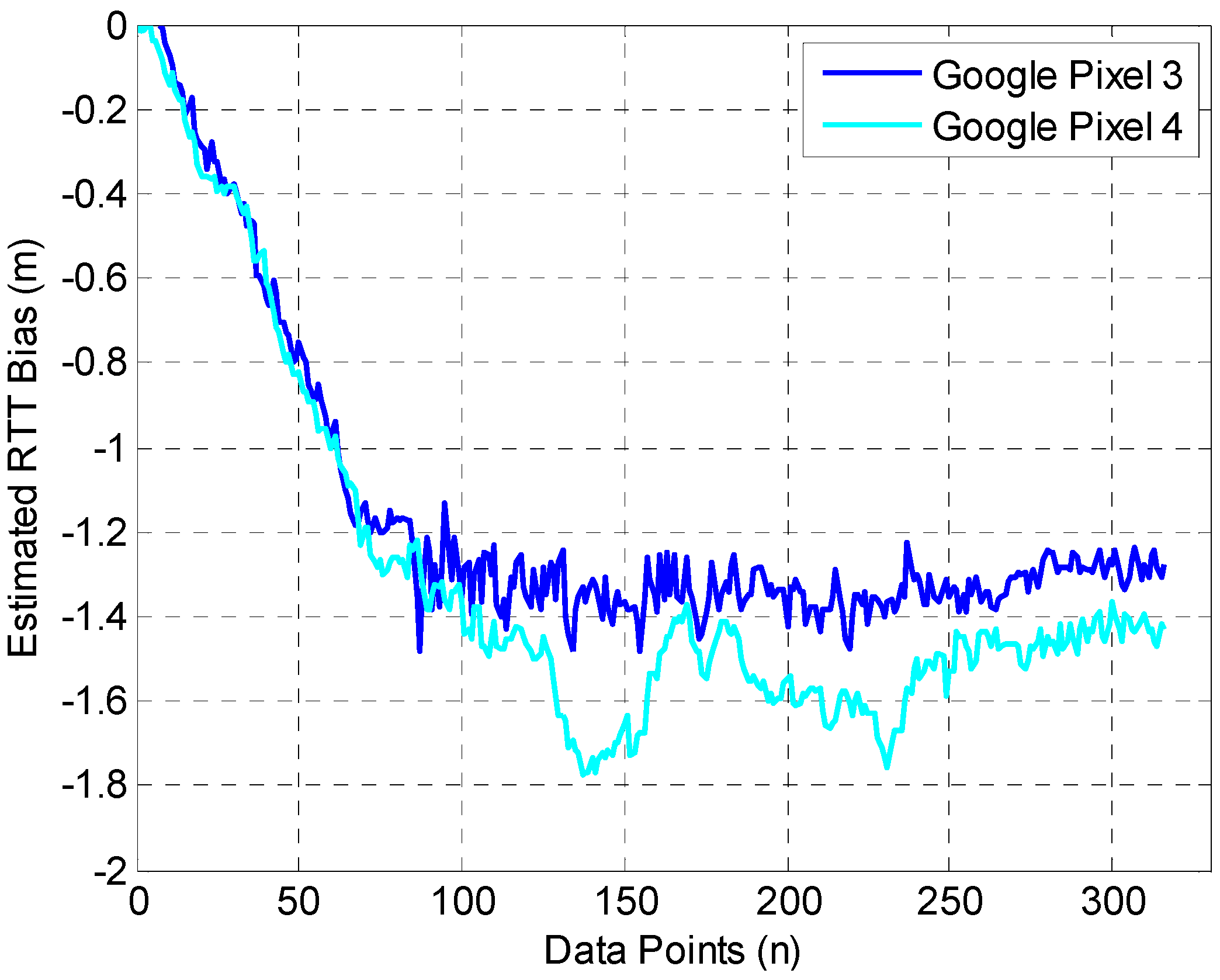
The performance of SM-WRFS is evaluated based on a comprehensive 3D indoor scene shown in Figure 4, in which the crowdsourced Wi-Fi fingerprinting database was constructed using the deep-learning model. To estimate the performance of RTT bias self-calibration, the tester walked around the office scene which is covered by the Wi-Fi-FTM-based location sources, and the RTT bias calibration results using different smartphones are shown in Figure 10.

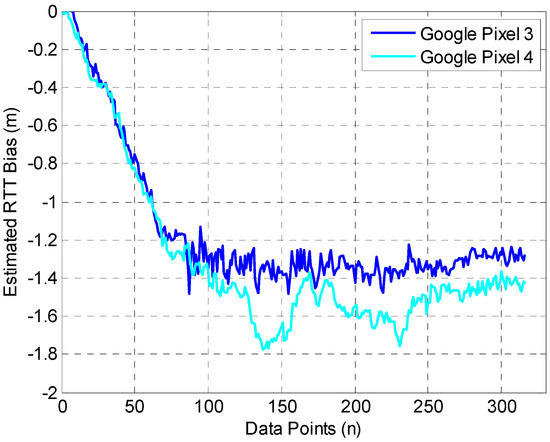
Figure 10. Performance of RTT Bias Calibration.

Figure 10 shows that the estimated RTT biases under different smartphones gradually converge at −1.3 m and −1.4 m with the procedure of multi-source fusion in the office scene. In addition, the static polynomial fitting method applied in [15] is applied as the comparison, which obtains the RTT biases of −1.25 m and −1.35 m, similar to the calibration algorithm in our work.

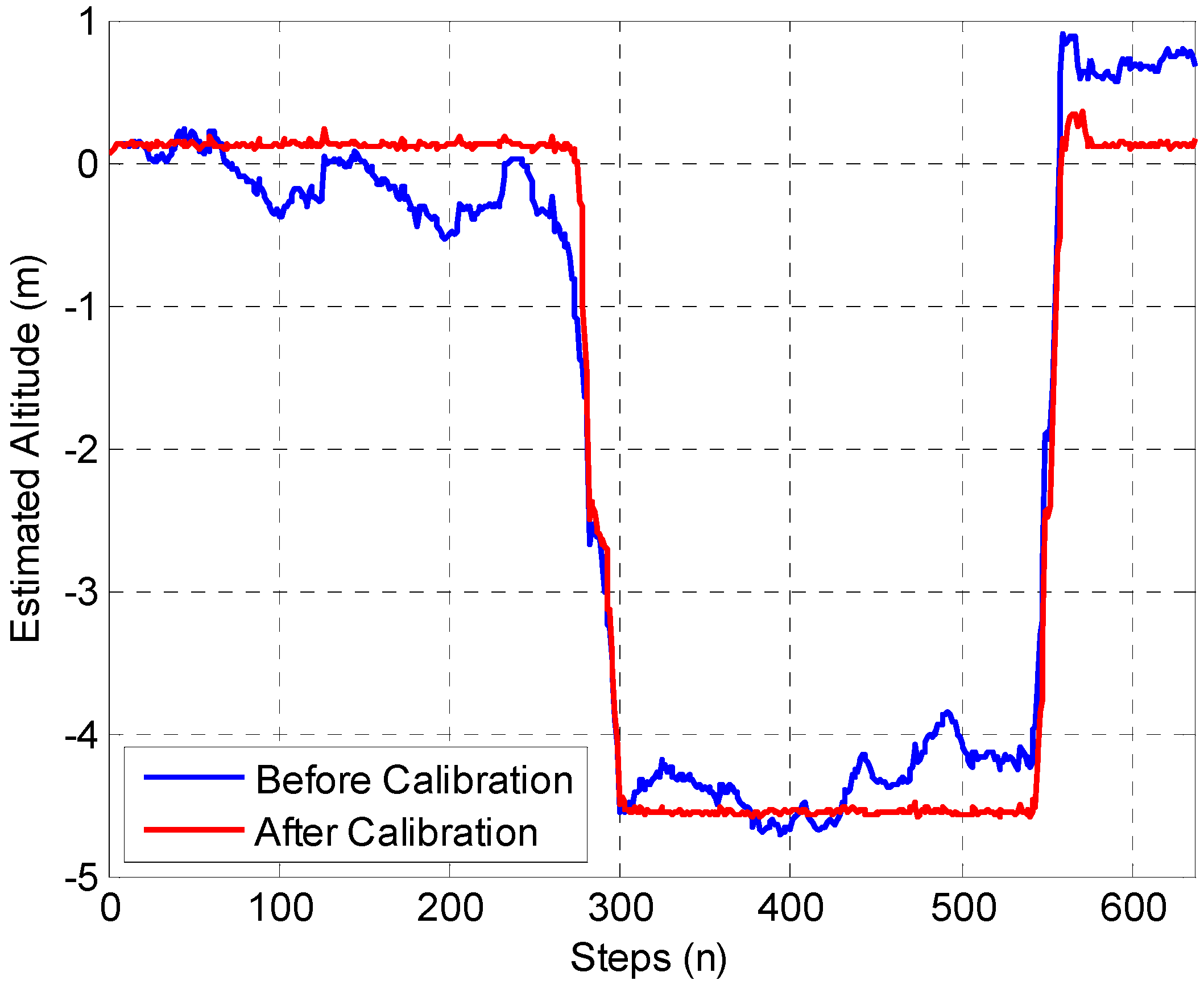
In the final experiment, the pedestrian walked past the Wi-Fi fingerprinting and ranging covered indoor areas, and the self-calibrated integration model is proposed to achieve real-time 3D localization. The walking route of the tester started with point A, passed by points B, E, F, G, H, I, F, G, H, I, F, J, E, C, D, K, O, N, M, P, O, R, Q, P, K, D, C, E, and B, and returned to point A. The calibration performance of the proposed H-ZUPT algorithm is shown in Figure 11.

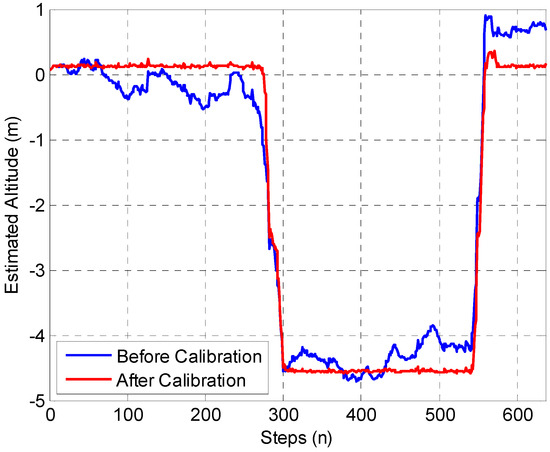
Figure 11. Performance of Altitude Bias Calibration.

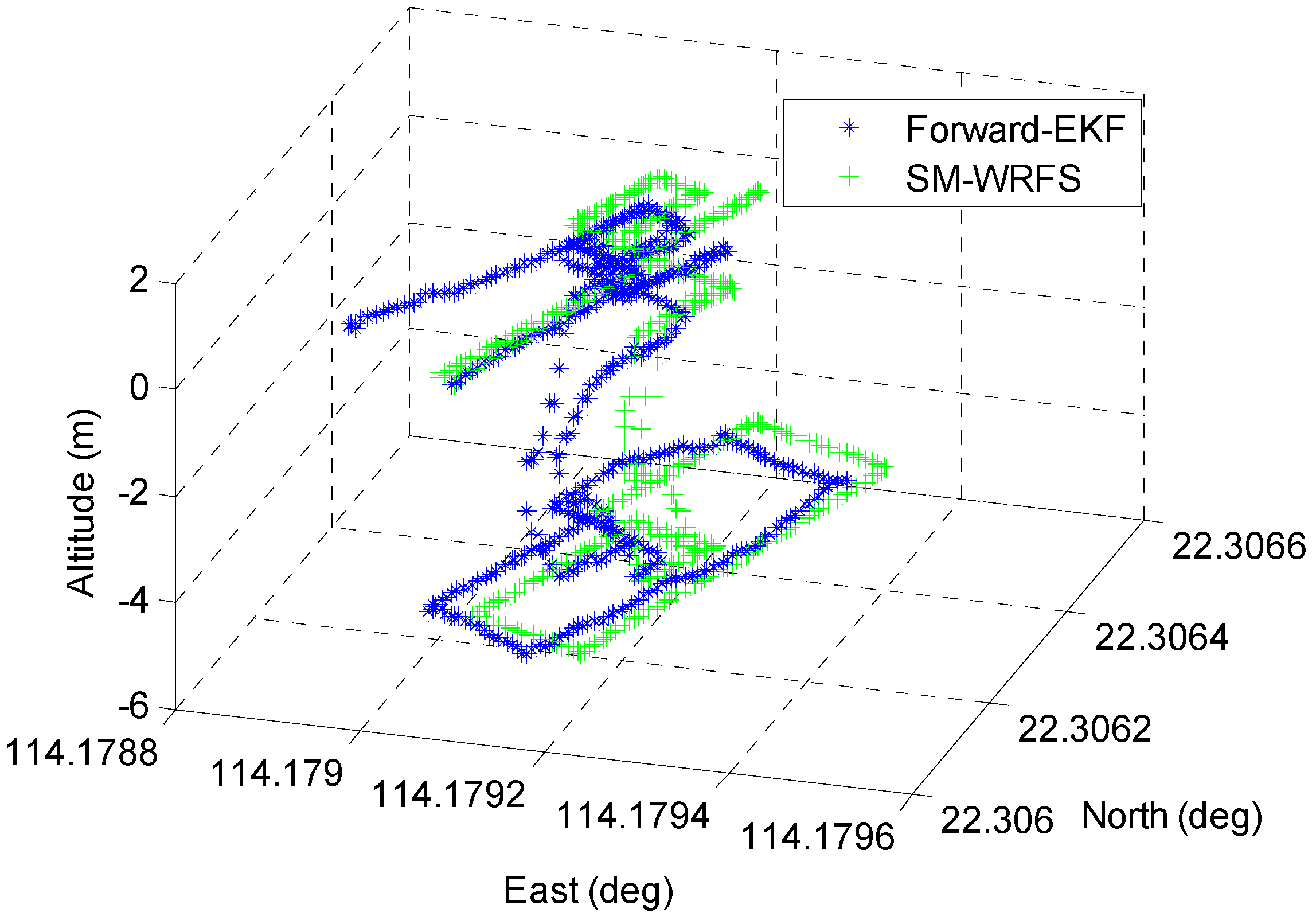
Figure 11 shows that a large improvement is realized by the proposed H-ZUPT algorithm, and the 3D localization comparison between forward-EKF without the self-calibration algorithm, and Wi-Fi fingerprinting, Wi-Fi FTM triangulation, and self-calibration algorithm assisted SM-WRFS is shown in Figure 12.

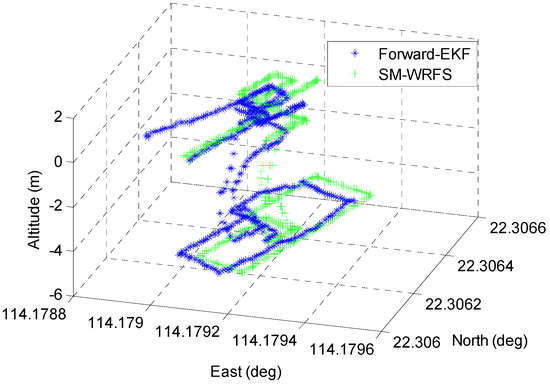
Figure 12. Performance of Proposed SM-WRFS.

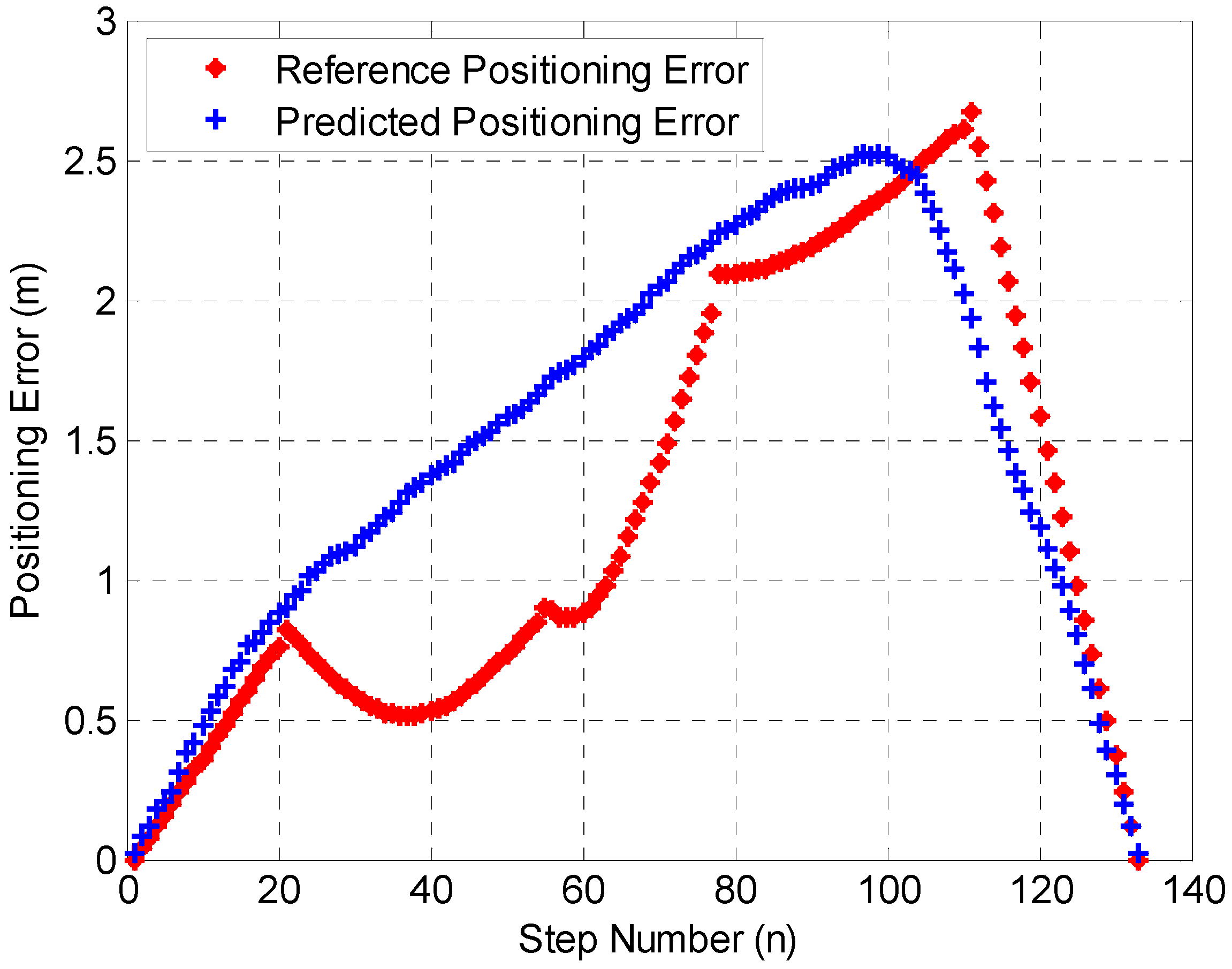
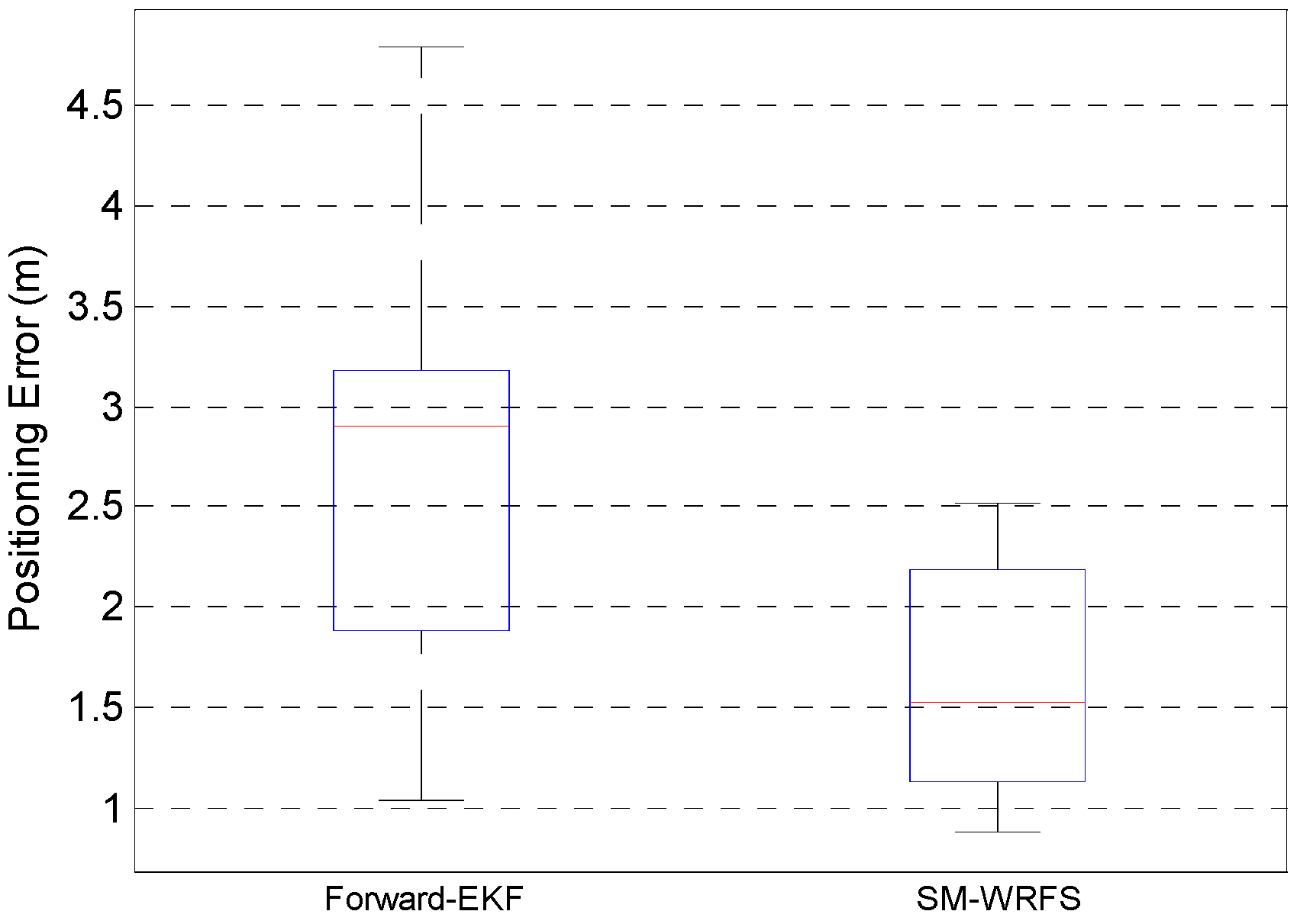
It can be seen in Figure 12 that the proposed forward-EKF also exists in the cumulative error, while the proposed SM-WRFS effectively increases the robustness of the multi-floor localization. The positioning error comparison results between forward-EKF and the final self-calibrated model SM-WRFS are described in Figure 13.

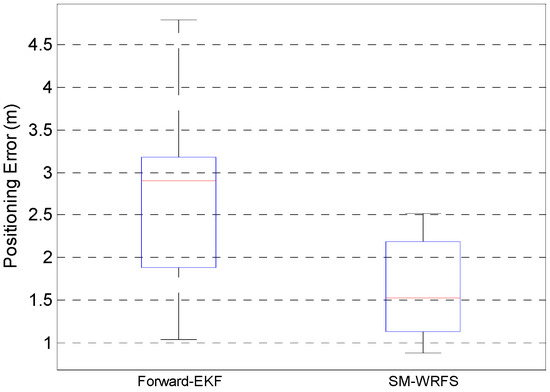
Figure 13. Positioning Errors Comparison.

Figure 13 describes the positioning errors comparison under complex 3D indoor environments using uncalibrated forward-EKF model and final self-calibrated model SM-WRFS which reach 3.18 m in 75% and 2.19 m in 75%, respectively.

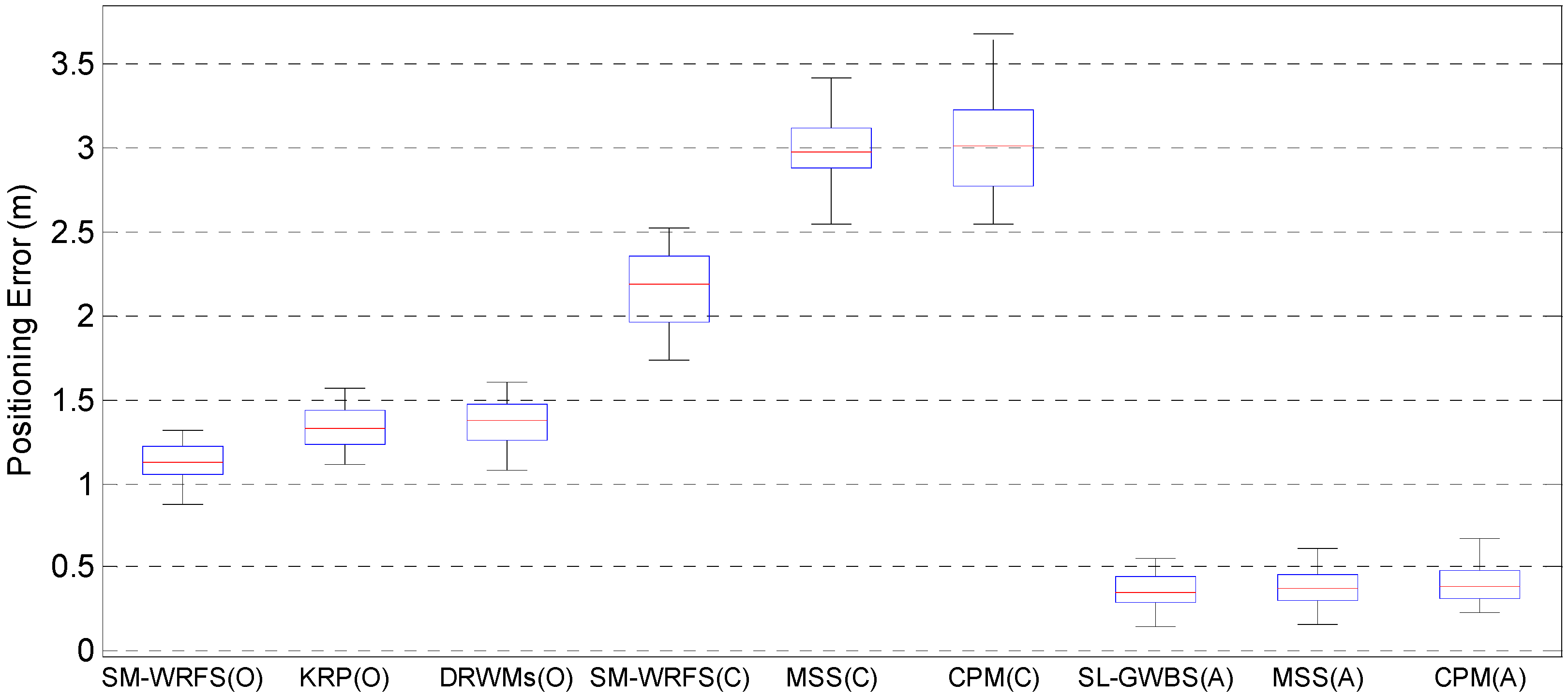
Finally, the proposed SM-WRFS structure is compared with two state-of-art positioning algorithms in the office scene and 3D corridor scene, in which the Kalman-filter-based RTT and PDR fusion algorithm (KRP) [17] and unscented Kalman-filter-based multi-source fusion algorithm (DRWMs) [36] are compared in the office scene, and the multi-sensor multi-floor system (MSS) [27] and cross-layer positioning method (CPM) [37] are compared in the corridor scene. The staircase under the corridor scene almost does not exist in the fingerprinting database coverage due to the distribution characteristics of deployed local Wi-Fi APs. The accuracy comparison of 2D localization and altitude estimation are shown in Figure 14.

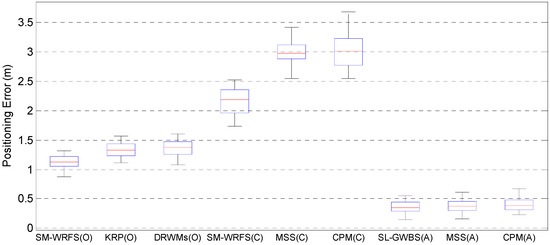
Figure 14. Performance Comparison between State-of-art Algorithms.

Figure 14 proves that the proposed SM-WRFS achieves a more accurate 2D positioning and altitude estimation accuracy in different positioning scenes. In the office scene, the positioning error of SM-WRFS reaches 1.22 m in 75%, compared with 1.44 m of KRP in 75%, and 1.47 m of DRWMs in 75%; in the corridor scene, the 2D positioning errors of the proposed SM-WRFS, KRP, and CPM are 2.36 m, 3.12 m, and 3.23 m in 75%, respectively, and the positioning accuracy of SM-WRFS is maintained in the staircase under corridor scene with nearly no database coverage, and the altitude estimation errors are similar, which were 0.44 m, 0.45 m, and 0.48 m in 75%, respectively.

5. Conclusions

The performance of crowdsourcing-based multi-floor indoor positioning is subject to cumulative error, hardware deviation and environmental interference. To solve these problems, this paper presents the SM-WRFS framework, which includes following contributions:

(1)

The EKF-based forward localization and backward smoothing using QR codes based landmarks, and the accuracy of optimized trajectories are autonomously evaluated by the deep-learning based error prediction algorithm for the navigation database generation.

(2)

The localization parameters, such as step-length scale factor, heading and altitude biases, and Wi-Fi ranging bias are calibrated in real-time to eliminate the cumulative error and hardware deviation effects of multi-source fusion.

(3)

Two different integration models are proposed, aiming at providing more accurate and universal multi-floor indoor localization performance. The designed experiments achieve a 2D localization error lower than 1.22 m in the office scene and 2.36 m in the corridor scene, respectively.