A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes
Abstract
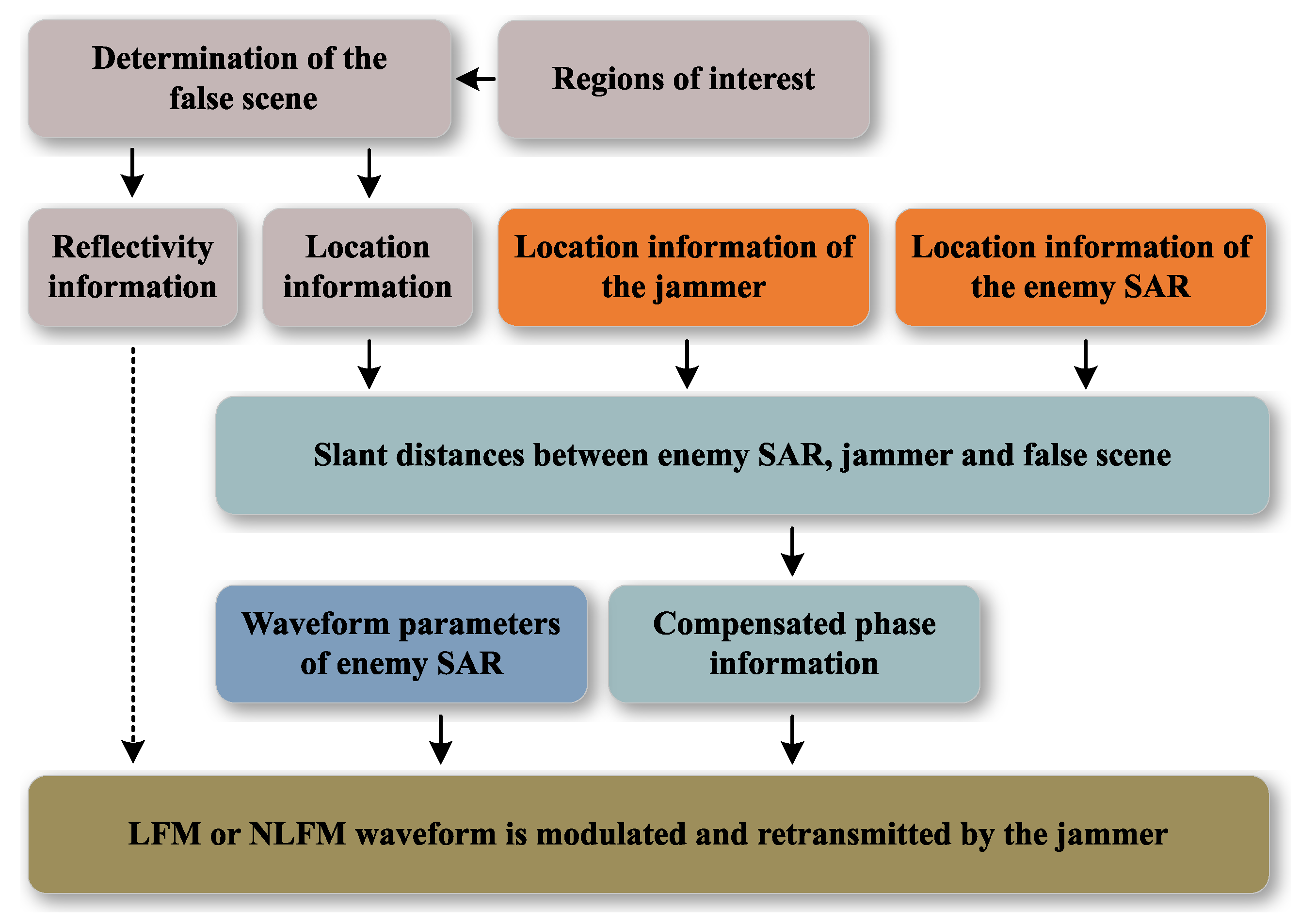
1. Introduction
2. Design Method for NLFM Waveforms
2.1. Coding Model
2.2. Correlation Function
2.3. Optimization
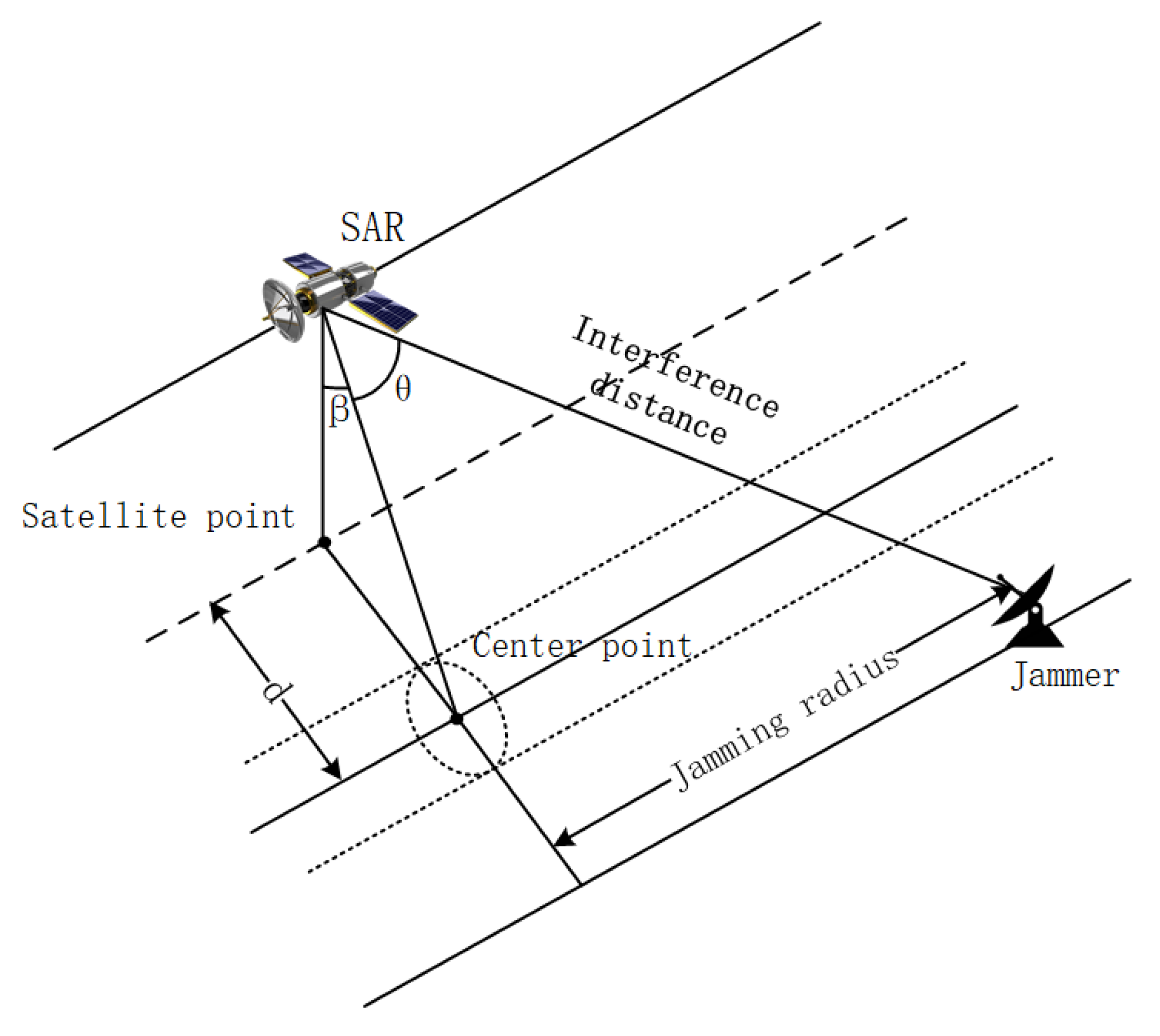
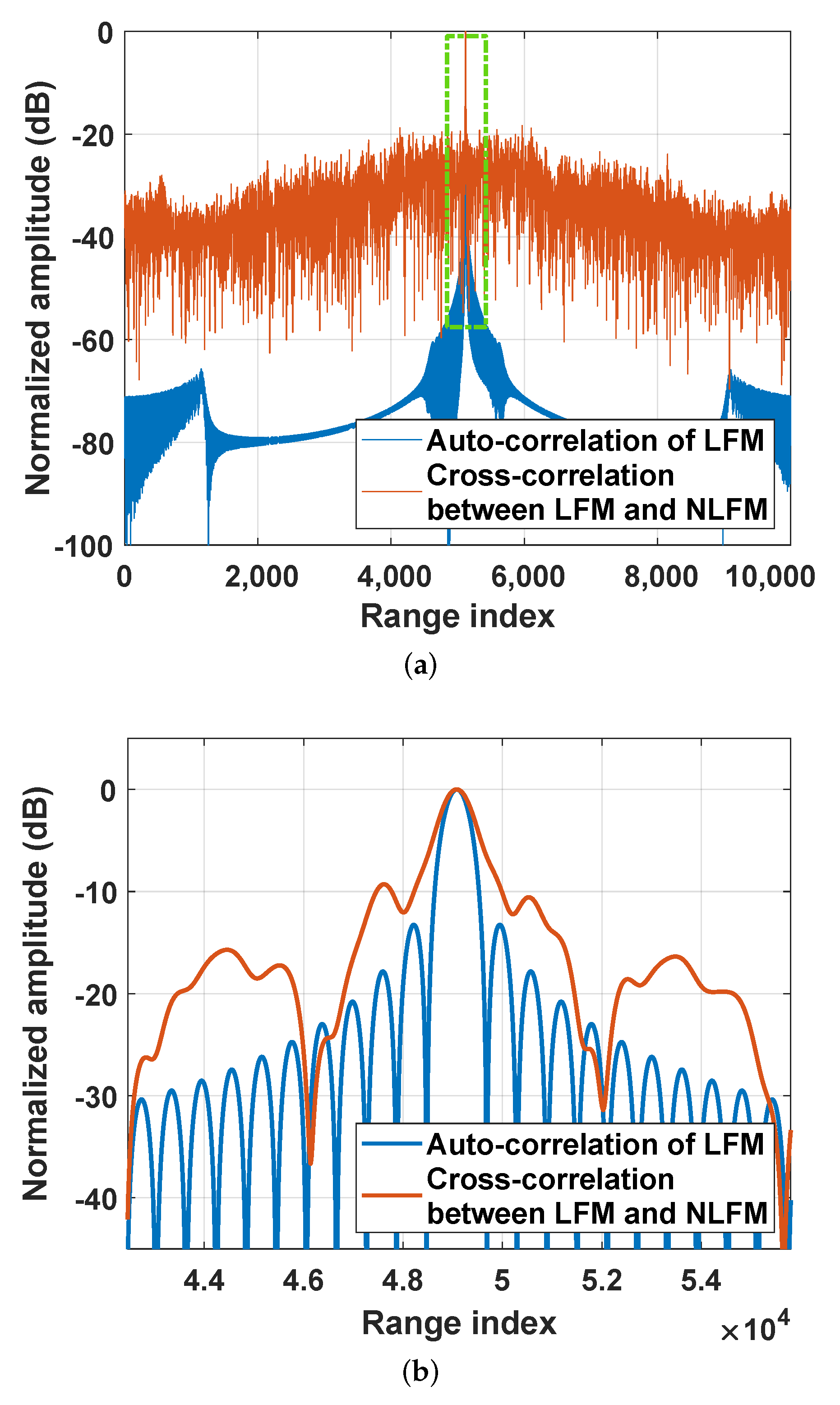
3. Simulations and Analysis
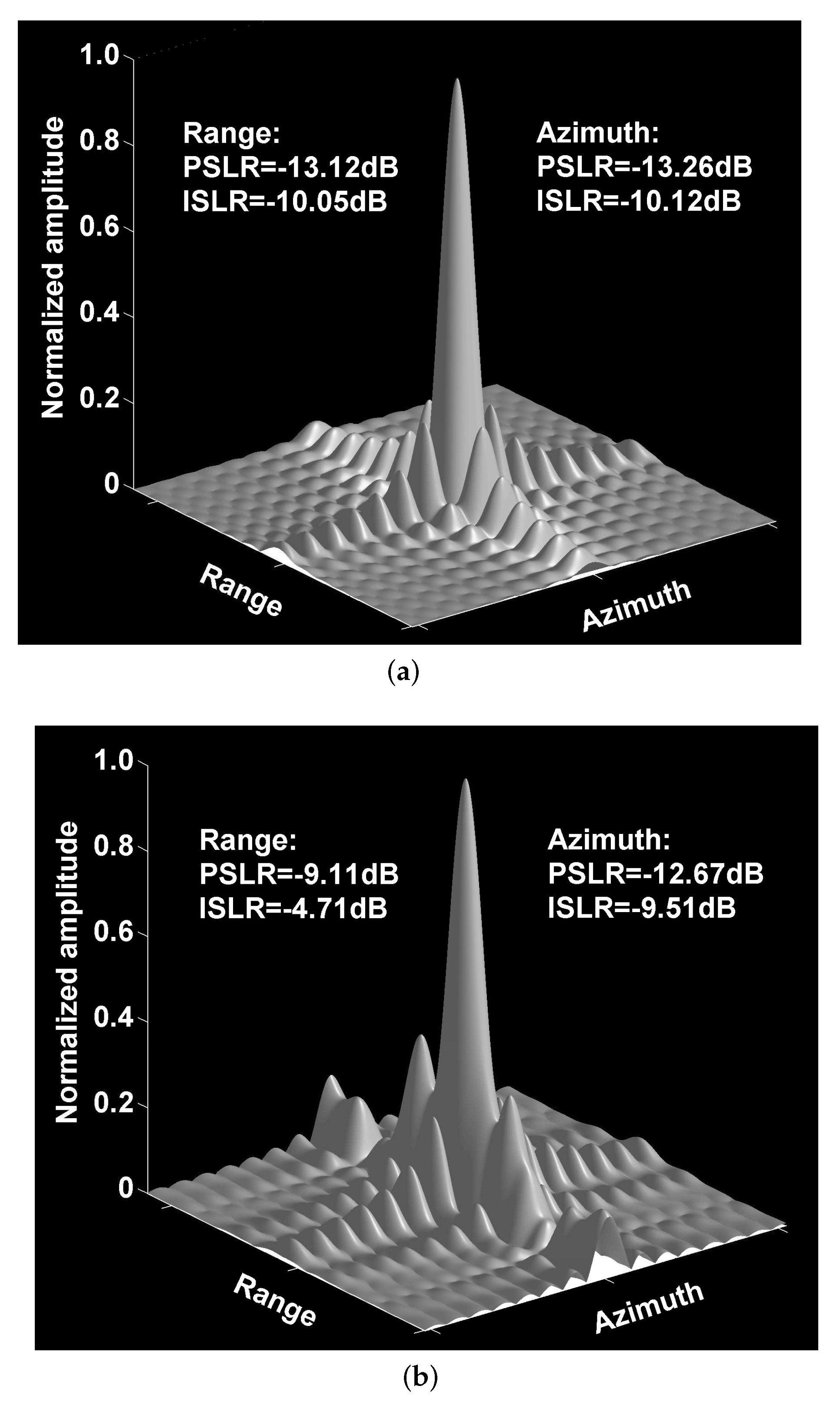
3.1. Point Target Simulation
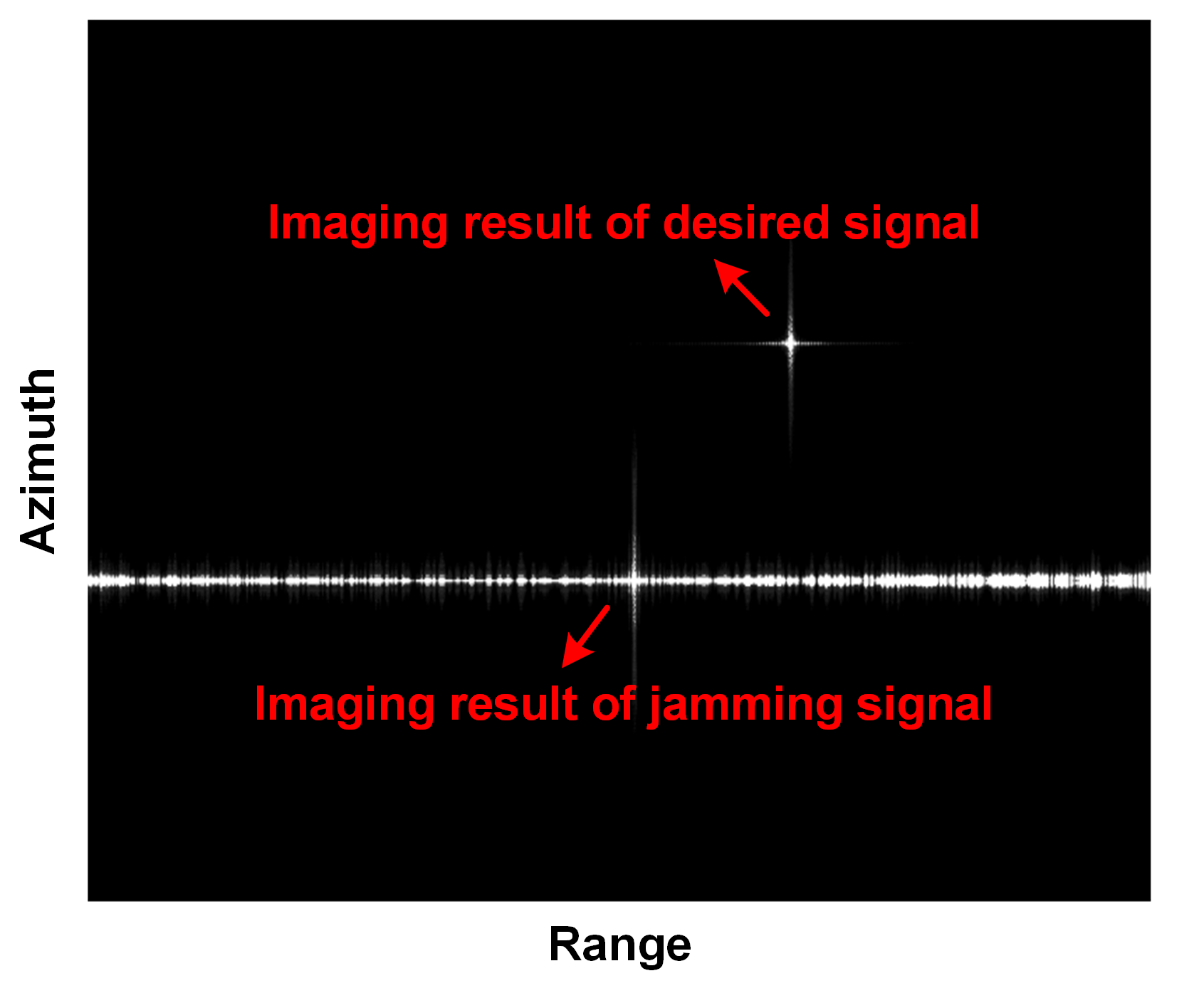
3.2. Distributed Scene Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAR | Synthetic aperture radar |
| NLFM | Nonlinear frequency modulation |
| LFM | Linear-frequency-modulated |
| Quad-Pol | Quadrature-polarimetric |
| DRFM | Digital radio frequency memory |
| PSD | Power spectral density |
| POSP | Principle of stationary phase |
| ALGA | Augmented Lagrangian genetic algorithm |
| CCE | Cross-correlation energy |
| PWL | Piecewise linear |
References
- Stimson, G.W. Introduction to Airborne Radar; SciTech Publishing, Inc.: Mendham, NJ, USA, 1998. [Google Scholar]
- Jin, G.; Deng, Y.; Wang, W.; Wang, R.; Zhang, Y.; Long, Y. Segmented Phase Code Waveforms: A Novel Radar Waveform for Spaceborne MIMO-SAR. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5764–5779. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, D.; Jin, G.; Yu, Q.; Wang, P.; Niu, S.; Cheng, Y.; Wu, D. A Robust Digital Beamforming on Receive in Elevation for Airborne MIMO SAR System. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 5233619. [Google Scholar] [CrossRef]
- Song, C.; Wu, Y.; Zhou, L.; Li, R.; Yang, J.; Liang, W.; Ding, C. A multicomponent micro-Doppler signal decomposition and parameter estimation method for target recognition. Sci. China Inf. Sci. 2019, 62, 29304. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H.C. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Boston, MA, USA, 2005; pp. 473–476. [Google Scholar]
- Jin, G.; Deng, Y.; Wang, W.; Zhang, Y.; Liang, D.; Wang, R. A Novel Spaceborne MIMO-SAR Imaging Scheme Based on Improved OFDM Waveforms. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2122–2126. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, F.; Xiang, D.; Yin, Q.; Zhou, Y. Fast task-specific region merging for SAR image segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5222316. [Google Scholar] [CrossRef]
- Yang, H.; Tao, M.; Chen, S.; Xi, F.; Liu, Z. On the Mutual Interference Between Spaceborne SARs: Modeling, Characterization, and Mitigation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8470–8485. [Google Scholar] [CrossRef]
- Yang, H.; Li, K.; Li, J.; Du, Y.; Yang, J. BSF: Block Subspace Filter for Removing Narrowband and Wideband Radio Interference Artifacts in Single-Look Complex SAR Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5211916. [Google Scholar] [CrossRef]
- Wang, R.; Wang, X.; Cheng, S.; Meng, Y.; Zhang, G.; Zhou, Y. Plasma Passive Jamming for SAR Based on the Resonant Absorption Effect. IEEE Trans. Plasma Sci. 2018, 46, 928–933. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, F.; Yin, Q.; Xiang, D.; Zhou, Y. Fast SAR image segmentation with deep task-specific superpixel sampling and soft graph convolution. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5214116. [Google Scholar] [CrossRef]
- Sjögren, T.K.; Vu, V.T.; Pettersson, M.I.; Wang, F.; Murdin, D.J.G.; Gustavsson, A.; Ulander, L.M.H. Suppression of Clutter in Multichannel SAR GMTI. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4005–4013. [Google Scholar] [CrossRef]
- Ender, J.; Berens, P.; Brenner, A.; Rossing, L.; Skupin, U. Multi-channel SAR/MTI system development at FGAN: From AER to PAMIR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 3, pp. 1697–1701. [Google Scholar] [CrossRef]
- Huang, L.; Dong, C.; Shen, Z.; Zhao, G. The Influence of Rebound Jamming on SAR GMTI. IEEE Geosci. Remote Sens. Lett. 2015, 12, 399–403. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhu, D.; Jin, G.; Zhang, J.; Niu, S.; Wang, Y. A Novel Intrapulse Repeater Mainlobe-Jamming Suppression Method With MIMO-SAR. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4507805. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, B.; Tao, M.; Bai, X.; Chen, B.; Sun, G. A Large Scene Deceptive Jamming Method for Space-Borne SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4486–4495. [Google Scholar] [CrossRef]
- Li, Z.; Xie, J.; Liu, W.; Zhang, H.; Xiang, H. Transmit Antenna Selection and Power Allocation for Joint Multi-Target Localization and Discrimination in MIMO Radar with Distributed Antennas under Deception Jamming. Remote Sens. 2022, 14, 3904. [Google Scholar] [CrossRef]
- Yang, K.; Ma, F.; Ran, D.; Ye, W.; Li, G. Fast Generation of Deceptive Jamming Signal Against Spaceborne SAR Based on Spatial Frequency Domain Interpolation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Wang, P.; Long, Y.; Zhang, Z.M.; Zhang, Y. An Advanced Nonlinear Frequency Modulation Waveform for Radar Imaging With Low Sidelobe. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6155–6168. [Google Scholar] [CrossRef]
- Fowle, E. The design of FM pulse compression signals. IEEE Trans. Inf. Theory 1964, 10, 61–67. [Google Scholar] [CrossRef]
- de Buda, R. Stationary phase approximations of FM spectra. IEEE Trans. Inf. Theory 1966, 12, 305–311. [Google Scholar] [CrossRef]
- Vizitiu, I.; Anton, L.; Popescu, F.; Iubu, G. The synthesis of some NLFM laws using the stationary phase principle. In Proceedings of the 2012 10th International Symposium on Electronics and Telecommunications, Kuala Lumpur, Malaysia, 24–27 June 2012; pp. 377–380. [Google Scholar] [CrossRef]
- Kurdzo, J.M.; Cheong, B.L.; Palmer, R.D.; Zhang, G. Optimized NLFM pulse compression waveforms for high-sensitivity radar observations. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Luna, F.; Zavala, G.R.; Nebro, A.J.; Durillo, J.J.; Coello, C.A.C. Distributed Multi-Objective Metaheuristics for Real-World Structural Optimization Problems. Comput. J. 2016, 59, 777–792. [Google Scholar] [CrossRef]
- Saeedi, J.; Faez, K. Synthetic aperture radar imaging using nonlinear frequency modulation signal. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 99–110. [Google Scholar] [CrossRef]
- Jin, G.; Liu, K.; Deng, Y.; Sha, Y.; Wang, R.; Liu, D.; Wang, W.; Long, Y.; Zhang, Y. Nonlinear Frequency Modulation Signal Generator in LT-1. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1570–1574. [Google Scholar] [CrossRef]
- Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An Advanced Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1735–1746. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Zhang, Y.; Long, Y.; Liang, D. Mitigating Range Ambiguities With Advanced Nonlinear Frequency Modulation Waveform. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1230–1234. [Google Scholar] [CrossRef]
- Bordoni, F.; Younis, M.; Krieger, G. Ambiguity Suppression by Azimuth Phase Coding in Multichannel SAR Systems. IEEE Trans. Geosci. Remote Sens. 2012, 50, 617–629. [Google Scholar] [CrossRef]
- Jin, G.; Zhu, D.; Yan, H.; Mao, X.; Deng, Y.; Wang, W.; Wang, R. New Insights Into SAR Alternate Transmitting Mode Based on Waveform Diversity. IEEE Trans. Geosci. Remote Sens. 2021, 1, 5209209. [Google Scholar] [CrossRef]
- Jin, G.; Aubry, A.; De Maio, A.; Wang, R.; Wang, W. Quasi-Orthogonal Waveforms for Ambiguity Suppression in Spaceborne Quad-Pol SAR. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 5204617. [Google Scholar] [CrossRef]
- Boersma, J. Computation of Fresnel integrals. Math. Comput. 1960, 14, 380. [Google Scholar] [CrossRef]
- Ugray, Z.; Lasdon, L.; Plummer, J.; Glover, F.; Kelly, J.; Martí, R. Scatter search and local NLP solvers: A multistart framework for global optimization. INFORMS J. Comput. 2007, 19, 328–340. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, D.; Jin, G.; Niu, S.; Wang, X.; Cheng, Y.; Wu, D. Improved DBF-MIMO-SAR Waveform Transmission Scheme for Reducing the Cost of DOF in the Elevation. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–15. [Google Scholar] [CrossRef]

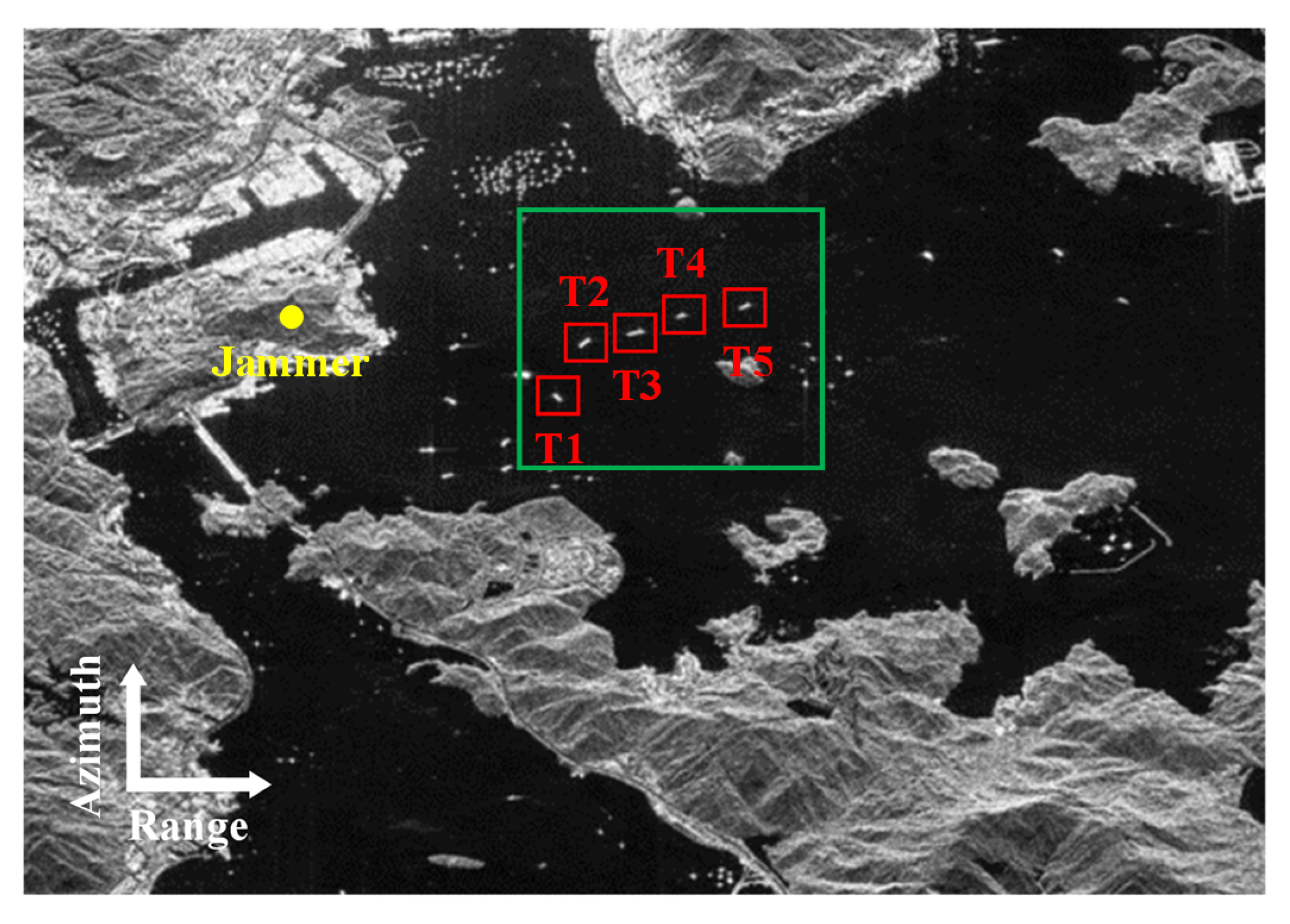


| Parameters | Value |
|---|---|
| Orbit height | 607 Km |
| Center frequency | 1.26 GHz |
| SAR pulse width | 80 s |
| Bandwidth | 60 MHz |
| Sampling rate | 72 MHz |
| PRF | 3320 Hz |
| Antenna type | Planar |
| Antenna length in azimuth | 10 |
| Antenna length in elevation | 5 |
| Look angle | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Wang, Y.; Jin, G.; Wang, Y.; Dong, Q.; Wang, B.; Zhou, L.; Lu, P.; Wu, Y. A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes. Remote Sens. 2022, 14, 5370. https://doi.org/10.3390/rs14215370
Song C, Wang Y, Jin G, Wang Y, Dong Q, Wang B, Zhou L, Lu P, Wu Y. A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes. Remote Sensing. 2022; 14(21):5370. https://doi.org/10.3390/rs14215370
Chicago/Turabian StyleSong, Chen, Yu Wang, Guodong Jin, Yu Wang, Qinghai Dong, Bingnan Wang, Liangjiang Zhou, Pingping Lu, and Yirong Wu. 2022. "A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes" Remote Sensing 14, no. 21: 5370. https://doi.org/10.3390/rs14215370
APA StyleSong, C., Wang, Y., Jin, G., Wang, Y., Dong, Q., Wang, B., Zhou, L., Lu, P., & Wu, Y. (2022). A Novel Jamming Method against SAR Using Nonlinear Frequency Modulation Waveform with Very High Sidelobes. Remote Sensing, 14(21), 5370. https://doi.org/10.3390/rs14215370









