Figure 1.
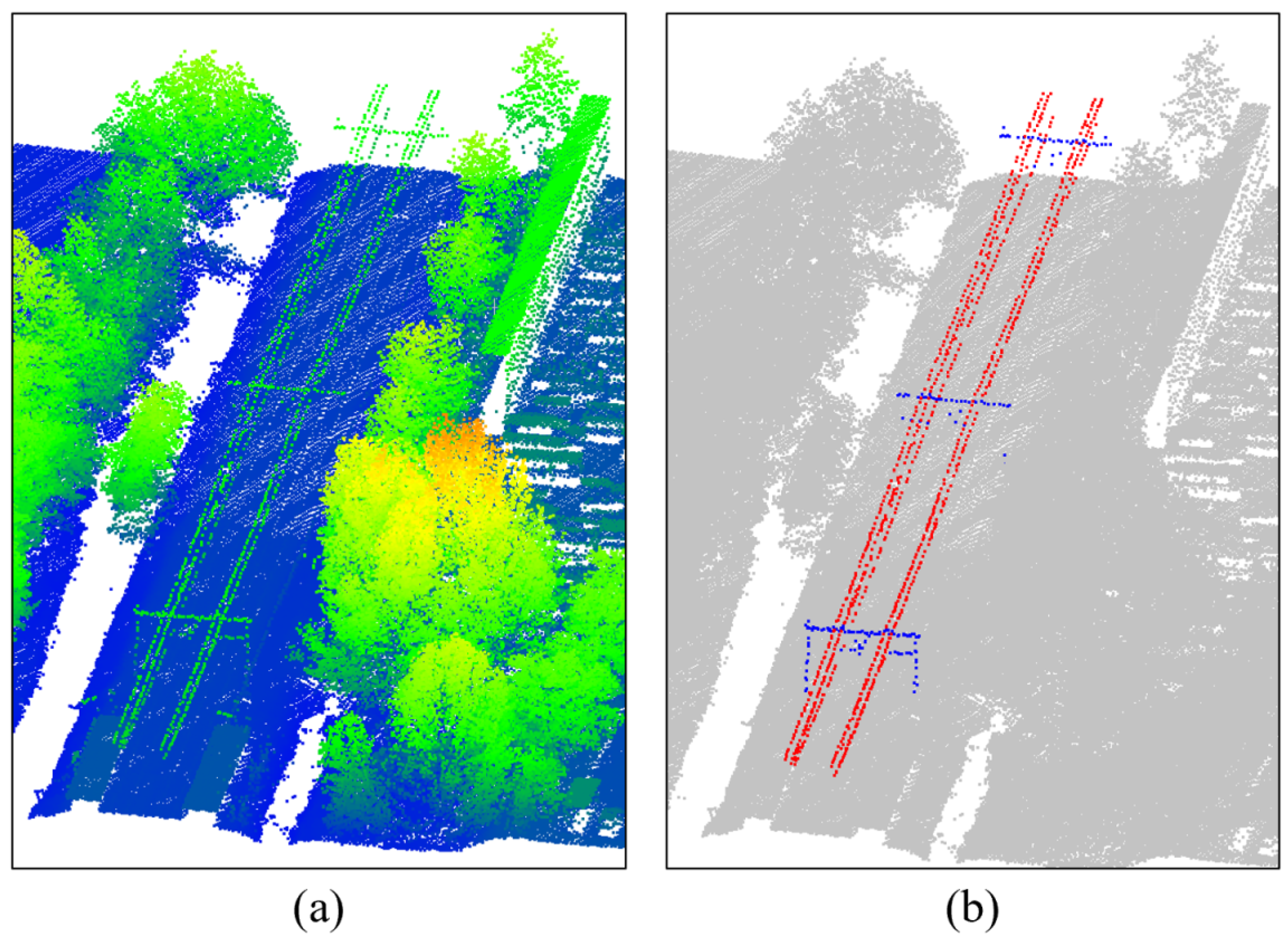
An applicable scenario of the proposed methodology. (a) point cloud data of a railway scenario (The points are colorized by height from red to blue); (b) overhead wires are automatically segmented and reconstructed by the proposed method.
Figure 1.
An applicable scenario of the proposed methodology. (a) point cloud data of a railway scenario (The points are colorized by height from red to blue); (b) overhead wires are automatically segmented and reconstructed by the proposed method.
Figure 2.
The overall procedure of the proposed method. First, raw data are preprocessed to obtain training data. Then, training data are fed into the proposed model for wire segmentation. Consecutively, the segmentation results are used for wire reconstruction.
Figure 2.
The overall procedure of the proposed method. First, raw data are preprocessed to obtain training data. Then, training data are fed into the proposed model for wire segmentation. Consecutively, the segmentation results are used for wire reconstruction.
Figure 3.
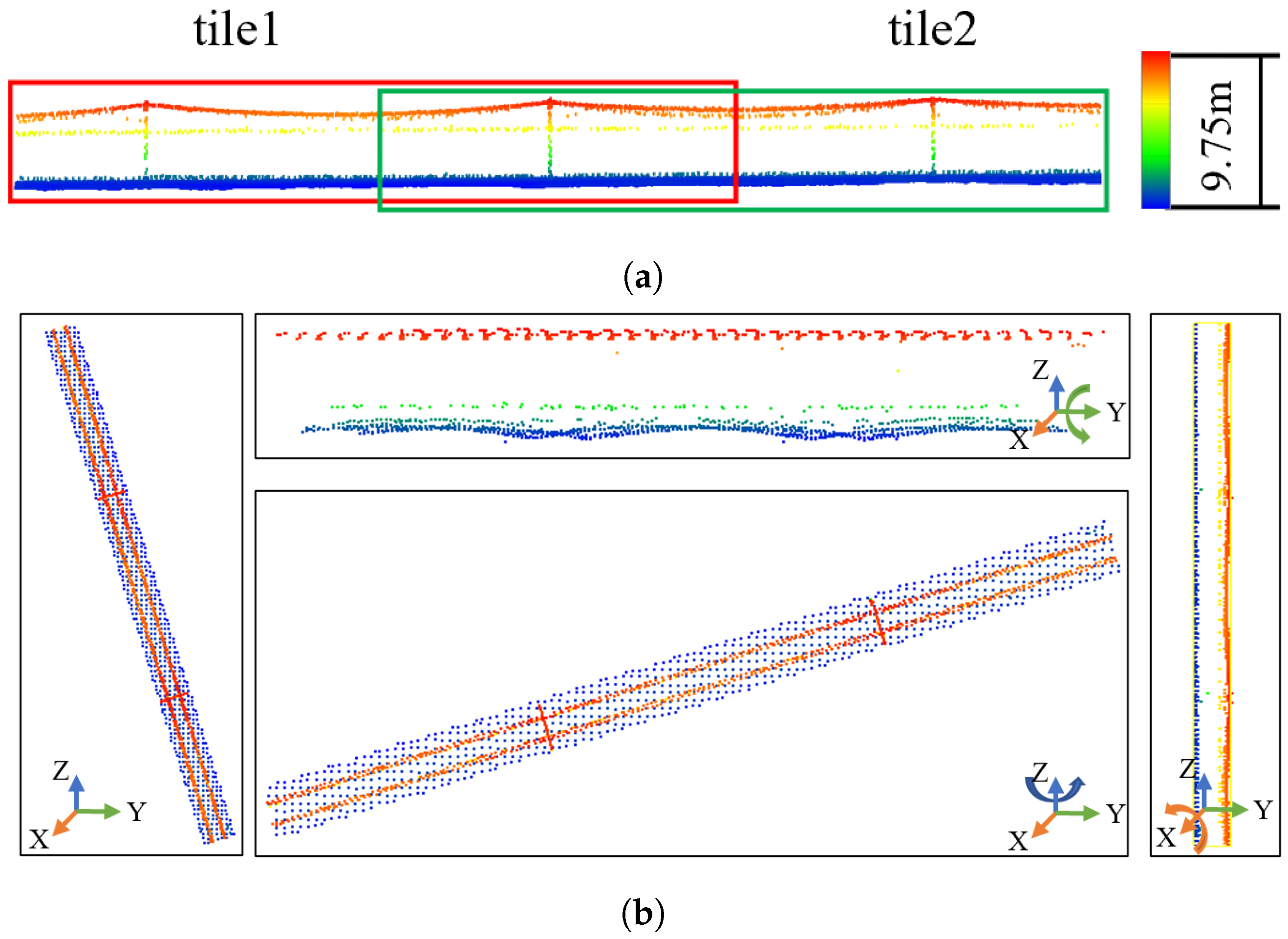
Data augmentation. (a) training data re-tiling; (b) rotation amplification. The four images are the visualization of the original tile and the rotated tile on the XOY plane.
Figure 3.
Data augmentation. (a) training data re-tiling; (b) rotation amplification. The four images are the visualization of the original tile and the rotated tile on the XOY plane.
Figure 4.
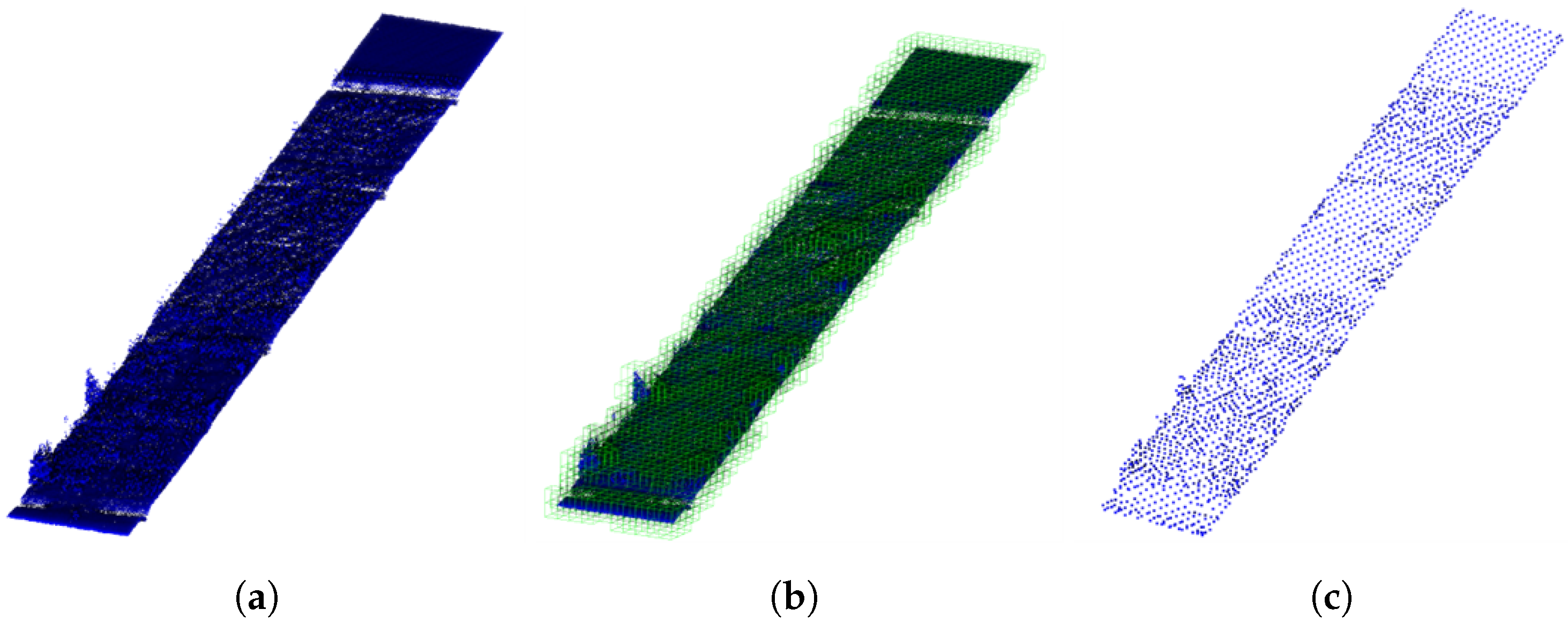
Ground point downsampling. (a) original ground point cloud; (b) an Octree space division of the ground points; (c) downsampling the ground points.
Figure 4.
Ground point downsampling. (a) original ground point cloud; (b) an Octree space division of the ground points; (c) downsampling the ground points.
Figure 5.
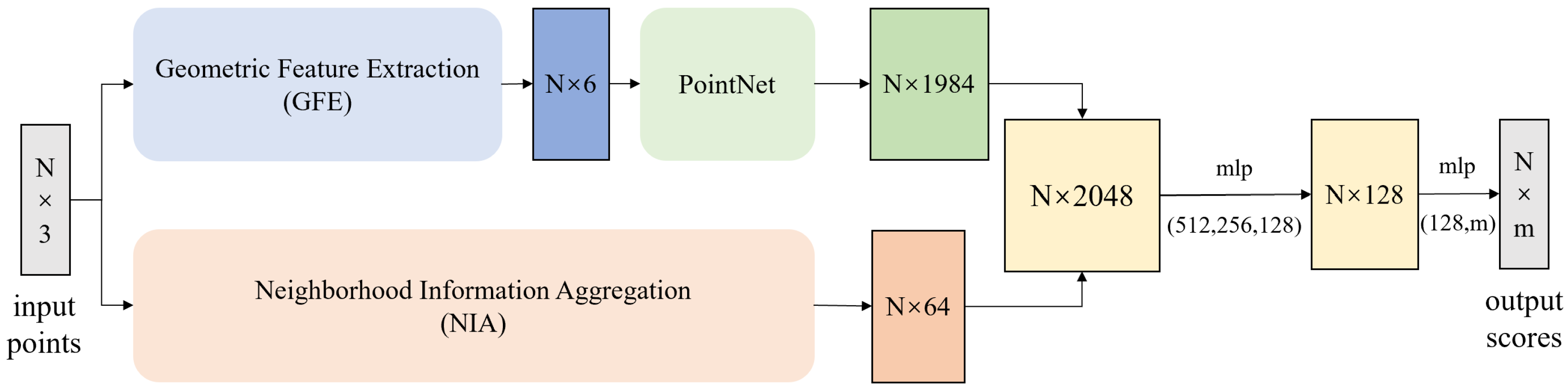
Flowchart of the presented model in this work. The GFE module extracts local geometric features of point cloud. The NIA module aggregates neighborhood feature information. The PointNet module outputs each class score through MLP.
Figure 5.
Flowchart of the presented model in this work. The GFE module extracts local geometric features of point cloud. The NIA module aggregates neighborhood feature information. The PointNet module outputs each class score through MLP.
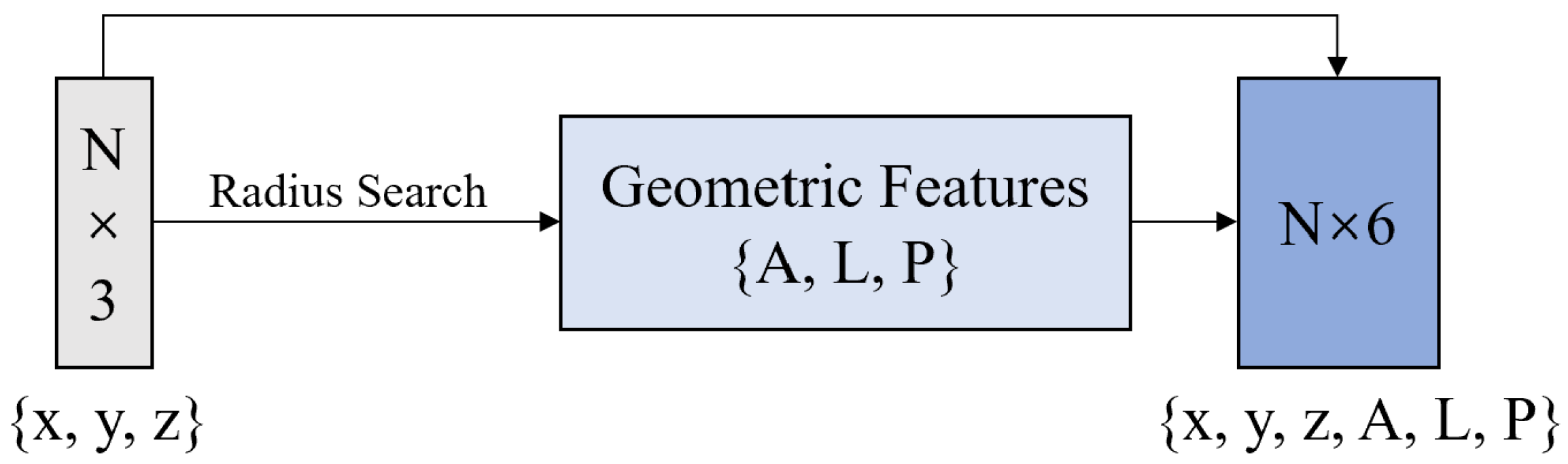
Figure 6.
Network structure of the GFE module.
Figure 6.
Network structure of the GFE module.
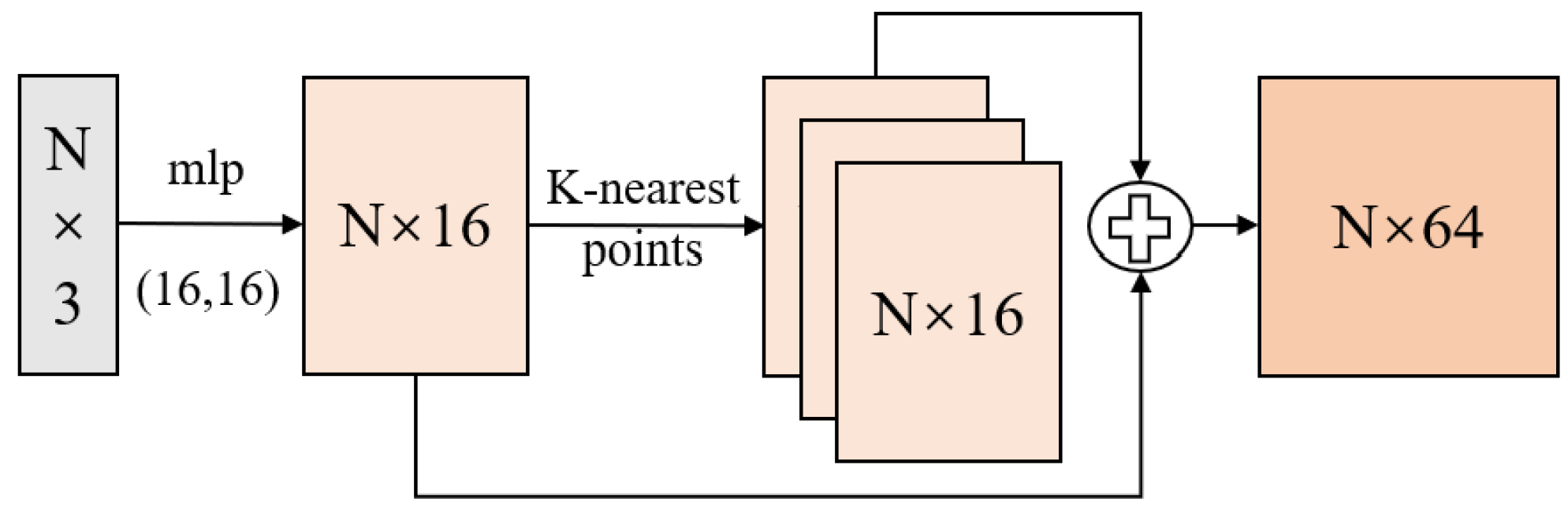
Figure 7.
Network structure of the NIA module.
Figure 7.
Network structure of the NIA module.
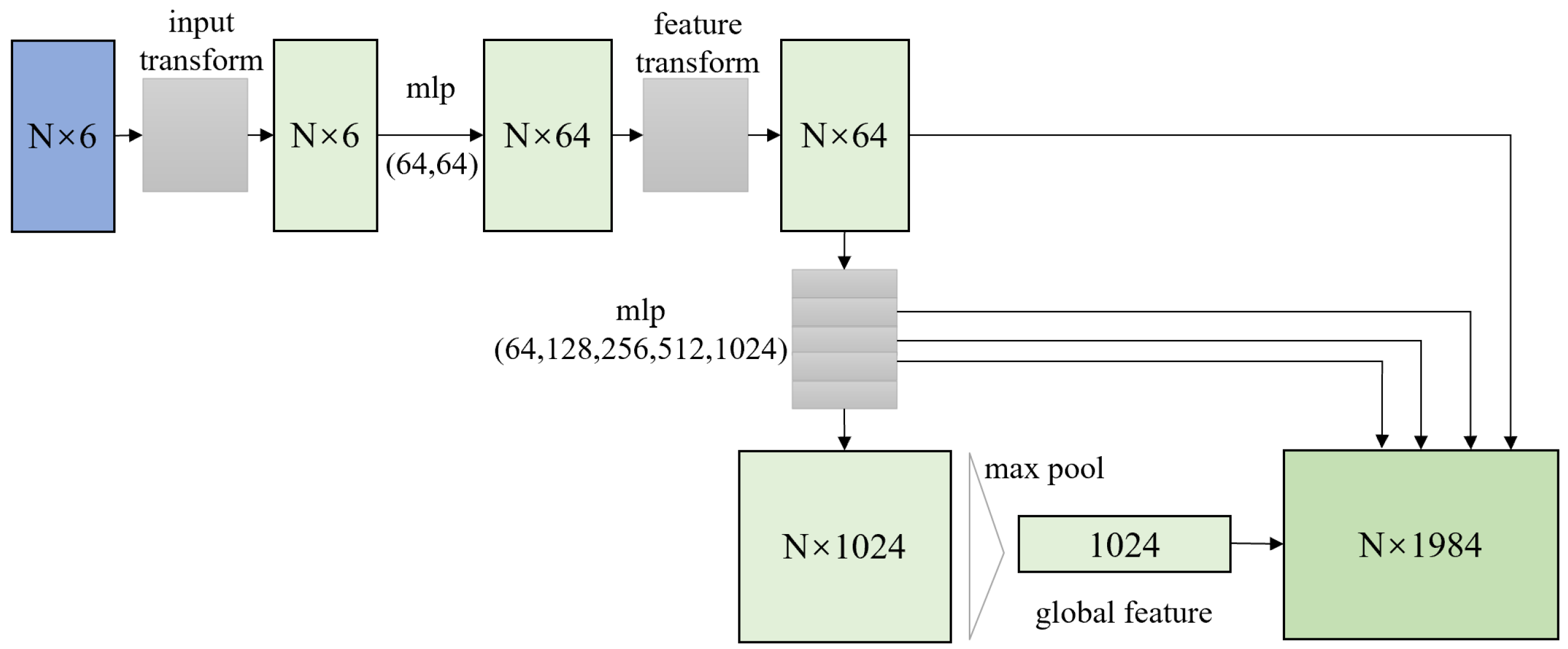
Figure 8.
Network structure of the PointNet module.
Figure 8.
Network structure of the PointNet module.
Figure 9.
Multi-layer perception (MLP) structure.
Figure 9.
Multi-layer perception (MLP) structure.
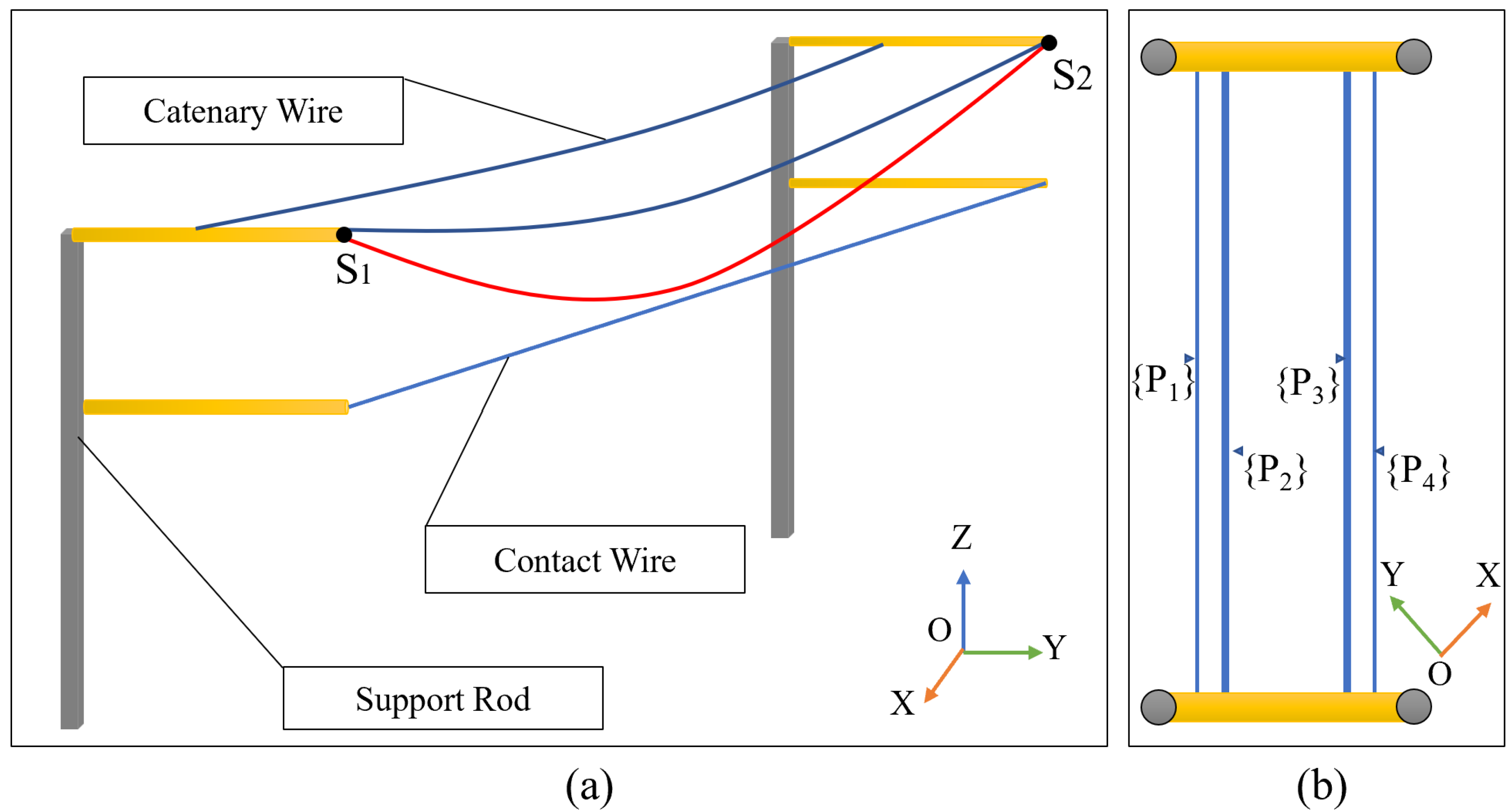
Figure 10.
Schematic diagram of the structure of the railway overhead wires (a) side view; (b) top view.
Figure 10.
Schematic diagram of the structure of the railway overhead wires (a) side view; (b) top view.
Figure 11.
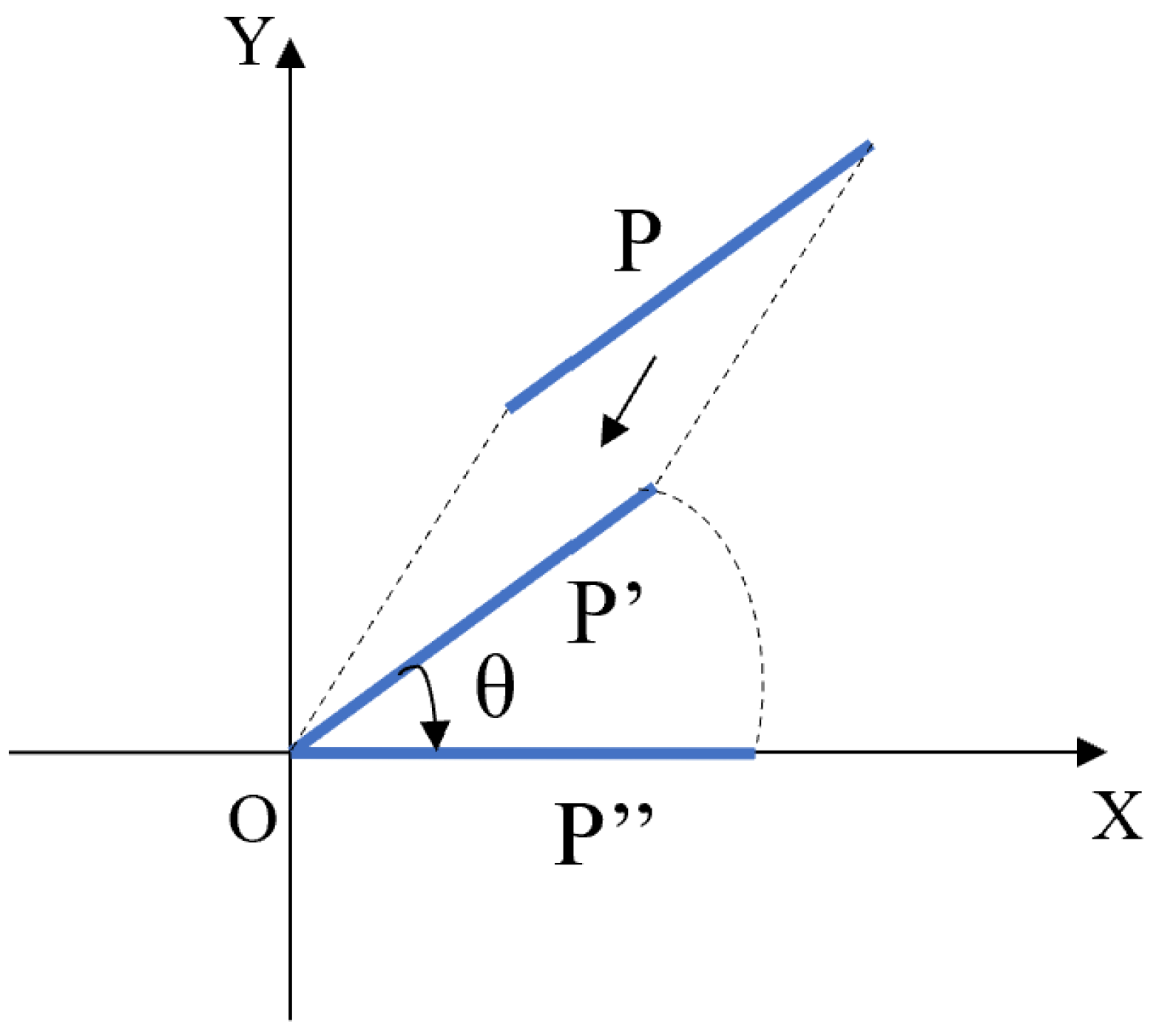
Transformation procedures of the point set in the XOY plane.
Figure 11.
Transformation procedures of the point set in the XOY plane.
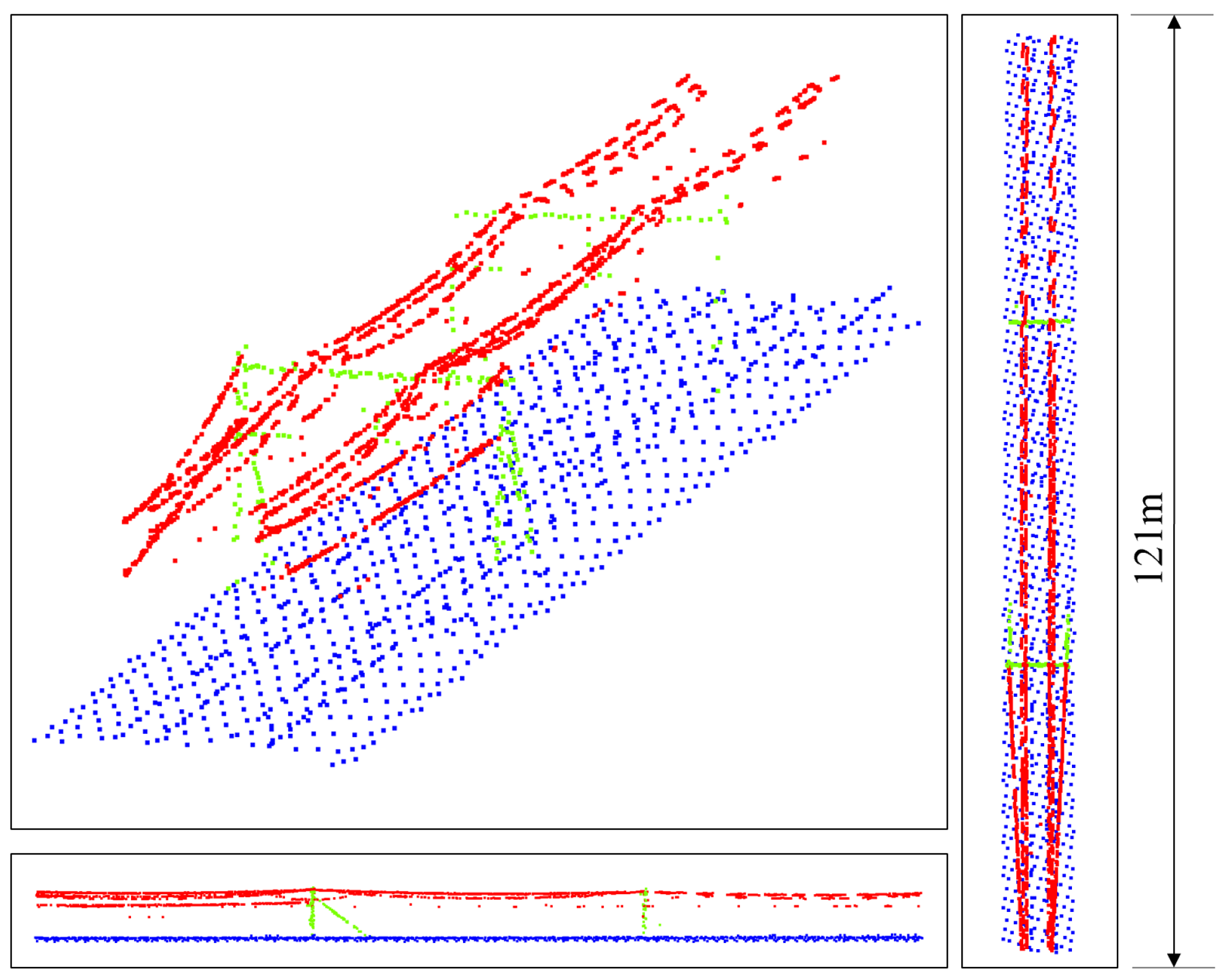
Figure 12.
The railway dataset used by the proposed method.
Figure 12.
The railway dataset used by the proposed method.
Figure 13.
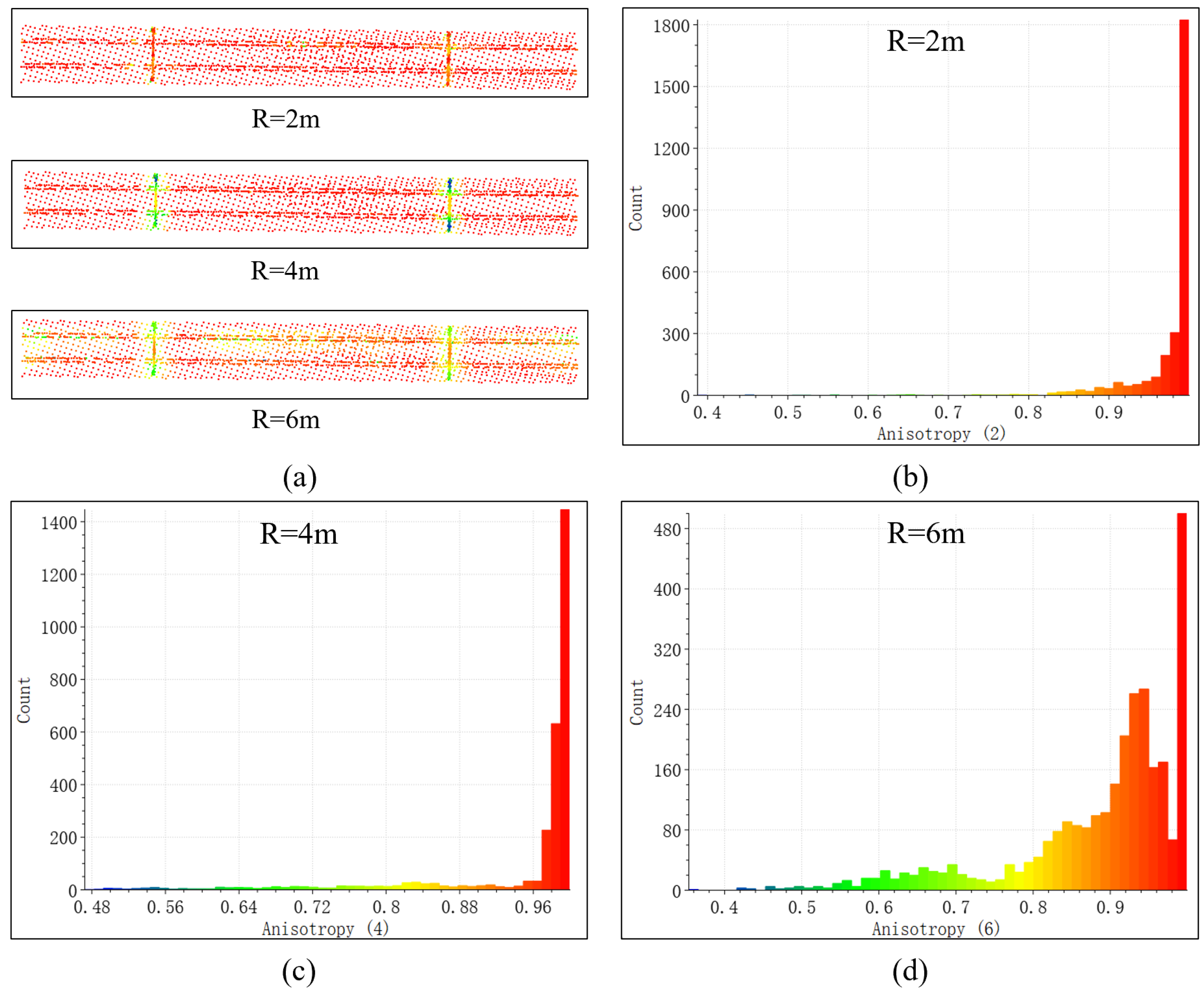
The anisotropy value with different neighbourhood radius. (a) anisotropy values with radius 2, 4, and 6 m; (b–d) are the distributions of anisotropy value with the radius, respectively.
Figure 13.
The anisotropy value with different neighbourhood radius. (a) anisotropy values with radius 2, 4, and 6 m; (b–d) are the distributions of anisotropy value with the radius, respectively.
Figure 14.
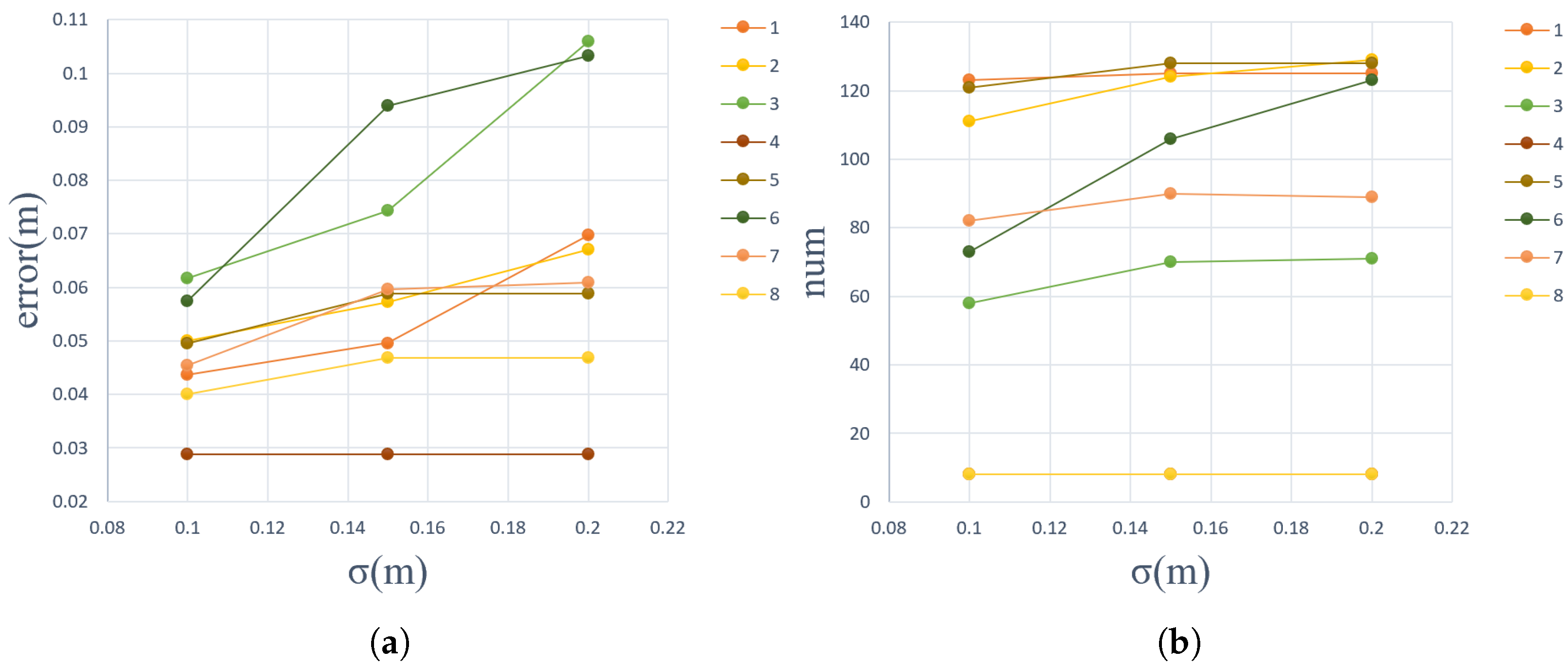
The influence of the choice of on the fitting effect. (a) the average fitting error of a single wire under different ; (b) the number of points fitted by a single wire under different (1–8 represent 8 wires in a span respectively).
Figure 14.
The influence of the choice of on the fitting effect. (a) the average fitting error of a single wire under different ; (b) the number of points fitted by a single wire under different (1–8 represent 8 wires in a span respectively).
Figure 15.
Training data from different perspectives after preprocessing (red, green and blue points represent wire, pylon, and ground points, respectively).
Figure 15.
Training data from different perspectives after preprocessing (red, green and blue points represent wire, pylon, and ground points, respectively).
Figure 16.
The trend of the training and test sets loss/accuracy during the model training.
Figure 16.
The trend of the training and test sets loss/accuracy during the model training.
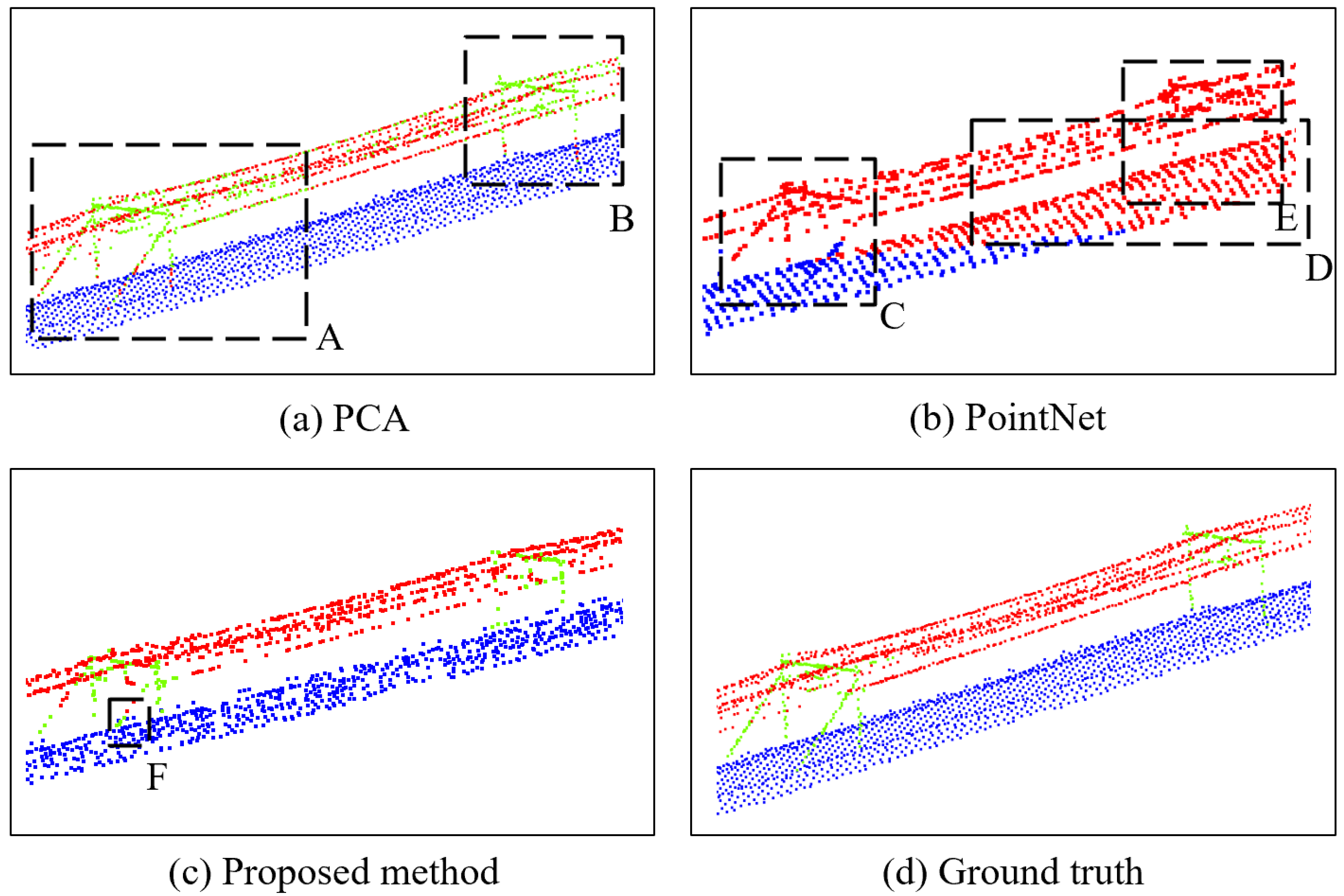
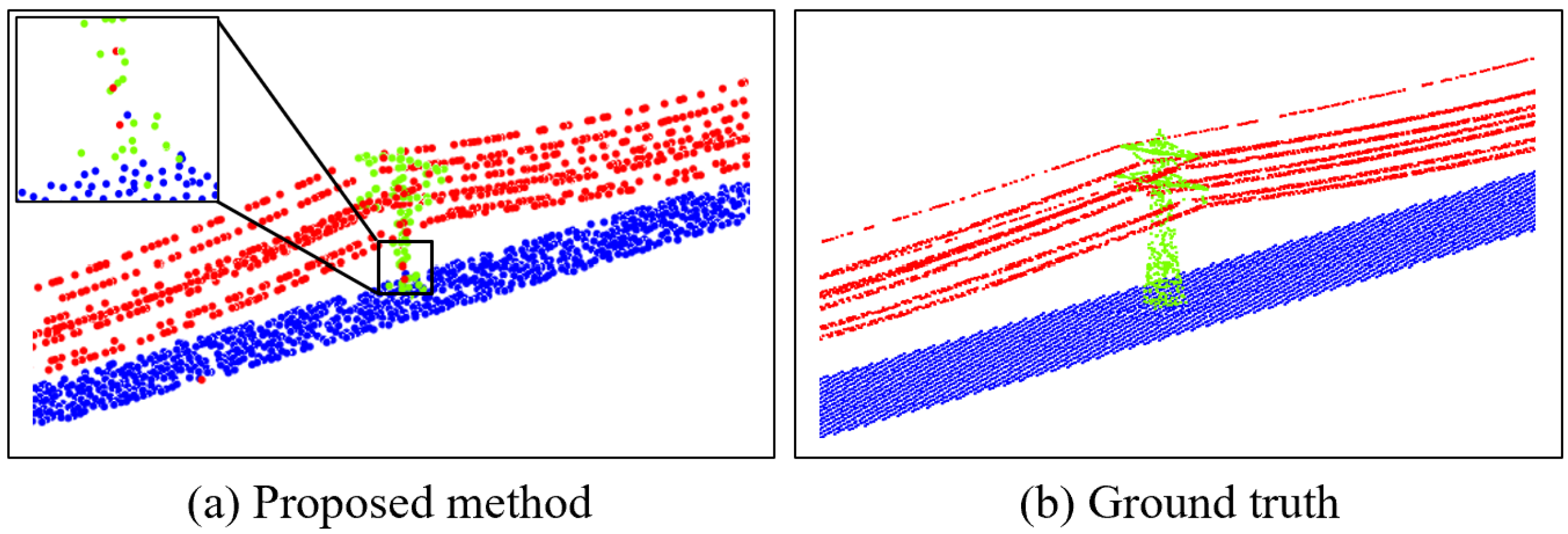
Figure 17.
The results of different wire segmentation methods. The wire, pylon, and ground are colored with red, green, and blue, respectively. The black dotted frame indicates points that are classified with error.
Figure 17.
The results of different wire segmentation methods. The wire, pylon, and ground are colored with red, green, and blue, respectively. The black dotted frame indicates points that are classified with error.
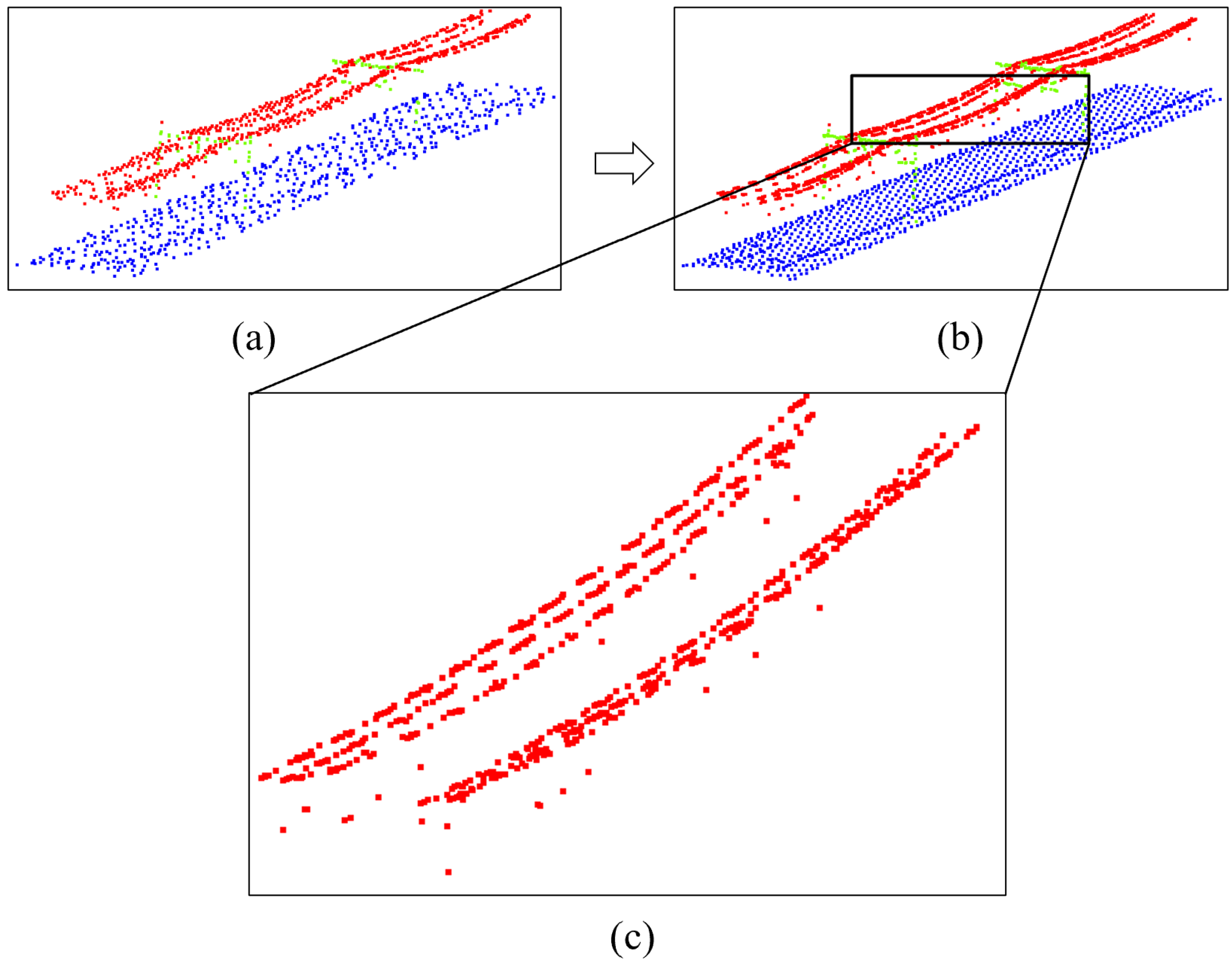
Figure 18.
Raw wire reverse mapping and span extraction. (a) wire point cloud after segmentation by the proposed model; (b) wire segmentation results of the original dataset after reverse mapping; (c) span extraction results.
Figure 18.
Raw wire reverse mapping and span extraction. (a) wire point cloud after segmentation by the proposed model; (b) wire segmentation results of the original dataset after reverse mapping; (c) span extraction results.
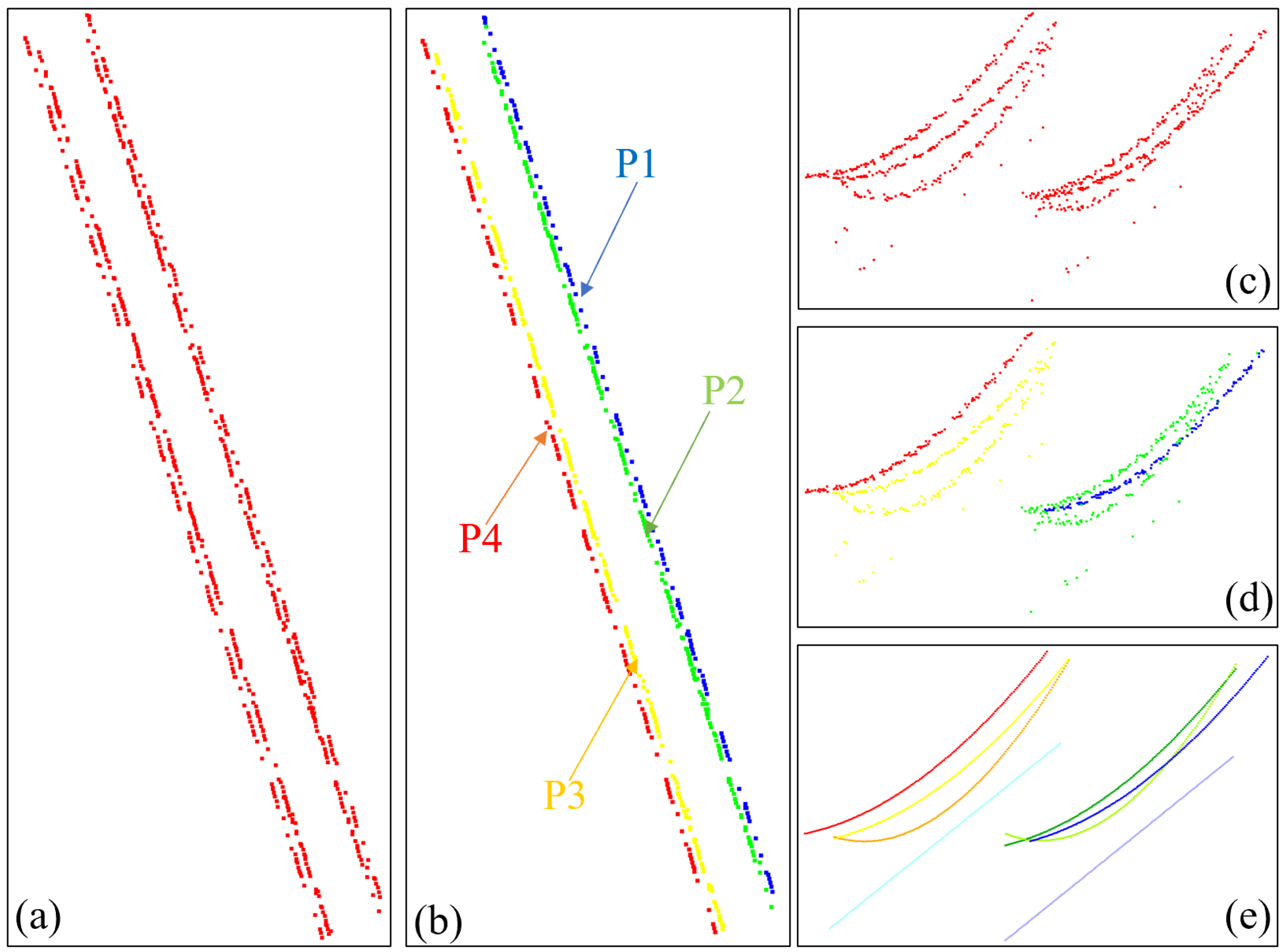
Figure 19.
Wire individualization and reconstruction. (a) wire points distribution on the XOY plane; (b) wire individualization based on the XOY plane; (c) side view of (a); (d) side view of (b); (e) wire reconstruction results.
Figure 19.
Wire individualization and reconstruction. (a) wire points distribution on the XOY plane; (b) wire individualization based on the XOY plane; (c) side view of (a); (d) side view of (b); (e) wire reconstruction results.
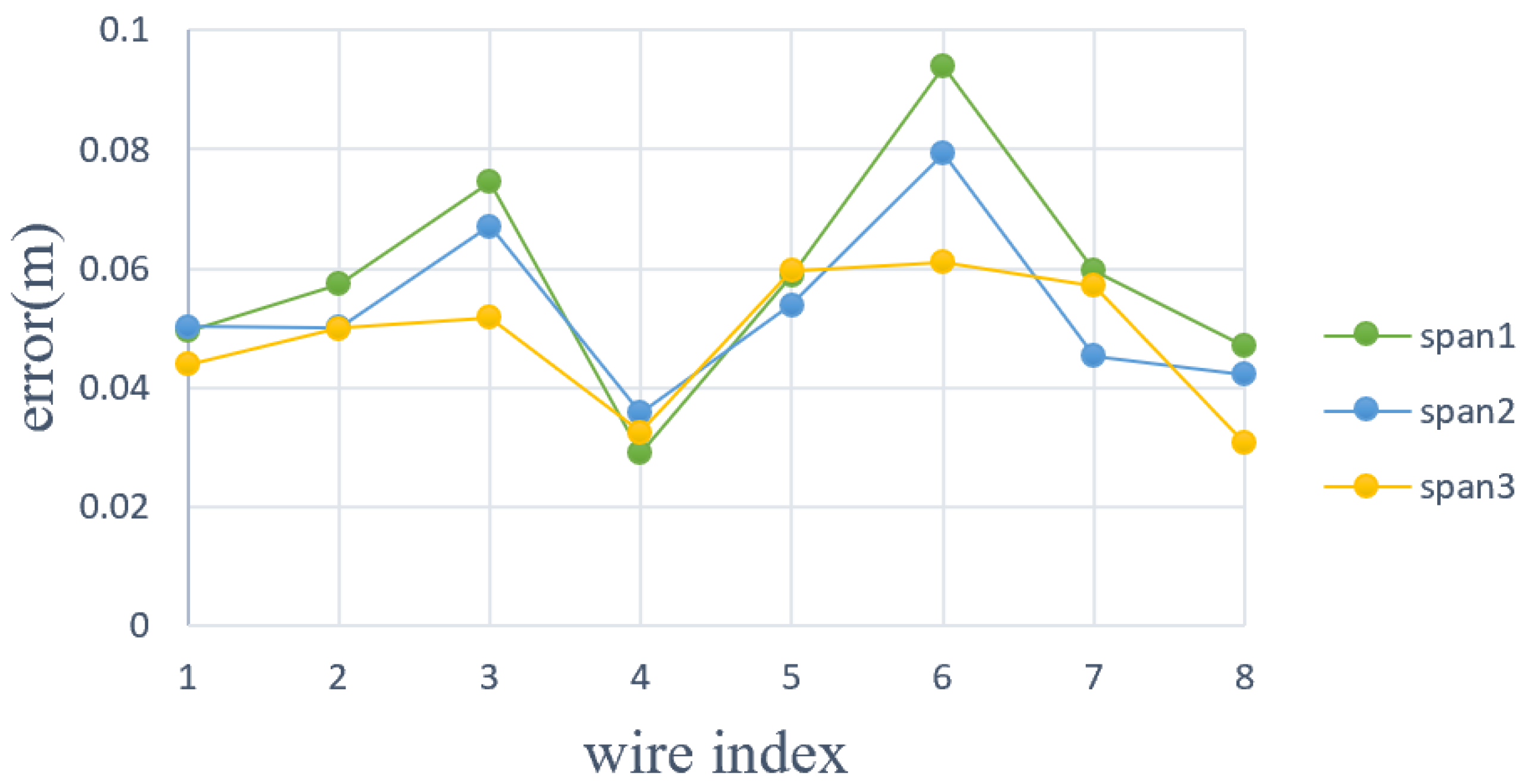
Figure 20.
Fitting error for eight wires at each span.
Figure 20.
Fitting error for eight wires at each span.
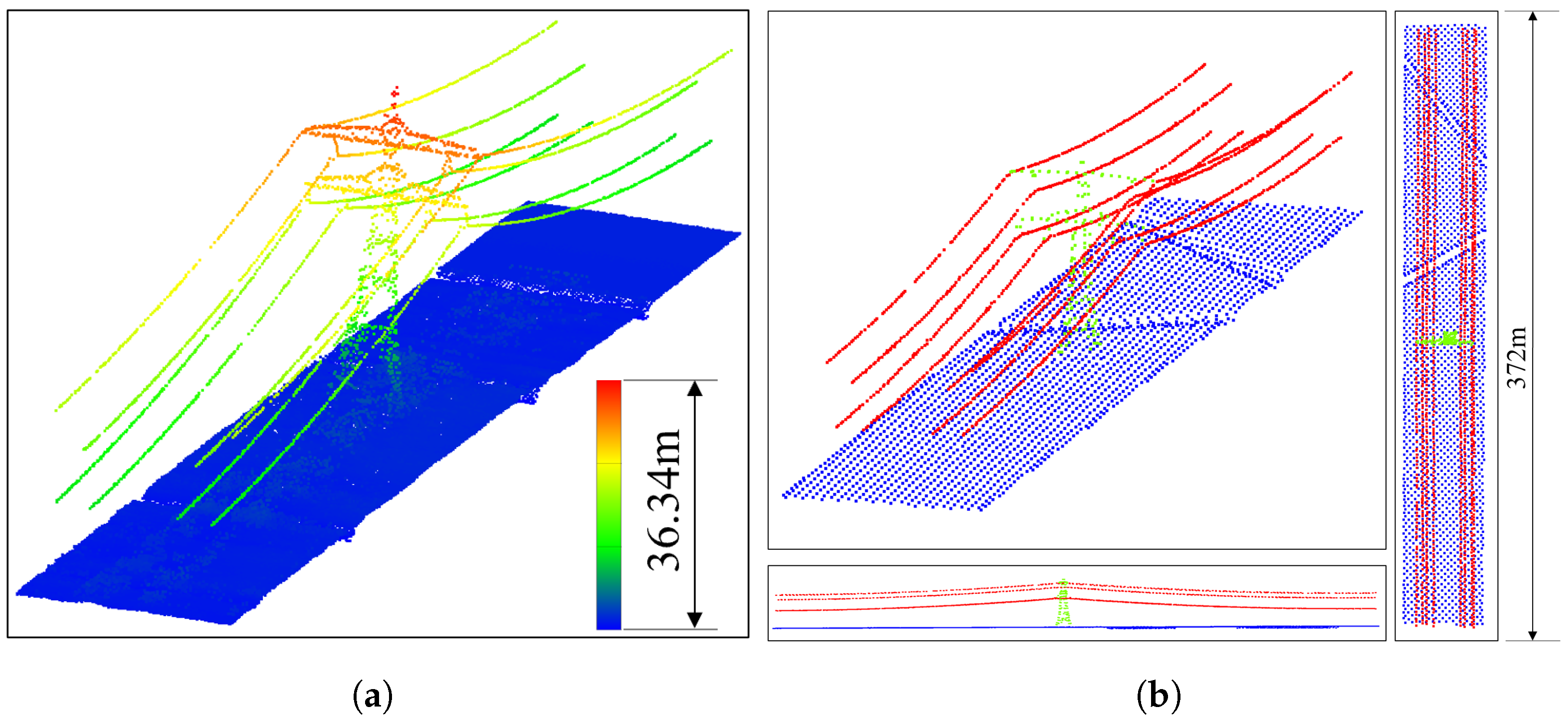
Figure 21.
(a) High-voltage powerline scenario; (b) pre-processing result.
Figure 21.
(a) High-voltage powerline scenario; (b) pre-processing result.
Figure 22.
The results of proposed powerline segmentation methods. The powerline, pylon, and ground are colored with red, green, and blue, respectively. The black dotted frame indicates points that are classified by error.
Figure 22.
The results of proposed powerline segmentation methods. The powerline, pylon, and ground are colored with red, green, and blue, respectively. The black dotted frame indicates points that are classified by error.
Table 1.
Summary of powerline extraction methods.
Table 1.
Summary of powerline extraction methods.
| Methods | Data | Characteristic |
|---|
| Model fitting based methods | Melzer and Briese [25] | ALS | Iteratively bottom-up HT strategy |
| Jing et al. [26] | ALS | LSM-Based line fitting |
| Sohn et al. [27] | ALS | Integrated HT, eigenvectors, and point density |
| Yadav and Chousalkar [28] | MLS | HT-based powerline extraction |
| Lehtomäki et al. [29] | MLS | Voxelization, PCA and RANSAC |
| Clustering based methods | Cheng et al. [33] | MLS | Bottom-up clustering |
| Guan et al. [34] | MLS | Integrates height filters, spatial density filters, size and shape filters |
| Liang et al. [35] | ALS | Euclidean distance-based clustering |
| Machine Learning based methods | Guo et al. [36] | ALS | Joint-Boost classification using 26 features |
| Wang et al. [37] | ALS | SVM-based extraction |
| Peng et al. [38] | ALS | RF-based classification |
| Li et al. [23] | ALS | Graph convolution-based identification |
| Proposed method | ALS | Deep learning based method for extraction and RANSAC based wire fitting |
Table 2.
Descriptions of the dataset.
Table 2.
Descriptions of the dataset.
| Parameters | Value |
|---|
| Length(km) | 7 |
| Number of points (million) | 0.18 |
| Density () | 15 |
| Number of pylons | 106 |
Table 3.
Specifications of the experimental environment.
Table 3.
Specifications of the experimental environment.
| Experiment Environment | Configurations |
|---|
| Operating System | Ubuntu20.04 |
| CPU | Inter®Xeon(R)Silver 4210R CPU@2.40GHZ×40 |
| GPU | NVIDIA Corporation GV100[TITAN V] |
| RAM | 64GB |
| VRAM | 12GB |
| Deep Learning Platform | PyTorch |
| Python | Python3.6 |
Table 4.
Parameter settings.
Table 4.
Parameter settings.
| Part | Parameter | Value |
|---|
| Pre-processing | segment standard (contain pylon numbers) | 2 |
| rotation amplification | 3 times |
| training data | 392 tiles |
| Segmentation | moment estimation | 0.9 |
| learning rate | 0.001 |
| batch size | 40 |
| epoch | 200 |
| R | 4 m |
| k | 3 |
| Reconstruction | | 0.15 m |
| t | 50 times |
Table 5.
Comparison of the number of various targets in the original data and after downsampling.
Table 5.
Comparison of the number of various targets in the original data and after downsampling.
| Dataset | Raw Point Clouds | Downsampled Results |
|---|
| Line | Pylon | Ground | Total | Line | Pylon | Ground | Total |
|---|
| 1 | 564 | 154 | 14,655 | 15,373 | 564 | 154 | 2204 | 2922 |
| 2 | 1465 | 637 | 28,021 | 30,123 | 1465 | 637 | 4543 | 6645 |
| 3 | 921 | 419 | 18,745 | 20,085 | 921 | 419 | 1395 | 2735 |
Table 6.
Comparison of the MIoU and ACC of the three different wire segmentation methods.
Table 6.
Comparison of the MIoU and ACC of the three different wire segmentation methods.
| Dataset | PCA | PointNet | Proposed Method |
|---|
| MIoU | ACC | MIoU | ACC | MIoU | ACC |
|---|
| Railway | 0.6029 | 0.8438 | 0.4460 | 0.7394 | 0.8265 | 0.9689 |
Table 7.
The performance of different modules proposed in this work in aspects of MIoU and ACC.
Table 7.
The performance of different modules proposed in this work in aspects of MIoU and ACC.
| Dataset | PointNet | PointNet+GFE | PointNet+GFE+NIA | PointNet(C)+GFE+NIA |
|---|
| MIoU | ACC | MIoU | ACC | MIoU | ACC | MIoU | ACC |
|---|
| Railway | 0.4460 | 0.7394 | 0.8012 | 0.9613 | 0.8123 | 0.9653 | 0.8265 | 0.9689 |
Table 8.
Fitting rate and fitting error of the railway overhead wires at each span.
Table 8.
Fitting rate and fitting error of the railway overhead wires at each span.
| Data Set | Raw Points | Fit Points | Fitting Rate (%) | Fitting Error (m) |
|---|
| span1 | 693 | 667 | 96.24 | 0.058 |
| span2 | 705 | 681 | 96.59 | 0.052 |
| span3 | 658 | 632 | 96.04 | 0.048 |
| average | 685 | 660 | 96.31 | 0.053 |
Table 9.
MIoU and ACC of the proposed method in a high-voltage powerline scenario.
Table 9.
MIoU and ACC of the proposed method in a high-voltage powerline scenario.
| Dataset | Proposed Method |
|---|
| MIoU | ACC |
|---|
| High-voltage | 0.8994 | 0.9852 |