Understanding Water Level Changes in the Great Lakes by an ICA-Based Merging of Multi-Mission Altimetry Measurements
Abstract
1. Introduction
2. Data and Methods
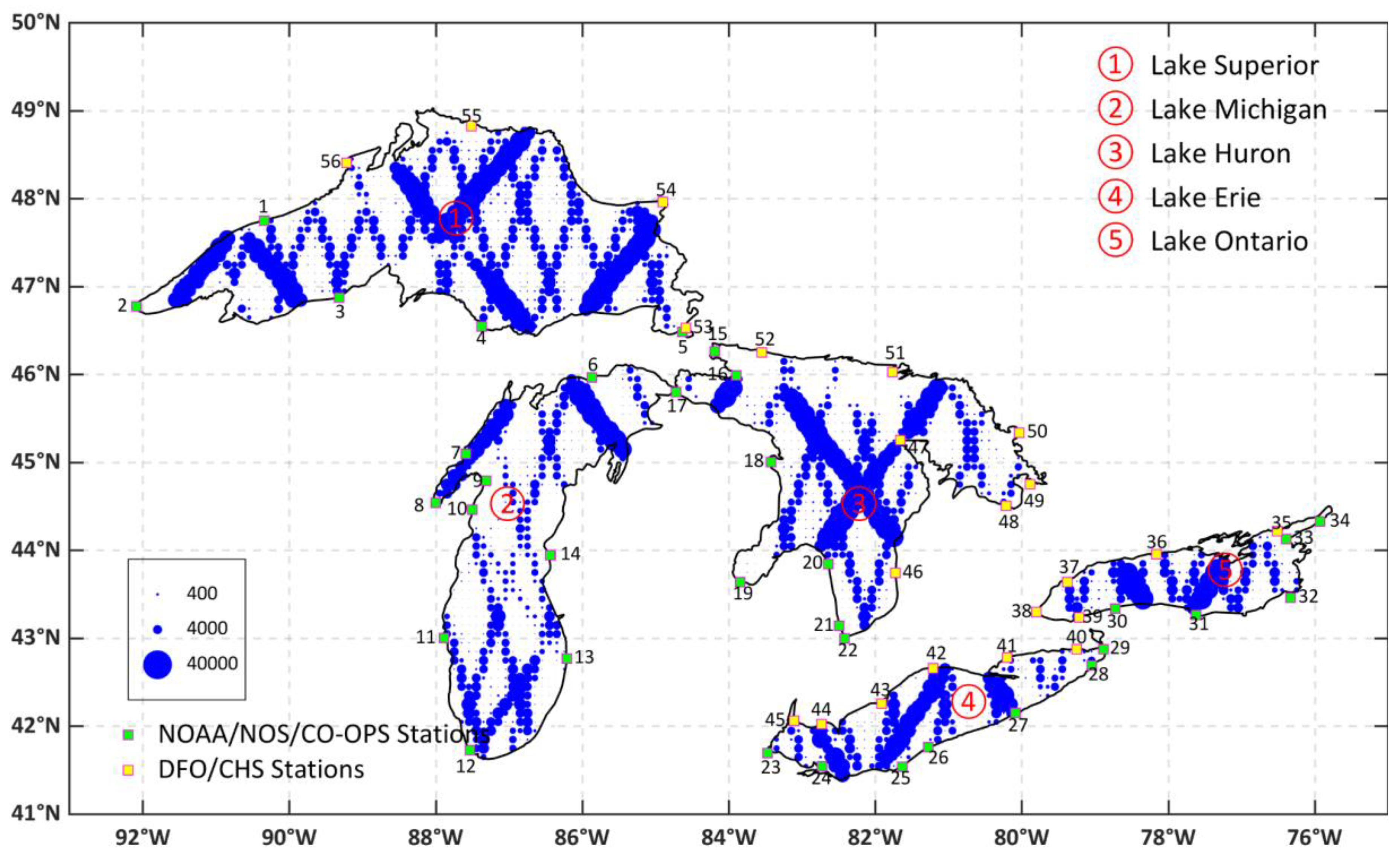
2.1. Study Area
2.2. Radar Altimetry Data
2.3. Water Level Stations
2.4. Glacial Isostatic Adjustment
2.5. Multivariate ENSO Index
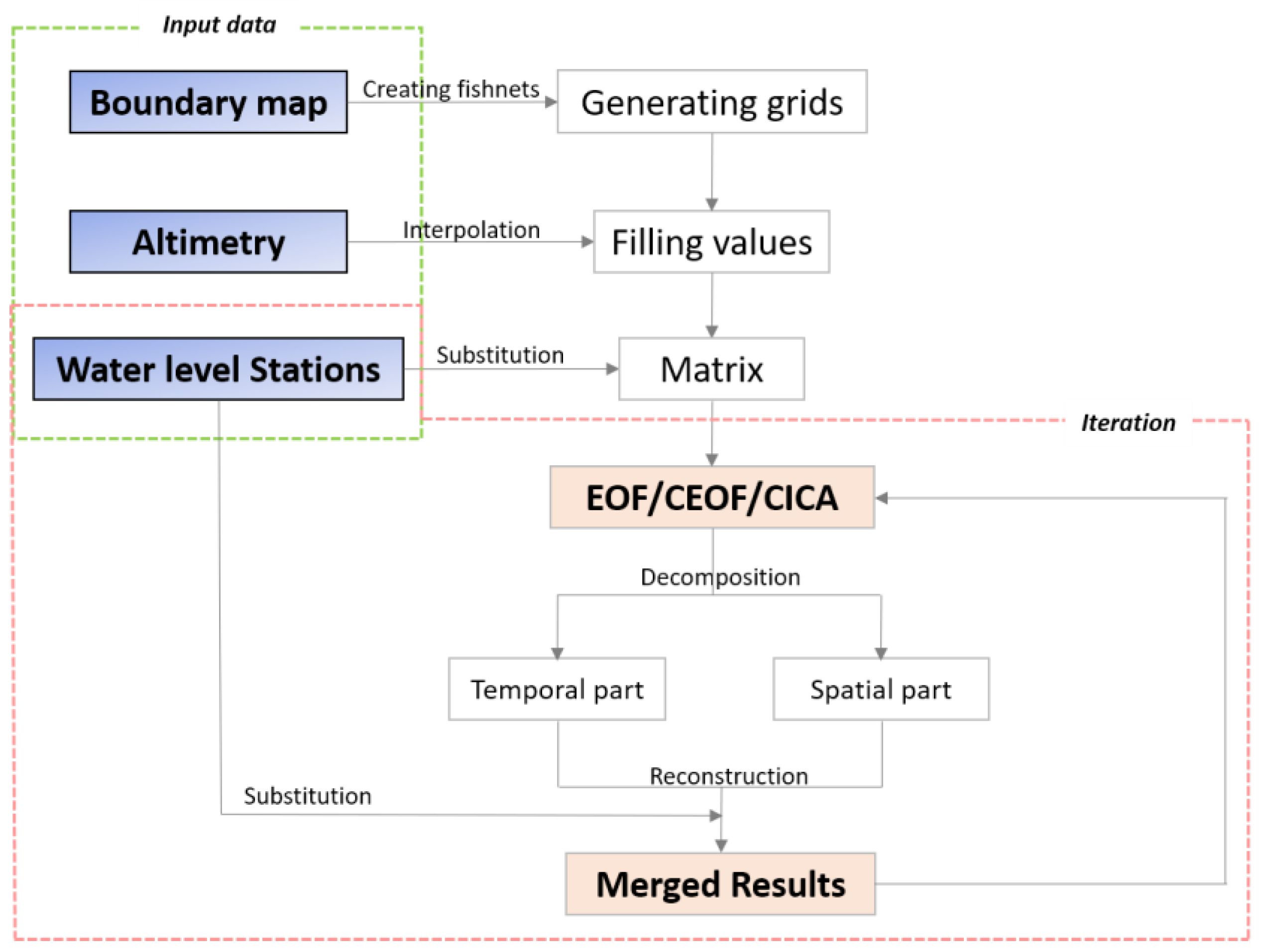
2.6. The Reconstructed Methods
3. Results
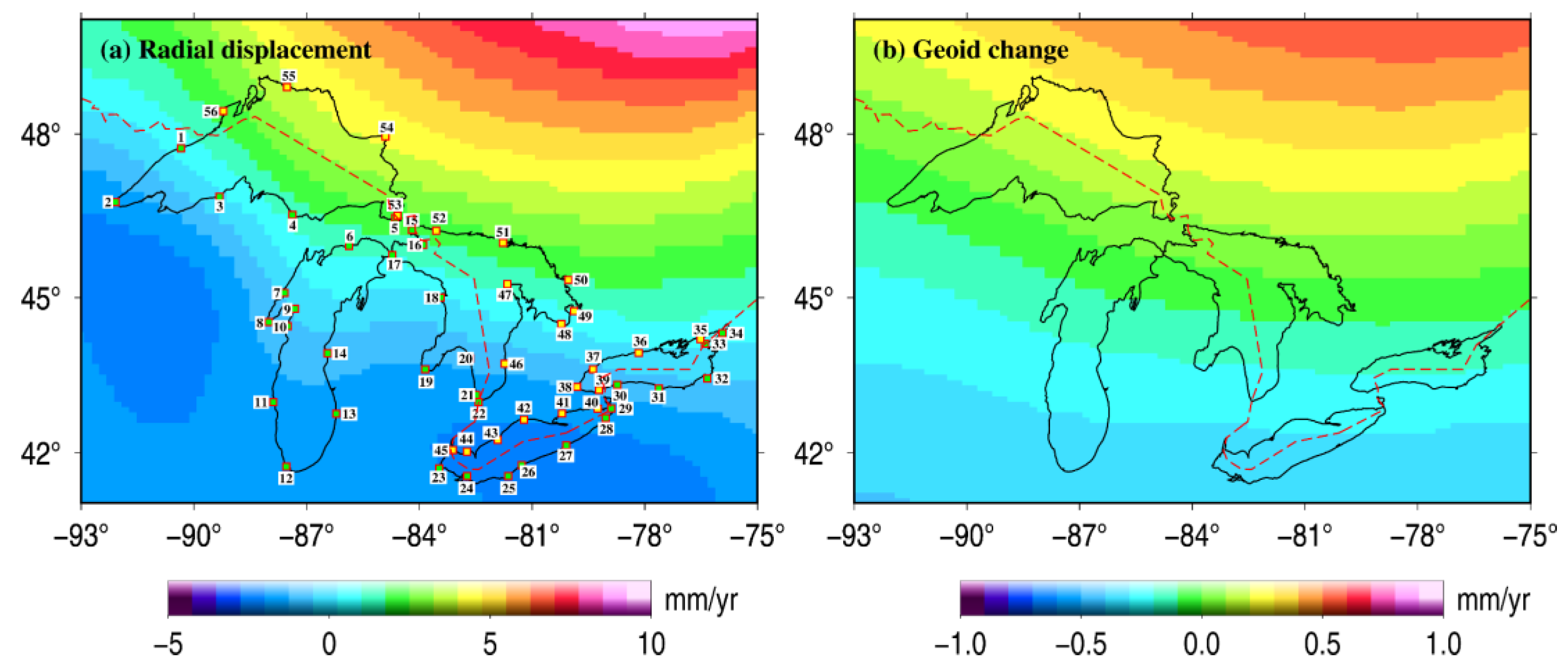
3.1. Effects of GIA on the Great Lakes
3.2. The Reconstructed Lake Surface Height
4. Discussion
4.1. Corrections of Vertical Motion Resulting from GIA
4.2. Impacts from ENSO on the Great Lakes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Description of EOF/CEOF/CICA
Appendix B. Description of M-SSA
References
- Waples, J.T.; Eadie, B.; Klump, J.V.; Squires, M.; Cotner, J.; McKinley, G. The Laurentian Great Lakes. In Continental Margins: A Synthesis and Planning Workshop, North American Continental Margins Working Group for the US Carbon Cycle Scientific Steering Group and Interagency Working Group; US Carbon Cycle Program: Washington, DC, USA, 2008; pp. 73–81. Available online: http://www.glerl.noaa.gov/pubs/fulltext/2008/20080024.pdf (accessed on 15 December 2020).
- Gershunov, A.; Barnett, T.P. Interdecadal modulation of ENSO teleconnections. Bull. Am. Meteorol. Soc. 1998, 79, 2715–2726. [Google Scholar] [CrossRef]
- De Loë, R.C.; Kreutzwiser, R.D. Climate Variability, Climate Change and Water Resource Management in the Great Lakes. Clim. Chang. 2000, 45, 163–179. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Stow, C.A. Water Loss from the Great Lakes. Science 2014, 343, 1084–1085. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Bowling, L.C. Detection of changes in hydrologic system memory associated with urbanization in the Great Lakes region. Water Resour. Res. 2014, 50, 3750–3763. [Google Scholar] [CrossRef]
- Quinn, F.H. Secular changes in Great Lakes water level seasonal cycles. J. Great Lakes Res. 2002, 28, 451–465. [Google Scholar] [CrossRef]
- Burton, T.M. The effects of water level fluctuations on Great Lakes coastal marshes. In Coastal Wetlands; Lewis Publishers: Chelsea, MI, USA, 2018; pp. 3–13. [Google Scholar]
- Kayastha, M.B.; Ye, X.; Huang, C.; Xue, P. Future rise of the Great Lakes water levels under climate change. J. Hydrol. 2022, 612, 128205. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Rood, R.B. Recent water level changes across Earth’s largest lake system and implications for future variability. J. Great Lakes Res. 2019, 45, 1–3. [Google Scholar] [CrossRef]
- Hwang, C.; Peng, M.-F.; Ning, J.; Luo, J.; Sui, C.-H. Lake level variations in China from TOPEX/Poseidon altimetry: Data quality assessment and links to precipitation and ENSO. Geophys. J. Int. 2005, 161, 1–11. [Google Scholar] [CrossRef]
- Wang, H.; Chu, Y.; Huang, Z.; Chao, N. Robust, Long-term Lake Level Change from Multiple Satellite Altimeters in Tibet: Observing the Rapid Rise of Ngangzi Co over a New Wetland. Remote Sens. 2019, 11, 558. [Google Scholar] [CrossRef]
- Sun, M.; Guo, J.; Yuan, J.; Liu, X.; Wang, H.; Li, C. Detecting Lake Level Change From 1992 to 2019 of Zhari Namco in Tibet Using Altimetry Data of TOPEX/Poseidon and Jason-1/2/3 Missions. Front. Earth Sci. 2021, 9, 640553. [Google Scholar] [CrossRef]
- Herdendorf, C.E. Great lakes estuaries. Estuaries 1990, 13, 493–503. [Google Scholar] [CrossRef]
- Ault, T.W.; Czajkowski, K.P.; Benko, T.; Coss, J.; Struble, J.; Spongberg, A.; Templin, M.; Gross, C. Validation of the MODIS snow product and cloud mask using student and NWS cooperative station observations in the Lower Great Lakes Region. Remote Sens. Environ. 2006, 105, 341–353. [Google Scholar] [CrossRef]
- Morris, C.S.; Gill, S.K. Variation of Great Lakes water levels derived from Geosat altimetry. Water Resour. Res. 1994, 30, 1009–1017. [Google Scholar] [CrossRef]
- Jekeli, C.; Dumrongchai, P. On monitoring a vertical datum with satellite altimetry and water-level gauge data on large lakes. J. Geodesy 2003, 77, 447–453. [Google Scholar] [CrossRef]
- Kuo, C.-Y.; Shum, C.; Braun, A.; Cheng, K.-C.; Yi, Y. Vertical Motion Determined Using Satellite Altimetry and Tide Gauges. Terr. Atmospheric Ocean. Sci. 2008, 19, 21–35. [Google Scholar] [CrossRef]
- Cheng, K.-C.; Kuo, C.-Y.; Tseng, H.-Z.; Yi, Y.; Shum, C. Lake Surface Height Calibration of Jason-1 and Jason-2 Over the Great Lakes. Mar. Geodesy 2010, 33, 186–203. [Google Scholar] [CrossRef]
- Jia, Y.; Shum, C.K.; Chu, P. Monitoring water level variations over the Great Lakes using contemporary satellite geodetic observations. In AGU Fall Meeting Abstracts; AGU Publisher: Washington, DC, USA, 2018; p. H31K-2074. [Google Scholar]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, RG2002. [Google Scholar] [CrossRef]
- Lee, H.; Beighley, R.E.; Alsdorf, D.; Jung, H.C.; Shum, C.; Duan, J.; Guo, J.; Yamazaki, D.; Andreadis, K. Characterization of terrestrial water dynamics in the Congo Basin using GRACE and satellite radar altimetry. Remote Sens. Environ. 2011, 115, 3530–3538. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W.; Livezey, R.E.; Stokes, D.C. Reconstruction of historical sea surface temperatures using empirical orthogonal functions. J. Clim. 1996, 9, 1403–1420. [Google Scholar] [CrossRef]
- Wenzel, M.; Schröter, J. Reconstruction of regional mean sea level anomalies from tide gauges using neural networks. J. Geophys. Res. Earth Surf. 2010, 115, C08013. [Google Scholar] [CrossRef]
- Kaplan, A.; Kushnir, Y.; Cane, M.A. Reduced Space Optimal Interpolation of Historical Marine Sea Level Pressure: 1854–1992. J. Clim. 2000, 13, 2987–3002. [Google Scholar] [CrossRef]
- Chambers, D.P.; Mehlhaff, C.A.; Urban, T.J.; Fujii, D.; Nerem, R.S. Low-frequency variations in global mean sea level: 1950–2000. J. Geophys. Res. Ocean. 2002, 107, 1-1–1-10. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J.; Coleman, R.; Lambeck, K.; Mitrovica, J.X. Estimates of the regional distribution of sea level rise over the 1950–2000 period. J. Clim. 2004, 17, 2609–2625. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Cheon, S.H.; Thompson, P.R.; Merrifield, M.A.; Nerem, R.S.; Leben, R.R.; Kim, K.Y. An ongoing shift in Pacific Ocean Sea level. J. Geophys. Res. Ocean. 2016, 121, 5084–5097. [Google Scholar] [CrossRef]
- Forootan, E. Statistical Signal Decomposition Techniques for Analyzing Time-Variable Satellite Gravimetry Data. Ph.D. Thesis, Universitäts-und Landesbibliothek Bonn, Bonn, Germany, 2014. [Google Scholar]
- Von Storch, H.; Navarra, A. (Eds.) Analysis of Climate Variability: Applications of Statistical Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Forootan, E.; Kusche, J.; Talpe, M.; Shum, C.K.; Schmidt, M. Developing a Complex Independent Component Analysis (CICA) Technique to Extract Non-stationary Patterns from Geophysical Time Series. Surv. Geophys. 2017, 39, 435–465. [Google Scholar] [CrossRef]
- Horel, J.D. Complex Principal Component Analysis: Theory and Examples. J. Clim. Appl. Meteorol. 1984, 23, 1660–1673. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of statistical analysis in climate research. In Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–26. [Google Scholar]
- Merrifield, M.A.; Guza, R.T. Detecting Propagating Signals with Complex Empirical Orthogonal Functions: A Cautionary Note. J. Phys. Oceanogr. 1990, 20, 1628–1633. [Google Scholar] [CrossRef]
- Hannachi, A.; Jolliffe, I.; Stephenson, D. Empirical orthogonal functions and related techniques in atmospheric science: A review. Int. J. Climatol. A J. R. Meteorol. Soc. 2007, 27, 1119–1152. [Google Scholar] [CrossRef]
- Aires, F.; Rossow, W.; Scott, N.; Chedin, A. Remote sensing from the infrared atmospheric sounding interferometer instrument 2. Simultaneous retrieval of temperature, water vapor, and ozone atmospheric profiles. J. Geophys. Res. Earth Surf. 2002, 107, ACH 7-1–ACH 7-12. [Google Scholar] [CrossRef]
- Forootan, E.; Kusche, J. Separation of global time-variable gravity signals into maximally independent components. J. Geodesy 2011, 86, 477–497. [Google Scholar] [CrossRef]
- Westra, S.; Brown, C.; Lall, U.; Sharma, A. Modeling multivariable hydrological series: Principal component analysis or independent component analysis? Water Resour. Res. 2007, 43, W06429. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Forootan, E.; Awange, J.; Kusche, J.; Heck, B.; Eicker, A. Independent patterns of water mass anomalies over Australia from satellite data and models. Remote Sens. Environ. 2012, 124, 427–443. [Google Scholar] [CrossRef]
- Williamson, J. The Inland Seas of North America: And the Natural and Industrial Productions of Canada, with the Real Foundations for Its Future Prosperity; Duff, J., Ed.; H. Ramsay: Montreal, QC, Cananda, 1854. [Google Scholar]
- Dolan, D.M.; Chapra, S.C. Great Lakes total phosphorus revisited: 1. Loading analysis and update (1994–2008). J. Great Lakes Res. 2012, 38, 730–740. [Google Scholar] [CrossRef]
- Birkett, C. The contribution of TOPEX/POSEIDON to the global monitoring of climatically sensitive lakes. J. Geophys. Res. Earth Surf. 1995, 100, 25179–25204. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Fortin, V.; Lofgren, B.; Clites, A.; Stow, C.A.; Quinn, F. Coasts, water levels, and climate change: A Great Lakes perspective. Clim. Chang. 2013, 120, 697–711. [Google Scholar] [CrossRef]
- Simons, M.; Hager, B.H. Localization of the gravity field and the signature of glacial rebound. Nature 1997, 390, 500. [Google Scholar] [CrossRef]
- Peltier, W.; Argus, D.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef]
- Trenberth, K.; Jones, P.; Ambenje, P.; Bojariu, R.; Easterling, D.; Klein Tank, A.; Parker, D.; Rahimzadeh, F.; Renwick, J.; Rusticucci, M. Observations: Surface and atmospheric climate change. In Climate Change; Cambridge University Press: Cambridge, UK, 2007; pp. 235–336. [Google Scholar]
- Cayan, D.R.; Redmond, K.T.; Riddle, L.G. ENSO and Hydrologic Extremes in the Western United States. J. Clim. 1999, 12, 2881–2893. [Google Scholar] [CrossRef]
- Li, X.; Zhong, S.; Bian, X.; Heilman, W. Climate and climate variability of the wind power resources in the Great Lakes region of the United States. J. Geophys. Res. Earth Surf. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Gill, S.K. Gap Analysis of the Great Lakes Component of the National Water Level Observation Network; NOAA: Silver Spring, MD, USA, 2014. [Google Scholar]
- Bruxer, J.; Southam, C. Analysis of Great Lakes Volume Changes Resulting from Glacial Isostatic Adjustment. In Data Technical Work Group; International Upper Great Lakes Study: Burlington, VT, USA, 2008. [Google Scholar]
- Wang, J.; Bai, X.; Hu, H.; Clites, A.; Colton, M.; Lofgren, B. Temporal and Spatial Variability of Great Lakes Ice Cover, 1973–2010. J. Clim. 2012, 25, 1318–1329. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Angel, J.R. Relationship of ENSO to snowfall and related cyclone activity in the contiguous United States. J. Geophys. Res. Earth Surf. 1999, 104, 19425–19434. [Google Scholar] [CrossRef]
- Ma, J.; Venkatesh, S.; Jantunen, L. Evidence of the impact of ENSO events on temporal trends of hexachlorobenzene air concentrations over the Great Lakes. Sci. Total Environ. 2003, 313, 177–184. [Google Scholar] [CrossRef]
- Smith, S.R.; Legler, D.M.; Remigio, M.J.; O’Brien, J.J. Comparison of 1997–98 U.S. Temperature and Precipitation Anomalies to Historical ENSO Warm Phases. J. Clim. 1999, 12, 3507–3515. [Google Scholar] [CrossRef]
- Groth, A.; Ghil, M. Multivariate singular spectrum analysis and the road to phase synchronization. Phys. Rev. E 2011, 84, 036206. [Google Scholar] [CrossRef] [PubMed]
- Alvera-Azcárate, A.; Barth, A.; Rixen, M.; Beckers, J.M. Reconstruction of incomplete oceanographic data sets using empirical orthogonal functions: Application to the Adriatic Sea surface temperature. Ocean. Model. 2005, 94, 325–346. [Google Scholar] [CrossRef]
- Erhardt, E.B.; Rachakonda, S.; Bedrick, E.J.; Allen, E.A.; Adali, T.; Calhoun, V.D. Comparison of multi-subject ICA methods for analysis of fMRI data. Hum. Brain Mapp. 2011, 3212, 2075–2095. [Google Scholar] [CrossRef]
- Pandžić, K.; Likso, T. Eastern Adriatic typical wind field patterns and large-scale atmospheric conditions. Int. J. Clim. 2005, 25, 81–98. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, Y.; Wang, D.; Wu, H.; Lin, A.; He, L. Using Principal Components Analysis and IDW Interpolation to Determine Spatial and Temporal Changes of Surface Water Quality of Xin’anjiang River in Huangshan, China. Int. J. Environ. Res. Public Health 2020, 17, 2942. [Google Scholar] [CrossRef]
- Cardoso, J.F.; Souloumiac, A. Blind beamforming for non-Gaussian signals. Proc. IEEE 1993, 140, 362–370. [Google Scholar] [CrossRef]
- Cardoso, J.F.; Souloumiac, A. Jacobi angles for simultaneous diagonalization. SIAM J. Matrix Anal. Appl. 1996, 17, 161–164. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 3-1–3-41. [Google Scholar] [CrossRef]

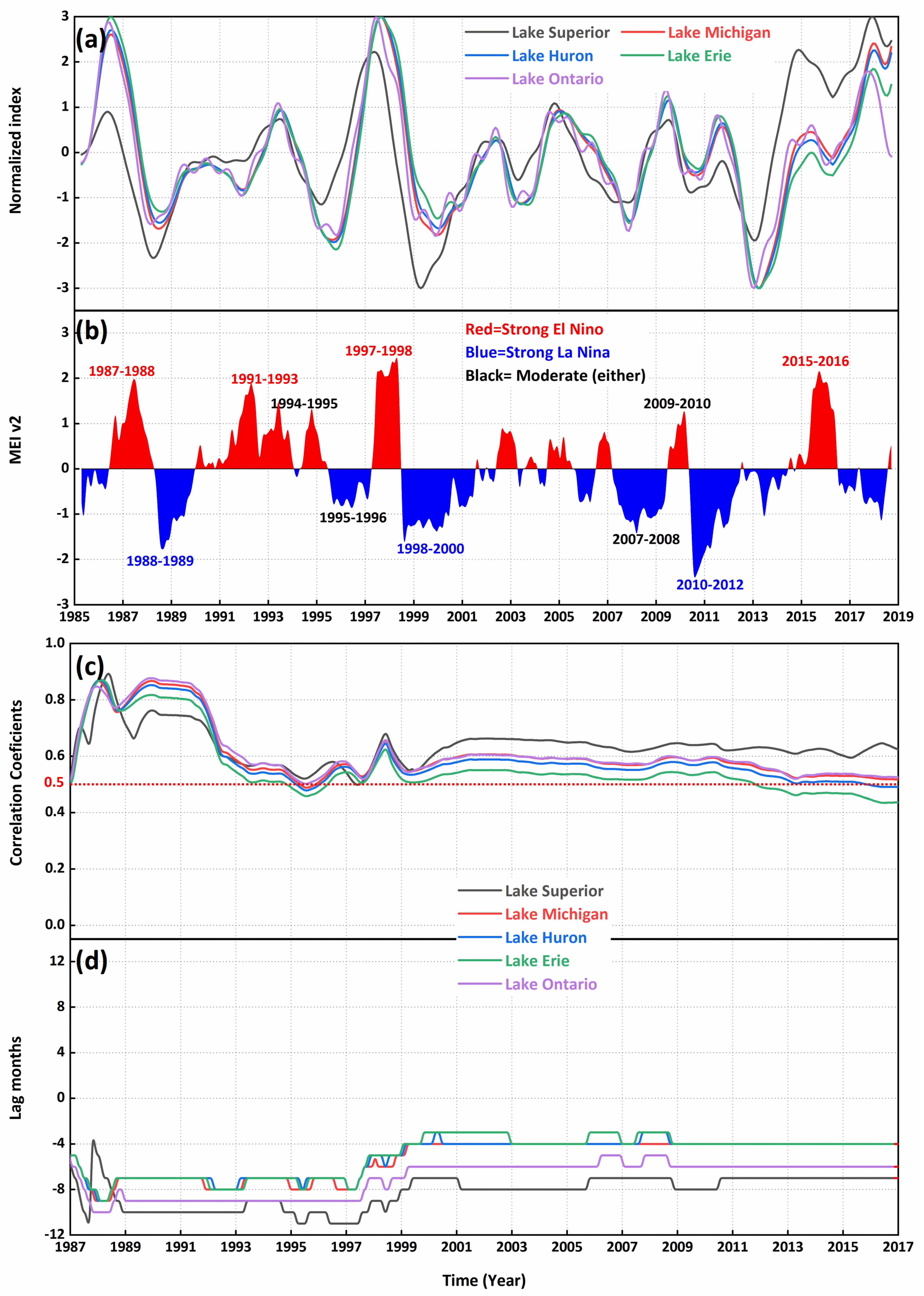
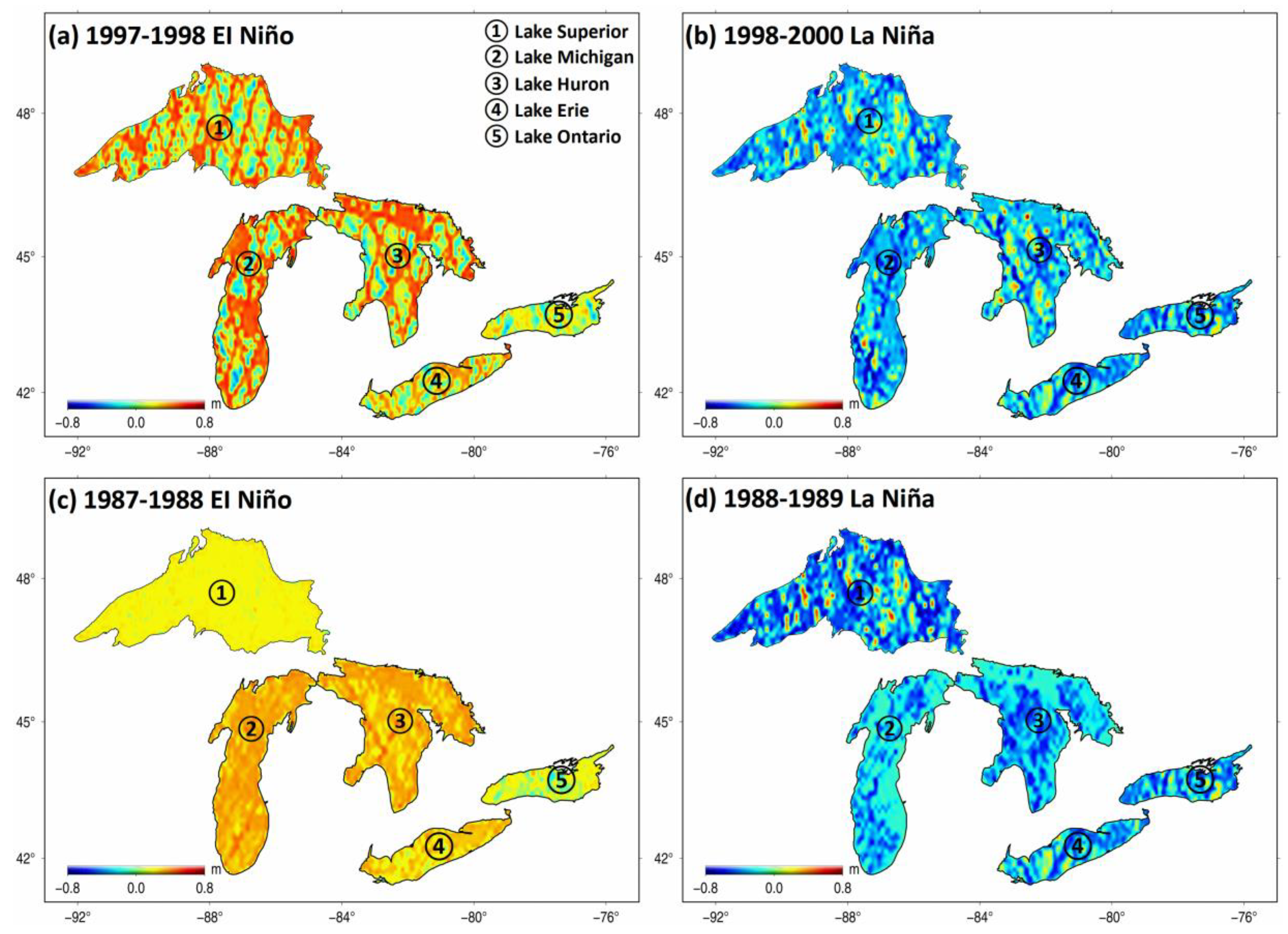
| GIA Effects | Lake Superior | Lake Michigan | Lake Huron | Lake Erie | Lake Ontario |
|---|---|---|---|---|---|
| Radial displacement | 2.02 ± 2.85 mm/year | −0.59 ± 1.83 mm/year | 0.66 ± 2.12 mm/year | −2.07 ± 0.31 mm/year | −0.36 ± 0.81 mm/year |
| Geoid change | 0.12 ± 0.17 mm/year | −0.19 ± 0.21 mm/year | −0.05 ± 0.17 mm/year | −0.32 ± 0.05 mm/year | −0.19 ± 0.05 mm/year |
| Great Lakes | Method | CC (95% CI) | RMSE (cm) |
|---|---|---|---|
| Lake Superior | Altimetry | 0.90 | 10.80 |
| EOF Rec | 0.92 | 8.69 | |
| CEOF Rec | 0.92 | 8.81 | |
| CICA Rec | 0.96 | 6.07 | |
| Lake Michigan | Altimetry | 0.93 | 14.99 |
| EOF Rec | 0.98 | 8.69 | |
| CEOF Rec | 0.98 | 8.42 | |
| CICA Rec | 0.99 | 4.89 | |
| Lake Huron | Altimetry | 0.93 | 16.45 |
| EOF Rec | 0.97 | 9.49 | |
| CEOF Rec | 0.97 | 10.08 | |
| CICA Rec | 0.97 | 9.27 | |
| Lake Erie | Altimetry | 0.90 | 13.94 |
| EOF Rec | 0.96 | 11.17 | |
| CEOF Rec | 0.96 | 11.16 | |
| CICA Rec | 0.97 | 7.71 | |
| Lake Ontario | Altimetry | 0.82 | 16.52 |
| EOF Rec | 0.94 | 11.82 | |
| CEOF Rec | 0.94 | 11.26 | |
| CICA Rec | 0.95 | 9.89 |
| Great Lakes | ICE-6G | ICE-5G | ICE-4G | ICE-3G | Stations |
|---|---|---|---|---|---|
| Lake Superior | 1.75 | 1.81 | 1.30 | 2.30 | 1.60 |
| Lake Michigan | −0.67 | −0.94 | 0.00 | −1.40 | −0.70 |
| Lake Huron | 0.47 | 0.58 | 0.90 | 2.00 | 1.10 |
| Lake Erie | −2.19 | −2.50 | −0.30 | −0.60 | 0.10 |
| Lake Ontario | −0.15 | −0.31 | 0.20 | 0.70 | 1.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Shum, C.K.; Forootan, E.; Feng, W.; Zhong, M.; Jia, Y.; Li, W.; Guo, J.; Wang, C.; Li, Q.; et al. Understanding Water Level Changes in the Great Lakes by an ICA-Based Merging of Multi-Mission Altimetry Measurements. Remote Sens. 2022, 14, 5194. https://doi.org/10.3390/rs14205194
Chen W, Shum CK, Forootan E, Feng W, Zhong M, Jia Y, Li W, Guo J, Wang C, Li Q, et al. Understanding Water Level Changes in the Great Lakes by an ICA-Based Merging of Multi-Mission Altimetry Measurements. Remote Sensing. 2022; 14(20):5194. https://doi.org/10.3390/rs14205194
Chicago/Turabian StyleChen, Wei, C. K. Shum, Ehsan Forootan, Wei Feng, Min Zhong, Yuanyuan Jia, Wenhao Li, Junyi Guo, Changqing Wang, Quanguo Li, and et al. 2022. "Understanding Water Level Changes in the Great Lakes by an ICA-Based Merging of Multi-Mission Altimetry Measurements" Remote Sensing 14, no. 20: 5194. https://doi.org/10.3390/rs14205194
APA StyleChen, W., Shum, C. K., Forootan, E., Feng, W., Zhong, M., Jia, Y., Li, W., Guo, J., Wang, C., Li, Q., & Liang, L. (2022). Understanding Water Level Changes in the Great Lakes by an ICA-Based Merging of Multi-Mission Altimetry Measurements. Remote Sensing, 14(20), 5194. https://doi.org/10.3390/rs14205194








