Common Latent Space Exploration for Calibration Transfer across Hyperspectral Imaging-Based Phenotyping Systems
Abstract
1. Introduction
2. Materials and Methods
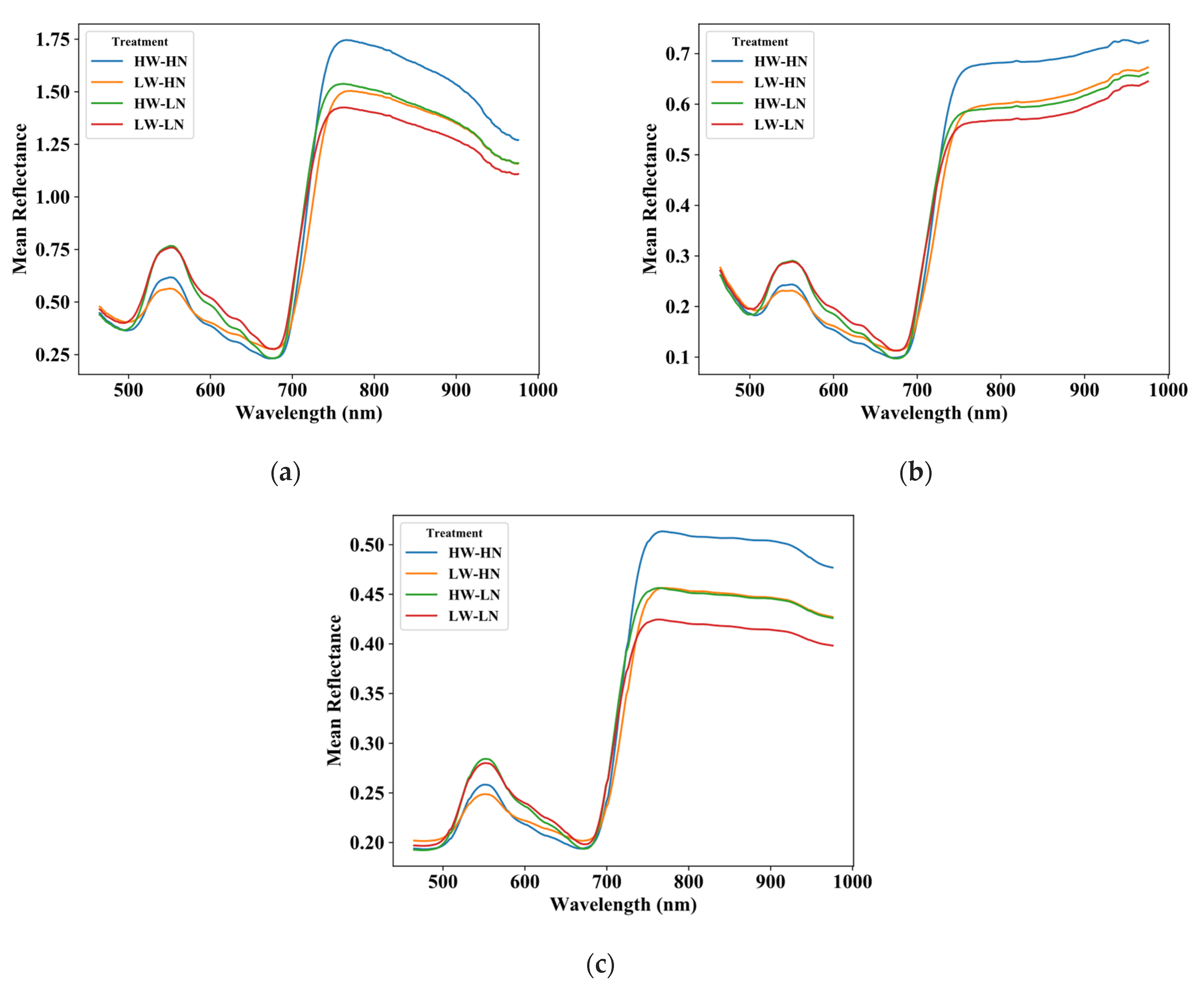
2.1. Hyperspectral Image Acquisition and Processing
2.2. Experimental Design and Plant Materials
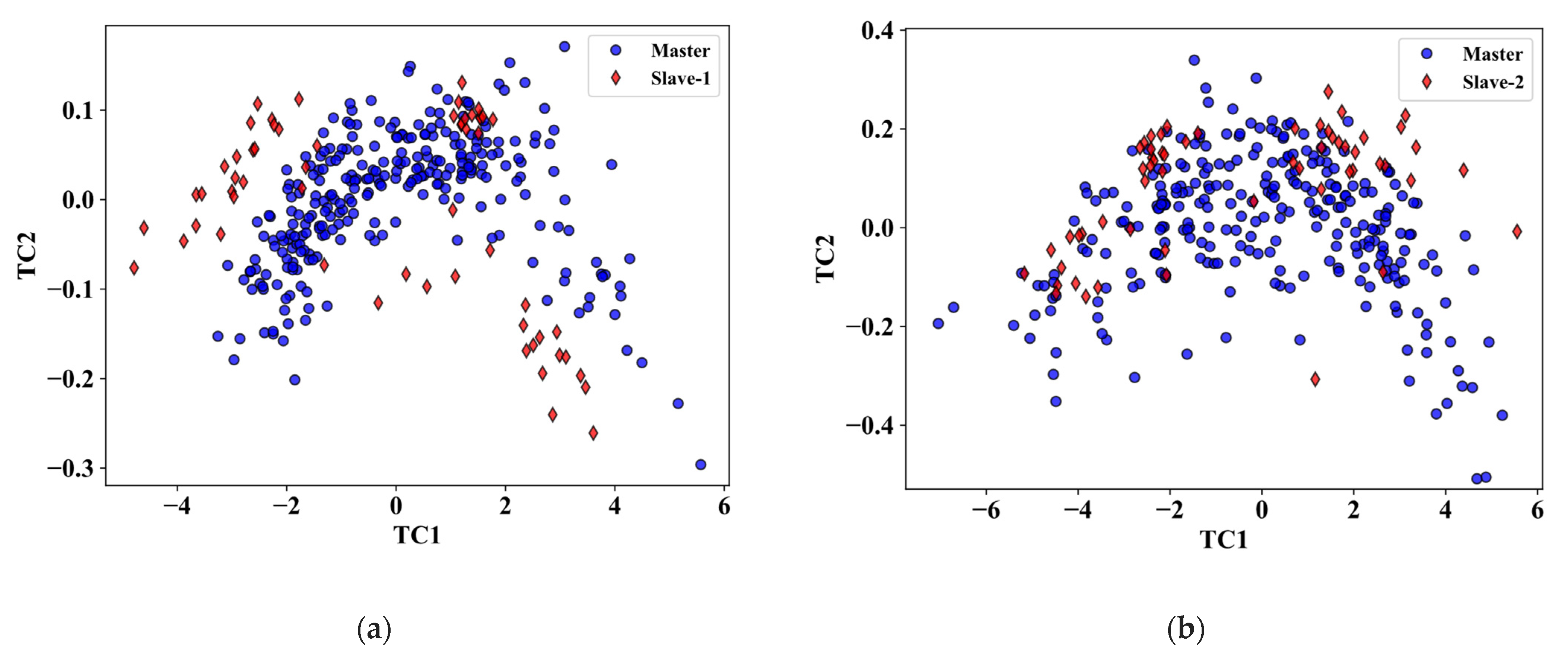
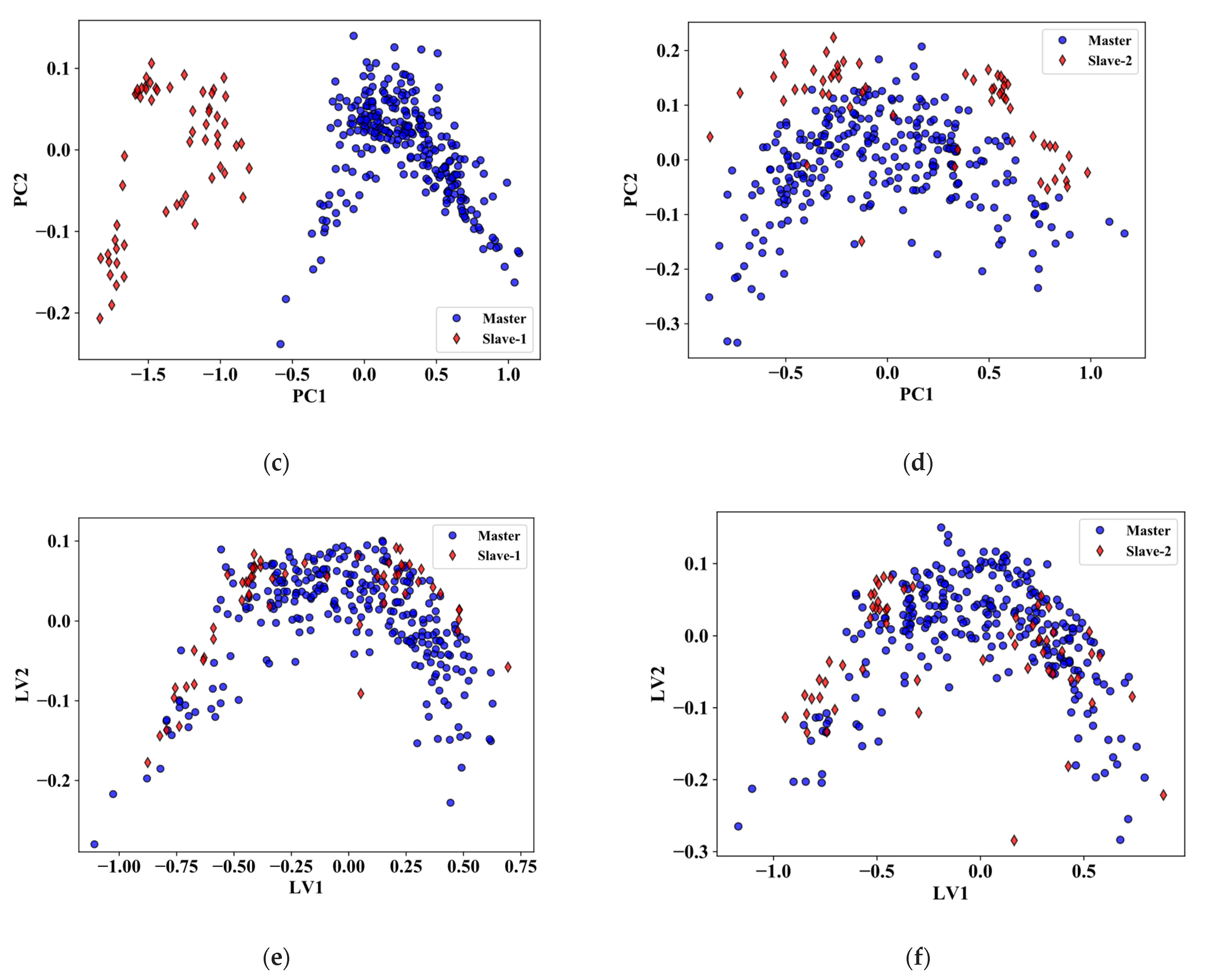
2.3. Common Latent Space Search
2.3.1. Notations
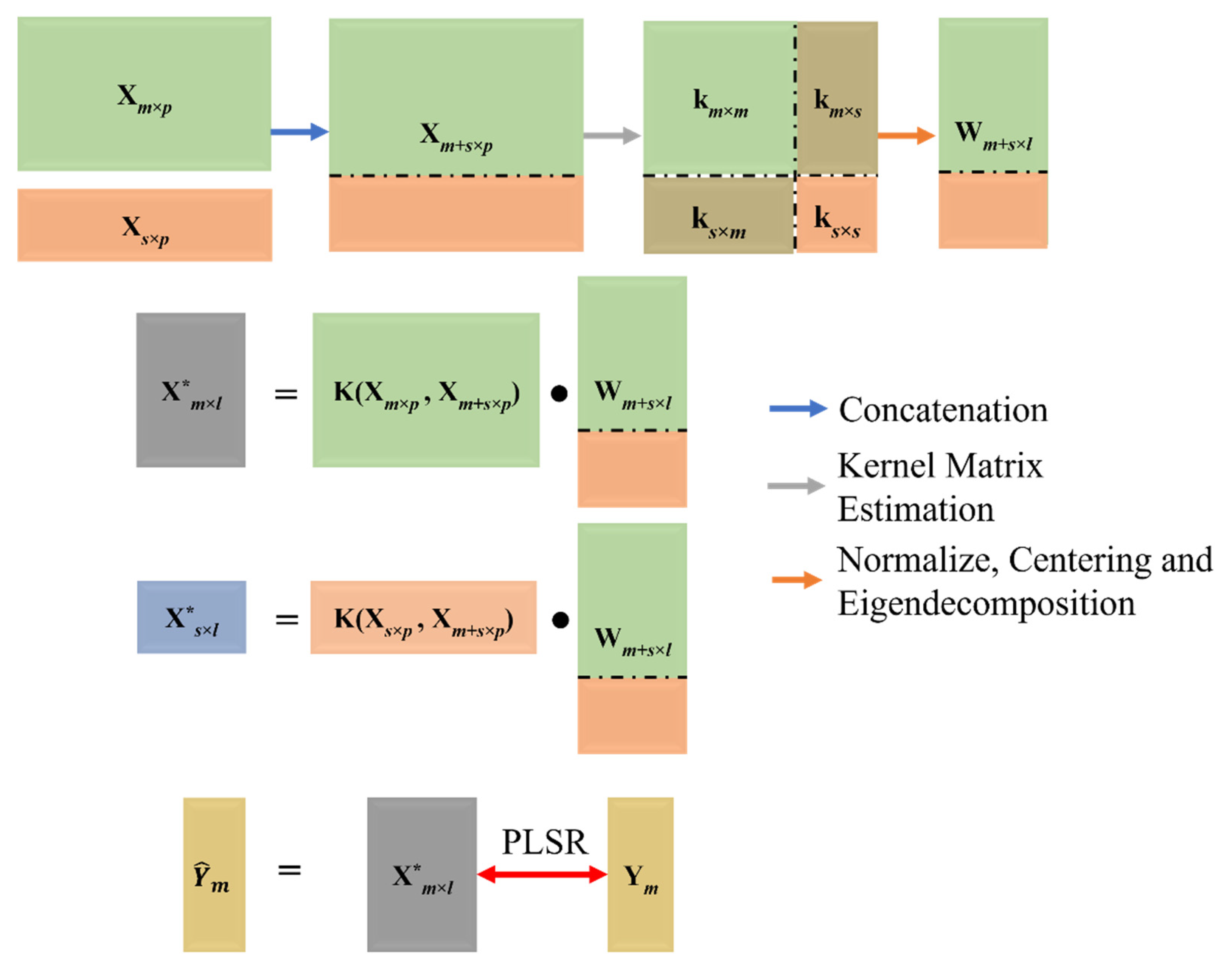
2.3.2. Transfer Component Analysis (TCA)
2.3.3. Combined Principal Component Analysis (c-PCA)
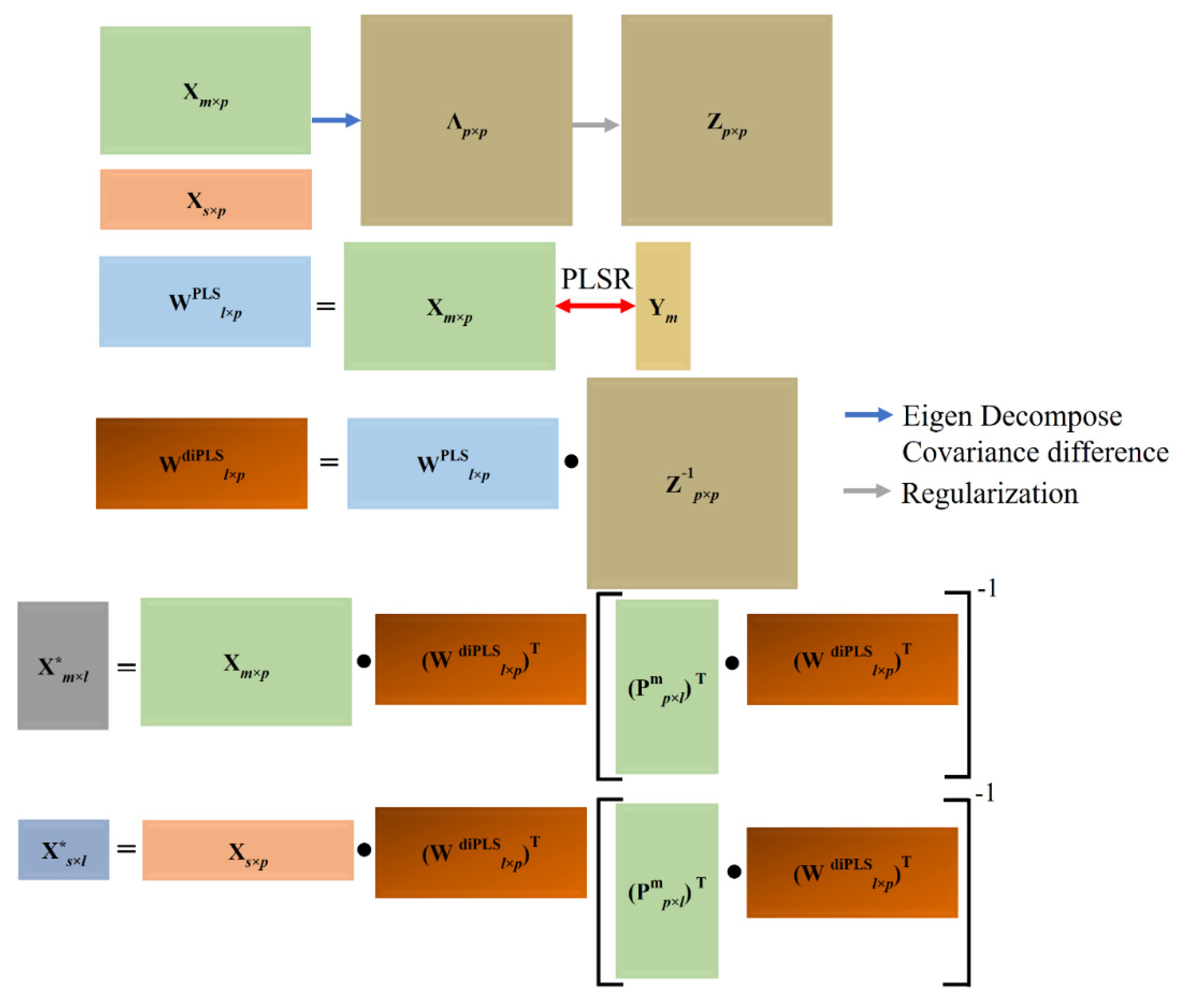
2.3.4. Domain Invariant Partial Least Squares Regression (di-PLSR)
2.4. Calibration Models
3. Results
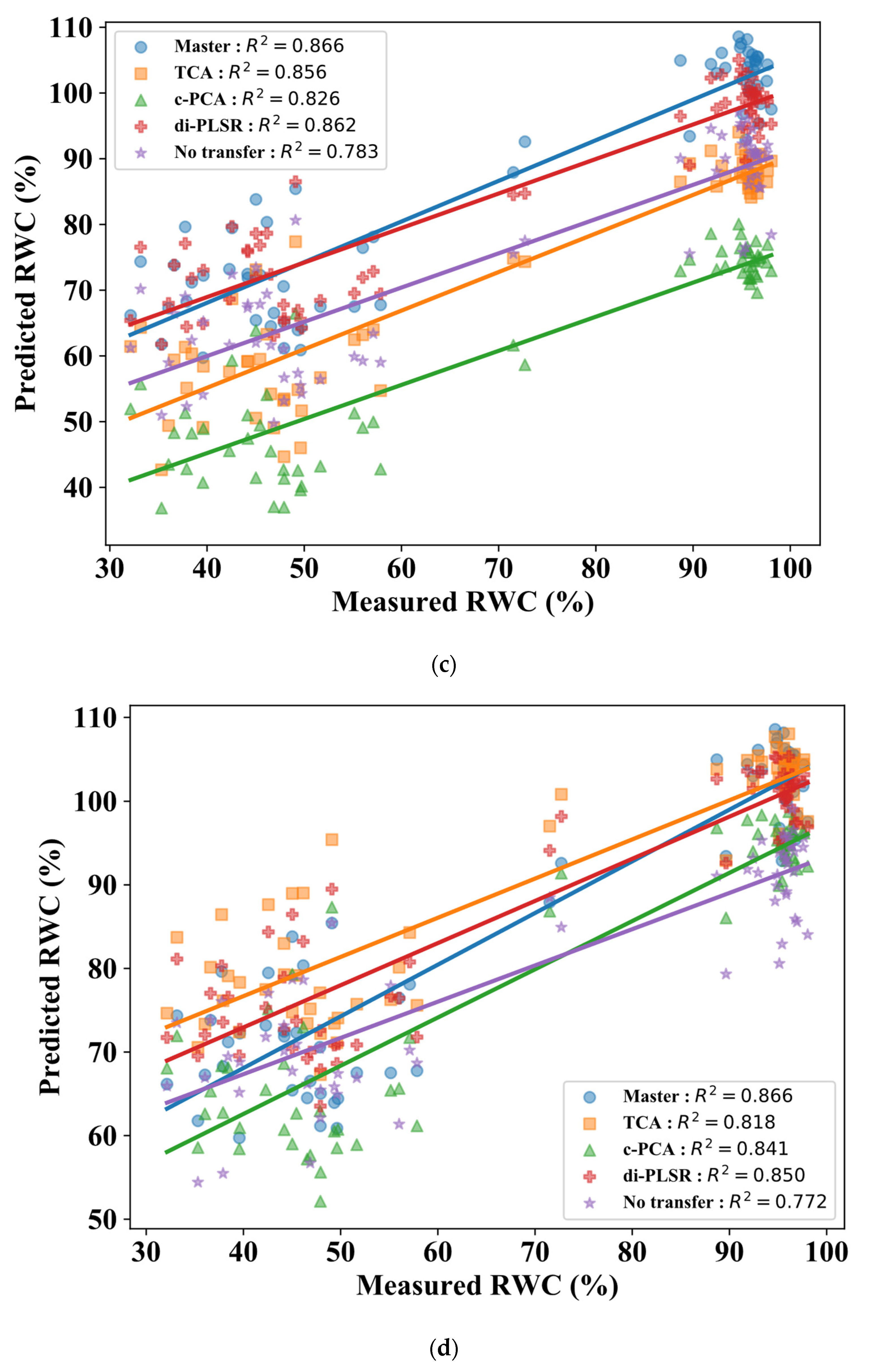
3.1. Comparison of Calibration Transfer Methods for RWC
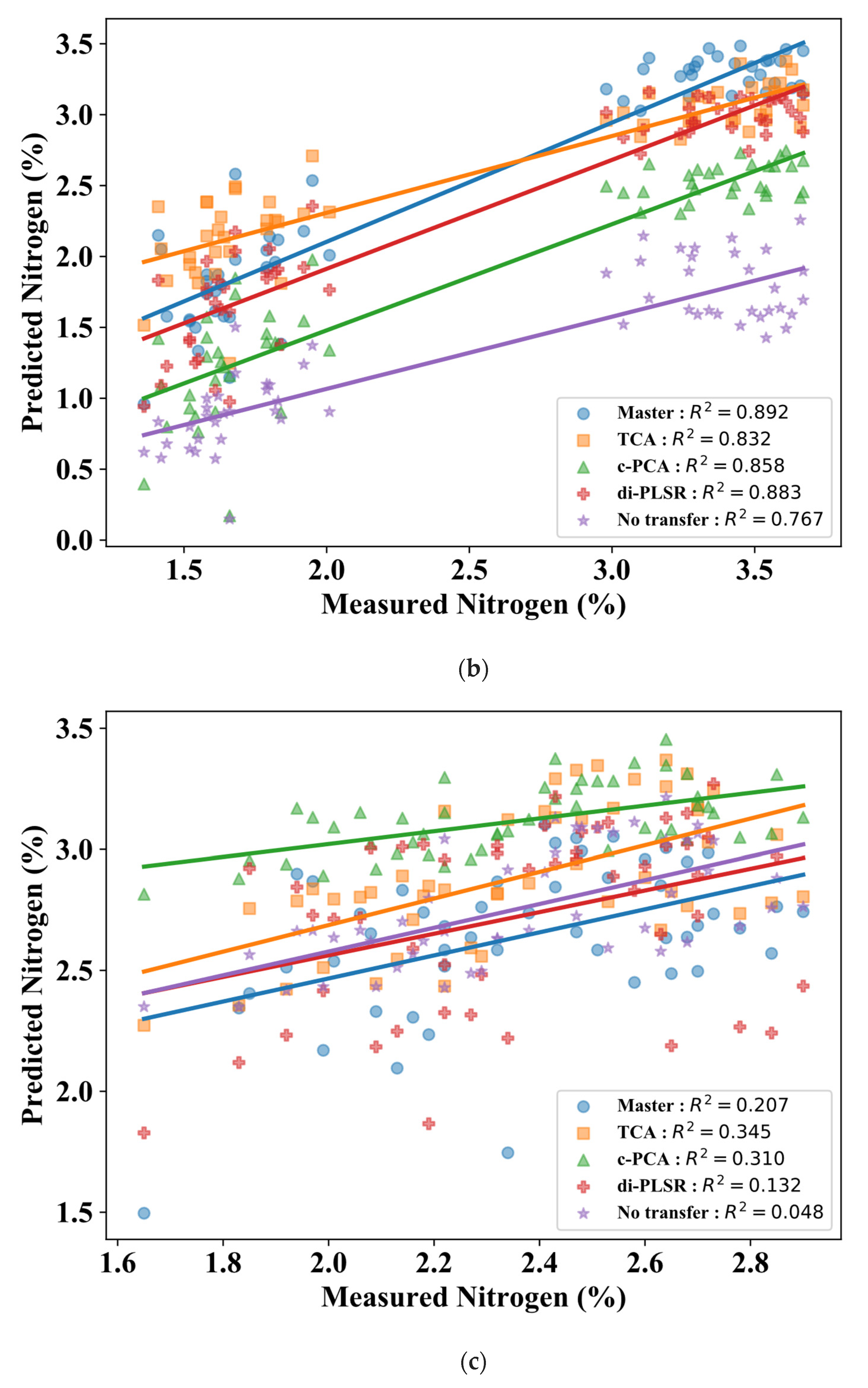
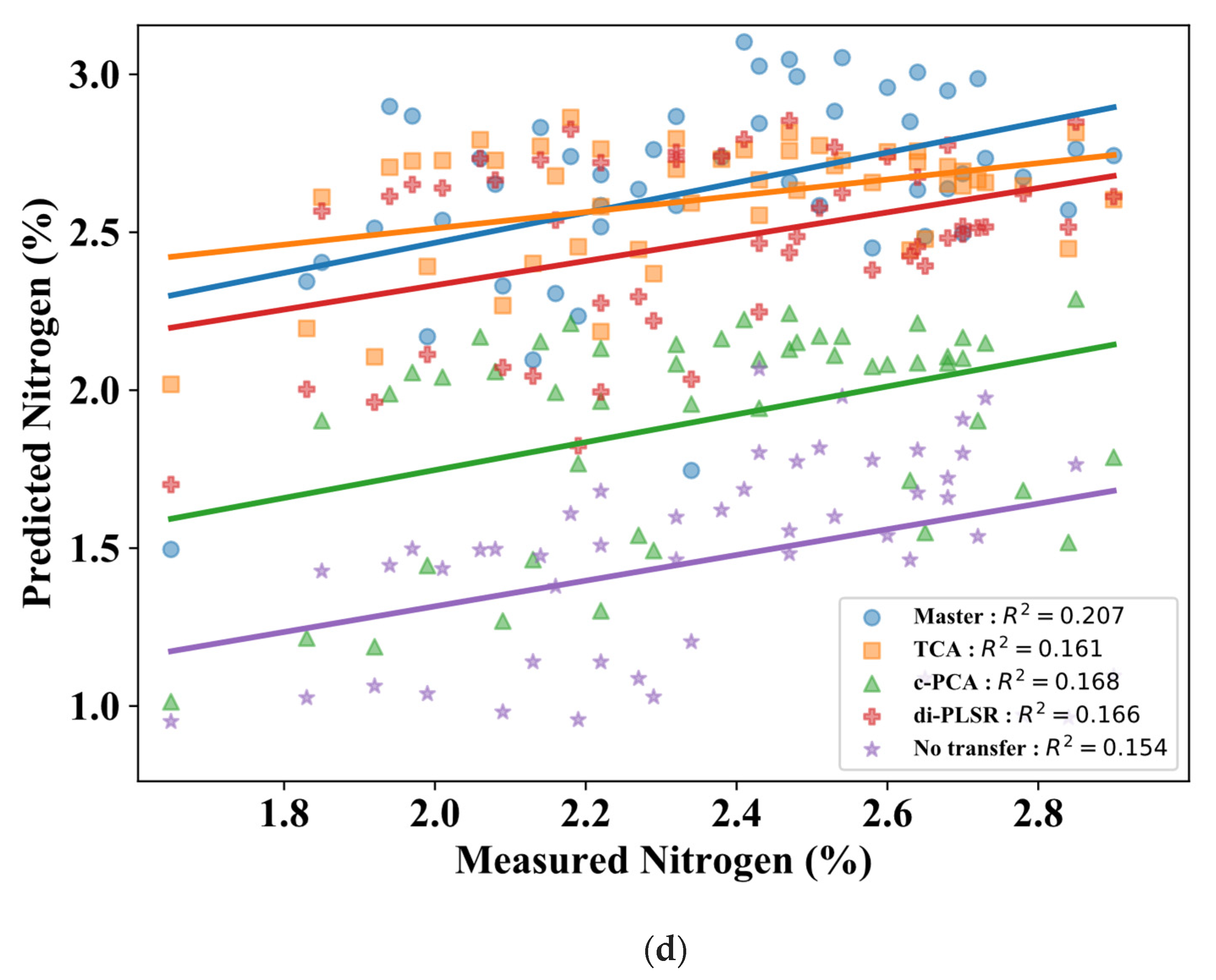
3.2. Comparison of Calibration Transfer Methods for Nitrogen
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fiorani, F.; Schurr, U. Future Scenarios for Plant Phenotyping. Annu. Rev. Plant Biol. 2013, 64, 267–291. [Google Scholar] [CrossRef]
- Walter, A.; Liebisch, F.; Hund, A. Plant Phenotyping: From Bean Weighing to Image Analysis. Plant Methods 2015, 11, 14. [Google Scholar] [CrossRef]
- Costa, C.; Schurr, U.; Loreto, F.; Menesatti, P.; Carpentier, S. Plant Phenotyping Research Trends, a Science Mapping Approach. Front. Plant Sci. 2019, 9, 1933. [Google Scholar] [CrossRef]
- Roitsch, T.; Cabrera-Bosquet, L.; Fournier, A.; Ghamkhar, K.; Jiménez-Berni, J.; Pinto, F.; Ober, E.S. Review: New Sensors and Data-Driven Approaches—A Path to next Generation Phenomics. Plant Sci. 2019, 282, 2–10. [Google Scholar] [CrossRef]
- das Choudhury, S.; Samal, A.; Awada, T. Leveraging Image Analysis for High-Throughput Plant Phenotyping. Front. Plant Sci. 2019, 10, 508. [Google Scholar] [CrossRef]
- Rehman, T.U.; Zhang, L.; Ma, D.; Wang, L.; Jin, J. Calibration Transfer across Multiple Hyperspectral Imaging-Based Plant Phenotyping Systems: I—Spectral Space Adjustment. Comput. Electron. Agric. 2020, 176, 105685. [Google Scholar] [CrossRef]
- Ge, Y.; Atefi, A.; Zhang, H.; Miao, C.; Ramamurthy, R.K.; Sigmon, B.; Yang, J.; Schnable, J.C. High-Throughput Analysis of Leaf Physiological and Chemical Traits with VIS-NIR-SWIR Spectroscopy: A Case Study with a Maize Diversity Panel. Plant Methods 2019, 15, 66. [Google Scholar] [CrossRef]
- Zhang, L.; Rao, Z.; Ji, H. NIR Hyperspectral Imaging Technology Combined with Multivariate Methods to Study the Residues of Different Concentrations of Omethoate on Wheat Grain Surface. Sensors 2019, 19, 3147. [Google Scholar] [CrossRef] [PubMed]
- Rehman, T.U.; Ma, D.; Wang, L.; Zhang, L.; Jin, J. Predictive Spectral Analysis Using an End-to-End Deep Model from Hyperspectral Images for High-Throughput Plant Phenotyping. Comput. Electron. Agric. 2020, 177, 105713. [Google Scholar] [CrossRef]
- Nikzad-Langerodi, R.; Zellinger, W.; Lughofer, E.; Saminger-Platz, S. Domain-Invariant Partial-Least-Squares Regression. Anal. Chem. 2018, 90, 6693–6701. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zhang, R.; Ge, J.; Chen, W.; Yang, W.; Du, Y. Calibration Transfer Based on the Weight Matrix (CTWM) of PLS for near Infrared (NIR) Spectral Analysis. Anal. Methods 2018, 10, 2169–2179. [Google Scholar] [CrossRef]
- Li, X.Y.; Ren, G.X.; Fan, P.P.; Liu, Y.; Sun, Z.L.; Hou, G.L.; Lv, M.R. Study on the Calibration Transfer of Soil Nutrient Concentration from the Hyperspectral Camera to the Normal Spectrometer. J. Spectrosc. 2020, 2020, 8137142. [Google Scholar] [CrossRef]
- Murphy, R.J.; Schneider, S.; Monteiro, S.T. Consistency of Measurements of Wavelength Position from Hyperspectral Imagery: Use of the Ferric Iron Crystal Field Absorption at ~900 Nm as an Indicator of Mineralogy. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2843–2857. [Google Scholar] [CrossRef]
- Buddenbaum, H.; Watt, M.S.; Scholten, R.C.; Hill, J. Preprocessing Ground-Based Visible/near Infrared Imaging Spectroscopy Data Affected by Smile Effects. Sensors 2019, 19, 1543. [Google Scholar] [CrossRef] [PubMed]
- Fearn, T. Standardisation and Calibration Transfer for near Infrared Instruments: A Review. J. Near Infrared Spectrosc. 2001, 9, 229–244. [Google Scholar] [CrossRef]
- Alamar, M.C.; Bobelyn, E.; Lammertyn, J.; Nicolaï, B.M.; Moltó, E. Calibration Transfer between NIR Diode Array and FT-NIR Spectrophotometers for Measuring the Soluble Solids Contents of Apple. Postharvest Biol. Technol. 2007, 45, 38–45. [Google Scholar] [CrossRef]
- Ji, W.; Viscarra Rossel, R.A.; Shi, Z. Improved Estimates of Organic Carbon Using Proximally Sensed Vis-NIR Spectra Corrected by Piecewise Direct Standardization. Eur. J. Soil Sci. 2015, 66, 670–678. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; Shao, X. Correcting Multivariate Calibration Model for near Infrared Spectral Analysis without Using Standard Samples. J. Near Infrared Spectrosc. 2015, 23, 285–291. [Google Scholar] [CrossRef]
- Pu, Y.Y.; Sun, D.W.; Riccioli, C.; Buccheri, M.; Grassi, M.; Cattaneo, T.M.P.; Gowen, A. Calibration Transfer from Micro NIR Spectrometer to Hyperspectral Imaging: A Case Study on Predicting Soluble Solids Content of Bananito Fruit (Musa Acuminata). Food Anal. Methods 2018, 11, 1021–1033. [Google Scholar] [CrossRef]
- Workman, J.J. A Review of Calibration Transfer Practices and Instrument Differences in Spectroscopy. Appl. Spectrosc. 2018, 72, 340–365. [Google Scholar] [CrossRef]
- Fan, S.; Li, J.; Xia, Y.; Tian, X.; Guo, Z.; Huang, W. Long-Term Evaluation of Soluble Solids Content of Apples with Biological Variability by Using near-Infrared Spectroscopy and Calibration Transfer Method. Postharvest Biol. Technol. 2019, 151, 79–87. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.P.; Zhong, L.J.; Wang, S.X.; Yu, R.Q.; Nordon, A.; Littlejohn, D.; Holden, M. Maintaining the Predictive Abilities of Multivariate Calibration Models by Spectral Space Transformation. Anal. Chim. Acta 2011, 690, 64–70. [Google Scholar] [CrossRef]
- Folch-Fortuny, A.; Vitale, R.; de Noord, O.E.; Ferrer, A. Calibration Transfer between NIR Spectrometers: New Proposals and a Comparative Study. J. Chemom. 2017, 31, e2874. [Google Scholar] [CrossRef]
- Ma, D.; Carpenter, N.; Amatya, S.; Maki, H.; Wang, L.; Zhang, L.; Neeno, S.; Tuinstra, M.R.; Jin, J. Removal of Greenhouse Microclimate Heterogeneity with Conveyor System for Indoor Phenotyping. Comput. Electron. Agric. 2019, 166, 104979. [Google Scholar] [CrossRef]
- Zhang, L.; Maki, H.; Ma, D.; Sánchez-Gallego, J.A.; Mickelbart, M.V.; Wang, L.; Rehman, T.U.; Jin, J. Optimized Angles of the Swing Hyperspectral Imaging System for Single Corn Plant. Comput. Electron. Agric. 2019, 156, 349–359. [Google Scholar] [CrossRef]
- Rehman, T.U.; Zhang, L.; Wang, L.; Ma, D.; Maki, H.; Sánchez-Gallego, J.A.; Mickelbart, M.V.; Jin, J. Automated Leaf Movement Tracking in Time-Lapse Imaging for Plant Phenotyping. Comput. Electron. Agric. 2020, 175, 105623. [Google Scholar] [CrossRef]
- Bin, J.; Li, X.; Fan, W.; Zhou, J.H.; Wang, C.W. Calibration Transfer of Near-Infrared Spectroscopy by Canonical Correlation Analysis Coupled with Wavelet Transform. Analyst 2017, 142, 2229–2238. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Borgwardt, K.M.; Gretton, A.; Rasch, M.J.; Kriegel, H.P.; Schölkopf, B.; Smola, A.J. Integrating Structured Biological Data by Kernel Maximum Mean Discrepancy. Bioinformatics 2006, 22, e49–e57. [Google Scholar] [CrossRef] [PubMed]
- Steinwart, I. On the Influence of the Kernel on the Consistency of Support Vector Machines. J. Mach. Learn. Res. 2002, 2, 67–93. [Google Scholar] [CrossRef][Green Version]
- Nikzad-Langerodi, R.; Zellinger, W.; Saminger-Platz, S.; Moser, B.A. Domain Adaptation for Regression under Beer–Lambert’s Law. Knowl.-Based Syst. 2020, 210, 106447. [Google Scholar] [CrossRef]
- Mishra, P.; Roger, J.M.; Rutledge, D.N.; Woltering, E. Two Standard-Free Approaches to Correct for External Influences on near-Infrared Spectra to Make Models Widely Applicable. Postharvest Biol. Technol. 2020, 170, 111326. [Google Scholar] [CrossRef]
- Shi, G.; Cao, J.; Li, C.; Liang, Y. Compression Strength Prediction of Xylosma Racemosum Using a Transfer Learning System Based on Near-Infrared Spectral Data. J. For. Res. 2020, 31, 1061–1069. [Google Scholar] [CrossRef]
- Mishra, P.; Nikzad-Langerodi, R. Partial Least Square Regression versus Domain Invariant Partial Least Square Regression with Application to Near-Infrared Spectroscopy of Fresh Fruit. Infrared Phys. Technol. 2020, 111, 103547. [Google Scholar] [CrossRef]
- Sun, X.; Subedi, P.; Walker, R.; Walsh, K.B. NIRS Prediction of Dry Matter Content of Single Olive Fruit with Consideration of Variable Sorting for Normalisation Pre-Treatment. Postharvest Biol. Technol. 2020, 163, 111140. [Google Scholar] [CrossRef]
- Li, L.; Jang, X.; Li, B.; Liu, Y. Wavelength Selection Method for Near-Infrared Spectroscopy Based on Standard-Sample Calibration Transfer of Mango and Apple. Comput. Electron. Agric. 2021, 190, 106448. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Yang, X.; He, Y. Boosting the Generalization Ability of Vis-NIR-Spectroscopy-Based Regression Models through Dimension Reduction and Transfer Learning. Comput. Electron. Agric. 2021, 186, 106157. [Google Scholar] [CrossRef]



| Models | Validation 1 | Test | Validation 1 | Test | ||||
|---|---|---|---|---|---|---|---|---|
| Slave–1 | Slave–2 | |||||||
| RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | |
| Non- transferred | 10.183 | 10.072 | 11.772 | 12.685 | 10.083 | 8.765 | 9.054 | 7.896 |
| TCA | 9.987 | 10.243 | 14.525 | 16.359 | 5.766 | 5.309 | 5.890 | 6.296 |
| c-PCA | 24.466 | 25.657 | 26.308 | 30.353 | 7.708 | 7.670 | 7.494 | 7.965 |
| di-PLSR | 2.598 | 2.234 | 4.126 | 4.138 | 2.767 | 2.468 | 3.949 | 4.122 |
| Models | Validation 1 | Test | Validation 1 | Test | ||||
|---|---|---|---|---|---|---|---|---|
| Slave–1 | Slave–2 | |||||||
| RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | RMSE (%) | MAPE (%) | |
| Non-transferred | 0.511 | 22.202 | 0.493 | 10.733 | 1.276 | 48.405 | 1.212 | 44.512 |
| TCA | 0.394 | 17.460 | 0.407 | 12.486 | 0.313 | 13.448 | 0.258 | 8.331 |
| c-PCA | 0.513 | 23.042 | 0.546 | 19.787 | 0.693 | 28.598 | 0.789 | 27.983 |
| di-PLSR | 0.193 | 7.117 | 0.277 | 9.580 | 0.297 | 9.721 | 0.286 | 8.535 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, T.U.; Zhang, L.; Ma, D.; Jin, J. Common Latent Space Exploration for Calibration Transfer across Hyperspectral Imaging-Based Phenotyping Systems. Remote Sens. 2022, 14, 319. https://doi.org/10.3390/rs14020319
Rehman TU, Zhang L, Ma D, Jin J. Common Latent Space Exploration for Calibration Transfer across Hyperspectral Imaging-Based Phenotyping Systems. Remote Sensing. 2022; 14(2):319. https://doi.org/10.3390/rs14020319
Chicago/Turabian StyleRehman, Tanzeel U., Libo Zhang, Dongdong Ma, and Jian Jin. 2022. "Common Latent Space Exploration for Calibration Transfer across Hyperspectral Imaging-Based Phenotyping Systems" Remote Sensing 14, no. 2: 319. https://doi.org/10.3390/rs14020319
APA StyleRehman, T. U., Zhang, L., Ma, D., & Jin, J. (2022). Common Latent Space Exploration for Calibration Transfer across Hyperspectral Imaging-Based Phenotyping Systems. Remote Sensing, 14(2), 319. https://doi.org/10.3390/rs14020319






