Abstract
GPS can be used to measure land motions induced by mass loading variations on the Earth’s surface. This paper presents an independent component analysis (ICA)-based inversion method that uses vertical GPS coordinate time series to estimate the change of terrestrial water storage (TWS) in the Sichuan-Yunnan region in China. The ICA method was applied to extract the hydrological deformation signals from the vertical coordinate time series of GPS stations in the Sichuan-Yunnan region from the Crustal Movement Observation Network of China (CMONC). These vertical deformation signals were then inverted to TWS variations. Comparative experiments were conducted based on Gravity Recovery and Climate Experiment (GRACE) data and a hydrological model for validation. The results demonstrate that the TWS changes estimated from GPS(ICA) deformations are highly correlated with the water variations derived from the GRACE data and hydrological model in Sichuan-Yunnan region. The TWS variations are overestimated by the vertical GPS observations the northwestern Sichuan-Yunnan region. The anomalies are likely caused by inaccurate atmospheric loading correction models or residual tropospheric errors in the region with high topographic variability and can be reduced by ICA preprocessing.
1. Introduction
Terrestrial water storage (TWS) variations play an important role in the study of the global water cycle and water resource management [1,2]. Modern space-geodetic satellites provide an effective and efficient approach to monitor and quantify TWS variations. For instance, Gravity Recovery and Climate Experiment (GRACE) data have been widely used to measure the variations of large-scale water storage [3,4,5]. However, GRACE-derived TWS values have low spatial resolution (300–500 km) and low temporal resolution (monthly). Another popular method is the use of hydrological assimilation models, such as Global Land Data Assimilation Systems (GLDAS) [6], to understand the water cycle process and effect of land surface processes on climate [5]. However, GLDAS models neglect either reservoir water or groundwater and lack comprehensive in-situ measurements.
TWS variations can deform the Earth’s surfaces, especially in the vertical direction. These elastic responses can be precisely monitored by GPS measurements. Some studies have used continuous GPS measurements to investigate hydrological deformations on the Earth’s surface in regions with significant water variations, and the results are in good agreement with the GRACE-derived displacements [7,8,9,10]. These studies indicate that GPS is a useful real-time tool to estimate TWS variations. Chew and Small [11] used vertical GPS observations to assess the TWS anomalies in the High Plains (United States) caused by the 2012 drought. In that study, the vertical GPS time series were assumed to be linearly correlated with TWS variations, but an explanation of their theoretical relationships was not provided. Argus et al. [12] proposed that the TWS inversion method uses vertical GPS time series of land motions based on Green’s functions [13] and successfully applied the method to monitor the TWS in California. Fu et al. [14] used GPS as an independent measuring method to estimate the TWS variations in the Washington and Oregon areas and made synthetic tests of the inversion method. Jin and Zhang [15] used continuous GPS observations to estimate the TWS variations in the southwestern U.S., and the inversion results showed good agreement with the GRACE-derived TWS and hydrological models. Zhang et al. [16] estimated the annual EWH (equivalent water height) changes of the lower Three-Rivers headwater region in southwestern China using the vertical displacements of GPS time series obtained from the Crustal Movement Observation Network of China (CMONOC). Zhong et al. [17] analyzed GPS-inverted mass changes under different density distributions of GPS stations and compared the inversion results with GRACE/GFO solutions in spatial and temporal domains.
To improve the accuracy of TWS inversion using GPS observations, Fok and Liu [18] proposed using terrain-corrected GPS and GRACE-derived ”virtual GPS stations” to solve the problem of irregularly distributed GPS stations and the neglect of the terrain effect in southwestern China. Liu et al. [19] introduced external TWS-derived displacements and used them as pseudo GPS sites in the inversion process. To improve the TWS inversion results in the boundary regions, Shen et al. [20] developed a boundary-included inversion model that accounts for the mass change effect from the near but exterior region. Lai et al. [21] applied truncated singular value decomposition regularization to more stably solve the inversion problem.
Relatively few studies have discussed the reliability in obtaining hydrological deformation information from GPS observations. Most previous studies considered TWS variations to be the main cause of such elastic deformations on the Earth’s surface. The existing TWS inversion methods therefore generally assume that the vertical GPS coordinate changes are identical to the hydrological deformations [12,14,15,16,18,19,20]. However, other mass loading changes, such as atmospheric loading (ATML) [22,23] cannot be neglected. An estimation of the ATML and corresponding corrections are sometimes necessary, but accurate ATML correction models are typically difficult to obtain due to the limited atmospheric pressure data resolution and terrain change complexities [24]. Continuous GPS time series also include other (seasonal) error sources, such as non-tidal ocean loading (NTOL), higher-order ionospheric effects, bedrock thermal expansion, and errors in the antenna phase center variation models [25,26]. Ignoring these effects is conducive to accurately estimating TWS variations. Independent component analysis (ICA) has been proposed to extract the hydrological signals from regional GPS network observations [27,28,29,30]. Previous studies [31,32,33] have confirmed that ICA is an effective method to extract hydrological deformations from continuous GPS time series.
In this paper, we propose to extract hydrological deformations from regional GPS networks and use the independent GPS displacements to estimate the TWS variations (hereafter referred to as GPS(ICA)). A case study is carried out in the Sichuan-Yunnan region, and the results are compared with those from the GRACE and GLDAS models.
2. Data and Methods
2.1. Continuous GPS Observation and Inversion Method
The study area is located in the Sichuan-Yunnan region of China, as shown in Figure 1. We selected 47 GPS sites from CMONOC to obtain their six-year vertical coordinate time series (2011–2016). GAMIT/GLOBK software was used to generate the daily solutions in ITRF2008 reference frame, with main parameters including the station coordinates, zenith tropospheric delays (one per hour), and gradients (one per day in the N/S and E/W directions). Tropospheric delays were corrected using the Vienna Mapping Function HGMF and DGMF. The ANTEX model was used to correct the antenna phase center variations. Non-tidal surface loading effects and high-order ionospheric delays are not corrected in the time series.
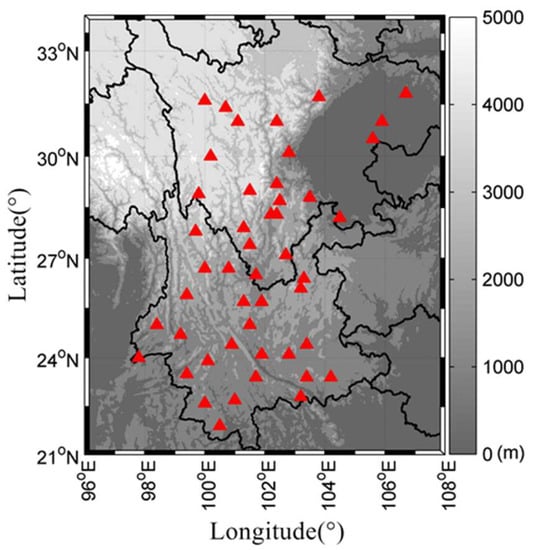
Figure 1.
Study area map. The red triangles are the GPS sites use in the inversion calculation in the Sichuan-Yunnan region. The background colors show the surface topography.
Cycle variations in the continuous GPS time series are mainly caused by mass loading changes on the Earth’s surface. The deformations caused by mass loading can be computed based on elastic theory [13]. The deformations observed by GPS can therefore be used to study the mass loading changes on the Earth’s surface. The elastic deformation induced by mass loading can be calculated by:
where is the angular distance between the point load and location, is the mass load, and are the radius and mass of the Earth, respectively, and and are the elastic Love numbers and Legendre polynomials, respectively. Equation (1) can be expressed as , where represents the Green’s functions and is the surface grid mass load. In this paper, we used the code provided by Chanard et al. [34] to compute the Green’s functions [35] based on the Preliminary Reference Earth Model (PREM) [36]. Furthermore, as elastic vertical motion rapidly decreases with distance from a load [14], we thus extended the studied area by 2° in both longitude and latitude when computing the Green’s functions to avoid the edge effect [14].
The elastic deformation is contributed from the total mass load on the surface. Suppose that there are grids and GPS sites in the inversion region. The displacement at the th GPS site position can then be expressed as:
where is the design matrix, is the angular distance between a grid mass in the inversion area and the th GPS site position, and is the grid mass load in the inversion area, because the distant mass load is neglected. The grid mass load derived displacements at the GPS sites can be expressed as:
where , and .
Considering that there is usually a limited number of GPS sites in the inversion, a regularization constraint is applied to obtain the TWS variations across the study area. The inversion model in Equation (3) with constraints thus becomes:
where is the design matrix consisting of Green’s functions, is the unknown mass load at each grid cell, is the vertical displacement at each GPS site, and is the Laplacian operator [37]. The templates of the Laplacian smoothing constraints on neighboring grids are shown in Figure 2.
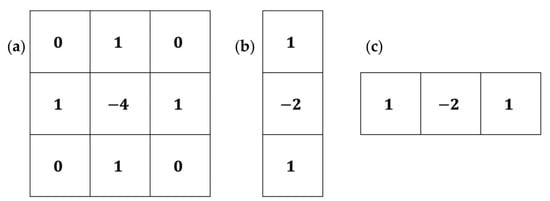
Figure 2.
The templates of Laplacian operator: (a) is the template for the internal grids; (b,c) are for the boundary grids.
The regularized solution to estimate the grid mass load in Equation (4) is used to minimize the combination in Equation (5):
where is a roughness factor that specifies by how much the neighboring pixels values may differ, and is the weight matrix. The roughness factor balances the relative importance between data misfit () and smoothness () and is selected based on the L-curve method [38] in our study. Figure 3 shows the changes of misfit and smoothness with different roughness factors. We evaluated a group of roughness factors and selected in our study.
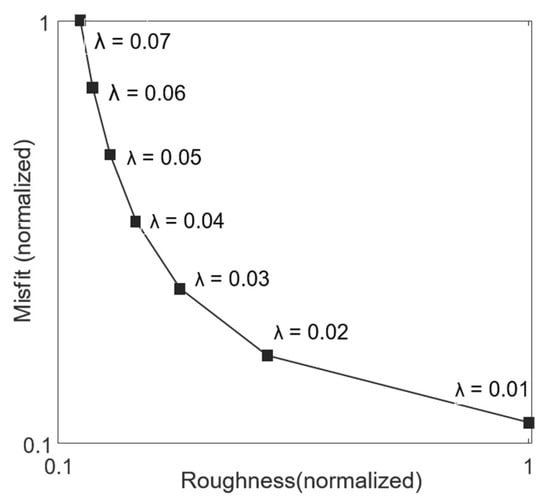
Figure 3.
Trade-off curve between roughness and misfit. Both the roughness and misfit have been normalized.
The final TWS variations can be estimated by:
The covariance matrix of the final estimation can be expressed as [39]:
where is the variance of unit weight. In the case of a certain number of grids to be inverted, the more GPS sites number means the more observation equations, and the inversion would be with better precision and stability.
2.2. Inversion Method Based on ICA
The TWS inversion method using GPS measurements is based on the assumption that the deformations monitored by GPS are caused by TWS variations. ICA has been proven to be a useful tool for extracting geophysical signals from observed geophysical series, such as GPS time series [27,28,29,30,31,32,40], GRACE time series [41,42,43], and InSAR monitoring data [44,45]. In this paper, ICA is used to extract hydrological deformations from GPS time series, and the FastICA algorithm [46,47] is applied in the separation. Regional GPS time series are used as mixed signals and treated as ICA inputs. Some temporally independent components (ICs) can be separated from the GPS coordinate time series by , where represents the GPS coordinate time series and is the separating matrix. Then the inputs can be expressed as:
where the row vectors in are ICs estimated by ICA processing and the column vectors in the invert matrix of are the spatial responses of ICs. Principal component analysis (PCA) was used to preprocess the inputs before we performed ICA and an appropriate number of principal components (PCs) need to remain for the following ICA processing. We used a trial and error approach to select the number of PCs [48], and found that in most cases the choice of the number of remaining PCs had little effect on the separation of the top several ICs. The contribution of each IC to the GPS observations can be characterized using ratio values defined as:
where the displacement GPSICk is the product of ICk and the corresponding spatial response. A smaller ratio value implies a more significant contribution for the corresponding IC [28], and the ICs are reordered in ascending order [40]. The top six ICs are shown in Figure 4a and the ratio values of the GPSICs are shown in Figure 4b. We found IC1 contributes most for the GPS coordinate time series.
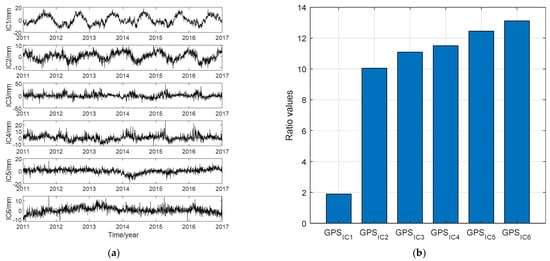
Figure 4.
(a) The top six ICs extracted from vertical GPS coordinate time series; (b) the ratio value of each displacement GPSICs.
The separated ICs were compared with external data to trace their potential geophysical causes. We computed the daily hydrological loadings at each GPS site and compared the results with GPSIC1, as shown in Figure 5. The averaged hydrological loading displacement is consistent with GPSIC1 in terms of its amplitude and phase, and the correlation coefficient is 0.78. The term GPSIC1 is therefore thought to represent hydrological deformation, and GPSIC1 is then used in the subsequent inversion step.
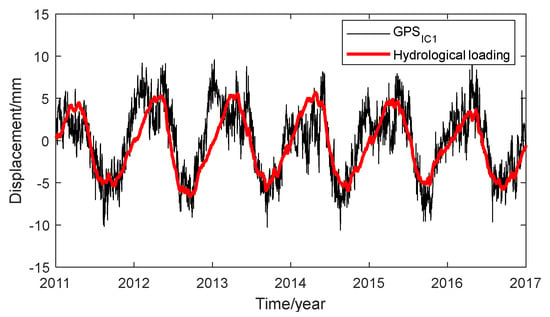
Figure 5.
The comparison between modeled daily land water storage loading (LWS) displacement (http://massloading.net/, accessed on 16 November 2021) and GPSIC1. For LWS, we use the GEOS-FPIT model developed by the Global Modeling and Assimilation Office at NASA Goddard Space Flight Center.
An inversion result using mass loading-corrected displacements is also applied for comparison. The ATML and NTOL were computed using the International Mass Loading Service [49] in the center-of-figure (CF) frame using the model of Modern Era Retrospective-analysis for Research and Applications (MERRA) and the Max Planck Institute Ocean Model (MPIOM) 06, respectively. We averaged the ATML and NTOL series into daily results and removed them from the GPS time series. The corrected GPS time series was then used to invert the TWS variation in the Sichuan-Yunnan Region. Previous studies on the thermal effect on the vertical displacements of GPS stations in China [50,51] indicate that the effect of thermal expansion on the vertical GPS coordinate time series is limited in low-latitude areas. The thermal expansion effect is thus not considered in our case study of the Sichuan-Yunnan region.
2.3. GRACE Measurements and GLDAS Hydrological Models
The GRACE-derived TWS variations and products of the GLDAS hydrological models were used to compare with our inversion results. For the GRACE TWS data, we used the surface mass change data based on the spherical harmonics from JPL (maximum degree/order: n = 60) [52,53] (available at https://grace.jpl.nasa.gov/, accessed on 16 November 2021). For the products, the non-tidal variability was corrected using the time variable background model known as Atmosphere and Ocean De-aliasing Level-1B (AOD1B). The degree 1 coefficients were estimated from Sun et al. [54]. The C20 (degree 2 order 0) and C30 coefficients were replaced with satellite laser ranging solutions [55]. We multiplied the GRACE data by the provided scaling grid product. A detailed description of the data processing, scaling factor derivation, and caveats are available in [52]. The missing month was then interpolated from the adjacent two months. The TWS was also estimated using the sum of soil moisture in all layers, accumulated snow, and plant canopy surface water from the GLDAS model, and further used to compare with the GRACE and GPS-derived TWS variation results. We used the products of the monthly data from the GLDAS-2.1 Noah model with a spatial resolution of 1° × 1°.
3. Inversion Results and Discussion
3.1. Estimated TWS Variations in the Sichuan-Yunnan Region Using Different Methods
We estimated the monthly TWS variations of year 2011 based on the inversion theory and hydrological deformation extracted from the vertical GPS coordinate time series in Section 2.2. The results are shown in Figure 6. We also adopted the conventional approach to invert the TWS variations using GPS observations, in which the ATML and NTOL were removed. The inversion results are shown in Figure 7. The GRACE and GLDAS-derived TWS variations in the Sichuan-Yunnan are presented in Figure 8 and Figure 9, respectively. Note that there are differences in the color bar scale in Figure 6, Figure 7, Figure 8 and Figure 9.
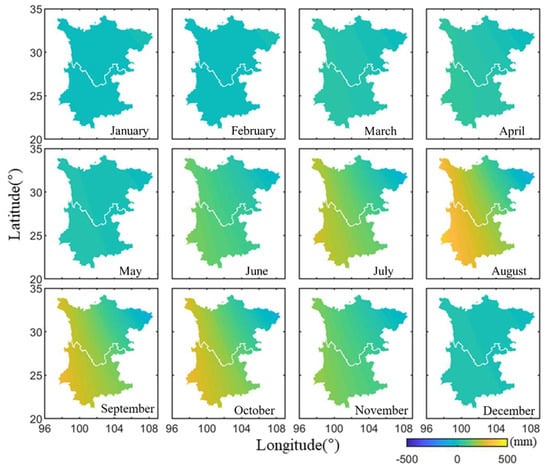
Figure 6.
Monthly variations (2011) of the TWS in Sichuan-Yunnan estimated by GPS based on ICA.
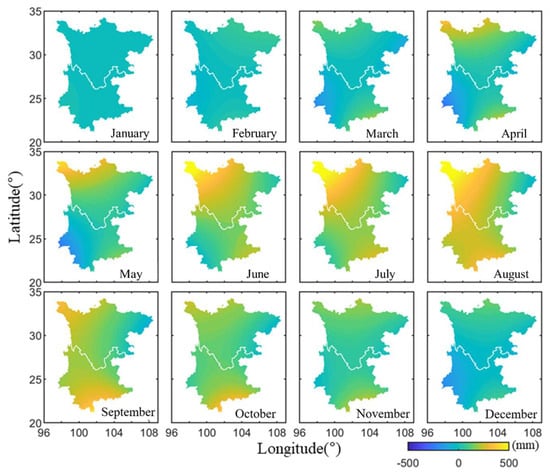
Figure 7.
Monthly variations (2011) of the TWS in Sichuan-Yunnan estimated by GPS after removing the ATML and NTOL.
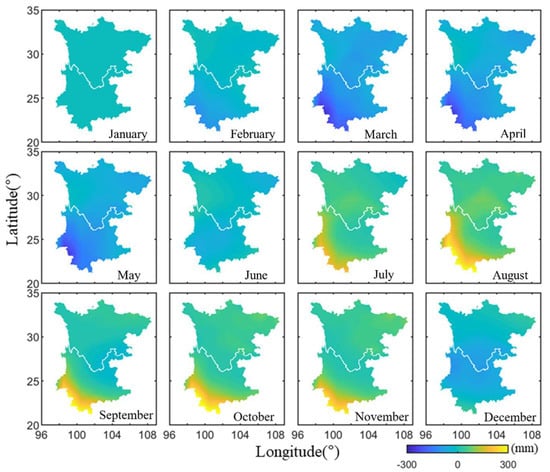
Figure 8.
Monthly variations (2011) of the TWS in Sichuan-Yunnan estimated by GRACE.
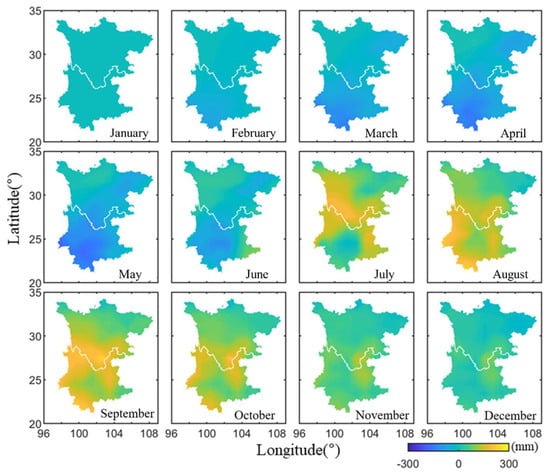
Figure 9.
Monthly variations (2011) of the TWS in Sichuan-Yunnan estimated by GLDAS.
A comparison of the monthly TWS variations obtained by the four different methods in Figure 6, Figure 7, Figure 8 and Figure 9 shows that the monthly changes and spatial variations are similar overall. In general, the TWS gradually increases from northeast to southwest, and the variations in the southwest of Yunnan Province are the most apparent. However, the TWS variation results obtained by the GPS inversion exhibit abnormal changes in the northwestern region of Sichuan-Yunnan, where there is very complex terrain and some GPS sites are located above 4000 m. Additional comparisons of the TWS variations in the northwestern Sichuan-Yunnan region are analyzed and presented in the next section. We spatially averaged the TWS grid data in the Sichuan-Yunnan region to analyze the TWS change rules of the four different results in terms of temporal pattern. The average monthly TWS variations for the different methods are shown in Figure 10a. The temporal change rules of the TWS obtained using the different methods are in good agreement; all reach a minimum in February–March (winter), and a maximum in August–October (late summer). By computing the difference between the TWS values in September and March in each grid, we obtained the distribution of the maximum TWS for each method. The results are shown in Figure 10b.
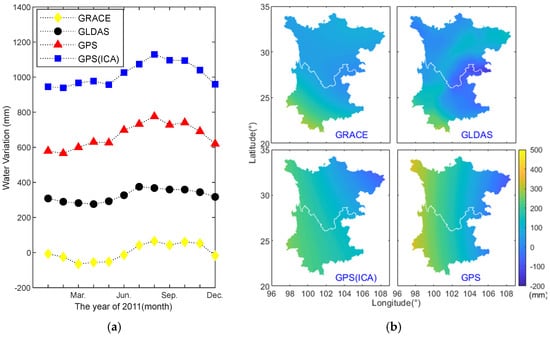
Figure 10.
TWS variations results obtained using different methods. (a) Monthly variations of the TWS grid value in Sichuan-Yunnan from different methods; (b) peak-to-peak values (September minus March) of TWS for different methods.
Figure 10 further illustrates the spatiotemporal distribution of the TWS variation rules of the four methods. The TWS inverted by the GPS and GPS(ICA) methods are found to vary the most, with a range of approximately 500 mm, whereas the range of GRACE and GLDAS results are approximately 300 mm. The change in GLDAS is the least notable and may be because the water changes in the rivers and reservoirs are not fully considered in the GLDAS-derived TWS result.
3.2. Northwestern Sichuan-Yunnan Region
Another clear difference among the four inverted results is the abnormal TWS change of the GPS inverted results in northwestern Sichuan Yunnan, as shown in Figure 10. To further investigate this anomaly, we compare the TWS change in the northwestern part of the Sichuan-Yunnan region and the entire region. We average the monthly TWS results in northwestern Sichuan-Yunnan (longitude: 99.5° E–101.5° E, latitude: 29.5° N–31.5° N) and the entire region for all of the investigated years. The results are shown in Figure 11, in which the legends of northwestern Sichuan-Yunnan results are marked with an asterisk.
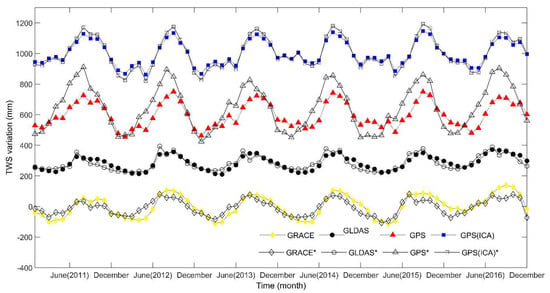
Figure 11.
TWS variations in northwestern Sichuan-Yunnan and the entire region from 2011 to 2016. The averaged grid data of monthly TWS variations in northwestern Sichuan-Yunnan (* mark) and in the entire region.
There is no significant difference between the TWS variations in northwestern Sichuan-Yunnan and the entire Sichuan-Yunnan region for the results obtained using GPS(ICA), GRACE, and GLDAS. In contrast, the variations of GPS-inverted TWS in northwestern Sichuan-Yunnan are higher than those in the entire region from April to August for all six years. The comparisons indicate that the GPS(ICA) inversion results are more consistent with those of GRACE and GLDAS than that of the GPS (ATML and NTOL corrected) observations.
To quantitatively compare the estimated TWS variations in northwestern Sichuan-Yunnan and the entire region using the different methods, referring to the fitting model for GPS coordinate time series [56], we fit the series in Figure 11 according to:
where are the coefficients and can be estimated using the least squares method. We can obtain the annual amplitude for each series by .
The annual amplitudes of the estimated TWS variations for the different methods in northwestern Sichuan-Yunnan and the entire region are shown in Table 1. The in Table 1 is defined as . The seasonal amplitude of the GPS-derived TWS in northwestern Sichuan-Yunnan region shows significant difference, nearly 50% larger than the results of the entire region, whereas no such notable discrepancy is found in the results obtained using the other three methods.

Table 1.
Comparisons between the estimated TWS variations in northwestern Sichuan-Yunnan and the entire region for the different methods.
3.3. Discussion
The anomalies of the GPS-derived TWS variations in northwestern Sichuan-Yunnan indicate that the coordinate time series used in the inversion contains deformation information or errors other than hydrological deformation. Considering the fact that northwestern Sichuan-Yunnan is near the Qinghai-Tibet Plateau and the terrain is extremely complex (Figure 1), the inaccurate ATML correction in this area may be the cause of anomalies in the GPS inversion result. The height of the GPS sites in northwestern Sichuan-Yunnan is generally around 3000 m, and the discrepancies between these sites and others can reach 2000–3000 m. In the ATML calculation, the atmospheric pressure data usually do not reflect the real atmospheric pressure in the Sichuan-Yunnan region. The ATML is therefore often inaccurately estimated in areas with complex terrain changes such as the Sichuan-Yunnan region [24].
We computed the averaged NTOL and ATML displacements and their RMS values at each site, as shown in Figure 12. The effect of the NTOL is found to be limited in the Sichuan-Yunnan region, the amplitude of which is only approximately 1 mm. The period from April to August is found to have large ATML variations, which is consistent with the time period of the TWS anomalies that occurred in the northwestern Sichuan-Yunnan region. If the ATML during this period in the northwestern Sichuan-Yunnan region is overestimated, the elastic responses observed by GPS would also be overestimated, which would be thought to be hydrological deformations. The inverted TWS will therefore be overestimated, which reasonably explains why there are anomalies in the northwestern Sichuan-Yunnan region from April to August.
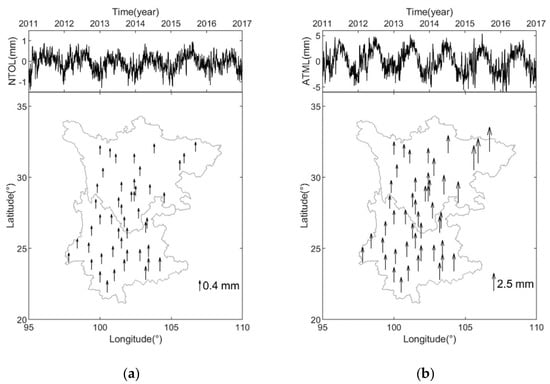
Figure 12.
Averaged (a) NTOL and (b) ATML series and the RMS values of these two loading displacements for each GPS sites.
Another possible reason for the anomaly in northwestern Sichuan-Yunnan may be the effect of high topographic variability that can cause more residual tropospheric errors in processing GPS observations.
4. Conclusions
GPS can be used to measure elastic deformation caused by mass loading variations on the Earth’s surface. Accurate hydrological deformation information from the GPS coordinate time series is the most critical step in TWS inversion. We propose a TWS inversion method using GPS observations based on independent component analysis (ICA). The ICA method is first used to separate the hydrological deformations from GPS coordinate time series. The TWS variations are then quantitatively estimated using the separated hydrological deformation displacements.
We estimate the TWS variations in the Sichuan-Yunnan region in China using different approaches, including GPS, GPS(ICA), GRACE, and GLDAS methods. The overall results of the four methods show similar change patterns in the spatial and temporal domain. Some differences are found in the results due to the completely different observation methods and implied sampling and process-representations. The TWS variations inverted by GPS and GPS(ICA) show more notable variations compared with the GRACE and GLDAS results. We find that anomalies occur in the northwestern Sichuan-Yunnan region for the GPS inversion results, where GPS sites are located within extreme and complex terrain changes.
We quantitatively evaluate the differences between the amplitude of the four different method-derived TWS variations in northwestern Sichuan-Yunnan and the entire region and find that the annual amplitude of the GPS-inverted TWS in the northwestern region is nearly twice that of the entire region. The anomalies in the GPS inversion results are further explored, and we suggest that the extreme and complex terrain changes may be the main cause of the GPS inverted TWS anomalies in the northwestern Sichuan-Yunnan region. The proposed GPS(ICA) method attenuates this problem and more accurately estimates the TWS variation results in the Sichuan-Yunnan region, which provides a new method for estimating regional TWS variations using GPS observations.
Author Contributions
Conceptualization, B.L. and W.Y.; methodology, B.L.; software, B.L.; validation, B.L. and W.Y.; formal analysis, B.L. and W.Y.; investigation, X.X., W.D. and C.K.; data curation, X.X.; writing—original draft preparation, B.L. and W.Y.; writing—review and editing, W.D., X.X. and C.K.; supervision, W.D., X.X. and C.K.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by the National Natural Science Foundation of China (Grant No. 41904003, 42074033, 41774040), the Natural Science Foundation of Hunan Province, China (Grant No. 2020JJ5571), and Open Fund of Engineering Laboratory of Spatial Information Technology of Highway Geological Disaster Early Warning in Hunan Province (Changsha University of Science & Technology) (Grant No. KFJ190602).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Thanks to the GNSS data product service platform of China Earthquake Administration for providing data support. The time series of the 47 GPS stations used in this paper are uploaded to Figshare, and readers can download the data from https://doi.org/10.6084/m9.figshare.13490442.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sterling, S.M.; Ducharne, A.; Polcher, J. The impact of global land-cover change on the terrestrial water cycle. Nat. Clim. Chang. 2012, 3, 385–390. [Google Scholar] [CrossRef]
- Jin, S.; Feng, G. Large-scale variations of global groundwater from satellite gravimetry and hydrological models, 2002–2012. Glob. Planet. Chang. 2013, 106, 20–30. [Google Scholar] [CrossRef]
- Anyah, R.O.; Forootan, E.; Awange, J.L.; Khaki, M. Understanding linkages between global climate indices and terrestrial water storage changes over Africa using GRACE products. Sci. Total Environ. 2018, 635, 1405–1416. [Google Scholar] [CrossRef] [Green Version]
- Swenson, S.; Yeh, P.J.F.; Wahr, J.; Famiglietti, J.S. A comparison of terrestrial water storage variations from GRACE with in situ measurements from Illinois. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.E.; Meng, C.J.; Arsenault, K.R.; Cosgrove, B.; Radakovich, J.D.; Bosilovich, M.G.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Tregoning, P.; Watson, C.S.; Ramillien, G.; Mcqueen, H.; Zhang, J. Detecting hydrologic deformation using GRACE and GPS. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Tesmer, V.; Steigenberger, P.; Van Dam, T.; Mayer-Gürr, T. Vertical deformations from homogeneously processed GRACE and global GPS long-term series. J. Geod. 2011, 85, 291–310. [Google Scholar] [CrossRef]
- Fu, Y.; Freymueller, J.T. Seasonal and long-term vertical deformation in the Nepal Himalaya constrained by GPS and GRACE measurements. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Pan, Y.; Shen, W.; Shum, C.K.; Chen, R. Spatially varying surface seasonal oscillations and 3-D crustal deformation of the Tibetan Plateau derived from GPS and GRACE data. Earth Planet. Sci. Lett. 2018, 502, 12–22. [Google Scholar] [CrossRef]
- Chew, C.; Small, E.E. Terrestrial water storage response to the 2012 drought estimated from GPS vertical position anomalies. Geophys. Res. Lett. 2014, 41, 6145–6151. [Google Scholar] [CrossRef]
- Argus, D.F.; Fu, Y.; Landerer, F.W. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Landerer, F.W. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. J. Geophys. Res. 2014, 120, 552–566. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, T. Terrestrial Water Storage Anomalies Associated with Drought in Southwestern USA from GPS Observations. Surv. Geophys. 2016, 37, 1139–1156. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y.; Fok, H.S.; Hu, Y.; Chen, Q. Potential Seasonal Terrestrial Water Storage Monitoring from GPS Vertical Displacements: A Case Study in the Lower Three-Rivers Headwater Region, China. Sensors 2016, 16, 1526. [Google Scholar] [CrossRef]
- Zhong, B.; Li, X.; Chen, J.; Li, Q.; Liu, T. Surface Mass Variations from GPS and GRACE/GFO: A Case Study in Southwest China. Remote Sens. 2020, 12, 1835. [Google Scholar] [CrossRef]
- Fok, H.S.; Liu, Y. An Improved GPS-Inferred Seasonal Terrestrial Water Storage Using Terrain-Corrected Vertical Crustal Displacements Constrained by GRACE. Remote Sens. 2019, 11, 1433. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Fok, H.S.; Tenzer, R.; Chen, Q.; Chen, X. Akaike’s Bayesian Information Criterion for the Joint Inversion of Terrestrial Water Storage Using GPS Vertical Displacements, GRACE and GLDAS in Southwest China. Entropy 2019, 21, 664. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Yan, H.; Peng, P.; Feng, W.; Zhang, Z.; Song, Y.; Bai, X. Boundary-Included Enhanced Water Storage Changes Inferred by GPS in the Pacific Rim of the Western United States. Remote Sens. 2020, 12, 2492. [Google Scholar] [CrossRef]
- Lai, Y.R.; Wang, L.; Bevis, M.; Fok, H.S.; Alanazi, A. Truncated Singular Value Decomposition Regularization for Estimating Terrestrial Water Storage Changes Using GPS: A Case Study over Taiwan. Remote Sens. 2020, 12, 3861. [Google Scholar] [CrossRef]
- van Dam, T.M.; Blewitt, G.; Heflin, M.B. Atmospheric pressure loading effects on Global Positioning System coordinate determinations. J. Geophys. Res. 1994, 99, 23939–23950. [Google Scholar] [CrossRef]
- Zerbini, S.; Richter, B.; Negusini, M.; Romagnoli, C.; Simon, D.; Domenichini, F.; Schwahn, W. Height and gravity variations by continuous GPS, gravity and environmental parameter observations in the southern Po Plain, near Bologna, Italy. Earth Planet. Sci. Lett. 2001, 192, 267–279. [Google Scholar] [CrossRef]
- van Dam, T.; Altamimi, Z.; Collilieux, X.; Ray, J. Topographically induced height errors in predicted atmospheric loading effects. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. 2002, 107, 2075. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Chen, W.; Zhu, Y.; Zhang, W.; Zhong, M. Contributions of thermal expansion of monuments and nearby bedrock to observed GPS height changes. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Dai, W.; Peng, W.; Meng, X. Spatiotemporal analysis of GPS time series in vertical direction using independent component analysis. Earth Planets Space 2015, 67, 189. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Dai, W.; Liu, N. Extracting seasonal deformations of the Nepal Himalaya region from vertical GPS position time series using Independent Component Analysis. Adv. Space Res. 2017, 60, 2910–2917. [Google Scholar] [CrossRef]
- Liu, B.; King, M.A.; Dai, W. Common mode error in Antarctic GPS coordinate time-series on its effect on bedrock-uplift estimates. Geophys. J. Int. 2018, 214, 1652–1664. [Google Scholar] [CrossRef]
- Peng, W.; Dai, W.; Santerre, R.; Cai, C.; Kuang, C. GNSS Vertical Coordinate Time Series Analysis Using Single-Channel Independent Component Analysis Method. Pure Appl. Geophys. 2017, 174, 723–736. [Google Scholar] [CrossRef]
- Gualandi, A.; Serpelloni, E.; Belardinelli, M.E. Blind source separation problem in GPS time series. J. Geod. 2016, 90, 323–341. [Google Scholar] [CrossRef]
- Gualandi, A.; Avouac, J.; Galetzka, J.; Genrich, J.F.; Blewitt, G.; Adhikari, L.B.; Koirala, B.P.; Gupta, R.; Upreti, B.N.; Prattsitaula, B. Pre- and post-seismic deformation related to the 2015, Mw7.8 Gorkha earthquake, Nepal. Tectonophysics 2017, 714–715, 90–106. [Google Scholar] [CrossRef]
- Yan, J.; Dong, D.; Bürgmann, R.; Materna, K.; Tan, W.; Peng, Y.; Chen, J. Separation of Sources of Seasonal Uplift in China Using Independent Component Analysis of GNSS Time Series. J. Geophys. Res. Solid Earth 2019, 124, 11951–11971. [Google Scholar] [CrossRef]
- Chanard, K.; Avouac, J.P.; Ramillien, G.; Genrich, J. Modeling deformation induced by seasonal variations of continental water in the Himalaya region: Sensitivity to Earth elastic structure. J. Geophys. Res. Solid Earth 2014, 119. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.Y.; Li, Y.B.; Huang, Y.; Deng, H.T.; Xu, S.Q.; Ning, J.S. Green’s function of the deformation of the Earth as a result of atmospheric loading. Geophys. J. Int. 2004, 159, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Harris, R.A.; Segall, P. Detection of a locked zone at depth on the Parkfield, California, segment of the San Andreas Fault. J. Geophys. Res. 1987, 92, 7945–7962. [Google Scholar] [CrossRef]
- Hansen, P.C.; Oleary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, G. Regularization and adjustment. In Sciences of Geodesy-II; Xu, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 293–337. [Google Scholar] [CrossRef]
- Liu, B.; Xing, X.M.; Tan, J.B.; Xia, Q. Modeling Seasonal Variations in Vertical GPS Coordinate Time Series Using Independent Component Analysis and Varying Coefficient Regression. Sensors 2020, 20, 5627. [Google Scholar] [CrossRef]
- Forootan, E.; Awange, J.L.; Kusche, J.; Heck, B.; Eicker, A. Independent patterns of water mass anomalies over Australia from satellite data and models. Remote Sens. Environ. 2012, 124, 427–443. [Google Scholar] [CrossRef] [Green Version]
- Forootan, E.; Kusche, J. Separation of global time-variable gravity signals into maximally independent components. J. Geod. 2012, 86, 477–497. [Google Scholar] [CrossRef]
- Boergens, E.; Rangelova, E.; Sideris, M.G.; Kusche, J. Assessment of the capabilities of the temporal and spatiotemporal ICA method for geophysical signal separation in GRACE data. J. Geophys. Res. Solid Earth 2014, 119, 4429–4447. [Google Scholar] [CrossRef]
- Gaddes, M.E.; Hooper, A.; Bagnardi, M.; Inman, H.; Albino, F. Blind Signal Separation Methods for InSAR: The Potential to Automatically Detect and Monitor Signals of Volcanic Deformation. J. Geophys. Res. 2018, 123, 10226–10251. [Google Scholar] [CrossRef] [Green Version]
- Ebmeier, S.K. Application of independent component analysis to multitemporal InSAR data with volcanic case studies. J. Geophys. Res. Solid Earth 2016, 121, 8970–8986. [Google Scholar] [CrossRef]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [Green Version]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Barnie, T.; Oppenheimer, C. Extracting High Temperature Event radiance from satellite images and correcting for saturation using Independent Component Analysis. Remote Sens. Environ. 2015, 158, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Petrov, L. The International Mass Loading Service. In REFAG 2014; Springer: Cham, Switzerland, 2015; pp. 79–83. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Chen, W.; Zhu, Y.; Zhang, W.; Zhong, M.; Liu, G. Thermal Effects on Vertical Displacement of GPS Stations in China. Chin. J. Geophys. 2010, 53, 252–262. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, K.; Deng, L.; Li, Z. Impact on Nonlinear Vertical Variation of GNSS Reference Stations Caused by Thermal Expansion. Acta Geod. Cartogr. Sin. 2015, 44, 473–480. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, WR011453. [Google Scholar] [CrossRef]
- Landerer, F. CSR TELLUS GRACE Level-3 Monthly Ocean Bottom Pressure Anomaly Release 6.0 Version 04 in netCDF/ASCII/GeoTIFF Formats; Physical Oceanography Distributed Active Archive Center: Pasadena, CA, USA, 2021. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef] [Green Version]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B.; Sabaka, T.J. The Critical Role of Satellite Laser Ranging for Correcting and Validating GRACE & GRACE-FO Gravity Products and Bridging the Data Gap; American Geophysical Union: San Francisco, CA, USA, December 2019. [Google Scholar]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System; University of California: San Diego, CA, USA, 2002. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).