Automatic Mapping and Characterisation of Linear Depositional Bedforms: Theory and Application Using Bathymetry from the North West Shelf of Australia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
2.1.1. Synthetic DEM
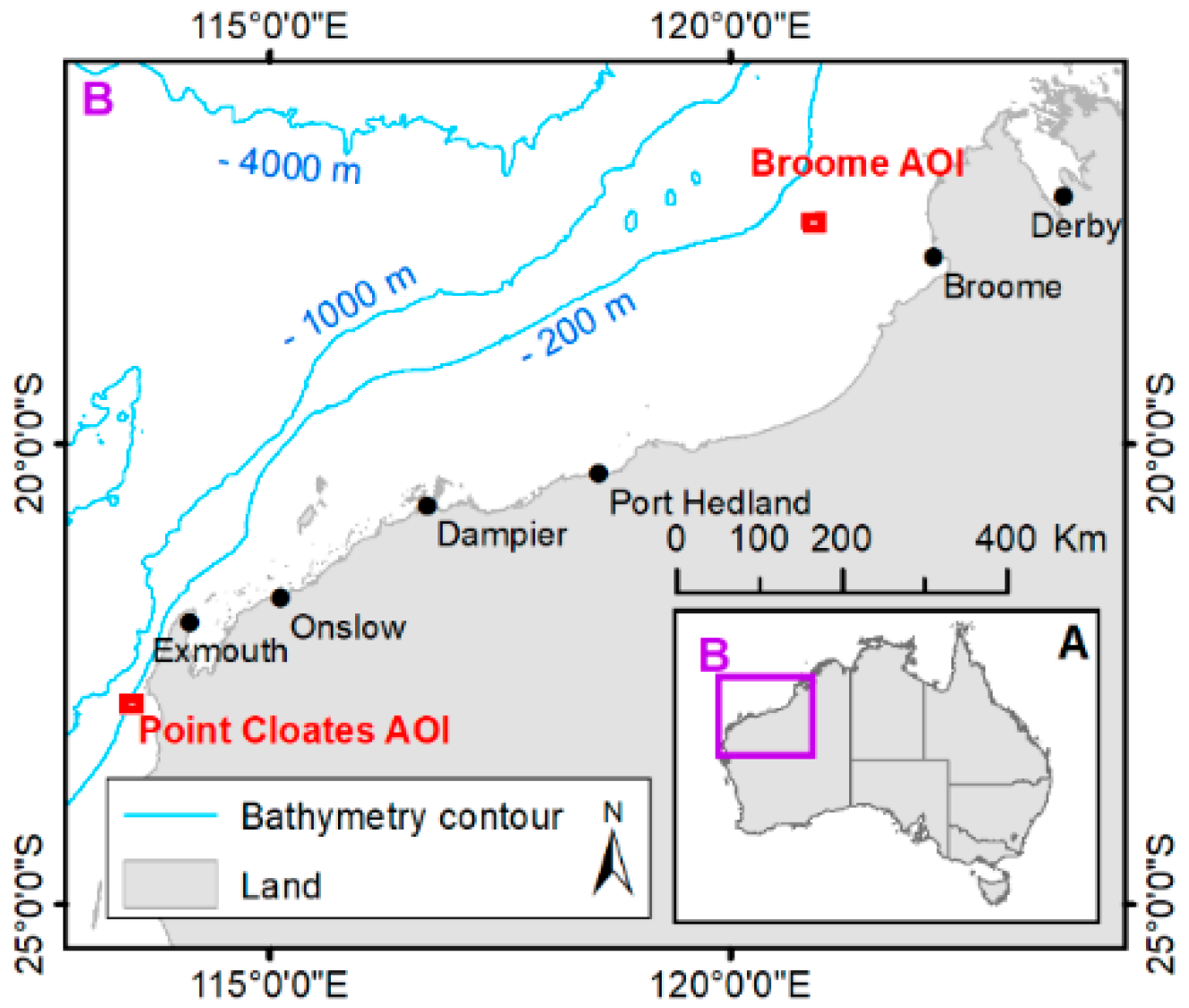
2.1.2. Broome Bathymetry
2.1.3. Point Cloates Bathymetry
2.2. Processing Tools
3. Methods
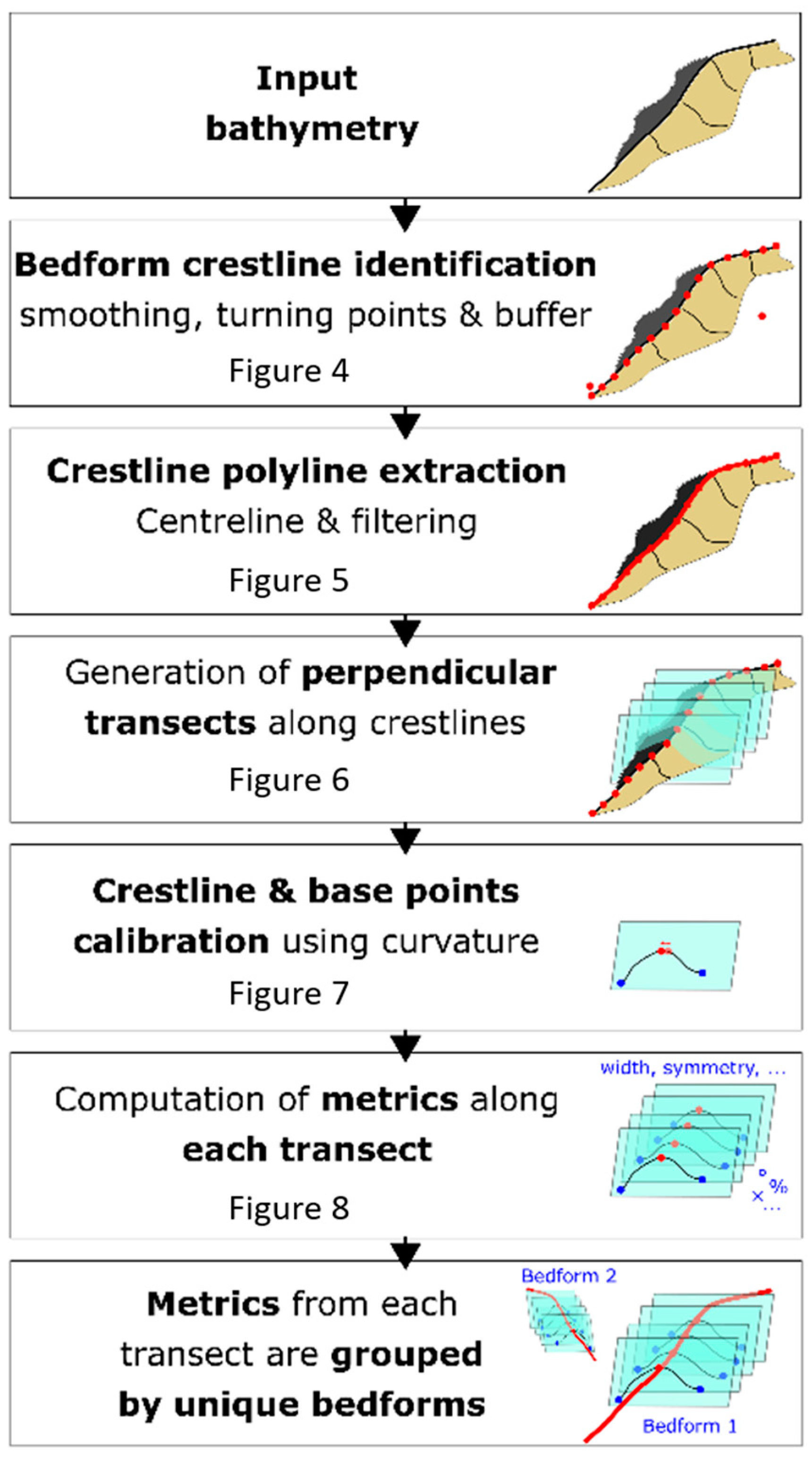
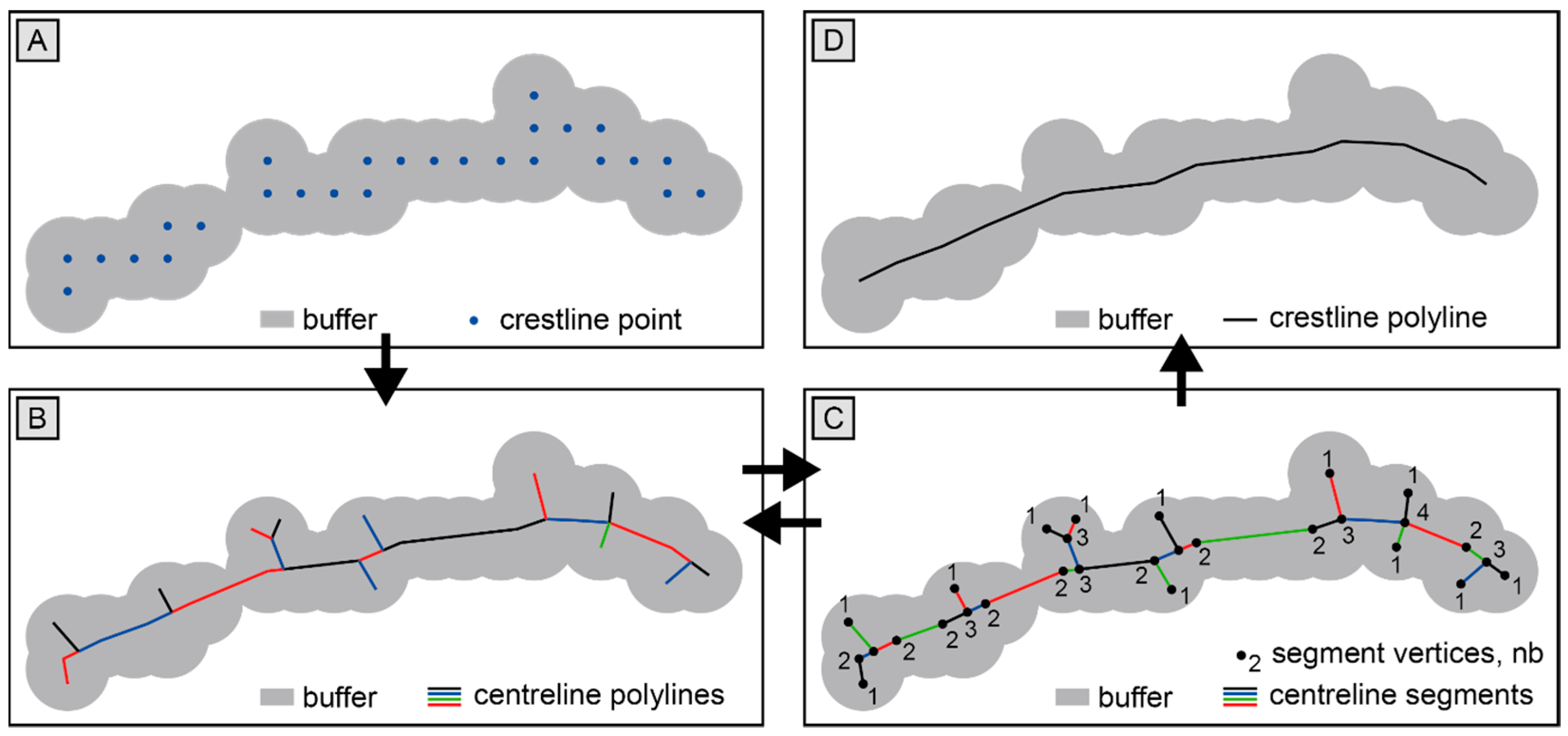
3.1. Extraction of Bedform Crestlines
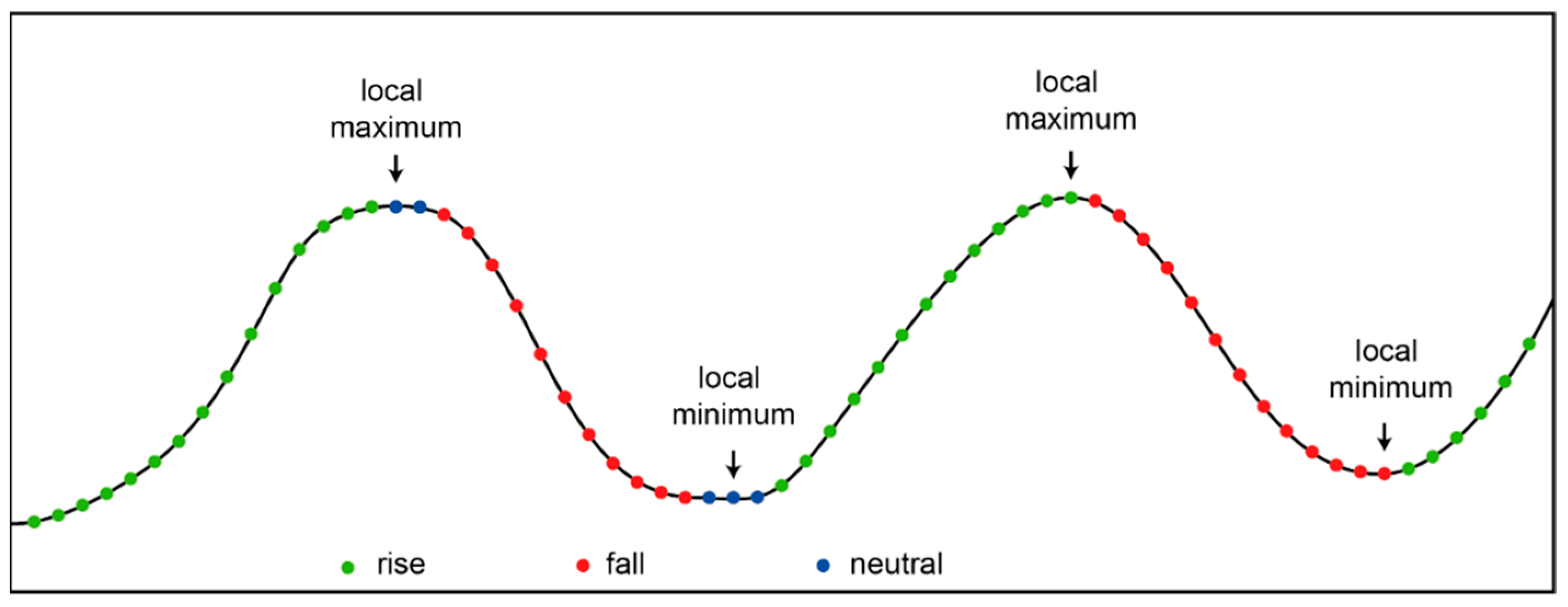
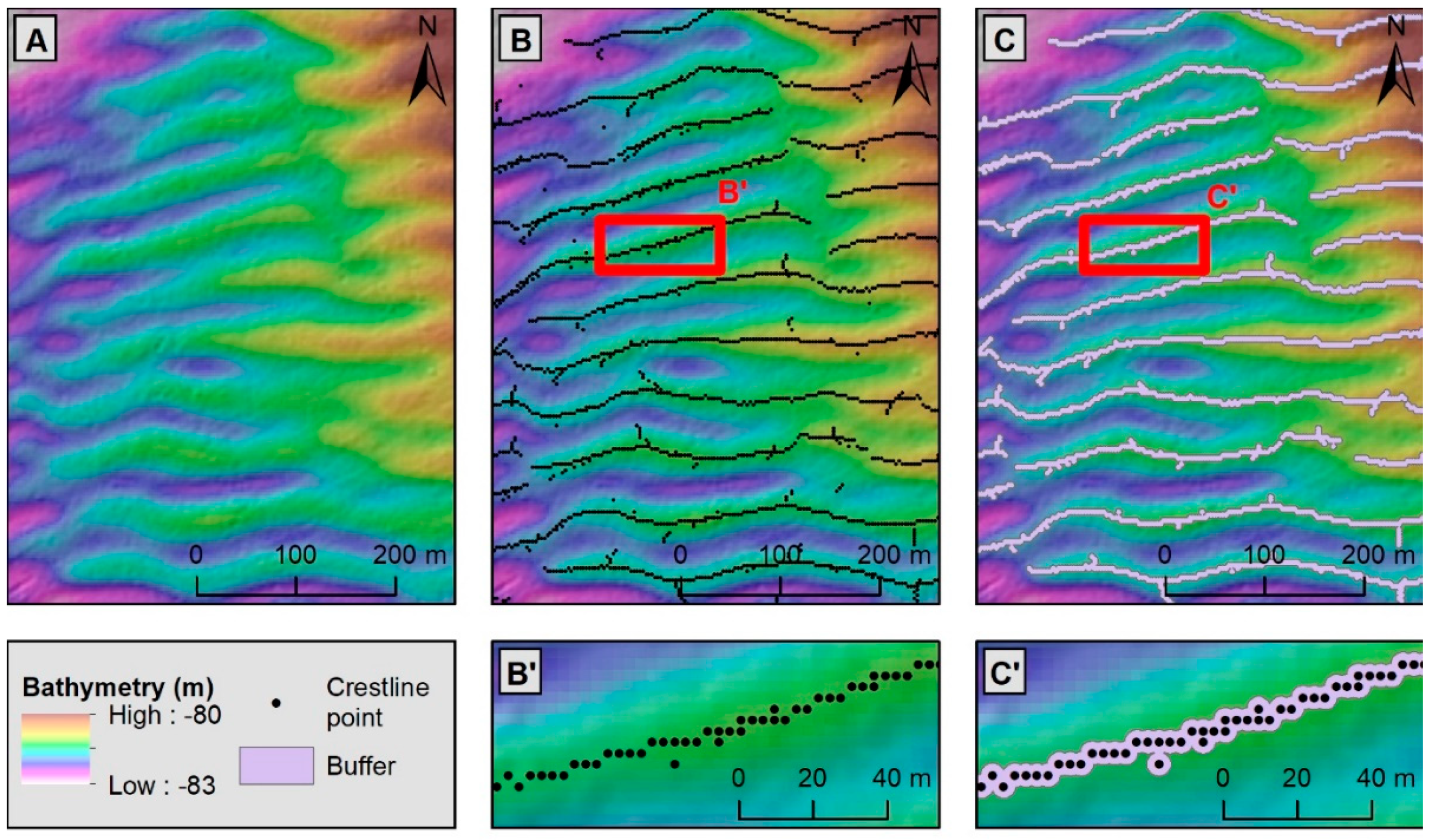
3.1.1. Identification of Bedform Crestline Points
3.1.2. Generation of Crestline Polylines
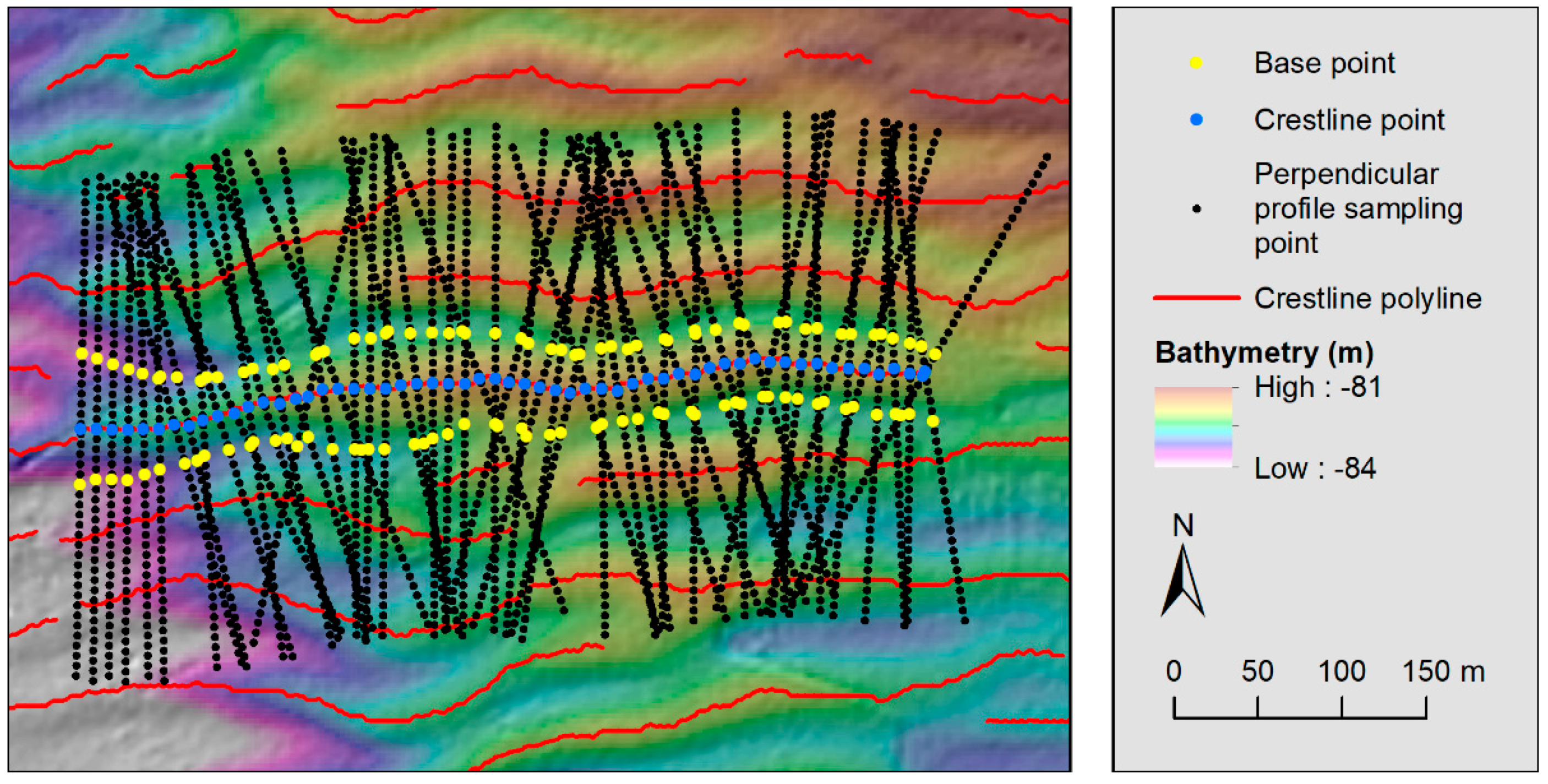
3.2. Extraction of Bedform Metrics
3.2.1. Generation of Perpendicular Transects
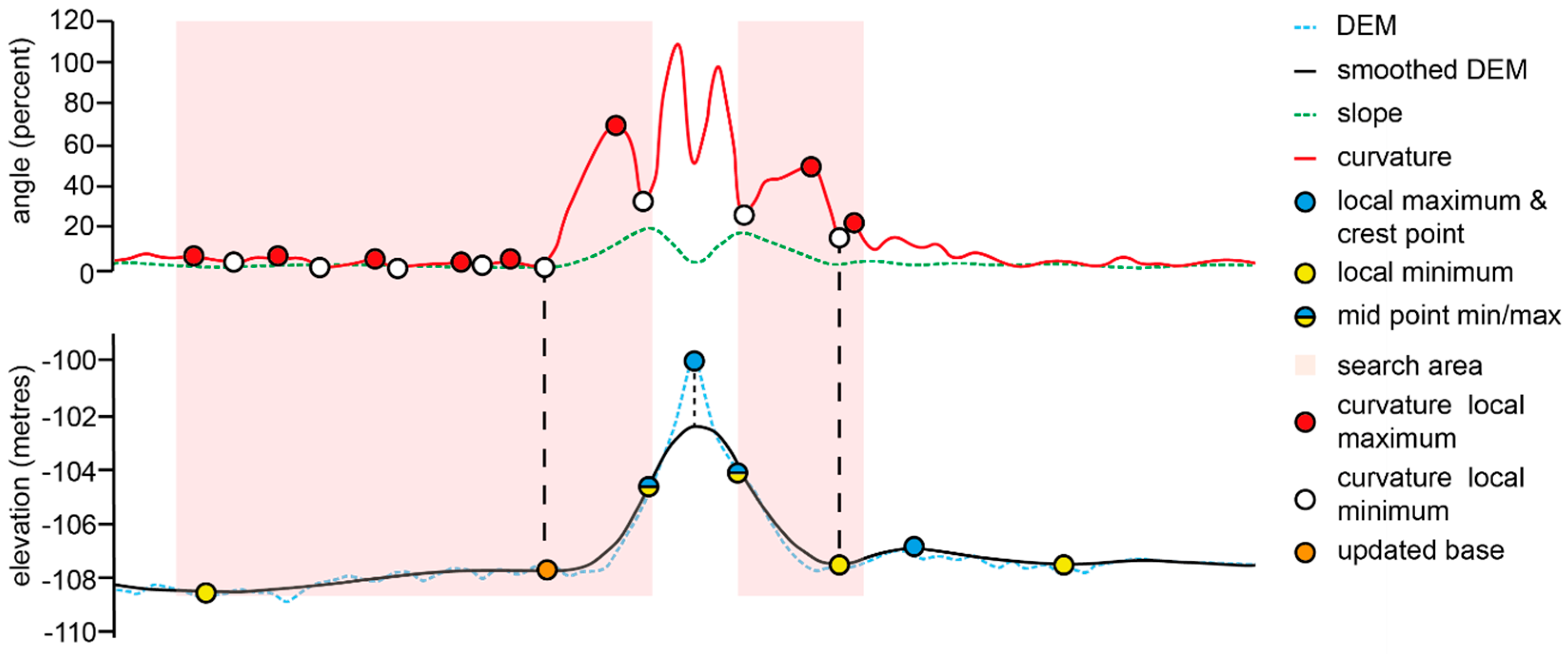
3.2.2. Identification of the Bedform Base and Crestline Points
- Whether it corresponds to a concave change of the bathymetry. In such cases, the elevation of the CGM would be lower than the average elevation of the surrounding values. This criterion is assessed by comparing the elevation of the CGM with the average elevation of the six surrounding values (three on either side).
- Whether elevation values on the crestline side of the curvature local maximum are higher than elevations on the base side in order to ensure CGM is related to the target crest.
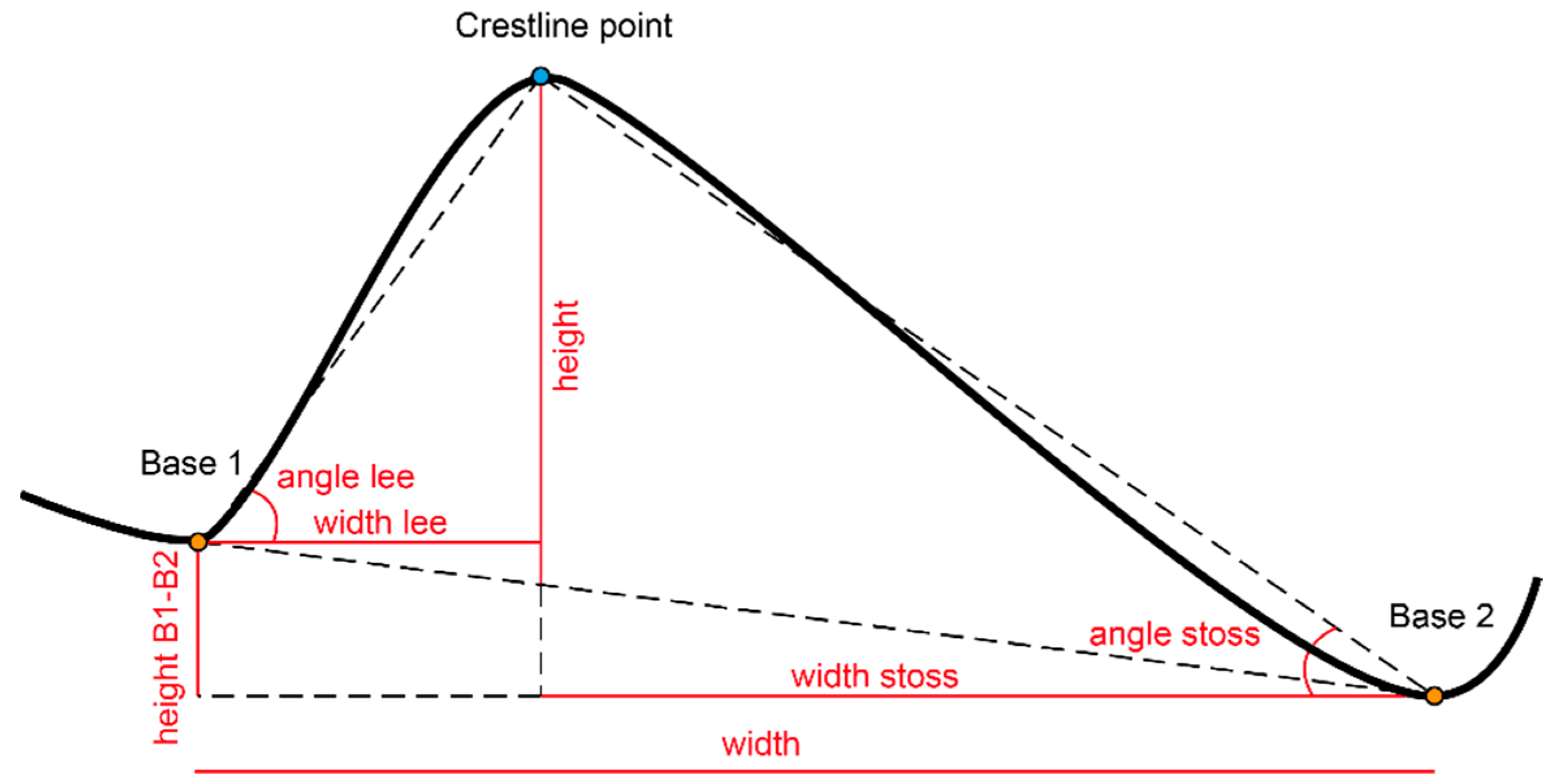
3.2.3. Computation of the Metrics
- Length: Cumulative distance between crestline points;
- Sinuosity index: Total length divided by the distance between the first and last crestline point of a bedform, sensu [51];
- Orientation: Azimuth of the line connecting the first and last crestline points;
- Width: Distance between both bases, along a horizontal plan;
- Width Lee/Stoss: Distance between the respective base and the associated crestline point, along a horizontal plan;
- Angle Lee/Stoss: Angle between a line joining a base and the associated crestline point and the horizontal axis, on either side on the bedform;
- Height: Difference in elevation between a crestline point and a point marking the intersection of a vertical line going through the peak and the line connecting both base points, calculated using a regressive function connecting both bases;
- Symmetry index: Ratio between the lee and stoss side. The direction of the asymmetry is indicated by the field symmetry direction, which specifies the direction of the lee. A value of 1 indicates a symmetrical bedform while a value > 1 highlights an asymmetrical bedform;
- Length to width ratio: Length divided by width;
- Width to height ratio: Width divided by height;
- Length to height ratio Length divided by height;
- Base elevations: Elevation of each base.
4. Results
4.1. Case Study 1: Synthetic DEM
4.2. Case Study 2: Broome
4.2.1. Bedform Identification
4.2.2. Calculation of Metrics and Classification
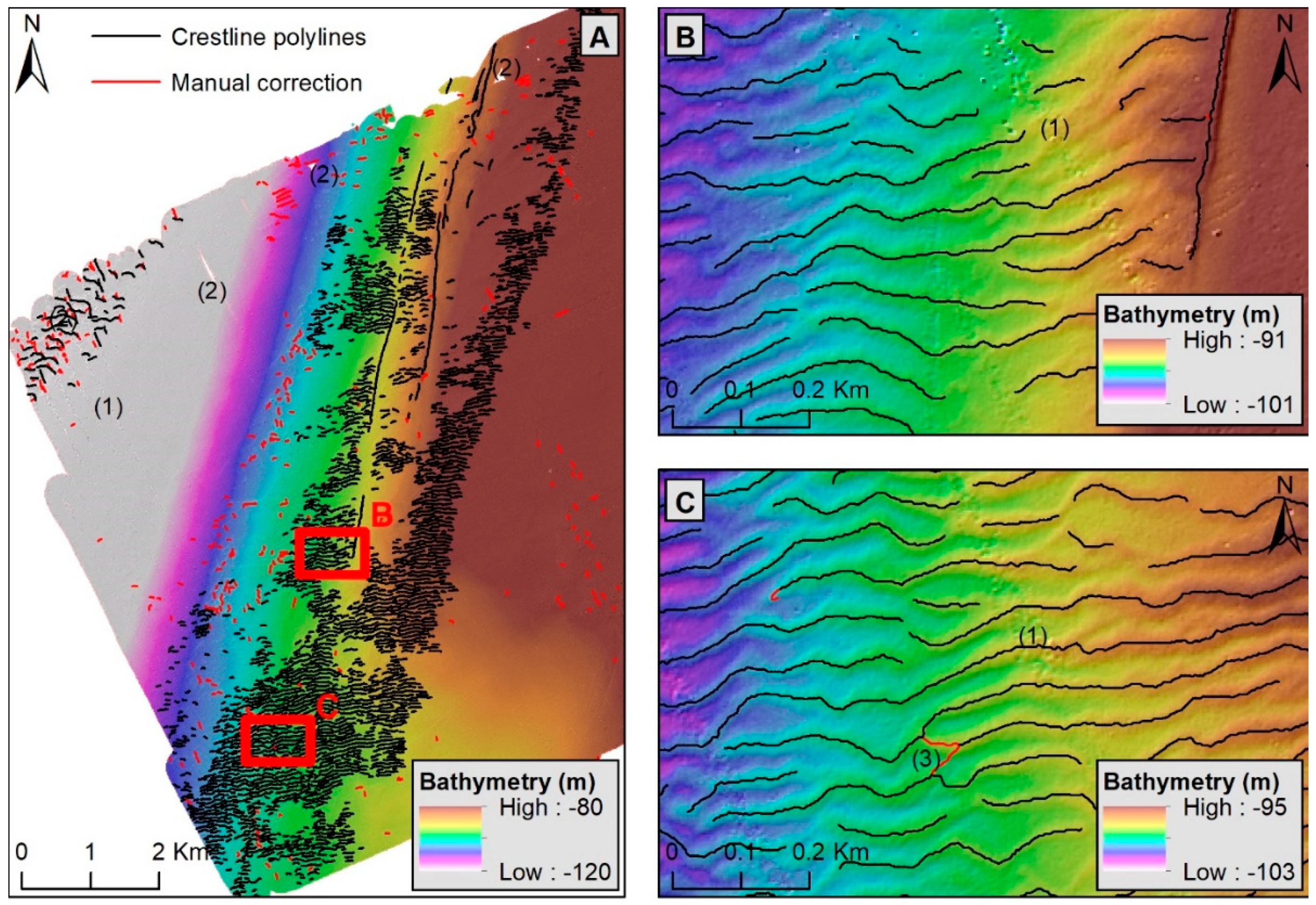
4.3. Case Study 2: Point Cloates
4.3.1. Bedform Identification
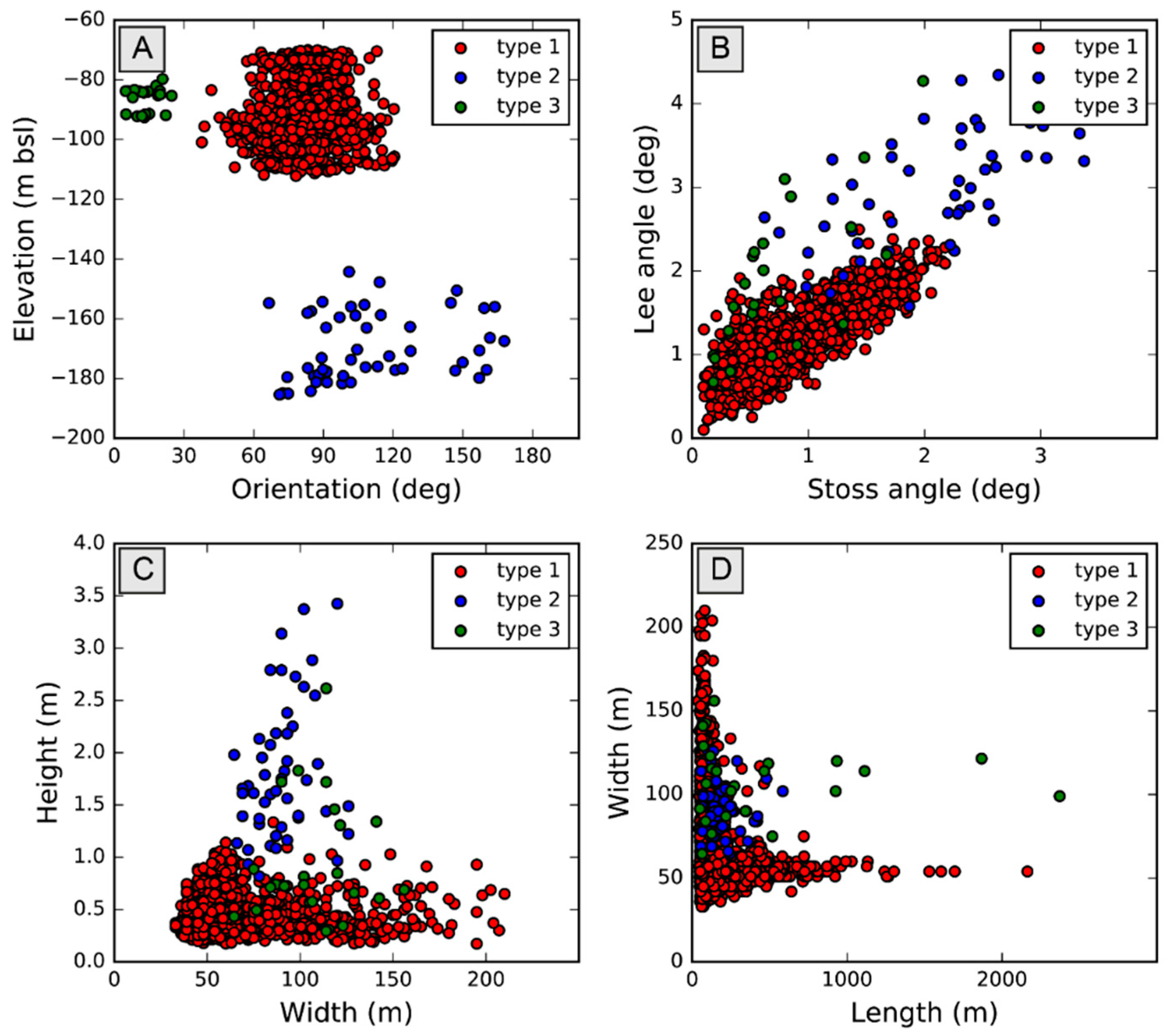
4.3.2. Calculation of Metrics and Classification
5. Discussions
5.1. Bedform Identification
5.2. Generation of Metrics
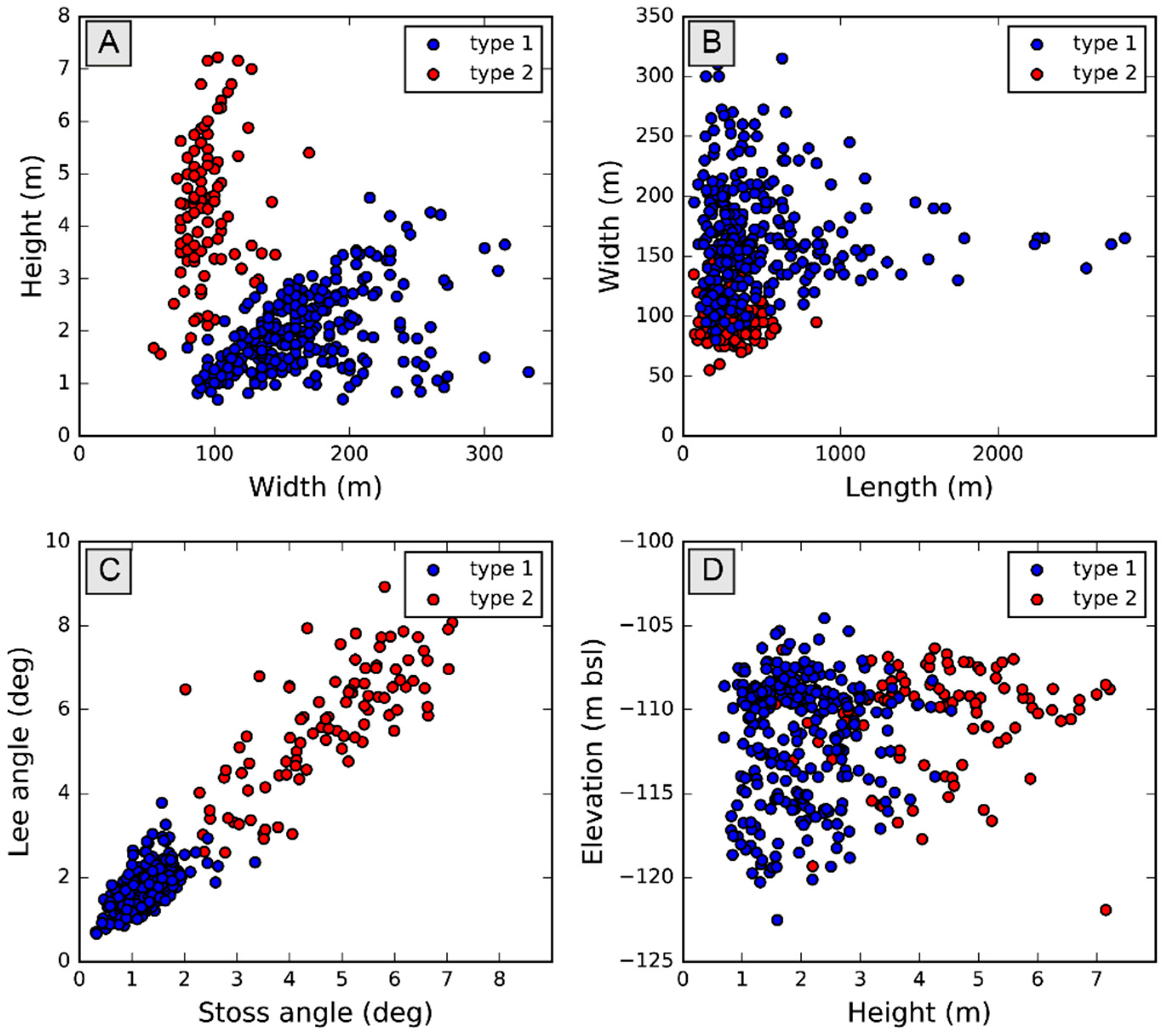
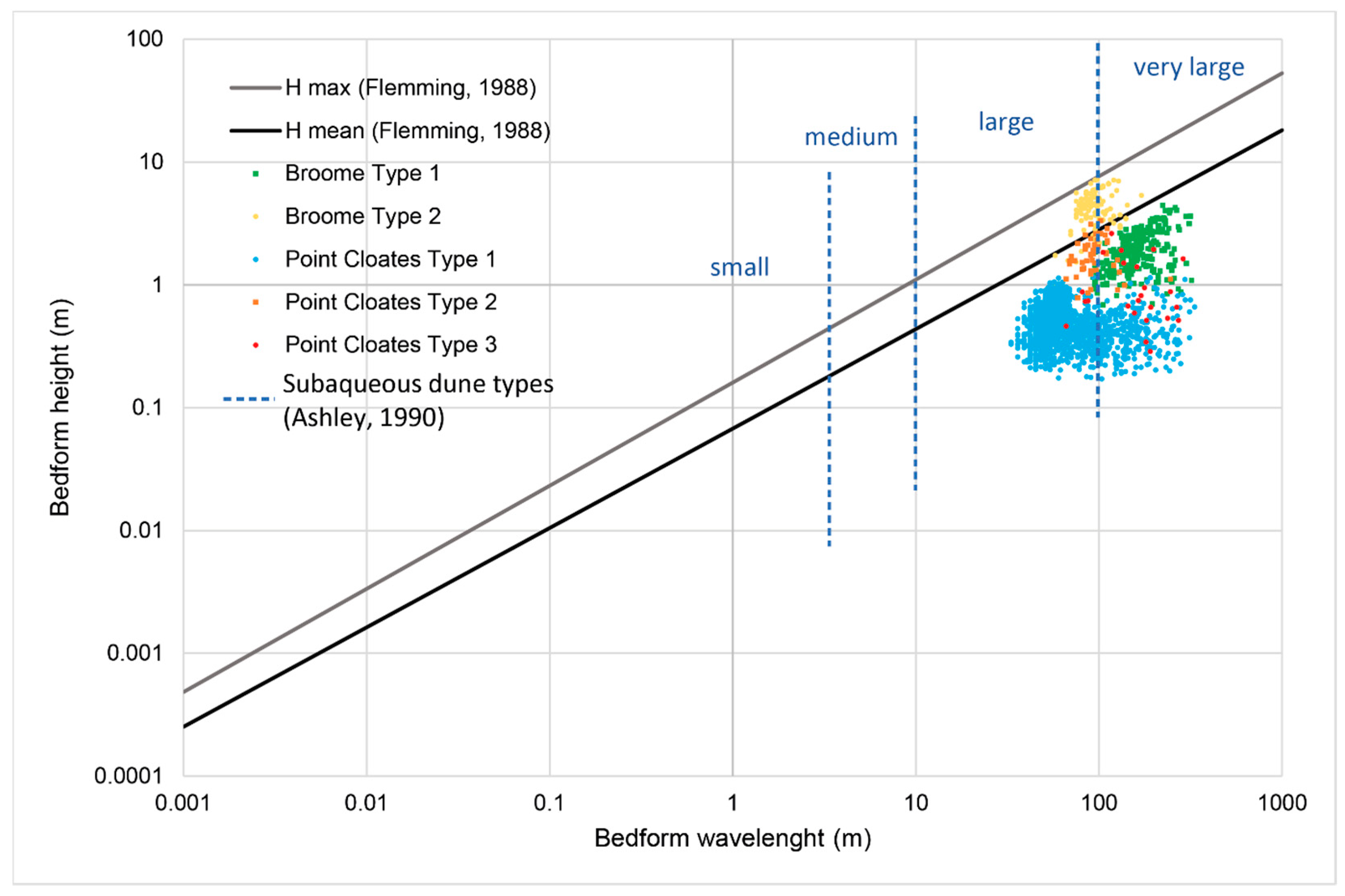
5.3. Comparison of Bedform Properties
5.4. Toward New Classifications
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Charru, F.; Andreotti, B.; Claudin, P. Sand Ripples and Dunes. Annu. Rev. Fluid Mech. 2013, 45, 469–493. [Google Scholar] [CrossRef] [Green Version]
- van Dijk, T.A.G.P.; Best, J.; Baas, A.C.W. Subaqueous and Subaerial Depositional Bedforms. In Encyclopedia of Geology; Elsevier: Amsterdam, The Netherlands, 2021; pp. 771–786. [Google Scholar] [CrossRef]
- Dyer, K.R.; Huntley, D.A. The origin, classification and modelling of sand banks and ridges. Cont. Shelf Res. 1999, 19, 1285–1330. [Google Scholar] [CrossRef]
- Malikides, M.; Harris, P.T.; Jenkins, C.J.; Keene, J.B. Carbonate sandwaves in Bass Strait. Aust. J. Earth Sci. 1988, 35, 303–311. [Google Scholar] [CrossRef]
- Stow, D.; Hernández-Molina, F.; Llave, E.; Sayago-Gil, M.; del Río, V.D.; Branson, A. Bedform-velocity matrix: The estimation of bottom current velocity from bedform observations. Geology 2009, 37, 327–330. [Google Scholar] [CrossRef]
- Allen, J.R.L. Sand waves: A model of origin and internal structure. Sediment. Geol. 1980, 26, 281–328. [Google Scholar] [CrossRef]
- Damen, J.M.; van Dijk, T.A.G.P.; Hulscher, S.J.M.H. Spatially Varying Environmental Properties Controlling Observed Sand Wave Morphology. J. Geophys. Res. Earth Surf. 2018, 123, 262–280. [Google Scholar] [CrossRef]
- Bellec, V.K.; Bøe, R.; Bjarnadóttir, L.R.; Albretsen, J.; Dolan, M.; Chand, S.; Thorsnes, T.; Jakobsen, F.W.; Nixon, C.; Plassen, L.; et al. Sandbanks, sandwaves and megaripples on Spitsbergenbanken, Barents Sea. Mar. Geol. 2019, 416, 105998. [Google Scholar] [CrossRef]
- Kenyon, N.H.; Cooper, B. Sand Banks, Sand Transport and Offshore Wind Farms; Report by ABP Marine Environmental Research Ltd. (ABPmer) and Kenyon MarineGeo. 2005. Available online: https://www.researchgate.net/publication/285584613_Sand_banks_sand_transport_and_offshore_wind_farms (accessed on 28 November 2021).
- Velegrakis, A.F.; Ballay, A.; Poulos, S.E.; Radzevičius, R.; Bellec, V.K.; Manso, F. European marine aggregates resources: Origins, usage, prospecting and dredging techniques. J. Coast. Res. 2010, SI 51, 1–15. [Google Scholar]
- van Dijk, T.A.G.P.; van Dalfsen, J.A.; Van Lancker, V.; van Overmeeren, R.A.; van Heteren, S.; Doornenbal, P.J. Benthic Habitat Variations over Tidal Ridges, North Sea, the Netherlands. In Seafloor Geomorphology as Benthic Habitat; Elsevier: London, UK, 2012; pp. 241–249. [Google Scholar]
- Duran Vinent, O.; Andreotti, B.; Claudin, P.; Winter, C. A unified model of ripples and dunes in water and planetary environments. Nat. Geosci. 2019, 12, 345–350. [Google Scholar] [CrossRef] [Green Version]
- Knaapen, M.A.F. Sandwave migration predictor based on shape information. J. Geophys. Res. Earth Surf. 2005, 110, F04S11. [Google Scholar] [CrossRef] [Green Version]
- Malarkey, J.; Baas, J.H.; Hope, J.A.; Aspden, R.J.; Parsons, D.R.; Peakall, J.; Paterson, D.M.; Schindler, R.J.; Ye, L.; Lichtman, I.D.; et al. The pervasive role of biological cohesion in bedform development. Nat. Commun. 2015, 6, 6257. [Google Scholar] [CrossRef] [Green Version]
- Ashley, G.M. Classification of large-scale subaqueous bedforms; a new look at an old problem. J. Sediment. Res. 1990, 60, 160–172. [Google Scholar] [CrossRef]
- Flemming, B. Zur Klassifikation subaquatischer, strömungstransversaler Transportkörper. In Proceedings of the Bochumer Geologishe und Geotechnishe Arbeiten, Bochum, Germany, May 1988; pp. 44–47. Available online: https://www.researchgate.net/publication/281282722_Zementstratigraphie_und_Kathodolumineszenz_des_Korallenoolith_Malm_im_Sudniedersachsischen_Bergland (accessed on 28 November 2021).
- Belderson, R.H.; Johnson, M.A.; Kenyon, N. Bedforms. In Offshore Tidal Sands, Processes and Deposit; Stride, A.H., Ed.; Chapman Hall: London, UK, 1982; pp. 27–57. [Google Scholar]
- Van Dijk, T.A.G.P.; Lindenbergh, R.C.; Egberts, P.J.P. Separating bathymetric data representing multiscale rhythmic bed forms: A geostatistical and spectral method compared. J. Geophys. Res. Earth Surf. 2008, 113, F04017. [Google Scholar] [CrossRef]
- Duffy, G. Patterns of Morphometric Parameters in a Large Bedform Field: Development and Application of a Tool for Automated Bedform Morphometry. Ir. J. Earth Sci. 2012, 30, 31–39. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Q.; Zhang, Y.; Flemming, B.W.; Wang, Y.; Gao, S. An automated procedure to calculate the morphological parameters of superimposed rhythmic bedforms. Earth Surf. Processes Landf. 2020, 45, 3496–3509. [Google Scholar] [CrossRef]
- Gutierrez, R.R.; Mallma, J.A.; Núñez-González, F.; Link, O.; Abad, J.D. Bedforms-ATM, an open source software to analyze the scale-based hierarchies and dimensionality of natural bed forms. SoftwareX 2018, 7, 184–189. [Google Scholar] [CrossRef]
- Lisimenka, A.; Kubicki, A. Estimation of dimensions and orientation of multiple riverine dune generations using spectral moments. Geo-Mar. Lett. 2017, 37, 59–74. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Musa, M.; Guala, M. Scale-Dependent Bedform Migration and Deformation in the Physical and Spectral Domains. J. Geophys. Res. Earth Surf. 2021, 126, e2020JF005811. [Google Scholar] [CrossRef]
- Scheiber, L.; Lojek, O.; Götschenberg, A.; Visscher, J.; Schlurmann, T. Robust methods for the decomposition and interpretation of compound dunes applied to a complex hydromorphological setting. Earth Surf. Processes Landf. 2021, 46, 478–489. [Google Scholar] [CrossRef]
- Evans, W.; Benetti, S.; Sacchetti, F.; Jackson, D.W.T.; Dunlop, P.; Monteys, X. Bedforms on the northwest Irish Shelf: Indication of modern active sediment transport and over printing of paleo-glacial sedimentary deposits. J. Maps 2015, 11, 561–574. [Google Scholar] [CrossRef] [Green Version]
- Dong, P. Automated measurement of sand dune migration using multi-temporal lidar data and GIS. Int. J. Remote Sens. 2015, 36, 5426–5447. [Google Scholar] [CrossRef]
- Yan, G.; Cheng, H.; Teng, L.; Xu, W.; Jiang, Y.; Yang, G.; Zhou, Q. Analysis of the Use of Geomorphic Elements Mapping to Characterize Subaqueous Bedforms Using Multibeam Bathymetric Data in River System. Appl. Sci. 2020, 10, 7692. [Google Scholar] [CrossRef]
- Di Stefano, M.; Mayer, L.A. An Automatic Procedure for the Quantitative Characterization of Submarine Bedforms. Geosciences 2018, 8, 28. [Google Scholar] [CrossRef] [Green Version]
- Cassol, W.N.; Daniel, S.; Guilbert, É. A Segmentation Approach to Identify Underwater Dunes from Digital Bathymetric Models. Geosciences 2021, 11, 361. [Google Scholar] [CrossRef]
- Jasiewicz, J.; Stepinski, T.F. Geomorphons—A pattern recognition approach to classification and mapping of landforms. Geomorphology 2013, 182, 147–156. [Google Scholar] [CrossRef]
- Gallant, J.C.; Dowling, T.I. A multiresolution index of valley bottom flatness for mapping depositional areas. Water Resour. Res. 2003, 39, 1347. [Google Scholar] [CrossRef]
- Weiss, A. Topographic position and landforms analysis. In Proceedings of the Poster Presentation, ESRI User Conference, San Diego, CA, USA, 9–13 July 2001. [Google Scholar]
- Debese, N.; Jacq, J.-J.; Garlan, T. Extraction of sandy bedforms features through geodesic morphometry. Geomorphology 2016, 268, 82–97. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.-C.; Sinha, G. A visual basic program for ridge axis picking on DEM data using the profile-recognition and polygon-breaking algorithm. Comput. Geosci. 2007, 33, 229–237. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Song, G.-S.; Hsu, S.-K. Automatic extraction of ridge and valley axes using the profile recognition and polygon-breaking algorithm. Comput. Geosci. 1998, 24, 83–93. [Google Scholar] [CrossRef]
- Baker, C.; Potter, A.; Tran, M.; Heap, A.D. Sedimentology and Geomorphology of the Northwest Marine Region of Australia; Geoscience Australia: Canberra, Australia, 2008; Volume Record 2008/7, p. 220.
- Condie, S.A.; Andrewartha, J.R. Circulation and connectivity on the Australian North West Shelf. Cont. Shelf Res. 2008, 28, 1724–1739. [Google Scholar] [CrossRef]
- Holloway, P.E. A regional model of the semidiurnal internal tide on the Australian North West Shelf. J. Geophys. Res. Ocean. 2001, 106, 19625–19638. [Google Scholar] [CrossRef] [Green Version]
- Katsumata, K. Tidal stirring and mixing on the Australian North West Shelf. Mar. Freshw. Res. 2006, 57, 243–254. [Google Scholar] [CrossRef]
- Wijeratne, S.; Pattiaratchi, C.; Proctor, R. Estimates of Surface and Subsurface Boundary Current Transport Around Australia. J. Geophys. Res. Ocean. 2018, 123, 3444–3466. [Google Scholar] [CrossRef]
- Suppiah, R. The Australian summer monsoon: A review. Prog. Phys. Geogr. 1992, 16, 283–318. [Google Scholar] [CrossRef]
- James, N.P.; Bone, Y.; Kyser, T.K.; Dix, G.R.; Collins, L.B. The importance of changing oceanography in controlling late Quaternary carbonate sedimentation on a high-energy, tropical, oceanic ramp: North-western Australia. Sedimentology 2004, 51, 1179–1205. [Google Scholar] [CrossRef]
- Baines, P.G. Satellite observations of internal waves on the Australian north-west shelf. Mar. Freshw. Res. 1981, 32, 457–463. [Google Scholar] [CrossRef] [Green Version]
- Belde, J.; Reuning, L.; Back, S. Bottom currents and sediment waves on a shallow carbonate shelf, Northern Carnarvon Basin, Australia. Cont. Shelf Res. 2017, 138, 142–153. [Google Scholar] [CrossRef]
- Lebrec, U.; Riera, R.; Paumard, V.; O’Leary, M.J.; Lang, S.C. Morphology and distribution of submerged palaeoshorelines: Insights from the North West Shelf of Australia. Earth-Sci. Rev. 2022, 224, 103864. [Google Scholar] [CrossRef]
- Lebrec, U.; Paumard, V.; O’Leary, M.J.; Lang, S.C. Towards a regional high-resolution bathymetry of the North West Shelf of Australia based on Sentinel-2 satellite images, 3D seismic surveys, and historical datasets. Earth Syst. Sci. Data 2021, 13, 5191–5212. [Google Scholar] [CrossRef]
- Jones, A.T.; Kennard, J.M.; Logan, G.A.; Grosjean, E.; Marshall, J. Fluid expulsion features associated with sand waves on Australia’s central North West Shelf. Geo-Mar. Lett. 2009, 29, 233–248. [Google Scholar] [CrossRef]
- Lucieer, V.; Porter-Smith, R.; Nichol, S.L.; Monk, J.; Barrett, N.S. Collation of Existing Shelf Reef Mapping Data and Gap Identification. Phase 1 Final Report-Shelf Reef Key Ecological Features. 2016. Available online: https://www.nespmarine.edu.au/document/collation-existing-shelf-reef-mapping-data-and-gap-identification-phase-1-final-report (accessed on 28 November 2021).
- Brooke, B.; Nichol, S.; Hughes, M.; McArthur, M.; Anderson, T.; Przeslawski, R.; Siwabessy, P.J.; Heyward, A.; Battershill, C.; Colquhoun, J.; et al. Carnarvon Shelf Survey Post-Survey Report. Geosci. Aust. Rec. 2009, 2, 90. [Google Scholar]
- Timo. Finding Turning Points of an Array in Python. Available online: https://stackoverflow.com/a/48360671 (accessed on 28 November 2021).
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braided, Meandering, and Straight; US Government Printing Office: Washington, DC, USA, 1957; p. 50.
- Cisneros, J.; Best, J.; van Dijk, T.; de Almeida, R.P.; Amsler, M.; Boldt, J.; Freitas, B.; Galeazzi, C.; Huizinga, R.; Ianniruberto, M.; et al. Dunes in the world’s big rivers are characterized by low-angle lee-side slopes and a complex shape. Nat. Geosci. 2020, 13, 156–162. [Google Scholar] [CrossRef]
- Griffin, D.A.; Herzfeld, M.; Hemer, M.; Engwirda, D. Australian tidal currents–assessment of a barotropic model (COMPAS v1.3.0 rev6631) with an unstructured grid. Geosci. Model Dev. Discuss. 2021, 2021, 1–39. [Google Scholar] [CrossRef]
- Picard, K.; Nichol, S.; Hashimoto, R.; Carroll, A.G.; Bernardel, G.; Jones, L.; Siwabessy, P.J.; Radke, L.; Nicholas, T.; Carey, M.; et al. Seabed environments and shallow geology of the Leveque Shelf, Browse Basin, Western Australia: Ga0340/SOL5754-Post-survey report. Geosci. Aust. Rec. 2014, 10, 145. [Google Scholar] [CrossRef]
- Nicholas, T.; Carroll, A.G.; Radke, L.; Tran, M.; Howard, F.; Przeslawski, R.; Chen, J.; Siwabessy, P.J.; Nichol, S. Seabed Environments and Shallow Geology of the Leveque Shelf, Browse Basin, Western Australia: GA0340 Interpretative Report. Geosci. Aust. Rec. 2016, 10, 157. [Google Scholar] [CrossRef]
- Daniell, J.J.; Hughes, M. The morphology of barchan-shaped sand banks from western Torres Strait, northern Australia. Sediment. Geol. 2007, 202, 638–652. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, X.; Zhuang, L.; Yan, J. Sand waves near the shelf break of the northern South China Sea: Morphology and recent mobility. Geo-Mar. Lett. 2019, 39, 19–36. [Google Scholar] [CrossRef]
- Reeder, D.B.; Ma, B.B.; Yang, Y.J. Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves. Mar. Geol. 2011, 279, 12–18. [Google Scholar] [CrossRef]
- Miramontes, E.; Jorry, S.J.; Jouet, G.; Counts, J.W.; Courgeon, S.; Le Roy, P.; Guerin, C.; Hernández-Molina, F.J. Deep-water dunes on drowned isolated carbonate terraces (Mozambique Channel, south-west Indian Ocean). Sedimentology 2019, 66, 1222–1242. [Google Scholar] [CrossRef]
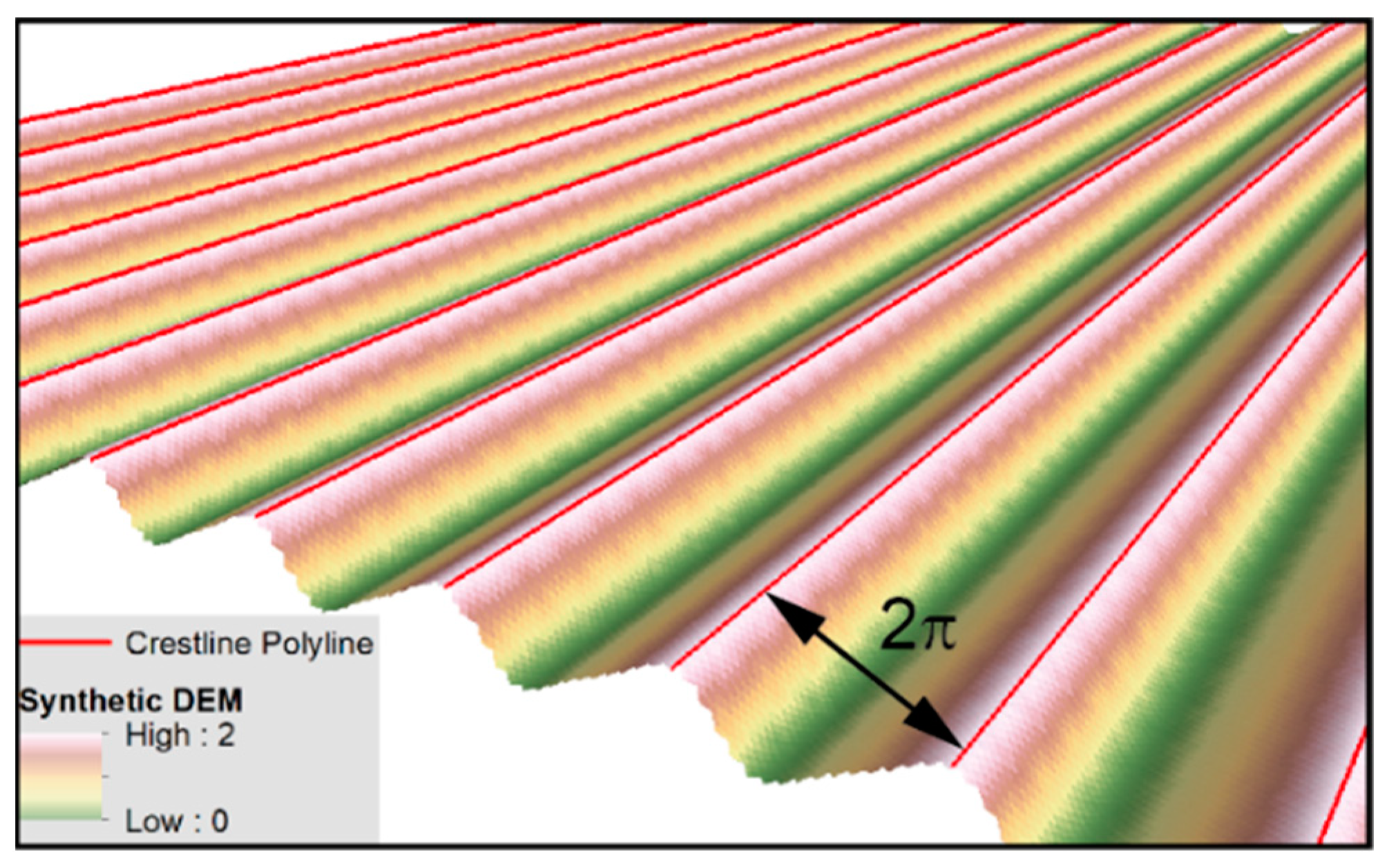

| Theory | Automated | |
|---|---|---|
| n | 12 | 12 |
| height | 2 m | 1.99 m |
| width | 6.28 m | 6.26 m |
| symmetry | 1.80 | 1.78 |
| orientation | 45° | 44.99° |
| n | Delta Height | Delta Width | Delta Sym. | Delta Dir. |
|---|---|---|---|---|
| 22 | 8.79% | 9.09% | 18.42% | 9.05° |
| Metrics | n | Width (m) | Height (m) | W/H Ratio | Length (m) | L/W Ratio | Orientation (deg.) | |
| Type 1 | Auto | 283 | 160 | 1.90 | 79.19 | 362.30 | 2.29 | 38.19° |
| Manual | 20 | 133 | 3.1 | 43.8 | 1306 | 10.2 | Na | |
| Type 2 | Auto | 98 | 90 | 4.41 | 21.2 | 275.50 | 3.22 | 44.41° |
| Manual | 20 | 90 | 6.7 | 13.5 | 402 | 4.7 | Na | |
| Metrics | Angle lee (deg.) | Angle stoss (deg.) | W lee (m) | W stoss (m) | Sym. ind. | Sym. dir. (deg.) | Sinuosity ind. | |
| Type 1 | Auto | 1.72 | 1.31 | 65 | 85 | 1.26 | 301 | 1.12 |
| Manual | 5.0 | 3.0 | 53.2 | 80.2 | 1.66 | Na | Na | |
| Type 2 | Auto | 5.84 | 4.94 | 40 | 50 | 1.17 | 139 | 1.1 |
| Manual | 12.3 | 8.8 | 42.2 | 47.2 | 1.42 | Na | Na | |
| n | Delta Height | Delta Width | Delta Sym. | Delta Dir. |
|---|---|---|---|---|
| 38 | 5.95% | 4.39% | 10.88% | 10.86° |
| Metrics | n | Width (m) | Height (m) | W/H Ratio | Length (m) | L/W Ratio | Orientation (North) |
| Type 1 | 1506 | 56.99 | 0.45 | 129.82 | 125.55 | 2.09 | 82.82° |
| Type 2 | 49 | 89.99 | 1.65 | 50.16 | 155.16 | 1.81 | 101.85° |
| Type 3 | 24 | 110.24 | 0.73 | 132.47 | 187.30 | 2.04 | 13.87° |
| Metrics | Angle lee (deg.) | Angle stoss (deg.) | L. lee (m) | L. stoss (m) | Sym. Ind. | Sym. Dir. | Sinuosity ind. |
| Type 1 | 1.09 | 0.82 | 24 | 30 | 1.25 | 173.6 | 1.05 |
| Type 2 | 2.99 | 2.26 | 33 | 51 | 1.49 | 177.48 | 1.11 |
| Type 3 | 1.61 | 0.57 | 24 | 79 | 3.33 | 103.87 | 1.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lebrec, U.; Riera, R.; Paumard, V.; O'Leary, M.J.; Lang, S.C. Automatic Mapping and Characterisation of Linear Depositional Bedforms: Theory and Application Using Bathymetry from the North West Shelf of Australia. Remote Sens. 2022, 14, 280. https://doi.org/10.3390/rs14020280
Lebrec U, Riera R, Paumard V, O'Leary MJ, Lang SC. Automatic Mapping and Characterisation of Linear Depositional Bedforms: Theory and Application Using Bathymetry from the North West Shelf of Australia. Remote Sensing. 2022; 14(2):280. https://doi.org/10.3390/rs14020280
Chicago/Turabian StyleLebrec, Ulysse, Rosine Riera, Victorien Paumard, Michael J. O'Leary, and Simon C. Lang. 2022. "Automatic Mapping and Characterisation of Linear Depositional Bedforms: Theory and Application Using Bathymetry from the North West Shelf of Australia" Remote Sensing 14, no. 2: 280. https://doi.org/10.3390/rs14020280
APA StyleLebrec, U., Riera, R., Paumard, V., O'Leary, M. J., & Lang, S. C. (2022). Automatic Mapping and Characterisation of Linear Depositional Bedforms: Theory and Application Using Bathymetry from the North West Shelf of Australia. Remote Sensing, 14(2), 280. https://doi.org/10.3390/rs14020280






