Optimization of Remote Sensing Image Segmentation by a Customized Parallel Sine Cosine Algorithm Based on the Taguchi Method
Abstract
1. Introduction
- A parallel SCA (PSCA) with three different communication strategies is proposed to solve the unimodal, multimodal, and complex problems;
- Using Taguchi’s method to obtain a customized parallel SCA scheme (TPSCA);
- A high-performance remote sensing image segmentation model is constructed by combining TPSCA with PCNN.
2. Related Works
2.1. Sine Cosine Algorithm (SCA)
2.2. Taguchi Method
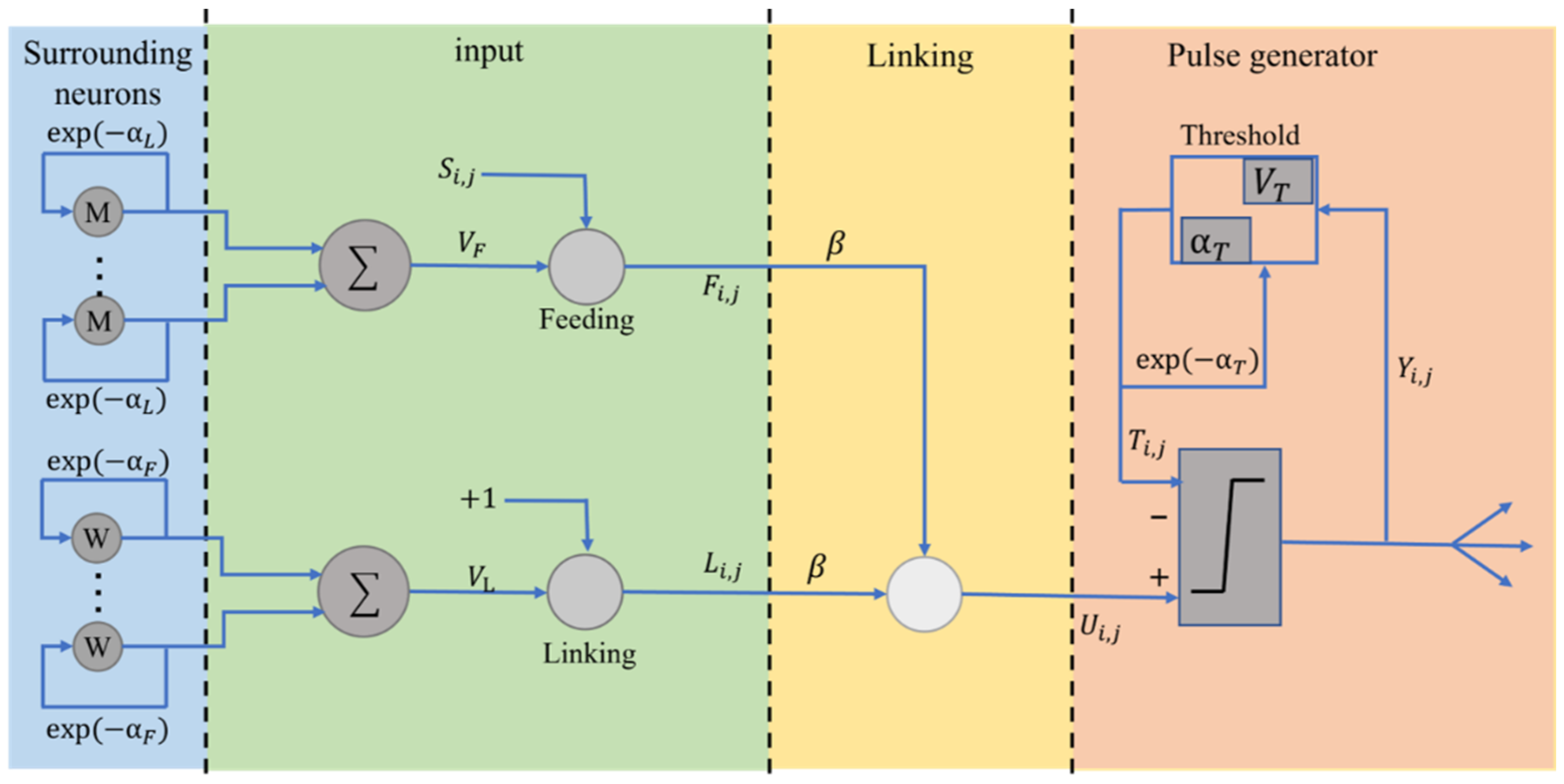
2.3. Pulse-Coupled Neural Networks (PCNNs)
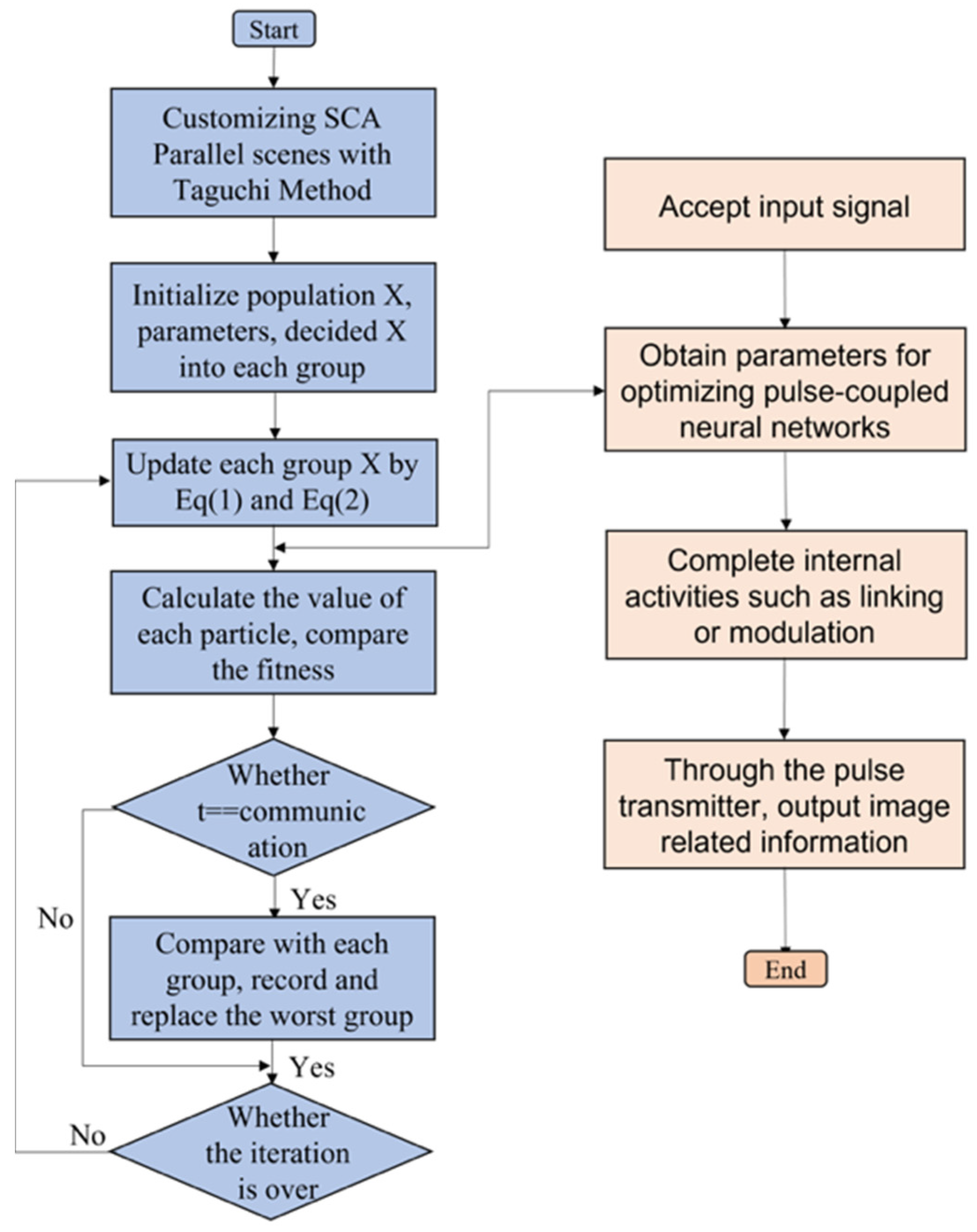
3. Customized Parallel SCA (TPSCA) Based on the Taguchi Method
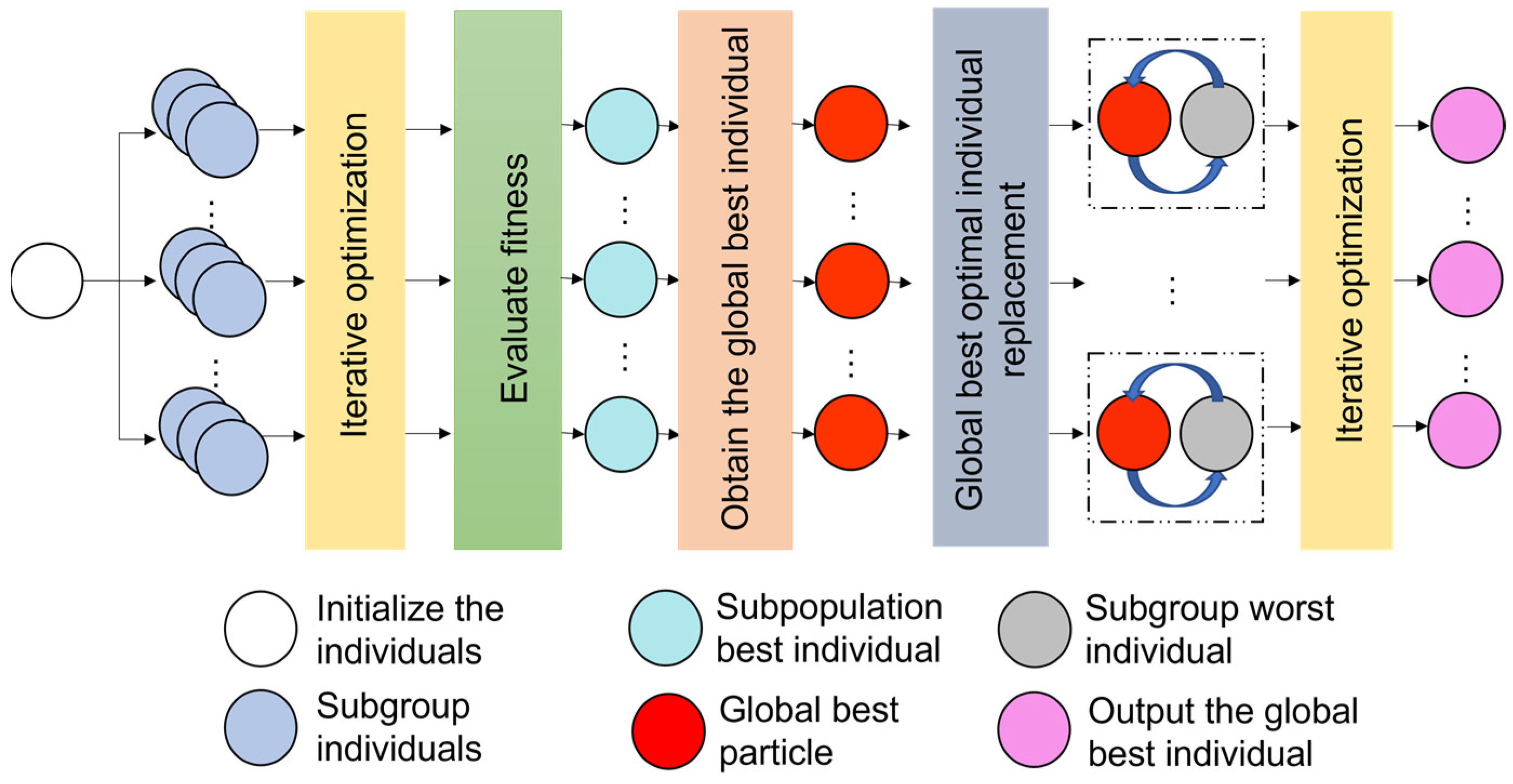
3.1. Parallel Sine Cosine Algorithm (PSCA)
- Dividing population: dividing the whole population into several subpopulations;
- Communication: exchange between subpopulations every generation during the iterative process;
- Integration: update the population based on the results of the communication.
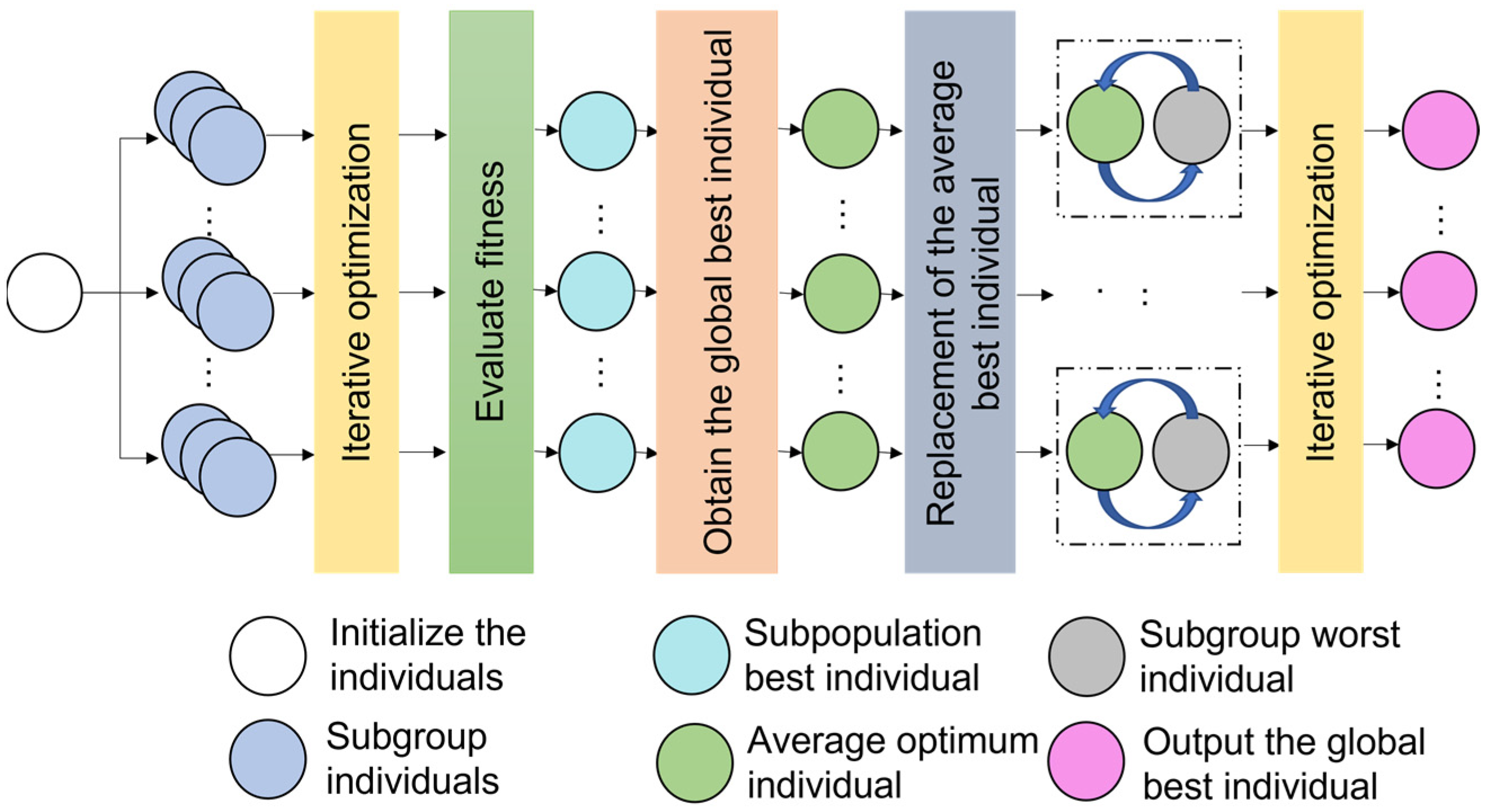
3.2. Custom SCA Parallel Scheme (TPSCA)
4. The Experiments and Results of the TPSCA
5. Combination of TPSCA and PCNN (TPSCA–PCNN)
6. Remote Sensing Image Segmentation Model Based on TPSCA–PCNN
6.1. Image Segmentation Evaluation Metrics
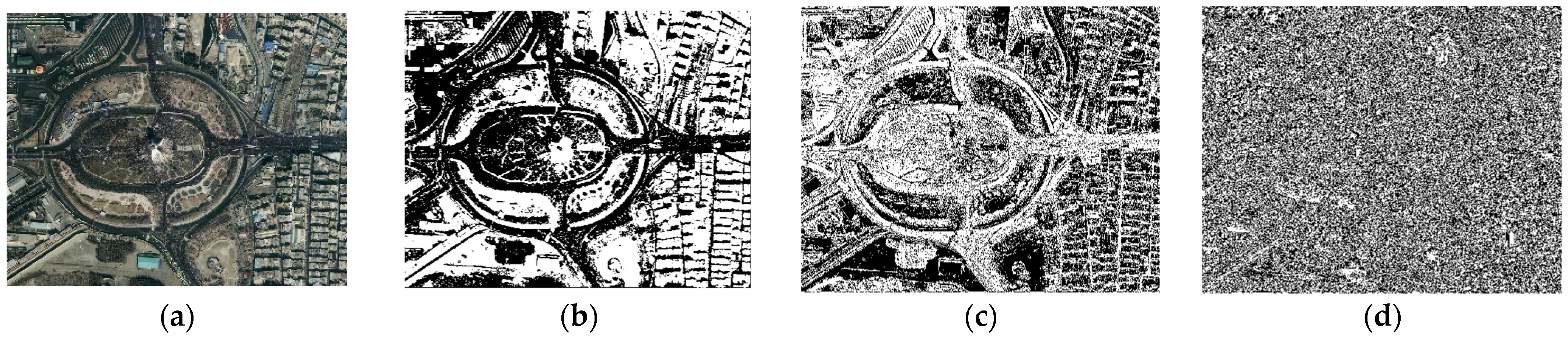
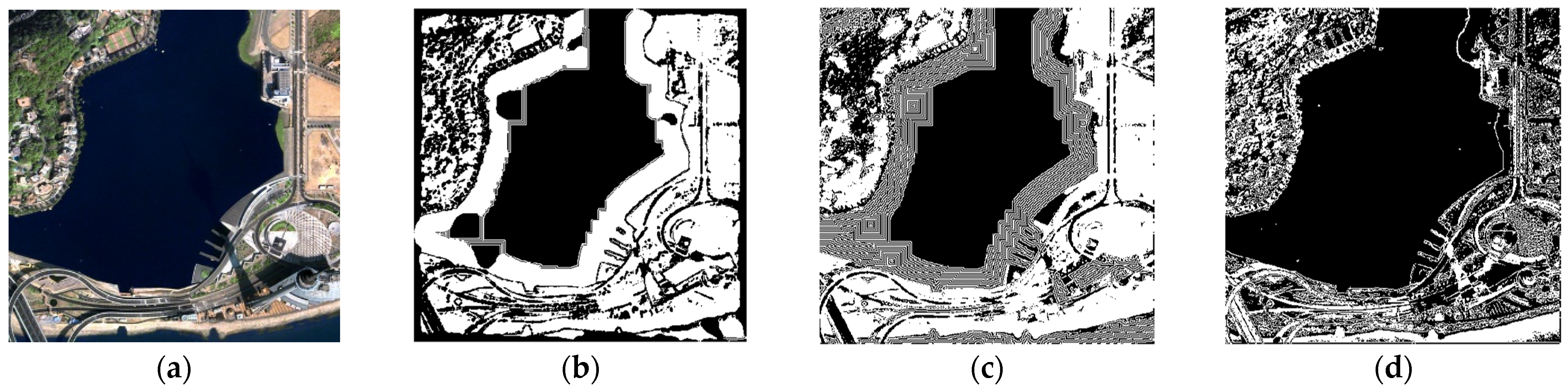
6.2. Remote Sensing Image Datasets
6.3. Image Preprocessing
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, J.; Gao, S.; Zhu, Y.; Ma, C. A Survey of Remote Sensing Image Classification Based on CNNs. Big Earth Data 2019, 3, 232–254. [Google Scholar] [CrossRef]
- Prabhu, R.; Alagu Raja, R.A. Urban Slum Detection Approaches from High-Resolution Satellite Data Using Statistical and Spectral Based Approaches. J. Indian Soc. Remote Sens. 2018, 46, 2033–2044. [Google Scholar] [CrossRef]
- Lian, J.; Yang, Z.; Liu, J.; Sun, W.; Zheng, L.; Du, X.; Yi, Z.; Shi, B.; Ma, Y. An Overview of Image Segmentation Based on Pulse-Coupled Neural Network. Arch. Comput. Methods Eng. 2021, 28, 387–403. [Google Scholar] [CrossRef]
- Yokoya, N.; Levine, M.D. Range Image Segmentation Based on Differential Geometry: A Hybrid Approach. J. Indian Soc. Remote Sens. 2018, 46, 2033–2044. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, M.; Wang, Y.; Shang, J.; Liu, X.; Li, B.; Song, A.; Li, Q. Automated Delineation of Agricultural Field Boundaries from Sentinel-2 Images Using Recurrent Residual U-Net. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102557. [Google Scholar] [CrossRef]
- Mittal, H.; Saraswat, M. An Optimum Multi-Level Image Thresholding Segmentation Using Non-Local Means 2D Histogram and Exponential Kbest Gravitational Search Algorithm. Eng. Appl. Artif. Intell. 2018, 71, 226–235. [Google Scholar] [CrossRef]
- Kim, W.; Kanezaki, A.; Tanaka, M. Unsupervised Learning of Image Segmentation Based on Differentiable Feature Clustering. IEEE Trans. Image Processing 2020, 29, 8055–8068. [Google Scholar] [CrossRef]
- Liu, C.; Liu, W.; Xing, W. A Weighted Edge-Based Level Set Method Based on Multi-Local Statistical Information for Noisy Image Segmentation. J. Vis. Commun. Image Represent. 2019, 59, 89–107. [Google Scholar] [CrossRef]
- Yu, H.; He, F.; Pan, Y. A Scalable Region-Based Level Set Method Using Adaptive Bilateral Filter for Noisy Image Segmentation. Multimed. Tools Appl. 2020, 79, 5743–5765. [Google Scholar] [CrossRef]
- Alshehhi, R.; Marpu, P.R. Hierarchical Graph-Based Segmentation for Extracting Road Networks from High-Resolution Satellite Images. ISPRS J. Photogramm. Remote Sens. 2017, 126, 245–260. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Li, X.; Lu, S.; Ye, Y.; Ban, Y. Cloud Detection Approach for Remote Sensing Images. Knowl.-Based Syst. 2022, 238, 107890. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Xia, J.; Yang, D.; Zhou, H.; Chen, Y.; Zhang, H.; Liu, T.; Heidari, A.A.; Chen, H.; Pan, Z. Evolving Kernel Extreme Learning Machine for Medical Diagnosis via a Disperse Foraging Sine Cosine Algorithm. Comput. Biol. Med. 2022, 141, 105137. [Google Scholar] [CrossRef]
- Zheng, H.; Gao, J.; Xiong, J.; Yao, G.; Cui, H.; Zhang, L. An Enhanced Artificial Electric Field Algorithm with Sine Cosine Mechanism for Logistics Distribution Vehicle Routing. Appl. Sci. 2022, 12, 6240. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Ewees, A.A.; Al-qaness, M.A.A.; Abualigah, L.; Ibrahim, R.A. Sine–Cosine-Barnacles Algorithm Optimizer with Disruption Operator for Global Optimization and Automatic Data Clustering. Expert Syst. Appl. 2022, 207, 117993. [Google Scholar] [CrossRef]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A Nested U-Net Architecture for Medical Image Segmentation. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2018; Volume 11045, pp. 3–11. [Google Scholar]
- Jha, D.; Riegler, M.A.; Johansen, D.; Halvorsen, P.; Johansen, H.D. DoubleU-Net: A Deep Convolutional Neural Network for Medical Image Segmentation. In Proceedings of the IEEE Symposium on Computer-Based Medical Systems, Rochester, MN, USA, 28–30 July 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; Volume 2020, pp. 558–564. [Google Scholar]
- Jia, H.; Xing, Z.; Song, W. Three Dimensional Pulse Coupled Neural Network Based on Hybrid Optimization Algorithm for Oil Pollution Image Segmentation. Remote Sens. 2019, 11, 1046. [Google Scholar] [CrossRef]
- Deng, X.; Yang, Y.; Zhang, H.; Ma, Y. PCNN Double Step Firing Mode for Image Edge Detection. Multimed. Tools Appl. 2022, 81, 27187–27213. [Google Scholar] [CrossRef]
- Zhou, D.; Shao, Y. Region Growing for Image Segmentation Using an Extended PCNN Model. IET Image Process. 2018, 12, 729–737. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, S.; Chaudhuri, S.S. Multi-Level Thresholding with a Decomposition-Based Multi-Objective Evolutionary Algorithm for Segmenting Natural and Medical Images. Appl. Soft Comput. J. 2017, 50, 142–157. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Y.; Liu, D.; Wang, L. Fast Threshold Image Segmentation Based on 2D Fuzzy Fisher and Random Local Optimized QPSO. IEEE Trans. Image Process. 2017, 26, 1355–1362. [Google Scholar] [CrossRef]
- Sun, Y.; Chu, S.-C.; Hu, P.; Watada, J.; Si, M.; Pan, J.-S. Overview of Parallel Computing for Meta-Heuristic Algorithms. Taiwan Ubiquitous Inf. 2022, 7, 656–684. [Google Scholar]
- Fan, F.; Chu, S.C.; Pan, J.S.; Yang, Q.; Zhao, H. Parallel Sine Cosine Algorithm for the Dynamic Deployment in Wireless Sensor Networks. J. Internet Technol. 2021, 22, 499–512. [Google Scholar] [CrossRef]
- Chu, S.C.; Xu, X.W.; Yang, S.Y.; Pan, J.S. Parallel Fish Migration Optimization with Compact Technology Based on Memory Principle for Wireless Sensor Networks. Knowl.-Based Syst. 2022, 241, 108124. [Google Scholar] [CrossRef]
- Yang, W.H.; Tarng, Y.S. Design Optimization of Cutting Parameters for Turning Operations Based on the Taguchi Method. J. Mater. Process. Technol. 1998, 84, 122–129. [Google Scholar] [CrossRef]
- Belazzoug, M.; Touahria, M.; Nouioua, F.; Brahimi, M. An Improved Sine Cosine Algorithm to Select Features for Text Categorization. J. King Saud Univ. Comput. Inf. Sci. 2020, 32, 454–464. [Google Scholar] [CrossRef]
- Qu, C.; Zeng, Z.; Dai, J.; Yi, Z.; He, W. A Modified Sine-Cosine Algorithm Based on Neighborhood Search and Greedy Levy Mutation. Comput. Intell. Neurosci. 2018, 2018, 4231647. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Tu, J.; Zhou, H.; Gui, W.; Liang, G.; Chen, H.; Wang, M. An Adaptive Chaotic Sine Cosine Algorithm for Constrained and Unconstrained Optimization. Complexity 2020, 2020, 6084917. [Google Scholar] [CrossRef]
- Chegini, S.N.; Bagheri, A.; Najafi, F. PSOSCALF: A New Hybrid PSO Based on Sine Cosine Algorithm and Levy Flight for Solving Optimization Problems. Appl. Soft Comput. J. 2018, 73, 697–726. [Google Scholar] [CrossRef]
- Dey, B.; Bhattacharyya, B. Comparison of Various Electricity Market Pricing Strategies to Reduce Generation Cost of a Microgrid System Using Hybrid WOA-SCA. Evol. Intell. 2021, 15, 1587–1604. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Zhu, J. Multiobjective Design Optimization of an IPMSM for EVs Based on Fuzzy Method and Sequential Taguchi Method. IEEE Trans. Ind. Electron. 2021, 68, 10592–10600. [Google Scholar] [CrossRef]
- Balaram Naik, A.; Chennakeshava Reddy, A. Optimization of Tensile Strength in TIG Welding Using the Taguchi Method and Analysis of Variance (ANOVA). Therm. Sci. Eng. Prog. 2018, 8, 327–339. [Google Scholar] [CrossRef]
- Tsai, P.W.; Pan, J.S.; Chen, S.M.; Liao, B.Y. Enhanced Parallel Cat Swarm Optimization Based on the Taguchi Method. Expert Syst. Appl. 2012, 39, 6309–6319. [Google Scholar] [CrossRef]
- Diao, K.; Sun, X.; Lei, G.; Bramerdorfer, G.; Guo, Y.; Zhu, J. Robust Design Optimization of Switched Reluctance Motor Drive Systems Based on System-Level Sequential Taguchi Method. IEEE Trans. Energy Convers. 2021, 36, 3199–3207. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Beltran, A.A.; Paglinawan, A.C. A Robust Design of Maximum Power Point Tracking Using Taguchi Method for Stand-Alone PV System. Appl. Energy 2018, 211, 50–63. [Google Scholar] [CrossRef]
- Gao, H.; Zhao, H.; Chen, S. Image Denoising Method of Auto-Evolving PCNN Model Based on Quantum Selfish Herd Algorithm. In Advances in Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2022; pp. 128–138. [Google Scholar]
- Nie, R.; He, M.; Cao, J.; Zhou, D.; Liang, Z. Pulse Coupled Neural Network Based MRI Image Enhancement Using Classical Visual Receptive Field for Smarter Mobile Healthcare. J. Ambient Intell. Humaniz. Comput. 2019, 10, 4059–4070. [Google Scholar] [CrossRef]
- Panigrahy, C.; Seal, A.; Mahato, N.K. MRI and SPECT Image Fusion Using a Weighted Parameter Adaptive Dual Channel PCNN. IEEE Signal Process. Lett. 2020, 27, 690–694. [Google Scholar] [CrossRef]
- Deng, X.; Ye, J. A Retinal Blood Vessel Segmentation Based on Improved D-MNet and Pulse-Coupled Neural Network. Biomed. Signal Process. Control 2022, 73, 103467. [Google Scholar] [CrossRef]
- Deng, X.; Yang, Y.; Sun, H. An Adaptive Threshold Setting Algorithm Based on PCNN Edge Detection Model. In Proceedings of the ACM International Conference Proceeding Series, Association for Computing Machinery, New York, NY, USA, 20 February 2021; pp. 34–41. [Google Scholar]
- Zhang, D.; Wang, D.; Gu, C.; Jin, N.; Zhao, H.; Chen, G.; Liang, H.; Liang, D. Using Neural Network to Identify the Severity of Wheat Fusarium Head Blight in the Field Environment. Remote Sens. 2019, 11, 2375. [Google Scholar] [CrossRef]
- Xu, X.; Liang, T.; Wang, G.; Wang, M.; Wang, X. Self-Adaptive PCNN Based on the ACO Algorithm and Its Application on Medical Image Segmentation. Intell. Autom. Soft Comput. 2017, 23, 303–310. [Google Scholar] [CrossRef]
- Low, K.S.; Zhuang, H. Real Time Runway Detection in Satellite Images Using Multi-Channel PCNN. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; ISBN 9781479943159. [Google Scholar]
- Gu, X. Feature Extraction Using Unit-Linking Pulse Coupled Neural Network and Its Applications. Neural Process. Lett. 2008, 27, 25–41. [Google Scholar] [CrossRef]
- Pan, J.S.; Hu, P.; Chu, S.C. Novel Parallel Heterogeneous Meta-Heuristic and Its Communication Strategies for the Prediction of Wind Power. Processes 2019, 7, 845. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Chang, J.-F.; Chu, S.-C.; Roddick, J.F.; Pan, J.-S. A Parallel Particle Swarm Optimization Algorithm with Communication Strategies. J. Inf. Sci. Eng. 2005, 21, 9. [Google Scholar]
- Wang, X.; Pan, J.S.; Chu, S.C. A Parallel Multi-Verse Optimizer for Application in Multilevel Image Segmentation. IEEE Access 2020, 8, 32018–32030. [Google Scholar] [CrossRef]
- Zhang, X.; Han, L.; Dong, Y.; Shi, Y.; Huang, W.; Han, L.; González-Moreno, P.; Ma, H.; Ye, H.; Sobeih, T. A Deep Learning-Based Approach for Automated Yellow Rust Disease Detection from High-Resolution Hyperspectral UAV Images. Remote Sens. 2019, 11, 1554. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Kang, L.; Li, Y.; Jiang, Z.; Sun, K. Pulse Coupled Neural Network Based on Harris Hawks Optimization Algorithm for Image Segmentation. Multimed. Tools Appl. 2020, 79, 28369–28392. [Google Scholar] [CrossRef]
- Natteshan, N.V.S.; Suresh Kumar, N. Effective SAR Image Segmentation and Classification of Crop Areas Using MRG and CDNN Techniques. Eur. J. Remote Sens. 2020, 53, 126–140. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Chu, S.-C.; Du, Z.-G.; Peng, Y.-J.; Pan, J.-S. Fuzzy Hierarchical Surrogate Assists Probabilistic Particle Swarm Optimization for Expensive High Dimensional Problem. Knowl.-Based Syst. 2021, 220, 106939. [Google Scholar]
- Wang, H.; Liang, M.; Sun, C.; Zhang, G.; Xie, L. Multiple-Strategy Learning Particle Swarm Optimization for Large-Scale Optimization Problems. Complex Intell. Syst. 2021, 7, 1–16. [Google Scholar] [CrossRef]







| Function | Dim | |
|---|---|---|
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 |
| Function | Dim | |
|---|---|---|
| 20 | −418.9829 × 5 | |
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 | |
| 20 | 0 |
| Function | Dim | |
|---|---|---|
| 2 | 0 | |
| 4 | 0.0003 | |
| 2 | −1.0316 | |
| 2 | 0.398 | |
| 2 | 3 | |
| 3 | −3.86 | |
| 6 | −3.32 | |
| 4 | −10.1532 | |
| 4 | −10.4028 | |
| 4 | −10.5363 |
| Function | Algorithm | Best Fitness | Mean | STD |
|---|---|---|---|---|
| F1 | SCA | |||
| PSCA-Best | ||||
| PSCA-Mean | ||||
| PSCA-Hybrid | ||||
| F2 | SCA | |||
| PSCA-Best | ||||
| PSCA-Mean | ||||
| PSCA-Hybrid | ||||
| F8 | SCA | |||
| PSCA-Best | ||||
| PSCA-Mean | ||||
| PSCA-Hybrid | ||||
| F12 | SCA | |||
| PSCA-Best | ||||
| PSCA-Mean | ||||
| PSCA-Hybrid | ||||
| F21 | SCA | |||
| PSCA-Best | ||||
| PSCA-Mean | ||||
| PSCA-Hybrid | ||||
| F22 | SCA | |||
| PSCA-Best | ||||
| PSCA-Mean | ||||
| PSCA-Hybrid |
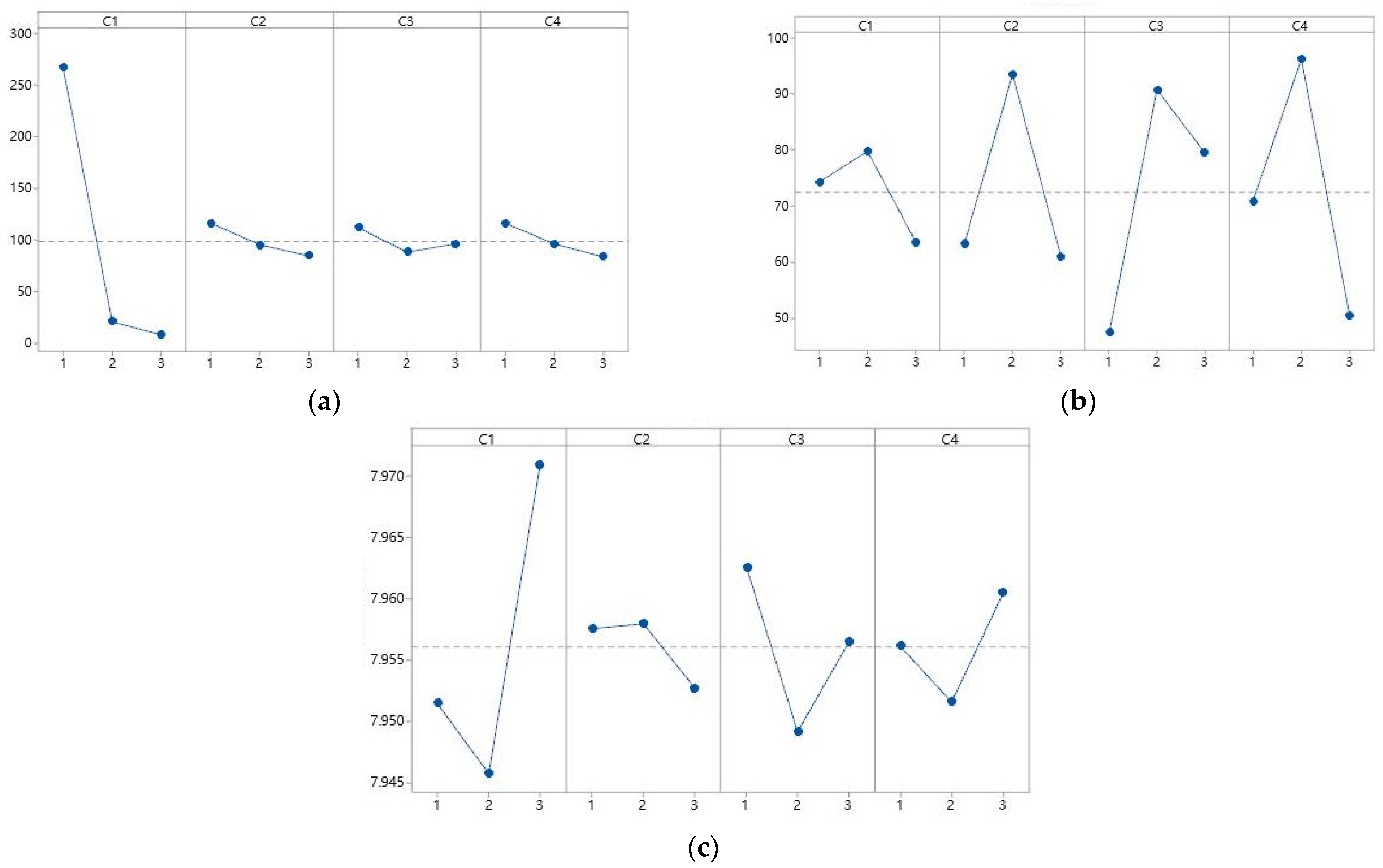
| Level | ||||
|---|---|---|---|---|
| Level 1 | 2 | 30 | PSCA-Best | |
| Level 2 | 4 | 50 | PSCA-Mean | |
| Level 3 | 8 | 60 | PSCA-Hybrid |
| Experiment Group | Considered Factors | |||
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 1 | 3 | 2 |
| 3 | 3 | 1 | 2 | 3 |
| 4 | 1 | 2 | 2 | 1 |
| 5 | 2 | 2 | 1 | 3 |
| 6 | 3 | 2 | 3 | 2 |
| 7 | 1 | 3 | 1 | 3 |
| 8 | 2 | 3 | 3 | 1 |
| 9 | 3 | 3 | 2 | 2 |
| Function | Values | Algorithm | ||||
|---|---|---|---|---|---|---|
| SCA | TPSCA | PPSO | PMVO | |||
| F1 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F2 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F3 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F4 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F5 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F6 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F7 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F8 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F9 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F10 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F11 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F12 | Best | |||||
| Avg | ||||||
| STD | 0 | |||||
| F13 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F14 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F15 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F16 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F17 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F18 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F19 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F20 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F21 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F22 | Best | |||||
| Avg | ||||||
| STD | ||||||
| F23 | Best | |||||
| Avg | ||||||
| STD | ||||||
| Statistics of the number of wins | Algorithm | Best | Avg | STD | ||
| SCA | 4 | 2 | 1 | |||
| TPSCA | 22 | 22 | 17 | |||
| PPSO | 3 | 1 | 1 | |||
| PMVO | 4 | 0 | 3 | |||
| Source | SS | df | Ms | Chi-sq | Prob < Chi-sq |
|---|---|---|---|---|---|
| Groups | 3.0 | 0.94 | 0.044 | ||
| Error | 88 | ||||
| Total | 91 |
| Source | SS | df | Ms | Chi-sq | Prob < Chi-sq |
|---|---|---|---|---|---|
| Groups | 53.47 | 3.0 | 17.82 | 38.44 | |
| Error | 42.52 | 66 | 0.64 | ||
| Total | 96 | 91 |
| Dataset | Model | Evaluation Metrics | |||||
|---|---|---|---|---|---|---|---|
| Image 1 | TPSCA–PCNN | 88.25% | 96.28% | 79.79% | 77.69% | 77.40% | 82.48% |
| PCNN | 43.98% | 42.87% | 35.81% | −12.19% | 24.24% | 44.77% | |
| ELM | 13.52% | 10.57% | 8.26% | −72.98% | 4.86% | 15.64% | |
| Image 2 | TPSCA–PCNN | 95.83% | 99.29% | 99.28% | 91.88% | 91.68% | 92.85% |
| PCNN | 35.45% | 4.95% | 10.00% | −39.65% | 3.42% | 61.64% | |
| ELM | 48.99% | 48.97% | 45.28% | −2.01% | 30.77% | 49.01% | |
| Image 3 | TPSCA–PCNN | 85.13% | 99.59% | 70.40% | 73.41% | 70.02% | 77.28% |
| PCNN | 43.42% | 40.47% | 28.54% | −13.86% | 20.10% | 45.02% | |
| ELM | 25.47% | 32.07% | 45.28% | −45.28% | 13.15% | 21.89% | |
| Image 4 | TPSCA–PCNN | 86.16% | 99.79% | 40.64% | 50.27% | 40.59% | 62.56% |
| PCNN | 38.68% | 22.18% | 9.06% | −2.82% | 6.88% | 42.24% | |
| ELM | 26.83% | 0.56% | 2.08% | −50.35% | 1.54% | 32.27% | |
| Image 5 | TPSCA–PCNN | 84.59% | 89.69% | 72.19% | 64.44% | 61.69% | 73.24% |
| PCNN | 10.91% | 2.67% | 0.22% | −79.39% | 1.22% | 16.69% | |
| ELM | 11.77% | 5.03% | 4.52% | −77.11% | 2.58% | 16.06% | |
| Image 6 | TPSCA–PCNN | 85.67% | 99.70% | 71.54% | 74.36% | 71.38% | 77.83% |
| PCNN | 54.31% | 23.69% | 31.66% | −5.29% | 15.68% | 71.42% | |
| ELM | 71.37% | 79.85% | 57.22% | 44.56% | 50.00% | 66.63% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, F.; Liu, G.; Geng, J.; Zhao, H.; Liu, G. Optimization of Remote Sensing Image Segmentation by a Customized Parallel Sine Cosine Algorithm Based on the Taguchi Method. Remote Sens. 2022, 14, 4875. https://doi.org/10.3390/rs14194875
Fan F, Liu G, Geng J, Zhao H, Liu G. Optimization of Remote Sensing Image Segmentation by a Customized Parallel Sine Cosine Algorithm Based on the Taguchi Method. Remote Sensing. 2022; 14(19):4875. https://doi.org/10.3390/rs14194875
Chicago/Turabian StyleFan, Fang, Gaoyuan Liu, Jiarong Geng, Huiqi Zhao, and Gang Liu. 2022. "Optimization of Remote Sensing Image Segmentation by a Customized Parallel Sine Cosine Algorithm Based on the Taguchi Method" Remote Sensing 14, no. 19: 4875. https://doi.org/10.3390/rs14194875
APA StyleFan, F., Liu, G., Geng, J., Zhao, H., & Liu, G. (2022). Optimization of Remote Sensing Image Segmentation by a Customized Parallel Sine Cosine Algorithm Based on the Taguchi Method. Remote Sensing, 14(19), 4875. https://doi.org/10.3390/rs14194875











