Figure 1.
Example categories in samples. Nodes within each circle represent the categories involved in each sample. Each sample contains a small number of category nodes, and categories in different samples are quite different.
Figure 1.
Example categories in samples. Nodes within each circle represent the categories involved in each sample. Each sample contains a small number of category nodes, and categories in different samples are quite different.
Figure 2.
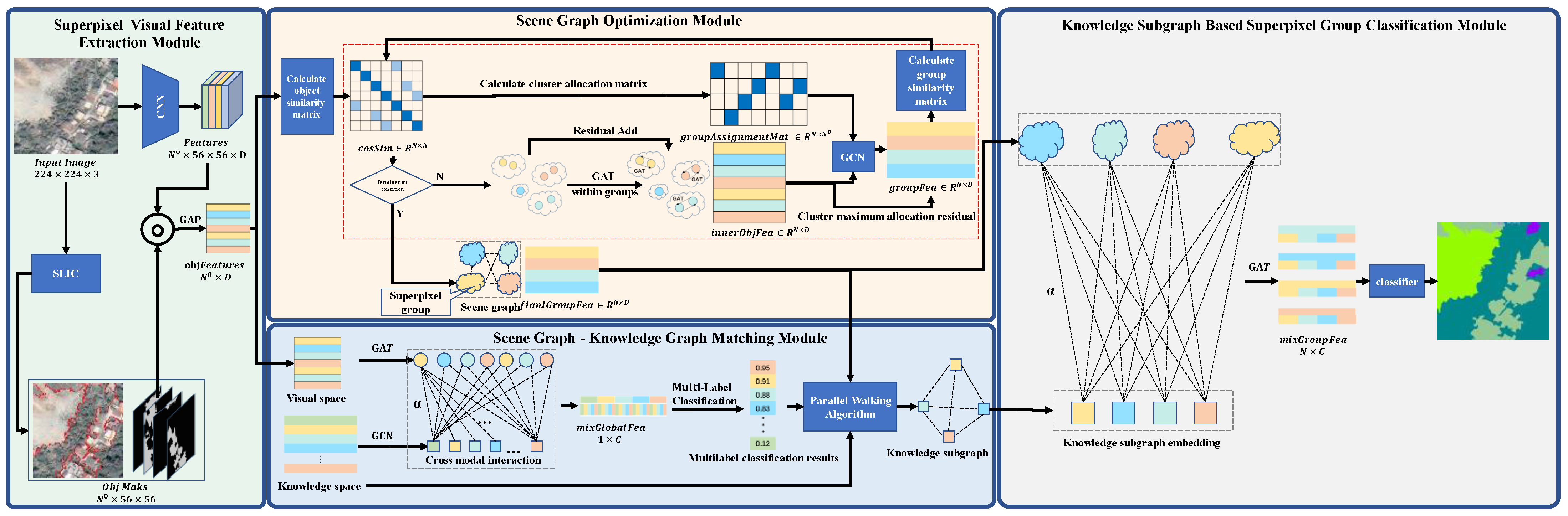
Network structure of the PWGM. The Superpixel Visual Feature Extraction Module performs superpixel segmentation on the sample and extracts the superpixel feature using the pretrained CNN network, which constructs the initial sample scene graph and provides input for the Scene Graph Optimization Module. The Scene Graph Optimization Module optimizes the initial scene graph, clusters the superpixel objects into superpixel clusters using graph pooling, and the optimized sample scene graph provides scene graph information for the Scene Graph—Knowledge Graph Matching Module. The Scene Graph—Knowledge Graph Matching Module outputs the knowledge subgraph matched with the sample scene graph, which provides the Knowledge Subgraph-Based Cross Modality Superpixel Group Classification Module.
Figure 2.
Network structure of the PWGM. The Superpixel Visual Feature Extraction Module performs superpixel segmentation on the sample and extracts the superpixel feature using the pretrained CNN network, which constructs the initial sample scene graph and provides input for the Scene Graph Optimization Module. The Scene Graph Optimization Module optimizes the initial scene graph, clusters the superpixel objects into superpixel clusters using graph pooling, and the optimized sample scene graph provides scene graph information for the Scene Graph—Knowledge Graph Matching Module. The Scene Graph—Knowledge Graph Matching Module outputs the knowledge subgraph matched with the sample scene graph, which provides the Knowledge Subgraph-Based Cross Modality Superpixel Group Classification Module.
Figure 3.
Structure of Scene Graph Optimization Module. This module provides a cosine similarity-based graph pooling algorithm to optimize the scene graph generated from the Superpixel Visual Feature Extraction Module. Through GAT and cluster allocation matrix, it reduces the redundant nodes in the scene graph and provides the optimized scene graph for the Scene Graph—Knowledge Graph Matching Module.
Figure 3.
Structure of Scene Graph Optimization Module. This module provides a cosine similarity-based graph pooling algorithm to optimize the scene graph generated from the Superpixel Visual Feature Extraction Module. Through GAT and cluster allocation matrix, it reduces the redundant nodes in the scene graph and provides the optimized scene graph for the Scene Graph—Knowledge Graph Matching Module.
Figure 4.
The structure of the Scene Graph—Knowledge Graph Matching Module. The information of visual and knowledge space is generated by GAT and GCN. After the cross modal interaction process, the knowledge subgraph is extracted through a parallel walking algorithm using multilabel classification.
Figure 4.
The structure of the Scene Graph—Knowledge Graph Matching Module. The information of visual and knowledge space is generated by GAT and GCN. After the cross modal interaction process, the knowledge subgraph is extracted through a parallel walking algorithm using multilabel classification.
Figure 5.
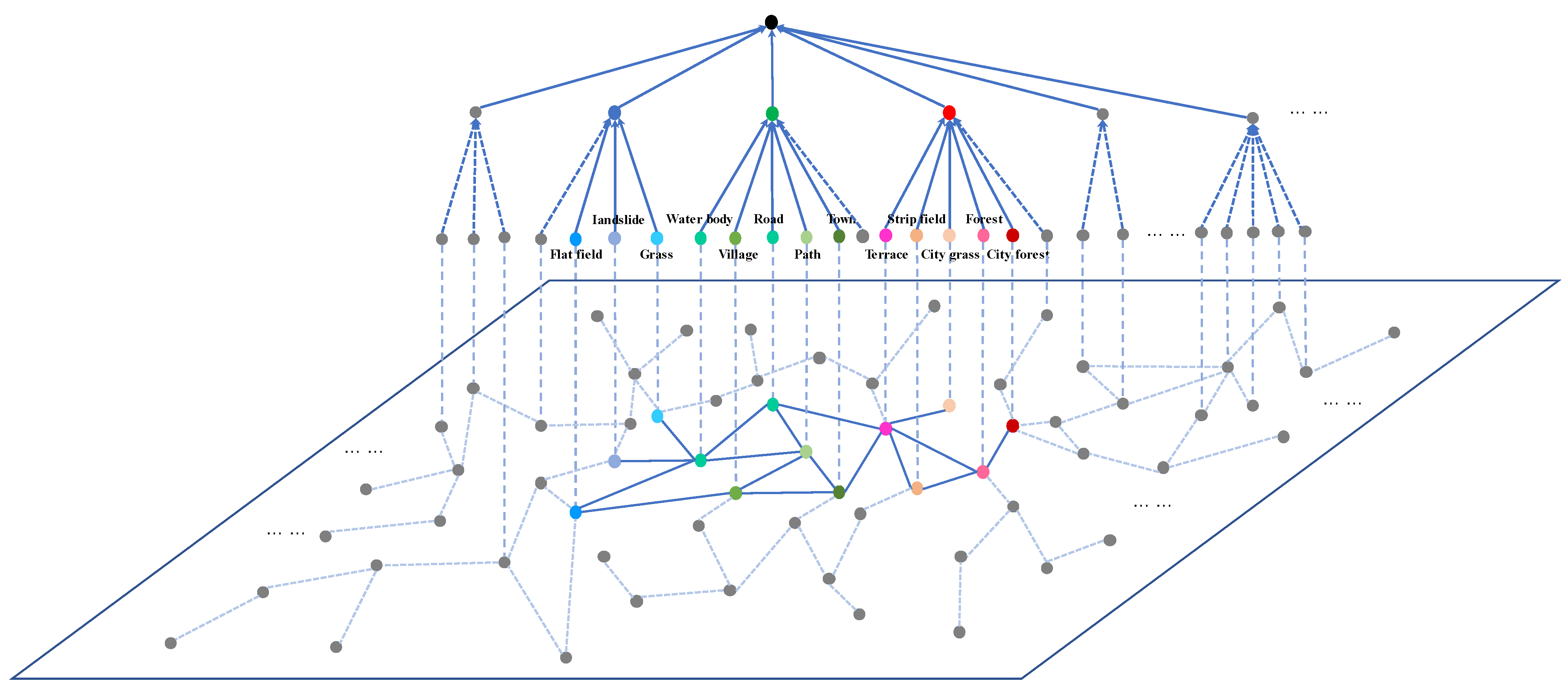
The structure of the knowledge subgraph. Nodes of different levels represent categories in different levels. The nodes on the plane represent the entire category knowledge graph, and the colored nodes, except for the gray ones, represent the subgraph of the knowledge map to be searched.
Figure 5.
The structure of the knowledge subgraph. Nodes of different levels represent categories in different levels. The nodes on the plane represent the entire category knowledge graph, and the colored nodes, except for the gray ones, represent the subgraph of the knowledge map to be searched.
Figure 6.
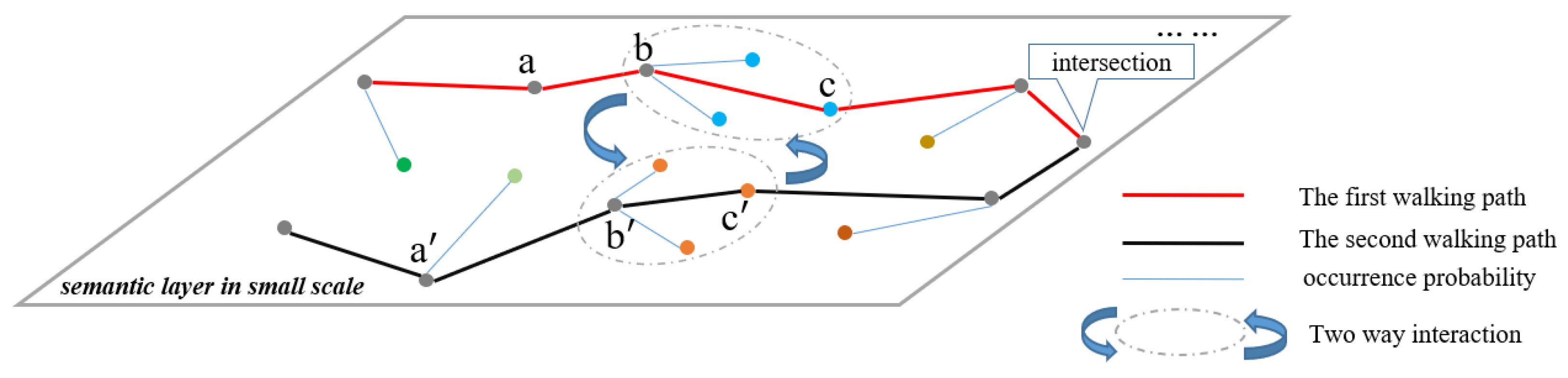
Process of parallel walking algorithm. The two walking paths represent two different scenes. Nodes in different paths represent different categories belonging to each scene. We apply our parallel walking algorithm to each path and filter out the possible categories in the corresponding scenes.
Figure 6.
Process of parallel walking algorithm. The two walking paths represent two different scenes. Nodes in different paths represent different categories belonging to each scene. We apply our parallel walking algorithm to each path and filter out the possible categories in the corresponding scenes.
Figure 7.
Structure of Knowledge Subgraph-Based Superpixel Group Classification Module. This module achieves semantic classification of superpixel groups based on cross modality information generated by GAT. Within the superpixel group, the nodes are classified the same.
Figure 7.
Structure of Knowledge Subgraph-Based Superpixel Group Classification Module. This module achieves semantic classification of superpixel groups based on cross modality information generated by GAT. Within the superpixel group, the nodes are classified the same.
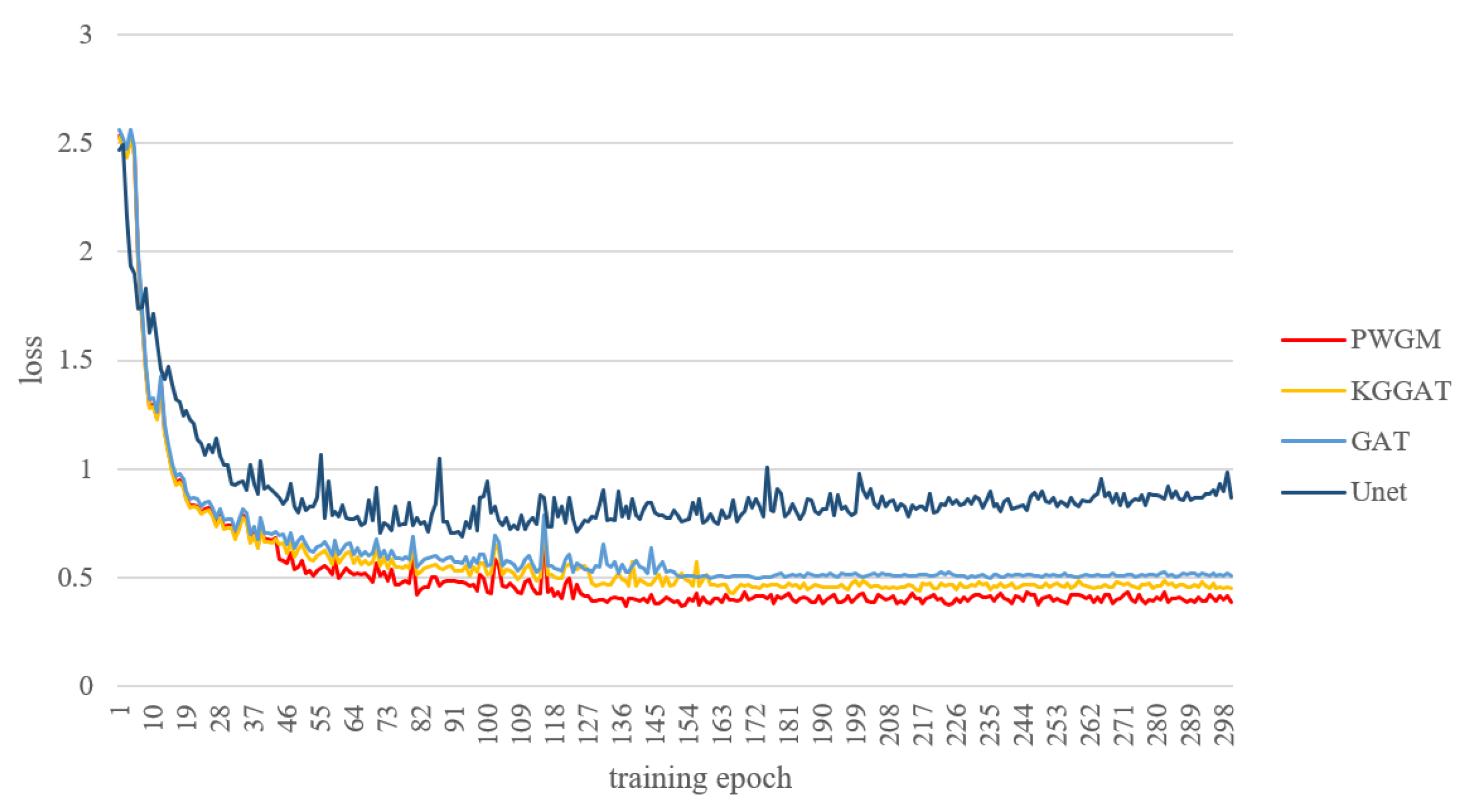
Figure 8.
Loss curves. The figure shows the loss function value in the process of model training. The Unet shows the highest loss value, while our PWGM shows the lowest loss value.
Figure 8.
Loss curves. The figure shows the loss function value in the process of model training. The Unet shows the highest loss value, while our PWGM shows the lowest loss value.
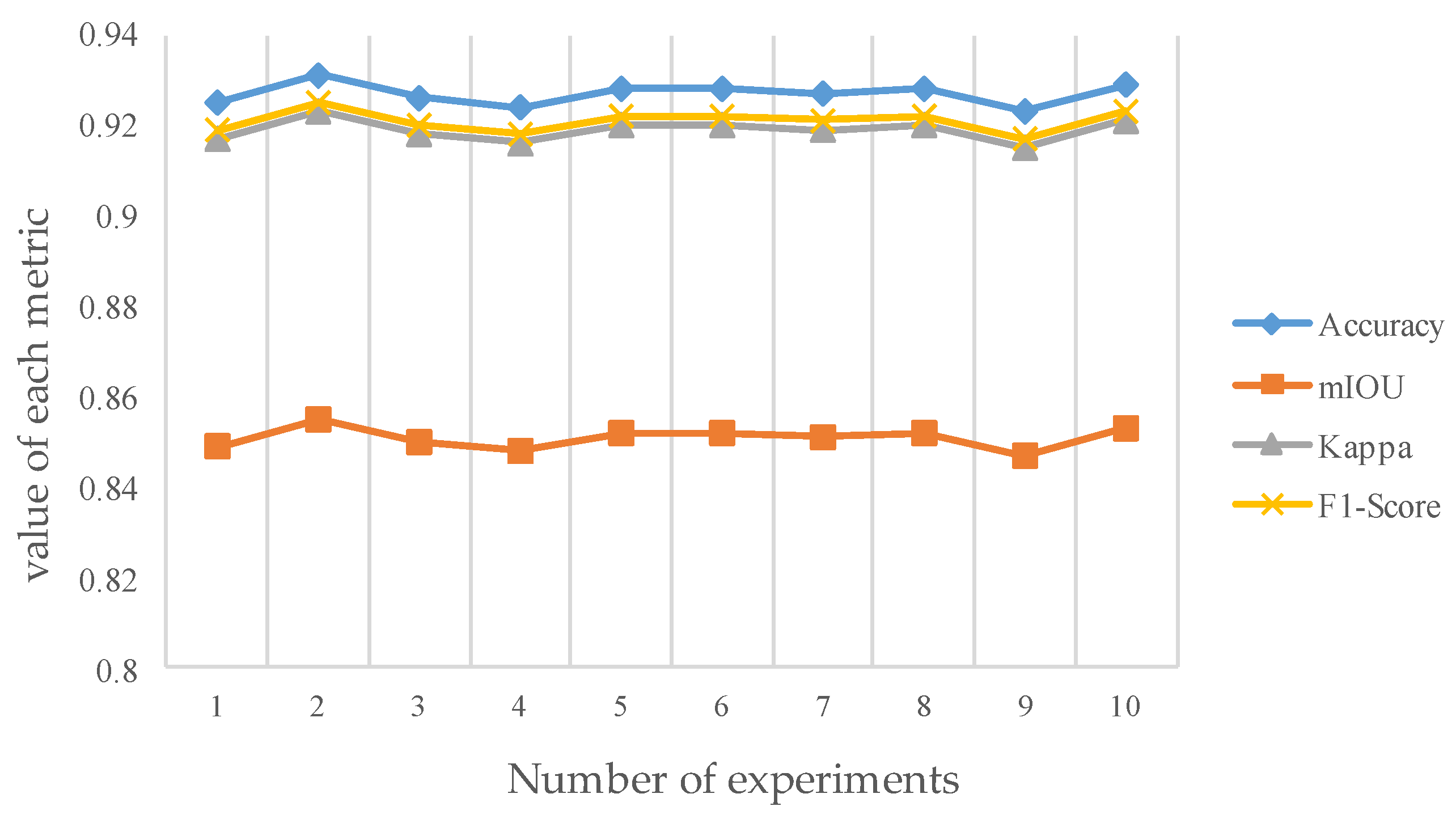
Figure 9.
Results of Monte Carlo experiments. For each experiment, we calculate the accuracy, mIOU, Kappa and F1-Score to describe the robustness of the model. The average values are close to the previous experimental results of PWGM.
Figure 9.
Results of Monte Carlo experiments. For each experiment, we calculate the accuracy, mIOU, Kappa and F1-Score to describe the robustness of the model. The average values are close to the previous experimental results of PWGM.
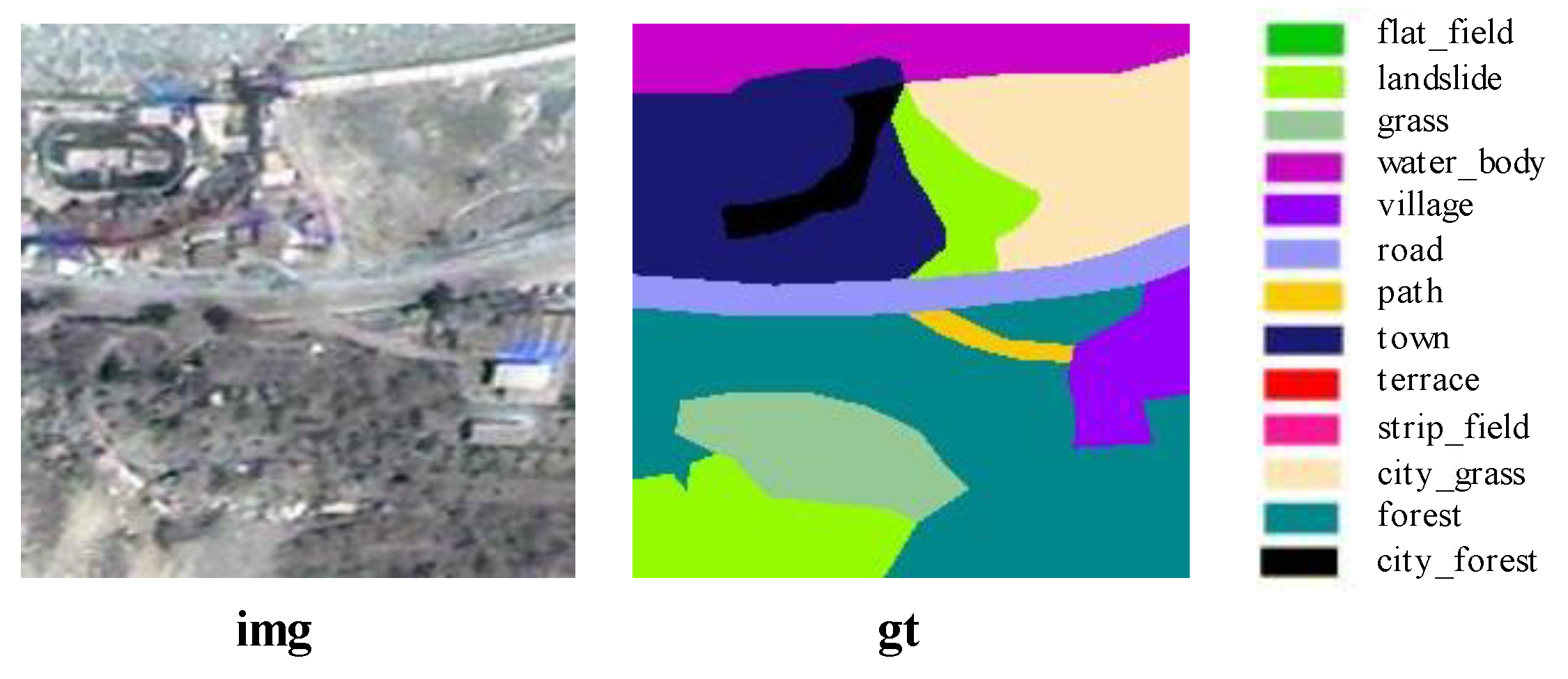
Figure 10.
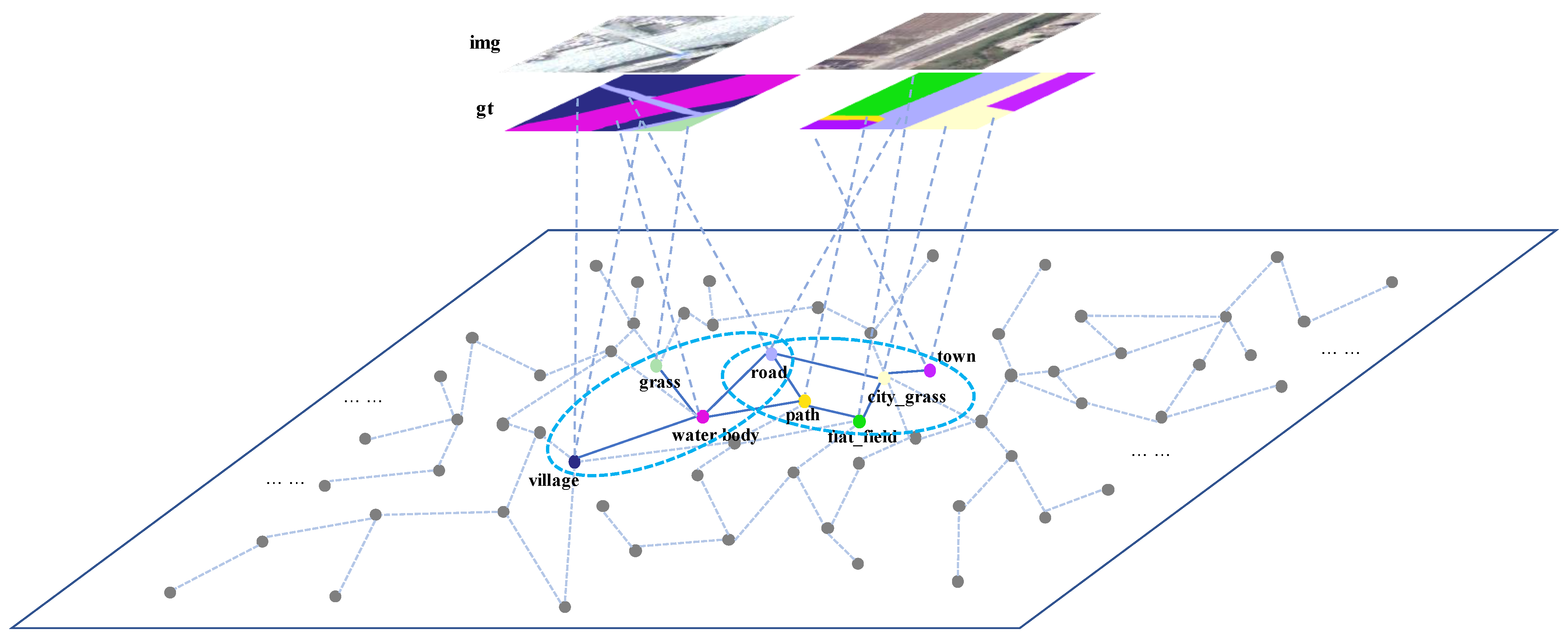
Sample I for the analysis of the solidified walking scene. This figure shows a specific solidified scene; “img” represents the remote sensing image and “gt” represents the ground truth image. The legend is on the right of the figure.
Figure 10.
Sample I for the analysis of the solidified walking scene. This figure shows a specific solidified scene; “img” represents the remote sensing image and “gt” represents the ground truth image. The legend is on the right of the figure.
Figure 11.
Surroundings of sample II. This figure shows a specific complex scene. The categories in the red box include town, grass, city grass, village, flat field and path. It involves the phenomenon of “different objects with the same spectrum” between grass and city grass.
Figure 11.
Surroundings of sample II. This figure shows a specific complex scene. The categories in the red box include town, grass, city grass, village, flat field and path. It involves the phenomenon of “different objects with the same spectrum” between grass and city grass.
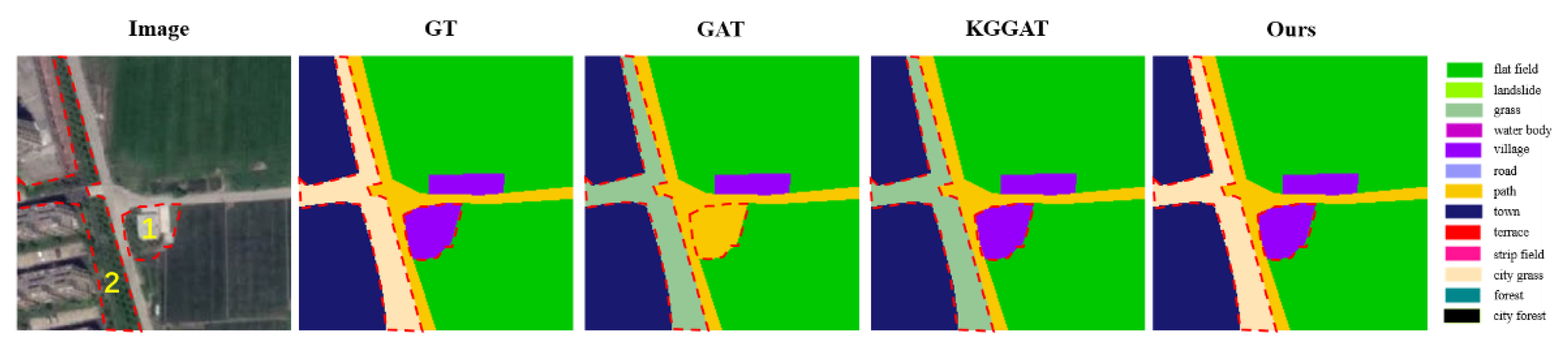
Figure 12.
Prediction of sample II. This figure shows the prediction results of the above models. For the city grass on the center left and the village on the center of the image, our PWGM predicts both correctly.
Figure 12.
Prediction of sample II. This figure shows the prediction results of the above models. For the city grass on the center left and the village on the center of the image, our PWGM predicts both correctly.
Table 1.
Introduction of references.
Table 1.
Introduction of references.
| Research Field | References |
|---|
| Remote sensing semantic segmentation | [1,2,3,4,5,6,7,8,11,15,47] |
| Graph neural network | [9,10,11,12,14,16,43,48,49] |
| Graph construction method | [13,24,46] |
| Research on geographical knowledge graph | [17,18,19,20,21,22,23,25] |
| Graph pooling method | [26,27,28,29,30,31,32,33,34,35] |
| Scene graph–knowledge graph matching method | [36,42,43,44,45] |
| Graph walking method | [37,38,39,40,41] |
| Graph matching method | [43] |
Table 2.
Table of notations.
Table 2.
Table of notations.
| Symbol | Meaning |
|---|
| the visual feature of nodes in the scene graph |
| global average pooling |
| convolutional neural network model |
| x | image samples |
| the superpixel mask |
| the sample scene graph structure |
| the node set of the scene graph |
| the edge set of the scene graph |
| the visual feature cosine similarity |
| the edge between nodes i and j |
| |
| the feature dimension of the vector |
| group mask matrix |
| cosine similarity matrix |
| clustering threshold |
| the node features updated from neighbor nodes within the group |
| activation function |
| learnable matrix |
| the assignment weight of node i which belongs to the superpixel group |
| the superpixel group feature matrix |
| the structure of knowledge graphs for remote sensing semantic segmentation |
| the node set of the knowledge graph |
| the edge set of the knowledge graph |
| the category cooccurrence probability between nodes and |
| the number of samples that include categories and |
| the number of samples that include category α |
| the classification score of category |
| the cooccurrence probability of categories b and c |
| the next node score of the multilabel classification |
| hyperparameters |
| the final mixed feature |
| attention function |
| the final superpixel group feature |
| the word embedding features of nodes in the knowledge graph |
| graph attention network |
| the result of classification |
| normalization function |
| the cross-entropy loss function of superpixel groups semantic classification |
| the label of the superpixel groups semantic classification |
| the prediction result of the superpixel groups semantic classification |
Table 3.
Sample statistics of complex scenes.
Table 3.
Sample statistics of complex scenes.
| Scene Name | Number of Samples | Categories Involved | Definition of Scene | Type of Scene |
|---|
| Cultivated Scene | 51 | flat field (1), grass (3), terrace (9), strip field (10) | No village construction in cultivated scene | simple scene |
| Landslide scene | 65 | landslide (2), grass (3), water body (4), forest (12) | Surrounding environment of landslide | simple scene |
| Urban Scene | 83 | road (6), town (8), water body (4), city forest (13), city grass (11) | Surrounding environment of urban buildings | simple scene |
| Rural Scene | 70 | path (7), village (5), water body (4), forest (12), grass (3), flat field (1) | Surrounding environment of village construction | simple scene |
| Urban–rural scene | 256 | road (6), town (8), water body (4), city forest (13), city grass (11), path (7), village (5), forest (12), grass (3), flat field (1) | Urban rural fringe | complex scene |
| Landslide-influenced scenes | 210 | path (7), village (5), water body (4), forest (12), grass (3), flat field (1), landslide (2), road (6), town (8) | Surrounding environment of affected by landslides | complex scene |
| … | … | … | … | … |
Table 4.
The OA, mIoU, Kappa, and F1-Score of four networks.
Table 4.
The OA, mIoU, Kappa, and F1-Score of four networks.
| | OA | mIoU | Kappa | F1-Score |
|---|
| Unet | 0.796 | 0.635 | 0.778 | 0.713 |
| GAT | 0.878 | 0.801 | 0.862 | 0.890 |
| KGGAT | 0.897 | 0.820 | 0.885 | 0.892 |
| PWGM (Ours) | 0.929 | 0.853 | 0.920 | 0.923 |
Table 5.
The pixel-based classification confusion matrix of Unet.
Table 5.
The pixel-based classification confusion matrix of Unet.
| | Flat Field | Landslide | Grass | Water Body | Village | Road | Path | Town | Terrace | Strip Field | City Grass | Forest | City Forest | Sum of Pixel | Accuracy |
|---|
| flat field | 1,795,560 | 1960 | 46,141 | 0 | 96,535 | 384 | 13,023 | 1748 | 13,098 | 461 | 15 | 44,768 | 130 | 2,013,823 | 0.891 |
| landslide | 4580 | 2,241,286 | 164,516 | 35,051 | 19,178 | 15,028 | 19,650 | 13,532 | 9295 | 10,167 | 7503 | 104,177 | 1334 | 2,645,297 | 0.847 |
| grass | 106,861 | 145,475 | 1,808,823 | 58,420 | 181,062 | 32,265 | 23,533 | 44,042 | 116,883 | 33,267 | 33,731 | 274,054 | 12,880 | 2,871,296 | 0.629 |
| water body | 972 | 18,642 | 28,330 | 1,371,473 | 2167 | 11,214 | 6 | 9207 | 1062 | 590 | 5112 | 6035 | 1801 | 1,456,611 | 0.941 |
| village | 92,896 | 2602 | 74,016 | 3927 | 1,238,335 | 7329 | 12,876 | 102,389 | 8146 | 6975 | 4642 | 147,308 | 5675 | 1,707,116 | 0.725 |
| road | 858 | 16,843 | 14,393 | 15,741 | 7393 | 152,166 | 3868 | 56,565 | 77 | 158 | 4504 | 3339 | 1409 | 277,314 | 0.548 |
| path | 25,255 | 18,275 | 17,185 | 4 | 36,583 | 5569 | 140,362 | 7878 | 9974 | 9176 | 33 | 8589 | 75 | 278,958 | 0.503 |
| town | 216 | 7003 | 11,177 | 13,718 | 72,131 | 24,440 | 101 | 1,522,105 | 0 | 18 | 28,560 | 35,469 | 41,879 | 1,756,817 | 0.866 |
| terrace | 53,041 | 1949 | 66,821 | 420 | 25,583 | 152 | 14,894 | 66 | 1,329,939 | 45,428 | 176 | 86,662 | 8 | 1,625,139 | 0.818 |
| strip field | 29,573 | 636 | 28,184 | 795 | 9033 | 195 | 10,505 | 45 | 40,645 | 1,684,747 | 419 | 48,252 | 3 | 1,853,032 | 0.909 |
| city grass | 651 | 486 | 23,239 | 8752 | 6151 | 6389 | 127 | 28,094 | 0 | 9 | 31,922 | 18,352 | 21,579 | 145,751 | 0.219 |
| forest | 50,139 | 65,758 | 247,138 | 8712 | 164,772 | 2277 | 5226 | 12,698 | 37,719 | 50,944 | 8855 | 3,451,530 | 31,395 | 4,137,163 | 0.834 |
| city forest | 2658 | 996 | 9136 | 4543 | 3119 | 1916 | 39 | 27,834 | 0 | 104 | 12,970 | 42,667 | 80,197 | 186,179 | 0.430 |
Table 6.
The pixel-based classification confusion matrix of GAT.
Table 6.
The pixel-based classification confusion matrix of GAT.
| | Flat Field | Landslide | Grass | Water Body | Village | Road | Path | Town | Terrace | Strip Field | City Grass | Forest | City Forest | Sum of Pixel | Accuracy |
|---|
| flat field | 1,730,815 | 5368 | 195,214 | 5325 | 24,563 | 1353 | 8085 | 0 | 26,665 | 0 | 0 | 16,434 | 0 | 2,013,823 | 0.859 |
| landslide | 0 | 2,440,442 | 155,939 | 174 | 11,845 | 17,897 | 6523 | 832 | 0 | 0 | 4453 | 7191 | 0 | 2,645,297 | 0.922 |
| grass | 32,385 | 83,124 | 2,125,012 | 70,160 | 64,089 | 6196 | 6776 | 5605 | 87,151 | 66,073 | 22,039 | 265,881 | 36,805 | 2,871,296 | 0.740 |
| water body | 0 | 9801 | 178,107 | 1,259,104 | 233 | 7377 | 0 | 0 | 0 | 0 | 1988 | 0 | 0 | 1,456,611 | 0.864 |
| village | 13,902 | 28,614 | 44,088 | 10,312 | 1,530,321 | 1443 | 3663 | 2382 | 3122 | 45,761 | 2508 | 20,907 | 93 | 1,707,116 | 0.896 |
| road | 0 | 6431 | 1267 | 1546 | 12,057 | 214,633 | 10,225 | 29,362 | 0 | 0 | 1792 | 0 | 0 | 277,314 | 0.773 |
| path | 10,354 | 14,579 | 25,524 | 0 | 9076 | 2405 | 207,048 | 5783 | 0 | 820 | 0 | 3369 | 0 | 278,958 | 0.742 |
| town | 0 | 1288 | 8762 | 2778 | 160,059 | 11,771 | 369 | 1,499,408 | 0 | 0 | 31,389 | 14,305 | 26,688 | 1,756,817 | 0.853 |
| terrace | 29,411 | 0 | 47,731 | 2432 | 2020 | 0 | 226 | 0 | 1,443,793 | 21,769 | 0 | 77,757 | 0 | 1,625,139 | 0.888 |
| strip field | 0 | 2465 | 10,189 | 0 | 4051 | 0 | 571 | 0 | 12,771 | 1,799,280 | 0 | 23,705 | 0 | 1,853,032 | 0.970 |
| city grass | 0 | 5576 | 56,948 | 5248 | 2566 | 2026 | 0 | 4267 | 0 | 0 | 51,012 | 4085 | 14,023 | 145,751 | 0.350 |
| forest | 14,881 | 9140 | 444,613 | 0 | 21,741 | 1225 | 0 | 2244 | 12,945 | 46,345 | 0 | 3,510,969 | 73,060 | 4,137,163 | 0.848 |
| city forest | 0 | 0 | 3693 | 0 | 0 | 0 | 0 | 11,763 | 0 | 5509 | 0 | 46,737 | 118,477 | 186,179 | 0.636 |
Table 7.
The pixel-based classification confusion matrix of KGGAT.
Table 7.
The pixel-based classification confusion matrix of KGGAT.
| | Flat Field | Landslide | Grass | Water Body | Village | Road | Path | Town | Terrace | Strip Field | City Grass | Forest | City Forest | Sum of Pixel | Accuracy |
|---|
| flat field | 1,859,030 | 5368 | 67,272 | 5325 | 24,563 | 1353 | 7813 | 0 | 26,665 | 0 | 0 | 16,434 | 0 | 2,013,823 | 0.923 |
| landslide | 0 | 2,571,005 | 27,091 | 174 | 11,845 | 16,183 | 6523 | 832 | 0 | 0 | 4453 | 7191 | 0 | 2,645,297 | 0.972 |
| grass | 15,003 | 88,590 | 2,317,620 | 70,160 | 61,935 | 2950 | 5941 | 5605 | 87,151 | 55,245 | 22,039 | 112,018 | 27,039 | 2,871,296 | 0.807 |
| water body | 0 | 9801 | 18,394 | 1,418,818 | 233 | 7377 | 0 | 0 | 0 | 0 | 1988 | 0 | 0 | 1,456,611 | 0.974 |
| village | 13,902 | 28,614 | 34,019 | 10,312 | 1,546,318 | 1443 | 3663 | 39,263 | 3122 | 3125 | 2508 | 20,827 | 0 | 1,707,116 | 0.906 |
| road | 0 | 6431 | 1267 | 1546 | 8057 | 239,535 | 10,225 | 8461 | 0 | 0 | 1792 | 0 | 0 | 277,314 | 0.864 |
| path | 12,697 | 11,397 | 24,016 | 0 | 19,076 | 10,060 | 191,740 | 5783 | 0 | 820 | 0 | 3369 | 0 | 278,958 | 0.687 |
| town | 0 | 1288 | 8762 | 2778 | 40,203 | 6102 | 369 | 1,625,390 | 0 | 0 | 31,389 | 14,305 | 26,231 | 1,756,817 | 0.925 |
| terrace | 29,411 | 0 | 77,731 | 2432 | 2020 | 0 | 226 | 0 | 1,410,698 | 21,769 | 0 | 80,852 | 0 | 1,625,139 | 0.868 |
| strip field | 0 | 2465 | 20,189 | 0 | 14,051 | 0 | 571 | 0 | 2053 | 1,756,553 | 0 | 57,150 | 0 | 1,853,032 | 0.948 |
| city grass | 0 | 5576 | 13,321 | 5248 | 2566 | 2026 | 0 | 14,267 | 0 | 0 | 83,515 | 7033 | 12,199 | 145,751 | 0.573 |
| forest | 9951 | 9140 | 214,321 | 0 | 21,539 | 1225 | 0 | 2244 | 12,945 | 33,414 | 0 | 3,763,354 | 69,030 | 4,137,163 | 0.910 |
| city forest | 0 | 0 | 13,693 | 0 | 0 | 0 | 0 | 11,763 | 0 | 5509 | 0 | 22,289 | 132,935 | 186,179 | 0.714 |
Table 8.
The pixel-based classification confusion matrix of PWGM.
Table 8.
The pixel-based classification confusion matrix of PWGM.
| | Flat Field | Landslide | Grass | Water Body | Village | Road | Path | Town | Terrace | Strip Field | City Grass | Forest | City Forest | Sum of Pixel | Accuracy |
|---|
| flat field | 1,893,895 | 5368 | 59,827 | 5325 | 17,209 | 852 | 6205 | 0 | 9311 | 0 | 0 | 15,831 | 0 | 2,013,823 | 0.940 |
| landslide | 0 | 2,573,213 | 28,624 | 174 | 10,662 | 16,183 | 6073 | 832 | 0 | 0 | 2345 | 7191 | 0 | 2,645,297 | 0.973 |
| grass | 10,655 | 58,342 | 2,512,137 | 16,401 | 33,411 | 1558 | 1187 | 5605 | 56,699 | 11,583 | 1915 | 146,989 | 14,814 | 2,871,296 | 0.875 |
| water body | 0 | 2065 | 21,887 | 1,425,049 | 233 | 7377 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1,456,611 | 0.978 |
| village | 13,902 | 18,639 | 26,863 | 10,248 | 1,598,267 | 1088 | 2768 | 14,071 | 408 | 3125 | 2358 | 15,379 | 0 | 1,707,116 | 0.936 |
| road | 0 | 5898 | 1267 | 643 | 12,057 | 245,738 | 7018 | 4693 | 0 | 0 | 0 | 0 | 0 | 277,314 | 0.886 |
| path | 12,697 | 15,389 | 16,741 | 0 | 13,853 | 0 | 210,639 | 5783 | 0 | 487 | 0 | 3369 | 0 | 278,958 | 0.755 |
| town | 0 | 1288 | 7974 | 2390 | 13,520 | 6102 | 369 | 1,661,090 | 0 | 0 | 31,389 | 6464 | 26,231 | 1,756,817 | 0.946 |
| terrace | 28,102 | 0 | 34,449 | 2432 | 2020 | 0 | 0 | 0 | 1,466,610 | 8484 | 0 | 83,042 | 0 | 1,625,139 | 0.903 |
| strip field | 0 | 0 | 0 | 0 | 14,051 | 0 | 0 | 0 | 1280 | 1,823,359 | 0 | 14,342 | 0 | 1,853,032 | 0.984 |
| city grass | 0 | 451 | 22,298 | 2327 | 2566 | 74 | 0 | 12,750 | 0 | 0 | 55,645 | 12,041 | 37,599 | 145,751 | 0.382 |
| forest | 9951 | 6581 | 155,856 | 0 | 20,331 | 1225 | 0 | 98 | 2041 | 28,826 | 0 | 3,865,463 | 46,791 | 4,137,163 | 0.934 |
| city forest | 0 | 0 | 13,448 | 0 | 0 | 0 | 0 | 11,422 | 0 | 5509 | 0 | 9129 | 146,671 | 186,179 | 0.788 |
Table 9.
The accuracies of each category in four networks.
Table 9.
The accuracies of each category in four networks.
| | Flat Field | Landslide | Grass | Water Body | Village | Road | Path | Town | Terrace | Strip Field | City Grass | Forest | City Forest |
|---|
| Unet | 0.891 | 0.847 | 0.629 | 0.941 | 0.725 | 0.548 | 0.503 | 0.866 | 0.818 | 0.909 | 0.219 | 0.834 | 0.430 |
| GAT | 0.859 | 0.922 | 0.740 | 0.864 | 0.896 | 0.773 | 0.742 | 0.853 | 0.888 | 0.970 | 0.350 | 0.848 | 0.636 |
| KGGAT | 0.923 | 0.972 | 0.807 | 0.974 | 0.906 | 0.864 | 0.687 | 0.925 | 0.868 | 0.948 | 0.573 | 0.91 | 0.714 |
| PWGM | 0.940 | 0.973 | 0.875 | 0.978 | 0.936 | 0.886 | 0.755 | 0.946 | 0.903 | 0.984 | 0.702 | 0.934 | 0.788 |
Table 10.
The performance of four networks.
Table 10.
The performance of four networks.
| Model | Parameters (M) | GPU Memory Cost (G) | Average Training Time per Epoch (S) | Total Training Time (Min) |
|---|
| Unet | 8.64 | 8.88 | 40 | 200 |
| GAT | 0.02 | 1.47 | 24 | 120 |
| KGGAT | 0.02 | 1.51 | 30 | 150 |
| PWGM | 0.02 | 0.88 | 15 | 75 |
Table 12.
Scene distribution statistics of double anchors in a test set.
Table 12.
Scene distribution statistics of double anchors in a test set.
| Scene Type | Number of Complex Scene Samples | Number of Scenes with Anchors in the Same Scene | Number of Scenes with Anchors in Different Scenes |
|---|
| Simple scene | 165 | 165 | 0 |
| Complex scene | 260 | 0 | 260 |
Table 13.
Statistical results of the ablation experiment of .
Table 13.
Statistical results of the ablation experiment of .
| Factor Combination | Number of Landslide-Influenced Scenes | Number of Samples in Solidified Walking Scene | Number of Unresolved Samples | Scene Solidified Rate (%) |
|---|
| 81 | 21 | 60 | 32.1 |
| 81 | 73 | 8 | 90.1 |
Table 15.
Experimental results of the influence of the intersection factor on the parallel walking algorithm.
Table 15.
Experimental results of the influence of the intersection factor on the parallel walking algorithm.
| Method | Number of Complex Scene Samples | Number of Intersection Samples | Intersection Rate |
|---|
| 260 | 143 | 0.550 |
| 260 | 143 | 0.550 |
| 260 | 260 | 1.000 |
Table 16.
Statistical results of samples in which the intersection category separates different scenes.
Table 16.
Statistical results of samples in which the intersection category separates different scenes.
| Method Type | Number of Complex Scene Samples | Number of Scenes in Which the Intersection Separates Different Scenes | Ratio of Scenes in Which the Intersection Separates Different Scenes | Walking Accuracy before Intersection |
|---|
| 260 | 143 | 0.550 | 0.803 |
| 260 | 260 | 1.000 | 0.962 |
Table 17.
Ablation experiment of terminating condition based on valid junction.
Table 17.
Ablation experiment of terminating condition based on valid junction.
| Valid Junction in Termination Condition | Number of Complex Samples | Number of Knowledge Subgraph Nodes | Reduction Comparison |
|---|
| No | 260 | 2730 | 0 |
| YES | 260 | 2043 | 25.2% |
Table 18.
Pixel proportion of category in sample II.
Table 18.
Pixel proportion of category in sample II.
| Category | Flat Field | Town | City Grass | Path | Village |
|---|
| Proportion | 56% | 21% | 10% | 8% | 5% |
Table 19.
Relevant cooccurrence probability for the analysis of object 1.
Table 19.
Relevant cooccurrence probability for the analysis of object 1.
| Category | Flat Field | Road | Village |
|---|
| village | 0.81 | 0.42 | 1.00 |
| path | 0.58 | 1.0 | 0.42 |
Table 20.
Relevant cooccurrence probability for the analysis of object 2.
Table 20.
Relevant cooccurrence probability for the analysis of object 2.
| Category | Village | Flat Field | Town | Path |
|---|
| grass | 0.56 | 0.12 | 0.12 | 0.29 |
| city grass | 0.13 | 0.01 | 0.95 | 0.01 |
Table 21.
Parallel walking result of sample II with different methods.
Table 21.
Parallel walking result of sample II with different methods.
| Methods | Label | Number of Superpixel Groups | First Walking Path | Second Walking Path | Highest Score in First Path | Highest
Score in
Second Path | Intersection Category | Accuracy |
|---|
| 1, 5, 7, 8, 11 | 5 | 1, 5, 7, 3, 8 | 8, 3, 5, 1, 7 | 5.66, 3.0, 2.63, 0.86, 0.09 | 4.71, 3.38, 2.01, 1.23, 0.09 | 3 | 80% |
| 1, 5, 7, 8, 11 | 5 | 1, 5, 7, 8, 11 | 8, 11, 7, 1, 5 | 5.66, 3.0, 2.78, 1.2, 0.61 | 4.71, 3.38, 2.57, 1.43, 0.57 | 7 | 100% |
Table 22.
Prediction of object 2 in KGGAT and PWGM in detail.
Table 22.
Prediction of object 2 in KGGAT and PWGM in detail.
| Model | Label | Prediction | Categories in Knowledge Subgraph | Categories of 3 Highest Probabilities | 3 Highest Probabilities for Each Category |
|---|
| KGGAT | city grass (11) | grass (3) | all | 3, 11, 1 | 1.00, 0.00, 0.00 |
| PWGM | city grass (11) | city grass (11) | 1, 5, 7, 8, 11 | 11, 1, 7 | 1.00, 0.00, 0.00 |
Table 23.
Distribution statistics of typical samples using .
Table 23.
Distribution statistics of typical samples using .
| Scene Type | Number of Scenes in Which the Intersection Separates Different Scenes | Proportion of Samples of Road Category | Proportion of Samples of Path Category | Proportion of Samples of Water Body Category | Proportion of Samples of Simple Scene before Intersection |
|---|
| Urban–rural | 143 | 39.9% | 34% | 26.1% | 1.0 |
| Landslide-influenced | 117 | 28.2% | 39% | 32.8% | 1.0 |
Table 24.
Comparison of Node2Vec and PWGM in complex scene samples.
Table 24.
Comparison of Node2Vec and PWGM in complex scene samples.
| Method | Scene Solidified Rate | Intersection Rate |
|---|
| (Node2Vec) | 0.321 | 0.550 |
| 0.901 | 0.550 |
| (PWGM) | 0.901 | 1.000 |
Table 25.
Comparisons of relevant models.
Table 25.
Comparisons of relevant models.
| Model | Accuracy | mIOU | Kappa | F1-Score |
|---|
| GAT | 0.873 | 0.799 | 0.883 | 0.885 |
| Multi-source GAT | 0.886 | 0.829 | 0.897 | 0.900 |
| KSPGAT | 0.911 | 0.846 | 0.916 | 0.914 |
| PWGM | 0.929 | 0.853 | 0.920 | 0.923 |