Feasibility of Bi-Temporal Airborne Laser Scanning Data in Detecting Species-Specific Individual Tree Crown Growth of Boreal Forests
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description and Field Data
2.2. Airborne Laser Scanning Data
2.3. Establishing a Monitoring Framework at the Individual Tree-Level
2.3.1. Bi-Temporal ALS Data Processing
2.3.2. Species-Specific Tree-to-Tree Matching
2.3.3. Extracting Canopy Metrics
2.3.4. Crown Growth Estimation and Statistical Analysis
3. Results
3.1. Crown Growth Detection within Different Species Groups
3.2. Relative Crown Growth Changes between Different Species Groups
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, C.; Apps, M.J. Modelling the Response of Net Primary Productivity (NPP) of Boreal Forest Ecosystems to Changes in Climate and Fire Disturbance Regimes. Ecol. Modell. 1999, 122, 175–193. [Google Scholar] [CrossRef]
- Pretzsch, H. Growing Space and Competitive Situation of Individual Trees. In Forest Dynamics, Growth and Yield; Springer: Berlin/Heidelberg, Germany, 2009; pp. 291–336. [Google Scholar]
- Coops, N.C. Characterizing Forest Growth and Productivity Using Remotely Sensed Data. Curr. For. Rep. 2015, 1, 195–205. [Google Scholar] [CrossRef]
- Harris, N.L.; Gibbs, D.A.; Baccini, A.; Birdsey, R.A.; de Bruin, S.; Farina, M.; Fatoyinbo, L.; Hansen, M.C.; Herold, M.; Houghton, R.A.; et al. Global Maps of Twenty-First Century Forest Carbon Fluxes. Nat. Clim. Chang. 2021, 11, 234–240. [Google Scholar] [CrossRef]
- Wensel, L.C.; Meerschaert, W.J.; Biging, G.S. Tree Height and Diameter Growth Models for Northern California Conifers. Hilgardia 1987, 55, 1–20. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Hann, D.W.; Kershaw Jr, J.A.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Tompalski, P.; Coops, N.; White, J.; Wulder, M. Enhancing Forest Growth and Yield Predictions with Airborne Laser Scanning Data: Increasing Spatial Detail and Optimizing Yield Curve Selection through Template Matching. Forests 2016, 7, 255. [Google Scholar] [CrossRef]
- Munro, D.D. Growth Models for Tree and Stand Simulation. For. Res. 1974, 30, 7–21. [Google Scholar]
- Peng, C. Growth and Yield Models for Uneven-Aged Stands: Past, Present and Future. For. Ecol. Manag. 2000, 132, 259–279. [Google Scholar] [CrossRef]
- Jimenez-Perez, J.; Aguirre-Calderon, O.; Kramer, H. Tree Crown Structure Indicators in a Natural Uneven-Aged Mixed Coniferous Forest in Northeastern Mexico. In Monitoring Science and Technology Symposium: Unifying Knowledge for Sustainability in the Western Hemisphere Proceedings RMRS-P-42CD; Aguirre-Bravo, C., Pellicane, P.J., Burns, D.P., Draggan, S., Eds.; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; Volume 42, pp. 649–654. [Google Scholar]
- Biging, G.S.; Dobbertin, M. Evaluation of Competition Indices in Individual Tree Growth Models. For. Sci. 1995, 41, 360–377. [Google Scholar]
- Perin, J.; Hébert, J.; Brostaux, Y.; Lejeune, P.; Claessens, H. Modelling the Top-Height Growth and Site Index of Norway Spruce in Southern Belgium. For. Ecol. Manag. 2013, 298, 62–70. [Google Scholar] [CrossRef]
- Socha, J.; Pierzchalski, M.; Bałazy, R.; Ciesielski, M. Modelling Top Height Growth and Site Index Using Repeated Laser Scanning Data. For. Ecol. Manag. 2017, 406, 307–317. [Google Scholar] [CrossRef]
- Wulder, M.A.; Franklin, S.E. (Eds.) Remote Sensing of Forest Environments: Concepts and Case Studies; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-1-4613-5014-9. [Google Scholar]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating Canopy Structure of Douglas-Fir Forest Stands from Discrete-Return LiDAR. Trees 2007, 21, 295. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of Methods of Small-footprint Airborne Laser Scanning for Extracting Forest Inventory Data in Boreal Forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- García, M.; Saatchi, S.; Casas, A.; Koltunov, A.; Ustin, S.; Ramirez, C.; Balzter, H. Extrapolating Forest Canopy Fuel Properties in the California Rim Fire by Combining Airborne LiDAR and Landsat OLI Data. Remote Sens. 2017, 9, 394. [Google Scholar] [CrossRef]
- Kruper, A.; McGaughey, R.J.; Crumrine, S.; Bormann, B.T.; Bennett, K.; Bobsin, C.R. Using Airborne LiDAR to Map Red Alder in the Sappho Long-Term Ecosystem Productivity Study. Remote Sens. 2022, 14, 1591. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Tymen, B.; Blanc, L.; Fauset, S.; Feldpausch, T.R.; Monteagudo, A.; Phillips, O.L.; Richard, H.; Chave, J. Using Repeated Small-Footprint LiDAR Acquisitions to Infer Spatial and Temporal Variations of a High-Biomass Neotropical Forest. Remote Sens. Environ. 2015, 169, 93–101. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of Forest Biomass Dynamics in Subtropical Forests Using Multi-Temporal Airborne LiDAR Data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.; Marshall, P.; White, J.; Wulder, M.; Bailey, T. Combining Multi-Date Airborne Laser Scanning and Digital Aerial Photogrammetric Data for Forest Growth and Yield Modelling. Remote Sens. 2018, 10, 347. [Google Scholar] [CrossRef]
- Vastaranta, M.; Yrttimaa, T.; Saarinen, N.; Yu, X.; Karjalainen, M.; Nurminen, K.; Karila, K.; Kankare, V.; Luoma, V.; Pyörälä, J.; et al. Airborne Laser Scanning Outperforms the Alternative 3D Techniques in Capturing Variation in Tree Height and Forest Density in Southern Boreal Forests. Balt. For. 2018, 24, 268–277. [Google Scholar]
- Dassot, M.; Constant, T.; Fournier, M. The Use of Terrestrial LiDAR Technology in Forest Science: Application Fields, Benefits and Challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Gatziolis, D.; Fried, J.S.; Monleon, V.S. Challenges to Estimating Tree Height via LiDAR in Closed-Canopy Forests: A Parable from Western Oregon. For. Sci. 2010, 56, 139–155. [Google Scholar]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.W. Multi-Temporal Terrestrial Laser Scanning for Modeling Tree Biomass Change. For. Ecol. Manag. 2014, 318, 304–317. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å. Identifying Species of Individual Trees Using Airborne Laser Scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K. A Voxel-Based Lidar Method for Estimating Crown Base Height for Deciduous and Pine Trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Kato, A.; Moskal, L.M.; Schiess, P.; Swanson, M.E.; Calhoun, D.; Stuetzle, W. Capturing Tree Crown Formation through Implicit Surface Reconstruction Using Airborne Lidar Data. Remote Sens. Environ. 2009, 113, 1148–1162. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Cook, B.D.; Hurtt, G.C.; Dubayah, R.O. An Efficient, Multi-Layered Crown Delineation Algorithm for Mapping Individual Tree Structure across Multiple Ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Frew, M.S.; Evans, D.L.; Londo, H.A.; Cooke, W.H.; Irby, D. Measuring Douglas-Fir Crown Growth with Multitemporal LiDAR. For. Sci. 2016, 62, 200–212. [Google Scholar] [CrossRef]
- Jung, S.-E.; Kwak, D.-A.; Park, T.; Lee, W.-K.; Yoo, S. Estimating Crown Variables of Individual Trees Using Airborne and Terrestrial Laser Scanners. Remote Sens. 2011, 3, 2346–2363. [Google Scholar] [CrossRef]
- Londo, H.A. The Suitability of LiDAR-Derived Forest Attributes for Use in Individual-Tree Distance-Dependent Growth-and-Yield Modeling. Doctor of Philosophy, Mississippi State University, Mississippi State, MS, USA, 2010. [Google Scholar]
- NASSET, E.; GOBAKKEN, T. Estimating Forest Growth Using Canopy Metrics Derived from Airborne Laser Scanner Data. Remote Sens. Environ. 2005, 96, 453–465. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kaartinen, H.; Maltamo, M.; Hyyppä, H. Obtaining Plotwise Mean Height and Volume Growth in Boreal Forests Using Multi-temporal Laser Surveys and Various Change Detection Techniques. Int. J. Remote Sens. 2008, 29, 1367–1386. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of Tropical Forest Height and Biomass Dynamics Using Lidar Remote Sensing at La Selva, Costa Rica. J. Geophys. Res. Biogeosciences 2010, 115. [Google Scholar] [CrossRef]
- Zhao, K.; Suarez, J.C.; Garcia, M.; Hu, T.; Wang, C.; Londo, A. Utility of Multitemporal Lidar for Forest and Carbon Monitoring: Tree Growth, Biomass Dynamics, and Carbon Flux. Remote Sens. Environ. 2018, 204, 883–897. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Tao, S.; Guo, Q. Quantifying Individual Tree Growth and Tree Competition Using Bi-Temporal Airborne Laser Scanning Data: A Case Study in the Sierra Nevada Mountains, California. Int. J. Digit. Earth 2018, 11, 485–503. [Google Scholar] [CrossRef]
- Maltamo, M.; Vartiainen, P.; Packalen, P.; Korhonen, L. Estimation of Periodic Annual Increment of Tree Ring Widths by Airborne Laser Scanning. Can. J. For. Res. 2022, 52, 644–651. [Google Scholar] [CrossRef]
- Duncanson, L.; Dubayah, R. Monitoring Individual Tree-based Change with Airborne Lidar. Ecol. Evol. 2018, 8, 5079–5089. [Google Scholar] [CrossRef] [PubMed]
- COOMES, D.A.; ALLEN, R.B. Effects of Size, Competition and Altitude on Tree Growth. J. Ecol. 2007, 95, 1084–1097. [Google Scholar] [CrossRef]
- Stephenson, N.L.; Das, A.J.; Condit, R.; Russo, S.E.; Baker, P.J.; Beckman, N.G.; Coomes, D.A.; Lines, E.R.; Morris, W.K.; Rüger, N.; et al. Rate of Tree Carbon Accumulation Increases Continuously with Tree Size. Nature 2014, 507, 90–93. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Hyyppä, J.; Karjalainen, M.; Nurminen, K.; Karila, K.; Vastaranta, M.; Kankare, V.; Kaartinen, H.; Holopainen, M.; Honkavaara, E.; et al. Comparison of Laser and Stereo Optical, SAR and InSAR Point Clouds from Air- and Space-Borne Sources in the Retrieval of Forest Inventory Attributes. Remote Sens. 2015, 7, 15933–15954. [Google Scholar] [CrossRef]
- Laasasenaho, J. Taper Curve and Volume Functions for Pine, Spruce and Birch. Commun. Inst. For. Fenn. 1982, 108, 1–74. [Google Scholar]
- Axelsson, P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models. Int. Arch. Photogramm. Remote Sens. Spat. 2000, 33, 110–117. [Google Scholar]
- Isenburg, M. Use Buffers When Processing LiDAR in Tiles. Available online: https://rapidlasso.com/2015/08/07/use-buffers-when-processing-lidar-in-tiles/ (accessed on 27 September 2022).
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M. Generating Spike-Free Digital Surface Models Using LiDAR Raw Point Clouds: A New Approach for Forestry Applications. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 104–114. [Google Scholar] [CrossRef]
- Isenburg, M. Rasterizing Perfect Canopy Height Models from LiDAR. Available online: https://rapidlasso.com/2014/11/04/rasterizing-perfect-canopy-height-models-from-lidar/ (accessed on 27 September 2022).
- Roussel, J.R.; Auty, D. LidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. 2018. Available online: https://cran.r-project.org/web/packages/lidR/index.html (accessed on 27 September 2022).
- Meyer, F.; Beucher, S. Morphological Segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Goodbody, T.R.H.; Hennigar, C.R.; Wulder, M.A.; Socha, J.; Woods, M.E. Estimating Changes in Forest Attributes and Enhancing Growth Projections: A Review of Existing Approaches and Future Directions Using Airborne 3D Point Cloud Data. Curr. For. Rep. 2021, 7, 1–24. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kaartinen, H.; Maltamo, M. Automatic Detection of Harvested Trees and Determination of Forest Growth Using Airborne Laser Scanning. Remote Sens. Environ. 2004, 90, 451–462. [Google Scholar] [CrossRef]
- Pyörälä, J.; Saarinen, N.; Kankare, V.; Coops, N.C.; Liang, X.; Wang, Y.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Variability of Wood Properties Using Airborne and Terrestrial Laser Scanning. Remote Sens. Environ. 2019, 235, 111474. [Google Scholar] [CrossRef]
- ESRI Spatial Join (Analysis). Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/analysis/spatial-join.htm (accessed on 27 September 2022).
- Vastaranta, M.; Holopainen, M.; Yu, X.; Hyyppä, J.; Mäkinen, A.; Rasinmäki, J.; Melkas, T.; Kaartinen, H.; Hyyppä, H. Effects of Individual Tree Detection Error Sources on Forest Management Planning Calculations. Remote Sens. 2011, 3, 1614–1626. [Google Scholar] [CrossRef]
- Jakubowski, M.; Li, W.; Guo, Q.; Kelly, M. Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-Based Segmentation Approaches. Remote Sens. 2013, 5, 4163–4186. [Google Scholar] [CrossRef]
- Zimmerman, D.W. A Note on the Influence of Outliers on Parametric and Nonparametric Tests. J. Gen. Psychol. 1994, 121, 391–401. [Google Scholar] [CrossRef]
- Fernández-Sarría, A.; Martínez, L.; Velázquez-Martí, B.; Sajdak, M.; Estornell, J.; Recio, J.A. Different Methodologies for Calculating Crown Volumes of Platanus Hispanica Trees Using Terrestrial Laser Scanner and a Comparison with Classical Dendrometric Measurements. Comput. Electron. Agric. 2013, 90, 176–185. [Google Scholar] [CrossRef]
- Yrttimaa, T.; Luoma, V.; Saarinen, N.; Kankare, V.; Junttila, S.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Monitoring Tree Growth Allometry Using Two-Date Terrestrial Laser Scanning. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Niemistö, P.; Kilpeläinen, H.; Poutiainen, E. Effect of First Thinning Type and Age on Growth, Stem Quality and Financial Performance of a Scots Pine Stand in Finland. Silva Fenn. 2018, 52, 21. [Google Scholar] [CrossRef]
- Pommerening, A.; Muszta, A. Methods of Modelling Relative Growth Rate. For. Ecosyst. 2015, 2, 5. [Google Scholar] [CrossRef]
- Kim, T.K.; Park, J.H. More about the Basic Assumptions of T-Test: Normality and Sample Size. Korean J. Anesthesiol. 2019, 72, 331–335. [Google Scholar] [CrossRef]
- Triola, M.F.; Goodman, W.M.; Law, R.; Labute, G. Elementary Statistics, 13th ed.; Pearson/Addison-Wesley Reading: Boston, FL, USA, 2006. [Google Scholar]
- Olejnik, S.; Algina, J. Generalized Eta and Omega Squared Statistics: Measures of Effect Size for Some Common Research Designs. Psychol. Methods 2003, 8, 434–447. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Kwak, D.A.; Lee, W.K.; Cho, H.K.; Lee, S.H.; Son, Y.; Kafatos, M.; Kim, S.R. Estimating Stem Volume and Biomass of Pinus Koraiensis Using LiDAR Data. J. Plant Res. 2010, 123, 421–432. [Google Scholar] [CrossRef]
- Getzin, S.; Wiegand, K. Asymmetric Tree Growth at the Stand Level: Random Crown Patterns and the Response to Slope. For. Ecol. Manag. 2007, 242, 165–174. [Google Scholar] [CrossRef]
- Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Response of a Boreal Forest to Canopy Opening: Assessing Vertical and Lateral Tree Growth with Multi-Temporal Lidar Data. Ecol. Appl. 2011, 21, 99–121. [Google Scholar] [CrossRef] [PubMed]
- Rapp, J.M.; Silman, M.R.; Clark, J.S.; Girardin, C.A.J.; Galiano, D.; Tito, R. Intra- and Interspecific Tree Growth across a Long Altitudinal Gradient in the Peruvian Andes. Ecology 2012, 93, 2061–2072. [Google Scholar] [CrossRef] [PubMed]
- Kaitaniemi, P.; Lintunen, A. Neighbor Identity and Competition Influence Tree Growth in Scots Pine, Siberian Larch, and Silver Birch. Ann. For. Sci. 2010, 67, 604. [Google Scholar] [CrossRef]
- Aakala, T.; Fraver, S.; D’Amato, A.W.; Palik, B.J. Influence of Competition and Age on Tree Growth in Structurally Complex Old-Growth Forests in Northern Minnesota, USA. For. Ecol. Manag. 2013, 308, 128–135. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing. In Topographic Laser Ranging and Scanning; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–590. [Google Scholar] [CrossRef]
- Csanyi, N.; Toth, C.K. LiDAR Data Accuracy: The Impact of Pulse Repetition Rate. In Proceedings of the MAPPS/ASPRS 2006 Fall Conference, San Antonio, TX, USA, 6–10 November 2006. [Google Scholar]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.H.; Martinuzzi, S.; Falkowski, M.J. Quantifying Aboveground Forest Carbon Pools and Fluxes from Repeat LiDAR Surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- Fekety, P.A.; Falkowski, M.J.; Hudak, A.T. Temporal Transferability of LiDAR-Based Imputation of Forest Inventory Attributes. Can. J. For. Res. 2015, 45, 422–435. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Kukko, A.; Maltamo, M.; Kaartinen, H. Change Detection Techniques for Canopy Height Growth Measurements Using Airborne Laser Scanner Data. Photogramm. Eng. Remote Sens. 2006, 72, 1339–1348. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef]
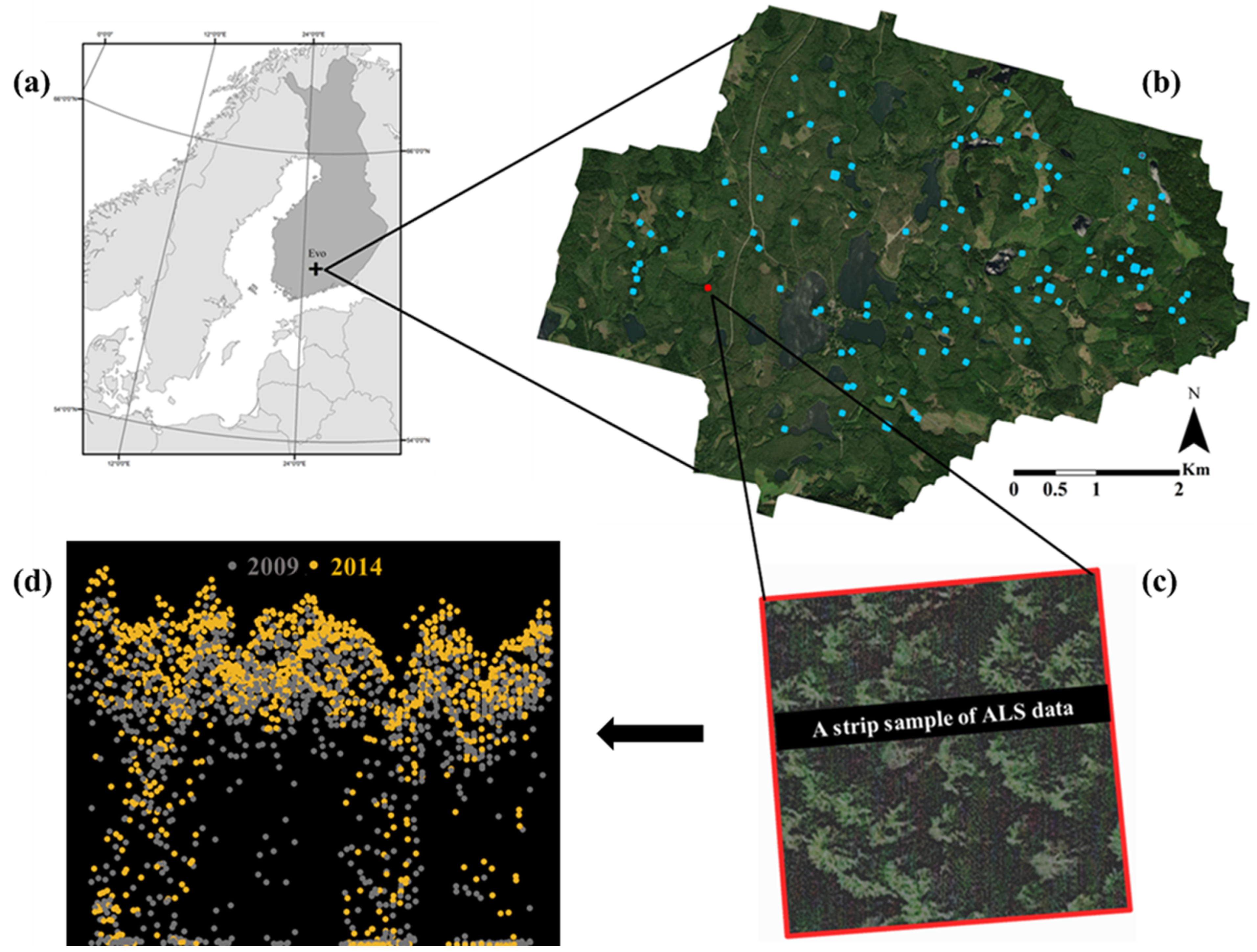
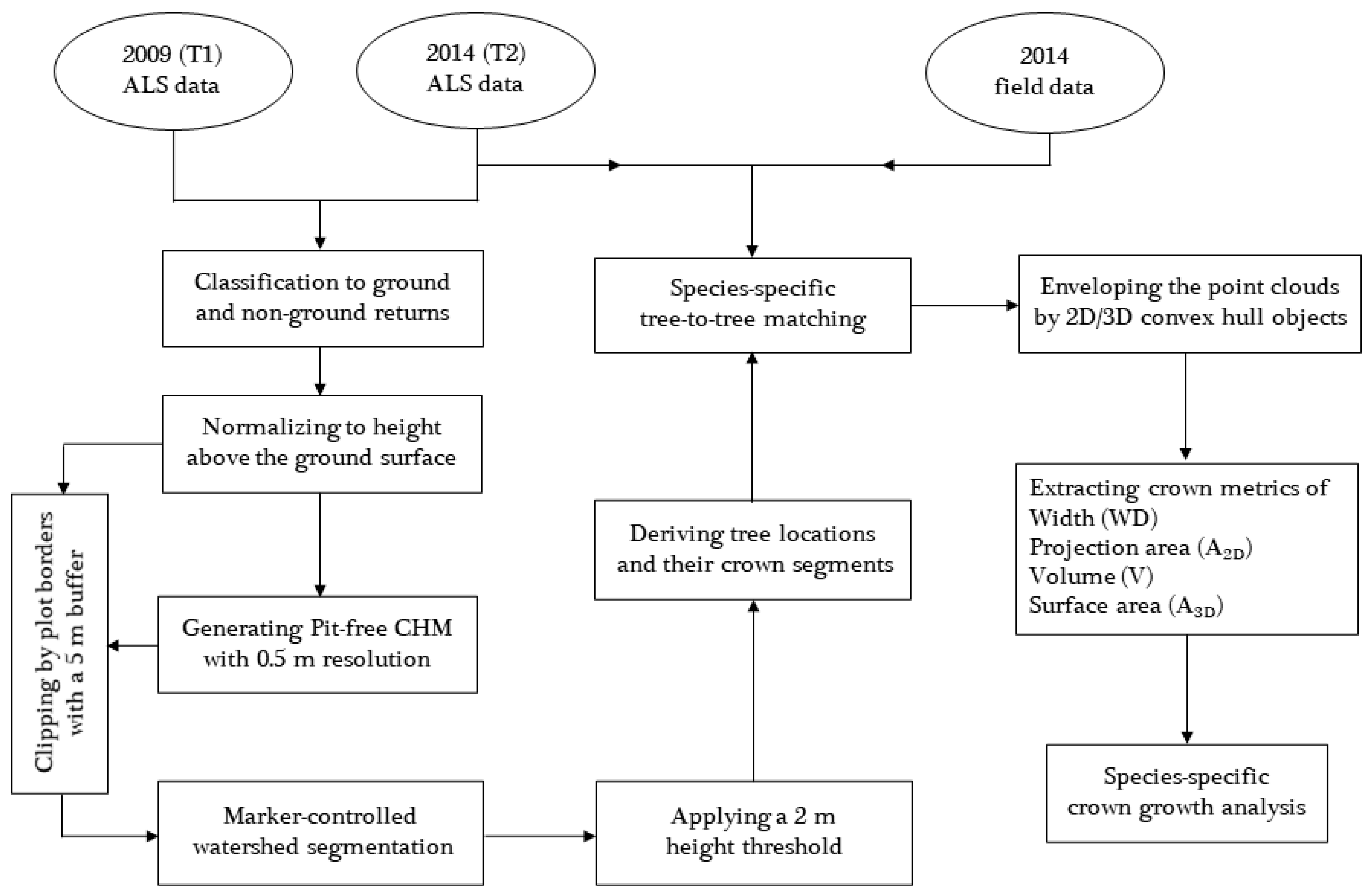

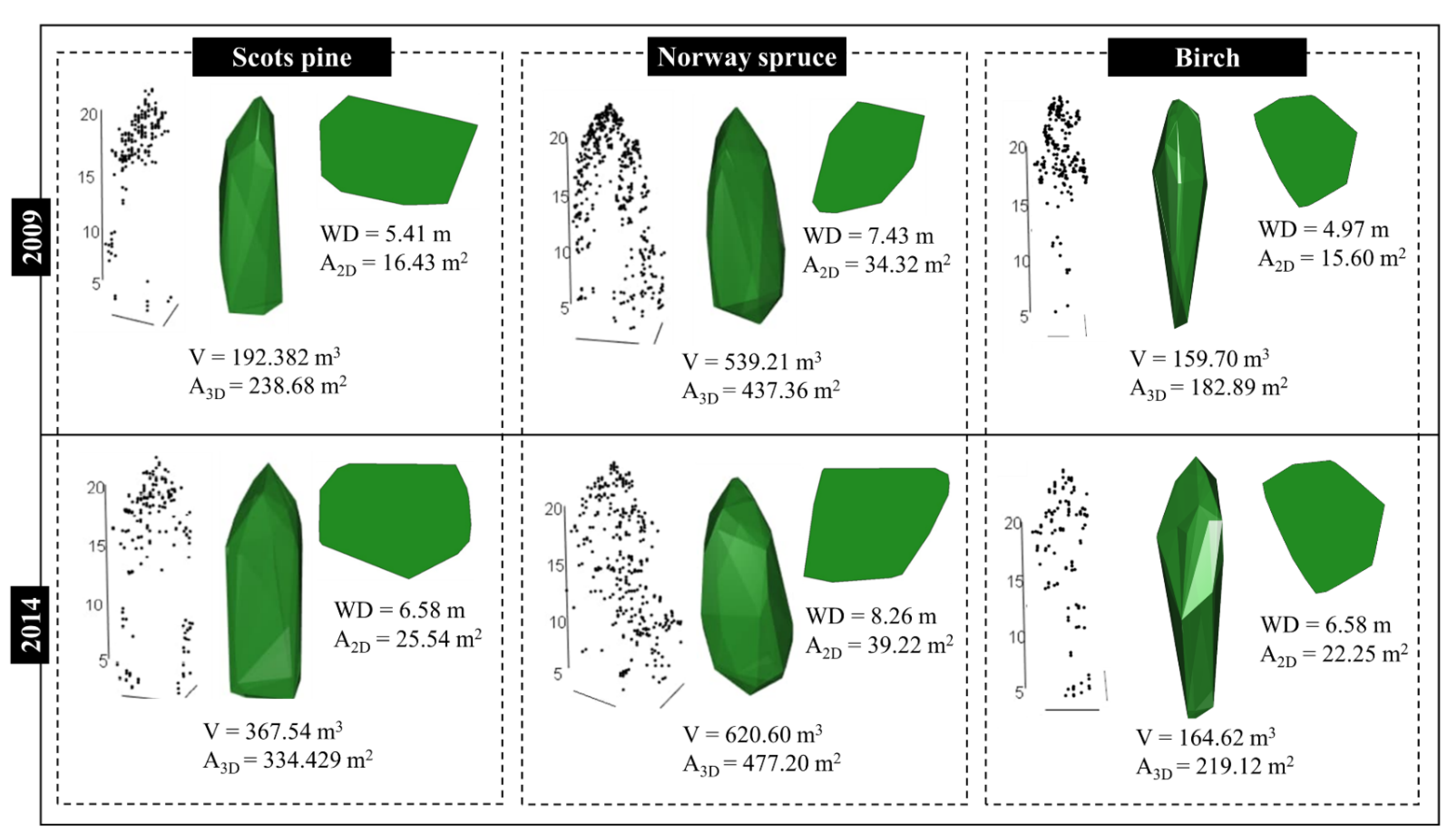
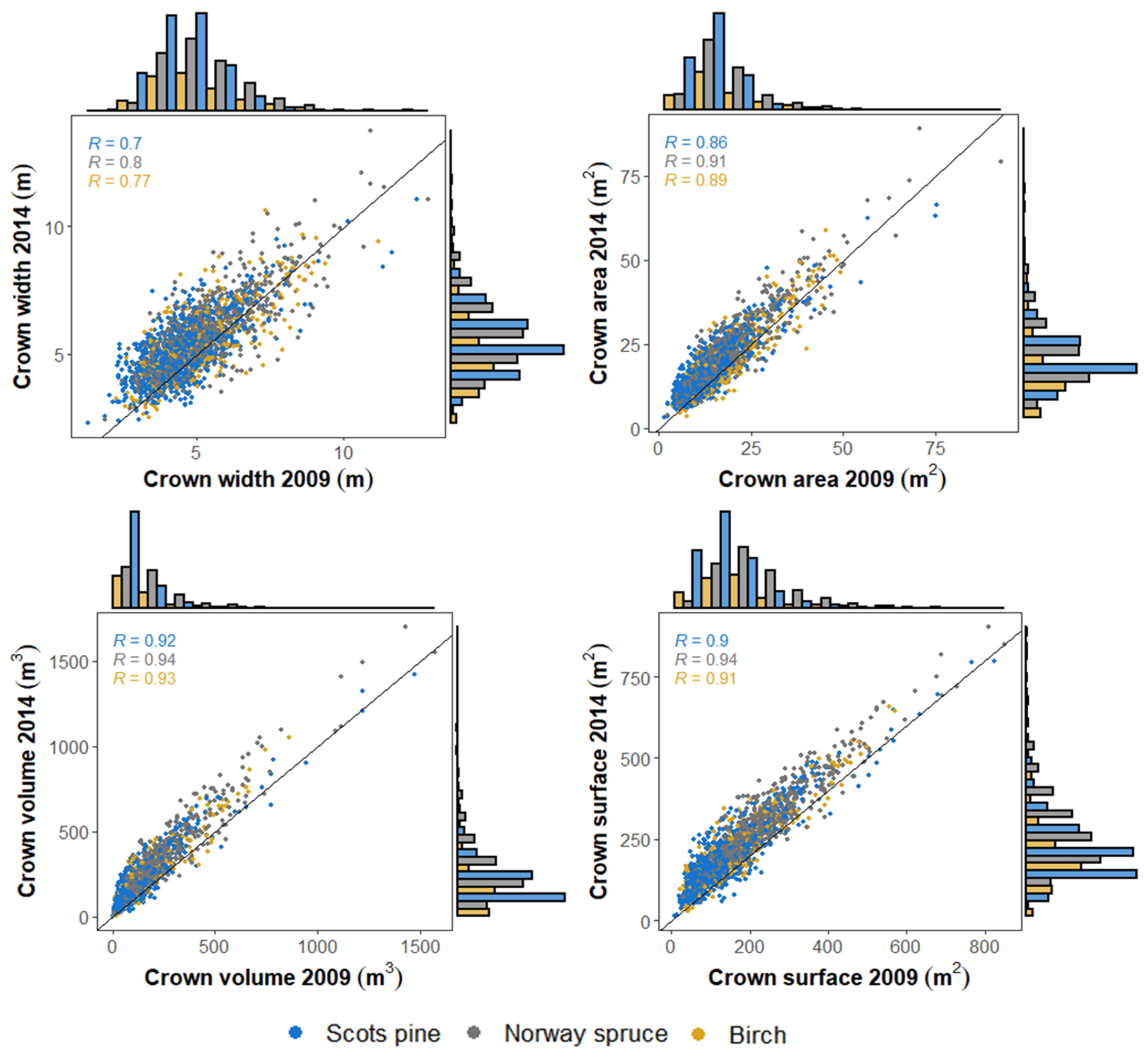
| Attribute | Min | Max | Mean | S.D. |
|---|---|---|---|---|
| Number of trees (n ha−1) | 342 | 3076 | 943 | 556 |
| Mean volume (m3 ha−1) | 34.46 | 518.39 | 271.49 | 110.73 |
| Basal-area-weighted mean dbh (cm) | 13.91 | 46.42 | 25.79 | 7.51 |
| Basal-area-weighted mean height (m) | 10.02 | 31.09 | 21.10 | 4.42 |
| Year | 2009 | 2014 |
|---|---|---|
| Sensor | Leica ALS50II SN058 | Leica ALS70-HA |
| Date | 25 July 2009 | 5 September 2014 |
| Laser pulse frequency | 150,000 kHz | 240 kHz |
| Scan frequency | 52.2 Hz | 59.90 Hz |
| Beam divergence | 0.22 mrad | 0.15 mrad |
| Flying altitude | 400 m | 900 m |
| Scanning angle | 30° | 30° |
| Average pulse density | 10 | 6 |
| Species Group | Diameter at Breast Height (cm) | Volume (m3) | Height (m) | |||
|---|---|---|---|---|---|---|
| Mean | S.D. | Mean | S.D. | Mean | S.D. | |
| Scots pine (n = 947) | 21.74 | 6.77 | 0.41 | 0.36 | 19.65 | 4.27 |
| Norway spruce (n = 749) | 20.42 | 10.37 | 0.46 | 0.50 | 22.09 | 5.66 |
| Birch (n = 402) | 15.73 | 6.46 | 0.22 | 0.24 | 19.71 | 4.10 |
| Species Group | Metrics | T1 | T2 | Δ | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Cohen’s D | ||
| Scots pine (n = 947) | WD | 4.56 | 1.20 | 5.12 | 1.14 | 0.56 **** | 0.90 | 0.62 |
| A2D | 14.00 | 7.34 | 17.57 | 7.35 | 3.57 **** | 3.85 | 0.93 | |
| V | 106.84 | 120.76 | 168.75 | 137.07 | 61.90 **** | 54.26 | 1.14 | |
| A3D | 136.45 | 90.02 | 189.62 | 94.94 | 53.17 **** | 41.63 | 1.28 | |
| Norway spruce (n = 749) | WD | 5.30 | 1.45 | 5.75 | 1.46 | 0.45 **** | 0.91 | 0.50 |
| A2D | 18.82 | 9.73 | 22.09 | 10.35 | 3.27 **** | 4.37 | 0.75 | |
| V | 199.53 | 166.32 | 285.83 | 199.53 | 86.30 **** | 70.64 | 1.22 | |
| A3D | 215.76 | 108.30 | 276.21 | 117.73 | 60.44 **** | 41.48 | 1.46 | |
| Birch (n = 402) | WD | 5.04 | 1.43 | 5.35 | 1.39 | 0.30 **** | 0.96 | 0.32 |
| A2D | 17.27 | 9.07 | 19.08 | 9.58 | 1.81 **** | 4.35 | 0.42 | |
| V | 147.78 | 132.07 | 210.64 | 156.86 | 62.86 **** | 57.73 | 1.09 | |
| A3D | 168.40 | 96.96 | 220.14 | 101.25 | 51.73 **** | 41.20 | 1.26 | |
| All trees (n = 2098) | WD | 4.92 | 1.38 | 5.39 | 1.34 | 0.47 **** | 0.92 | 0.51 |
| A2D | 16.35 | 8.86 | 19.47 | 9.18 | 3.13 **** | 4.19 | 0.75 | |
| V | 147.78 | 146.61 | 218.58 | 173.58 | 70.80 **** | 62.28 | 1.14 | |
| A3D | 170.89 | 104.37 | 226.38 | 111.69 | 55.49 **** | 41.64 | 1.33 | |
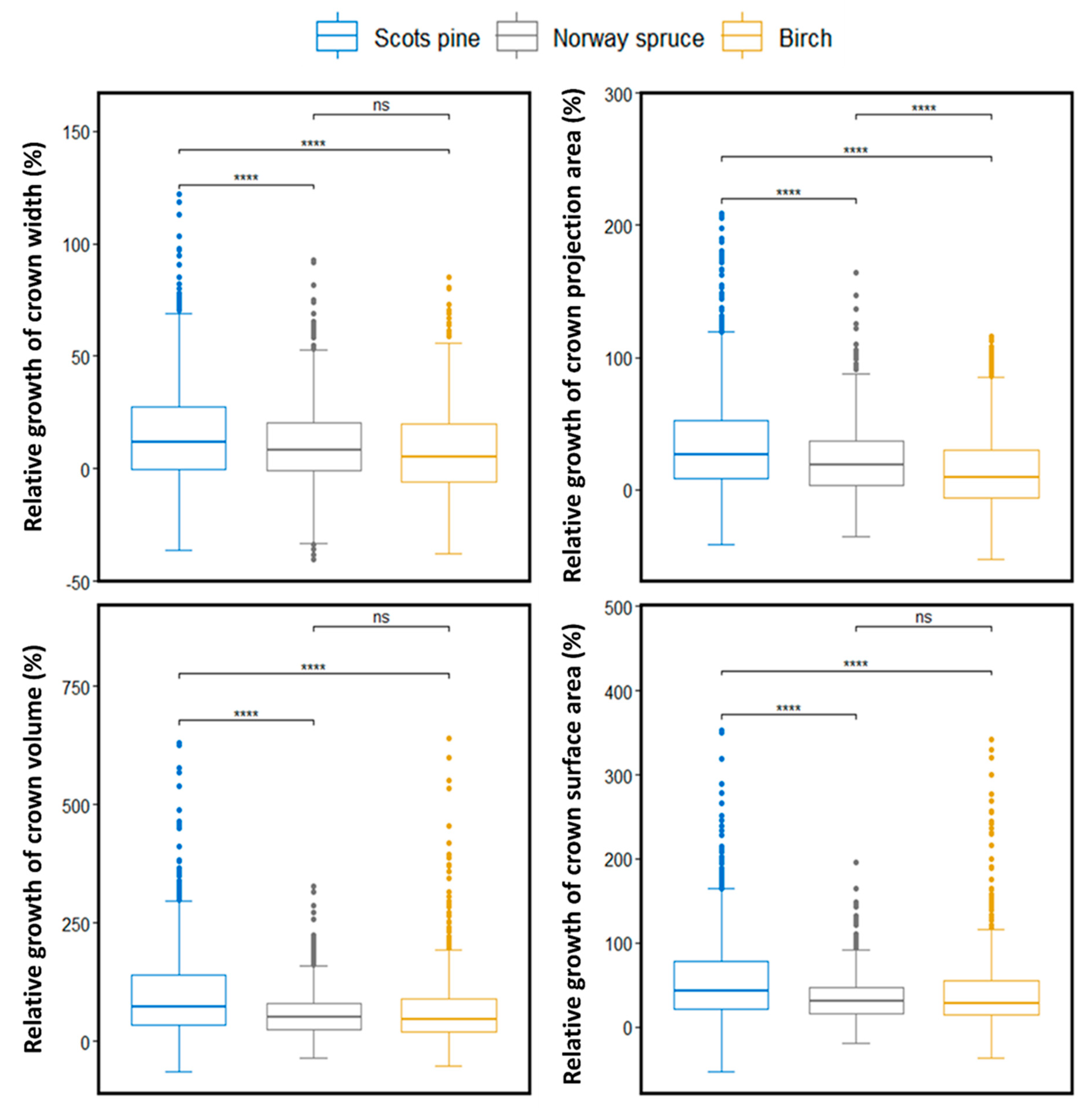
| Species Group | Metrics | rΔ (%) | p-Value | η2 | |
|---|---|---|---|---|---|
| Mean | S.D. | ||||
| WD | Scots pine | 15.38 | 23.30 | 2.18 × 10−8 | 0.02 |
| Norway spruce | 10.50 | 18.50 | |||
| Birch | 8.54 | 20.89 | |||
| A2D | Scots pine | 35.42 | 41.05 | 2.4 × 10−22 | 0.05 |
| Norway spruce | 21.96 | 26.98 | |||
| Birch | 15.64 | 32.16 | |||
| V | Scots pine | 97.67 | 94.77 | 1.93 × 10−16 | 0.03 |
| Norway spruce | 58.21 | 48.32 | |||
| Birch | 74.97 | 96.86 | |||
| A3D | Scots pine | 55.80 | 53.48 | 1.73 × 10−19 | 0.04 |
| Norway spruce | 34.14 | 27.24 | |||
| Birch | 46.89 | 58.91 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poorazimy, M.; Ronoud, G.; Yu, X.; Luoma, V.; Hyyppä, J.; Saarinen, N.; Kankare, V.; Vastaranta, M. Feasibility of Bi-Temporal Airborne Laser Scanning Data in Detecting Species-Specific Individual Tree Crown Growth of Boreal Forests. Remote Sens. 2022, 14, 4845. https://doi.org/10.3390/rs14194845
Poorazimy M, Ronoud G, Yu X, Luoma V, Hyyppä J, Saarinen N, Kankare V, Vastaranta M. Feasibility of Bi-Temporal Airborne Laser Scanning Data in Detecting Species-Specific Individual Tree Crown Growth of Boreal Forests. Remote Sensing. 2022; 14(19):4845. https://doi.org/10.3390/rs14194845
Chicago/Turabian StylePoorazimy, Maryam, Ghasem Ronoud, Xiaowei Yu, Ville Luoma, Juha Hyyppä, Ninni Saarinen, Ville Kankare, and Mikko Vastaranta. 2022. "Feasibility of Bi-Temporal Airborne Laser Scanning Data in Detecting Species-Specific Individual Tree Crown Growth of Boreal Forests" Remote Sensing 14, no. 19: 4845. https://doi.org/10.3390/rs14194845
APA StylePoorazimy, M., Ronoud, G., Yu, X., Luoma, V., Hyyppä, J., Saarinen, N., Kankare, V., & Vastaranta, M. (2022). Feasibility of Bi-Temporal Airborne Laser Scanning Data in Detecting Species-Specific Individual Tree Crown Growth of Boreal Forests. Remote Sensing, 14(19), 4845. https://doi.org/10.3390/rs14194845








