A Novel Slow-Growing Gross Error Detection Method for GNSS/Accelerometer Integrated Deformation Monitoring Based on State Domain Consistency Theory
Abstract
1. Introduction
2. Method
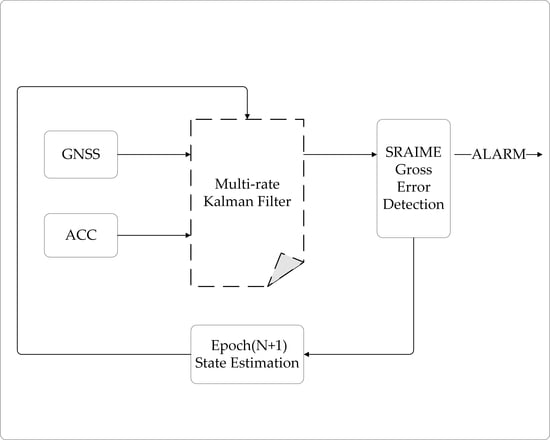
2.1. GNSS/Accelerometer Integration Algorithm Based on Kalman Filter
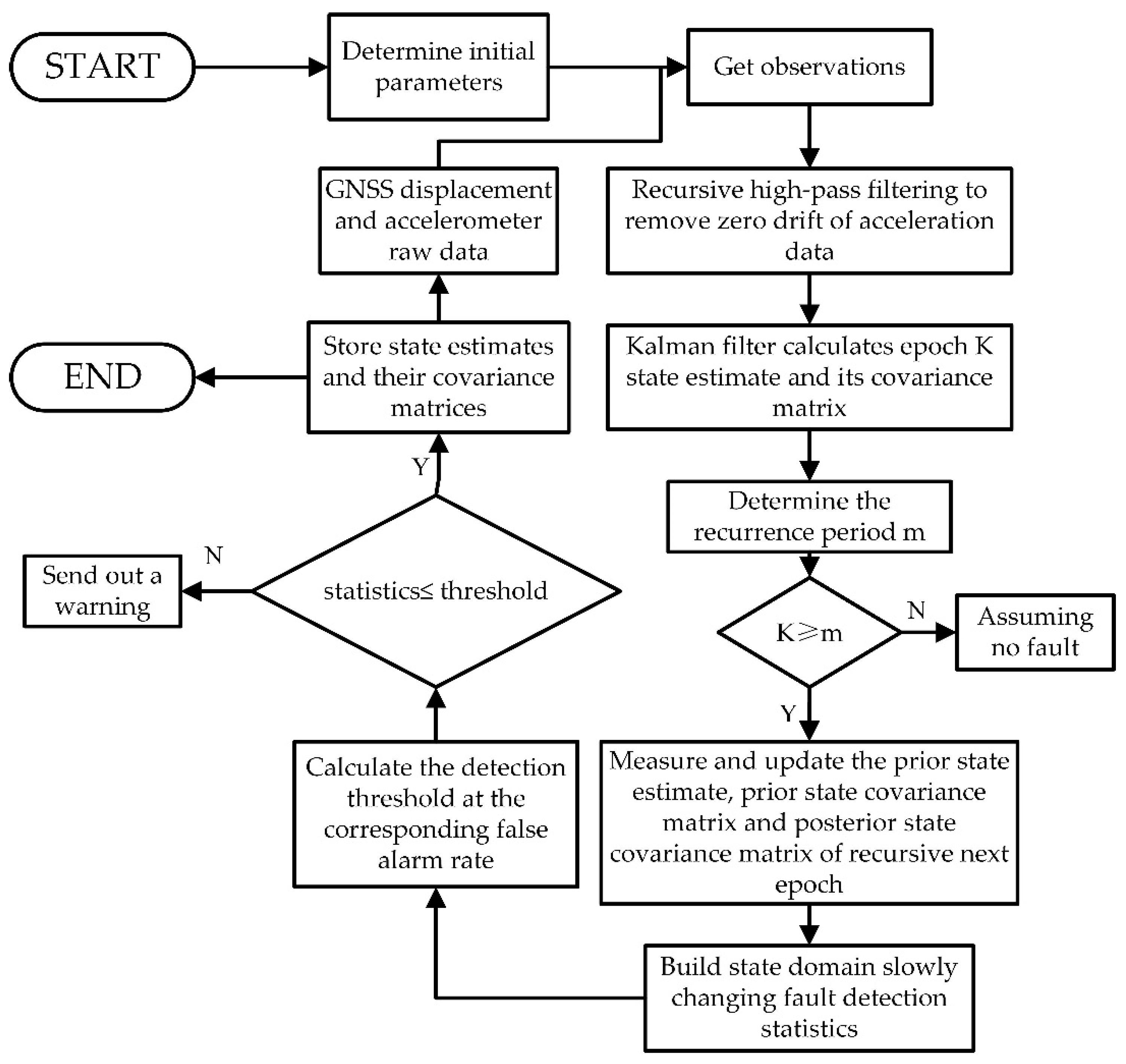
2.2. Slow-Growing Gross Error Detection Algorithm Based on State Domain
- 1.
- Determine the false alarm rate according to the bridge monitoring environment;
- 2.
- Obtain the estimated value of epoch k and its covariance matrix through GNSS/accelerometer fusion Kalman filter;
- 3.
- Determine the recurrence period . Assuming that epoch has no faults, the multi-step extrapolation estimated value and its covariance matrix from epoch to epoch k can be obtained by calculating the estimated value of epoch k-m and its covariance matrix :
- 4.
- Calculate and its covariance matrix :
- 5.
- Construct the slow-growing fault detection statistic in the state domain, where singular value decomposition is used when inverting to increase the calculation stability:
- 6.
- Calculate the fault detection threshold under the false alarm rate , where is the cumulative distribution function of , the operator inf represents the lower bound, and is the fault detection threshold,
- 7.
- Compare the state test statistic with the threshold : If , it is considered that there is no fault and no slow-growing gross error; if , it is considered that there is a slow-growing fault and a slow-growing gross error.
3. Experiments and Discussion
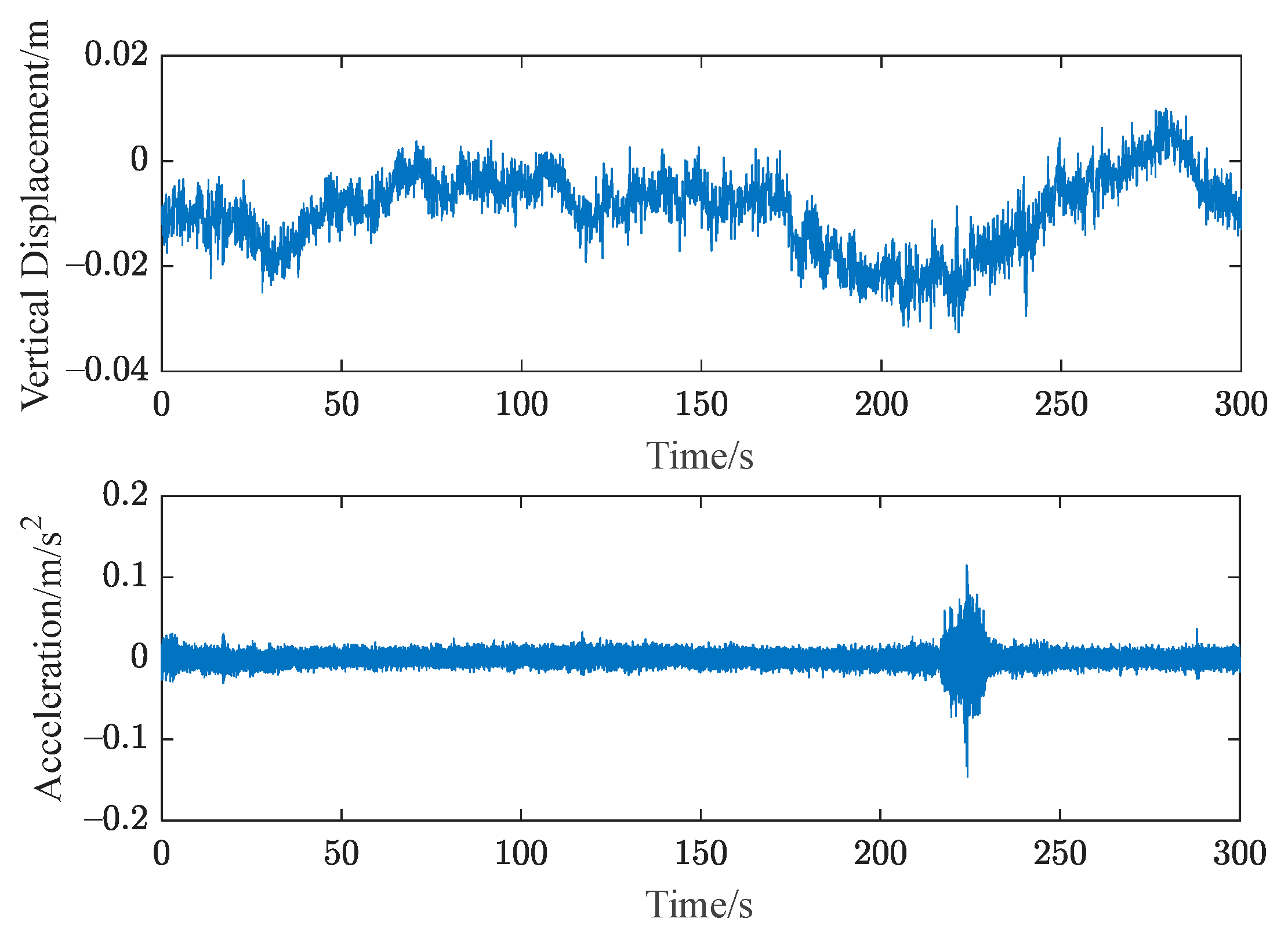
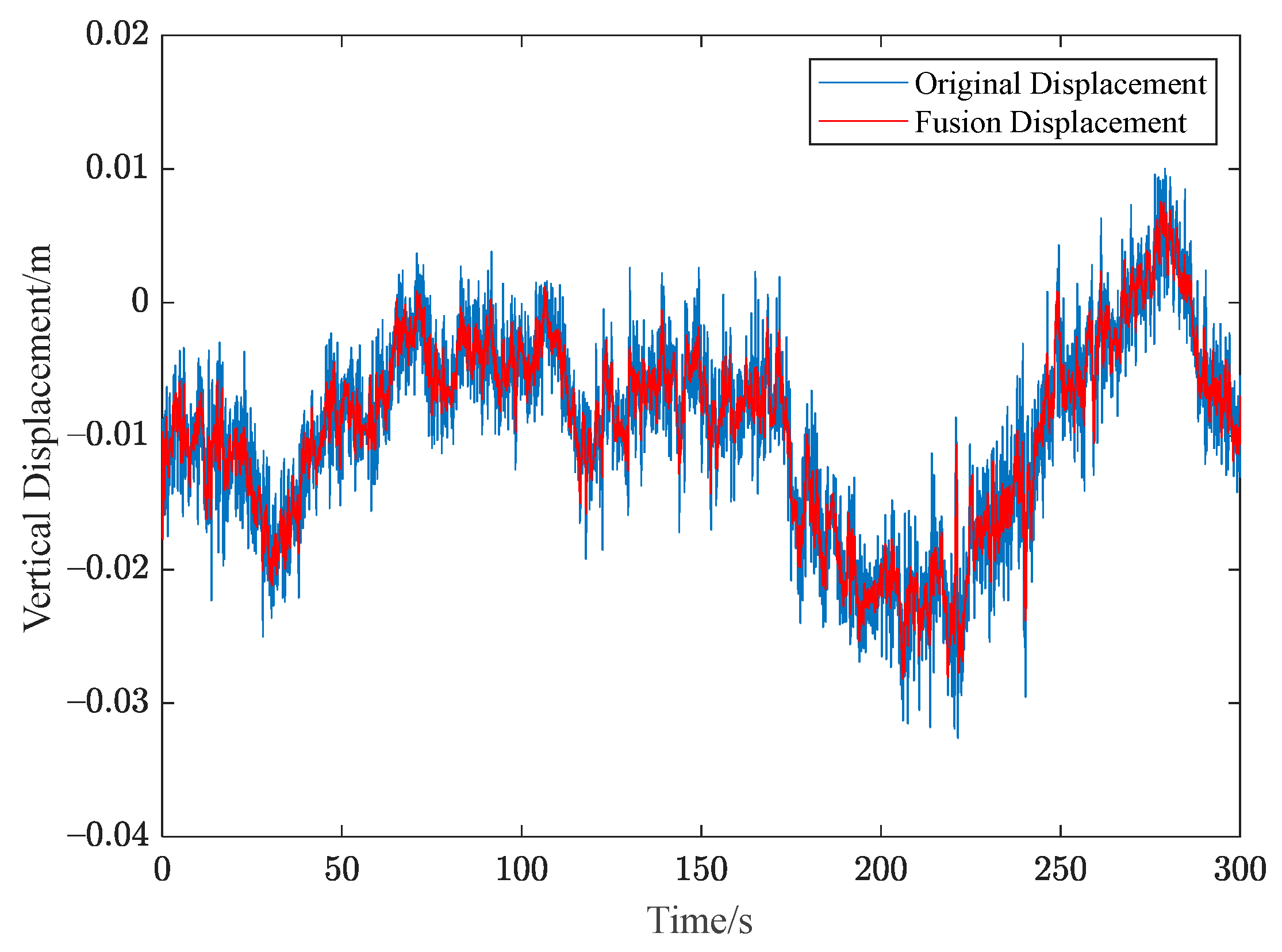
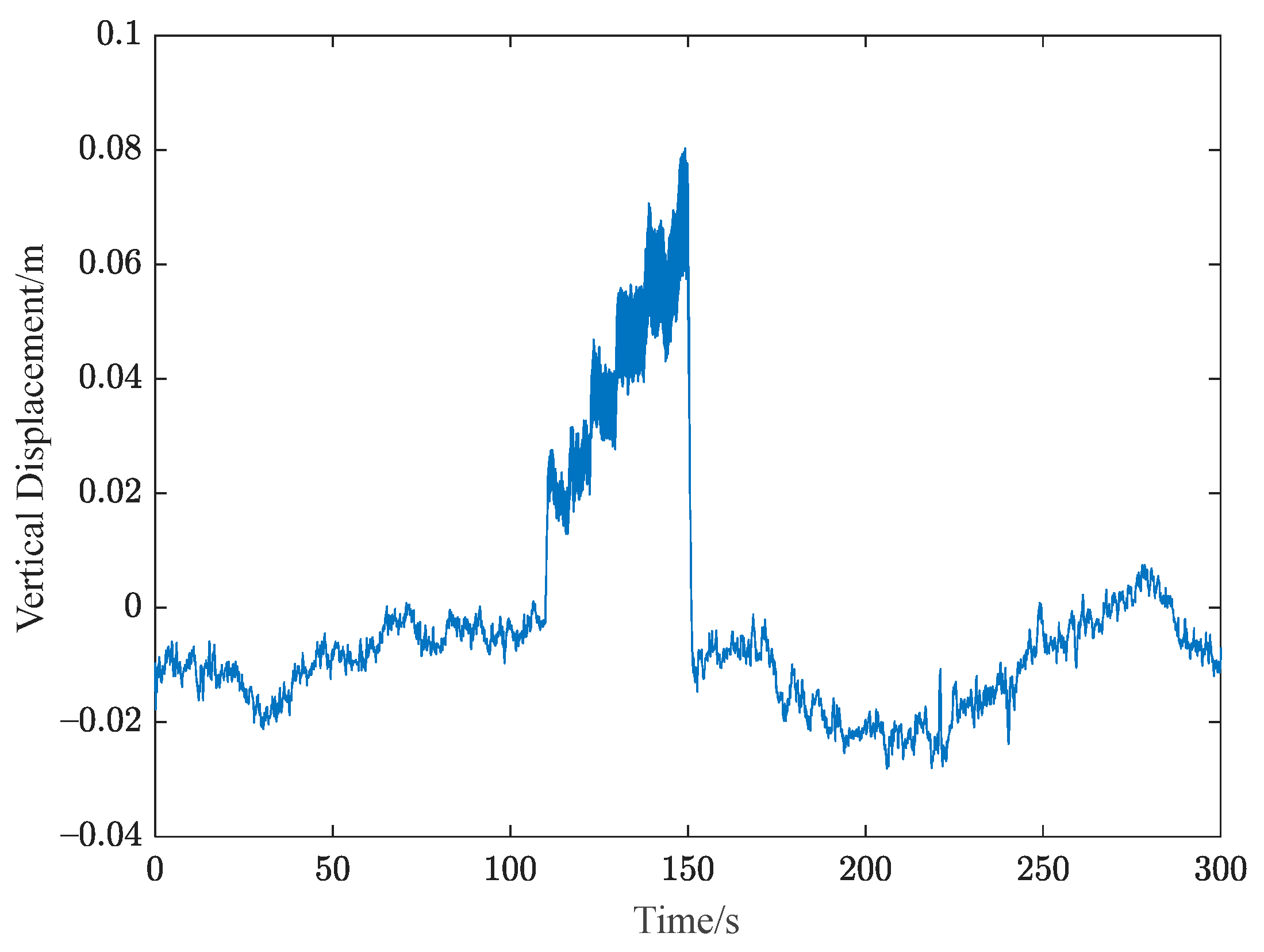
3.1. Analysis of Experimental Results of Anhui Suntuan River Bridge
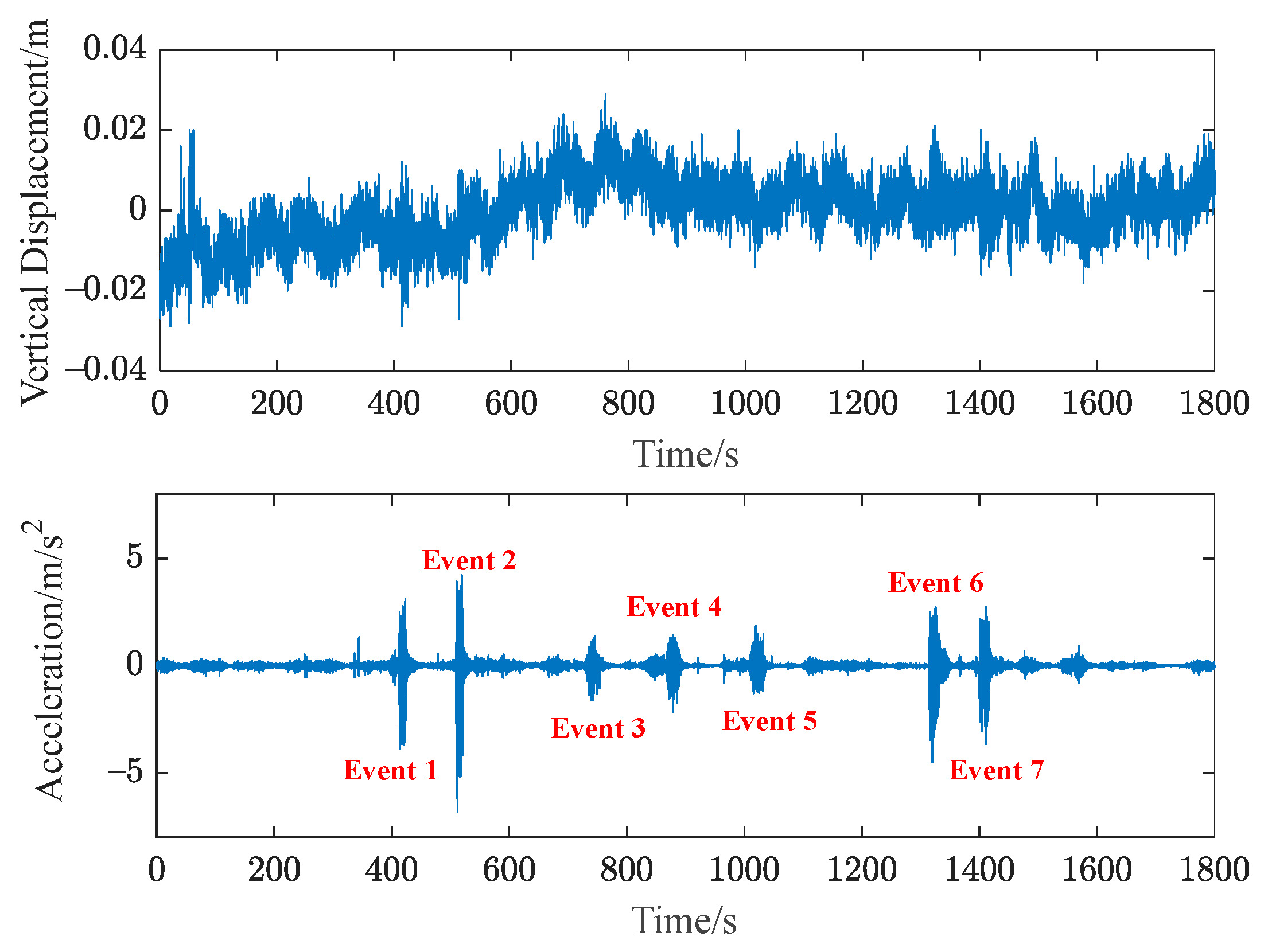
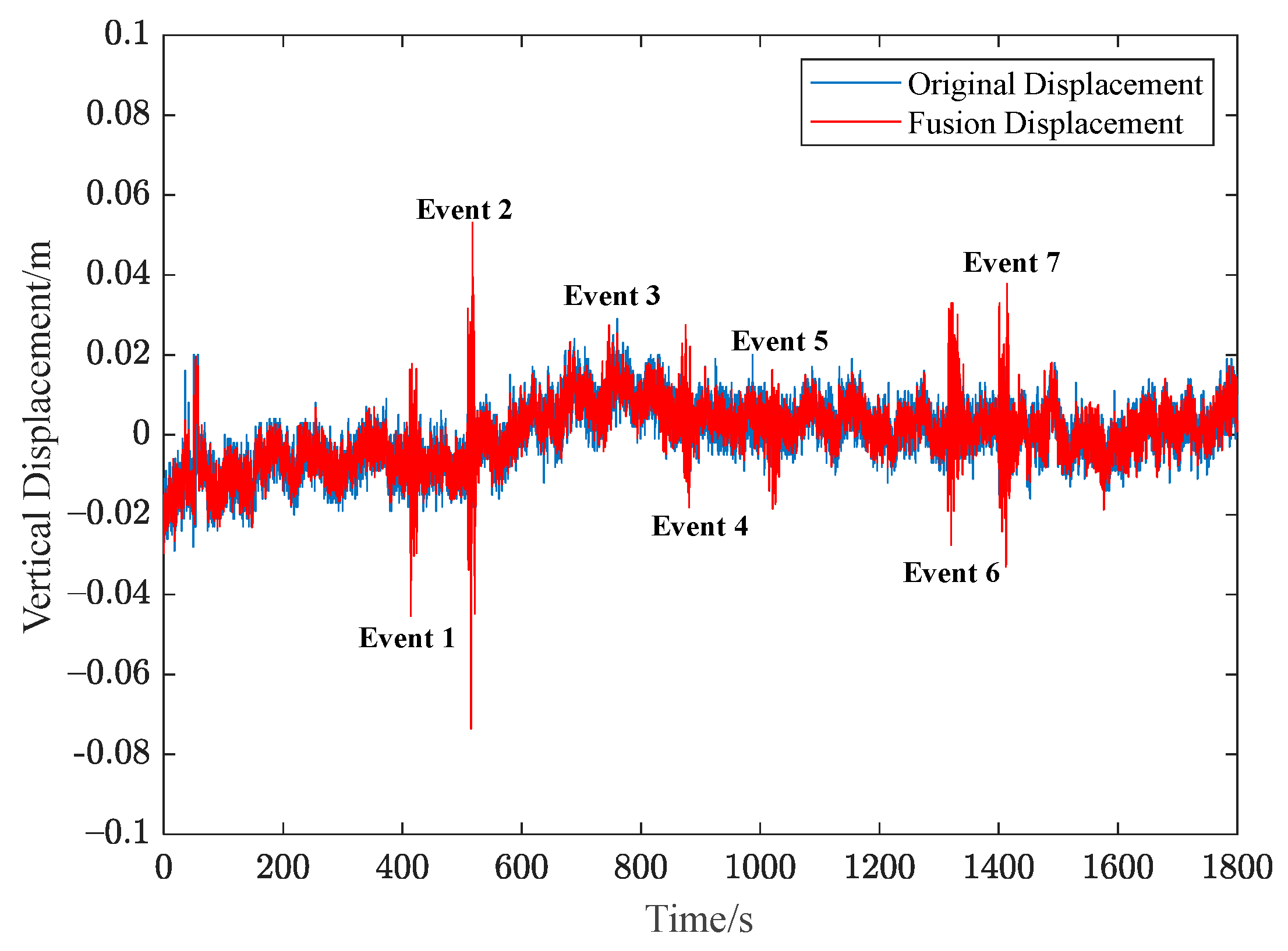
3.2. Analysis of Experimental Results of Wilford Bridge, UK
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, J.; Meng, X.; Yan, B.; Xu, B.; Fan, Q.; Xie, Y. Global Navigation Satellite System-based Positioning Technology for Structural Health Monitoring: A Review. Struct. Control Health Monit. 2020, 27, e2467. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, Q.; Gao, W.; Li, J.; Xu, Y.; Sun, B. Principle and Performance of BDSBAS and PPP-B2b of BDS-3. Satell. Navig. 2022, 3, 5. [Google Scholar] [CrossRef]
- Yu, J.Y.; Shao, X.D.; Meng, X.L.; Li, L.F. Experimental research on dynamic monitoring of bridges using gnss and accelerometer. China J. Highw. Transp. 2014, 27, 62–69. [Google Scholar]
- Yang, Y.; Mao, Y.; Sun, B. Basic Performance and Future Developments of BeiDou Global Navigation Satellite System. Satell. Navig. 2020, 1, 1–8. [Google Scholar] [CrossRef]
- Tolman, B.W.; Craig, B.K. An integrated GPS/accelerometer system for low dynamics applications. In Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics, and Navigation, Banff, AB, Canada, 5–8 June 2001; pp. 151–159. [Google Scholar]
- Li, X.; Ge, L.; Ambikairajah, E.; Rizos, C.; Tamura, Y.; Yoshida, A. Full-Scale Structural Monitoring Using an Integrated GPS and Accelerometer System. Gps Solut. 2006, 10, 233–247. [Google Scholar] [CrossRef]
- Chan, W.S.; Xu, Y.L.; Ding, X.L.; Dai, W.J. An Integrated GPS-Accelerometer Data Processing Technique for Structural Deformation Monitoring. J. Geod. 2006, 80, 705–719. [Google Scholar] [CrossRef]
- Dai, W.J.; Wu, X.X.; Luo, F.Y. Integration of GPS and accelerometer for high building vibration monitoring. J. Vib. Shock. 2011, 30, 223–226, 249. [Google Scholar]
- Moschas, F.; Stiros, S. Measurement of the Dynamic Displacements and of the Modal Frequencies of a Short-Span Pedestrian Bridge Using GPS and an Accelerometer. Eng. Struct. 2011, 33, 10–17. [Google Scholar] [CrossRef]
- Han, H.Z.; Wang, J.; Meng, X.L. Reconstruction of bridge dynamics using integrated GPS and accelerometer. J. China Univ. Min. Technol. 2015, 44, 549–556. [Google Scholar]
- Xu, Y.; Brownjohn, J.M.W.; Hester, D.; Koo, K.Y. Long-Span Bridges: Enhanced Data Fusion of GPS Displacement and Deck Accelerations. Eng. Struct. 2017, 147, 639–651. [Google Scholar] [CrossRef]
- Kim, K.; Choi, J.; Chung, J.; Koo, G.; Bae, I.-H.; Sohn, H. Structural Displacement Estimation through Multi-Rate Fusion of Accelerometer and RTK-GPS Displacement and Velocity Measurements. Measurement 2018, 130, 223–235. [Google Scholar] [CrossRef]
- Hou, H.; Kuang, C.; Zhou, Y.; Zhang, Y. Feasibility Study of Low Cost Receiver for Deformation Monitoring. In China Satellite Navigation Conference (CSNC) 2018 Proceedings; Lecture Notes in Electrical Engineering; Sun, J., Yang, C., Guo, S., Eds.; Springer: Singapore, 2018; Volume 497, pp. 129–138. ISBN 9789811300042. [Google Scholar]
- Notti, D.; Cina, A.; Manzino, A.; Colombo, A.; Bendea, I.H.; Mollo, P.; Giordan, D. Low-Cost GNSS Solution for Continuous Monitoring of Slope Instabilities Applied to Madonna Del Sasso Sanctuary (NW Italy). Sensors 2020, 20, 289. [Google Scholar] [CrossRef] [PubMed]
- Tu, R.; Wang, R.; Ge, M.; Walter, T.R.; Ramatschi, M.; Milkereit, C.; Bindi, D.; Dahm, T. Cost-effective Monitoring of Ground Motion Related to Earthquakes, Landslides, or Volcanic Activity by Joint Use of a Single-frequency GPS and a MEMS Accelerometer. Geophys. Res. Lett. 2013, 40, 3825–3829. [Google Scholar] [CrossRef]
- Tu, R.; Liu, J.; Zhang, R.; Fan, L.; Han, J. Real-Time Kinematic Positioning Algorithm with GNSS and High-Frequency Accelerometer Observations for Broadband Signals. Meas. Sci. Technol. 2019, 31, 035007. [Google Scholar] [CrossRef]
- Sun, K.T.; Gao, Y.; Wu, X.D. Application of MEMS Sensors in Abnormal Deformation Monitoring of Metro Tunnel Structure. In Proceedings of the International Conference on Smart Transportation and City Engineering 2021; Li, Z., Chen, X., Yan, K., Cen, F., Peng, L., Lin, N., Eds.; SPIE: Chongqing, China, 2021; p. 75. [Google Scholar]
- Lăpădat, A.M.; Tiberius, C.C.J.M.; Teunissen, P.J.G. Experimental Evaluation of Smartphone Accelerometer and Low-Cost Dual Frequency GNSS Sensors for Deformation Monitoring. Sensors 2021, 21, 7946. [Google Scholar] [CrossRef] [PubMed]
- Smyth, A.; Wu, M. Multi-Rate Kalman Filtering for the Data Fusion of Displacement and Acceleration Response Measurements in Dynamic System Monitoring. Mech. Syst. Signal Process. 2007, 21, 706–723. [Google Scholar] [CrossRef]
- Kogan, M.G.; Kim, W.-Y.; Bock, Y.; Smyth, A.W. Load Response on a Large Suspension Bridge during the NYC Marathon Revealed by GPS and Accelerometers. Seismol. Res. Lett. 2008, 79, 12–19. [Google Scholar] [CrossRef]
- Chang, C.C.; Xiao, X.H. An Integrated Visual-Inertial Technique for Structural Displacement and Velocity Measurement. Smart Struct. Syst. 2010, 6, 1025–1039. [Google Scholar] [CrossRef]
- Lai, T.; Ting-Hua, Y.I.; Wang, J.Y.; Lin, Y.X.; Hong-Nan, L.I. Data Fusion of Displacement and Acceleration Measurements Based on Multi-rate Kalman Filtering Technique. J. Disaster Prev. Mitig. Eng. 2012, 32, 707–713. [Google Scholar]
- Meng, X.; Wang, J.; Han, H. Optimal GPS/Accelerometer Integration Algorithm for Monitoring the Vertical Structural Dynamics. J. Appl. Geod. 2014, 8, 265–272. [Google Scholar] [CrossRef]
- Yang, A.; Wang, P.; Yang, H. Bridge Dynamic Displacement Monitoring Using Adaptive Data Fusion of GNSS and Accelerometer Measurements. IEEE Sens. J. 2021, 21, 24359–24370. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Meng, X.; Liu, H. Analysis of the Dynamic Response of a Long Span Bridge Using GPS/Accelerometer/Anemometer under Typhoon Loading. Eng. Struct. 2016, 122, 238–250. [Google Scholar] [CrossRef]
- Hide, C.; Moore, T.; Smith, M. Adaptive Kalman Filtering for Low-Cost INS/GPS. J. Navig. 2003, 56, 143–152. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Li, S.; Feng, S.; Wang, X.; Liao, J. GIL: A Tightly Coupled GNSS PPP/INS/LiDAR Method for Precise Vehicle Navigation. Satell. Navig. 2021, 2, 26. [Google Scholar] [CrossRef]
- Teunissen, P.; Salzmann, M. A Recursive Slippage Test for Use in State-Space Filtering. Manuscr. Geod. 1989, 14, 383–390. [Google Scholar]
- Brumback, B.; Srinath, M. A Chi-Square Test for Fault-Detection in Kalman Filters. IEEE Trans. Autom. Control 1987, 32, 552–554. [Google Scholar] [CrossRef]
- Li, P. Investigation of System Fault Detectionin INS/GNSS/SAR Integrated Navigation System. J. Proj. Rocket. Missiles Guid. 2005, 7, 309–312. [Google Scholar]
- Li, T.; Zhou, J.B.; Liu, Y.P. Federal Kalman Filter Based on Residual Chi-Square Test Method. Aerosp. Control. 2017, 35, 56–59. [Google Scholar]
- Xiong, H.; Bian, R.; Li, Y.; Du, Z.; Mai, Z. Fault-Tolerant GNSS/SINS/DVL/CNS Integrated Navigation and Positioning Mechanism Based on Adaptive Information Sharing Factors. IEEE Syst. J. 2020, 14, 3744–3754. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Kirubarajan, T.; Li, X.R. Estimation with Applications to Tracking and Navigation; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar]
- Li, X.R.; Zhao, Z. Evaluation of Estimation Algorithms. Part 1: Incomprehensive Measures of Performance. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1340–1358. [Google Scholar] [CrossRef]
- Chun, Y.; Lei, Z.; Jian, G.; Qingwei, C. Fault-tolerant integrated navigation algorithm using chi-square test with two state propagators and fuzzy adaptive filter. Control. Theory Appl. 2016, 33, 500–511. [Google Scholar]
- Diesel, J.; Dunn, G. GPS/IRS AIME: Certification for Sole Means and Solution to RF Interference. In Proceedings of the Proceedings of the 9th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1996), Kansas City, MO, USA, 17–20 September 1996; pp. 1599–1606. [Google Scholar]
- Liu, H.Y.; Feng, C.T.; Wang, H.N. Method of Inertial Aided Satellite Navigation and Its Integrity Monitoring. J. Astronaut. 2011, 32, 775–780. [Google Scholar]
- Zhong, L.N.; Liu, J.Y.; Li, R.B.; Wang, R. Approach for detection of slowly growing errors in INS/GNSS tightly-coupled system based on LS-SVM. J. Chin. Inert. Technol. 2012, 20, 754–758. [Google Scholar]
- Bhatti, U.I.; Ochieng, W.Y.; Feng, S. Performance of Rate Detector Algorithms for an Integrated GPS/INS System in the Presence of Slowly Growing Error. GPS Solut. 2012, 16, 293–301. [Google Scholar] [CrossRef]
- Li, X.; Zhao, X.; Pang, C.; He, Z. Integrity Monitoring of Integrated GNSS /SINS System Based on PBN. Electron. Opt. Control. 2013, 20, 44–48. [Google Scholar]
- Zhao, X.; Gao, C.; Pang, C.; Zhang, C.; Wang, Y. A double-threshold test method for soft faults assisted by BP neural network. Control. Decrsion 2020, 35, 1384–1390. [Google Scholar]

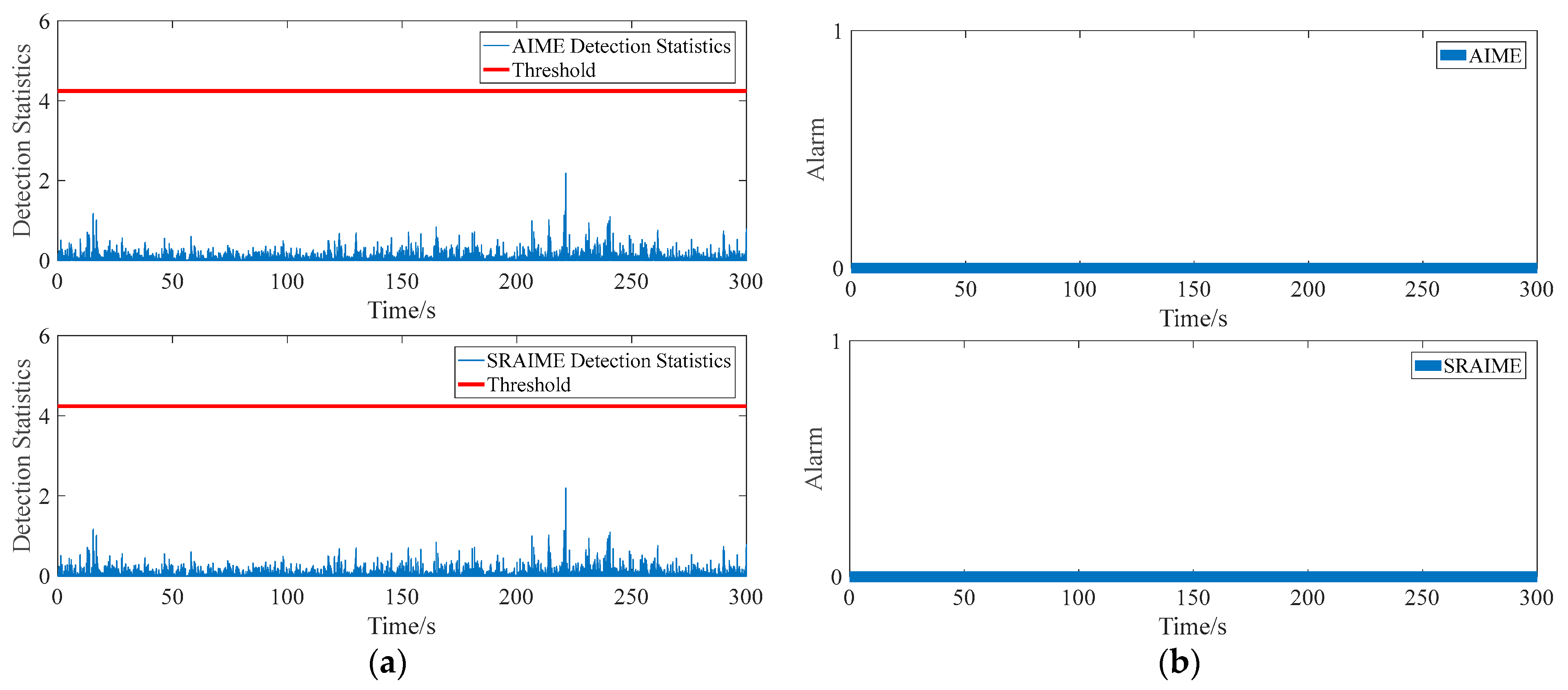



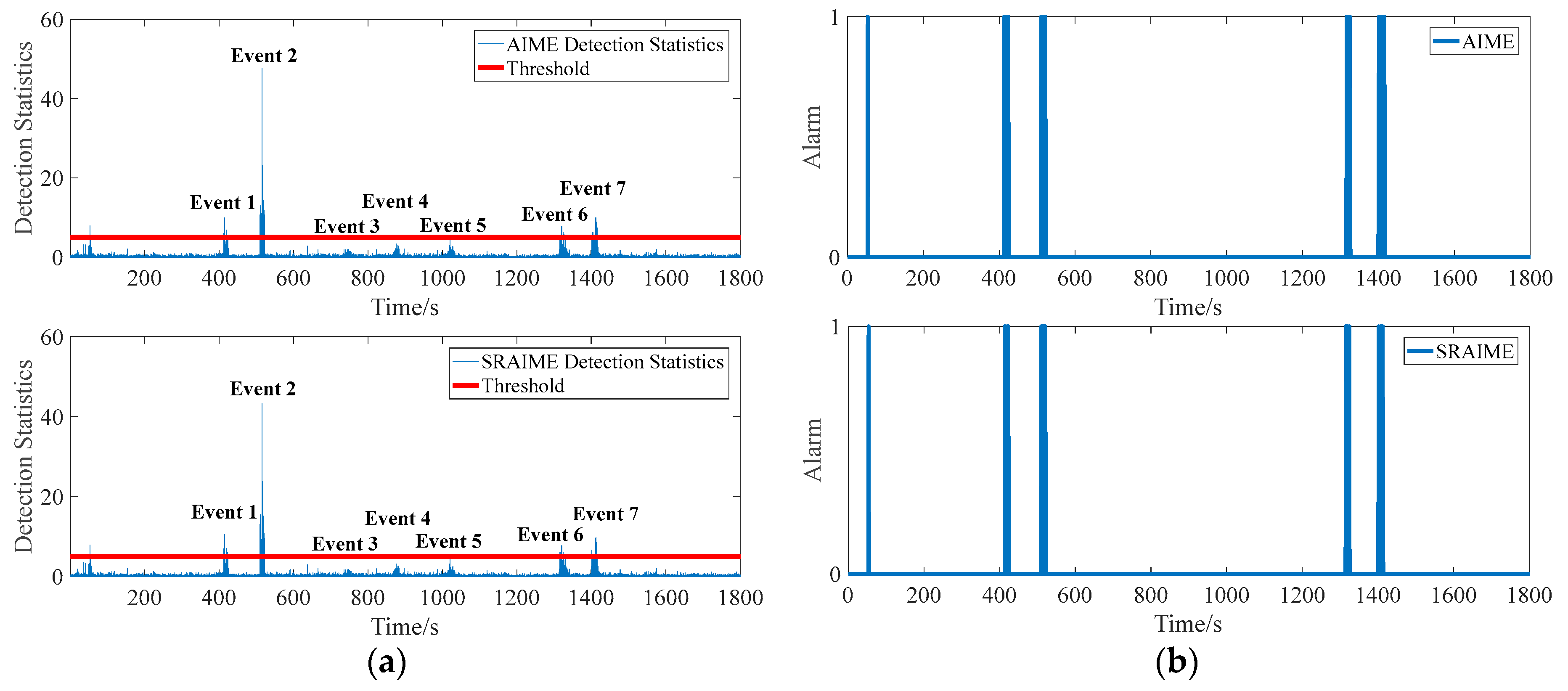

| First Alarm Time/Detection Statistics | Alert Threshold | |
|---|---|---|
| AIME | 110 s/4.63 | 4.24 |
| SRAIME | 110 s/4.63 | 4.24 |
| Experimental Event | Event Description |
|---|---|
| Event 1 | 30 people jumped at the midspan of the bridge, with a total weight of 2353 kg. |
| Event 2 | 30 people jumped at the midspan of the bridge, then 15 people left. |
| Event 3 | A column of 15 people ran from east to west to the middle span of the bridge, with a total weight of 1253 kg. |
| Event 4 | Located on the south side of the bridge, 15 people ran in a row from west to east. |
| Event 5 | Located in the northwest of the bridge, 15 people lined up to run from west to east. |
| Event 6 | 15 people jump on the bridge midspan. |
| Event 7 | 15 people jump on the bridge midspan. |
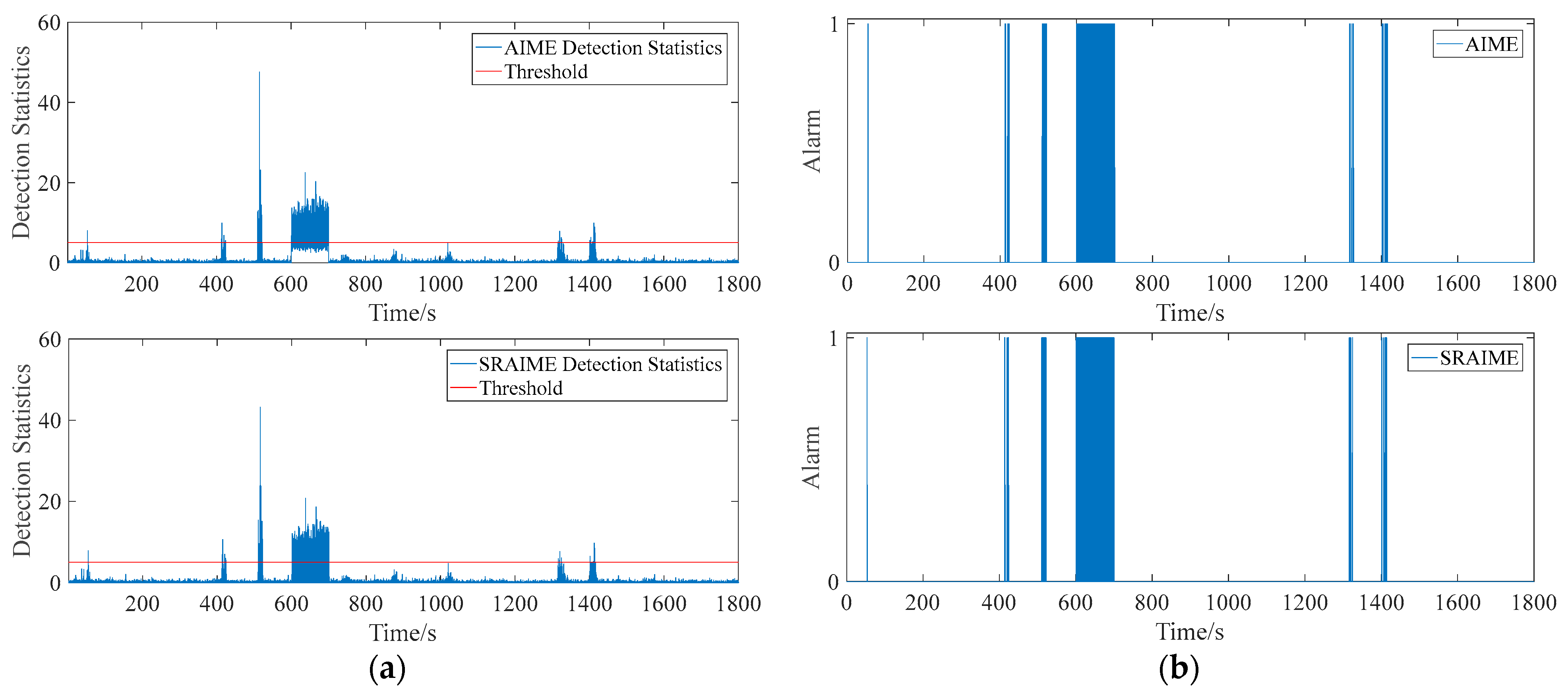
| First Alarm Time/Detection Statistics | Alert Threshold | |
|---|---|---|
| AIME | 600 s/5.07 | 5.05 |
| SRAIME | 600 s/5.07 | 5.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, A.; Zhang, Q.; Yu, Z.; Meng, X.; Liu, X.; Zhang, Y.; Xie, Y. A Novel Slow-Growing Gross Error Detection Method for GNSS/Accelerometer Integrated Deformation Monitoring Based on State Domain Consistency Theory. Remote Sens. 2022, 14, 4758. https://doi.org/10.3390/rs14194758
Sun A, Zhang Q, Yu Z, Meng X, Liu X, Zhang Y, Xie Y. A Novel Slow-Growing Gross Error Detection Method for GNSS/Accelerometer Integrated Deformation Monitoring Based on State Domain Consistency Theory. Remote Sensing. 2022; 14(19):4758. https://doi.org/10.3390/rs14194758
Chicago/Turabian StyleSun, Ao, Qiuzhao Zhang, Zhangjun Yu, Xiaolin Meng, Xin Liu, Yunlong Zhang, and Yilin Xie. 2022. "A Novel Slow-Growing Gross Error Detection Method for GNSS/Accelerometer Integrated Deformation Monitoring Based on State Domain Consistency Theory" Remote Sensing 14, no. 19: 4758. https://doi.org/10.3390/rs14194758
APA StyleSun, A., Zhang, Q., Yu, Z., Meng, X., Liu, X., Zhang, Y., & Xie, Y. (2022). A Novel Slow-Growing Gross Error Detection Method for GNSS/Accelerometer Integrated Deformation Monitoring Based on State Domain Consistency Theory. Remote Sensing, 14(19), 4758. https://doi.org/10.3390/rs14194758