Joint Inversion of 3D Gravity and Magnetic Data under Undulating Terrain Based on Combined Hexahedral Grid
Abstract
1. Introduction
2. Methods
2.1. Curved Hexahedron Forward Theory
2.2. Cross-Gradient Joint Inversion Method
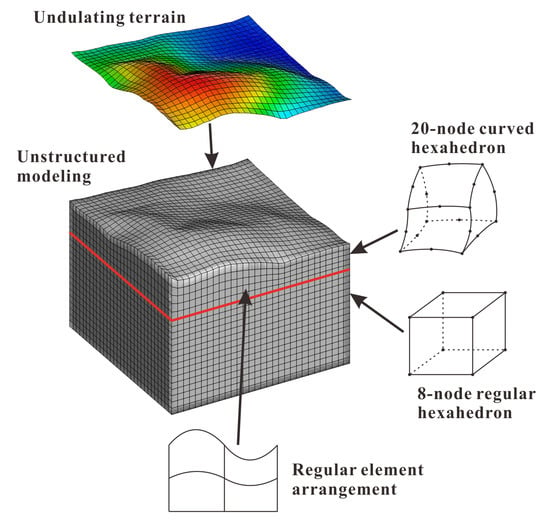
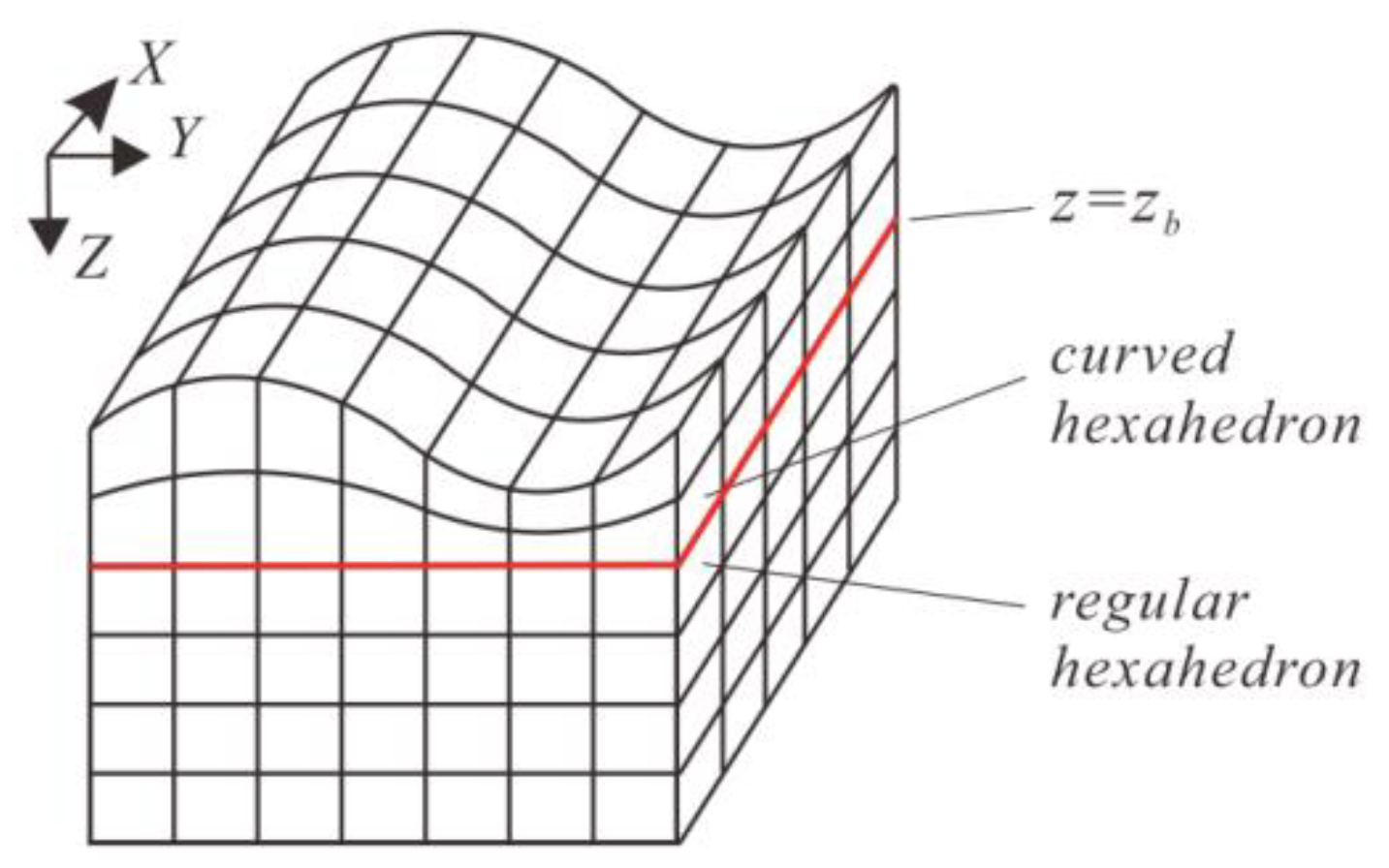
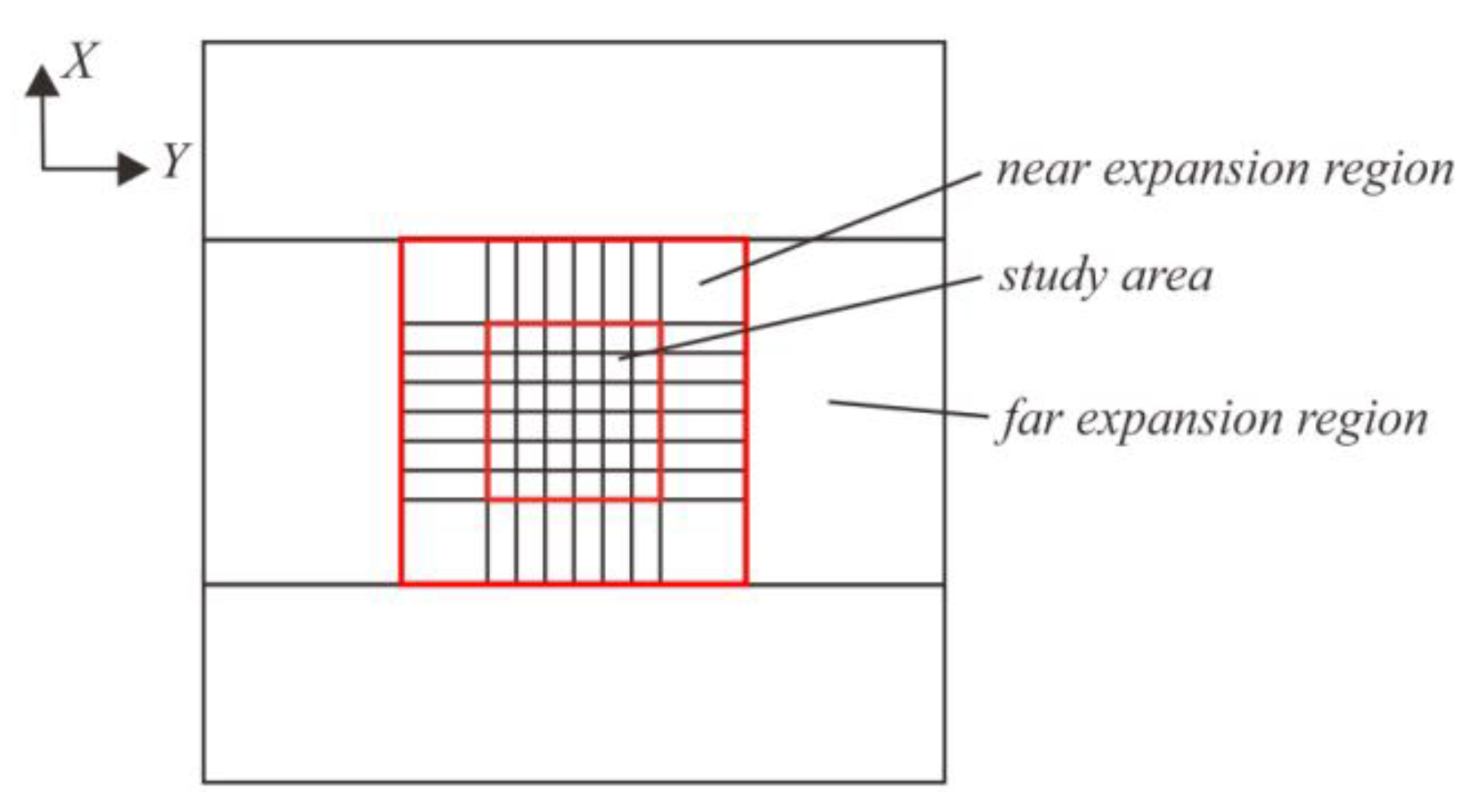
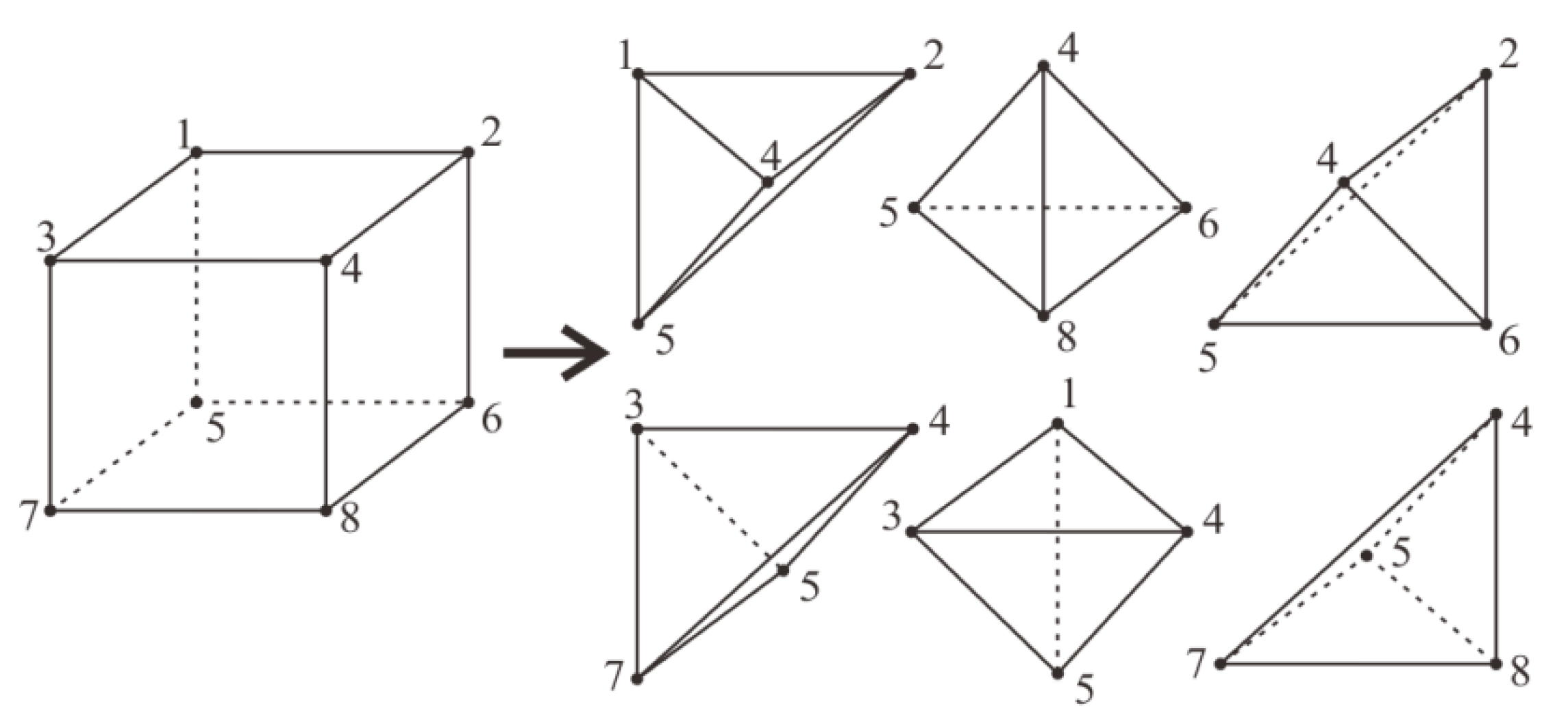
2.3. Combined Hexahedral Grid
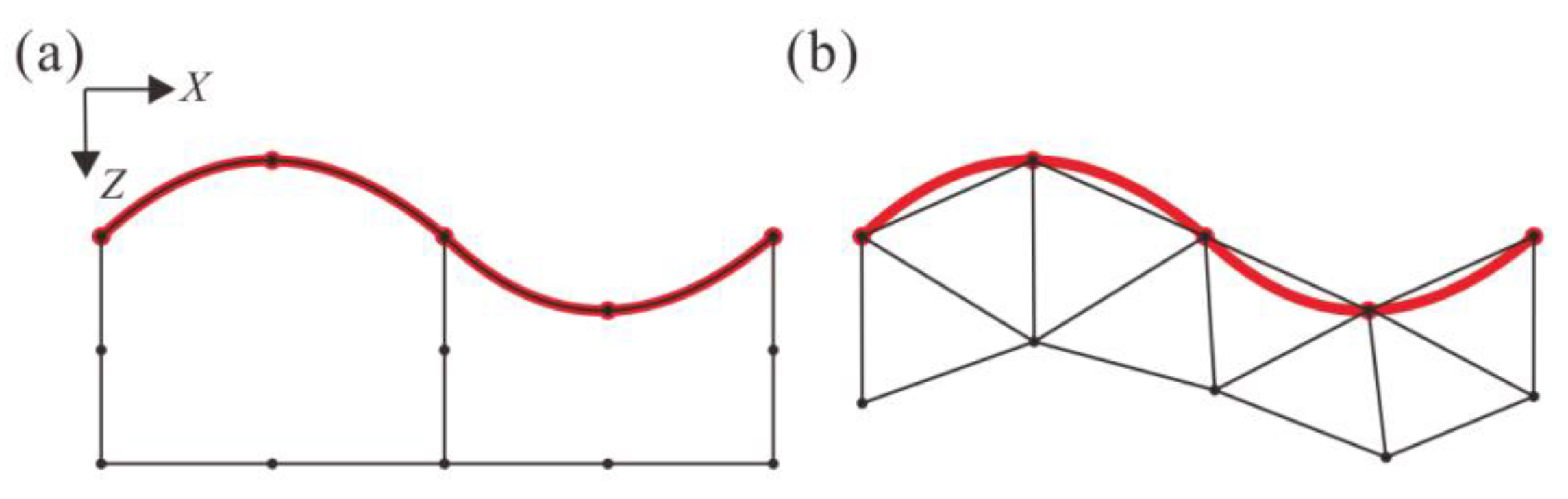
2.4. Element Volume Correction
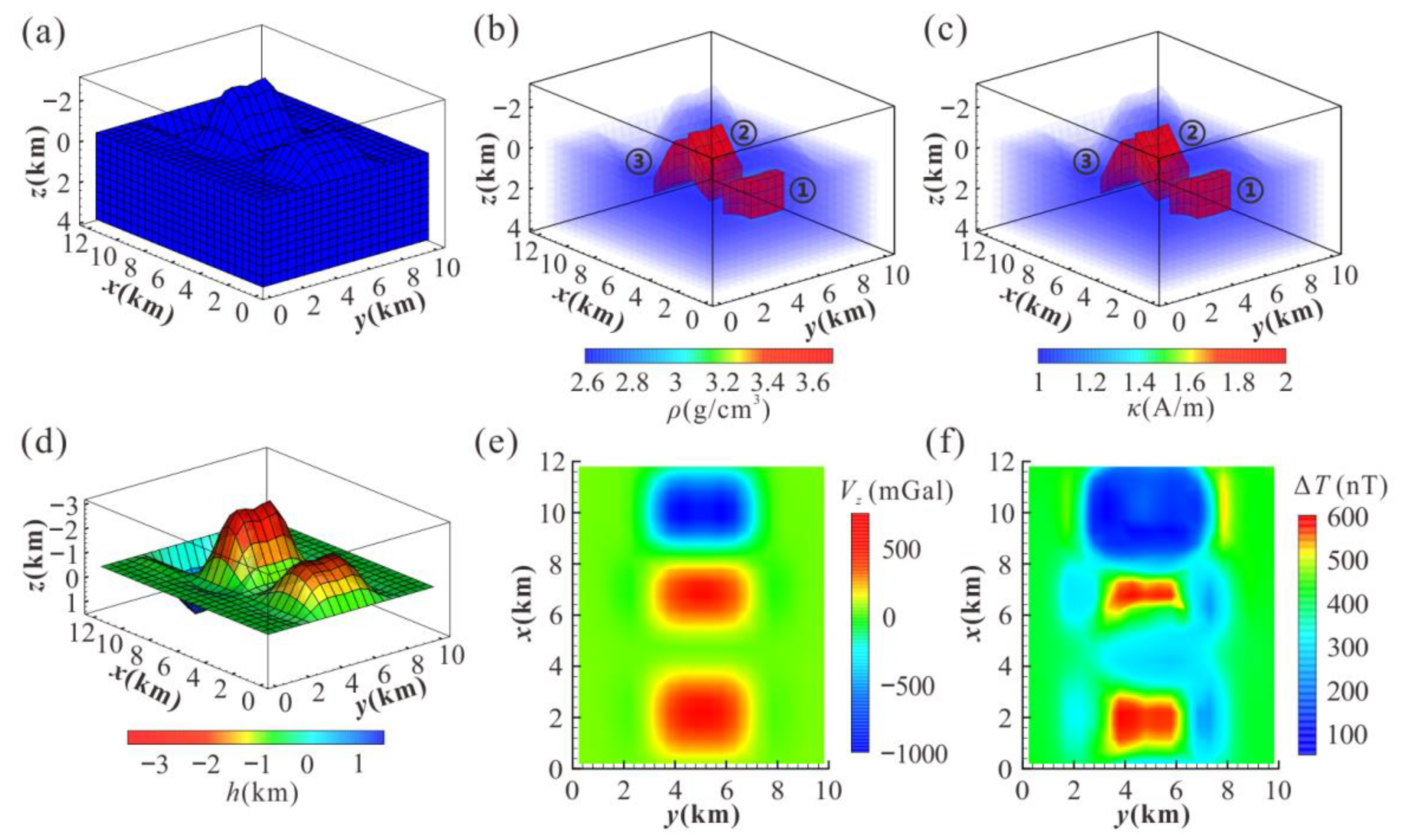
3. Results
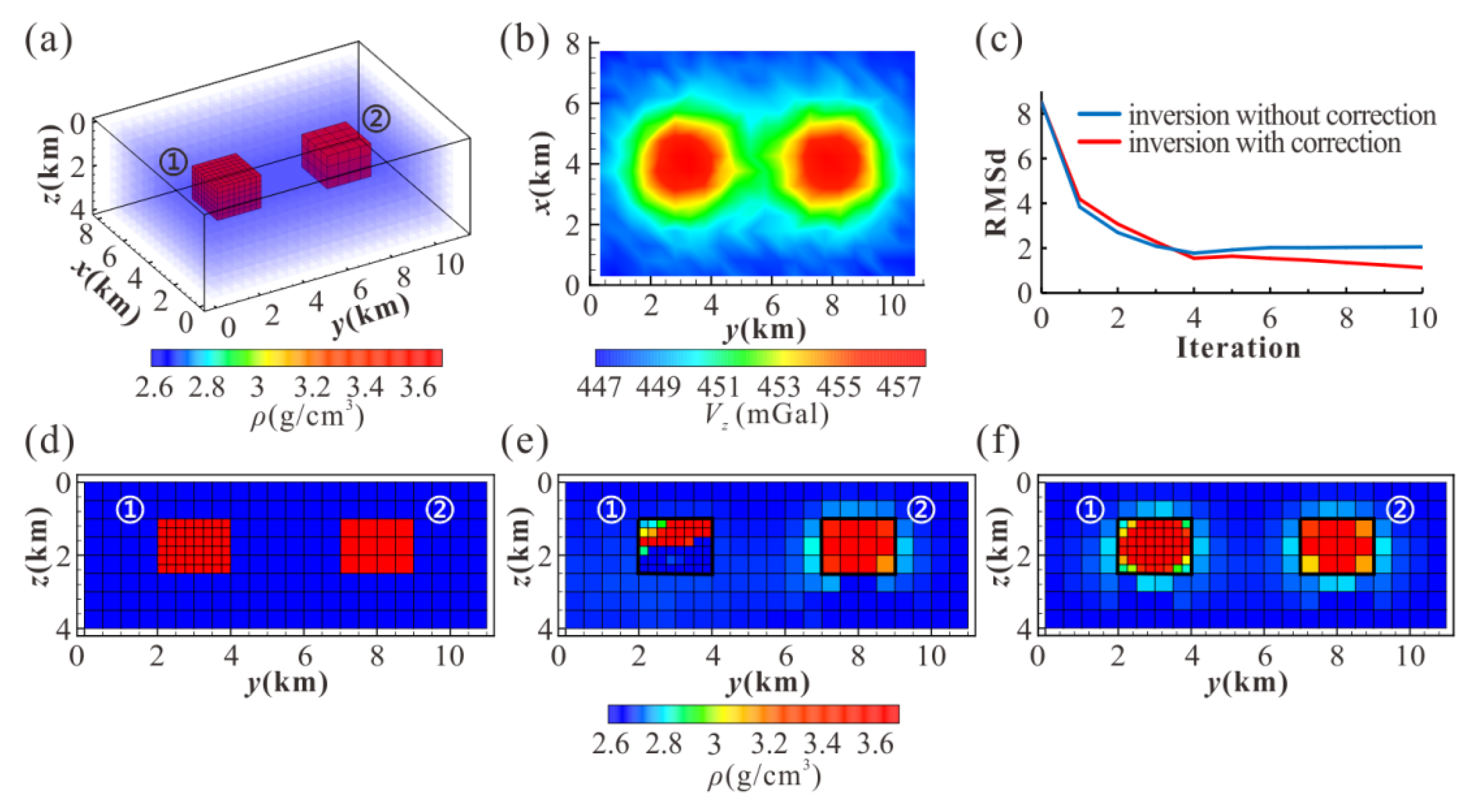
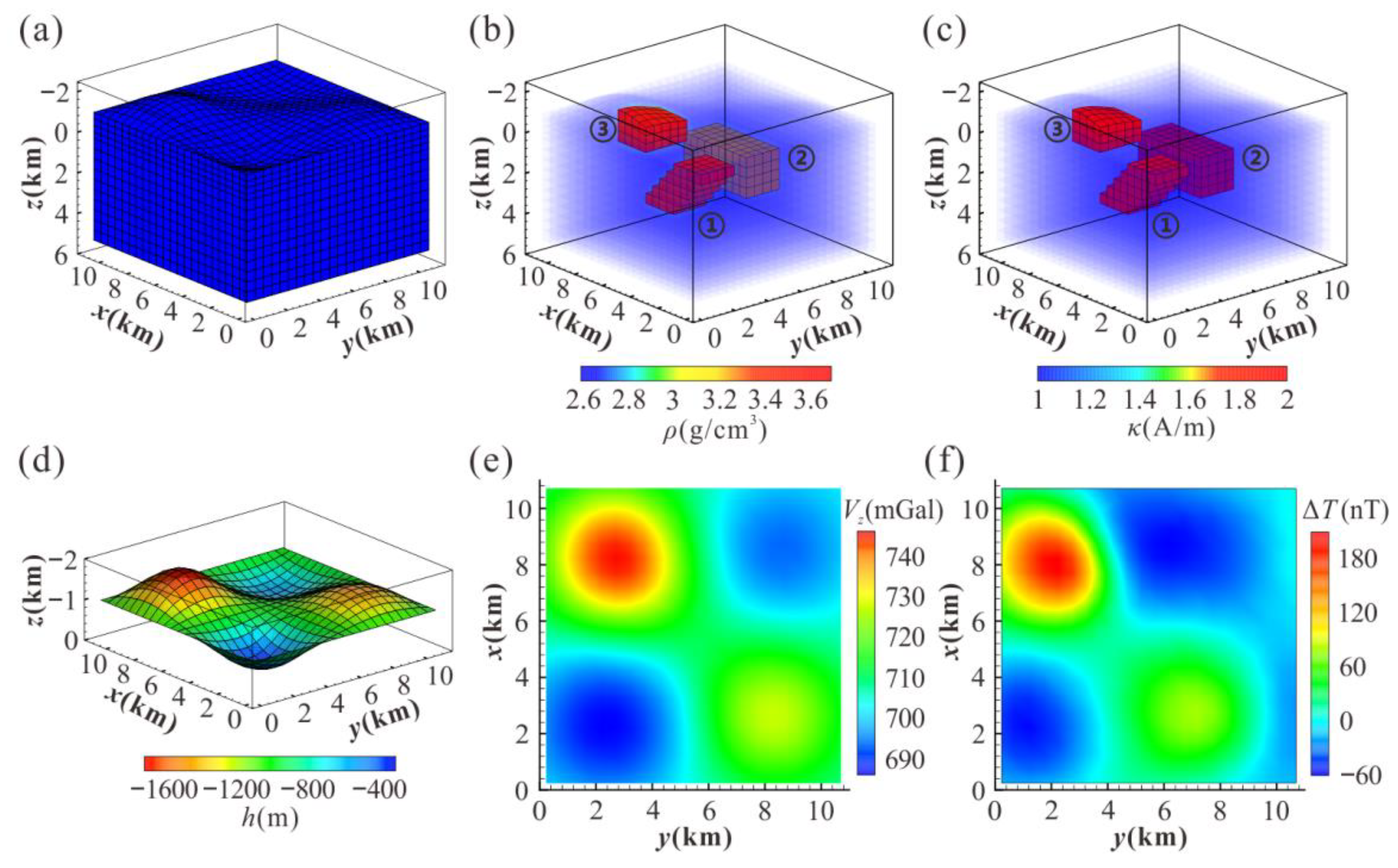
3.1. Effect Analysis of Element Volume Correction
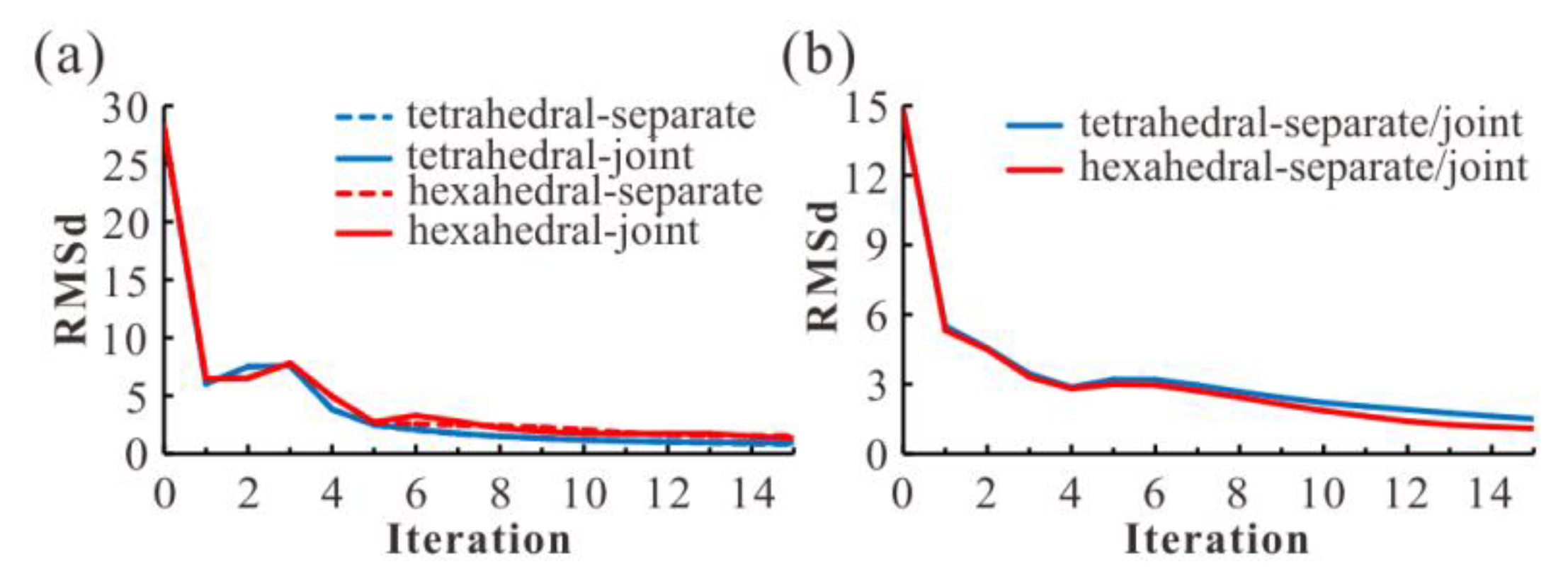
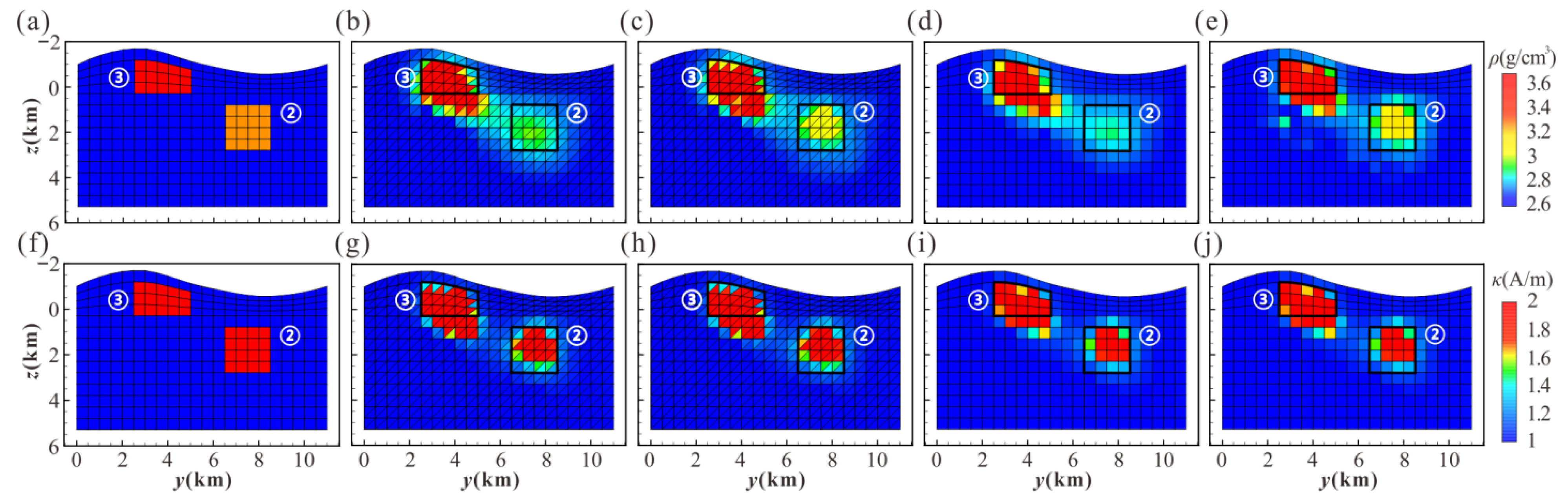
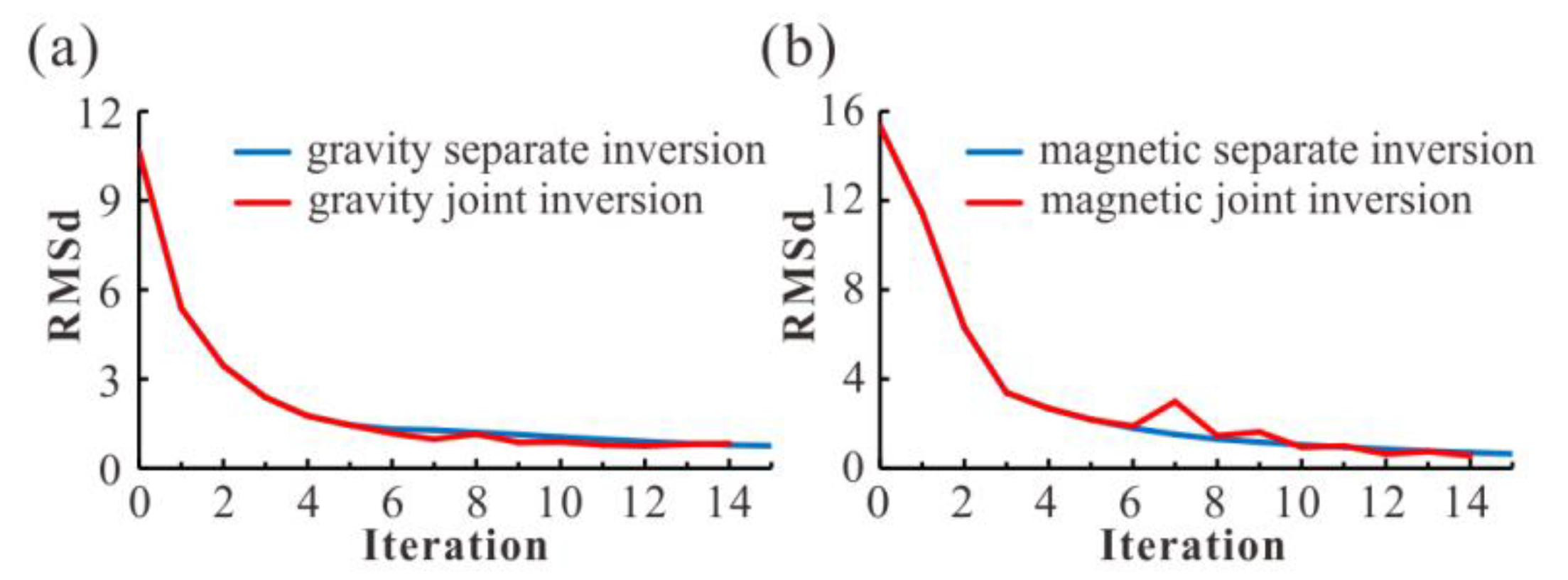
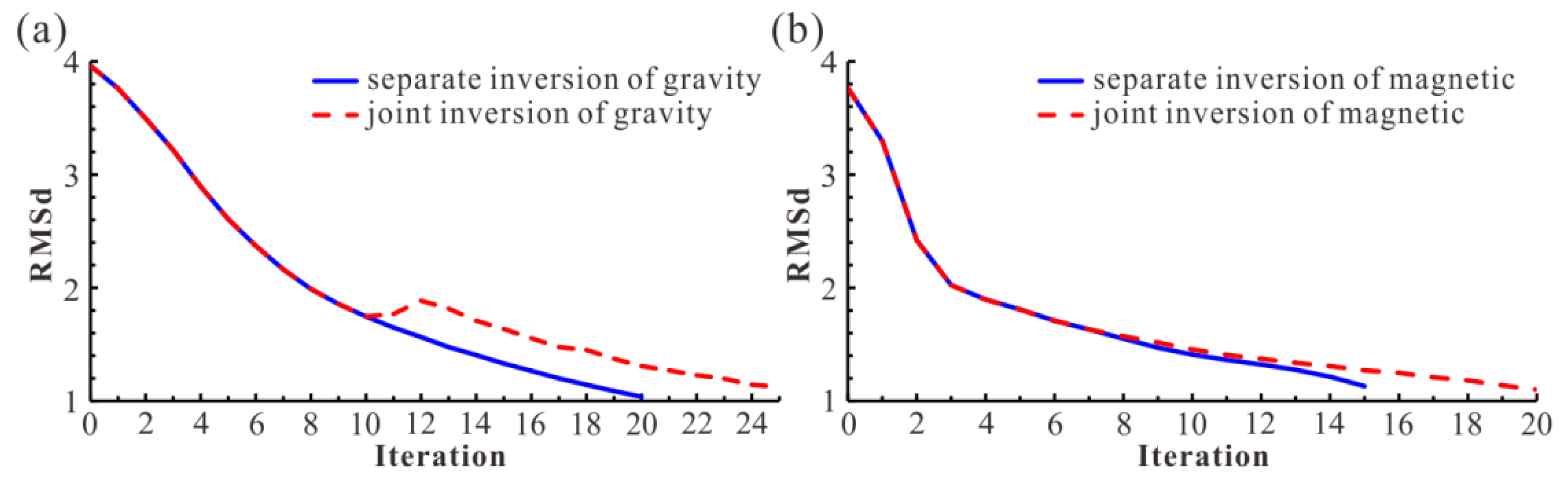
3.2. Effect Analysis of Joint Inversion Based on Combined Hexahedral Grid
3.3. Efficiency Analysis of Joint Inversion Based on Combined Hexahedral Grid
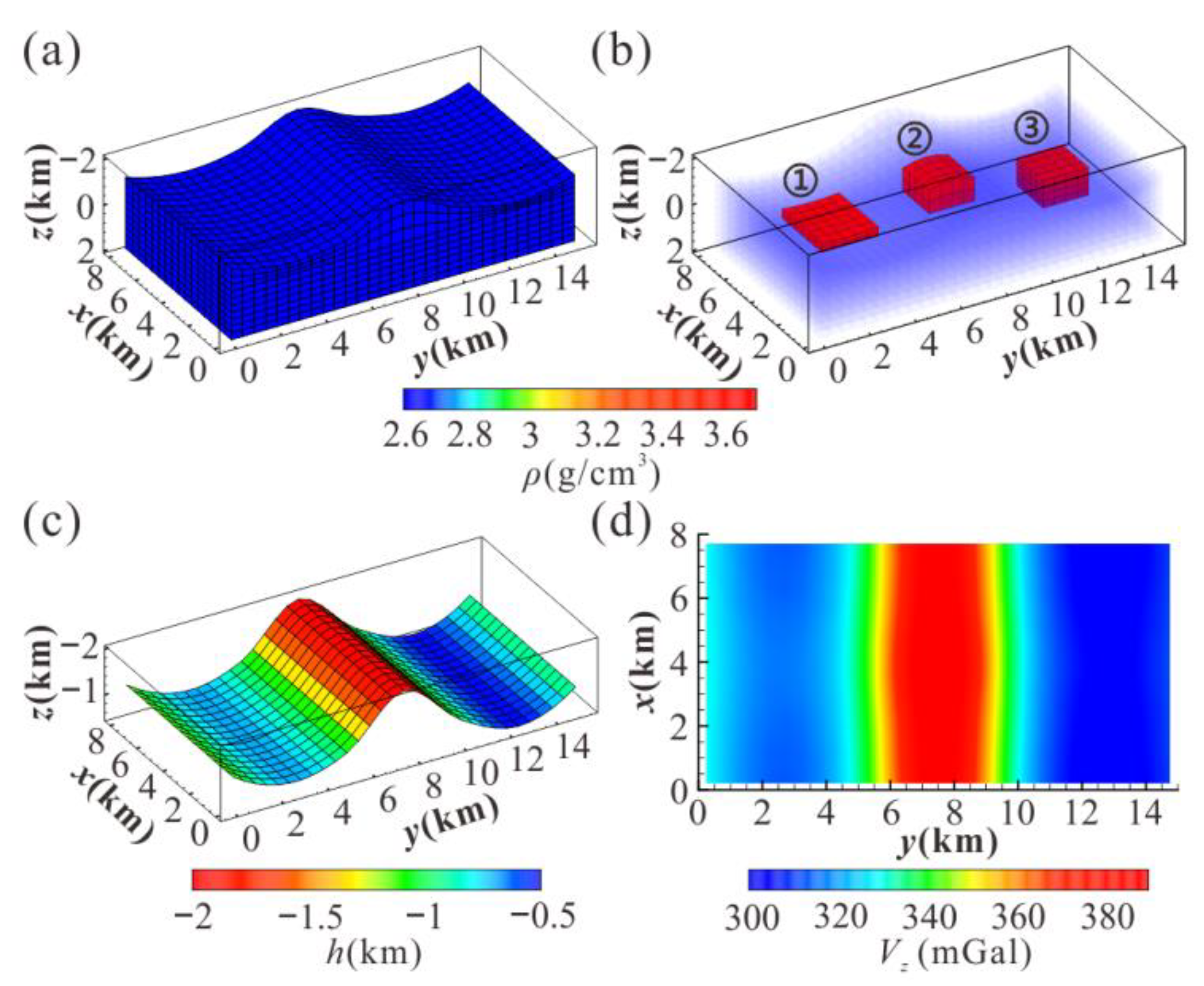
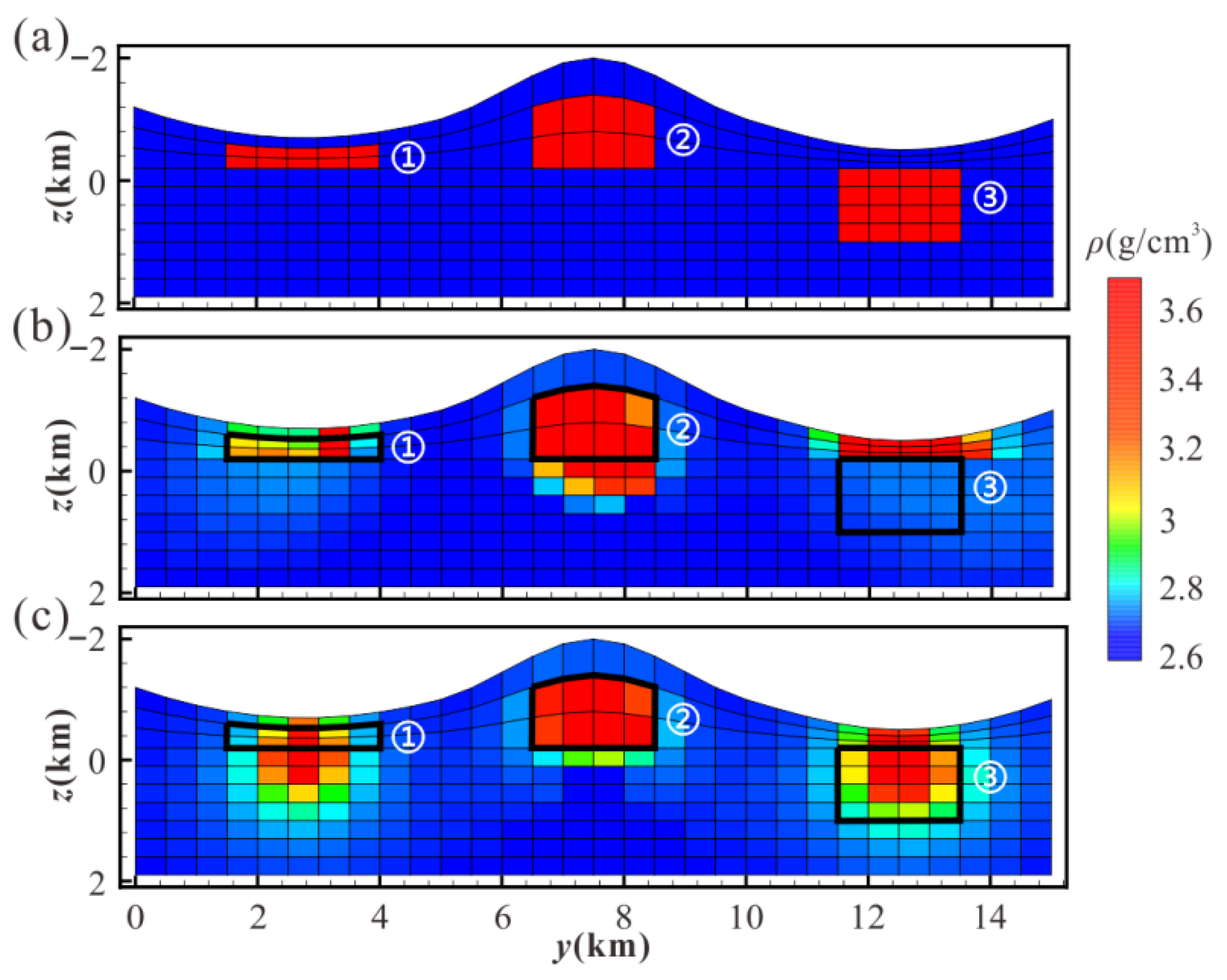
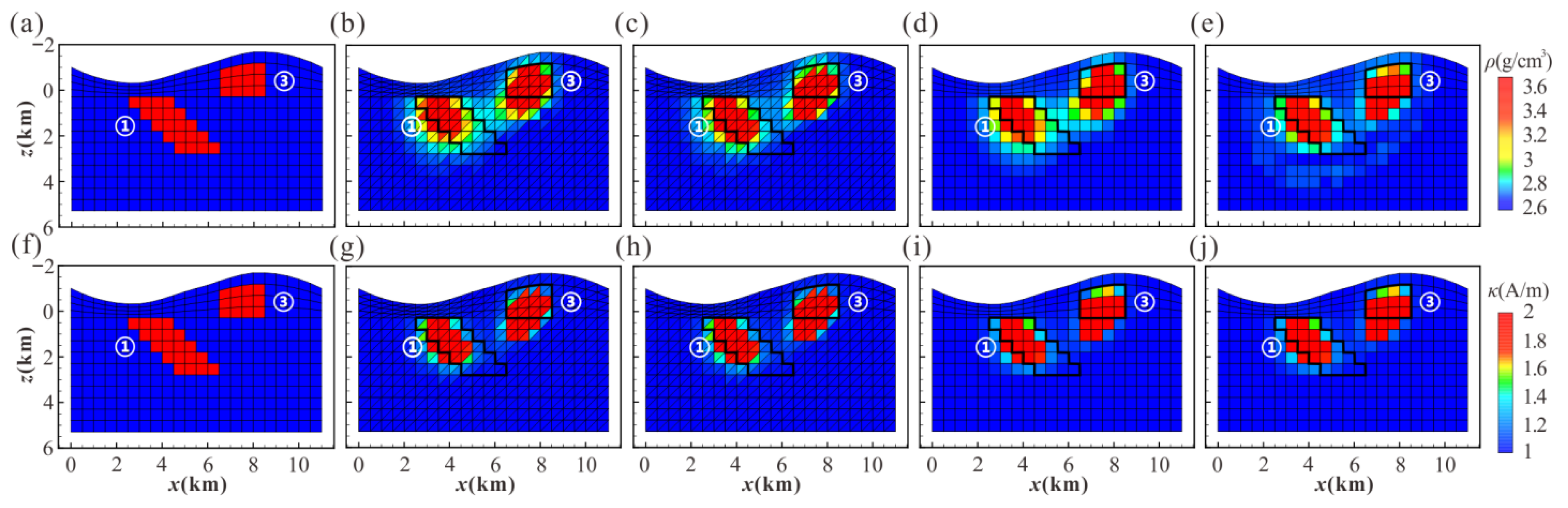
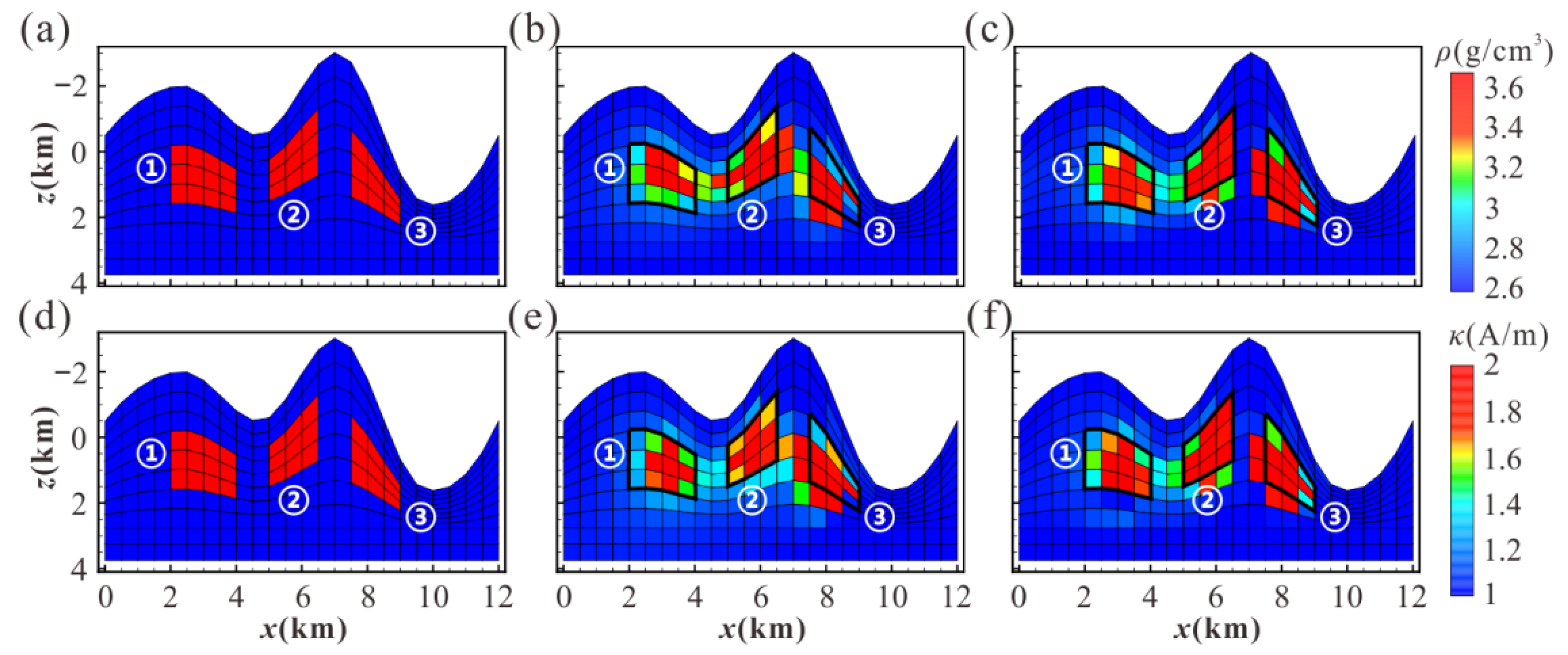
3.4. Effect Analysis of Application in Complex Terrain
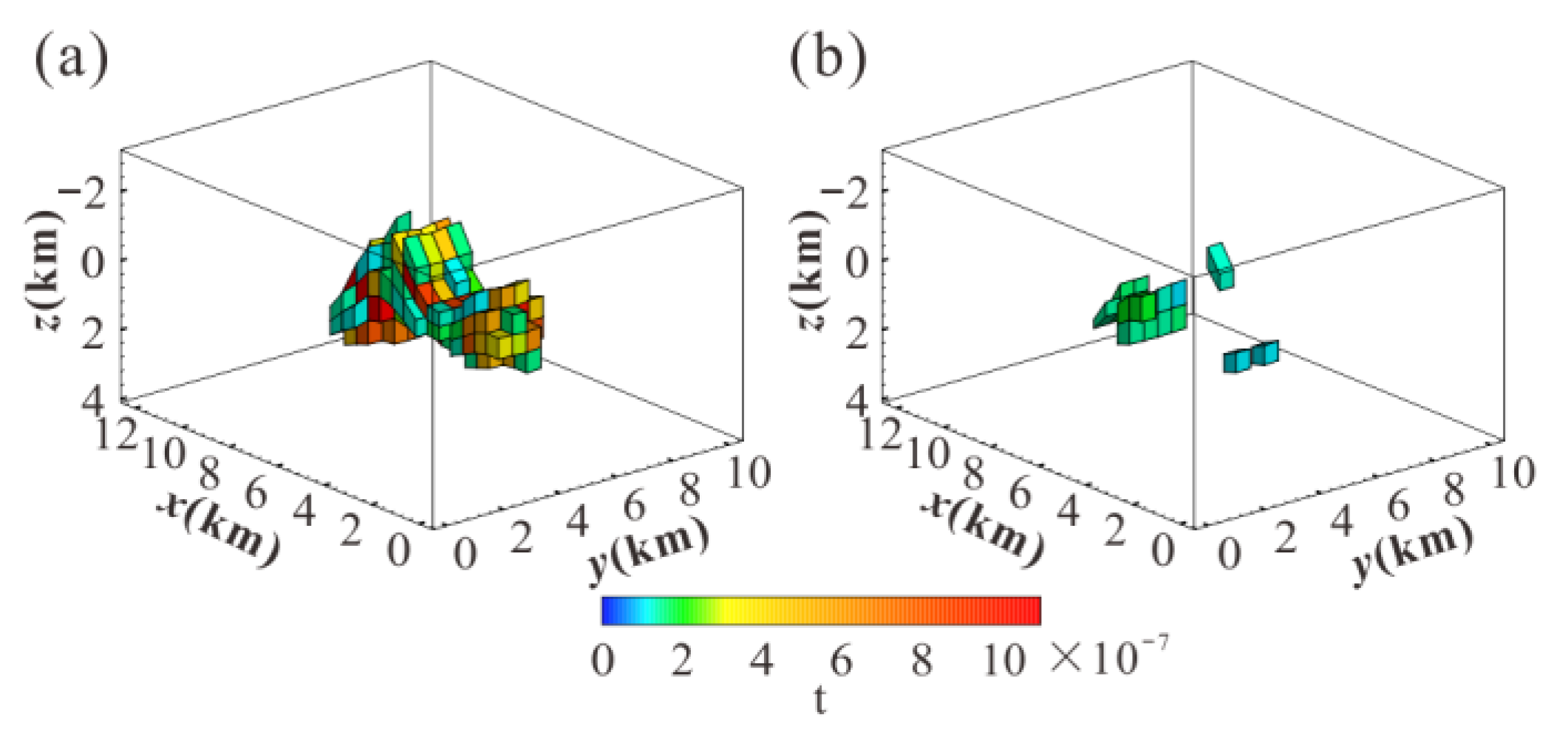
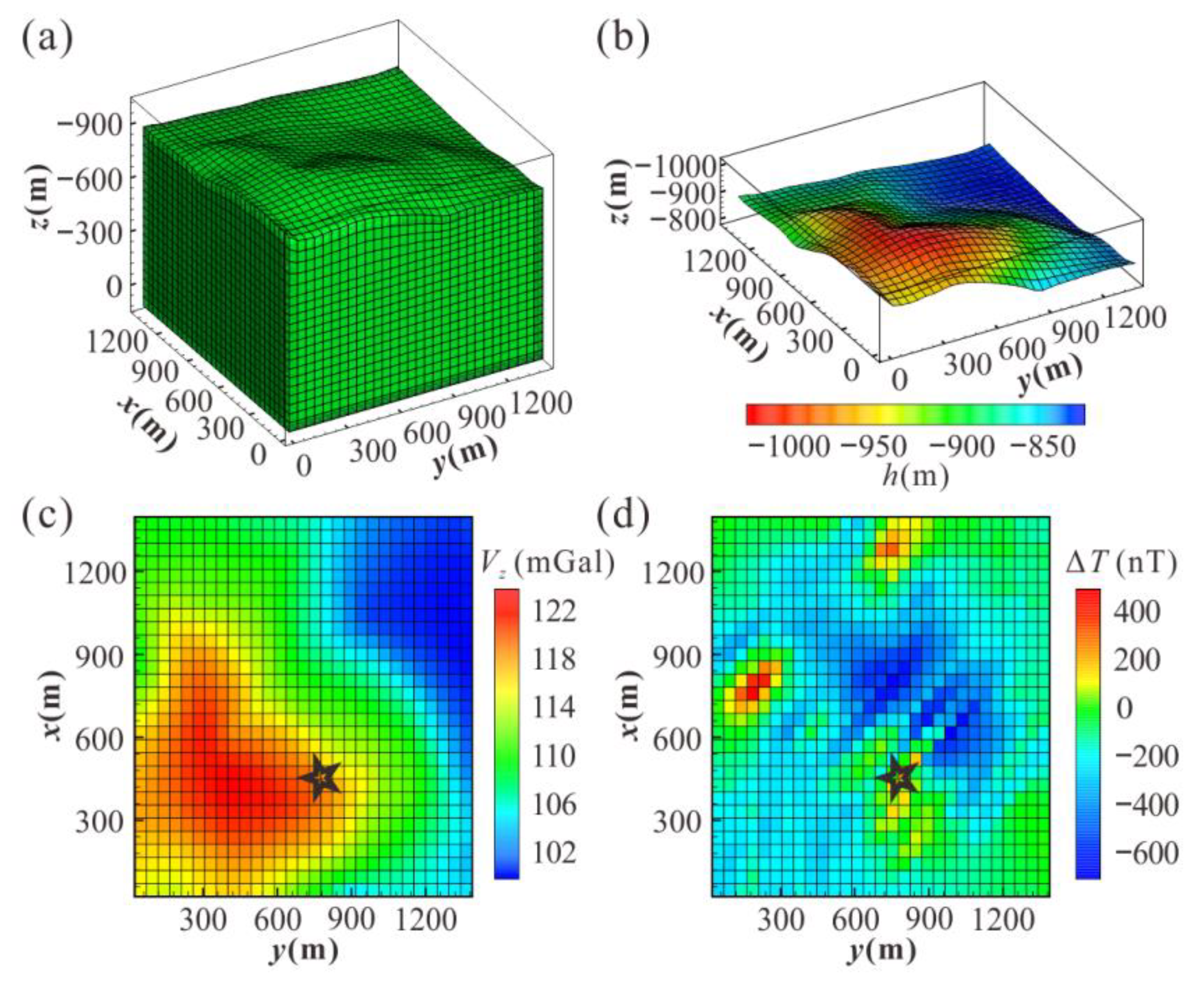
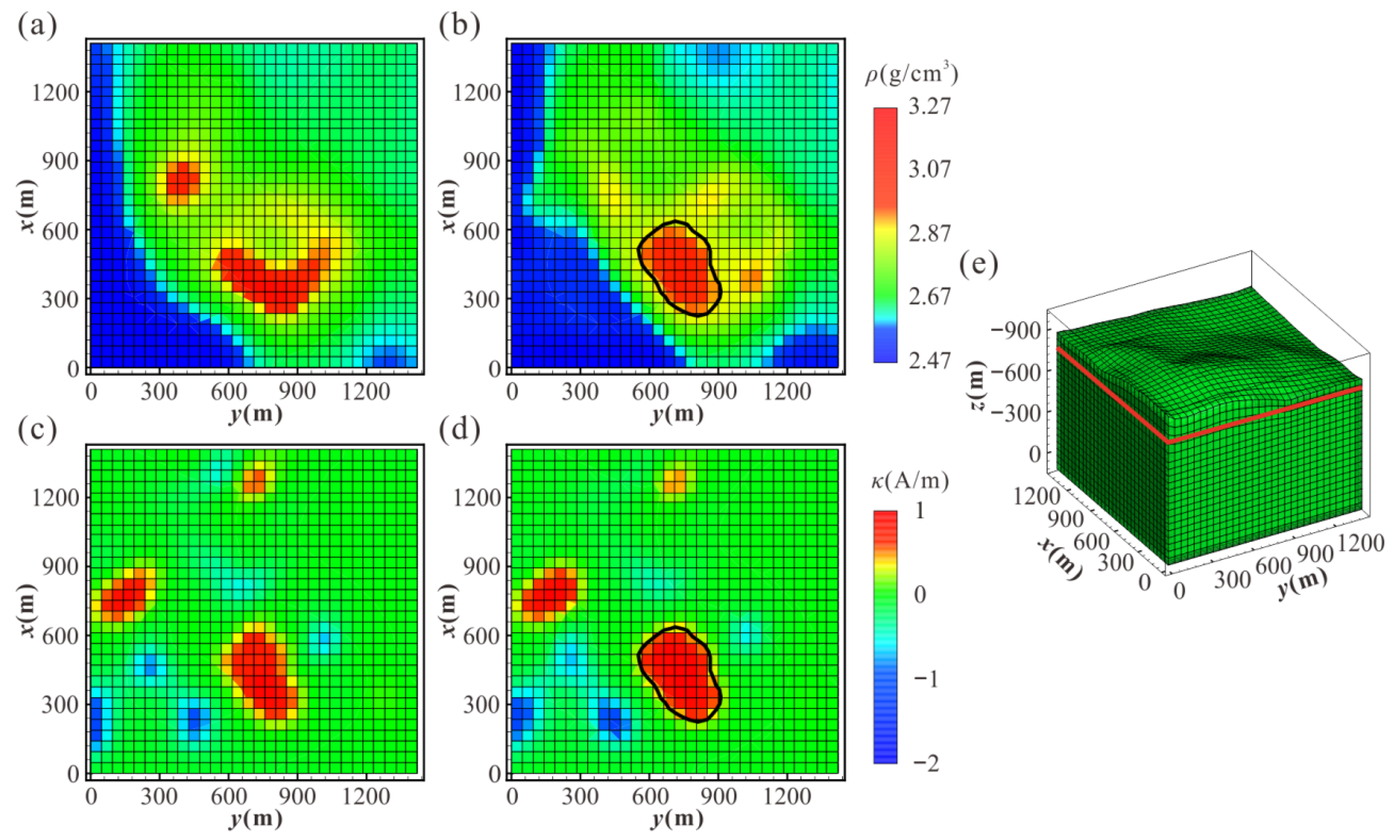
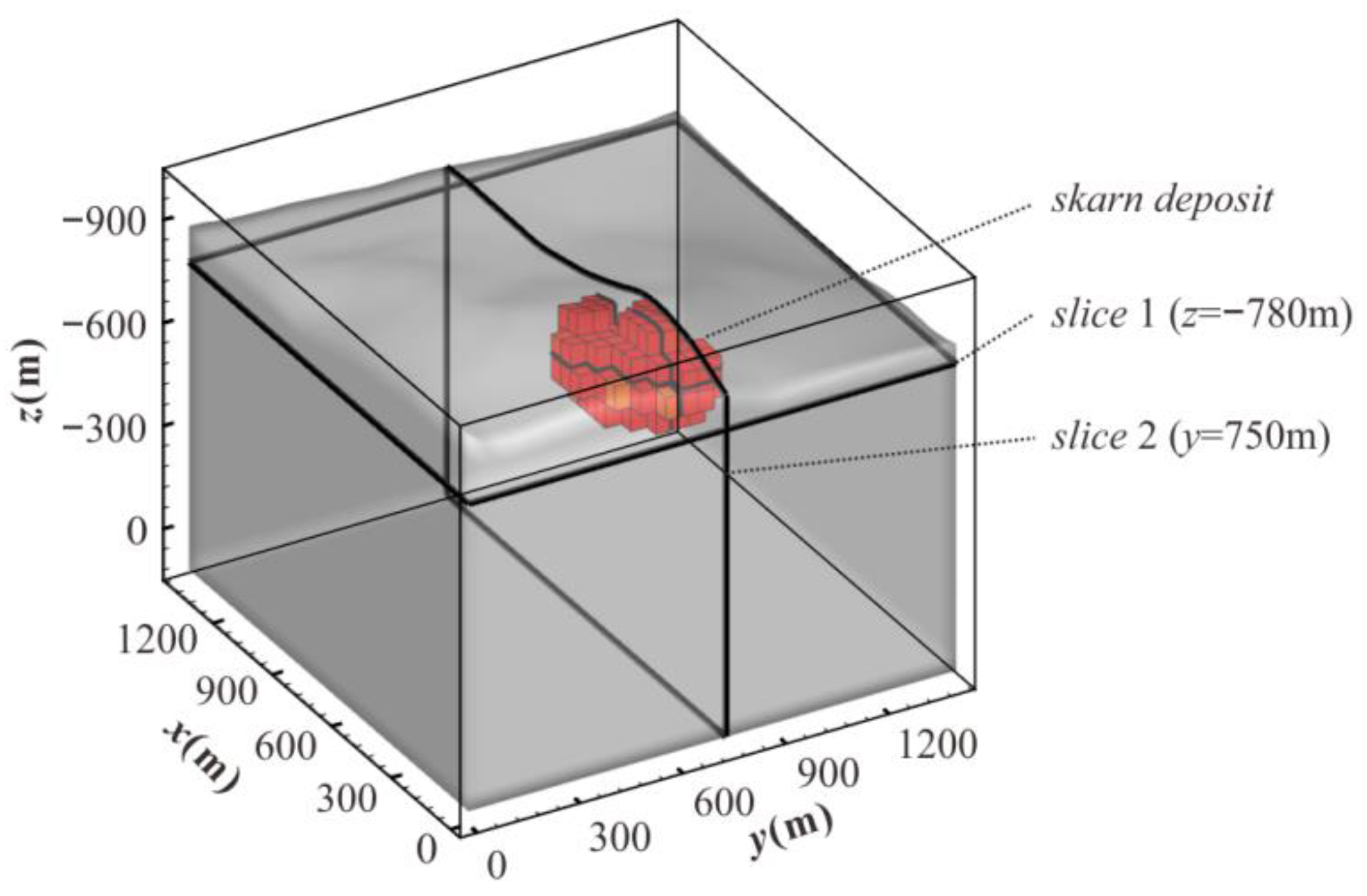
3.5. Real Data Application
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Okabe, M. Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translations into magnetic anomalies. Geophysics 1979, 44, 730–741. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. Forward modeling of gravity data using finite-volume and finite-element methods on unstructured grids. Geophysics 2013, 78, G69–G80. [Google Scholar] [CrossRef]
- Jahandari, H.; Bihlo, A.; Donzelli, F. Forward modelling of gravity data on unstructured grids using an adaptive mimetic finite-difference method. J. Appl. Geophys. 2021, 190, 104340. [Google Scholar] [CrossRef]
- Meng, Q.F.; Ma, G.Q.; Wang, T.H.; Xiong, S.Q. The Efficient 3D Gravity Focusing Density Inversion Based on Preconditioned JFNK Method under Undulating Terrain: A Case Study from Huayangchuan, Shaanxi Province, China. Minerals 2020, 10, 741. [Google Scholar] [CrossRef]
- Carrillo, J.; Perez, F.; Marco, A.; Gallardo, L.A.; Schill, E. Joint inversion of gravity and magnetic data using correspondence maps with application to geothermal fields. Geophys. J. Int. 2022, 228, 1621–1636. [Google Scholar] [CrossRef]
- Bosch, M.; Meza, R.; Jimenez, R.; Hoenig, A. Joint gravity and magnetic inversion in 3D using Monte Carlo methods. Geophysics 2006, 71, G153–G156. [Google Scholar] [CrossRef]
- Kamm, J.; Lundin, I.A.; Bastani, M.; Sadeghi, M.; Pedersen, L.B. Joint inversion of gravity, magnetic, and petrophysical data; a case study from a gabbro intrusion in Boden, Sweden. Geophysics 2015, 80, B131–B152. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Characterization of heterogeneous near-surface materials by joint 2D inversion of dc resistivity and seismic data. Geophys. Res. Lett. 2003, 30, 1658. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints. J. Geophys. Res. Solid Earth 2004, 109, B03311-n/a. [Google Scholar] [CrossRef]
- Pak, Y.C.; Li, T.L.; Kim, G.S. 2D data-space cross-gradient joint inversion of MT, gravity and magnetic data. J. Appl. Geophys. 2017, 143, 212–222. [Google Scholar] [CrossRef]
- Shi, Z.J.; Hobbs, R.W.; Moorkamp, M.; Tian, G.; Jiang, L. 3-D cross-gradient joint inversion of seismic refraction and DC resistivity data. J. Appl. Geophys. 2017, 141, 54–67. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, H.J. An efficient sequential strategy for realizing cross-gradient joint inversion; method and its application to 2-D cross borehole seismic traveltime and DC resistivity tomography. Geophys. J. Int. 2018, 213, 1044–1055. [Google Scholar] [CrossRef]
- Fregoso, E.; Gallardo, L.A. Cross-gradients joint 3D inversion with applications to gravity and magnetic data. Geophysics 2009, 74, L31–L42. [Google Scholar] [CrossRef]
- Zhou, J.J.; Meng, X.H.; Guo, L.H.; Zhang, S. Three-dimensional cross-gradient joint inversion of gravity and normalized magnetic source strength data in the presence of remanent magnetization. J. Appl. Geophys. 2015, 119, 51–60. [Google Scholar] [CrossRef]
- Joulidehsar, F.; Moradzadeh, A.; Ardejani, F.D. An Improved 3D Joint Inversion Method of Potential Field Data Using Cross-Gradient Constraint and LSQR Method. Pure Appl. Geophys. 2018, 175, 4389–4409. [Google Scholar] [CrossRef]
- Zhang, R.Z.; Li, T.L.; Liu, C.; Huang, X.G.; Jensen, K.; Sommer, M. 3-D Joint Inversion of Gravity and Magnetic Data Using Data-Space and Truncated Gauss-Newton Methods. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Tavakoli, M.; Nejati Kalateh, A.; Rezaie, M.; Gross, L.; Fedi, M. Sequential joint inversion of gravity and magnetic data via the cross-gradient constraint. Geophys. Prospect. 2021, 69, 1542–1559. [Google Scholar] [CrossRef]
- Vatankhah, S.; Liu, S.; Renaut, R.A.; Hu, X.Y.; Hogue, J.D.; Gharloghi, M. An Efficient Alternating Algorithm for the L-Norm Cross-Gradient Joint Inversion of Gravity and Magnetic Data Using the 2-D Fast Fourier Transform. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Ozyildirim, O.; Demirci, I.; Gundogdu, N.Y.; Candansayar, M.E. Two dimensional joint inversion of direct current resistivity and radiomagnetotelluric data based on unstructured mesh. J. Appl. Geophys. 2020, 172, 103885. [Google Scholar] [CrossRef]
- Lelievre, P.G.; Farquharson, C.G.; Hurich, C.A. Joint inversion of seismic traveltimes and gravity data on unstructured grids with application to mineral exploration. Geophysics 2012, 77, K1–K15. [Google Scholar] [CrossRef]
- Jordi, C.; Doetsch, J.; Guenther, T.; Schmelzbach, C.; Maurer, H.; Robertsson, J.O.A. Structural joint inversion on irregular meshes. Geophys. J. Int. 2020, 220, 1995–2008. [Google Scholar] [CrossRef]
- Yin, C.C.; Sun, S.Y.; Gao, X.H.; Liu, Y.H.; Chen, H. 3D joint inversion of magnetotelluric and gravity data based on local correlation constraints. Acta Geophys. Sin. 2018, 61, 358–367. [Google Scholar] [CrossRef]
- Lelievre, P.G.; Farquharson, C.G. Gradient and smoothness regularization operators for geophysical inversion on unstructured meshes. Geophys. J. Int. 2013, 195, 330–341. [Google Scholar] [CrossRef]
- Mehanee, S.; Golubev, N.; Zhdanov, M.S. Weighted regularized inversion of magnetotelluric data. SEG Annu. Meet. Expand. Tech. Program Abstr. Biogr. 1998, 68, 481–484. [Google Scholar]
- Li, Y.; Oldenburg, D.W. Joint inversion of surface and three-component borehole magnetic data. Geophysics 2000, 65, 540–552. [Google Scholar] [CrossRef]
- Kim, K.; Hu, X.Y.; Cho, G.; Nam, M.; Kang, J.; Kim, G.; Liu, H. Study on isoparametric finite-element integral algorithm of gravity and magnetic anomaly for a body with complex shape. Shiyou Diqiu Wuli Kantan 2009, 44, 231–239. [Google Scholar]
- Nagy, D. The gravitational attraction of a right rectangular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Bhattacharyya, B.K. Magnetic anomalies due to prism-shaped bodies with arbitrary polarization. Geophysics 1964, 29, 517–531. [Google Scholar] [CrossRef]
- Last, B.J.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef]
- Sampietro, D.; Capponi, M. Practical tips for 3D regional gravity inversion. Geophysics 2019, 9, 351. [Google Scholar] [CrossRef]
- Li, S.P.; Li, T.L.; Zheng, J.; Chen, H.B.; Zhang, Z.Y. Application of 3D inversion of gravity magnetism electric method in upper mining area of Xiagalai Aoyi River. Glob. Geol. 2020, 39, 437–443. [Google Scholar]
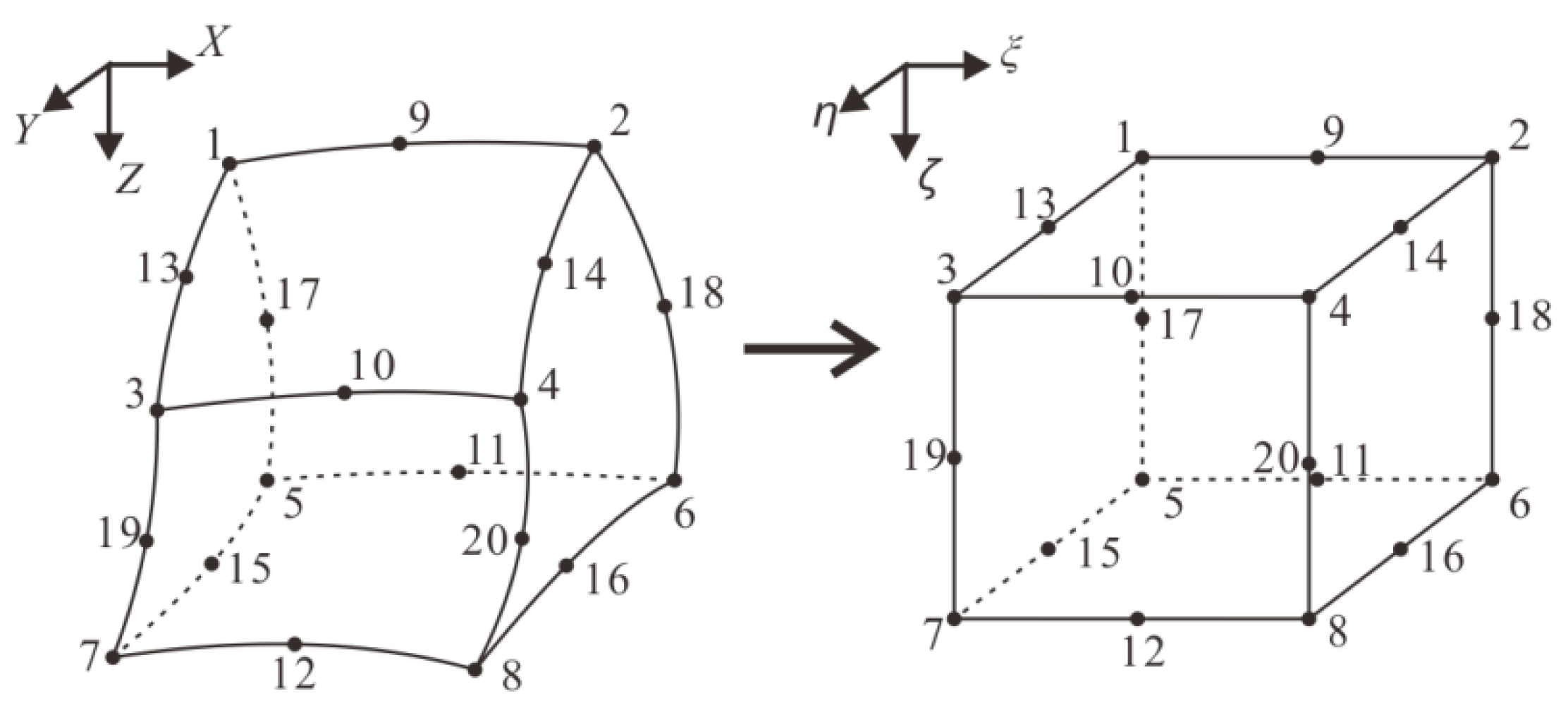




| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ξi | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | 0 | 0 | 0 | 0 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 |
| ηi | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | 1 | −1 | 1 | 0 | 0 | 0 | 0 | −1 | −1 | 1 | 1 |
| ζi | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Initial Model | Without Correction | With Correction | |
|---|---|---|---|
| RMSm_ρ | 18.03 | 19.10 | 14.49 |
| Initial Model | Separate Result (Tetrahedral) | Joint Result (Tetrahedral) | Separate Result (Combined Hexahedral) | Joint Result (Combined Hexahedral) | |
|---|---|---|---|---|---|
| RMSm_ρ | 16.83 | 12.38 | 11.99 | 12.78 | 11.51 |
| RMSm_κ | 20.47 | 13.36 | 13.36 | 13.03 | 13.03 |
| Real Model | Separate Result (Tetrahedral) | Joint Result (Tetrahedral) | Separate Result (Combined Hexahedral) | Joint Result (Combined Hexahedral) | |
|---|---|---|---|---|---|
| Pearson coefficient | 0.9687 | 0.8936 | 0.9420 | 0.8757 | 0.9577 |
| Tetrahedral Grid | Curved Hexahedral Grid | Combined Hexahedral Grid | |
|---|---|---|---|
| gravity (s) | 2.238 | 250.9 | 71.89 |
| magnetic (s) | 13.13 | 1160 | 329.1 |
| Tetrahedral Grid | Curved Hexahedral Grid | Combined Hexahedral Grid | |
|---|---|---|---|
| time cost (s) | 107.8 | 9.043 | 9.119 |
| Tetrahedral Grid | Curved Hexahedral Grid | Combined Hexahedral Grid | |
|---|---|---|---|
| time cost (s) | 525.5 | 1900 | 887.2 |
| Initial Model | Separate Inversion | Joint Inversion | |
|---|---|---|---|
| RMSm_ρ | 15.81 | 10.54 | 9.75 |
| RMSm_κ | 15.81 | 10.59 | 9.71 |
| Real Model | Separate Inversion | Joint Inversion | |
|---|---|---|---|
| Pearson coefficient | 1 | 0.9117 | 0.9908 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Li, T.; Zhang, R. Joint Inversion of 3D Gravity and Magnetic Data under Undulating Terrain Based on Combined Hexahedral Grid. Remote Sens. 2022, 14, 4651. https://doi.org/10.3390/rs14184651
He H, Li T, Zhang R. Joint Inversion of 3D Gravity and Magnetic Data under Undulating Terrain Based on Combined Hexahedral Grid. Remote Sensing. 2022; 14(18):4651. https://doi.org/10.3390/rs14184651
Chicago/Turabian StyleHe, Haoyuan, Tonglin Li, and Rongzhe Zhang. 2022. "Joint Inversion of 3D Gravity and Magnetic Data under Undulating Terrain Based on Combined Hexahedral Grid" Remote Sensing 14, no. 18: 4651. https://doi.org/10.3390/rs14184651
APA StyleHe, H., Li, T., & Zhang, R. (2022). Joint Inversion of 3D Gravity and Magnetic Data under Undulating Terrain Based on Combined Hexahedral Grid. Remote Sensing, 14(18), 4651. https://doi.org/10.3390/rs14184651