An Adversarial Generative Network Designed for High-Resolution Monocular Depth Estimation from 2D HiRISE Images of Mars
Abstract
1. Introduction
Is it possible to increase the resolution of the images by 4× and, at the same time, estimate a DTM, always by 4×, through a single end-to-end model?
Does a refinement learned from a low-resolution interpolated source during the training allow us to obtain better features?
Does using the GAN approach through the model proposal offer performance advantages over a classic generative architecture?
2. Data
2.1. Satellite Sources
2.2. The Dataset
2.3. Data Normalization
3. Methodology
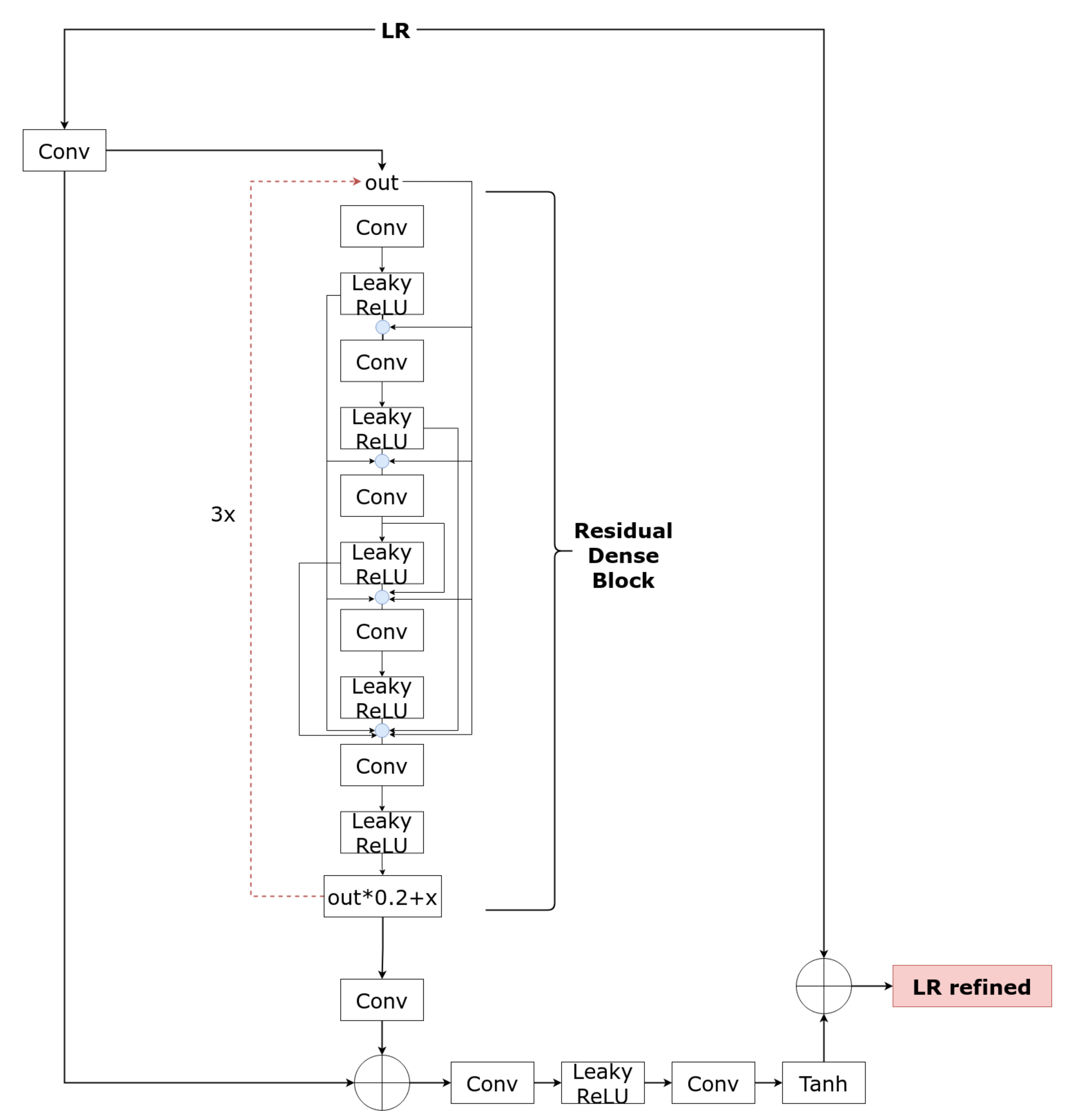
3.1. Refinement Learned Network
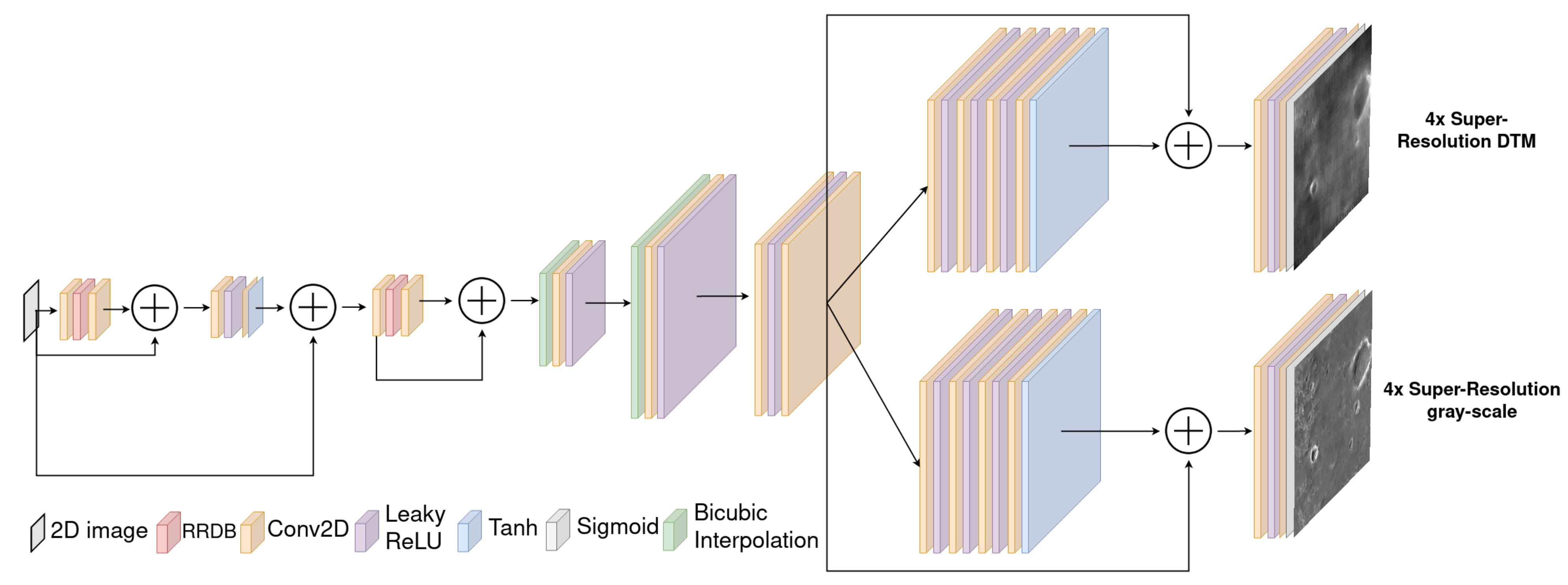
3.2. Generator Two Branches Network
4. Results
4.1. Quantitative Analysis
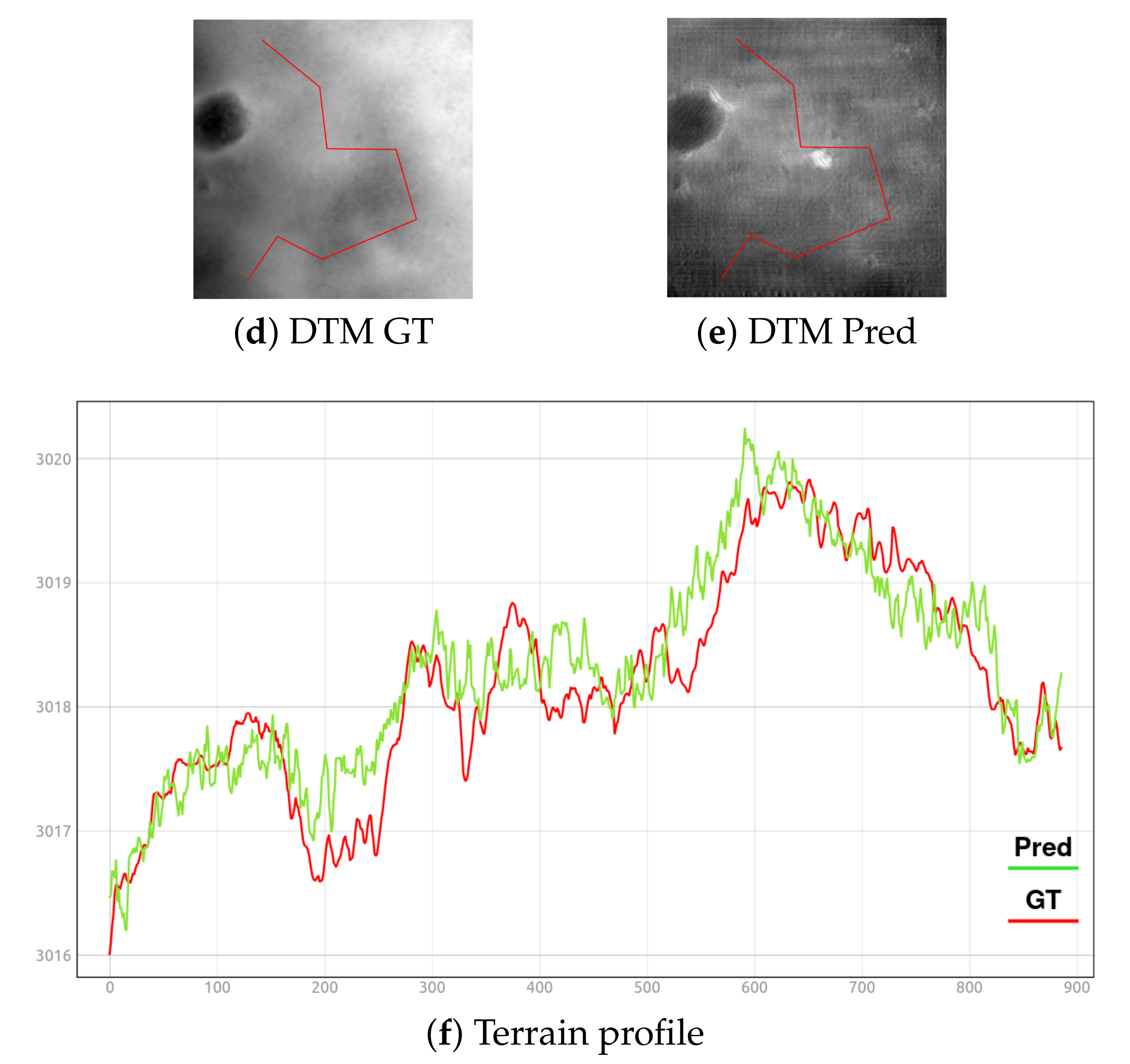
4.2. Science Case Study: Oxia Planum Site
Real Super-Resolution Experiment
4.3. Discussion
- Introduced a novel GAN model able to reproduce a super-resolution grey-scale image and predict DTM output by feeding into the network only a grey-scale source.
- Built sub-network that refines the interpolated grey-scale image (unsupervised approach) and feeds into a model that uses the GAN paradigm, taking advantage of the predicted super-resolution outputs.
- Improvements in terms of architectural design finalizing into two-branch models able to predict both super-resolution outputs (DTM and grey-scale).
- HiRISE dataset creation useful to train all models built.
- Quantitative/qualitative analysis of three model variations on HiRISE dataset and comparison with a monocular depth-estimation model known in the literature.
- Analysis on a scientific case study over the Oxia Planum site (ESA-selected landing site for a future mission).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, H.; Tang, X.; Shen, S. Depth-map completion for large indoor scene reconstruction. Pattern Recognit. 2020, 99, 107112. [Google Scholar] [CrossRef]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Förstner, W. A feature based correspondence algorithm for image matching. ISPRS ComIII Rovan. 1986, 150–166. [Google Scholar]
- Ackermann, F. Digital image correlation: Performance and potential application in photogrammetry. Photogramm. Rec. 1984, 11, 429–439. [Google Scholar] [CrossRef]
- Krystek, P. Fully automatic measurement of digital elevation models with MATCH-T. In Proceedings of the 43th Photogrammetric Week, Stuttgart, Germany, 9–14 September 1991; Institus für Photogrammetrie der Universität Stuttgart: Stuttgart, Germany, 1991; pp. 203–214. [Google Scholar]
- Simioni, E.; Re, C.; Mudric, T.; Cremonese, G.; Tulyakov, S.; Petrella, A.; Pommerol, A.; Thomas, N. 3DPD: A photogrammetric pipeline for a PUSH frame stereo cameras. Planet. Space Sci. 2021, 198, 105165. [Google Scholar] [CrossRef]
- Re, C.; Fennema, A.; Simioni, E.; Sutton, S.; Mège, D.; Gwinner, K.; Józefowicz, M.; Munaretto, G.; Pajola, M.; Petrella, A.; et al. CaSSIS-based stereo products for Mars after three years in orbit. Planet. Space Sci. 2022, 219, 105515. [Google Scholar] [CrossRef]
- Ming, Y.; Meng, X.; Fan, C.; Yu, H. Deep learning for monocular depth estimation: A review. Neurocomputing 2021, 438, 14–33. [Google Scholar] [CrossRef]
- Tao, Y.; Xiong, S.; Conway, S.J.; Muller, J.P.; Guimpier, A.; Fawdon, P.; Thomas, N.; Cremonese, G. Rapid Single Image-Based DTM Estimation from ExoMars TGO CaSSIS Images Using Generative Adversarial U-Nets. Remote Sens. 2021, 13, 2877. [Google Scholar] [CrossRef]
- Gwn Lore, K.; Reddy, K.; Giering, M.; Bernal, E.A. Generative adversarial networks for depth map estimation from RGB video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1177–1185. [Google Scholar]
- Tao, Y.; Muller, J.P.; Xiong, S.; Conway, S.J. MADNet 2.0: Pixel-Scale Topography Retrieval from Single-View Orbital Imagery of Mars Using Deep Learning. Remote Sens. 2021, 13, 4220. [Google Scholar] [CrossRef]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep ordinal regression network for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2002–2011. [Google Scholar]
- Bhat, S.F.; Alhashim, I.; Wonka, P. Adabins: Depth estimation using adaptive bins. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual Conference, 19–25 June 2021; pp. 4009–4018. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-esrgan: Training real-world blind super-resolution with pure synthetic data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1905–1914. [Google Scholar]
- Sun, W.; Chen, Z. Learned image downscaling for upscaling using content adaptive resampler. IEEE Trans. Image Process. 2020, 29, 4027–4040. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Ga, W.; Ahn, P.; Joo, D.; Chun, S.; Kim, J. Global-Local Path Networks for Monocular Depth Estimation with Vertical CutDepth. arXiv 2022, arXiv:2201.07436. [Google Scholar]
- McEwen, A.S.; Eliason, E.M.; Bergstrom, J.W.; Bridges, N.T.; Hansen, C.J.; Delamere, W.A.; Grant, J.A.; Gulick, V.C.; Herkenhoff, K.E.; Keszthelyi, L.; et al. Mars reconnaissance orbiter’s high resolution imaging science experiment (HiRISE). J. Geophys. Res. Planets 2007, 112. [Google Scholar] [CrossRef]
- HiRISE Repository. Available online: https://www.uahirise.org/dtm/ (accessed on 1 March 2022).
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization techniques in training dnns: Methodology, analysis and application. arXiv 2020, arXiv:2009.12836. [Google Scholar]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient backprop. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–48. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Aggarwal, A.; Mittal, M.; Battineni, G. Generative adversarial network: An overview of theory and applications. Int. J. Inf. Manag. Data Insights 2021, 1, 100004. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Source, H.O. HiRISE, Oxia Planum Site. Available online: https://www.uahirise.org/dtm/ESP_037070_1985 (accessed on 1 March 2022).
- La Grassa, R. Pytorch Code SRDiNet 2022. Available online: https://gitlab.com/riccardo2468/srdinet (accessed on 1 March 2022).






| Range (m) | Train Total Pixels | Percentage | Test Total Pixels | Percentage |
|---|---|---|---|---|
| (−7500; −6750] | 125,167,881 | 0.40% | 36,128,083 | 0.46 % |
| (−6750; −6000] | 402,230,537 | 1.27% | 98,323,693 | 1.25 % |
| (−6000; −5250] | 212,877,177 | 0.67% | 53,962,715 | 0.68 % |
| (−5250; −4500] | 1,638,429,900 | 5.19% | 380,020,058 | 4.82% |
| (−4500; −3750] | 4,373,169,629 | 13.86% | 1,108,666,596 | 14.06% |
| (−3750; −3000] | 4,249,001,383 | 13.47% | 1,056,827,070 | 13.41% |
| (−3000; −2250] | 4,455,583,194 | 14.12% | 1,131,272,379 | 14.35% |
| (−2250; −1500] | 4,086,800,593 | 12.95% | 1,014,990,398 | 12.88% |
| (−1500; −750] | 2,268,149,838 | 7.19% | 571,919,007 | 7.25% |
| (−750; 0] | 2,024,401,066 | 6.42% | 491,264,802 | 6.23% |
| (0; 750] | 1,963,805,715 | 6.22% | 480,032,232 | 6.09% |
| (750; 1500] | 2,664,539,777 | 8.45% | 674,413,972 | 8.56% |
| (1500; 2250] | 1,683,998,656 | 5.34% | 426,284,350 | 5.41% |
| (2250; 3000] | 504,330,832 | 1.60% | 136,542,305 | 1.73% |
| (3000; 3750] | 452,791,812 | 1.44% | 113,674,919 | 1.44% |
| (3750; 4500] | 274,299,407 | 0.87% | 70,333,088 | 0.89% |
| (4500; 5250] | 7,744,087 | 0.02% | 2,035,558 | 0.03% |
| (5250; 6000] | 32,818,301 | 0.10% | 6,395,581 | 0.08% |
| (6000; 6750] | 72,529,655 | 0.23% | 18,573,226 | 0.24% |
| (6750; 7500] | 55,574,528 | 0.18% | 11,534,336 | 0.15% |
| Model Type | RLNet | Generator | Discriminator |
|---|---|---|---|
| Model A | ✓ | ✓ | ✓ |
| Model B | ✓ | ✓ | |
| Model C | ✓ | ✓ |
| Metric (avg) | Model A | Model B | Model C |
|---|---|---|---|
| PSNR SR/HR ↑ | 25.400 | 26.456 | 25.689 |
| PSNR DTM SR/HR ↑ | 15.069 | 14.930 | 14.813 |
| RMSE SR/HR ↓ | 0.0567 | 0.0514 | 0.0552 |
| RMSE DTM SR/HR ↓ | 0.1859 | 0.1876 | 0.1903 |
| Absolute err. SR/HR ↓ | 0.0417 | 0.0371 | 0.0404 |
| Absolute err. DTM SR/HR ↓ | 0.1558 | 0.1574 | 0.1594 |
| s1 SR/HR ↑ | 0.9098 | 0.9233 | 0.9149 |
| s2 SR/HR ↑ | 0.9834 | 0.9853 | 0.9841 |
| s3 SR/HR ↑ | 0.9947 | 0.9951 | 0.9948 |
| s1 DTM SR/HR ↑ | 0.3967 | 0.3882 | 0.3834 |
| s2 DTM SR/HR ↑ | 0.6731 | 0.6697 | 0.6628 |
| s3 DTM SR/HR ↑ | 0.8208 | 0.8204 | 0.8158 |
| Metric (avg) | Model A | GLPDepth [17] |
|---|---|---|
| PSNR DTM SR/HR ↑ | 15.069 | 14.5610 |
| RMSE DTM SR/HR ↓ | 0.1859 | 0.2310 |
| Absolute err. DTM SR/HR ↓ | 0.1558 | 0.1590 |
| s1 DTM SR/HR ↑ | 0.3967 | 0.3729 |
| s2 DTM SR/HR ↑ | 0.6731 | 0.5907 |
| s3 DTM SR/HR ↑ | 0.8208 | 0.7312 |
| Range (m) | Model A | Model B | Model C |
|---|---|---|---|
| [−9000 −8200) | 0.1378 | 0.0621 | 0.1271 |
| [−8200 −7400) | 0.1531 | 0.0794 | 0.1499 |
| [−7400 −6600) | 0.1495 | 0.1012 | 0.1515 |
| [−6600 −5800) | 0.1501 | 0.1254 | 0.1524 |
| [−5800 −5000) | 0.1570 | 0.1434 | 0.1565 |
| [−5000 −4199.9) | 0.1607 | 0.1541 | 0.1609 |
| [−4199.9 −3399.9) | 0.1598 | 0.1593 | 0.1620 |
| [−3399.9 −2600) | 0.1588 | 0.1610 | 0.1621 |
| [−2600 −1800) | 0.1592 | 0.1619 | 0.1630 |
| [−1800 −1000) | 0.1605 | 0.1639 | 0.1652 |
| [−1000 −200) | 0.1635 | 0.1662 | 0.1685 |
| [−200 600) | 0.1672 | 0.1695 | 0.1715 |
| [600 1400) | 0.1706 | 0.1709 | 0.1745 |
| [1400 2200) | 0.1732 | 0.1673 | 0.1763 |
| [2200 3000) | 0.1749 | 0.1582 | 0.1775 |
| [3000 3800) | 0.1781 | 0.1437 | 0.1791 |
| [3800 4600) | 0.1817 | 0.1240 | 0.1817 |
| [4600 5400) | 0.1820 | 0.1015 | 0.1819 |
| [5400 6200) | 0.1609 | 0.0765 | 0.1785 |
| Metric (avg) | Model A | Model B | Model C | GLPDepth [17] |
|---|---|---|---|---|
| PSNR DTM SR/HR ↑ | 14.221 | 14.211 | 14.161 | 14.1184 |
| RMSE DTM SR/HR ↓ | 0.2011 | 0.2013 | 0.2026 | 0.2155 |
| Absolute err. DTM SR/HR ↓ | 0.1697 | 0.1700 | 0.1710 | 0.1787 |
| Model | Parameters (M) | GPUs | Batch-Size | Instances | Inference Time (s) |
|---|---|---|---|---|---|
| Model A/B | 15.35 | 4 | 4 | 500 | 246 |
| Model C | 12.39 | 4 | 4 | 500 | 218 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Grassa, R.; Gallo, I.; Re, C.; Cremonese, G.; Landro, N.; Pernechele, C.; Simioni, E.; Gatti, M. An Adversarial Generative Network Designed for High-Resolution Monocular Depth Estimation from 2D HiRISE Images of Mars. Remote Sens. 2022, 14, 4619. https://doi.org/10.3390/rs14184619
La Grassa R, Gallo I, Re C, Cremonese G, Landro N, Pernechele C, Simioni E, Gatti M. An Adversarial Generative Network Designed for High-Resolution Monocular Depth Estimation from 2D HiRISE Images of Mars. Remote Sensing. 2022; 14(18):4619. https://doi.org/10.3390/rs14184619
Chicago/Turabian StyleLa Grassa, Riccardo, Ignazio Gallo, Cristina Re, Gabriele Cremonese, Nicola Landro, Claudio Pernechele, Emanuele Simioni, and Mattia Gatti. 2022. "An Adversarial Generative Network Designed for High-Resolution Monocular Depth Estimation from 2D HiRISE Images of Mars" Remote Sensing 14, no. 18: 4619. https://doi.org/10.3390/rs14184619
APA StyleLa Grassa, R., Gallo, I., Re, C., Cremonese, G., Landro, N., Pernechele, C., Simioni, E., & Gatti, M. (2022). An Adversarial Generative Network Designed for High-Resolution Monocular Depth Estimation from 2D HiRISE Images of Mars. Remote Sensing, 14(18), 4619. https://doi.org/10.3390/rs14184619









