Study on the Impact of the Doppler Shift for CO2 Lidar Remote Sensing
Abstract
1. Introduction
2. Materials and Methods
2.1. Airborne Flight Overview
2.2. IPDA LIDAR Principle
2.3. Doppler Effect
3. Results
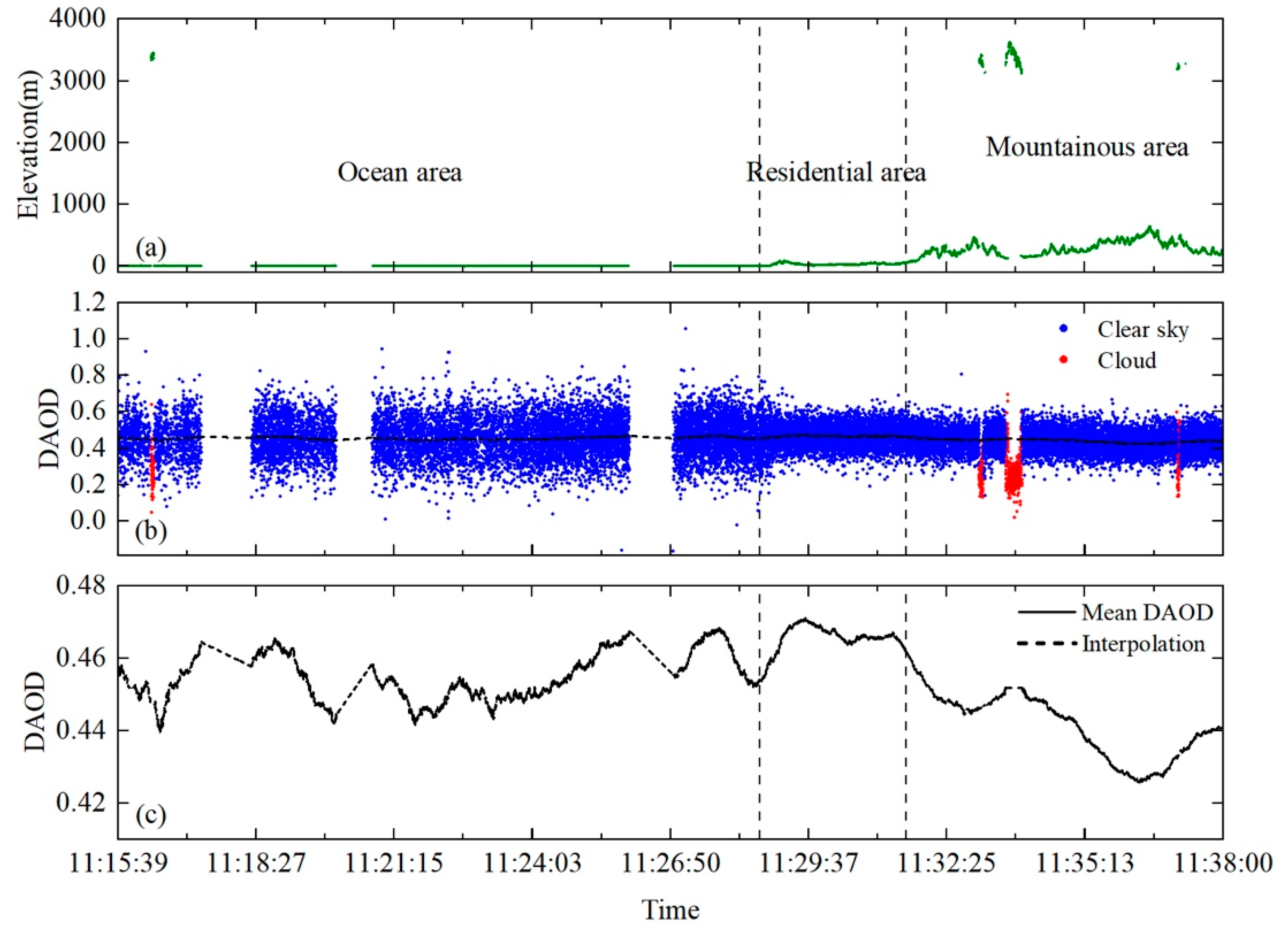
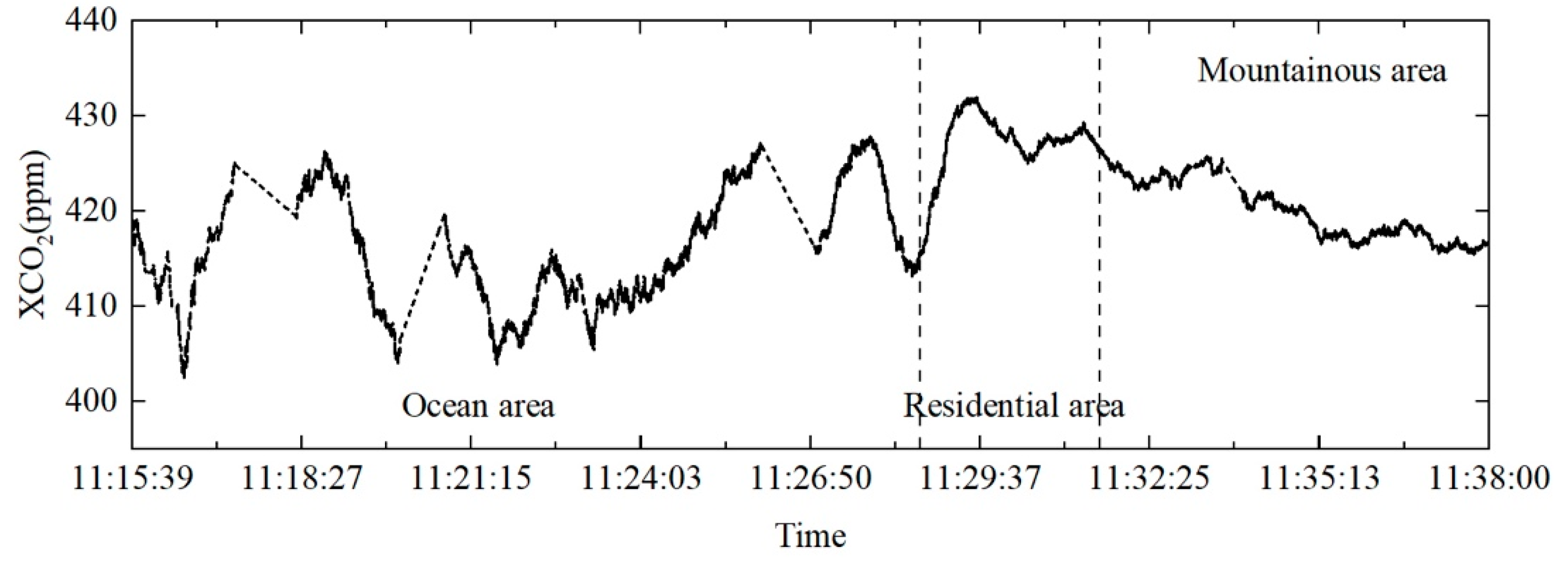
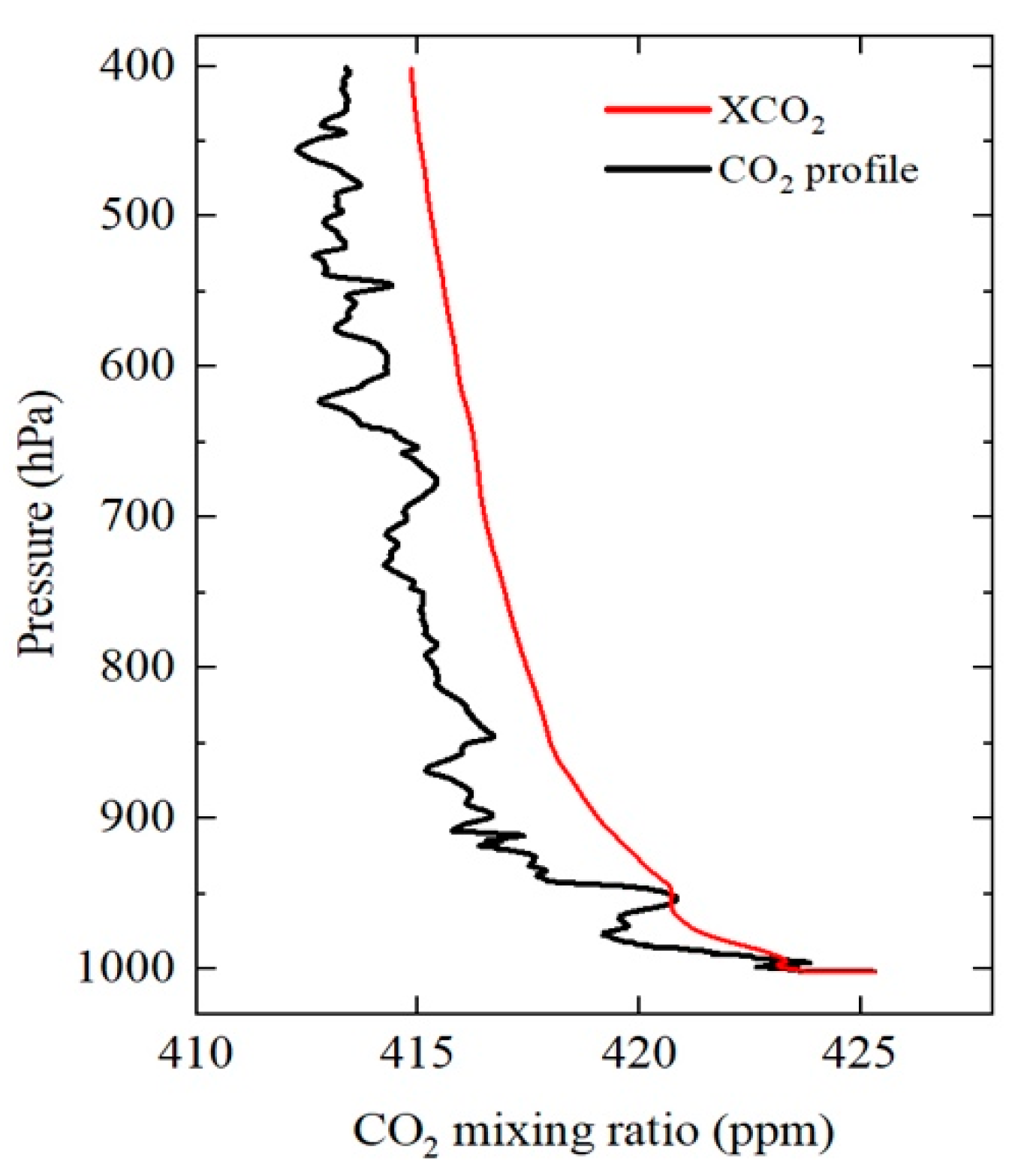
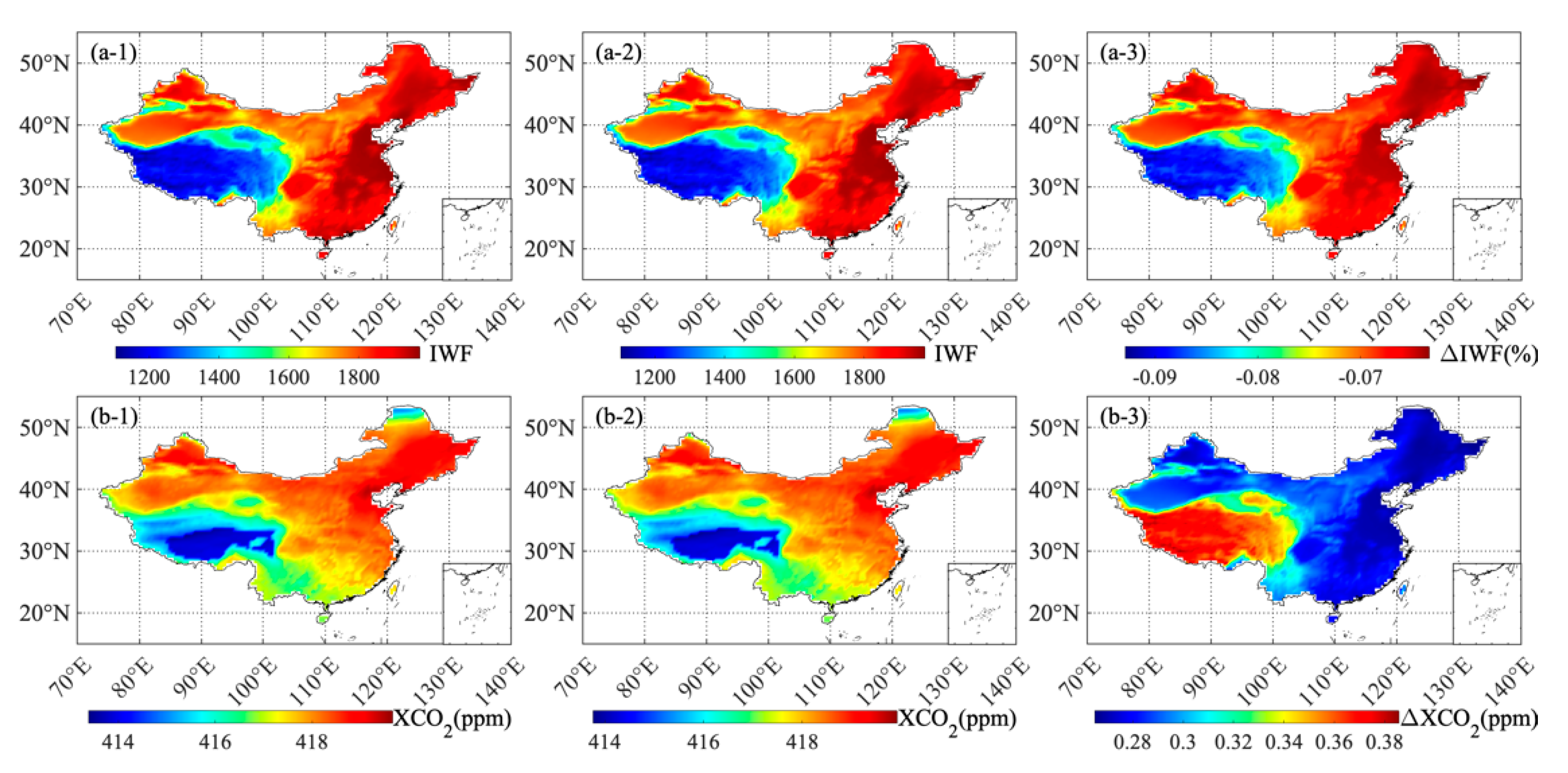
3.1. CO2 Retrieval Overview
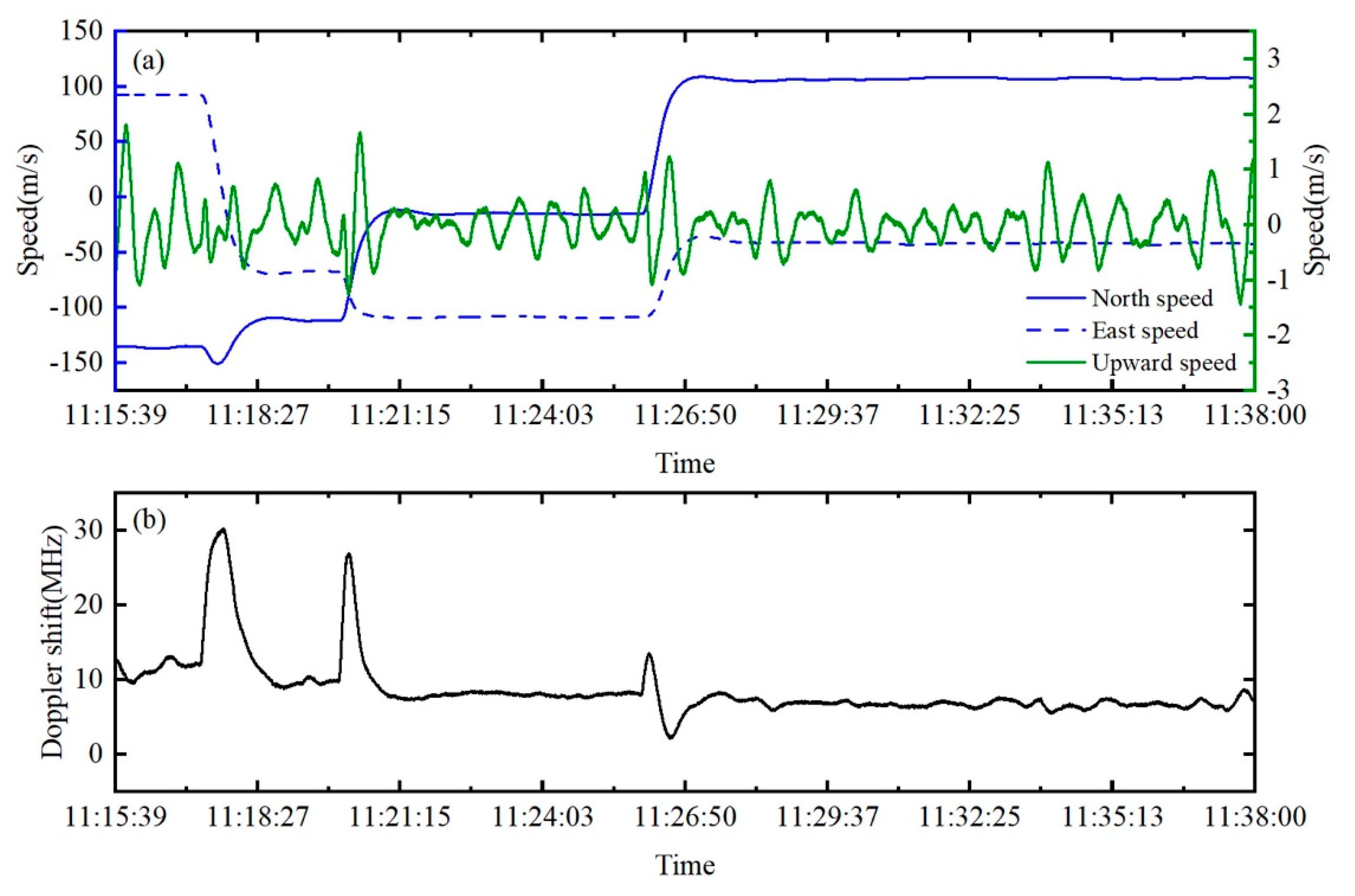
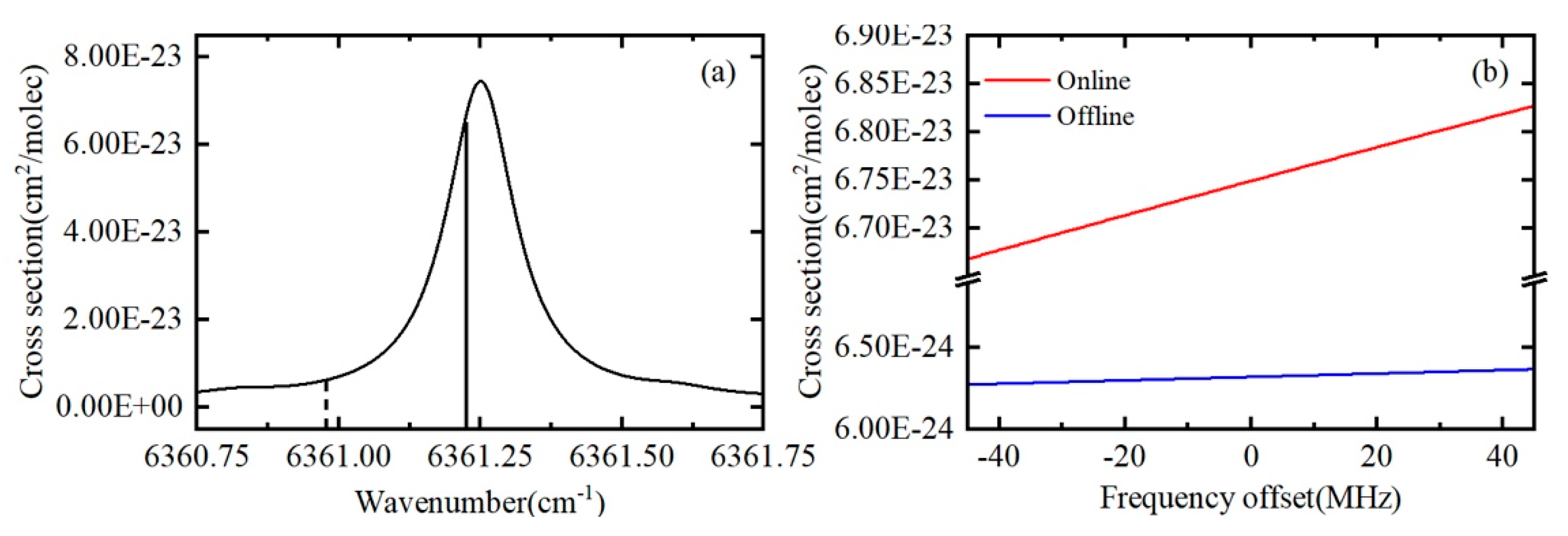
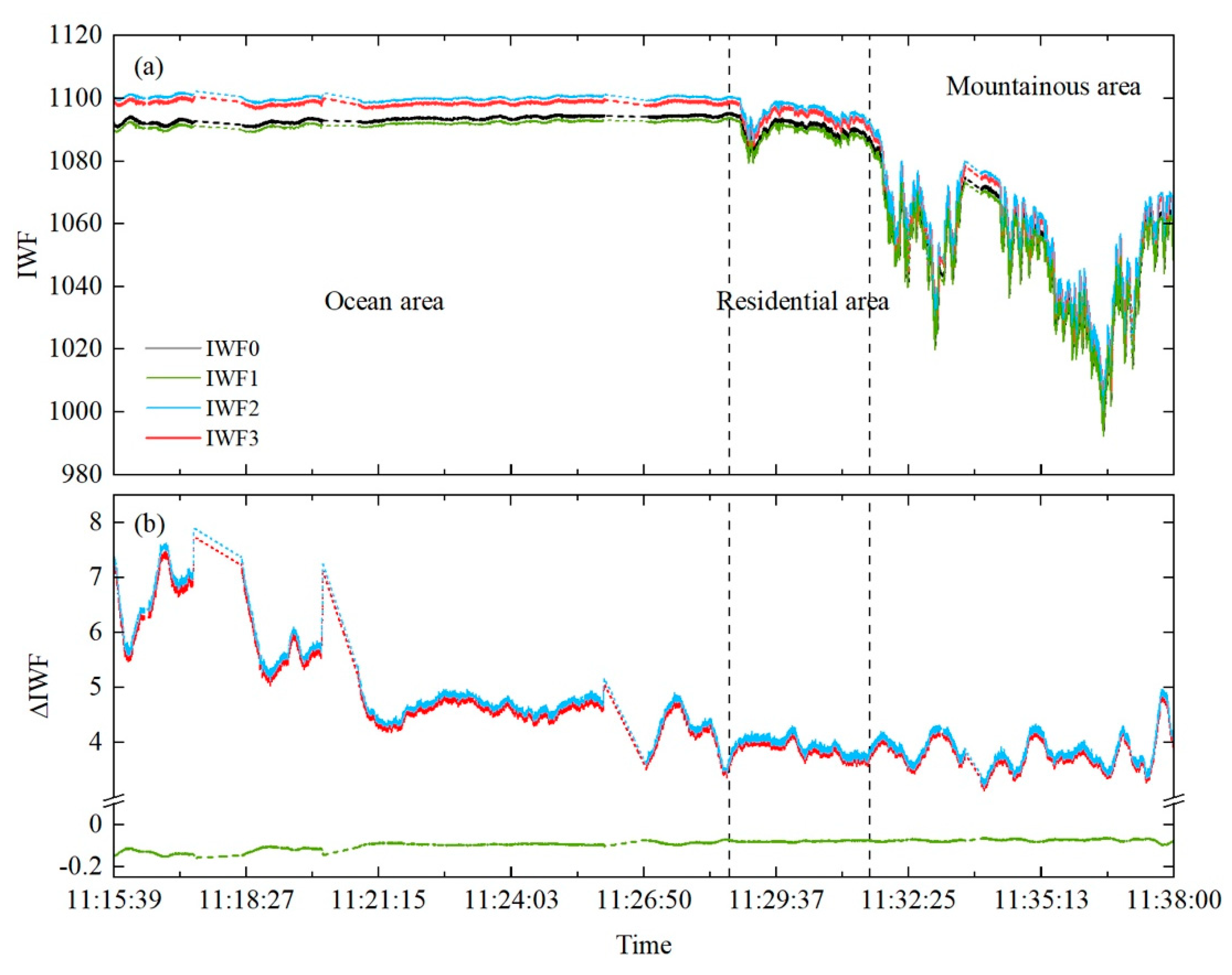
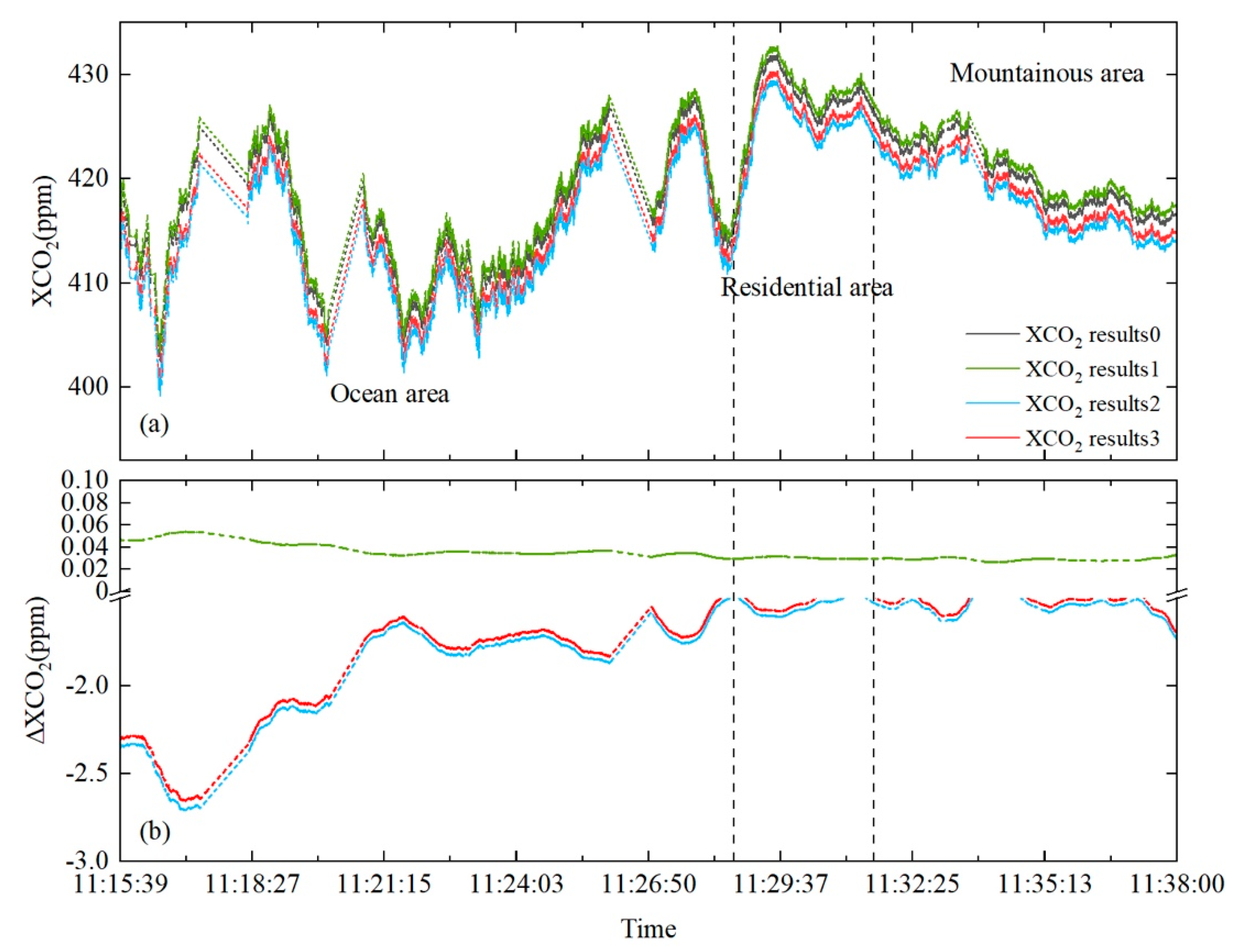
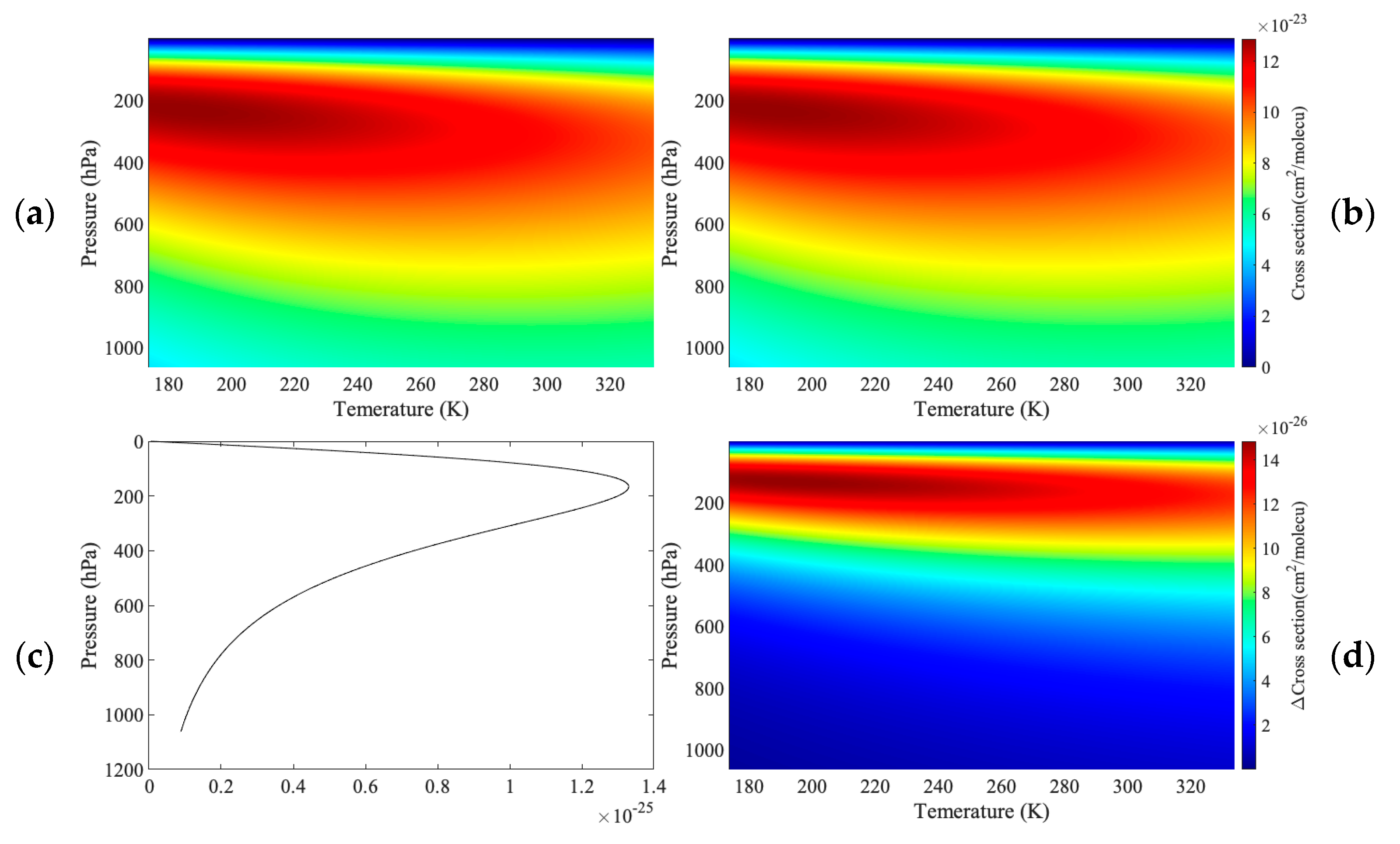
3.2. Impact of the Doppler Effect on Airborne Measurements
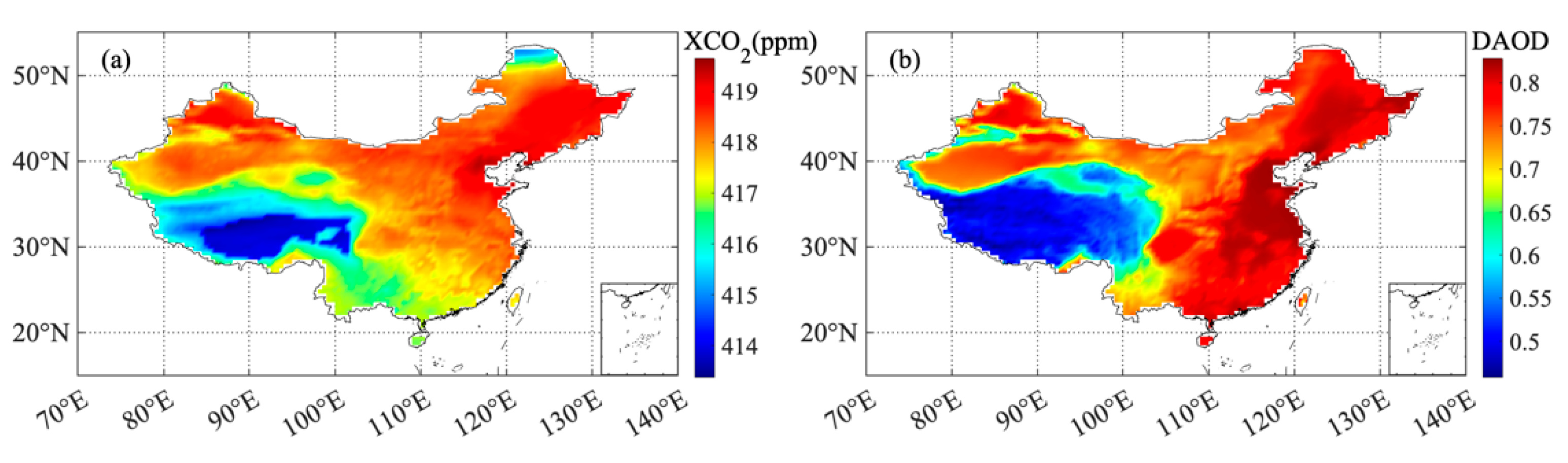
3.3. Impact of the Doppler Effect on Spaceborne Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Canadell, J.G.; Monteiro, P.M.; Costa, M.H.; Da Cunha, L.C.; Cox, P.M.; Alexey, V.; Henson, S.; Ishii, M.; Jaccard, S.; Koven, C. Global carbon and other biogeochemical cycles and feedbacks. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; United Nations Environment Programme: Nairobi, Kenya, 2021. [Google Scholar]
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M. Carbon and other biogeochemical cycles. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; pp. 465–570. [Google Scholar]
- Khalil, M. Non-CO2 greenhouse gases in the atmosphere. Annu. Rev. Environ. Resour. 1999, 24, 645. [Google Scholar] [CrossRef]
- Zhao, C.; Andrews, A.E.; Bianco, L.; Eluszkiewicz, J.; Hirsch, A.; MacDonald, C.; Nehrkorn, T.; Fischer, M.L. Atmospheric inverse estimates of methane emissions from Central California. J. Geophys. Res. Atmos. 2009, 114, D16302. [Google Scholar] [CrossRef]
- Montzka, S.A.; Dlugokencky, E.J.; Butler, J.H. Non-CO2 greenhouse gases and climate change. Nature 2011, 476, 43–50. [Google Scholar] [CrossRef]
- Jeong, S.; Zhao, C.; Andrews, A.E.; Bianco, L.; Wilczak, J.M.; Fischer, M.L. Seasonal variation of CH4 emissions from central California. J. Geophys. Res. Atmos. 2012, 117, D11306. [Google Scholar] [CrossRef]
- Jeong, S.; Zhao, C.; Andrews, A.E.; Dlugokencky, E.J.; Sweeney, C.; Bianco, L.; Wilczak, J.M.; Fischer, M.L. Seasonal variations in N2O emissions from central California. Geophys. Res. Lett. 2012, 39, L16805. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Z.-M.; Qiao, H.; Chen, B.; Hayat, T.; Alsaedi, A. China’s non-CO2 greenhouse gas emissions: Inventory and input–output analysis. Ecol. Inform. 2015, 26, 101–110. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Y.; Zhao, X.; Meng, J. Non-CO2 Greenhouse Gas Emissions in China 2012: Inventory and Supply Chain Analysis. Earth’s Future 2018, 6, 103–116. [Google Scholar] [CrossRef]
- Trends in Atmospheric Carbon Dioxide, National Oceanic and Atmospheric Administration, Earth System Research Laboratory (NOAA/ESRL). Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends/global.html (accessed on 25 October 2021).
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; et al. Global Carbon Budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Crevoisier, C.; Chédin, A.; Matsueda, H.; Machida, T.; Armante, R.; Scott, N.A. First year of upper tropospheric integrated content of CO2 from IASI hyperspectral infrared observations. Atmos. Chem. Phys. 2009, 9, 4797–4810. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Reuter, M.; Heymann, J.; Bovensmann, H.; Burrows, J.P. Long-term analysis of carbon dioxide and methane column-averaged mole fractions retrieved from SCIAMACHY. Atmos. Chem. Phys. 2011, 11, 2863–2880. [Google Scholar] [CrossRef]
- Crevoisier, C.; Heilliette, S.; Chédin, A.; Serrar, S.; Armante, R.; Scott, N.A. Midtropospheric CO2 concentration retrieval from AIRS observations in the tropics. Geophys. Res. Lett. 2004, 31, L17106. [Google Scholar] [CrossRef]
- Eldering, A.; Taylor, T.E.; O’Dell, C.W.; Pavlick, R. The OCO-3 mission: Measurement objectives and expected performance based on 1 year of simulated data. Atmos. Meas. Tech. 2019, 12, 2341–2370. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Feng, L.; Wang, J.; Yao, L.; Cai, Z.; Zhu, S.; Lu, N.; Lyu, D. The First Global Carbon Dioxide Flux Map Derived from TanSat Measurements. Adv. Atmos. Sci. 2021, 38, 1433–1443. [Google Scholar] [CrossRef]
- Kawa, S.R.; Abshire, J.B.; Baker, D.F.; Browell, E.V.; Crisp, D.; Crowell, S.M.; Hyon, J.J.; Jacob, J.C.; Jucks, K.W.; Lin, B. Active Sensing of CO2 Emissions over Nights, Days, and Seasons (ASCENDS): Final Report of the ASCENDS Ad Hoc Science Definition Team; NASA Technical Reports Server: Washington, DC, USA, 2018. [Google Scholar]
- Ingmann, P.; Bensi, P.; Durand, Y. Candidate Earth Explorer Core Missions–Reports for Assessment: A-SCOPE–Advanced Space Carbon and climate Observation of Planet Earth. ESA SP 2008, 1313. [Google Scholar]
- Amediek, A.; Fix, A.; Wirth, M.; Ehret, G. Development of an OPO system at 1.57 μm for integrated path DIAL measurement of atmospheric carbon dioxide. Appl. Phys. B 2008, 92, 295–302. [Google Scholar] [CrossRef]
- Amediek, A.; Fix, A.; Ehret, G.; Caron, J.; Durand, Y. Airborne lidar reflectance measurements at 1.57 μm in support of the A-SCOPE mission for atmospheric CO2. Atmos. Meas. Tech. 2009, 2, 755–772. [Google Scholar] [CrossRef]
- NRC. Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
- Jacob, J.; Spiers, G.D.; Menzies, R.T. Airborne Laser Absorption Spectrometer Measurements of Atmospheric CO2 Column Mole Fractions: Source and Sink Detection and Environmental Impacts on Retrievals. J. Atmos. Ocean. Technol. 2014, 31, 404–421. [Google Scholar] [CrossRef]
- Amediek, A.; Ehret, G.; Fix, A.; Wirth, M.; Budenbender, C.; Quatrevalet, M.; Kiemle, C.; Gerbig, C. CHARM-F-A new airborne integrated-path differential-absorption lidar for carbon dioxide and methane observations: Measurement performance and quantification of strong point source emissions. Appl. Opt. 2017, 56, 5182–5197. [Google Scholar] [CrossRef]
- Mao, J.; Ramanathan, A.; Abshire, J.B.; Kawa, S.R.; Riris, H.; Allan, G.R.; Rodriguez, M.; Hasselbrack, W.E.; Sun, X.; Numata, K.; et al. Measurement of atmospheric CO2 column concentrations to cloud tops with a pulsed multi-wavelength airborne lidar. Atmos. Meas. Tech. 2018, 11, 127–140. [Google Scholar] [CrossRef]
- Refaat, T.F.; Singh, U.N.; Yu, J.; Petros, M.; Remus, R.; Ismail, S. Double-pulse 2-μm integrated path differential absorption lidar airborne validation for atmospheric carbon dioxide measurement. Appl. Opt. 2016, 55, 4232–4246. [Google Scholar] [CrossRef]
- Spiers, G.D.; Menzies, R.T.; Jacob, J.; Christensen, L.E.; Phillips, M.W.; Choi, Y.; Browell, E.V. Atmospheric CO2 measurements with a 2 μm airborne laser absorption spectrometer employing coherent detection. Appl. Opt. 2011, 50, 2098–2111. [Google Scholar] [CrossRef] [PubMed]
- Abshire, J.B.; Ramanathan, A.K.; Riris, H.; Allan, G.R.; Sun, X.; Hasselbrack, W.E.; Mao, J.; Wu, S.; Chen, J.; Numata, K.; et al. Airborne measurements of CO2 column concentrations made with a pulsed IPDA lidar using a multiple-wavelength-locked laser and HgCdTe APD detector. Atmos. Meas. Tech. 2018, 11, 2001–2025. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, J.; Chen, X.; Zhu, X.; Zhang, J.; Li, S.; Sun, Y.; Hou, X.; Bi, D.; Bu, L.; et al. Airborne Validation Experiment of 1.57-μm Double-Pulse IPDA LIDAR for Atmospheric Carbon Dioxide Measurement. Remote Sens. 2020, 12, 1999. [Google Scholar] [CrossRef]
- Wang, Q.; Mustafa, F.; Bu, L.; Zhu, S.; Liu, J.; Chen, W. Atmospheric carbon dioxide measurement from aircraft and comparison with OCO-2 and CarbonTracker model data. Atmos. Meas. Tech. 2021, 14, 6601–6617. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, F.; Wang, W.; Huang, F.; Chen, B.; Gao, L.; Wang, S.; Yan, H.; Ye, H.; Si, F.; et al. The development and application of satellite remote sensing for atmospheric compositions in China. Atmos. Res. 2020, 245, 105056. [Google Scholar] [CrossRef]
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, CH4, and N2O by integrated path differential absorption lidar: A sensitivity analysis. Appl. Phys. B 2008, 90, 593–608. [Google Scholar] [CrossRef]
- Kiemle, C.; Quatrevalet, M.; Ehret, G.; Amediek, A.; Fix, A.; Wirth, M. Sensitivity studies for a space-based methane lidar mission. Atmos. Meas. Tech. 2011, 4, 2195–2211. [Google Scholar] [CrossRef]
- Zaccheo, T.S.; Pernini, T.; Snell, H.E.; Browell, E.V. Impact of atmospheric state uncertainties on retrieved XCO2 columns from laser differential absorption spectroscopy measurements. J. Appl. Remote Sens. 2014, 8, 083575. [Google Scholar] [CrossRef]
- Han, G.; Gong, W.; Lin, H.; Ma, X.; Xiang, Z. Study on Influences of Atmospheric Factors on Vertical CO2 Profile Retrieving From Ground-Based DIAL at 1.6 μm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3221–3234. [Google Scholar] [CrossRef]
- Zhu, Y. Research on Ground Verification Technology of Spaceborne CO2 Detection Lidar. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, June 2021. [Google Scholar]
- Yu, J.; Petros, M.; Singh, U.N.; Refaat, T.F.; Reithmaier, K.; Remus, R.G.; Johnson, W. An Airborne 2-μm Double-Pulsed Direct-Detection Lidar Instrument for Atmospheric CO2 Column Measurements. J. Atmos. Ocean. Technol. 2017, 34, 385–400. [Google Scholar] [CrossRef]
- Albrecht, H.-E.; Damaschke, N.; Borys, M.; Tropea, C. Laser Doppler and Phase Doppler Measurement Techniques; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Drain, L.E. The Laser Doppler Techniques; Wiley-Interscience: Chichester, UK, 1980. [Google Scholar]
- Ehret, G.; Bousquet, P.; Pierangelo, C.; Alpers, M.; Millet, B.; Abshire, J.; Bovensmann, H.; Burrows, J.; Chevallier, F.; Ciais, P.; et al. MERLIN: A French-German Space Lidar Mission Dedicated to Atmospheric Methane. Remote Sens. 2017, 9, 1052. [Google Scholar] [CrossRef]
- Tellier, Y.; Pierangelo, C.; Wirth, M.; Gibert, F.; Marnas, F. Averaging bias correction for the future space-borne methane IPDA lidar mission MERLIN. Atmos. Meas. Tech. 2018, 11, 5865–5884. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Zhang, L.; Zhang, X.; Yang, S.; Deng, Z.; Zhang, X.; Jiang, Y. Study on the Impact of the Doppler Shift for CO2 Lidar Remote Sensing. Remote Sens. 2022, 14, 4620. https://doi.org/10.3390/rs14184620
Cao X, Zhang L, Zhang X, Yang S, Deng Z, Zhang X, Jiang Y. Study on the Impact of the Doppler Shift for CO2 Lidar Remote Sensing. Remote Sensing. 2022; 14(18):4620. https://doi.org/10.3390/rs14184620
Chicago/Turabian StyleCao, Xifeng, Lu Zhang, Xingying Zhang, Sen Yang, Zhili Deng, Xin Zhang, and Yuhan Jiang. 2022. "Study on the Impact of the Doppler Shift for CO2 Lidar Remote Sensing" Remote Sensing 14, no. 18: 4620. https://doi.org/10.3390/rs14184620
APA StyleCao, X., Zhang, L., Zhang, X., Yang, S., Deng, Z., Zhang, X., & Jiang, Y. (2022). Study on the Impact of the Doppler Shift for CO2 Lidar Remote Sensing. Remote Sensing, 14(18), 4620. https://doi.org/10.3390/rs14184620




