Abstract
In transtensional regions, structures striking obliquely to the extension direction generally exhibit oblique or partitioned slips. However, their on-fault partitioning patterns and controlling factors are less known, hindering our understanding of the evolution of the rifting process. Here, we study the slip distribution of the 2021 Mw6.7 Lake Hovsgol (Mongolia) earthquake occurred in a pull-apart basin using InSAR observations. Our preferred slip model shows a remarkable feature, with three zones exhibiting distinct slip directions at different depths. The Coulomb stress change analysis reveals that this pattern is likely controlled by the left-lateral motion of the Mondy Fault to the north, which also inhibits the growth of a boundary fault to the east of the lake, shaping the asymmetric graben structure in this region. Our results imply the important role of major strike-slip faults bounding the pull-apart basin in the formation and evolution of the oblique rift.
1. Introduction
Pull-apart basins are topographic depressions due to the presence of the extension of two or more (en echelon) strike-slip fault systems and are bounded by diagonal transfer faults on their ends [1,2]. In a pull-apart basin, one common structure is a half graben bounded by a master normal fault on one side and a domain of hanging-wall beds dipping toward the master fault on the other side [3,4]. Accompanied by crustal thinning, a pull-apart basin may evolve into a rift zone [5,6]. During this process, oblique slips generally occur on the basin side at the ends of en echelon faults due to the transtensional movement [7], which is characterized by an irregular normal-slip fault at the basin margin [4,8,9]. Such irregular normal-slip faults play an important role in the formation and evolution of rift zones [10].
The Baikal Rift Zone (BRZ; [11]) is a SW–NE-oriented active rift in the Mongol-Siberian mountainous area (Figure 1). Previous studies proposed that the BRZ and its associated shear zone are related to both local sinistral shear and, on a larger scale, the far-field India–Eurasia collision in the Eocene time [12,13,14,15]. In the southwestern BRZ, the en echelon left-stepping, left-lateral strike-slip faults, including the Bolnay Fault (BF) in the south and the Mondy Fault (MF) in the north (Figure 1), foster a pull-apart tensional environment in northwestern Mongolia. Earthquakes with normal and strike-slip mechanisms prevail in this region ([16]; Figure 1a). The Hovsgol basin in the southwestern BRZ is oriented approximately perpendicular to the Tunga depression and the South Baikal basin ([17]). Formed in the Pliocene, it is a typical half graben bounded by the Hovsgol Fault system near the termination of the Mondy Fault [18,19,20]. Although historical earthquakes showed mixed mechanisms with a significant amount of rift-related normal slip surrounding Lake Hovsgol ([21,22]; Figure 1a), events with near-field observations are rare, hindering our understanding of the strain–release mechanism in the transtensional regime and its implication for the evolution of half-graben structures.
On 11 January 2021, an Mw6.7 earthquake shocked the Lake Hovsgol basin, which is the largest event that has been instrumentally recorded in this region. Aftershocks within two months after the mainshock distributed trending NW on the west bank of the lake (Figure 1a). Four months later, an Mw5.6 earthquake occurred nearby with a similar focal mechanism but at a greater depth (Table 1). Focal mechanisms proposed by the USGS, gCMT, and GFZ showed normal faulting with a significant strike-slip component (Table 1). The predominant double-couple component (~97% from the USGS) suggests that this event likely ruptured on a single fault plane. The field survey indicated that projections of the east-dipping nodal planes from different sources correlate well with the mapped old scarp of the Hovsgol Fault, yet with no primary coseismic surface rupture on the lake banks [23]. The results of joint inversion [24,25] using single-track InSAR and teleseismic data showed that the rupture fault was located between the West Range and the Doloon Uul Peninsula, oblique to the direction of maximum extension (Figure 1b). When the striking direction of the ruptured fault is oblique to the direction of maximum extension, fault-slip partitioning likely occurs [26]. Slip partitioning in oblique rifting is studied based on the inversion of seismic data [27], field-based observations [28], and stress analog modeling [29]. However, the relation between the fault slip distribution and regional stress regime is less investigated. The 2021 Mw6.7 Lake Hovsgol event provides a chance to probe the detailed slip distribution of an earthquake occurring near the termination of a major strike-slip fault that promotes the development of a pull-apart basin.

Table 1.
Source parameters of the 2021 Mw6.7 Hovsgol earthquake and the Mw5.6 aftershock from different sources.
Interferometric Synthetic Aperture Radar (InSAR) technology can provide high-resolution, near-field coseismic constraints to quantify fault geometry and slip distribution [30,31,32,33,34,35], especially in areas lacking seismological observations. The fault geometry and slip distribution of the 2021 Mw6.7 Lake Hovsgol earthquake were studied using Sentinel-1 InSAR data [24,25]. However, the published slip distribution models suffer from significant uncertainties due to the single-geometry constraint of InSAR, because the Sentinel-1 satellite only acquired descending images in this region. Specifically, Liu, G., et al. (2021) presented a strike-slip and dip-slip partitioning pattern [24], while Liu, X., et al. (2022) suggested a fault slip with a uniformly oblique slip [25]. The discrepancy in slip patterns hinders a deep discussion about the slip partitioning pattern and the mechanism behind it.
In this study, we obtain the additional ascending observations from the ALOS-2 satellite, which provide important constraints for the seismogenic fault geometry and slip distribution. The joining of InSAR observations using different geometries allows us to derive the east–west and vertical deformation across the seismogenic fault, leading to a better understanding of the faulting behavior of this event, for which the field investigation is difficult due to its inaccessibility. Moreover, to reveal the role of transform strike-slip faults in controlling the seismicity and tectonic evolution of the Lake Hovsgol pull-apart basin, we apply the Coulomb stress analysis based on the elastic dislocation model to a left-lateral strike-slip fault north of the epicenter region. Our in-depth analysis may shed new light on the understanding of oblique slip partitioning in transtensional regimes.
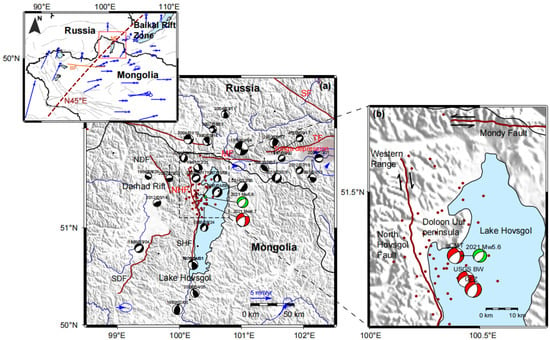
Figure 1.
Tectonic settings and historical earthquakes around the southwestern Baikal Rift Zone (BRZ). In the top-left plot, the red box shows the study area, while the blue arrows depict the GPS horizontal velocities with 95% confidence ellipses from [36]. The gray lines represent the active faults from [37], whereas the orange lines highlight the Mondy Fault (MF) and the Bolnay Fault (BF). (a) Map of the study area. The red and green beachballs display USGS-derived focal mechanisms of the 2021 Mw6.7 Lake Hovsgol and 2021 Mw5.6 earthquakes, respectively. The black beachballs indicate instances of historical seismicity from previous studies [38,39,40,41]. The dark red dots show aftershock locations according to the USGS within two months after the Mw6.7 earthquake. The dark red lines depict active faults in the southwestern BRZ. The main active faults in this region include the North Hovsgol Fault (NHF), South Hovsgol Fault (SHF), North Darhad Fault (NDF), South Darhad Fault (SDF), Tunga Fault (TF), and Sayan Fault (SF). (b) Enlarged view of the dashed black box in (a) showing the northern Lake Hovsgol with focal mechanisms of the Mw6.7 event from different sources.
2. Materials and Methods
2.1. Deformation Measurement
We collected SAR data from ascending ALOS-2 (AT555 and AT966) and descending Sentinel-1 (DT04) tracks covering the earthquake area (see Table 2 for information about InSAR data) to derive the coseismic surface deformation of the 2021 Mw6.7 earthquake. The pair of C-band Sentinel-1 images was acquired using the Terrain Observation by Progressive Scan (TOPS) technique and processed by the Sentinel-1 Interferometry Processor [42]. The primary and secondary Single Look Complexes (SLCs) were at first co-registered using a geometric approach with precise orbit ephemerides and the DEM from Shuttle Radar Topography Mission (SRTM; [43]). Then, an interferogram of each imaging burst was formed with its topographic component removed using the same DEM. Furthermore, all the interferograms were multilooked by a factor of 23 in range and 6 in azimuth, resulting in a ground pixel size of ~90 m, and were filtered using Goldstein interferogram filtering with a window size of 32 to further improve the signal-to-noise ratio (SNR) of the interferogram [44]. The ALOS-2 images were coregistered using a similar geometric method, and interferograms were also multilooked to a ~90 m ground resolution. We did not perform atmospheric correction; instead, we carried out linear trend removal using the integrated function in Geodetic Bayesian Inversion Software (GBIS; [45]). Finally, the interferograms were unwrapped using Statistical-Cost, Network-Flow Algorithm for Phase Unwrapping software (SNAPHU; [46]). Before the inversion, the ascending and descending deformations were downsampled using the quadtree decomposition algorithm [47], resulting in 6854 and 3655 data points for ascending and descending tracks, respectively.

Table 2.
Parameters of coseismic SAR images used for the 2021 Mw6.7 earthquake.
Due to the near-polar orbits of radar satellites, the InSAR observations are insensitive to the deformation in the north–south direction (Table 2). Therefore, we had to neglect the north–south deformation to derive the east–west and vertical deformation fields using SAR images from three independent tracks acquired by the ALOS-2 and Sentinel-1 satellites. The relationship between the east–west and vertical two-dimensional deformation and the satellite LOS deformation can be expressed as follows [48,49]:
where represents the line-of-sight deformation; and represent the surface deformation in the east–west and vertical directions, respectively; and represent the azimuth and incident angles of the satellite, respectively; subscript AT stands for ascending tracks (AT555 and AT966); and DT stands for descending track (DT04). Then, the 2D deformation fields were obtained using the least squares method [48,49,50]. The observation of the descending DT04 track from the Sentinel-1 satellite completely covered both the eastern and western regions of the lake, while the ascending observation from the ALOS-2 satellite covered the eastern (AT555) and western (AT966) regions of the lake, respectively. In the derivation of the 2D deformation field, we separated the observation of the descending orbit into the left and right sides of the lake, in order to avoid the rank deficiency of the matrix. The observation data were jointly inverted in the area where the coverages of these three orbits overlapped. We note that for an earthquake, the north–south coseismic deformation cannot be fully ignored, while for most cases, InSAR data can only be used to derive east–west and vertical deformation, unless pixel-offset tracking can be applied to constrain large north–south deformation [51,52,53]. For the 2021 Mw6.7 Lake Hovsgol earthquake, the surface deformation is clearly too small to be measured via pixel offset tracking. Therefore, other independent observations that are sensitive to the north–south direction would have to be required to better constrain the deformation decomposition if available.
2.2. Inversion of Fault Geometry and Slip Distribution
We adopted a two-step procedure to obtain the optimal fault geometry and slip distribution [47]. Based on the aftershock distribution, geological information, and InSAR deformation field, we inferred that the most likely ruptured fault of this event was the NW–SE trending NHF. With a fixed fault location, we searched for the model parameters using Geodetic Bayesian Inversion Software [45]. To obtain the coseismic slip distribution, we extended the fault plane to 50 km × 30 km in the strike and dip directions, respectively, and discretized it into patches with a size of 2 km × 2 km. We inverted for the slip distribution using the steepest descent method [54]. To quantitatively evaluate the data fitness, the dimensionless misfit was calculated according to [55], considering the data covariance matrix.
2.3. Coulomb Failure Stress Change
The major left-lateral strike-slip fault system, the Bolnay Fault (BF), and the Mondy Fault (MF) (Figure 1), play an important role in the formation and evolution of the pull-apart tensional environment. However, as the BF is ~340 km away from the NHF, posing insignificant stress changes to the NHF compared with the MF (Figure S1), we only focused on the role of the nearest Mondy Fault (MF) in affecting the observed slip partitioning pattern on the NHF, and we conducted simple dislocation modeling in an elastic half space [56,57] with constraints from field observations and historical earthquakes. We assumed a left-lateral slip of 1 m occurring on the EW-trending Mondy Fault from the surface down to a 30 km depth in accordance with the slip during the 1950 Mw6.9 Mondy event based on the empirical relation between slip and magnitude [58] as well as the GPS velocity at the Mondy station [36]. By doing so, we in fact assumed that the slip pattern of the 1950 earthquake represents the long-term motion of the Mondy Fault. Then, we calculated the effects of Coulomb, shear, and normal stress changes on the NHF due to slips on the Mondy Fault utilizing coulomb 3.3 software [59].
3. Results
3.1. Coseismic Deformation Mapping
Three interferograms from the descending Sentinel-1 and ascending ALOS-2 satellites covering the earthquake area were obtained to derive the surface deformation field of the 2021 Mw6.7 event (Figure 2). These interferograms consistently suggested a complex rupture rather than a simple normal-faulting event.
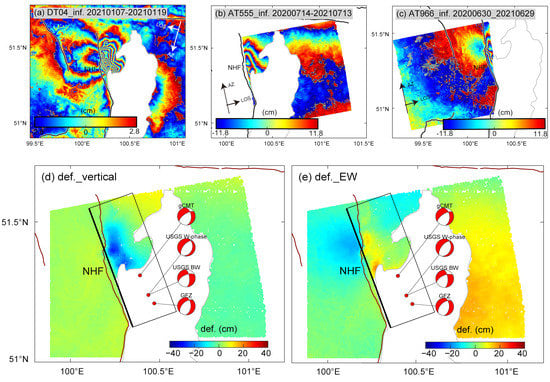
Figure 2.
Surface deformation associated with the 2021 Mw6.7 Lake Hovsgol earthquake obtained from Sentinel-1 and ALOS-2 SAR satellites. The water body was masked out manually. (a–c) Interferograms from descending Sentinel-1 (DT04) and ascending ALOS-2 (AT555 and AT966) tracks, respectively. Each fringe represents 2.8 cm for Sentinel-1 and 11.8 cm for ALOS-2 interferograms, respectively. (d,e) Vertical and east–west horizontal displacements computed using the observations in (a–c). The reddish color indicates the uplift/eastward movement, while bluish color is subsidence/westward movement. The black rectangle represents the surficial projection of our fault model. The beachballs display focal mechanisms of the Mw6.7 event from different institutions as indicated.
The descending Sentinel-1 interferogram captured the complete deformation field. A striking feature was that the dense fringes distributed northwest of Lake Hovsgol were separated by the North Hovsgol Fault (NHF). Particularly, east of the NHF, two distinct centers indicated that the whole area moved away from the satellite along the LOS direction, with the maximum deformation reaching ~0.21 m. South of these dense fringes, a slight slant-range shortening (~0.07 m) was distributed on both banks of Lake Hovsgol.
Two tracks of ascending ALOS-2 interferograms showed the deformation field resulted from the other geometry. The two deformation centers east of the NHF clearly indicated that this area also moved away from the ascending LOS direction (~0.26 m), suggesting subsidence. However, west of the NHF, an LOS lengthening of ~0.15 m could be identified, showing a different pattern from the descending interferogram. In addition, the east bank of Lake Hovsgol slightly moved away from the satellite, again in contrast with the descending observation, indicating that the deformation in these areas is dominated by horizontal movements.
Compared with previous studies [24,25], the combination of ascending and descending measurements provided us with an opportunity to derive the coseismic deformation in both the vertical and east–west directions (Figure 2d,e). The decomposition indicated that the dense fringes east of the NHF were a combination of subsidence (~0.4 m) and eastward movement (~0.15 m), while its west side was dominated by westward deformation (~0.16 m) without obvious vertical motion, reflecting the tensional feature of this event superimposed with local slips across the NHF.
3.2. Fault Geometry and Slip Distribution Model
The best-fitting fault plane followed the shallow NHF dipping ~53° to the northeast. The uniform slip model favored normal slip with a significant right-lateral strike-slip component (Table 3). Figure 3 shows the resulting slip distribution on our optimal fault plane. The model fitted the main features of the displacement field quite well (Figure 4), with a correlation coefficient of ~97%. The dimensionless misfits of the ascending and descending deformation fields were 1.2 and 0.8, respectively. The individual seismic moments attributed to the dip-slip and strike-slip components were 1.18 × 1019 N·m (corresponding to Mw6.68) and 5.76 × 1018 N·m (corresponding to Mw6.47), respectively, which meant that the accumulated transtensional stress was released at different crustal depths as dip and strike slips with a ratio of 2 between them. The estimated total seismic moment was 1.316 × 1019 N·m, corresponding to Mw6.71, which agreed with the previous solutions (Table 1).

Table 3.
The prior and initial values, maximum posterior probability solutions, and confidence intervals for our single fault model.
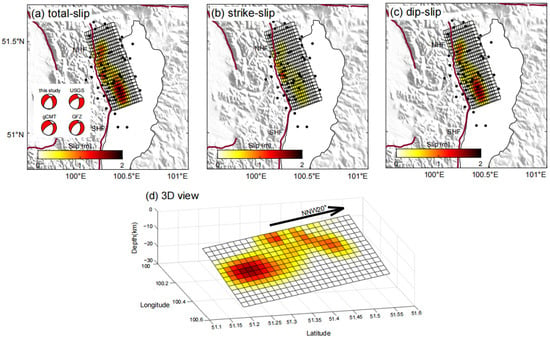
Figure 3.
Fault slip distribution of the preferred fault model. (a–c) Total, strike, and dip slips of the optimal fault model, respectively. The black dots represent aftershocks within 2 months after the mainshock. The beachballs in (a) display focal mechanisms of the Mw6.7 event from this study, USGS, Global CMT, and GFZ. (d) The 3D view of the fault slip distribution.
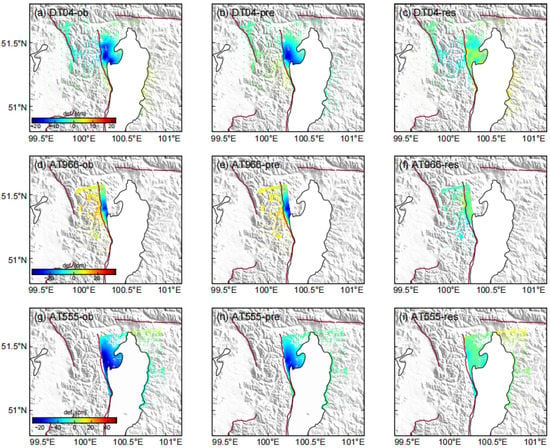
Figure 4.
Observed (a,d,g), predicted (b,e,h), and residual (c,f,i) maps based on our preferred model of tracks DT04, AT966, and AT555, respectively.
Overall, our slip model showed that the slip was partitioned into three areas at different depths on the fault plane with different mechanisms (Figure 3). Specifically, purely right-lateral slips were apparent at a shallow depth of 0–5 km bracketed by two oblique-slip patches below 5 km with a slip amount of ~1.5 m. The slips terminated at the two ends of the mapped NHF. Though complicated, the focal mechanism estimated from our slip distribution agreed with those from other institutions (beachballs in Figure 3a), supporting the observed slip partitioning pattern.
3.3. Stress Change Analysis
We calculated the Coulomb, shear, and normal stress changes in the NHF for dip-slip and strike-slip mechanisms due to slips on the Mondy Fault (Figure 5). When assuming a normal-faulting mechanism of the NHF, the Coulomb stress changes induced by the Mondy Fault were positive overall (Figure 5a,d), promoting normal slips as revealed in our slip model. However, assuming a right-lateral mechanism of the NHF, the positive Coulomb stress change only occurred in the middle section of the NHF, remarkably consistent with the distribution of a dextral strike-slip component (Figure 5b,e). Moreover, negative Coulomb stress changes appeared at two ends of the NHF, which may have prevented the propagation of the strike slip during the 2021 event. Therefore, the rupture pattern of the 2021 event was likely facilitated or even controlled by the slips on the Mondy Fault. In other words, the NHF accumulated transtensional strains non-uniformly, with a purely right-lateral shear strain at a shallow depth, which were released simultaneously during the 2021 Mw6.7 earthquake.
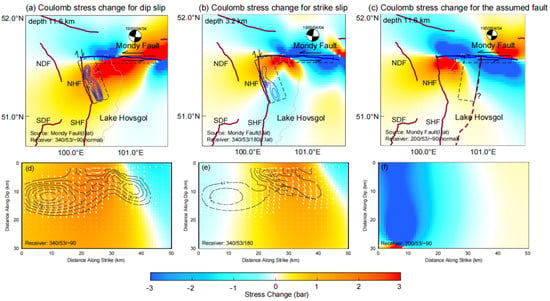
Figure 5.
Stress change analysis based on a simple dislocation model applied to the Mondy Fault, indicated by the blue line [24]. Warm (cold) color means facilitating (inhibiting) slips on the receiver faults. The beachball displays the focal mechanism of the 1950 Mw6.9 Mondy earthquake [39]. (a–c) Map views of the consequent Coulomb stress changes for purely dip and strike slips on the NHF and for normal slip on an assumed west-dipping fault east of Lake Hovsgol, respectively. For (a) and (b), the stress changes were calculated at the depths of 11.6 km and 3.2 km, respectively, where maximum dip and strike slips occurred in our slip model. The blue contours show the dip and strike slips, respectively. The depth for (c) is the same as in (a). The dark red dashed line represents the trace of the assumed west-dipping normal fault. The black rectangles represent the surface outlines of the source and receiver faults, respectively, with solid lines showing the upper boundaries. (d–f) Coulomb stress changes on the receiver fault planes as (a–c). The black contours show the coseismic dip and strike slips, respectively. The white arrows represent the slip directions of the fault patches depicted in Figure 3.
We also examined the effect of the Coulomb stress changes resulted from the motion of the Mondy Fault on a symmetrically oriented, west-dipping normal fault (dark red dashed line in Figure 5c) to the east of Lake Hovsgol. It was clear that the stress resulted from the motion of the Mondy Fault prevented a normal faulting on the assumed west-dipping fault, and the stress suppression was even stronger at greater depth (Figure 5c,f). We thus propose that the strike-slip Mondy Fault may inhibit the initiation and growth of a west-dipping normal fault east of Lake Hovsgol, thus shaping the half-graben structure.
Note that due to the inaccessibility of this region, different studies showed variant mapped traces of the Mondy Fault (Table 4). Reference [24] used the fault trace digitized from [36], while [25] used the data from the GEM Global Active Faults Database (GAF-DB; [37]). As for the uncertainties of faults mapped from field observations, we conducted three sets of Coulomb stress analysis based on the fault traces from [24] and GAF-DB [37] to determine the fault location that could best explain the stress effect of a major strike-slip fault on the boundary fault near its termination. Map views and profiles for the stress change on the NHF when utilizing our fault data (i.e., the middle and eastern segments of the MF from [24]) are displayed in Figure S2. Map views and profiles for the stress change on the NHF are presented in Figures S3 and S4 when utilizing the fault location from [24] and in Figures S5 and S6 when utilizing the fault location from GAF-DB. It was clear that when utilizing the middle and eastern segments of the MF from [24], the distribution of the stress changes matched best with the slip distribution. Granted, many other factors may have also led to the spatially partitioned slip pattern, such as frictional behavior (e.g., [60]), fault geometry (e.g., [61]), crustal heterogeneity (e.g., [4,62]), pre-existing asperity (e.g., [63]), and a deep-seated weak zone striking obliquely to the extension direction (e.g., [64,65]). Precisely determined fault geometry, slip rates, and paleo-stress analysis are needed to further quantify the transtensional strain for better understanding the fault development and structure evolution in actively transtensional regions. Nevertheless, the remarkable consistency of the Coulomb stress distribution with the coseismic slip pattern is hardly a coincidence and strongly suggests that the Mondy Fault plays an important role in the coseismic slip partitioning of the NHF.

Table 4.
Geometrical parameters of the Mondy Fault (MF) from different sources.
4. Discussion
The most prominent feature of the 2021 Mw6.7 Lake Hovsgol earthquake is the three asperities exhibiting distinct slip mechanisms at different depths on a single fault plane. It displays an interesting strain–release pattern starting from deep oblique slips in the south, drastically changing to the shallow right-lateral slips in the middle, and ending up in oblique slips at depth again in the north. Our slip model was consistent with the results derived from descending InSAR and teleseismic data [24] but revealed more details of the slip partitioning pattern, particularly in the northern part of the fault, thanks to the additional constraints from ascending InSAR observations. Note that according to the ascending ALOS-2 InSAR data spanning about half a year after the earthquake, the slip distribution may contain the influence from postseismic deformation such as that from afterslip or poroelastic rebound. To probe the magnitude of postseismic deformation, we processed a pair of descending Sentinel-1 interferograms spanning the period of 19 January 2021–31 January 2021, which showed no obvious afterslip signal (Figure S7). Moreover, the largest aftershock, the 2021 Mw5.6 event, occurred in the ALOS-2 ascending time span, yet it did not cause any obvious deformation in the ascending Sentinel-1 observations either (Table 5; Figure S8). Therefore, we suggest that the observed slip partitioning pattern is dominated by coseismic slips and that the influence from postseismic deformation is negligible.

Table 5.
Parameters of SAR images used for the 2021 Mw5.6 earthquake.
In transtensional regions, the accumulated strain can be released separately by normal and strike-slip events, such as the earthquakes that occurred in the Minto Flats Fault Zone in Central Alaska [66] and Lake Tahoe in the Sierra Nevada-Great Basin [67]; by an event with a uniformly oblique slip, such as the 2016 Mw5.9 Zaduo (Qinghai, China) earthquake [68]; or in the form of simultaneous ruptures of dip-slip and strike-slip motions in a multi-fault system, such as the 2016 Mw7.0 Kumamoto (Japan) earthquake [69] and the 2001 Mw7.8 Kokoxili (Qinghai, China) earthquake [70]. Note that in the third catalog, oblique motions are commonly partitioned into slips on two or more faults with different mechanisms [71], and the slip partitioning results from the elastoplastic upward propagation of an oblique slip at depth [70,72]. However, the 2021 Mw6.7 Lake Hovsgol event occurred on a boundary fault of the pull-apart basin with no obvious slip-partitioned surface break [23]. The co-existence of strike and normal slips on a single fault plane thus exhibits a different slip partitioning pattern.
Structures striking obliquely to the extension direction generally exhibit oblique slips or partitioned slips to compensate the accumulated stress (e.g., [26,73,74]). It is widely accepted that complex tectonic backgrounds and inhomogeneous stress fields in source regions lead to oblique slips during earthquakes on graben-boundary faults, which was observed in active oblique rift systems, e.g., [4,24,28,75,76,77]). Liu, G., et al. (2021) suggested that the reduced NS convergence across the Hovsgol basin may be attributed to normal faulting with a dextral strike-slip component in this region, consistent with the right-lateral strike slip seen on the ruptured fault [24]. However, the controlling factors of the specific slip pattern on the fault plane are still unknown.
To reveal the mechanism of dip and strike slips partitioning on a bending fault of the 2014 Northern Nagano (Japan) earthquake, Kobayashi et al. (2018) proposed that the shallow slip partitioning may be accounted for by the shear stress resulted from an oblique fault at depth. However, we did not have sufficient evidence indicating an oblique fault or detachment plane under the seismogenic fault in the Hovsgol basin. We instead investigated the stress distribution on the graben-boundary fault resulted from the major strike-slip fault. Our results revealed that shallow stress changes induced by the Mondy Fault contributed to the inhomogeneous shear and normal stress accumulation on the ruptured fault plane, fostering a slip partitioning. On the east coast of the lake, the stress resulted from the Mondy Fault inhibited the development of a west-dipping normal fault, consistent with the asymmetric graben structure of Lake Hovsgol. Our stress analysis suggested that the spatially partitioned slips on the graben-boundary fault could have resulted not only from the regional extension but also from the local stress change resulted from the adjacent, major strike-slip fault. A similar strain–release mode may occur in other transtensional regions with shallow strike slips, causing unexpected damage to pull-apart basins, which requires more attention in seismic hazard assessment.
5. Conclusions
The coseismic slip partitioning of right-lateral strike-slip and normal faulting was observed at distinct asperities on an east-dipping graben-boundary fault dipping ~53° to the northeast during the 2021 Mw6.7 Lake Hovsgol earthquake. The 2D deformation field derived using both ascending and descending observations revealed the maximum surface subsidence of ~0.4 m as well as an up to 0.15 m eastward movement east of the NHF, while westward deformation (~0.16 m) dominated the west side of the NHF. Based on a stress analysis, we inferred that left-lateral strike slips on the Mondy Fault to the north likely controlled the slip distribution of this event. The motion of the Mondy Fault also posed a restraining stress on the east boundary of Lake Hovsgol, facilitating the formation of the half-graben structure. The 2021 Mw6.7 Lake Hovsgol event thus represents an interesting case of slip partitioning on a single fault associated with an oblique pull-apart basin and highlights the non-negligible role of the shallow stress resulted from the boundary strike-slip fault. Our results have important implications for understanding the strain–release mechanism in oblique extensional tectonic settings and improving the assessment of geohazards.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14184553/s1, Figure S1: The shear stress change on NHF (black line) due to the Mondy Fault (MF, green line 2#) and Bolnay Fault (BF, green line 1#); Figure S2: The normal and shear stress change analyses for dip and strike slips on NHF based on the middle and eastern segment of Mondy Fault from Liu, G. et al. (2021) [24]. (a–d) Map views of normal and shear stress changes for purely dip and strike slips on the NHF caused by the MF at the depths of 11.6 km and 3.2 km, respectively, where maximum dip and strike slips occur in our slip model. Black rectangles represent the outlines of the NHF and MF, respectively, with solid lines showing the upper boundaries. The blue contours show the dip and strike slips, respectively. (e–h) are related stress change profiles of NHF fault plane based on the (a–d). The black contours show the dip and strike slips, respectively. The white arrows represent the slip directions of the fault patches depicted in Figure 3; Figure S3: The Coulomb (a,b), normal (c,d), and shear (e,f) stress change analyses for dip and strike slips on the NHF based on the Mondy Fault from Liu, G. et al. (2021) [24]. The stress changes are calculated at the depths of 11.6 km and 3.2 km, respectively, where the corresponding maximum dip and strike slips occur in our slip model. Blue line represents the fault location of Mondy Fault. Warm (cold) color means facilitating (inhibiting) slips on the receiver faults. Black rectangles show the surface projections of source (MF) and receiver (NHF) fault, respectively, with solid lines showing the upper boundaries; Figure S4: The Coulomb (a,b), normal (c,d), and shear (e,f) stress changes on the NHF fault plane according to Figure S3; Figure S5: The Coulomb (a,b), normal (c,d), and shear (e,f) stress change analyses for dip and strike slips on the NHF based on the Mondy Fault from GAF-DB. The stress changes are calculated at the depths of 11.6 km and 3.2 km, respectively, where the corresponding maximum dip and strike slips occurred in our slip model. The dark-red line represents the fault location of the Mondy Fault. Warm (cold) color means facilitating (inhibiting) slips on the receiver faults. Black rectangles show the surface projections of source (MF) and receiver (NHF) fault, respectively, with solid lines showing the upper boundaries; Figure S6: The Coulomb (a,b), normal (c,d), and shear (e,f) stress changes on the NHF fault plane according to Figure S5; Figure S7: Surface LOS deformation during the 19 January 2021–31 January 2021 obtained from Sentinel-1B SAR satellite; Figure S8: Surface LOS deformation associated with the 2021 Mw5.6 aftershock obtained from Sentinel-1B ascending orbit.
Author Contributions
Conceptualization, T.W.; methodology, Y.H.; software, Y.H.; validation, Y.H.; formal analysis, Y.H.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, T.W. and L.Z.; supervision, T.W. and L.Z.; funding acquisition, T.W. and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research study was funded by National Natural Science Foundation of China, grant Nos. U1939202 and 41974017.
Data Availability Statement
All data used in this study are open access. Sentinel-1 SAR images were copyrighted by the European Space Agency (ESA; https://scihub.copernicus.eu/dhus/) and processed with Sentinel-1 Interferometry Processor software (available at http://sarimggeodesy.github.io/software). The SAR images from ALOS-2 were downloaded from the Japan Aerospace Exploration Agency (JAXA; https://gportal.jaxa.jp/gpr/). Focal mechanism solutions came from the U.S. Geological Survey (USGS; https://earthquake.usgs.gov/earthquakes/map/), the Global Centroid Moment Tensor (Global CMT; https://www.globalcmt.org/CMTsearch.html), and the German Research Centre for Geosciences (GFZ; https://www.gfz-potsdam.de/en/). Figures were generated using Generic Mapping Tools 5.4.3 (http://www.soest.hawaii.edu/gmt/; [78]). The down-sampled InSAR observations and detailed fault slips are available at https://doi.org/10.5281/zenodo.6551945. All websites were last accessed on 23 July 2022.
Acknowledgments
The authors are grateful for insightful discussions with Heng Luo and Zhen Li from Peking University, China, and Taewook Kim from Kangwon National University, Korea.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rahe, B.; Ferrill, D.A.; Morris, A.P. Physical analog modeling of pull-apart basin evolution. Tectonophysics 1998, 285, 21–40. [Google Scholar] [CrossRef]
- Alper, G. Geometric characteristics of pull-apart basins. Lithosphere 2010, 2, 199–206. [Google Scholar]
- Groshong, R.H. Half-Graben Structures-Balanced Models of Extensional Fault-Bend Folds. Geol. Soc. Am. Bull. 1989, 101, 96–105. [Google Scholar] [CrossRef]
- Ring, U. The influence of preexisting structure on the evolution of the Cenozoic Malawi rift (East African rift system). Tectonics 1994, 13, 313–326. [Google Scholar] [CrossRef]
- Mann, P.J.; Hempton, M.R.; Bradley, D.C.; Burke, K.C. Development of Pull-Apart Basins. J. Geol. 1983, 91, 529–554. [Google Scholar] [CrossRef]
- Gartman, A.; Hein, J.R. Mineralization at Oceanic Transform Faults and Fracture Zones. In Transform Plate Boundaries and Fracture Zones; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Rodgers, D.A. Analysis of pull-apart basin development produced by en echelon strike-slip faults. Sediment. Obliq. Slip Mob. Zones 1980, 4, 27–41. [Google Scholar]
- Crowell, J.C. Origin of late cenozoic basins in southern california. Mod. Anc. Geosynclinal Sediment. 1974, 57, 190–204. [Google Scholar]
- Taghipour, K.; Khatib, M.M.; Heyhat, M.; Shabanian, E.; Vaezihir, A. Evidence for distributed active strike-slip faulting in NW Iran: The Maragheh and Salmas fault zones. Tectonophysics 2018, 742, 15–33. [Google Scholar] [CrossRef]
- Lavier, L.L.; Buck, W.R. Half graben versus large-offset low-angle normal fault: Importance of keeping cool during normal faulting. J. Geophys. Res. 2002, 107, 2122. [Google Scholar] [CrossRef]
- Seminsky, K.Z. Major factors of the evolution of basins and faults in the Baikal Rift Zone: Tectonophysical analysis. Geotecton 2009, 43, 486. [Google Scholar] [CrossRef]
- Tapponnier, P.; Molnar, P. Active Faulting and Tectonics in China. J. Geophys. Res. 1977, 82, 2905–2930. [Google Scholar] [CrossRef]
- Tapponnier, P.; Molnar, P. Active faulting and Cenozoic tectonics of the Tien Shan, Mongolia, and Baykal regions. J. Geophys. Res. 1979, 84, 3425–3459. [Google Scholar] [CrossRef]
- Hutchinson, D.R.; Golmshtok, A.J.; Zonenshain, L.P.; Moore, T.C.; Scholz, C.A.; Klitgord, K.D. Depositional and tectonic framework of the rift basins of Lake Baikal from multichannel seismic data. Geology 1992, 20, 589–592. [Google Scholar] [CrossRef]
- Mats, V.D. The structure and development of the Baikal rift depression. Earth-Sci. Rev. 1993, 34, 81–118. [Google Scholar] [CrossRef]
- Klyuchevskii, A.V.; Dem’yanovich, V.M. Stress-strain state of the lithosphere in the southern Baikal region and northern Mongolia from data on seismic moments of earthquakes. Izv.-Phys. Solid Earth 2006, 42, 416–428. [Google Scholar] [CrossRef]
- Krivonogov, S.K.; Safonova, I.Y. Basin structures and sediment accumulation in the Baikal Rift Zone: Implications for Cenozoic intracontinental processes in the Central Asian Orogenic Belt. Gondwana Res. 2017, 47, 267–290. [Google Scholar] [CrossRef]
- Zolotarev, A.G.; Kulakov, V.S.; Khilko, S.D. Khubsugul upland. Geomorphology of Mongolian People Republic. In Proceedings of the Join Soviet-Mongolian Scientific-Research Geological Expedition; Nauka: Moscow, Russia, 1982; Volume 28, pp. 109–122. (In Russian) [Google Scholar]
- Zorin, Y.A.; Tumtanov, E.K.; Arvisbaatar, N. Structure of Cenozoic basins of the Prekhubsugul region from gravity data. Geol. Geophys. 1989, 10, 130–136. (In Russian) [Google Scholar]
- Orkhonselenge, A.; Krivonogov, S.K.; Mino, K.; Kashiwaya, K.; Safonova, I.; Yamamoto, M.; Kashima, K.; Nakamura, T.; Kim, J. Holocene sedimentary records from Lake Borsog, eastern shore of Lake Khuvsgul, Mongolia, and their paleoenvironmental implications. Quat. Int. 2013, 290, 95–109. [Google Scholar] [CrossRef]
- Golenetsky, S.I.; Misharina, L.A. Seismicity and earthquake focal mechanisms in the Baikal rift zone. Tectonophysics 1978, 45, 71–85. [Google Scholar] [CrossRef]
- Demberel, S.; Klyuchevskii, A. Lithospheric stress in Mongolia, from earthquake source data. Geosci. Front. 2017, 8, 1323–1337. [Google Scholar]
- Battogtokh, D.; Bayasgalan, A.; Wang, K.; Ganzorig, D.; Bayaraa, J. The 2021 Mw 6.7 Khankh earthquake in the Khuvsgul rift, Mongolia. Mong. Geosci. 2021, 26, 46–61. [Google Scholar] [CrossRef]
- Liu, G.; Qiao, X.; Yu, P.; Zhou, Y.; Zhao, B.; Xiong, W. Rupture Kinematics of the 11 January 2021 Mw 6.7 Hovsgol, Mongolia, Earthquake and Implications in the Western Baikal Rift Zone, Seismol. Res. Lett. 2021, 92, 3318–3326. [Google Scholar] [CrossRef]
- Liu, X.; Xu, W.; Radziminovich, N.A.; Fang, N.; Xie, L. Transtensional coseismic fault slip of the 2021 Mw 6.7 Turt Earthquake and heterogeneous tectonic stress surrounding the Hovsgol Basin, Northwest Mongolia. Tectonophysics 2022, 836, 229407. [Google Scholar] [CrossRef]
- Philippon, M.; Willingshofer, E.; Sokoutis, D.; Corti, G.; Sani, F.; Bonini, M.; Cloetingh, S. Slip re-orientation in oblique rifts. Geology 2015, 42, 147–150. [Google Scholar] [CrossRef]
- Fanavoll, S.; Lippard, S.J. Possible oblique-slip faulting in the Skagerrak Graben, as interpreted from high resolution seismic data. Nor. Geol. Tidsskr. 1994, 74, 146–151. [Google Scholar]
- Rao, G.; He, C.; Cheng, Y.; Yu, Y.; Hu, J.; Chen, P.; Yao, Q. Active Normal Faulting along the Langshan Piedmont Fault, North China: Implications for Slip Partitioning in the Western Hetao Graben. J. Geol. 2018, 126, 99–118. [Google Scholar] [CrossRef]
- Brune, S. Evolution of stress and fault patterns in oblique rift systems: 3-D numerical lithosphericscale experiments from rift to breakup. Geochem. Geophys. Geosyst. 2014, 15, 3392–3415. [Google Scholar] [CrossRef]
- Elliott, J.R.; Walters, R.J.; Wright, T.J. The role of space-based observation in understanding and responding to active tectonics and earthquakes. Nat. Commun. 2016, 7, 13844. [Google Scholar] [CrossRef]
- Elliott, J.R.; Jolivet, R.; Gonzalez, P.J.; Avouac, J.P.; Hollingsworth, J.; Searle, M.P.; Stevens, V.L. Himalayan megathrust geometry and relation to topography revealed by the Gorkha earthquake. Nat. Geosci. 2016, 9, 174–180. [Google Scholar] [CrossRef]
- Daout, S.; Jolivet, R.; Lasserre, C.; Doin, M.; Barbot, S.; Tapponnier, P.E.; Peltzer, G.; Socquet, A.; Sun, J.F. Along-strike variations of the partitioning of convergence across the Haiyuan fault system detected by InSAR. Geophys. J. Int. 2016, 205, 536–547. [Google Scholar] [CrossRef]
- Wang, T.; Wei, S.J.; Jonsson, S. Coseismic displacements from SAR image offsets between different satellite sensors: Application to the 2001 Bhuj (India) earthquake. Geophys. Res. Lett. 2015, 42, 7022–7030. [Google Scholar] [CrossRef]
- Feng, G.; Hetland, E.A.; Ding, X.; Li, Z.; Zhang, L. Coseismic fault slip of the 2008 Mw 7.9 Wenchuan earthquake estimated from InSAR and GPS measurements. Geophys. Res. Lett. 2010, 37, L01302. [Google Scholar] [CrossRef]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Calais, É.; Vergnolle, M.; San’kov, V.; Lukhnev, A.V.; Miroshnitchenko, A.; Amarjargal, S.; Déverchère, J. GPS measurements of crustal deformation in the Baikal-Mongolia area (1994–2002): Implications for current kinematics of Asia. J. Geophys. Res. 2003, 108, 2501. [Google Scholar] [CrossRef]
- Styron, R.; Pagani, M. The GEM Global Active Faults Database. Earthq. Spectra 2020, 36 (Suppl. S1), 160–180. [Google Scholar] [CrossRef]
- Khilko, S.D.; Kurushin, R.A.; Kochetkov, V.M.; Misharina, L.A.; Melnikova, V.I.; Gileva, N.A.; Lastochkin, S.V.; Baljinnyam, I.; Monkhoo, D. Earthquakes and Principles of Seismic Zoning of Mongolia; Nauka: Moscow, Russia, 1985; 224p, (In Russian). Available online: http://refhub.elsevier.com/S0040-1951(22)00201-3/rf0100 (accessed on 21 January 2022).
- Delouis, B.; Deverchere, J.; Melnikova, V.; Radziminovitch, N.; Loncke, L.; Larroque, C.; Ritz, J.F.; San’kov, V. A reappraisal of the 1950 (Mw 6.9) Mondy earthquake, Siberia, and its relationship to the strain pattern at the south-western end of the Baikal rift zone. Terra Nova 2002, 14, 491–500. [Google Scholar] [CrossRef]
- Melnikova, V.; Gileva, N.A.; Arefyev, S.S.; Bykova, V.; Seredkina, A.I. The 27 August 2008, Mw = 6.3 Kultuk earthquake (South Baikal): The stress-strain state of the source area from the aftershock data. Izv. Phys. Solid Earth 2013, 49, 563–576. (In Russian) [Google Scholar] [CrossRef]
- Dobrynina, A.A.; Sankov, V.A.; Tcydypova, L.R.; German, V.I.; Chechelnitsky, V.V.; Ulzibat, M. Hovsgol earthquake 5 December 2014, MW = 4.9: Seismic and acoustic effects. J. Seismol. 2017, 22, 377–389. [Google Scholar] [CrossRef]
- Jiang, H.J.; Feng, G.C.; Wang, T.; Burgmann, R. Toward full exploitation of coherent and incoherent information in Sentinel-1 TOPS data for retrieving surface displacement: Application to the 2016 Kumamoto (Japan) earthquake, Geophys. Res. Lett. 2017, 44, 1758–1767. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Ro, E.C.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 361. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Bagnardi, M.; Hooper, A. Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: A Bayesian approach. Geochem. Geophy. Geosy. 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar] [CrossRef]
- Jonsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault slip distribution of the 1999 M-w 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Hector Mine earthquake, southern California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Liu, G.X.; Zhang, R.; Li, T.; Jia, H.G.; Nie, Y.J. Extracting 3D ground deformation velocity field by multi-platform persistent scatterer SAR interferometry. Chinese J. Geophys. 2012, 55, 2598–2610. (In Chinese) [Google Scholar] [CrossRef]
- Wang, T.; Wei, S.J.; Shi, X.H.; Qiu, Q.; Li, L.L.; Peng, D.J.; Weldon, R.J.; Barbot, S. The 2016 Kaikoura earthquake: Simultaneous rupture of the subduction interface and overlying faults. Earth Planet. Sci. Lett. 2018, 482, 44–51. [Google Scholar] [CrossRef]
- Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the Landers Earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef]
- Fielding, E.J.; Lundgren, P.R.; Taymaz, T.; Yolsal-Cevikbilen, S.; Owen, S.E. Fault-Slip Source Models for the 2011 M7.1 Van Earthquake in Turkey from SAR Interferometry, Pixel Offset Tracking, GPS, and Seismic Waveform Analysis. Seismol. Res. Lett. 2013, 84, 579–593. [Google Scholar] [CrossRef]
- Wang, T.; Jonsson, S. Improved SAR amplitude image offset measurements for deriving three-dimensional coseismic displacements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3271–3278. [Google Scholar] [CrossRef]
- Wang, L.; Wang, R.; Roth, F.; Enescu, B.; Hainzl, S.; Ergintav, S. Afterslip and viscoelastic relaxation following the 1999 M 7.4 Izmit earthquake from GPS measurements. Geophys. J. Int. 2009, 178, 1220–1237. [Google Scholar] [CrossRef]
- Xue, L.; Sun, J.B.; Shen, Z.K. InSAR coseismic deformation observation of the 12 January 2010 Haiti earthquake and its coseismic slip distribution inversion. Seismol. Geol. 2011, 33, 157–174, (In Chinese with English abstract). [Google Scholar]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Toda, S.; Stein, R.S.; Sevilgen, V.; Lin, J. Coulomb 3.3 Graphic-Rich Deformation and Stress-Change Software for Earthquake, Tectonic, and Volcano Research and Teaching—User Guide; U.S. Geological Survey Open-File Report 1060; U.S. Geological Survey: Menlo Park, CA, USA, 2011; 63p. Available online: https://pubs.usgs.gov/of/2011/1060/ (accessed on 21 January 2022).
- French, M.E.; Condit, C.B. Slip partitioning along an idealized subduction plate boundary at deep slow slip conditions. Earth Planet. Sci. Lett. 2019, 528, 115828. [Google Scholar] [CrossRef]
- Kobayashi, T.; Morishita, Y.; Yarai, H. SAR-revealed slip partitioning on a bending fault plane for the 2014 Northern Nagano earthquake at the northern Itoigawa-Shizuoka tectonic line. Tectonophysics 2018, 733, 85–99. [Google Scholar] [CrossRef]
- Smith, M.; Mosley, P. Crustal heterogeneity and basement influence on the development of the Kenya Rift, East Africa. Tectonics 1993, 12, 591–606. [Google Scholar] [CrossRef]
- Petit, C.; Déverchère, J.; Houdry, F.; Sankov, V.A.; Melnikova, V.I.; Delvaux, D. Present-day stress field changes along the baikal rift and tectonic implications. Tectonics 1996, 15, 1171–1191. [Google Scholar] [CrossRef]
- Corti, G.; Philippon, M.; Sani, F.; Keir, D.; Kidane, T. Re-orientation of the extension direction and pure extensional faulting at oblique rift margins: Comparison between the Main Ethiopian Rift and laboratory experiments. Terra Nova 2013, 25, 396–404. [Google Scholar] [CrossRef]
- Osagiede, E.E.; Rosenau, M.; Rotevatn, A.; Gawthorpe, R.; Jackson, C.A.-L.; Rudolf, M. Influence of zones of pre-existing crustal weakness on strain localization and partitioning during rifting: Insights from analog modeling using high-resolution 3D digital image correlation. Tectonics 2021, 40, e2021TC006970. [Google Scholar] [CrossRef]
- Tape, C.; Silwal, V.; Ji, C.; Keyson, L.H.; West, M.E.; Ruppert, N. Transtensional Tectonics of the Minto Flats Fault Zone and Nenana Basin, Central Alaska. Bull. Seismol. Soc. Am. 2015, 105, 2081–2100. [Google Scholar] [CrossRef]
- Schweickert, R.A.; Lahren, M.M.; Smith, K.D.; Howle, J.F.; Ichinose, G.A. Transtensional deformation in the Lake Tahoe region, California and Nevada, USA. Tectonophysics 2004, 392, 303–323. [Google Scholar] [CrossRef]
- Jiang, G.; Wen, Y.; Li, K.; Fang, L.; Xu, C.; Zhang, Y.; Xu, X. A NE-Trending Oblique-Slip Fault Responsible for the 2016 Zaduo Earthquake (Qinghai, China) Revealed by InSAR Data. Pure Appl. Geophys. 2018, 175, 4275–4288. [Google Scholar] [CrossRef]
- Toda, S.; Kaneda, H.; Okada, S.; Ishimura, D.; Mildon, Z.K. Slip-partitioned surface ruptures for the Mw 7.0 16 April 2016 Kumamoto, Japan, earthquake. Earth Planets Space 2016, 68, 1–11. [Google Scholar] [CrossRef]
- King, G.; Klinger, Y.; Bowman, D.; Tapponnier, P. Slip-partitioned surface breaks for the mw 7.8 2001 kokoxili earthquake, China. Bull. Seismol. Soc. Am. 2005, 95, 731–738. [Google Scholar] [CrossRef]
- Fitch, T. Plate convergence, transcurrent faults, and internal deformation adjacent to southeast Asia and the western Pacific. J. Geophys. Res. 1972, 77, 4432–4462. [Google Scholar] [CrossRef]
- Bowman, D.; King, G.; Tapponnier, P. Slip partinioning by elastoplastic propagation of oblique slip at depth. Science 2003, 300, 1121–1123. [Google Scholar] [CrossRef]
- Withjack, M.O.; Jamison, W.R. Deformation produced by oblique rifting. Tectonophysics 1986, 126, 99–124. [Google Scholar] [CrossRef]
- Tron, V.; Brun, J.P. Experiments on oblique rifting in brittle-ductile systems. Tectonophysics 1991, 188, 71–84. [Google Scholar] [CrossRef]
- Strecker, M.R.; Blisniuk, P.M.; Eisbacher, G.H. Rotation of extension direction in the central Kenya rift. Geology 1990, 18, 299–302. [Google Scholar] [CrossRef]
- Bonini, M.; Souriot, T.; Boccaletti, M.; Brun, J.P. Successive orthogonal and oblique extension episodes in a rift zone: Laboratory experiments with application to the Ethiopian Rift. Tectonics 1997, 16, 347–362. [Google Scholar] [CrossRef]
- Titus, S.; Fossen, H.; Pedersen, R.; Tikoff, B. Pull-apart formation and strike-slip partitioning in an obliquely divergent setting, Leka Ophiolite, Norway. Tectonophysics 2002, 354, 101–119. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. EOS Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).