Modelling and Assessment of a New Triple-Frequency IF1213 PPP with BDS/GPS
Abstract
:1. Introduction
2. Materials and Methods
2.1. General Observation Model
2.2. IF1213 Observation Model
2.3. TF-C: IF1213 PPP Model with PIFCB Estimation
2.4. TF-F: IF1213 PPP Model Ignoring the PIFCB
2.5. TF-CF: IF1213 PPP Model without the Full Estimation of PIFCB
2.6. TF-FP: IF1213 PPP Model with IGMAS Product Correction
2.7. Relationships in the IF1213 PPP Models
3. Results and Discussion
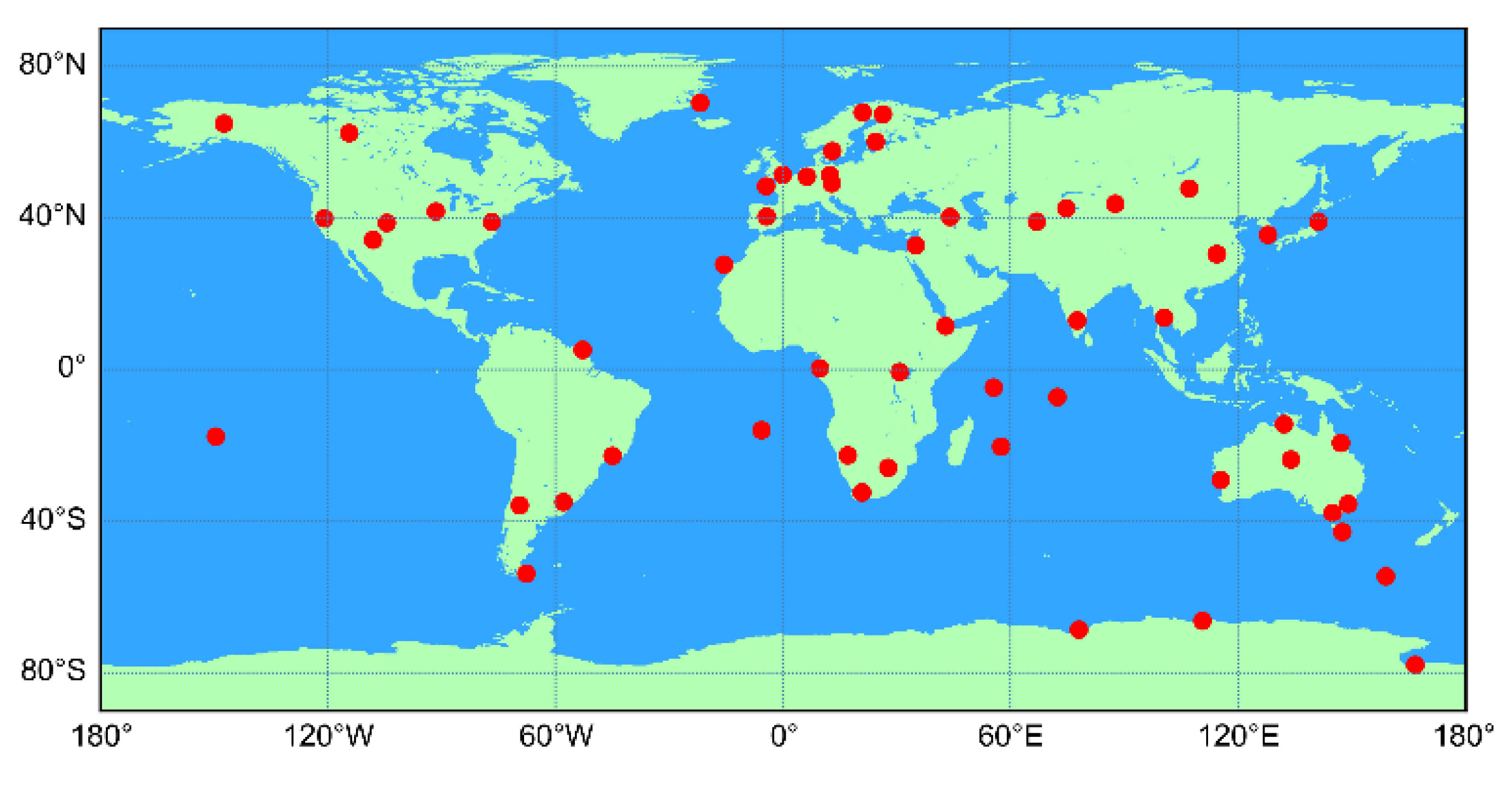
3.1. Data Processing Strategies
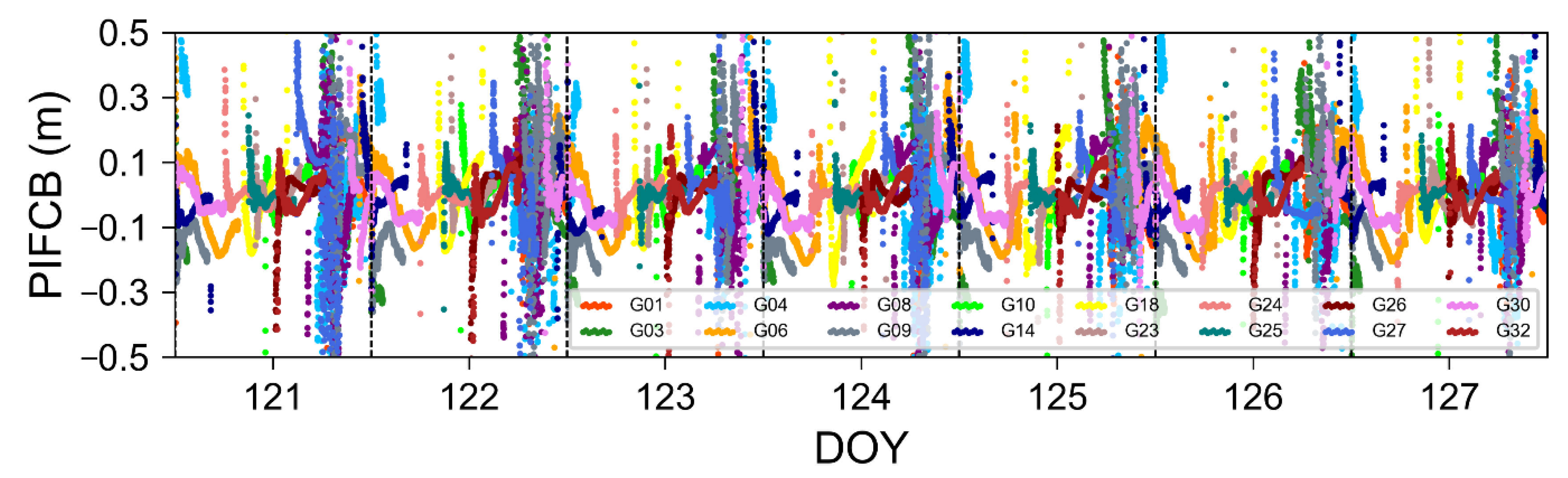
3.2. Influence of the Satellite PIFCB
3.2.1. Influence of the GPS PIFCB
3.2.2. Influence of the BDS-2 PIFCB in BDS
3.3. BDS/GPS PPP Performance
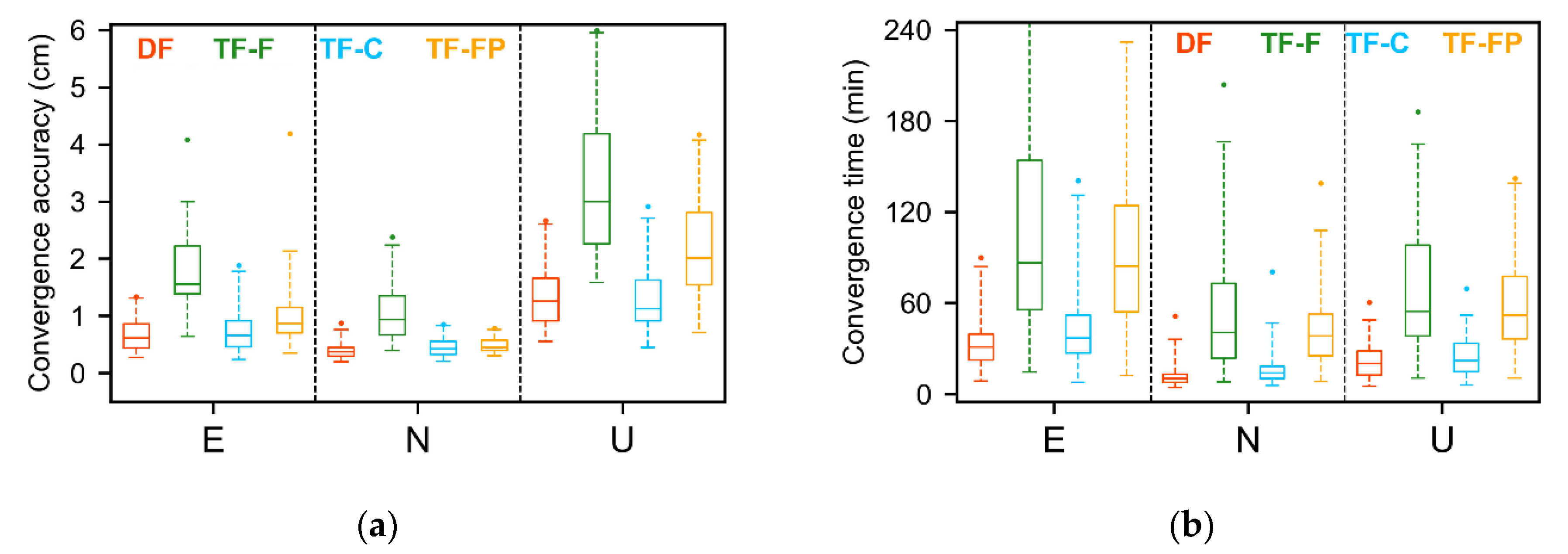
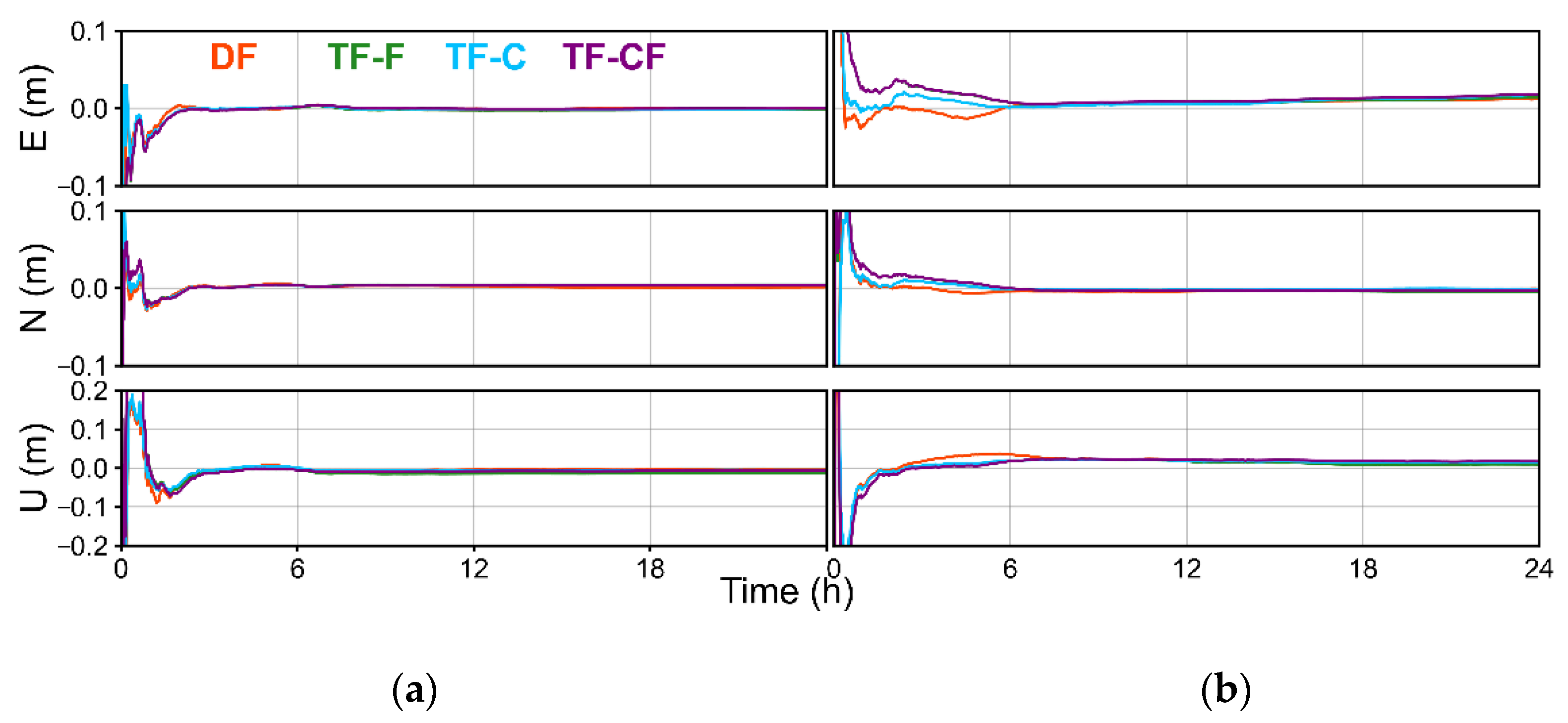
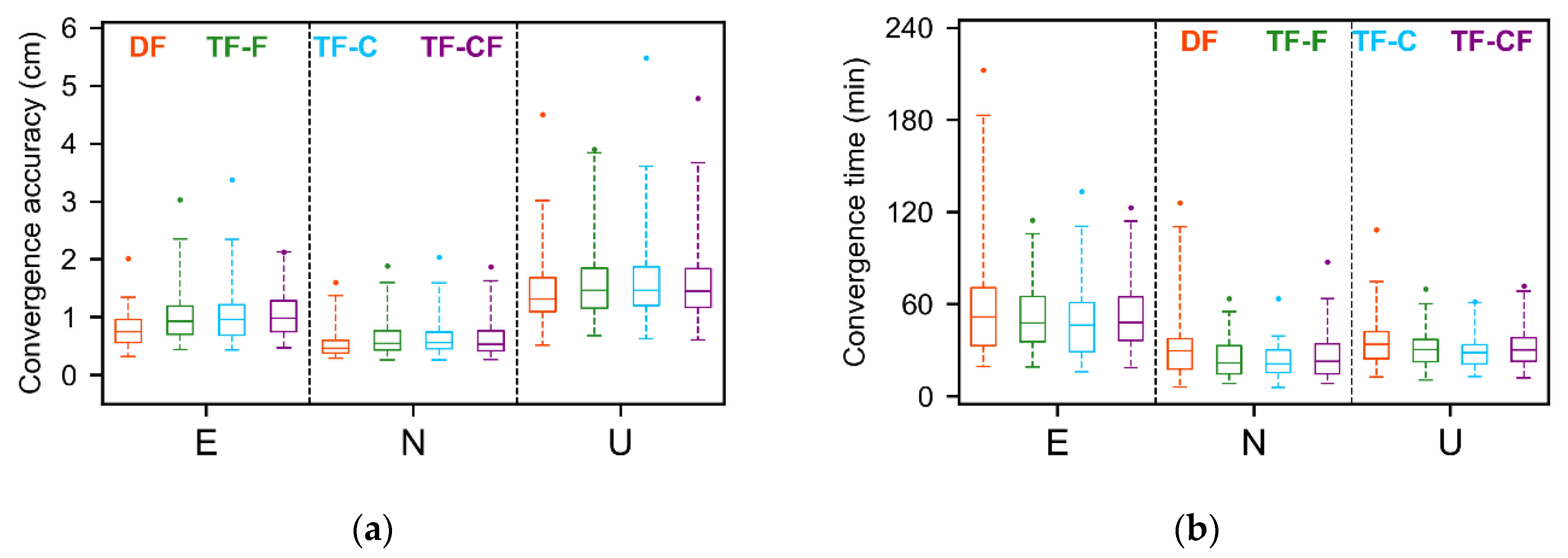
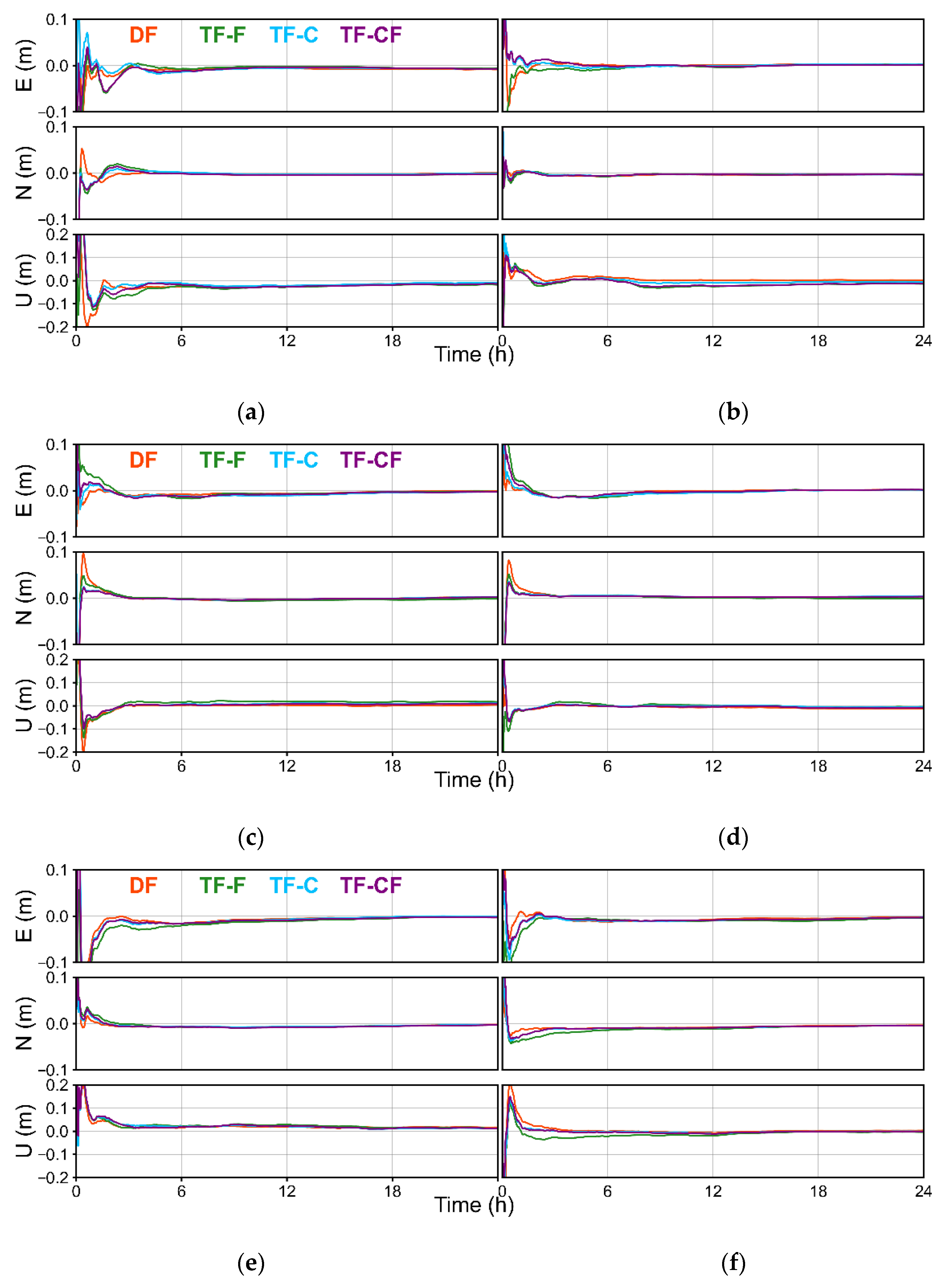
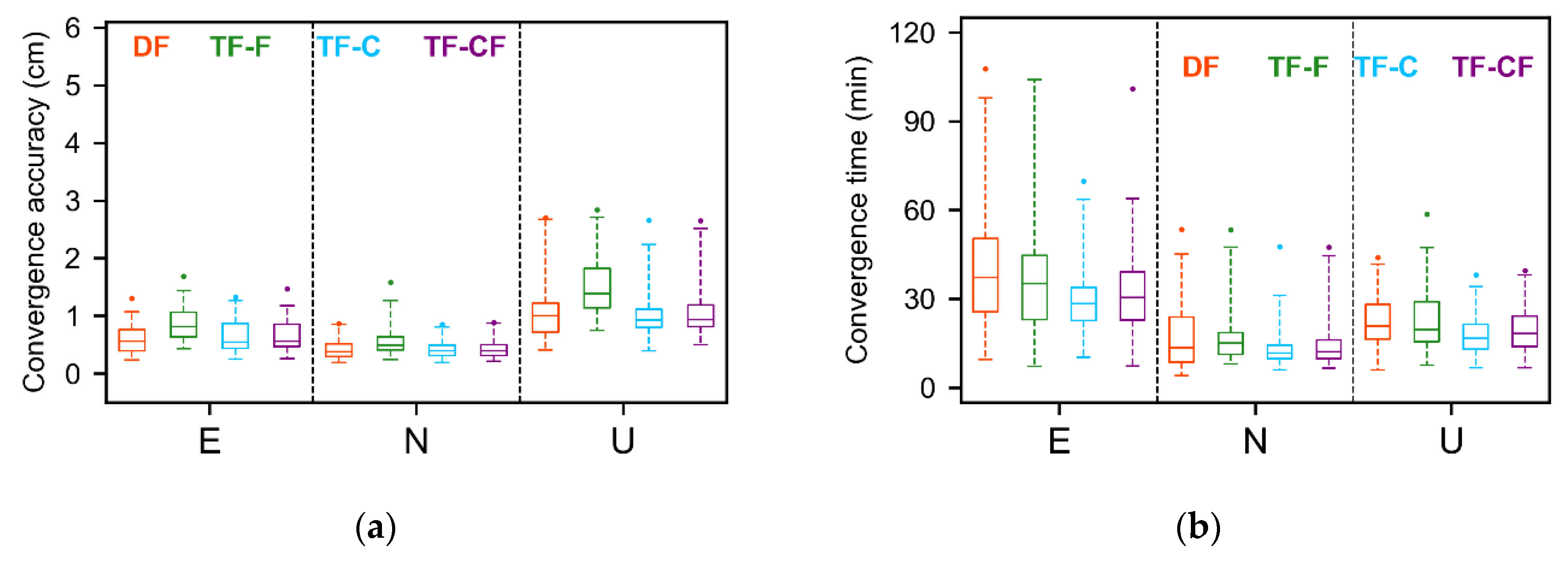
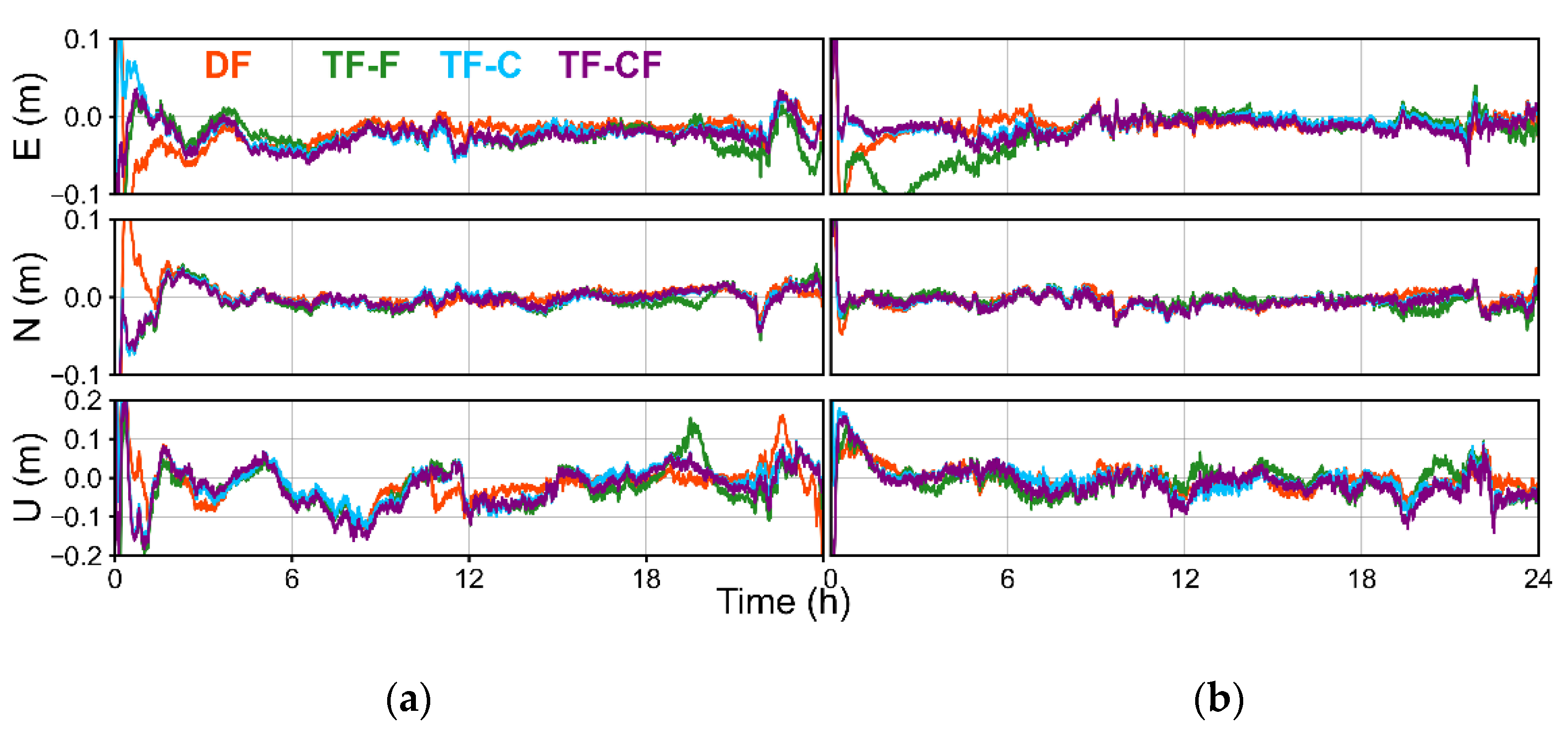
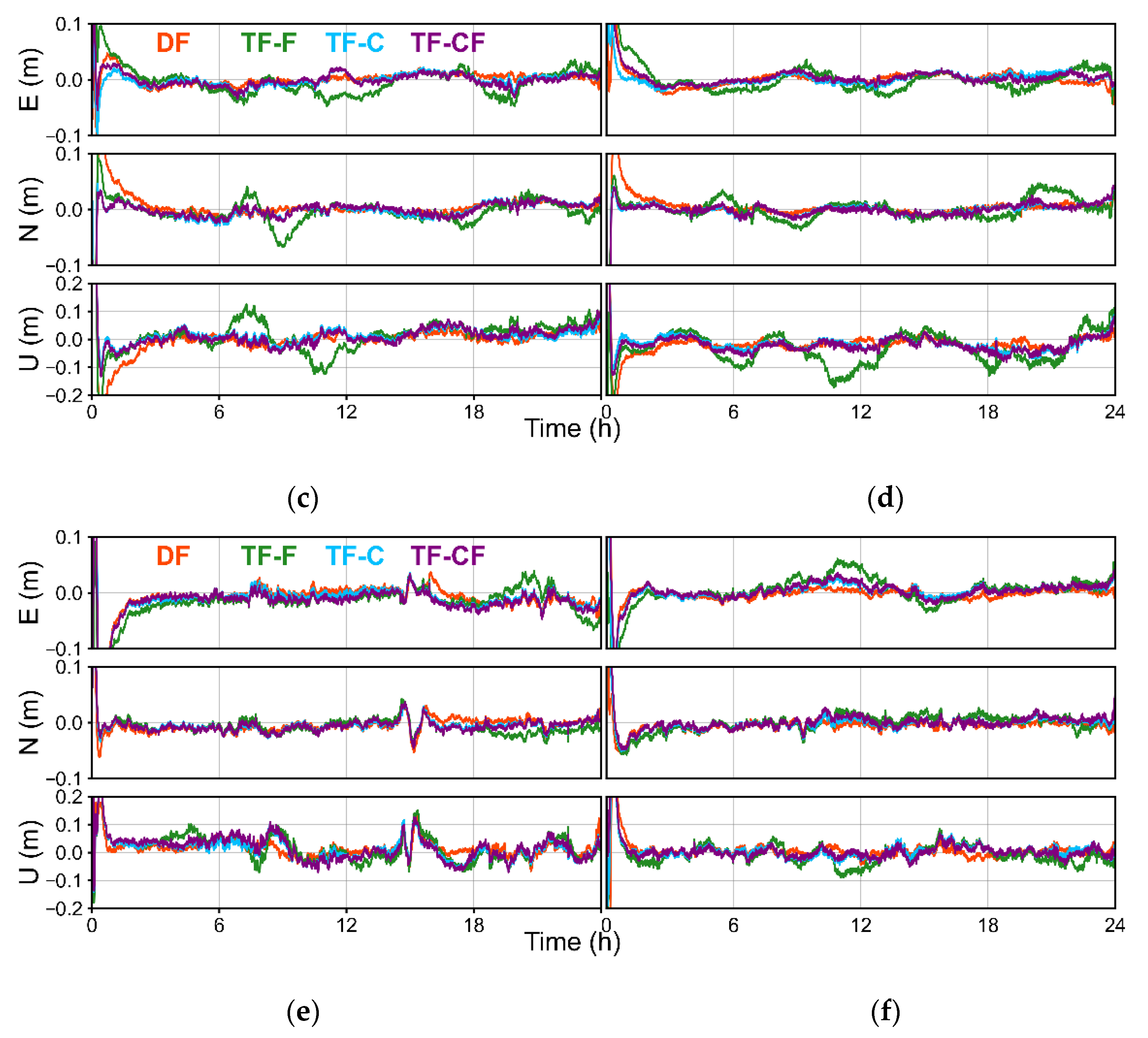
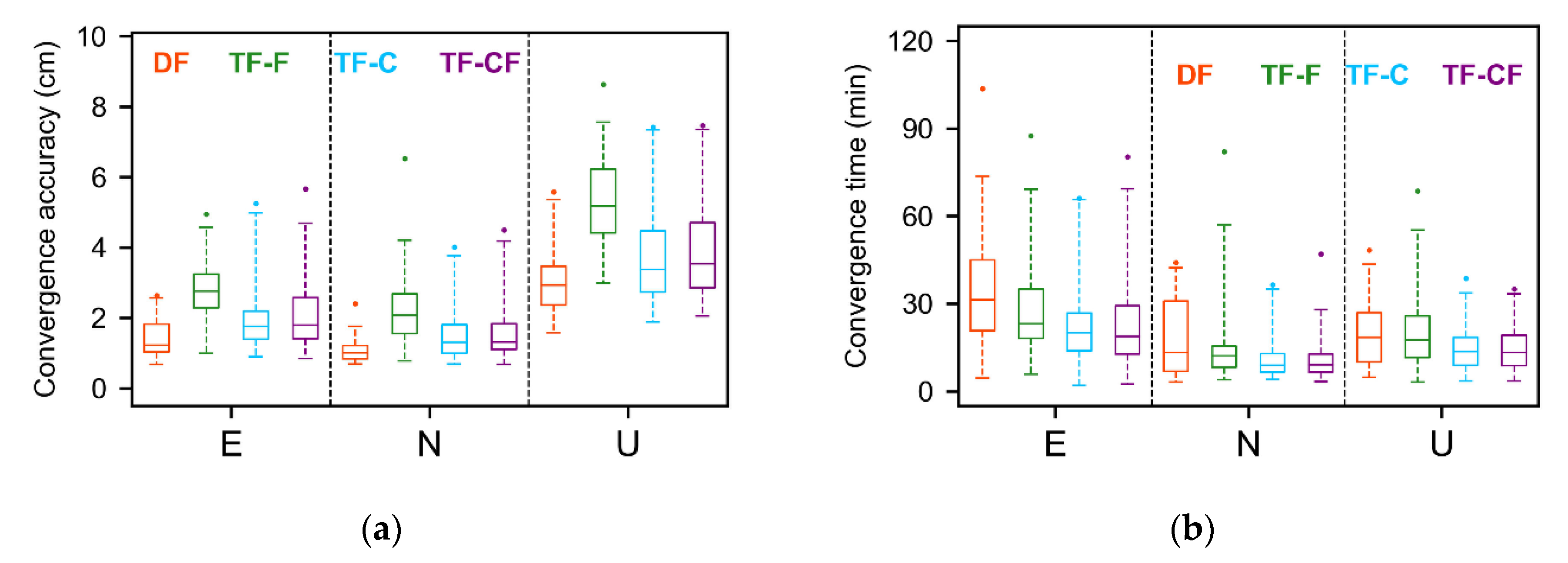
3.3.1. Static Mode
3.3.2. Kinematic Mode
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Malys, S.; Jensen, P.A. Geodetic point positioning with GPS carrier beat phase data from the CASA UNO Experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Deo, M.; El-Mowafy, A. Triple-frequency GNSS models for PPP with float ambiguity estimation: Performance comparison using GPS. Surv. Rev. 2018, 50, 249–261. [Google Scholar] [CrossRef]
- Xiao, G.R.; Li, P.; Gao, Y.; Heck, B. A Unified Model for Multi-Frequency PPP Ambiguity Resolution and Test Results with Galileo and BeiDou Triple-Frequency Observations. Remote Sens. 2019, 11, 116. [Google Scholar] [CrossRef]
- Liu, G.; Guo, F.; Wang, J.; Du, M.Y.; Qu, L.Z. Triple-Frequency GPS Un-Differenced and Uncombined PPP Ambiguity Resolution Using Observable-Specific Satellite Signal Biases. Remote Sens. 2020, 12, 2310. [Google Scholar] [CrossRef]
- Naciri, N.; Bisnath, S. An uncombined triple-frequency user implementation of the decoupled clock model for PPP-AR. J. Geod. 2021, 95, 1–17. [Google Scholar] [CrossRef]
- Tsai, Y.-H.; Yang, W.-C.; Chang, F.-R.; Ma, C.-L. Using multi-frequency for GPS positioning and receiver autonomous integrity monitoring. In Proceedings of the 2004 IEEE International Conference on Control Applications, Taipei, Taiwan, 2–4 September 2004; pp. 205–210. [Google Scholar]
- Zhao, Q.L.; Sun, B.Z.; Dai, Z.Q.; Hu, Z.G.; Shi, C.; Liu, J.N. Real-time detection and repair of cycle slips in triple-frequency GNSS measurements. GPS Solut. 2015, 19, 381–391. [Google Scholar] [CrossRef]
- Gu, X.Y.; Zhu, B.C. Detection and Correction of Cycle Slip in Triple-Frequency GNSS Positioning. IEEE Access 2017, 5, 12584–12595. [Google Scholar] [CrossRef]
- Li, P.; Jiang, X.; Zhang, X.; Ge, M.; Schuh, H. GPS + Galileo + BeiDou precise point positioning with triple-frequency ambiguity resolution. GPS Solut. 2020, 24, 78. [Google Scholar] [CrossRef]
- Spits, J.; Warnant, R. Total electron content monitoring using triple frequency GNSS data: A three-step approach. J. Atmos. Sol. Terr. Phys. 2008, 70, 1885–1893. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Langley, R. Three’s the challenge: A close look at GPS SVN62 triple-frequency signal combinations finds carrier-phase variations on the new L5. GPS World 2010, 21, 8–19. [Google Scholar]
- Montenbruck, O.; Hugentobler, U.; Dach, R.; Steigenberger, P.; Hauschild, A. Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite. GPS Solut. 2012, 16, 303–313. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.; Guo, F.; Liu, J. GPS inter-frequency clock bias estimation for both uncombined and ionospheric-free combined triple-frequency precise point positioning. J. Geod. 2019, 93, 473–487. [Google Scholar] [CrossRef]
- Steigenberger, P.; Hauschild, A.; Montenbruck, O.; Rodriguez-Solano, C.; Hugentobler, U. Orbit and Clock Determination of QZS-1 Based on the CONGO Network. Navigation 2013, 60, 31–40. [Google Scholar] [CrossRef]
- Cai, C.S.; He, C.; Santerre, R.; Pan, L.; Cui, X.Q.; Zhu, J.J. A comparative analysis of measurement noise and multipath for four constellations: GPS, BeiDou, GLONASS and Galileo. Surv. Rev. 2016, 48, 287–295. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, G.X.; Liu, Z.Z.; Hu, Z.G.; Dai, Z.Q.; Liu, J.N. Analysis of BeiDou Satellite Measurements with Code Multipath and Geometry-Free Ionosphere-Free Combinations. Sensors 2016, 16, 123. [Google Scholar] [CrossRef]
- Fan, L.; Wang, C.; Guo, S.; Fang, X.; Jing, G.; Shi, C. GNSS satellite inter-frequency clock bias estimation and correction based on IGS clock datum: A unified model and result validation using BDS-2 and BDS-3 multi-frequency data. J. Geod. 2021, 95, 135. [Google Scholar] [CrossRef]
- Gong, X.; Gu, S.; Lou, Y.; Zheng, F.; Yang, X.; Wang, Z.; Liu, J. Research on empirical correction models of GPS Block IIF and BDS satellite inter-frequency clock bias. J. Geod. 2020, 94, 36. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.H.; Li, X.X.; Liu, J.N.; Li, X. Characteristics of inter-frequency clock bias for Block IIF satellites and its effect on triple-frequency GPS precise point positioning. GPS Solut. 2017, 21, 811–822. [Google Scholar] [CrossRef]
- Lu, X.F.; Zhang, S.L.; Bao, Y.C. A New Method of Ambiguity Resolution for Triple-Frequency GPS PPP. ITM Web Conf. 2016, 7, 01010. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Zhang, X.H.; Wang, J.L.; Ren, X.D. Modeling and assessment of triple-frequency BDS precise point positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.H.; Liu, J.N. A comparison of three widely used GPS triple-frequency precise point positioning models. GPS Solut. 2019, 23, 1–13. [Google Scholar] [CrossRef]
- Cai, C.S.; Gao, Y.; Pan, L.; Zhu, J.J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar] [CrossRef]
- Ren, X.D.; Zhang, X.H.; Xie, W.L.; Zhang, K.K.; Yuan, Y.Q.; Li, X.X. Global Ionospheric Modelling using Multi-GNSS: BeiDou, Galileo, GLONASS and GPS. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Gao, X.; Dai, W.J.; Song, Z.Y.; Cai, C.S. Reference satellite selection method for GNSS high-precision relative positioning. Geod. Geodyn. 2017, 8, 125–129. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.H.; Liu, J.N.; Li, X.X.; Li, X. Performance Evaluation of Single-frequency Precise Point Positioning with GPS, GLONASS, BeiDou and Galileo. J. Navig. 2017, 70, 465–482. [Google Scholar] [CrossRef]
- Li, X.X.; Li, X.; Liu, G.G.; Feng, G.L.; Yuan, Y.Q.; Zhang, K.K.; Ren, X.D. Triple-frequency PPP ambiguity resolution with multi-constellation GNSS: BDS and Galileo. J. Geod. 2019, 93, 1105–1122. [Google Scholar] [CrossRef]
- Hu, C. An Investigation of Key Technologies Related to Combining BDS-2 and BDS-3 Observations in Data Processing; China University of Mining and Technology: Xuzhou, China, 2020. [Google Scholar]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, Z.; Wang, N. Multi-GNSS triple-frequency differential code bias (DCB) determination with precise point positioning (PPP). J. Geod. 2019, 93, 765–784. [Google Scholar] [CrossRef]
- Chen, L.; Li, M.; Zhao, Y.; Hu, Z.; Zheng, F.; Shi, C. Multi-GNSS real-time precise clock estimation considering the correction of inter-satellite code biases. GPS Solut. 2021, 25, 32. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, T. Modeling and assessment of GPS/BDS/Galileo treple-frequency precise point positioning. Acta Geod. Cartogr. Sin. 2021, 50, 61–70. [Google Scholar]
- Li, P.; Zhang, X.H.; Ge, M.R.; Schuh, H. Three-frequency BDS precise point positioning ambiguity resolution based on raw observables. J. Geod. 2018, 92, 1357–1369. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Dong, D.; Li, P.; Li, X.; Schuh, H. Influence of stochastic modeling for inter-system biases on multi-GNSS undifferenced and uncombined precise point positioning. GPS Solut. 2019, 23, 59. [Google Scholar] [CrossRef]
- Schmid, R.; Steigenberger, P.; Gendt, G.; Ge, M.; Rothacher, M. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. J. Geod. 2007, 81, 781–798. [Google Scholar] [CrossRef]
- Wu, J.-T.; Wu, S.-C.; Hajj, G.; Bertiger, W.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Astrodynamics 1991 1992, 91–98. [Google Scholar]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bulletin Géodésique (1946–1975) 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B.; Conventions, I. IERS Conventions (2010); Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Ashby, N. Relativity in the Global Positioning System. Living Rev. Relativ. 2003, 6, 1. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Shi, C.; Li, M.; Wang, C.; Zheng, F.; Jing, G.; Zhang, J. GPS satellite inter-frequency clock bias estimation using triple-frequency raw observations. J. Geod. 2019, 93, 2465–2479. [Google Scholar] [CrossRef]
- Chen, Y.; Mi, J.; Gu, S.; Li, B.; Li, H.; Yang, L.; Pang, Y. GPS, BDS-3, and Galileo Inter-Frequency Clock Bias Deviation Time-Varying Characteristics and Positioning Performance Analysis. Remote Sens. 2022, 14, 3991. [Google Scholar] [CrossRef]

| Number | GPS | BDS-2 | BDS-3 |
|---|---|---|---|
| 1 | L1 (1575.42) | B1I (1561.01) | B1I (1561.01) |
| 2 | L2 (1227.60) | B3I (1268.52) | B3I (1268.52) |
| 3 | L5 (1176.45) | B2I (1207.14) | B1C (1575.42) |
| System | PRN | Orbit Type |
|---|---|---|
| GPS | G01, G03, G04, G06, G08, G09, G10, G14, G18, G23, G24, G25, G26, G27, G30, G32. | Medium Earth Orbit (MEO) |
| BDS-2 | C01, C02, C03, C04, C05; | Geostationary Earth Orbit (GEO) |
| C06, C07, C08, C09, C10, C13, C16; | Inclined Geo-Synchronous Orbit (IGSO) | |
| C11, C12, C14; | MEO | |
| BDS-3 | C19, C20, C21, C22, C23, C24, C25, C26, C27, C28, C29, C30, C32, C33, C34, C35, C36, C37, C41, C42, C43, C44, C45, C46; | MEO |
| C38, C39, C40. | IGSO |
| Items | Strategy |
|---|---|
| Model | DF, TF-C, TF-F, TF-CF, TF-FP(GPS) |
| Satellite elevation mask | 15° |
| Estimator | Kalman filter |
| Weighting scheme | Elevation-dependent weight; 0.003 m and 0.3 m for raw phase and code, respectively |
| PCO/PCV | igs14_2196.atx according to Schmid et al. [37] |
| Phase windup | Corrected [38] |
| Satellite DCB corrections | Corrected with MGEX DCB products except TF-C model |
| Satellite orbit and clock | Products from WUM |
| Tropospheric delay | Zenith Hydrostatic Delays (ZHD) are corrected using the Saastamoinen model, and Zenith Wet Delays (ZWD) are estimated using random walk [39] |
| Tide effect | Solid Earth, pole and ocean tide [40] |
| Relativistic effect | Corrected [41] |
| Station coordinates | Static: estimated using constants; kinematic: estimated using white noise process |
| Receiver clock | Estimated using white noises |
| Receiver inter-frequency bias | Estimated using random walk |
| Inter-frequency clock bias | Estimated using random walk |
| Ambiguity | Estimated using a constant |
| Model | Convergence Accuracy (CM) | Convergence Time (Min) | ||||
|---|---|---|---|---|---|---|
| E | N | U | E | N | U | |
| DF | 0.61 | 0.37 | 1.26 | 30.86 | 10.17 | 20.14 |
| TF-F | 1.56 | 0.94 | 3.00 | 86.36 | 40.64 | 54.43 |
| TF-C | 0.66 | 0.42 | 1.12 | 36.93 | 14.00 | 22.21 |
| TF-FP | 0.86 | 0.45 | 2.01 | 84.25 | 38.21 | 51.79 |
| Model | Convergence Accuracy (CM) | Convergence Time (Min) | ||||
|---|---|---|---|---|---|---|
| E | N | U | E | N | U | |
| DF | 0.74 | 0.46 | 1.31 | 51.64 | 29.57 | 33.64 |
| TF-F | 0.93 | 0.54 | 1.46 | 47.59 | 21.69 | 30.36 |
| TF-C | 0.96 | 0.56 | 1.46 | 46.14 | 21.00 | 28.29 |
| TF-CF | 0.98 | 0.53 | 1.44 | 47.89 | 22.75 | 29.96 |
| Model | Convergence Accuracy (CM) | Convergence Time (Min) | ||||
|---|---|---|---|---|---|---|
| E | N | U | E | N | U | |
| DF | 0.56 | 0.38 | 1.00 | 37.18 | 13.43 | 20.80 |
| TF-F | 0.81 | 0.49 | 1.39 | 35.18 | 15.04 | 19.54 |
| TF-C | 0.54 | 0.39 | 0.93 | 28.43 | 11.61 | 16.68 |
| TF-CF | 0.56 | 0.39 | 0.93 | 30.46 | 12.12 | 18.29 |
| Model | Convergence Accuracy (CM) | Convergence Time (Min) | ||||
|---|---|---|---|---|---|---|
| E | N | U | E | N | U | |
| DF | 1.23 | 1.01 | 2.93 | 31.24 | 13.33 | 18.39 |
| TF-F | 2.75 | 2.08 | 5.17 | 23.07 | 12.13 | 17.47 |
| TF-C | 1.75 | 1.29 | 3.37 | 20.02 | 8.93 | 13.50 |
| TF-CF | 1.79 | 1.31 | 3.53 | 18.74 | 9.08 | 13.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, R.; Wang, Y.; Hu, C.; Liu, B. Modelling and Assessment of a New Triple-Frequency IF1213 PPP with BDS/GPS. Remote Sens. 2022, 14, 4509. https://doi.org/10.3390/rs14184509
Wang Z, Wang R, Wang Y, Hu C, Liu B. Modelling and Assessment of a New Triple-Frequency IF1213 PPP with BDS/GPS. Remote Sensing. 2022; 14(18):4509. https://doi.org/10.3390/rs14184509
Chicago/Turabian StyleWang, Zhongyuan, Ruiguang Wang, Yangyang Wang, Chao Hu, and Bingyu Liu. 2022. "Modelling and Assessment of a New Triple-Frequency IF1213 PPP with BDS/GPS" Remote Sensing 14, no. 18: 4509. https://doi.org/10.3390/rs14184509
APA StyleWang, Z., Wang, R., Wang, Y., Hu, C., & Liu, B. (2022). Modelling and Assessment of a New Triple-Frequency IF1213 PPP with BDS/GPS. Remote Sensing, 14(18), 4509. https://doi.org/10.3390/rs14184509