Abstract
The redistribution of surface mass (e.g., atmosphere, soil water, oceans, and groundwater) can cause load responses, resulting in vertical deformations of the crust. Indeed, the global navigation satellite system (GNSS)-based continuously operating reference stations (CORS) are able to accurately measure the vertical deformation caused by surface mass loads. In this study, the CORS was used to invert groundwater storage anomalies (GWSA), represented by the equivalent water height (EWH), after removing the effect of the non-groundwater surface mass load (atmospheric, groundwater, and non-tidal oceanic loads) from the vertical deformation monitored by CORS. In addition, the global and regional high-resolution surface mass models were combined to calculate the high-precision load deformation field in in western Yunnan using the remove–restore method, thereby obtaining more accurate surface mass load data and improving the accuracy of the inverted GWSA results. In order to assess the feasibility of the CORS inversion for the GWSA used, 66 CORS stations in western Yunnan Province were considered, presenting weekly GWSA data from 10 January 2018 to 31 December 2020. The results revealed significant seasonal variation in GWSA in the study area, showing an amplitude range of −200–200 mm. This approach is based on the already-established CORS network without requiring additional set-up costs. In addition, the reliability of CORS inverse results was assessed using Gravity Recovery and Climate Experiment (GRACE) inverse results and actual groundwater monitoring data. According to the obtained results, GWSA can be monitored by both CORS and GRACE data; however, CORS provided a more effective spatiotemporal resolution of GWSA. Therefore, the CORS network combined with surface mass load data is able to effectively monitor the spatiotemporal dynamics of GWSA in small-scale areas and provides important references for the study of hydrology.
1. Introduction
As a densely populated country, China is relatively poor in water resources per capita []. Moreover, China is characterized by an uneven spatiotemporal distribution of water resources due to the impacts of climatic and topographic characteristics. The GWSA (groundwater storage anomalies) aims to estimate groundwater storage, thereby maintaining the ecological balance of groundwater systems. The overexploitation of groundwater resources has seriously restrained sustainable development in many regions [,]. Therefore, the assessment of the spatiotemporal distribution of regional GWS (groundwater storage) is of great scientific importance for studying water circulation and groundwater allocation as well as for preventing groundwater droughts [,].
At present, the two main GWS monitoring approaches consist of in situ monitoring of groundwater level fluctuations and using Gravity Recovery and Climate Experiment (GRACE) and Global Land Data Assimilation System (GLDAS) data to invert the spatiotemporal characteristics of GWS [,]. In fact, consecutive groundwater level data, with relatively high accuracies, can be obtained at monitoring well stations using the first approach. However, this approach is costly since it requires several monitoring stations with high density to ensure accurate regional monitoring. Moreover, most well stations can be located in plains regions, making it challenging to monitor groundwater storage in mountainous areas. Meanwhile, due to the complex regional geological structures, some parameters (e.g., specific yield) are difficult to determine, making it difficult to effectively assess GWSA using discretely distributed well stations. On the other hand, the GRACE and GLDAS data-based approach is often applied to large-scale regional GWSA monitoring [,]. Although the quality of gravity satellite data is relatively high, there is considerable interference upon high-order spherical harmonic coefficients, resulting in low spatial resolutions. Furthermore, these satellite data have been lacking since 2011, with a data gap of nearly one year between GRACE/GRACE Follow-on (GRACE-FO), explaining the inability of GRACE data to provide high-resolution continuous monitoring the GWSA data in small-scale regions [,]. Therefore, given the complex physical conditions, high cost of monitoring groundwater storage through well stations, and the low-resolution GRACE monitoring data, the continuously operating reference system (CORS) inversion method for GWSA in small-scale areas requires further study and discussion.
The CORS is a ground observation system based on the global navigation satellite system (GNSS) observation system. These data are derived from long consecutive monitoring data of satellite navigation signals, providing real-time and periodic data through communication facilities. The CORS can monitor the dynamics of regional geodetic heights and their consecutive long-time series [,]. Indeed, several researchers have demonstrated the ability of the CORS network to obtain real-time information from selected monitoring stations in certain regions, providing references for monitoring spatial dynamics as well as comprehensive continuous regional observation data [,,]. In addition, the load-deformation theory demonstrated that changes in the surface environmental mass (e.g., atmosphere, surface water, groundwater, and ocean) lead to load vertical deformation, thereby influencing the seasonal periodic signals in the geodesic height variations of CORS stations [,,]. Argus [] used the seasonal signals of GNSS vertical data to invert the terrestrial water storage anomalies (TWSA) in California, showing consistent spatial distribution data with that inverted using GRACE. In addition, He [] inverted the changes in the TWSA in Yunnan Province from 2010 to 2014 and compared the GNSS data with those of GRACE and GLDAS, discussing the possibility of GNSS to separately operate and monitor the TWSA. Several studies have revealed consistent findings with the hypothesis that the seasonal vertical displacement of GNSS is strongly related to the load-deformation caused by TWSA and have assessed the reliability of GNSS data to invert the TWSA [,,,,,,]. However, studies on groundwater inversion have only assessed the correlation between seasonal GNSS and GWSA data due to the complexity of seasonal signals of GNSS vertical displacements, while only a few studies have inverted GWSA data using the CORS.
To address this challenge, this study aims to verify the feasibility and reliability of the combined CORS high-resolution surface mass load inversion for GWSA based on an already-established CORS network, thus avoiding additional establishment costs. Moreover, the density of CORS stations and their continuous and immediate high-precision observation make it possible to perform high-resolution GWSA monitoring in a small-scale region. Yunnan Province in China has experienced a severe water shortage and continuous drought. Indeed, the GWSAs have directly affected the regional economy and local ecological environment in Yunnan Province. Therefore, assessing the spatiotemporal distribution characteristics of the GWSA can provide important reference significance for human production activities as well as for relevant decision-makers in the regions. In order to improve the precision and stability of the CORS inversion, the global and regional high-resolution surface mass models were combined in this study to calculate the high-precision load deformation field in Yunnan Province based on the remove-restore method. Indeed, researchers have eliminated three surface mass loads (atmospheric, soil water, and non-tidal oceanic loads) from the non-linear time series of CORS geodetic heights through data processing, and then the CORS data were used to invert the GWSAs based on load deformation theory and inversion models [,]. To assess the applicability of the method, researchers have used data from 66 CORS stations in Western Yunnan Province and high-resolution surface mass load results and performed a weekly GWSA grid in the study area from 10 January 2018 to 31 December 2020 to assess the effectiveness and reliability of CORS inverse results using GRACE inverse results and groundwater monitoring station data.
2. Materials and Methods
2.1. Data Used
2.1.1. CORS Network Data
As is shown in Figure 1, the study region is circled by red lines. The data were collected from 66 CORS stations located in the study region, covering the 2018–2020 period. In addition, 15 international GNSS service (IGS) stations were selected in this study to obtain high-precision CORS coordinate time series and to resolve the solution of CORS data. The longitude and latitude coordinates of the IGS stations are reported in Table 1. GAMIT and GLOBK were also used in this study to process the collected data []. On the other hand, by correcting the daily errors of GNSS data for each station, a solution was achieved in some zones of the study region through GAMIT (Table 2). GLOBK was used for a global adjustment of the network and to present the time series of station coordinates in the international terrestrial reference frame (ITRF) []. As is shown in Table 2, the CORS data solution removed the influences of the solid, sea, and atmospheric tides, while the influences of non-tidal elements (e.g., atmosphere pressure, soil water, and sea level) were maintained.
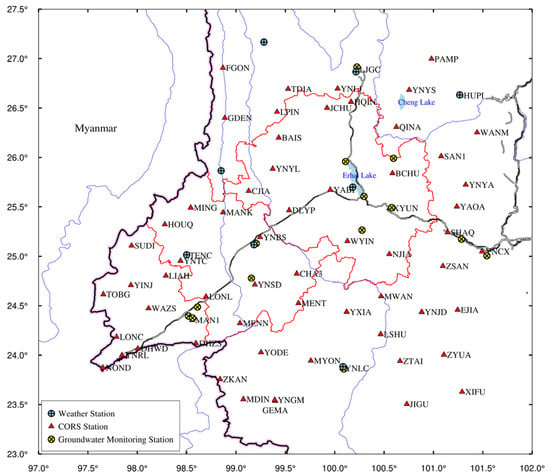
Figure 1.
Geographic location of the study region.

Table 1.
The 15 IGS sites used for the calculation of the CORS network in Western Yunnan Province.

Table 2.
The main parameters used in the GAMIT calculation.
2.1.2. Atmospheric Pressure Data
In order to calculate the effect of atmospheric load, the global atmospheric pressure data were derived in this study from ECMWF’s (European Centre for Medium-Range Weather Forecasts) re-analysis of the 0.25° × 0.25° ERA-interim surface pressure product data (https://www.ecmwf.int/, accessed on 15 May 2021), covering the 3 January 2018–30 December 2020 period []. The original data were averaged by week, which is reported by Wednesday of each week. Similar to the solutions of non-tidal oceanic and soil water loadings, the weekly grid time series of atmospheric loading were obtained using Equations (1) and (2).
On the other hand, the regional high-resolution atmospheric pressure data were downloaded from the CLDAS-V2.0 data (CLDAS Atmospheric Driving Field) product of the China Meteorological Administration Land Data Assimilation System (CLDAS) from the China Meteorological Data Network (http://data.cma.cn/, accessed on 15 May 2021). The product data consist of temperature, pressure, humidity, wind speed, precipitation, and other meteorological parameter data. The hourly product data cover the Asian region (0°~65°N, 60°~160°E), with a spatial resolution of 0.0625° × 0.0625°. The dataset includes data observed at over 2400 and 40,000 national and regional automatic meteorological stations, respectively, for operational assessment. By combining global and regional atmospheric pressure data, a high-resolution atmospheric loading deformation field of the study area was determined using the remove–restore method. The soil water loading was calculated using the same method.
2.1.3. Sea Level Anomaly Data
In order to calculate the effect of Non-tidal ocean load, the daily global sea-level anomaly (SLA) data were derived from the 0.25° × 0.25° archiving validation and interpretation of satellite oceanography (AVISO) data (https://www.aviso.altimetry.fr/, accessed on 15 May 2021), covering the 2 January 2018–30 December 2020 period. The AVISO data integrate not only multi-satellite-derived sea-level data (e.g., TOPEX/Poseidon, Jason-1/2, and Envisat) but also the associated geophysical correction, including tidal and inverse barometer corrections, thereby representing the effects of non-tidal ocean loading [,].
2.1.4. Soil Water Data
Calculation of soil water load requires soil water data. In this study, the V2.1 GLDAS/Noah model, provided by the National Aeronautics and Space Administration (NASA) and National Centers for Environmental Prediction (NCEP), was used to obtain the soil water data, with a spatial resolution of 0.25° × 0.25° (https://mirador.gsfc.nasa.gov, accessed on 15 May 2021) []. The GLDAS model takes into account soil water, canopy water, and snow water (ranging from 0 to 200 cm), while groundwater is excluded. The temporal resolutions of the data are 3-hourly and monthly. In this study, the 3-hourly resolution GLDAS data, from 3 January 2018 to 30 December 2020, were first downloaded, then averaged by week to obtain weekly soil water data. These data were used to determine the influence of soil water loading, whereas the monthly soil water data covered the January 2018–December 2020 period. Indeed, the monthly GLDAS data combined with the monthly GRACE data can be used to determine GWSA as well as to assess the validity and feasibility of the CORS inversion for GWSA.
On the other hand, the regional high-resolution surface water height data were downloaded in this study from the CLDAS data product of the China Meteorological Data Network, which consists of hourly soil moisture data covering the Asian region (0°–65°N, 60°–160°E), with a spatial resolution of 0.0625° × 0.0625°.
2.2. GRACE-FO Mascon Solutions
To compare and analyze the CORS and GRACE inverse results for GWSA, GRACE-FO RL06 mascon solutions, provided by the Center for Space Research (CSR) with a spatial resolution of 0.25° × 0.25°, were used to reflect the monthly changes in terrestrial water storage (http://www2.csr.utexas.edu/grace/RL06_mascons.html, accessed on 15 May 2021) []. The data covered the October 2018–December 2020 period. The collected data were corrected for degree-1, C20 (degree 2 order 0), C30 (degree 3 order 0), and GIA to reflect the dynamics of terrestrial water storage (Table 3). It should be noted that in comparison with GRACE, the GRACE-FO data processing added the C30 correction into its procedure. Therefore, the regional GWSA could be calculated through the combination of monthly data of terrestrial water storage and the monthly data of soil water provided by GLDAS.

Table 3.
The main corrections used in Mascon solutions.
2.3. Groundwater Monitoring Station Data
The daily data observed at 15 groundwater monitoring stations (Figure 1) from 26 September 2018 to 25 November 2020 were used in this study to assess the accuracy of the CORS inverse results for the GWSA. The collected data were averaged by week. The applicability and reliability of the integrated solution method can be assessed by comparing the observed data with those of the CORS inversion for the GWSA.
2.4. Precipitation Data from Weather Stations
To analyze the influences of precipitation on the spatiotemporal distribution of GWSA in the study region, daily precipitation data observed at eight weather stations in Yunnan Province from (Figure 1) 1 January 2018 to 31 December 2020 were used in this study (http://data.cma.cn, accessed on 15 May 2021).
3. Method
3.1. High-Resolution Surface Mass Load Based on the Remove–Restore Method
The spherical harmonic analysis method was expressed using Equation (1), reflecting the medium- and long-wave components at global scales, while Equation (2) is the load Green’s function method, which mainly reflects the short-wave components at small scales. Since equivalent water height (EWH) can reflect the changes in the mass of the surface environment (e.g., atmosphere, soil water, oceans, and groundwater) based on the load theory of spherical harmonic coefficients, the changes in geodetic heights caused by loads can be calculated using the following equation [,]:
where denotes the average density of the solid earth; is the gravitational constant; and is the average gravity of the ground.
On the other hand, the changes in the geodetic heights of CORS stations resulting from the changes in surface mass load can be expressed using the load Green’s function equation [,]:
where denotes the geodetic height; represents time; denotes the longitude and latitude of the calculated point; and denotes the load point on the ground. The density of water was considered as ; denotes the spherical angular distance between the calculated and load points; denotes the green function of the radial loads; and denotes the average earth radius.
The green function of the radial loads can be expressed as follows [,]:
where is radial load Love number; denotes the earth mass; and denotes the Legendre function.
In this study, the global and regional high-resolution models were combined to calculate the high-precision load deformation field in the study area using the remove–restore method. Figure 2 shows the procedure used in this study [,].
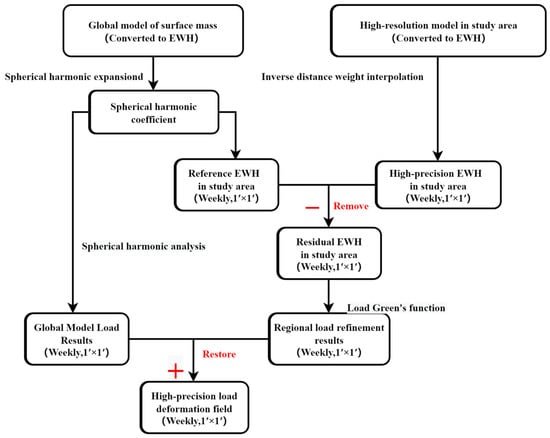
Figure 2.
Flowchart of the high-precision load deformation field solution.
First, the global EWH model was used to estimate the reference EWH and load vertical deformation in the study area using the spherical harmonic analysis method, thus obtaining the spatial long-wave component information. Second, the high-resolution regional EWH model was encrypted into a 1′ × 1′ grid before removing the reference EWH grid from the regional high-resolution EWH grid to obtain the residual EWH using the remove method. Third, the load impact of the residual EWH change on the geodetic height was estimated using the load Green’s function method, introducing the short wave components of the study area. Finally, the load impacts obtained in the first and third steps were added using the restore method. By using these steps, the high-resolution and high-precision load deformation field of the study area was obtained. This approach not only introduces the short-wave component of the study area and improves the applicability of the model in the small-scale study area but also effectively removes the truncation error generated during the spherical harmonic expansion and reduces the calculation uncertainties.
3.2. GWSA Inversion Using the Combined CORS and Surface Mass Load Method
EWH was used in this study to reflect the mass changes in the surface environment (atmospheric pressure, sea level, soil water, and groundwater levels) []. Based on load deformation theory, the normalized expansion formula of the spherical harmonic load was determined using the load-deformation theory, according to the following equations [,,]:
where denotes the geocentric latitude and longitude of the ground calculation point; are the load sphere harmonic coefficients, with degree and order; and denotes the associated Legendre function, with degree and order.
Different thicknesses and radius disks of the same mass were placed on the surface. Figure 3 shows the related load deformation and its relationship with distance, indicating clear load responses near fields. The load-deformation was 1/10 of that of the center at a distance from the center of the disk equal to three times its radius, while no load-deformation was observed at a distance from the center of disk equation to 10 times its radius. Therefore, the vertical displacement and load-deformation were mainly influenced by the load points within a limited distance range. The use of GNSS in the inversion of the regional GWS showed that stations on the edges of the study area tended to be simultaneously influenced by the inside and outside loads of the study area. By neglecting the influence of the outside mass changes, the outside loads can be restrained to the border region, thus leading to false inversion on the edges of the study area, explaining the larger inverted region than the study area. The expansion should consider the sensitive range of load responses. Therefore, the 66 CORS stations covered the study region and its peripheral areas.
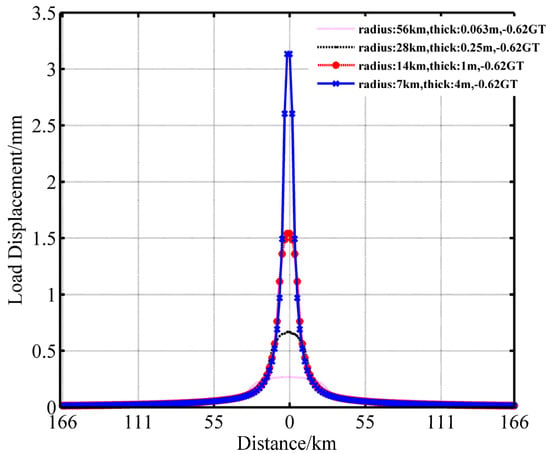
Figure 3.
Vertical deformation caused by disks of different masses.
The inversion model of Argus [] used in this paper:
where denotes the standard deviation of the observation value vector of geodetic height changes; denotes the coefficient matrix of the green function, which can be calculated using Equation (3); is the EWH of the corresponding grid point; denotes the observation value of the GNSS geodetic height changes of CORS stations; denotes the smoothing factor; and denotes the Laplace operator.
Due to the limited number of GPS observation stations in the study area, the number of equations is smaller than the number of unknowns, resulting in a rank loss of the coefficient matrix of the normal equation. The inversion of the equivalent water height changes using GNSS observation data is, therefore, an ill-posed equation problem. To address this challenge, the ridge estimation reported by Hoerl [] was used in this study, which is a classical regularized approach, to determine the solution of in Equation (5). Indeed, the L-curve method was used in previous studies to select the best-regularized parameters [].
The influence of surface mass changes was calculated using the load-deformation theory in Equation (1). Besides the impact of groundwater changes, atmospheric pressure, sea level, and soil water changes were considered in the present study, while other less influential factors (e.g., rivers, lakes, and reservoirs) were neglected. Based on the weekly geodetic height values, the non-linear time series of each CORS station were obtained. After removing the influences of the non-groundwater data, the residual time series were obtained, including load and non-load vertical deformations of groundwater. Afterward, Equations (2) and (5) were used to invert GWSA from the residual time series. The method used is illustrated in Figure 4. In this study, the integral radius of the load Green’s function and the smoothing factor (β) were set to 2° and 0.01, respectively.
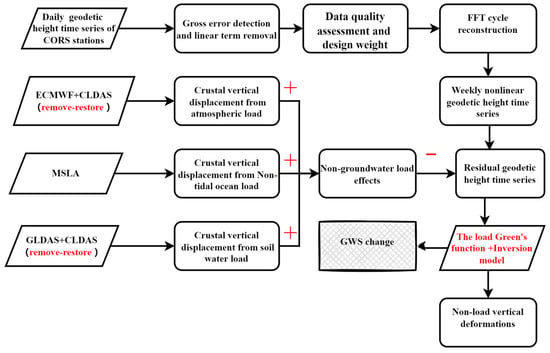
Figure 4.
Flowchart of CORS inversion for GWSA.
3.3. GWSA Inversion Using GRACE Product Data
The terrestrial water storages () are the summation of soi l water, groundwater, surface runoff, snow, and canopy water. Contrary to soil water and groundwater, the contributions of surface runoff and canopy water changes to TWS are minor, and thus they can be neglected. Indeed, TWS in the study region is mainly affected by soil water, snow water, and groundwater []. was calculated in this study using the following formula:
where is the groundwater storage; denotes the changes in TWS obtained from GRACE data; and denote the changes in soil water and snow water, respectively, obtained from GLDAS product data.
4. Results
4.1. GWSA Inversion Results Using CORS Data
The time series of non-linear geodetic height changes were first processed using gross error detection and linear item removal, as shown by the red points in Figure 5. The black curve in Figure 5 shows the time series of geodetic heights after the periodic fast Fourier transformation (FFT) reconstruction. According to the magnitude of the power spectral density, this paper uses the first eight periodic signals to reconstruct [,]. Indeed, the periodic FFT reconstruction is a low-pass filtering method used to decrease or inhibit the high-frequency noise of the time series, thus improving the stability of the inversion results. The geodetic heights of CORS stations corresponded to the temporal resolution of surface mass loads. In order to improve the accuracy of the CORS inversion, the influences of high-resolution surface mass loads, including atmospheric, soil water, and non-tidal oceanic loads, were removed from the reconstructed time series of non-linear geodetic heights, as shown by the purple, blue and green curves in Figure 5. The residual time series obtained after the removal process, according to Equations (2) and (5), can therefore be used to invert GWSA within the coverage of the CORS network, which is reflected by EWH.
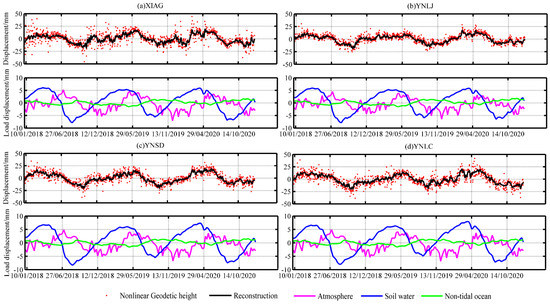
Figure 5.
Processed geodetic height changes of different CORS stations and surface mass loads.
Figure 6 shows the annual differences between the maximum and minimum values of the reconstructed geodetic height time series at the 66 CORS stations, ranging from 15 to 35 mm. According to Figure 5, the atmospheric and soil water loads revealed the highest effects among the three types of loads. The results revealed that the vertical deformation, caused by the soil water loads, ranged from −8 to 8 mm, while non-tidal oceanic load showed the lowest effect, with a vertical deformation range of −2–2 mm.
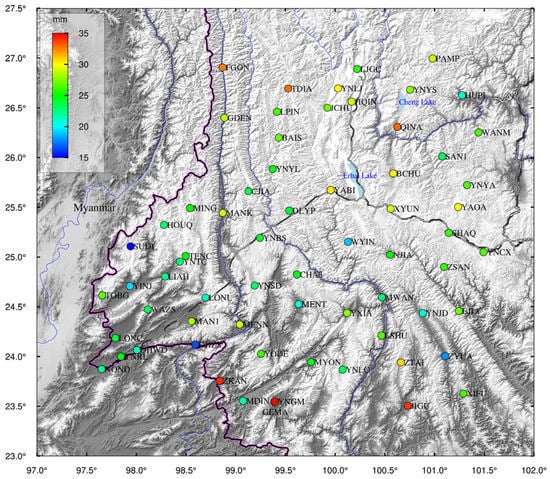
Figure 6.
Range of the reconstructed geodetic heights at each CORS station in the study area.
Surface mass loads, namely atmospheric, non-tidal oceanic, and soil water loads, showed different correlations with the geodetic height time series of CORS stations, demonstrating the influences of these surface mass loads. Therefore, in order to compare the obtained results, the influences of loads were first removed, then the WRMS ratio of the GNSS time series was calculated according to the following formula []:
where is the WRMS of the reconstructed GNSS geodetic height time series. Positive and negative values of indicate a decrease and increase in the WRMS of the GNSS time series, respectively. It should be noted that the absolute value of can reflect the load influences on the GNSS’s non-linear geodetic height time series.
On the other hand, the Pearson correlation coefficient () was computed in this study according to the following equation. It is widely used to measure the degree of correlation between two variables [,]:
where denotes the reconstructed time series of the observed GNSS geodetic heights; denotes the time series of the vertical deformation caused by surface mass loads. The R values range from −1 to 1, indicating strong negative and positive correlations, respectively, between the periodic phases of the two series.
In total, 12 stations were selected to assess the influences of the three surface mass loads on the reconstructed time series of CORS geodetic heights using R and WRMS values (Table 4). Unlike the non-tidal oceanic load, the and WRMS values of atmospheric and soil water loads were all positive. According to the obtained results, the and WRMS values of the atmospheric load ranged from 0.50 and 0.66 and 7.61 to 12.80%, respectively, whereas the and WRMS values of the soil water load ranged from 0.64 to 0.81 and 20.54 to 34.80%, respectively. On the other hand, the non-tidal oceanic load was negatively correlated with the reconstructed time series of the CORS geodetic heights, which is consistent with the reported by Munekane and Nordman [,]. However, the absolute WRMS value of the non-tidal oceanic load ranged from 3.24 to 6.39%, suggesting a low influence on the CORS geodetic heights. This result was due to the offsetting effects of the atmospheric and soil water loads, making the influence of the non-tidal oceanic load difficult to reflect in the time series of the CORS geodetic heights. In other words, atmospheric and soil water loads exhibited stronger influences than that of the non-tidal oceanic load. The R and WRMS values of total loads ranged from 0.81 to 0.89 and 33.84 and 43.93%, respectively (Table 4). On the other hand, by removing the surface mass loads, decreases in the values were observed. This finding demonstrates not only the reliability of the reconstructed CORS geodetic height time series and surface mass load deformations but also the effectiveness of the integrated solving process used in the present study.

Table 4.
Correlation coefficient and WRMS values between different loads and the reconstructed geodetic height time series.
In order to ensure the reliability of the inversion and reduce the influence of the low-quality CORS data, the quality of each CORS dataset was first evaluated before inversion, and then different weights were assigned to CORS stations. The initial weight of every station was set at 1, while the weight of the low-quality stations was decreased based on the entire time series data and their RMS values.
It was demonstrated earlier that the integration solution of the CORS data revealed a weekly GWSA grid over the 3 January 2018–30 December 2020 period was established, with the GWSA expressed in EWH. As is shown in Figure 7, the GWSA showed significant spatial and seasonal variations. The results revealed decreases in GWS from February to June each year, which might be due to the significant seasonal and spatial decreases in groundwater recharge (e.g., rainfall infiltration). From August to the next January, however, increases in GWS were observed in the study area from August to January due to the increase in rainfall amounts. In addition, the inverted GWS using the CORS network showed a relatively high spatial resolution (Figure 7).
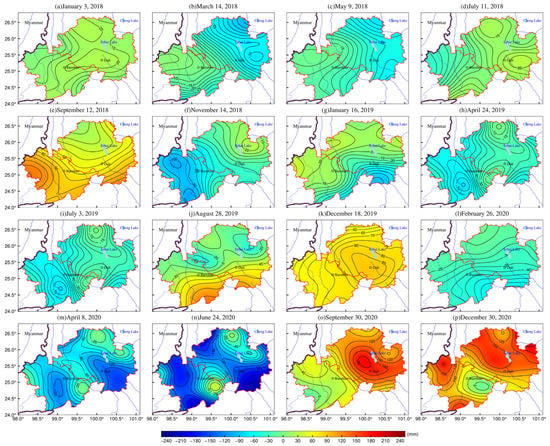
Figure 7.
Weekly GWSA over the January 2018-December 2020 period.
The errors generated from the GNSS data processing, the surface mass model, and the uncertainty in the CORS inversion model may affect the accuracy of the GWSA inversion. The inverse distance weight interpolation method was used in this study to map the time series of the GWSA of CORS stations. Table 5 shows the statistical results of the interpolated GWSA time series of 12 CORS stations. The maximum and minimum values of the inverted GWSA were −200 and 200 mm, respectively. In addition, there were some differences in the amplitude variation of GWSA at different CORS stations, indicating that the CORS inverse results had a high resolution. The mean and standard deviation (SD) values of GWSA at all CORS stations ranged from 3.16 to 15.03 mm and 55.87 to 110.39 mm, respectively. The reliability of the CORS inverse results was assessed in the subsequent part using the GRACE inverse results and groundwater monitoring station data.

Table 5.
Statistics of CORS inverse results for GWSA (mm).
In order to further analyze the temporal features of GWSA based on the sequence data of the GWSA grids, the study area was first divided into four sub-study areas, namely the eastern (BCHU, SYUN, and NJIA), northern (BAIS, YNYL, and JCHU), western (SUDI, YINJ, and TOBG), and southern (CHA3, MENT, and YNSD) sub-study areas, and then four CORS stations were selected randomly as examples. In Figure 8, the curves show the time series of GWSA at the corresponding stations, while the bar charts indicate the precipitation amounts in certain sub-study areas observed at nearby weather stations (Figure 1). In comparison with Figure 7, Figure 8 more directly reflects the temporal features of GWSA. The GWSA dynamics in different sub-study areas were relatively similar. Indeed, since groundwater recharge is derived mainly from precipitation in the study region, GWSA was strongly correlated with precipitation and exhibited significant seasonal differences. According to the obtained results, GWS exhibited main wave crest shapes. From February and March of each year, GWS showed the lowest values from February/March to June/July, then increased significantly from July to October due to the significant increase in the precipitation amounts, followed by a decrease in GWS in December and January. Therefore, precipitation was the main influencing factor on the GWSA in the study region.
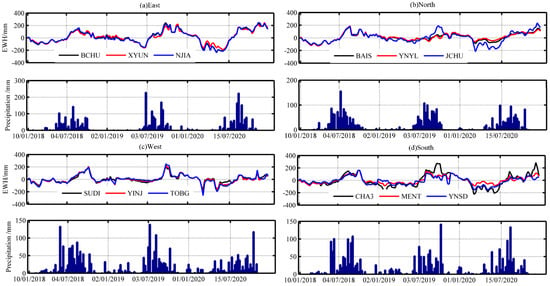
Figure 8.
GWSA at Different CORS stations and precipitation amounts in different sub-study areas.
In order to quantitatively analyze the groundwater drought in the study area within 3 years, the groundwater severity index (DSI) [] was used in this study. This index was calculated using the following formula:
where denotes the year from 2018 to 2020; represents the month from January to December; represents the groundwater drought index DSI; and represent the mean and standard deviation of GWSA, respectively. The classification results of groundwater drought, derived from DSI, are reported in Table 6. As reported above, the monthly GWSA data were obtained from the monthly average of the weekly GWSA time series.

Table 6.
Correlation coefficients and WRMS (%) between different mass surface loads and the reconstructed geodetic height time series.
Figure 9 shows the temporal variation of CORS-DSI in the study area from 2018 to 2020. The results showed a significant seasonal variation in CORS-DSI. In addition, the CORS-DSI values in the eastern and northern sub-regions of the study area were above 0.8 in most months, while only a few months showed CORS-DSI values slightly below 0.8, indicating a mild groundwater drought (Figure 9a,b). On the other hand, the western and southern sub-regions of the study area showed several months with CORS-DSI values below −0.8, while the southern sub-region exhibited relatively significant groundwater drought, with CORS-DSI close to −1.3 over the November 2018–February 2019 and April 2020–August 2020 periods (Figure 9c,d). It is worth noting that the groundwater drought analysis requires more than 10 years of observation data, while only 3 years of CORS station data were used in this study to invert the GWSA. Therefore, to obtain more detailed and accurate drought analysis results, it is suggested to consider long-term observation data in future groundwater drought analyses.
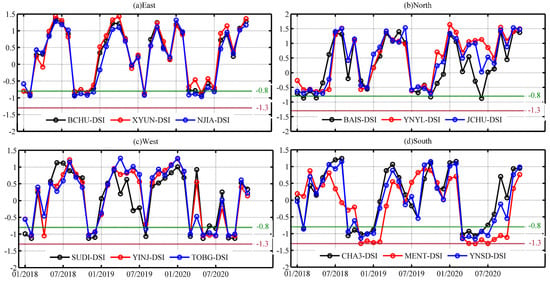
Figure 9.
CORS-DSI in different sub-study areas.
4.2. Comparison with GRACE Data
In order to assess the reliability of the CORS inverse results for GWSA, the GRACE inverse results for GWSA and the observed groundwater level data were used in this study. EWH is considered in the GRACE data to reflect the TWS. GWSA can be computed by removing soil water storage provided by the GLDAS data product. In this study, the period between October 2018 and December 2020 was considered due to the loss of data between GRACE and GRACE-FO. The monthly GRACE data were compared in this study with the monthly inverted CORS-based GWSA data during the year 2019. The obtained results are shown in Figure 10.
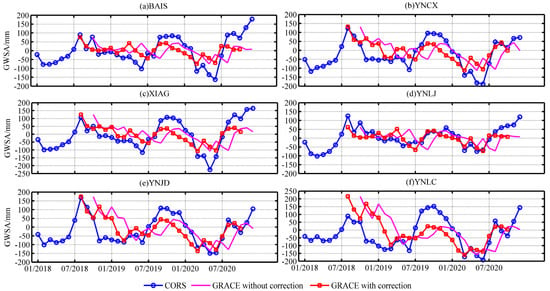
Figure 10.
Comparison between CORS and GRACE inverse results.
Feng [] showed a delay in the GRACE-based land water storage changes by 2 months compared to precipitation changes. Therefore, a 2-month phase delay was performed for the GRACE time series. As can be seen from Figure 10, relatively consistent GRACE- and CORS-based GWSA trends were obtained following the phase delay correction.
In total, 15 CORS were selected randomly as examples. The values in Table 7 indicate the correlation coefficients of the CORS- and GRACE-based GWSA results. Due to the missing data in 2018, the correlation coefficients were computed in this study based on the 2019 data. Compared with the inversion CORS-based data, the GRACE data had a 2-month phase delay. After phase delay correction, the coefficients were significantly improved. Except for FGON, LJGC, and YNRL, showing correlation coefficients of 0.68, 0.69, and 0.65, respectively, the correlation coefficients of all other stations were above 0.7. The highest correlation coefficient was 0.85 in YNJD, indicating a strong correlation. The computed correlation coefficients showed a spatial variation due to the low spatial resolution of the inversion GRACE-based on data. As is shown in Figure 10, the interpolation method used in this study resulted in relatively consistent trends of GRACE monitoring results at different sites without showing significant spatial differences. In addition, the CORS-based GWSA results were based on long-term monitoring GNSS data. Indeed, the density of the CORS stations in the study region allowed us to obtain a higher spatial resolution (Figure 7), showing clear differences in the GWSA time series that are also clearer (Figure 10).

Table 7.
Correlation coefficients between CORS and GRACE inverse results.
Figure 11 shows the annual variation in CORS- and GRACE-based GWSA from 2018 to 2020. The spatial distribution characteristics of the two monitoring results were slightly consistent, showing relatively large annual changes in GWSA in the eastern and southern parts of the study area. The main spatial differences between the two monitoring results were observed in the south-central part of the study area. Overall, the amplitude of the annual variation in CORS-based GWSA was greater than that of GRACE-based GWSA. This finding may be due to the different monitoring methods of the two data products. Indeed, GRACE measures the integrated regional effect of mass redistribution. Its low spatial resolution makes it difficult to comprehensively reflect the effective information of the small-scale region, whereas the CORS data product is based on GNSS measurement methods, which provides real-time geometric deformation information at different locations in the study area, thereby fully reflecting the signal changes in the region.
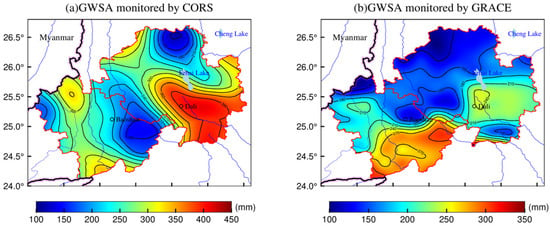
Figure 11.
Annual variation in CORS- and GRACE-based GWSA results.
In summary, both inverse results reflected the changes in GWSA. The results indicate that the GNSS-based CORS data are more sensitive to GWSA, showing obvious local spatial characteristics compared to those of the GRACE data.
4.3. Comparison with Groundwater Monitoring Data
In order to further assess the reliability of CORS-based GWSA results, the inverted GWSA data were interpolated and compared to groundwater levels observed at groundwater monitoring stations. The daily groundwater level data were collected from September 2018 to December 2020. These data were processed for gross error detection and weekly averaging. In order to quantitatively compare the groundwater level data with GWSA, it is necessary to convert the groundwater level data to equivalent water height by considering the specific yield of the area []. The specific yield value for the study area was set to 0.05 [,].
The blue curves in Figure 12 indicate the CORS-based GWSA results observed in four stations, while the red line indicates the result of multiplying the groundwater level by the specific yield value. Both results are the average values of data observed over the year 2019. The results revealed consistent trends of CORS-based GWSA and groundwater levels, showing the same order of amplitude changes. On the other hand, the correlation coefficients between the two data ranged from 0.62 to 0.82, indicating strong positive correlations (Table 8). Therefore, the results demonstrated that the combined CORS and high-resolution surface mass load data effectively invert GWSA in small-scale areas, providing accurate seasonal trends for GWSA.
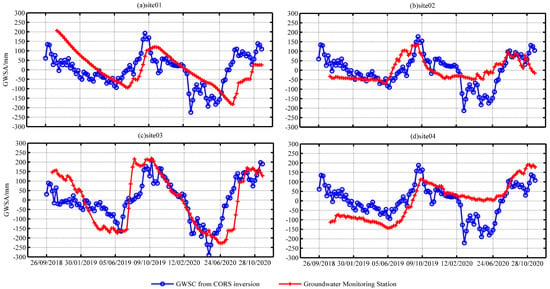
Figure 12.
Comparison between CORS-based GWSA and groundwater monitoring results.

Table 8.
Correlation coefficients between CORS-based GWSA and observed GWSA at groundwater monitoring stations.
5. Discussion
Considering the difficult physical conditions and high cost of constructing groundwater monitoring stations, as well as the low-resolution problem of the GRACE inversion results, the present study aims to assess the feasibility and reliability of CORS for GWSA inversion. Numerous studies have analyzed the correlation of TWSA or GWSA with GNSS vertical displacement [,,]. In addition, He [] inverted TWSA using GNSS vertical displacement. However, few studies have directly inverted GWSA using the CORS data product. Therefore, to improve the accuracy and stability of the inversion results, global and regional high-resolution surface mass models were combined to determine the high-precision load deformation field in western Yunnan using the remove–restore method. In addition, the reliability of CORS-based GWSA results was assessed using the observed groundwater levels. Although the obtained results showed accurate GWSA and demonstrated the validity and reliability of the methods used in this study, there are still some challenges to address. Data covering a period longer than 2.5 years were observed only at 15 stations among the 66 CORS stations, thereby affecting the accuracy of the inverse results for some months. Since the data processing is complicated, the study period considered in this study was only 3 years, resulting in non-obvious drought characteristics and trends. Therefore, this study focused mainly on the seasonal variation in GWSA in the study area. In addition, the specific yield in this study was set to 0.05 for the entire study area. It should be noted that the specific yield can vary significantly depending on the depth of groundwater wells and the lithological characteristic of the aquifers. Therefore, different specific yield values need to be provided for different groundwater wells to obtain more accurate GWSA results using groundwater monitoring data.
The correlation coefficients between GRACE- and CORS-based GWSA were above 0.65 following the 2-month delay phase correction. The variation in the EWH of GRACE- and CORS-based GWSA showed a consistent magnitude of variation. In addition, the annual variation in CORS-based GWSA results was slightly larger than that of GRACE-based GWSA results. Although the principles of GRACE and CORS methods used in the GWSA inversion are different, the results suggested that both methods can effectively reflect the seasonal trend of GWSA in the study area. Indeed, GRACE product data are based on remote sensing techniques to comprehensively reflect the regional effects with redistributed mass, resulting in a low spatial resolution and difficulties in effectively transmitting small-scale regional information. Moreover, the filtering process used in the GRACE data processing might affect the real signal. On the other hand, the CORS data product is derived from GNSS-based monitoring data, allowing us to obtain in real time the geodetic height changes at a certain location, thus assuring faster response and better performance in reflecting the inter-region signal dynamics. Both methods can reflect the GWSA trends. However, the signal intensity and GRACE trend monitoring results at different locations can be basically the same in small-scale areas, while the differences in CORS network monitoring results are more obvious. GRACE is ineffective in determining features of small-scale study areas due to its limited spatial resolution, while CORS network monitoring results exhibit higher spatiotemporal resolution, with continuous and high-precision observation data, making the CORS method advantageous. Moreover, the CORS method can capture local area signals that are difficult to monitor by remote sensing techniques (e.g., GRACE). In summary, the CORS-based GWSA results revealed higher spatiotemporal resolution than that of GRACE-based GWSA results and are more sensitive to groundwater storage changes.
6. Conclusions
The present study aims to invert GWSA in western Yunnan using CORS and high-precision surface mass load data. This approach is based on the already-established CORS network without requiring extra construction costs. This approach is, indeed, able to provide a high-resolution GWSA grid sequence within the coverage of the CORS network due to the high density of CORS stations and consecutive high-precision GNSS monitoring data. Western Yunnan Province was considered in the present study to assess the validity of the approach used. The results demonstrated that the approach is able to independently and effectively invert a high-resolution GWSA grid within the CORS network. In addition, the spatiotemporal distribution characteristics of GWSA were analyzed in this study using the precipitation data observed at meteorological stations in western Yunnan. Moreover, to test the reliability of the obtained results, the GRACE and groundwater monitoring data were used in the present study. The main conclusions are as follows:
- The correlation coefficients between the CORS geodetic height time series and the vertical deformation of the surface mass loads were all above 0.8, indicating strong positive correlations. In addition, the percentage of WRMS decreased from 33.84 to 43.93% following the load removal, demonstrating the effectiveness of the data processing used in the present study and the feasibility of CORS inversion for GWSA. The vertical deformations caused by surface mass loads contributed significantly to the seasonal signals of CORS geodetic height changes. Among the three surface mass loads, atmospheric and soil water loads were more influential, with an amplitude ranging from −8 to 8 mm, while the non-tidal oceanic load showed the lowest influence with an amplitude range of −2–2 mm.
- The GWSA results exhibited clear seasonal variations in the study area from January 2018 to December 2020. In addition, GWS values decreased and increased from February to July and from July to September due to the significant decrease and increase in precipitation, respectively, observed during these periods. These findings indicated that precipitation is the major factor influencing GWS in the study region. In addition, the GWSA trends were similar in the different sub-study areas, while differences were mainly observed in the annual variation magnitude of GWSA. The largest annual variation was observed mainly in the eastern part of the study area, reaching 450 mm.
- After performing a 2-month phase delay correction for GRACE inverse results, the correlation coefficient between GRACE- and CORS-GWSA results was over 0.65. Both methods were able to reflect the dynamics of GWSA in the study area. However, the CORS-based GWSA results reflected more accurately the GWSA changes in the study area, with a higher spatiotemporal resolution than those obtained using the GRACE data product.
- The CORS-based GWSA showed high positive correlations with those determined using groundwater monitoring stations, with a correlation coefficient range of 0.62–0.82. The amplitudes of both GWSA results were on the same order of magnitude. These findings demonstrated the effectiveness and reliability of the CORS inversion for GWSA.
Author Contributions
P.X., T.J. and C.Z. conceived and designed the experiments; P.X. performed the experiments, analyzed the data, and wrote the paper; T.J., W.L. and C.Z. helped in the discussion and revision. K.S. provided the data from the CORS network. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 42074020), the Open Fund Project of the Key Laboratory of Marine Environmental Survey Technology and Application of the Ministry of Natural Resources (MESTA-2020-A001), and the Comprehensive CORS network and multi-source data monitoring of surface stability changes and pilot analysis of geological disaster precursor capture (AR2114).
Data Availability Statement
The raw/processed CORS network and groundwater level data are available from the author upon reasonable request. Correspondence and requests for data should be addressed to T.J.
Acknowledgments
Thanks to the CORS network data provided by the Yunnan Technical Center of Base Surveying and Mapping and the data from groundwater monitoring stations provided by the China Geological Environment Monitoring Institute.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zheng, C.; Liu, J.; Cao, G.; Kendy, E.; Wang, H.; Jia, Y. Can China cope with its water crisis?—Perspectives from the North China Plain. Groundwater 2010, 48, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Doell, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59, 143–156. [Google Scholar] [CrossRef]
- Andermann, C.; Longuevergne, L.; Bonnet, L.; Crave, A.; Davy, P.; Gloaguen, R. Impact of transient groundwater storage on the discharge of Himalayan rivers. Nat. Geosci. 2012, 5, 127–132. [Google Scholar] [CrossRef]
- Hodnett, M.G.; Vendrame, I.; Filho, A.O.M.; Oyama, M.D.; Tomasella, J. Soil water storage and groundwater behaviour in a catenary sequence beneath forest in central Amazonia: I. Comparisons between plateau, slope and valley floor. Hydrol. Earth Syst. Sci. 1997, 1, 265–277. [Google Scholar] [CrossRef]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Sharda, V.N.; Kurothe, R.S.; Sena, D.R.; Pande, V.C.; Tiwari, S.P. Estimation of groundwater recharge from water storage structures in a semi-arid climate of India. J. Hydrol. 2006, 329, 224–243. [Google Scholar] [CrossRef]
- Kim, G.B.; Lee, K.K.; Lee, J.Y.; Yi, M.J. Case study for determination of a water level monitoring frequency for nationwide groundwater monitoring networks in Korea. J. Hydrol. 2007, 342, 223–237. [Google Scholar] [CrossRef]
- Strassberg, G. Evaluation of groundwater storage monitoring with the GRACE satellite: Case study of the High Plains aquifer, central United States. Water Resour. Res. 2009, 45, W05410. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. An analysis of terrestrial water storage variations in Illinois with implications for the Gravity Recovery and Climate Experiment (GRACE). Water Resour. 2001, 37, 1327–1339. [Google Scholar] [CrossRef]
- Wei, F.; Wang, C.; Mu, D.; Min, Z.; Xu, H. Groundwater storage variations in the North China Plain from GRACE with spatial constraints. Chin. J. Geophys. 2017, 60, 1630–1642. [Google Scholar] [CrossRef]
- Flechtner, F.; Neumayer, K.H.; Dahle, C.; Dobslaw, H.; Güntner, A.; Raimondo, J.C.; Fagiolini, E. What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? Surv. Geophys. Int. Rev. J. Geophys. Planet. Sci. 2016, 37, 263–280. [Google Scholar]
- Zhang, C.Y.; Wang, W.; Gan, W.J. Monitoring temporal and spatial changes of crustal deformation and gravity field caused by environmental load in the Three Gorges Reservoir Region based on CORS network. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 1287–1294. [Google Scholar] [CrossRef]
- Baniulis, R.; Galinauskas, K.; Marozas, L.; Parseliunas, E.; Puskorius, V. An Analysis of the Performance and Coordinates Time Series of CORS Network LitPOS. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 22–25. [Google Scholar]
- Métois, M.; Socquet, A.; Vigny, C.; Carrizo, D.; Peyrat, S.; Delorme, A.; Maureira, E.; Valderas-Bermejo, M.-C.; Ortega, I. Revisiting the North Chile seismic gap segmentation using GPS-derived interseismic coupling. Geophys. J. Int. 2013, 194, 1283–1294. [Google Scholar] [CrossRef]
- Daniélyan, Y.S.; Yanitskii, P.A. Stability of the interphase surface in the freezing of moist ground. J. Eng. Phys. 1980, 39, 781–785. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Jiang, T.; Ke, B.G.; Wang, W. The Analysis of Height System Definition and the High Precision GNSS Replacing Leveling Method. Acta Geod. Cartogr. Sin. 2017, 46, 11–17. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–791. [Google Scholar] [CrossRef]
- Blewitt, G.; Clarke, P. Inversion of Earth’s changing shape to weigh sea level in static equilibrium with surface mass redistribution. J. Geophys. Res. 2003, 108, 2311. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, C.Y.; Hu, M.Z.; Yang, Q.; Liang, S.M.; Kang, S.J. Monitoring and analysis of geological hazards in Three Gorges area based on load impact change. Nat. Hazards 2019, 97, 611–622. [Google Scholar] [CrossRef]
- Argus, D.F.; Fu, Y.; Landerer, F.W. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- He, S.Y.; Gu, Y.C.; Fan, D.M.; Zhao, H.; Zheng, R. Seasonal Variation of Terrestrial Water Storage in Yunnan Province lmferredfrom GPS Vertical Observations. Acta Geod. Cartogr. Sin. 2018, 47, 332–340. [Google Scholar] [CrossRef]
- Amos, C.B.; Audet, P.; Hammond, W.C.; Bürgmann, R.; Johanson, I.A.; Blewitt, G. Uplift and seismicity driven by groundwater depletion in central California. Nature 2014, 509, 483–486. [Google Scholar] [CrossRef] [PubMed]
- Gross, R.S.; Blewitt, G.; Clarke, P.J.; Lavallée, D. Degree-2 harmonics of the Earth’s mass load estimated from GPS and Earth rotation data. Geophys. Res. Lett. 2004, 31, L07601. [Google Scholar] [CrossRef]
- Liu, R.L.; Zou, R.; Li, J.C.; Zhang, C.H.; Zhao, B.; Zhang, Y.K. Vertical Displacements Driven by Groundwater Storage Changes in the North China Plain Detected by GPS Observations. Remote Sens. 2018, 10, 259. [Google Scholar] [CrossRef]
- Chanard, K.; Avouac, J.P.; Ramillien, G.; Genrich, J. Modeling deformation induced by seasonal variations of continental water in the Himalaya region: Sensitivity to Earth elastic structure. J. Geophys. Res. Solid Earth 2014, 119, 5097–5113. [Google Scholar] [CrossRef]
- Hew, C.C.; Small, E.E. Terrestrial water storage response to the 2012 drought estimated from GPS vertical position anomalies. Geophys. Res. Lett. 2014, 41, 6145–6151. [Google Scholar] [CrossRef]
- Davis, J.L. Climate-driven deformation of the solid Earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31, L24605. [Google Scholar] [CrossRef]
- Nahmani, S.; Bock, O.; Bouin, M.N.; Santamaría-Gómez, A.; Boy, J.P.; Collilieux, X.; Métivier, L.; Panet, I.; Genthon, P.; Linage, C.D.; et al. Hydrological deformation induced by the West African Monsoon: Comparison of GPS, GRACE and loading models. J. Geophys. Res. Solid Earth 2012, 117, 5409. [Google Scholar] [CrossRef]
- Dardanelli, G.; Brutto, M.L.; Pipitone, C. GNSS CORS network of the University of Palermo: Design and first analysis of data. Geogr. Tech. 2020, 15, 43–69. [Google Scholar] [CrossRef]
- Kenyeres, A.; Bellet, J.G.; Bruyninx, C.; Caporali, A.; Doncker, F.D.; Droscak, B.; Duret, A.; Franke, P.; Georgiec, I.; Bingley, R.; et al. Regional integration of long-term national dense GNSS network solutions. GPS Solut. 2019, 23, 122. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. Introduction to GAMIT/GLOBK; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018; Available online: http://geoweb.mit.edu/gg/Intro_GG.pdf (accessed on 15 May 2021).
- Altamimi, Z.; Collilieux, X.; Métiver, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Sheng, C. Characteristics of non-tectonic crustal deformation from surface loads around Chinese mainland and correction model. Recent Dev. World Seism. 2014, 11, 45–48. [Google Scholar]
- Lombard, A.; Garcia, D.; Ramillien, G.; Cazenave, A.; Biancale, R.; Lemoine, J.M.; Flechtner, F.; Schmidt, R.; Ishii, M. Estimation of steric sea level variations from combined GRACE and Jason-1 data. Earth Planet. Sci. Lett. 2007, 254, 194–202. [Google Scholar] [CrossRef]
- Rodell, M.; Beaudoing, H.K. NASA/GSFC/HSL. GLDAS Noah Land Surface Model L4 Monthly 0.25 × 0.25 Degree V2.1; Goddard Space Flight Center Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2016. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, 2075. [Google Scholar] [CrossRef]
- Blais, J.A.R.; Provins, D.A.; Soofi, M.A. Spherical harmonic transforms for discrete multiresolution applications. J. Supercomput. 2006, 38, 173–187. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometric 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Wang, Z.J.; Ou, J.K. Determining the RidgeParameter in a Ridge Estimation Using L-curve Method. Geomat. Inf. Sci. Wuhan Univ. 2004, 29, 235–238. [Google Scholar] [CrossRef]
- Nussbaumer, H.J. Fast Fourier Transform and Convolution Algorithms; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Tao, R.; Li, B.-Z.; Wang, Y. Spectral Analysis and Reconstruction for Periodic Nonuniformly Sampled Signals in Fractional Fourier Domain. IEEE Trans. Signal Process. 2007, 55, 3541–3547. [Google Scholar] [CrossRef]
- Dam, T.V.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. Solid Earth 2007, 112, B03404. [Google Scholar] [CrossRef]
- Kostadinov, T.S.; Lookingbill, T.R. Snow cover variability in a forest ecotone of the Oregon Cascades via MODIS Terra products. Remote Sens. Environ. 2015, 164, 55–169. [Google Scholar] [CrossRef][Green Version]
- Muhuri, A.; Gascoin, S.; Menzel, L.; Kostadinov, T.; Moreno, J.I.L. Performance Assessment of Optical Satellite-Based Operational Snow Cover Monitoring Algorithms in Forested Landscapes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7159–7178. [Google Scholar] [CrossRef]
- Munekane, H.; Matsuzaka, S. Nontidal ocean mass loading detected by GPS observations in the tropical Pacific region. Geophys. Res. Lett. 2004, 31, 289–291. [Google Scholar] [CrossRef]
- Nordman, M.; Mäkinen, J.; Virtanen, H.; Johansson, J.; Bilker-Koivula, M.; Virtanen, J. Crustal loading in vertical GPS time series in Fennoscandia. J. Geodyn. 2009, 48, 144–150. [Google Scholar] [CrossRef]
- Han, Z.M.; Hhuang, S.Z.; Huang, Q.; Leng, G.Y.; Wang, H.; Bai, Q.J.; Zhao, J.; Ma, L.; Wang, L.; Du, M. Propagation dynamics from meteorological to groundwater drought and their possible influence factors. J. Hydrol. 2019, 578, 124102. [Google Scholar] [CrossRef]
- Feng, W.; Lemoine, J.M.; Zhong, M.; Tou-Tse, H. Terrestrial water storage changes in the Amazon basin measured by GRACE during 2002–2010. Chin. J. Geophys. 2012, 55, 814–821. (In Chinese) [Google Scholar] [CrossRef]
- Gehlin, S.E.A.; Hellstrm, G. Influence on thermal response test by groundwater flow in vertical fractures in hard rock. Renew. Energy 2003, 28, 2221–2238. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; CHEN, X.; Zhang, Z.C. Numerical groundwater modeling in a small karst watershed of the Southwest China. Geotech. Investig. Surv. 2011, 4, 43–51. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).