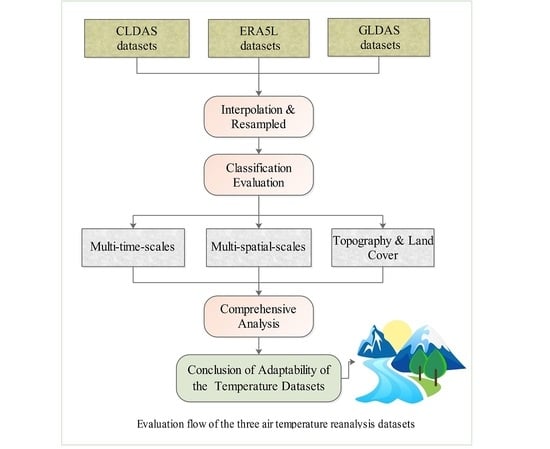
Evaluation of Three Air Temperature Reanalysis Datasets in the Alpine Region of the Qinghai–Tibet Plateau
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.1.1. Reanalysis of Surface Air Temperature
- CLDAS dataset
- 2.
- ERA5L dataset
- 3.
- GLDAS dataset
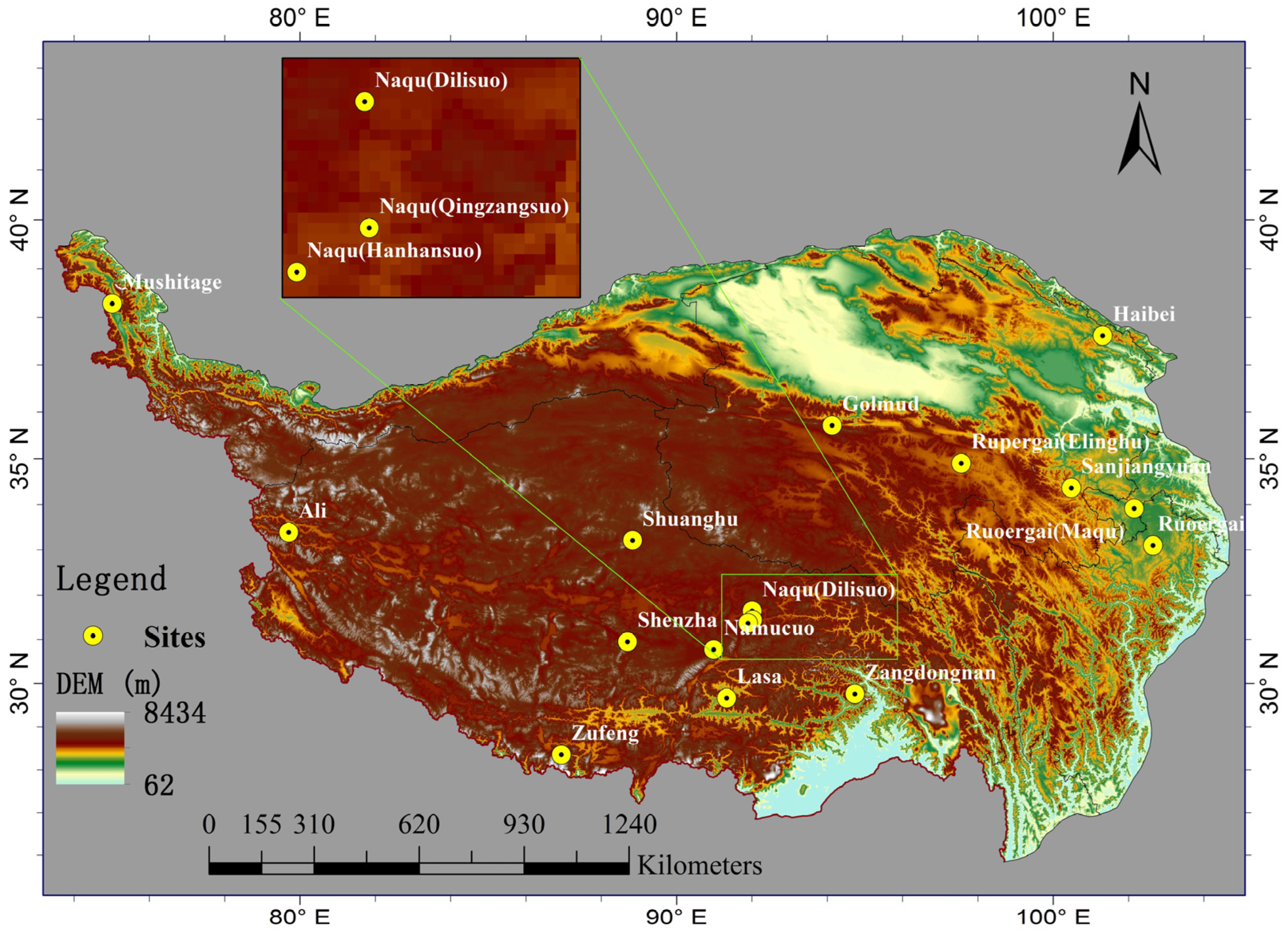
2.1.2. In-Situ Temperature Observations in the Alpine Region of the QTP
2.2. Methods
3. Results Analysis
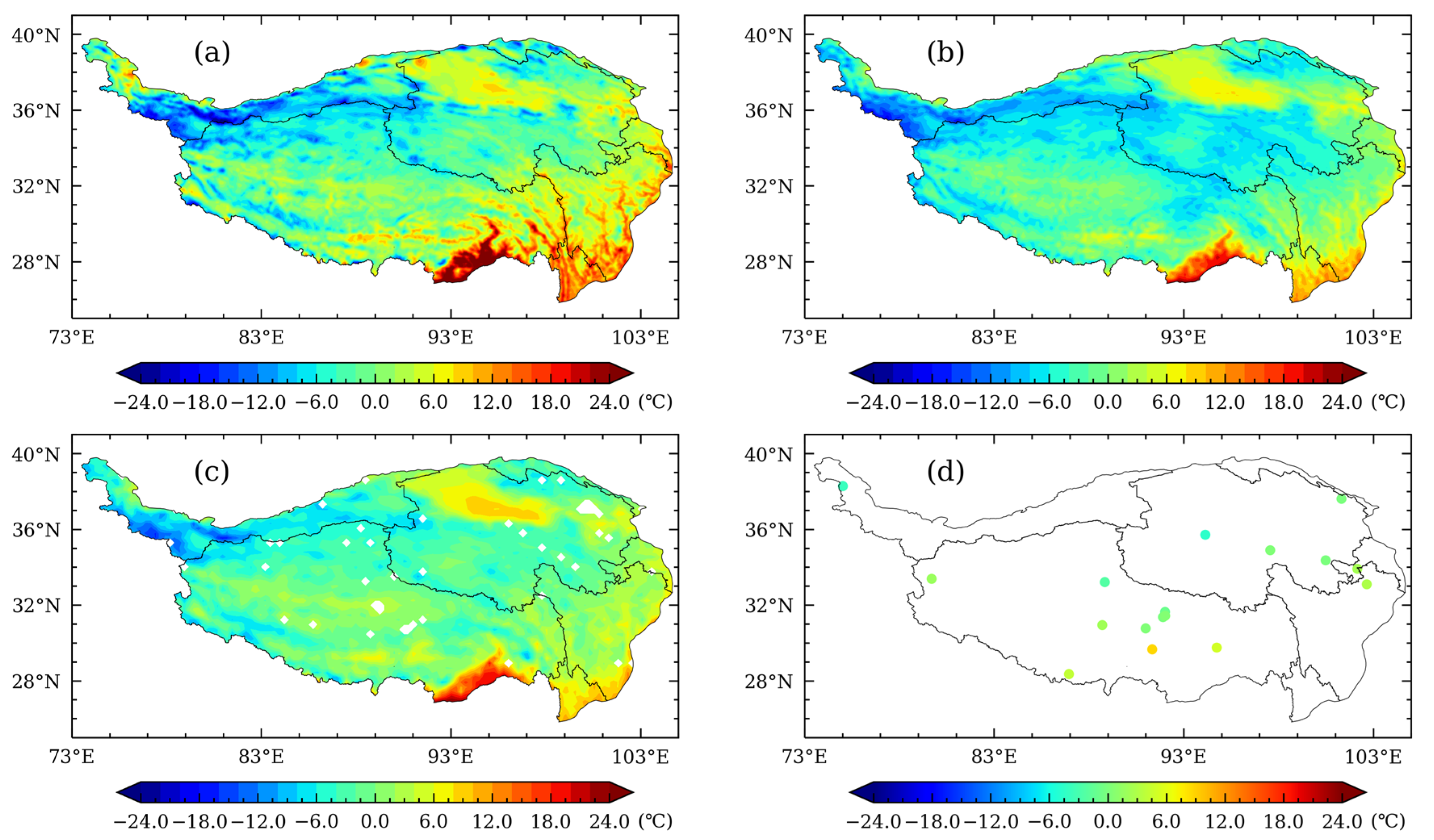
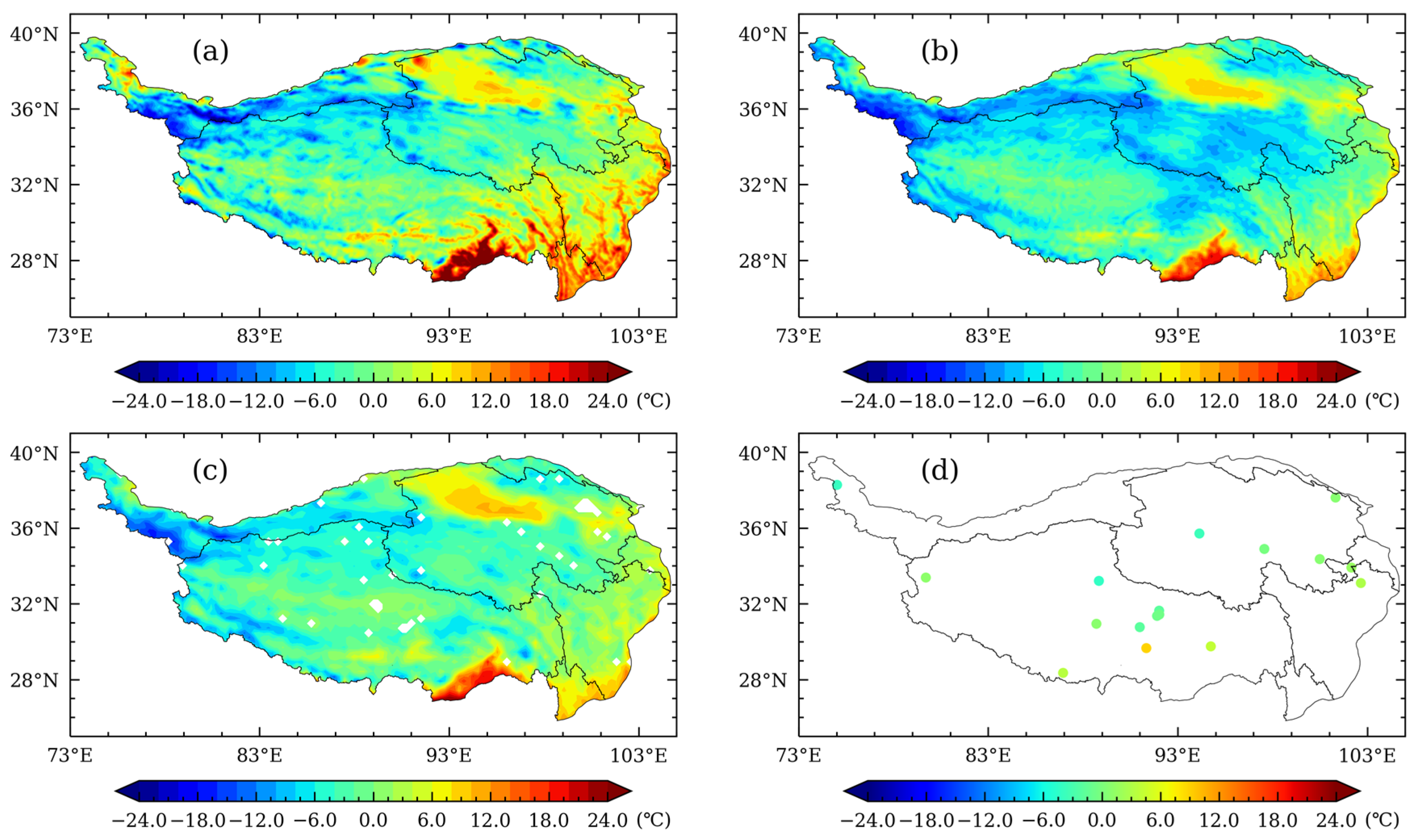
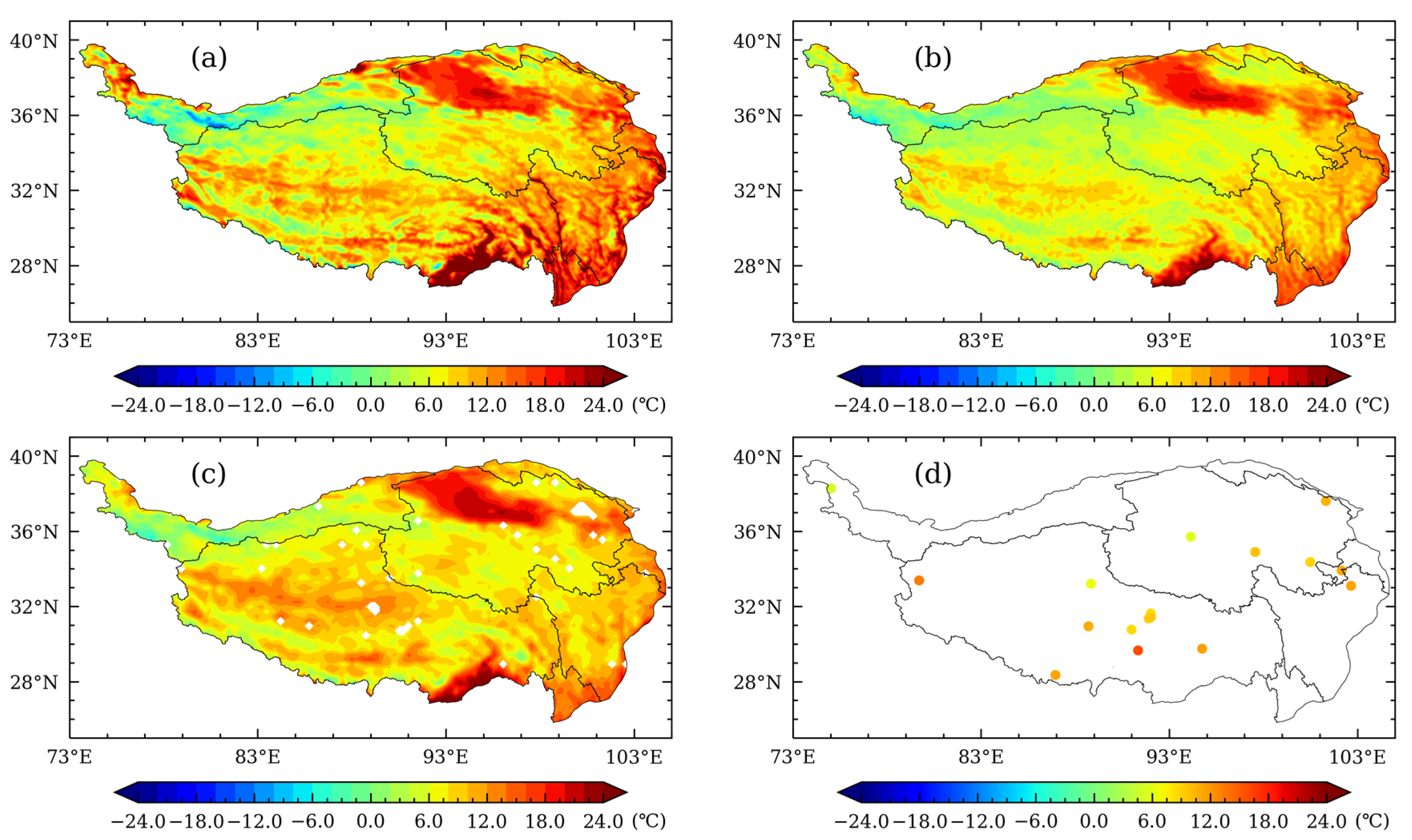
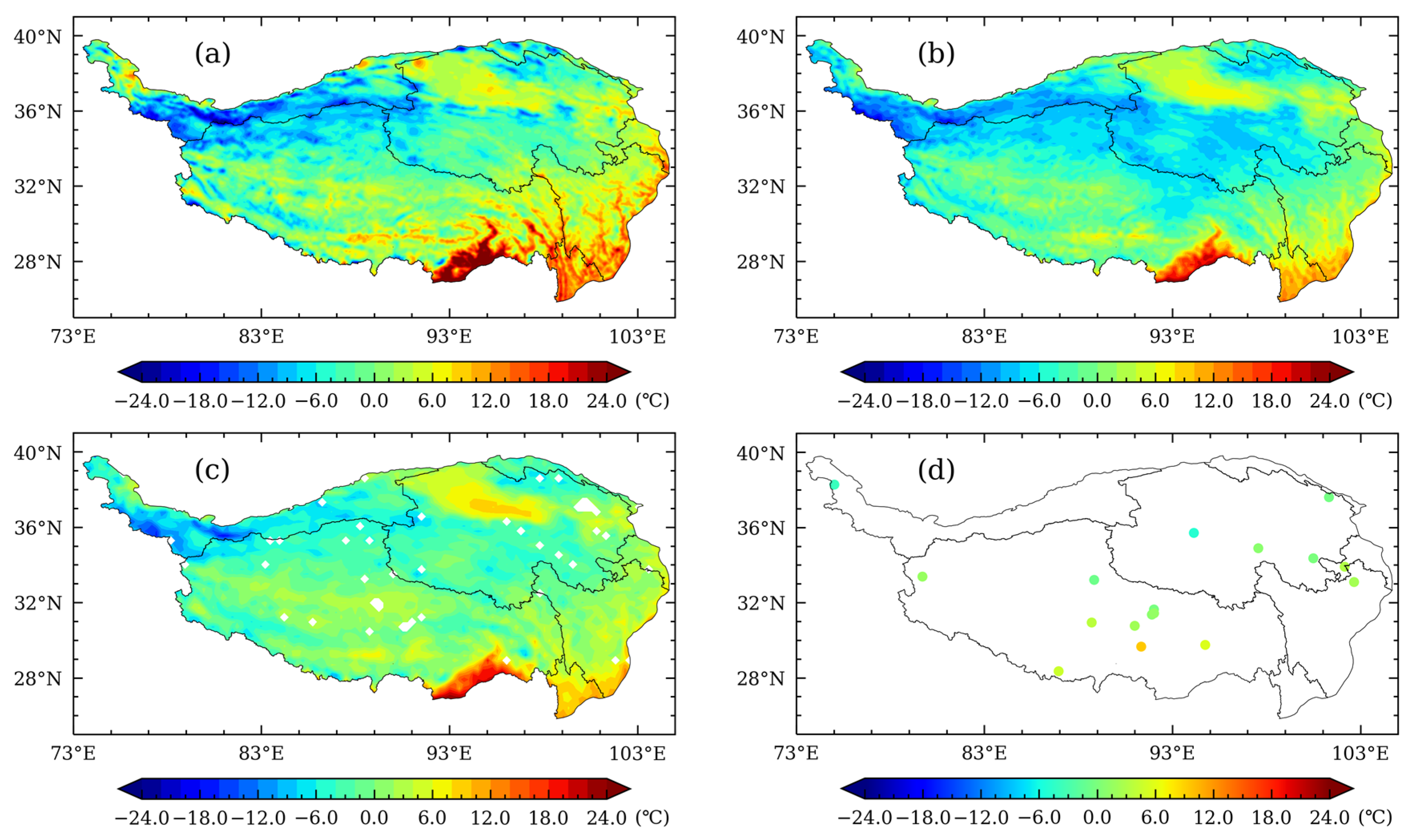
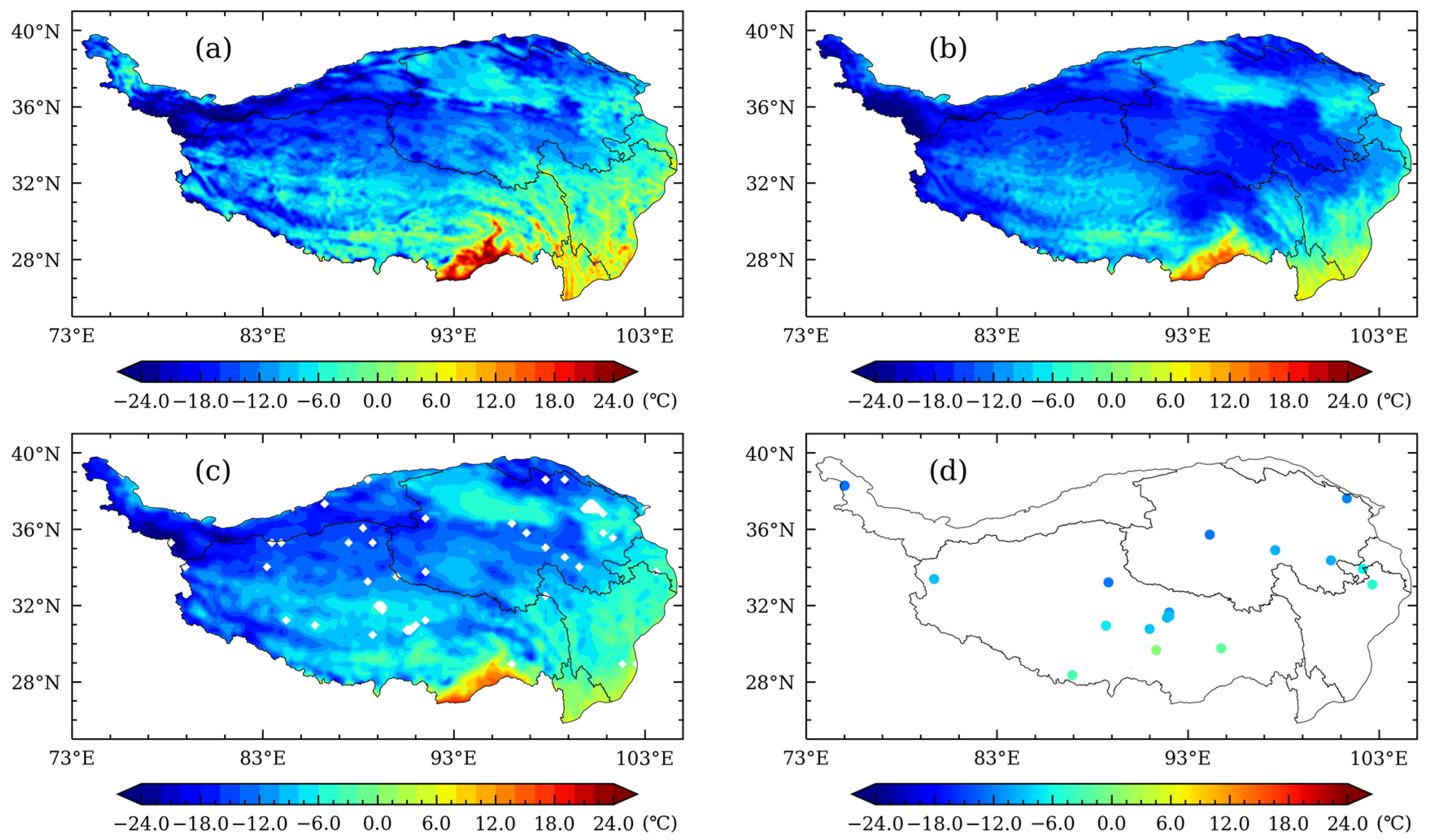
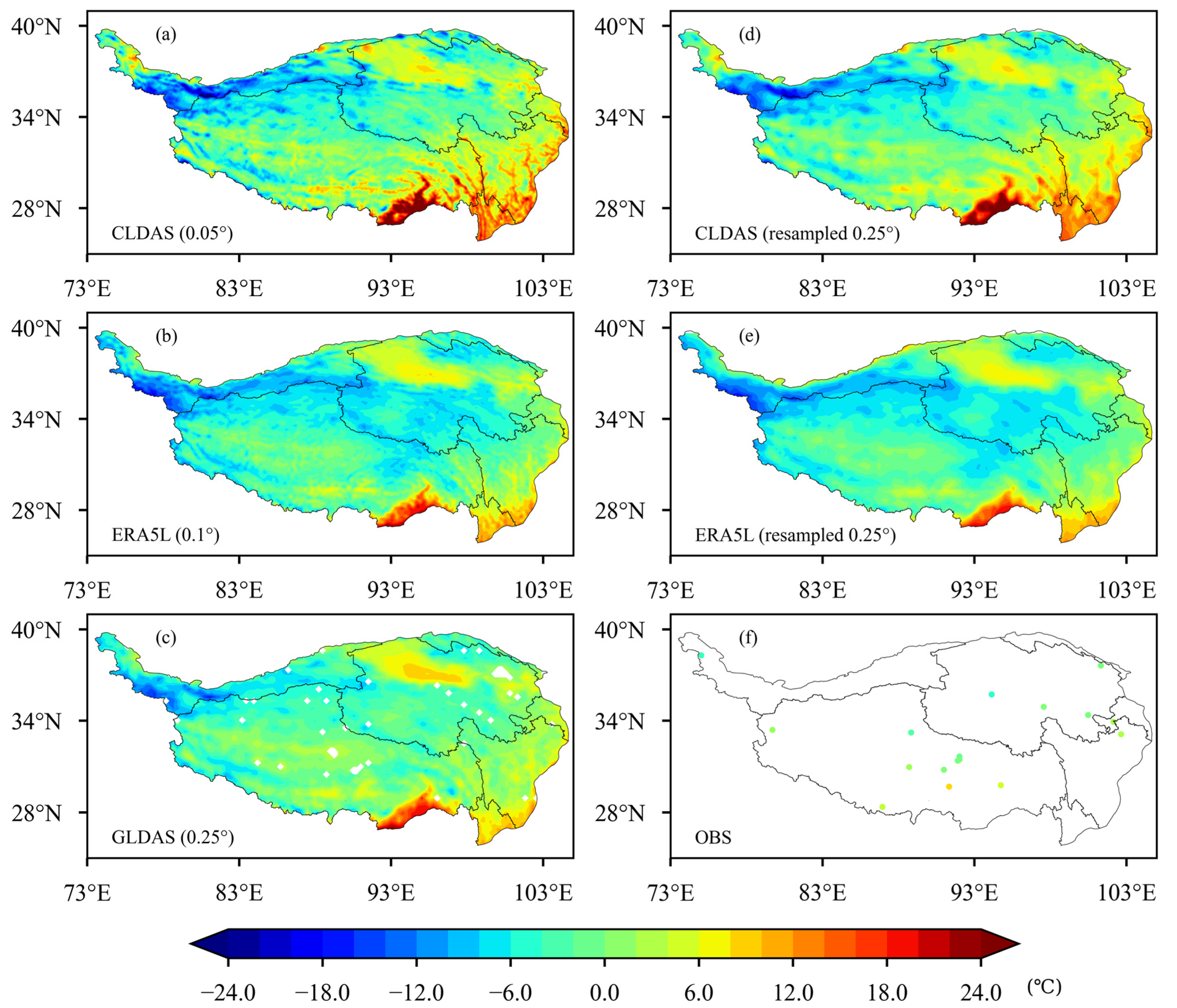
3.1. Comparative Analysis of Spatial Distribution Characteristics
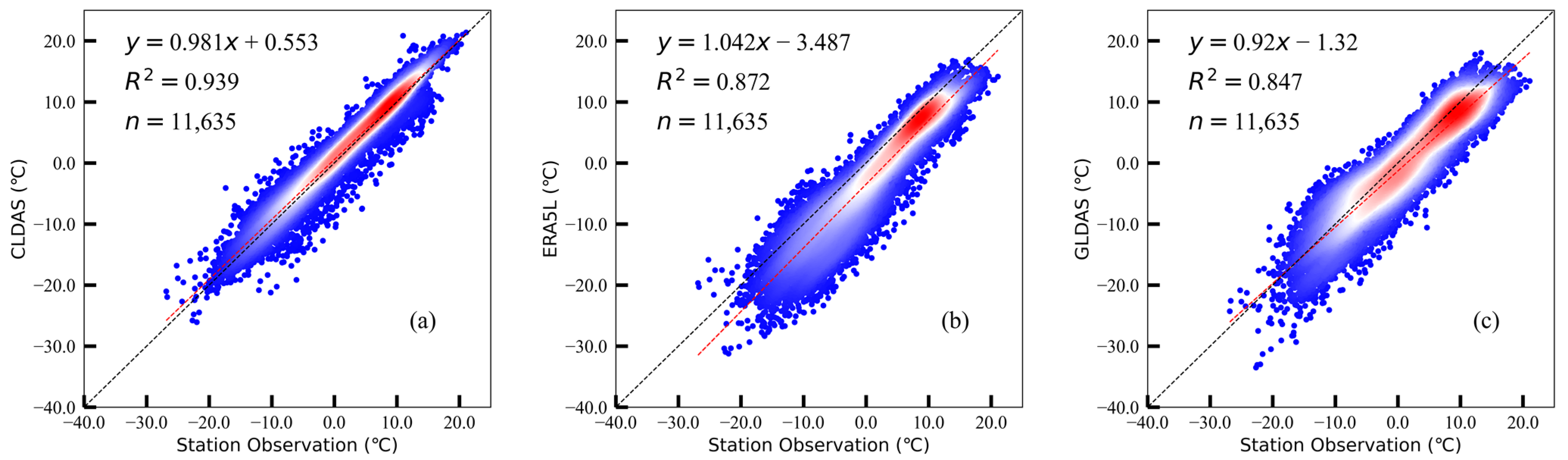
3.2. Accuracy of the Reanalysis Datasets for the Evaluation Period
3.3. Evaluation of Temporal Variation
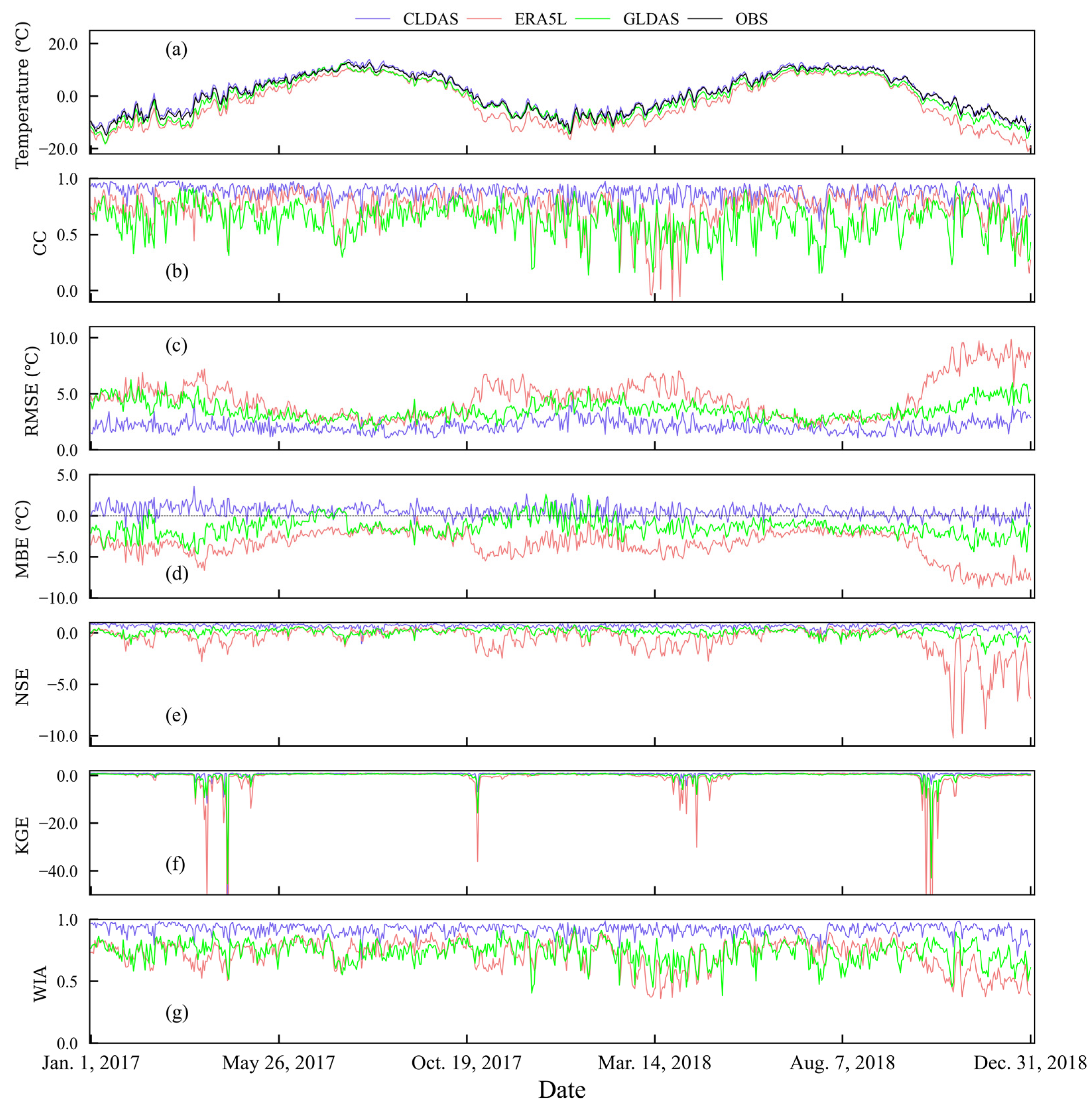
3.3.1. Daily Variation
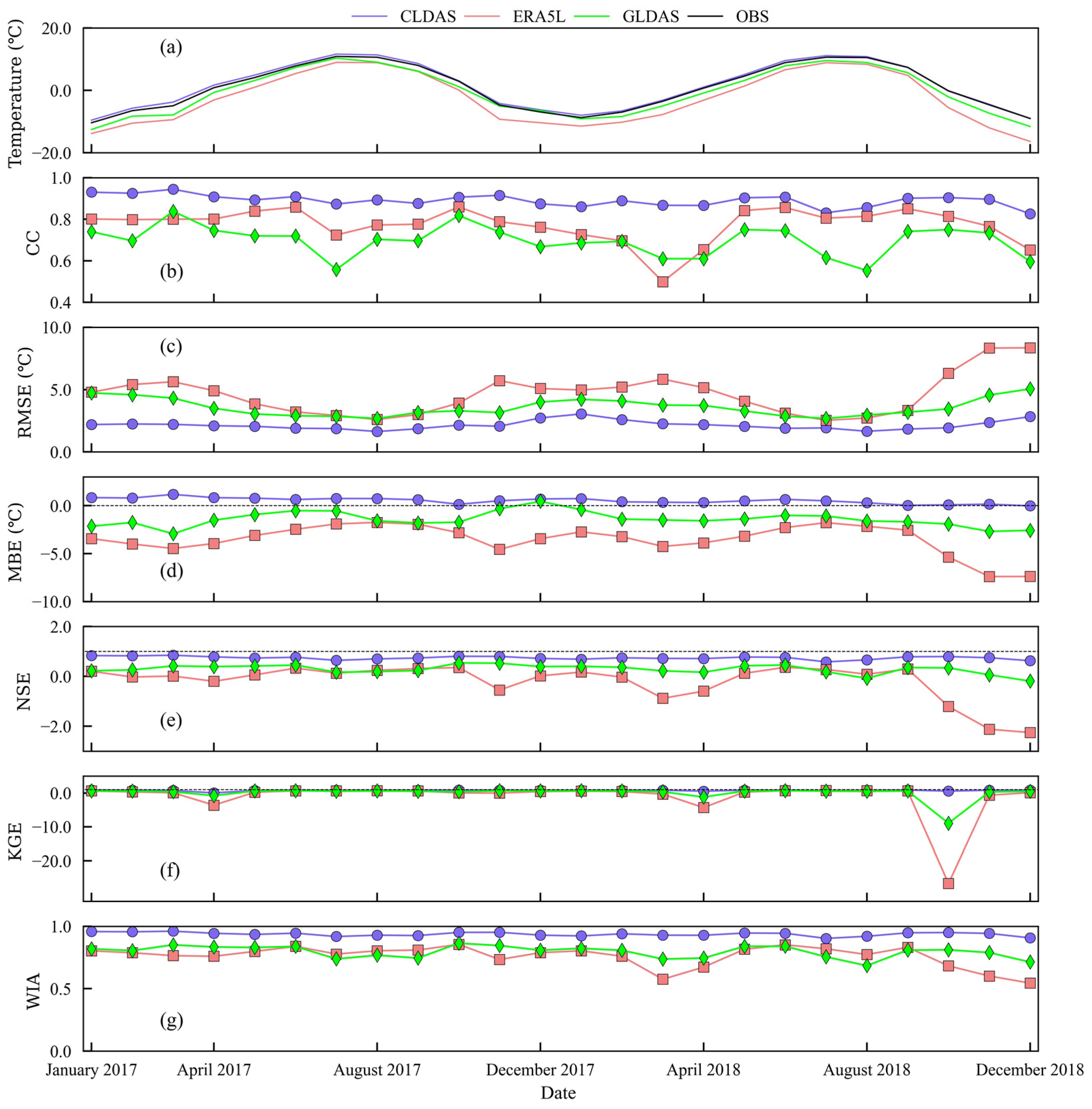
3.3.2. Monthly Variation
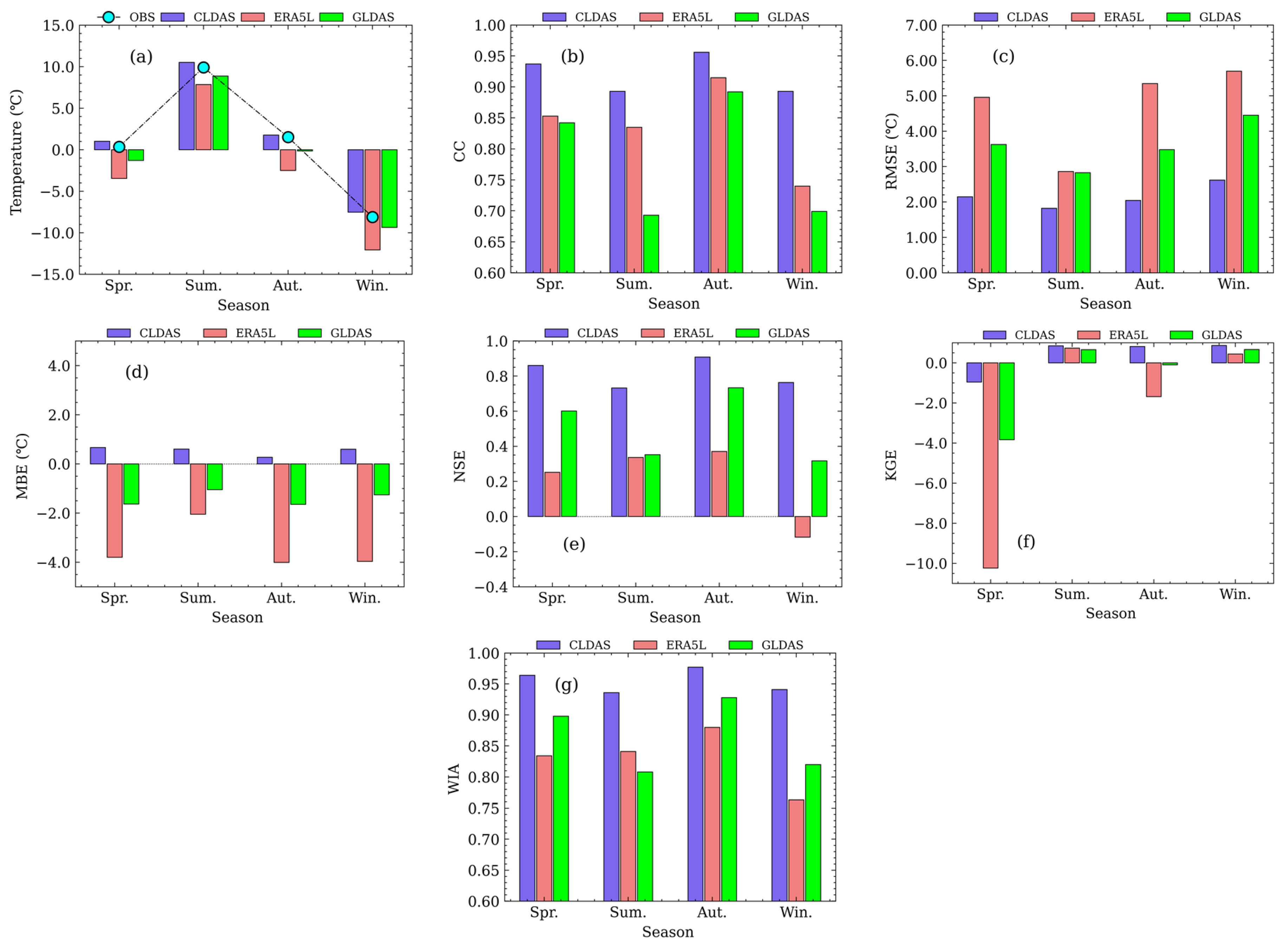
3.3.3. Seasonal Analysis
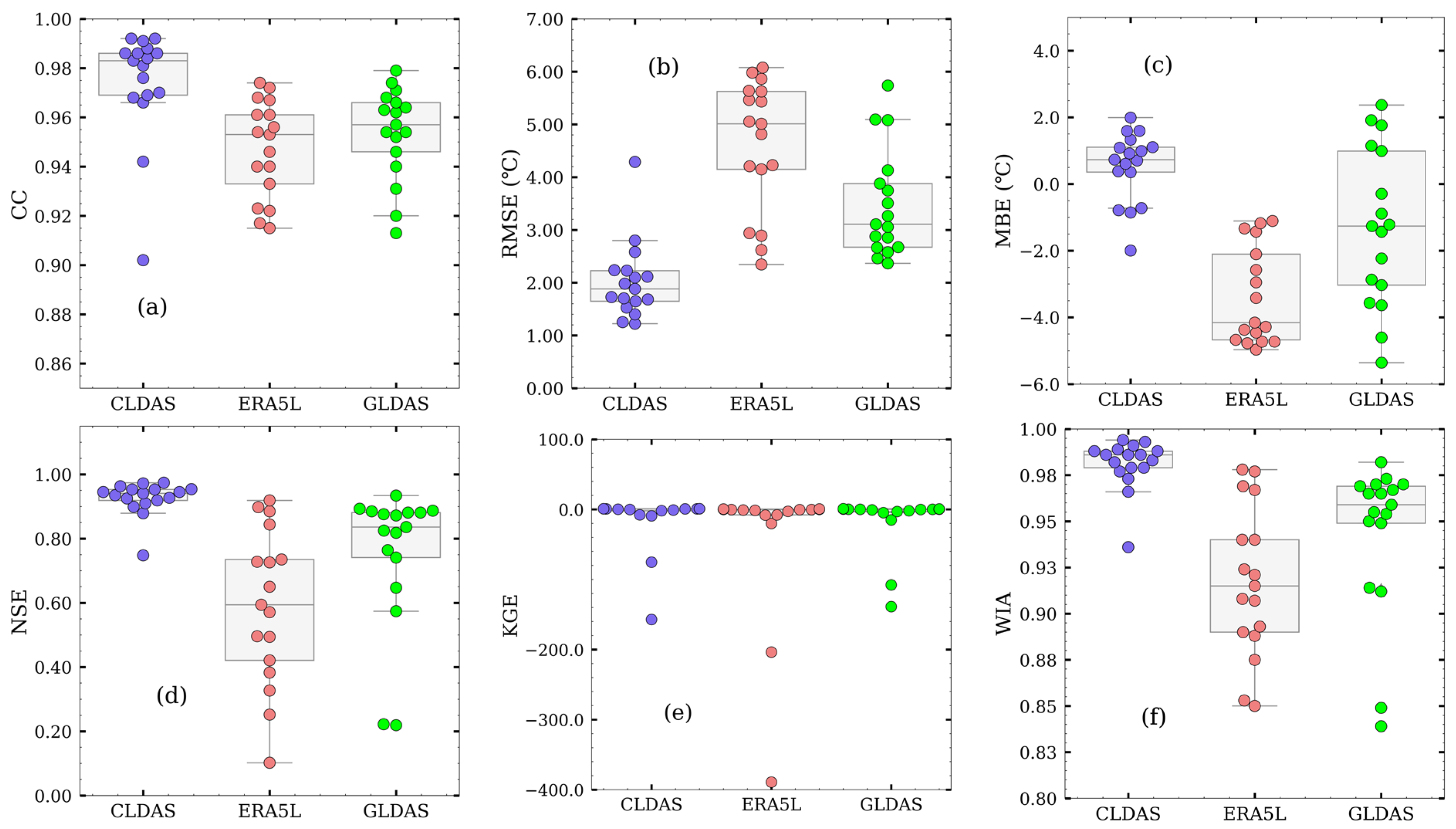
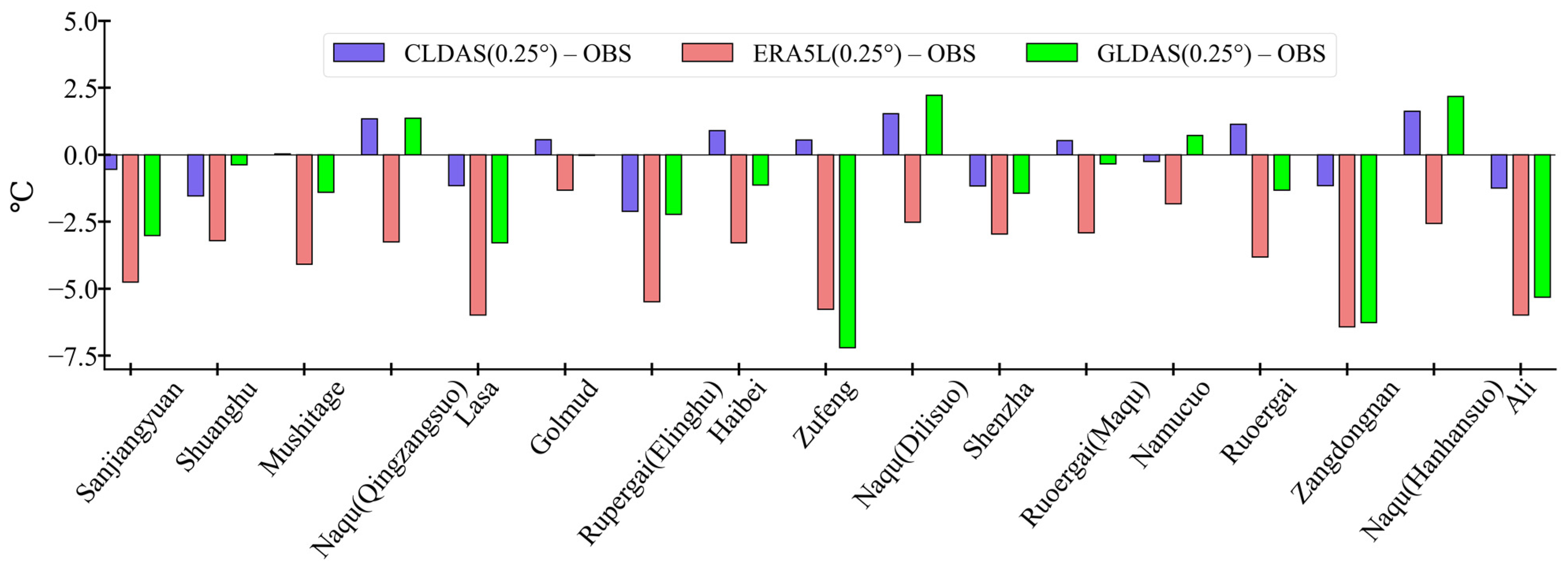
3.4. Comparative Reanalysis at Individual Sites
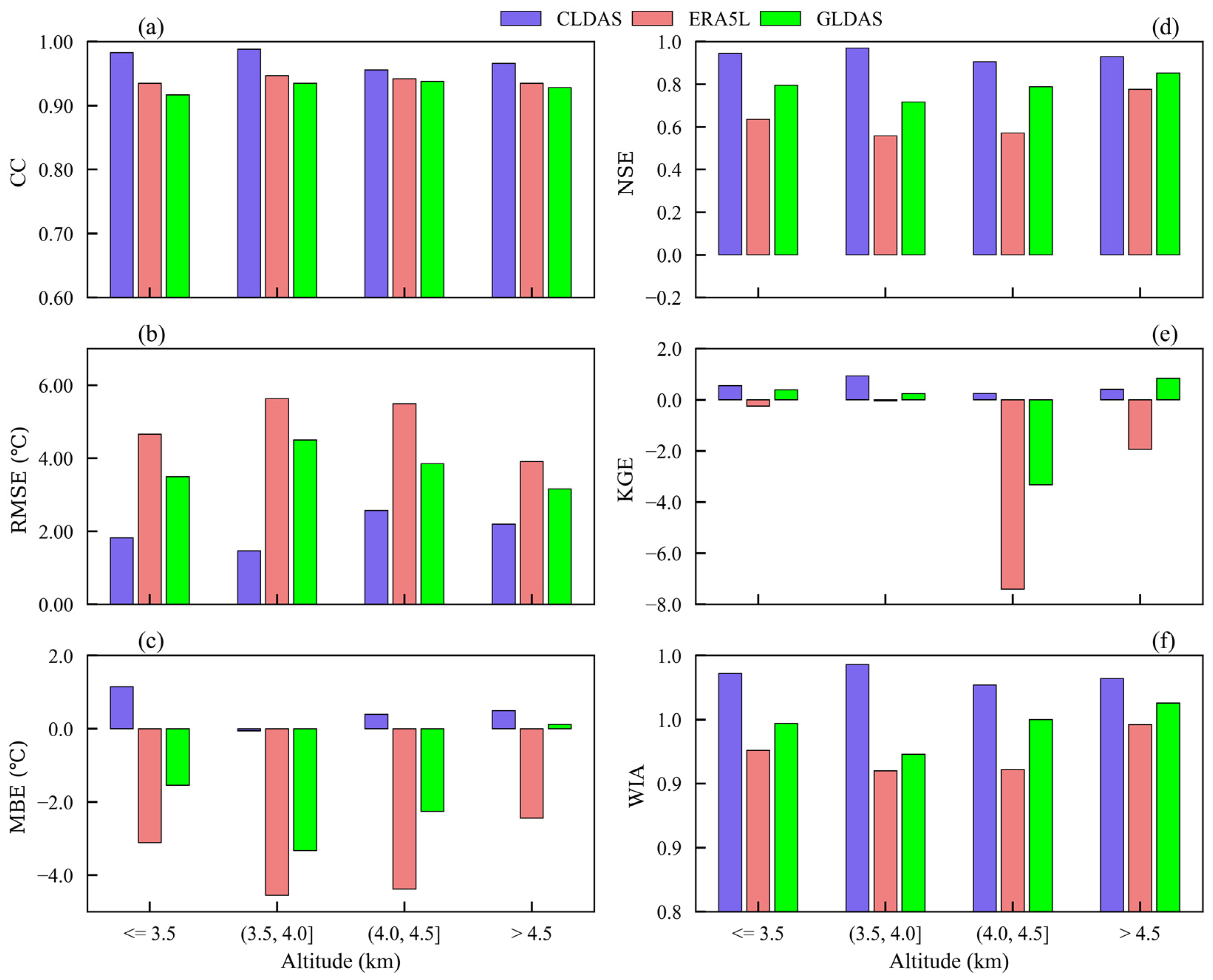
3.5. Comparative Reanalysis at Different Terrain Elevations
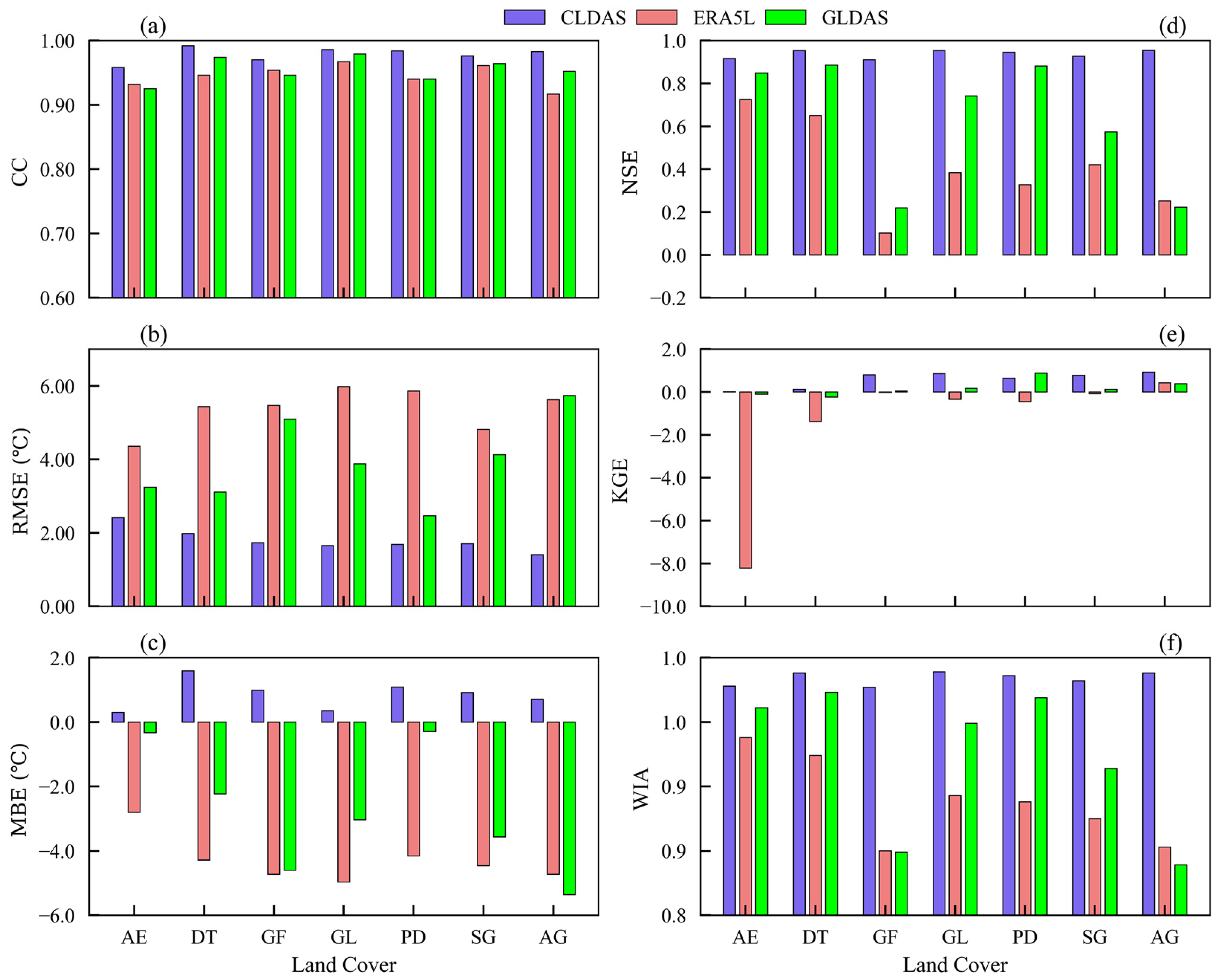
3.6. Comparative Reanalysis at Different Land Covers
4. Discussion
4.1. Inpact of Grid Resolutions on the Accuracy of the Reanalysis Datasets
4.2. Inpact of Interpolation Methods on the Accuracy of the Reanalysis Datasets
5. Conclusions
- (1)
- The spatial distributions of the three reanalysis datasets and the in-situ observations follow the change patterns of latitude and elevation. Temporal variations of average temperature and spatial distributions of temperature in the reanalysis datasets, as well as their correlations with and deviation from in-situ observations, all indicate that the three reanalysis datasets are consistent with observations and demonstrate reasonability. Despite some slight differences in local or regional scales, the magnitudes of the data and their spatial distributions remain consistent.
- (2)
- The spatial distributions of the three reanalysis datasets are consistent, while CLDAS is closer to, and more consistent with, observations than GLDAS and ERA5L are. In the spring, CLDAS temperature is higher than ERA5L and GLDAS over the entire study area except the Qaidam Basin and the low elevation area of southern Tibet. Compared to ERA5L and GLDAS, CLDAS shows smaller differences in spatial distribution. In the summer, spatial distributions of CLDAS and GLDAS are closer, while ERA5L is obviously lower. In the autumn, CLDAS and ERA5L become closer, while GLDAS is relatively low in the high-elevation area of the western QTP but relatively high in the low-elevation area of the southeastern QTP. In the winter, ERA5L is lower than CLDAS and GLDAS in southeastern Qinghai and northeastern Tibet.
- (3)
- Evaluation results on multi-time scales (daily, monthly, and seasonal) and multi-space scales (individual stations, elevations, and land covers) indicate that the accuracy and applicability of CLDAS are discernibly better than the other two datasets. GLDAS is better than ERA5L, but the difference between the two is small. However, the quality of the reanalysis datasets is different at observation sites.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qiu, J. China: The third pole. Nature 2008, 454, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Liu, Y.; Zhang, Q.; Duan, A.; Wang, T.; Wan, R.; Liu, X.; Li, W.; Wang, Z.; Liang, X. The influence of mechanical and thermal forcing by the Tibetan Plateau on Asian climate. J. Hydrometeorol. 2007, 8, 770–789. (In Chinese) [Google Scholar] [CrossRef]
- Xu, X.; Dong, L.; Zhao, Y.; Wang, Y. Effect of the Asian Water Tower over the Qinghai-Tibet Plateau and the characteristics of atmospheric water circulation. Chin. Sci. Bull. 2019, 64, 2830–2841. [Google Scholar] [CrossRef]
- Deliang, C.; Baiqing, X.; Tandong, Y.; ZhengTang, G.; Peng, C.; FaHu, C.; Zhang, R.; Zhang, X.; Zhang, Y.; Jie, F. Assessment of past, present and future environmental changes on the Tibetan Plateau. Chin. Sci. Bull. 2015, 60, 3025–3035. (In Chinese) [Google Scholar] [CrossRef]
- Ma, Y.; Hu, Z.; Tian, L.; Zhang, F.; Duan, A.; Yang, K.; Zhang, Y.; Yang, Y. Study progresses of the Tibet Plateau climate system change and mechanism of its impact on East Asia. Adv. Earth Sci. 2014, 29, 207–215. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, R.; Fengge, S.; Jiang, Z.; Xuejie, G.; Donglin, G.; Jian, N.; Qinglong, Y.; Cuo, L.; BoTao, Z. An overview of projected climate and environmental changes across the Tibetan Plateau in the 21st century. Chin. Sci. Bull. 2015, 60, 3036–3047. (In Chinese) [Google Scholar] [CrossRef]
- Yao, T.; Yu, W.; Wu, G.; Xu, B.; Yang, W.; Zhao, H.; Wang, W.; Li, S.; Wang, N.; Li, Z. Glacier anomalies and relevant disaster risks on the Tibetan Plateau and surroundings. Chin. Sci. Bull. 2019, 64, 2770–2782. (In Chinese) [Google Scholar] [CrossRef]
- Sheridan, S.C.; Lee, C.C.; Smith, E.T. A comparison between station observations and reanalysis data in the identification of extreme temperature events. Geophys. Res. Lett. 2020, 47, e2020GL088120. [Google Scholar] [CrossRef]
- Tandong, Y.; Shilong, P.; Miaogen, S.; Jing, G.; Wei, Y.; Guoqing, Z.; Yanbin, L.; Yang, G.; Liping, Z.; Baiqing, X. Chained impacts on modern environment of interaction between Westerlies and Indian Monsoon on Tibetan Plateau. Bull. Chin. Acad. Sci. 2017, 32, 976–984. (In Chinese) [Google Scholar] [CrossRef]
- Fu, Y.; Ma, Y.; Zhong, L.; Yang, Y.; Guo, X.; Wang, C.; Xu, X.; Yang, K.; Xu, X.; Liu, L. Land-surface processes and summer-cloud-precipitation characteristics in the Tibetan Plateau and their effects on downstream weather: A review and perspective. Natl. Sci. Rev. 2020, 7, 500–515. [Google Scholar] [CrossRef] [Green Version]
- DingYihui, Z. Intercomparison of the time for climate abrupt change between the Tibetan Plateau and other regions in China. Chin. J. Atmos. Sci. 2008, 32, 794–805. (In Chinese) [Google Scholar]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Chen, D.; Li, J.; Ji, Z. Several research frontiers of climate change over the Tibetan Plateau. J. Glaciol. Geocryol. 2021, 43, 885–901. (In Chinese) [Google Scholar] [CrossRef]
- Duo, C.; Yong, Y.; Jiancan, L.; Ciren, B. Applicability analysis of MERRA surface air temperature over the Qinghai-Xizang Plateau. Plateau Meteorol. 2016, 35, 337–350. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.; Pang, G.; Yang, M. Precipitation over the Tibetan Plateau during recent decades: A review based on observations and simulations. Int. J. Climatol. 2018, 38, 1116–1131. [Google Scholar] [CrossRef]
- Zhao, T.; Fu, C. Applicability evaluation of surface air temperature from several reanalysis datasets in China. Plateau Meteorol. 2009, 28, 594–606. (In Chinese) [Google Scholar]
- Zheng, R.; Li, D.; Jiang, Y. New characteristics of temperature change over Qinghai-Xizang Plateau on the background of global warming. Plateau Meteorol. 2015, 34, 1531–1539. (In Chinese) [Google Scholar] [CrossRef]
- Han, S.; Shi, C.; Sun, S.; Gu, J.; Xu, B.; Liao, Z.; Zhang, Y.; Xu, Y. Development and Evaluation of a Real-Time Hourly One-Kilometre Gridded Multisource Fusion Air Temperature Dataset in China Based on Remote Sensing DEM. Remote Sens. 2022, 14, 2480. [Google Scholar] [CrossRef]
- Gao, K.; Duan, A.; Chen, D.; Wu, G. Surface energy budget diagnosis reveals possible mechanism for the different warming rate among Earth’s three poles in recent decades. Sci. Bull. 2019, 64, 1140–1143. [Google Scholar] [CrossRef]
- Lai, H.-W.; Chen, H.W.; Kukulies, J.; Ou, T.; Chen, D. Regionalization of seasonal precipitation over the Tibetan Plateau and associated large-scale atmospheric systems. J. Clim. 2021, 34, 2635–2651. [Google Scholar] [CrossRef]
- Shi, C.; Pan, Y.; Gu, J.; Xu, B.; Han, S.; Zhu, Z.; Zhang, L.; Sun, S.; Jiang, Z. A review of multi-source meteorological data fusion products. Acta Meteorol. Sin. 2019, 77, 774–783. (In Chinese) [Google Scholar] [CrossRef]
- Xia, Y.; Hao, Z.; Shi, C.; Li, Y.; Meng, J.; Xu, T.; Wu, X.; Zhang, B. Regional and global land data assimilation systems: Innovations, challenges, and prospects. J. Meteorol. Res. 2019, 33, 159–189. [Google Scholar] [CrossRef]
- Jiang, Y.; Han, S.; Shi, C.; Gao, T.; Zhen, H.; Liu, X. Evaluation of HRCLDAS and ERA5 Datasets for Near-Surface Wind over Hainan Island and South China Sea. Atmosphere 2021, 12, 766. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Radu, R.; Schepers, D.; Simmons, A.; Soci, C. Global reanalysis: Goodbye ERA-Interim, hello ERA5. ECMWF Newsl. 2019, 159, 17–24. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B. From ERA-Interim to ERA5: The considerable impact of ECMWF’s next-generation reanalysis on Lagrangian transport simulations. Atmos. Chem. Phys. 2019, 19, 3097–3124. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data Discuss. 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Xu, W.; Lei, X.; Chen, S.; Zhang, M.; Jiang, L.; Bao, R.; Guan, X.; Ma, M.; Wei, J.; Feng, A. How well does the ERA5 reanalysis capture the extreme climate events over China? Part II: Extreme temperature. Front. Environ. Sci. 2022, 10, 756. [Google Scholar] [CrossRef]
- Pelosi, A.; Terribile, F.; D’Urso, G.; Chirico, G.B. Comparison of ERA5-Land and UERRA MESCAN-SURFEX reanalysis data with spatially interpolated weather observations for the regional assessment of reference evapotranspiration. Water 2020, 12, 1669. [Google Scholar] [CrossRef]
- Ghazanfari, S.; Pande, S.; Hashemy, M.; Sonneveld, B. Diagnosis of GLDAS LSM based aridity index and dryland identification. J. Environ. Manag. 2013, 119, 162–172. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Wu, Z.; Feng, H.; He, H.; Zhou, J.; Zhang, Y. Evaluation of Soil Moisture Climatology and Anomaly Components Derived from ERA5-Land and GLDAS-2.1 in China. Water Resour. Manag. 2021, 35, 629–643. [Google Scholar] [CrossRef]
- Shi, C.; Xie, Z.; Qian, H.; Liang, M.; Yang, X. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Han, S.; Shi, C.; Jiang, Z.; Xu, B.; Li, X.; Zhang, T.; Jiang, L.; Liang, X.; Zhu, Z.; Liu, J. Development and progress of high resolution CMA land surface data assimilation system. Adv. Meteorol. Sci. Technol. 2018, 8, 102–108 + 116. (In Chinese) [Google Scholar] [CrossRef]
- Sun, S.; Shi, C.; Pan, Y.; Bai, L.; Xu, B.; Zhang, T.; Han, S.; Jiang, L. Applicability assessment of the 1998–2018 CLDAS multi-source precipitation fusion dataset over China. J. Meteorol. Res. 2020, 34, 879–892. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W.; Xiao, C.; Ai, W. Evaluation of High-Resolution Crop Model Meteorological Forcing Datasets at Regional Scale: Air Temperature and Precipitation over Major Land Areas of China. Atmosphere 2020, 11, 1011. [Google Scholar] [CrossRef]
- Han, S.; Shi, C.; Xu, B.; Sun, S.; Zhang, T.; Jiang, L.; Liang, X. Development and Evaluation of Hourly and Kilometer Resolution Retrospective and Real-Time Surface Meteorological Blended Forcing Dataset(SMBFD) in China. J. Meteorol. Res. 2019, 33, 1168–1181. [Google Scholar] [CrossRef]
- Liu, L.; Gu, H.; Xie, J.; Xu, Y.P. How well do the ERA-Interim, ERA-5, GLDAS-2.1 and NCEP-R2 reanalysis datasets represent daily air temperature over the Tibetan Plateau? Int. J. Climatol. 2021, 41, 1484–1505. [Google Scholar] [CrossRef]
- Han, S.; Liu, B.; Shi, C.; Liu, Y.; Qiu, M.; Sun, S. Evaluation of CLDAS and GLDAS datasets for Near-surface Air Temperature over major land areas of China. Sustainability 2020, 12, 4311. [Google Scholar] [CrossRef]
- Huang, X.; Han, S.; Shi, C. Multiscale Assessments of Three Reanalysis Temperature Data Systems over China. Agriculture 2021, 11, 1292. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, C.; Wang, H.; Han, S. Applicability assessment of CLDAS temperature data in China. Trans. Atmos. Sci. 2021, 44, 540–548. (In Chinese) [Google Scholar] [CrossRef]
- Wang, W.; Gao, Y.; Xu, J. Applicability of GLDAS and climate change in the Qinghai-Xizang Plateau and its surrounding arid area. Plateau Meteorol. 2013, 32, 635–645. (In Chinese) [Google Scholar] [CrossRef]
- Peng, P.; Zhu, L. Observations of land surface processes of the Tibetan Plateau based on the field stations network. Sci. Technol. Rev. 2017, 35, 97–102. (In Chinese) [Google Scholar] [CrossRef]
- Peng, P.; Zhu, L. Meteorological Data of Surface Environment and Observation Network in China’s Cold Region (2018); National Tibetan Plateau Data Center: Beijing, China, 2020. [Google Scholar] [CrossRef]
- Rolland, C. Spatial and seasonal variations of air temperature lapse rates in Alpine regions. J. Clim. 2003, 16, 1032–1046. [Google Scholar] [CrossRef]
- Camargo, L.R.; Schmidt, J. Simulation of multi-annual time series of solar photovoltaic power: Is the ERA5-land reanalysis the next big step? Sustain. Energy Technol. Assess. 2020, 42, 100829. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, X.; Chen, X. Evaluation of GLDAS-1 and GLDAS-2 forcing data and Noah model simulations over China at the monthly scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]
- Rui, H.; Beaudoing, H. README Document for NASA GLDAS Version 2 Data Products. Available online: https://hydro1.gesdisc.eosdis.nasa.gov/data/GLDAS/README_GLDAS2.pdf (accessed on 10 July 2022).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Ji, L.; Senay, G.B.; Verdin, J.P.J.J.o.H. Evaluation of the Global Land Data Assimilation System (GLDAS) air temperature data products. J. Hydrometeorol. 2015, 16, 2463–2480. [Google Scholar] [CrossRef]
- You, Q.; Fraedrich, K.; Ren, G.; Pepin, N.; Kang, S. Variability of temperature in the Tibetan Plateau based on homogenized surface stations and reanalysis data. Int. J. Climatol. 2013, 33, 1337–1347. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Pepin, N.; Flügel, W.-A.; Yan, Y.; Behrawan, H.; Huang, J. Relationship between temperature trend magnitude, elevation and mean temperature in the Tibetan Plateau from homogenized surface stations and reanalysis data. Glob. Planet. Chang. 2010, 71, 124–133. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Lu, L. Spatial analysis of air temperature in the Qinghai-Tibet Plateau. Arct. Antarct. Alp. Res. 2005, 37, 246–252. [Google Scholar] [CrossRef]
- Yang, J.; Huang, M.; Zhai, P. Performance of the CRA-40/Land, CMFD, and ERA-Interim datasets in reflecting changes in surface air temperature over the Tibetan Plateau. J. Meteorol. Res. 2021, 35, 663–672. [Google Scholar] [CrossRef]
- Yin, H.; Sun, Y.; Donat, M.G. Changes in temperature extremes on the Tibetan Plateau and their attribution. Environ. Res. Lett. 2019, 14, 124015. [Google Scholar] [CrossRef]
- Ding, L.; Zhou, J.; Zhang, X.; Liu, S.; Cao, R. Downscaling of surface air temperature over the Tibetan Plateau based on DEM. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 136–147. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, L.; Wu, X.; Li, R.; Wu, T.; Su, Y.; Hao, J.J.T.; Climatology, A. Evaluation of reanalysis air temperature products in permafrost regions on the Qinghai-Tibetan Plateau. Theor. Appl. Climatol. 2019, 138, 1457–1470. [Google Scholar] [CrossRef]
- Peng, X.; Frauenfeld, O.W.; Jin, H.; Du, R.; Qiao, L.; Zhao, Y.; Mu, C.; Zhang, T. Assessment of temperature changes on the Tibetan Plateau during 1980–2018. Earth Space Sci. 2021, 8, e2020EA001609. [Google Scholar] [CrossRef]
- Ding, M.; Du, J.; Xiao, T. Applicability of the four reanalysis temperature data in Chang Tang Nature Reserve. J. Glaciol. Geocryol. 2020, 42, 1046–1056. (In Chinese) [Google Scholar] [CrossRef]
- Long, K.; Shi, C.; Han, S.; Huang, X.; Xu, X.; Sun, S.; Gu, J. Quality assessment of High Resolution Temperature Merged Grid Analysis Product in China. Plateau Mt. Meteorol. Res. 2019, 39, 67–74. (In Chinese) [Google Scholar] [CrossRef]
- Shi, G.; Sun, Z.; Qiu, X.; Zeng, Y.; Chen, P.; Liu, C. Comparison of two air temperature gridding methods over complex terrain in China. Theor. Appl. Climatol. 2018, 133, 1009–1019. [Google Scholar] [CrossRef]
- Gao, L.; Bernhardt, M.; Schulz, K. Elevation correction of ERA-Interim temperature data in complex terrain. Hydrol. Earth Syst. Sci. 2012, 16, 4661–4673. [Google Scholar] [CrossRef]
- Wang, A.; Zeng, X. Evaluation of multireanalysis products with in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2012, 117, d05102. [Google Scholar] [CrossRef]

| Dataset | Areal Coverage | Spatial Resolution | Temporal Resolution | Unit | Website for Download |
|---|---|---|---|---|---|
| GLDAS | 180°W–180°E; 60°S–90°N | 0.25° × 0.25° | 3 hourly | K | http://disc.sci.gsfc.nasa.gov/hydrology/data-holdings (accessed on 30 June 2022) |
| ERA5L | 180°W–180°E; 60°S–90°N | 0.1° × 0.1° | Hourly | K | https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-ERA5L?tab=form (accessed on 30 June 2022) |
| CLDAS | 70°E–140°E; 0°–60°N | 0.05° × 0.05° | Hourly | K | http://data.cma.cn/ (accessed on 30 June 2022) |
| NO. | Name | Longitude (°) | Latitude (°) | Elevation (m) | Height of the Sensor from the Ground (m) | Land Cover Type |
|---|---|---|---|---|---|---|
| 1 | Zangdongnan | 94.7363 | 29.7593 | 3326 | 1.3 | Grassland in forests |
| 2 | Namucuo | 90.9885 | 30.7740 | 4730 | 1.5 | Alpine meadow |
| 3 | Zufeng | 86.9422 | 28.3590 | 4276 | 1.5 | Sand and gravel |
| 4 | Golmud | 94.1333 | 35.7167 | 4538 | 2.0 | Alpine meadow |
| 5 | Lasa | 91.3333 | 29.6667 | 3688 | 1.5 | Artificial grassland |
| 6 | Mushitage | 75.0183 | 38.2868 | 4400 | 1.5 | Gravel |
| 7 | Ali | 79.7013 | 33.3917 | 4264 | 1.5 | Desert |
| 8 | Rupergai (Elinghu) | 97.5588 | 34.9021 | 4278 | 2.0 | Alpine meadow |
| 9 | Sanjiangyuan | 100.4833 | 34.3667 | 3958 | 1.5 | Alpine meadow |
| 10 | Shenzha | 88.7000 | 30.9500 | 4675 | 2.0 | Alpine meadow |
| 11 | Ruoergai | 102.6509 | 33.1026 | 3483 | 2.7 | Peatland |
| 12 | Ruoergai (Maqu) | 102.1515 | 33.9205 | 3430 | 2.0 | Alpine meadow |
| 13 | Naqu (Dilisuo) | 92.0097 | 31.6437 | 4602 | 1.8 | Alpine meadow |
| 14 | Naqu (Qingzangsuo) | 92.0170 | 31.4410 | 4500 | 1.5 | Alpine meadow |
| 15 | Shuanghu | 88.8322 | 33.2167 | 4939 | 2.0 | Alpine meadow |
| 16 | Haibei | 101.3167 | 37.6167 | 3220 | 1.5 | Alpine meadow |
| 17 | Naqu (Hanhansuo) | 91.9000 | 31.3700 | 4509 | 1.5 | Alpine meadow |
| Dataset | Mean Temperature (°C) | CC | MBE (°C) | RMSE (°C) | NSE | KGE | WIA |
|---|---|---|---|---|---|---|---|
| CLDAS | 1.49 | 0.969 | 0.534 | 2.175 | 0.933 | 0.44 | 0.983 |
| ERA5L | −2.491 | 0.934 | −3.447 | 4.827 | 0.67 | −2.609 | 0.927 |
| GLDAS | −0.44 | 0.92 | −1.396 | 3.638 | 0.813 | −0.463 | 0.952 |
| Dataset | CC | MBE (°C) | RMSE (°C) | NSE | KGE | WIA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nea | Bil | Nea | Bil | Nea | Bil | Nea | Bil | Nea | Bil | Nea | Bil | |
| CLDAS | 0.969 | 0.968 | 0.534 | 0.404 | 2.175 | 2.179 | 0.933 | 0.933 | 0.44 | 0.576 | 0.983 | 0.983 |
| ERA5L | 0.934 | 0.933 | −3.447 | −3.61 | 4.827 | 4.942 | 0.67 | 0.654 | −2.609 | −2.779 | 0.927 | 0.924 |
| GLDAS | 0.92 | 0.927 | −1.396 | −1.103 | 3.638 | 3.37 | 0.813 | 0.839 | −0.463 | −0.157 | 0.952 | 0.958 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Han, S.; Shi, C. Evaluation of Three Air Temperature Reanalysis Datasets in the Alpine Region of the Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 4447. https://doi.org/10.3390/rs14184447
Huang X, Han S, Shi C. Evaluation of Three Air Temperature Reanalysis Datasets in the Alpine Region of the Qinghai–Tibet Plateau. Remote Sensing. 2022; 14(18):4447. https://doi.org/10.3390/rs14184447
Chicago/Turabian StyleHuang, Xiaolong, Shuai Han, and Chunxiang Shi. 2022. "Evaluation of Three Air Temperature Reanalysis Datasets in the Alpine Region of the Qinghai–Tibet Plateau" Remote Sensing 14, no. 18: 4447. https://doi.org/10.3390/rs14184447
APA StyleHuang, X., Han, S., & Shi, C. (2022). Evaluation of Three Air Temperature Reanalysis Datasets in the Alpine Region of the Qinghai–Tibet Plateau. Remote Sensing, 14(18), 4447. https://doi.org/10.3390/rs14184447