Abstract
The high-precision geometric positioning of optical remote sensing satellites is the prerequisite to determine the application capability of satellite image products. Its positioning accuracy is related to the observation accuracy of each link in the imaging process, including satellite attitude, orbit measurement accuracy, time synchronization accuracy, camera measurement accuracy, and so on. Untimely and inaccurate on-orbit calibration will lead to great geometric positioning errors. To optimize the positioning accuracy of satellite images with the rational function model (RFM) under low positioning accuracy, our paper proposes an improved geometric quality model based on the reorientation of internal and external orientation elements in the RFM model of remote sensing images. By establishing the rational function positioning model, the external orientation model, and the internal orientation model, the original image can be reorientated. Then, we use the improved model to generate uniformly distributed virtual ground control points. By analyzing and verifying the relationship between each rational polynomial coefficient (RPC) and its influence on geometric positioning accuracy, we propose an RPC coefficients optimization method based on image offset correction and positioning dominant coefficients. Finally, we use the small satellite “MN200Sar-1” with low geometric accuracy for experimental verification. The results show that the model can effectively eliminate the errors of internal and external elements in the on-orbit calibration, and the positioning accuracy is improved from one hundred pixels to one pixel. At the same time, the rational polynomial dominant coefficient optimization method can improve geometric positioning accuracy without introducing additional compensation parameters.
1. Introduction
With the continuous rise of commercial remote sensing satellite technology, optical remote sensing satellite resolution is becoming higher and higher, imaging mode is becoming more and more diverse, and high-resolution remote sensing earth observation has become an important means of geospatial information acquisition. It is more urgent for the national economy and national defense construction to master the characteristics of spatial geographic information, which is widely used in change detection, multi-source data fusion, digital elevation map (DEMs) generation, image classification, and other fields [1]. Therefore, how to achieve high-precision satellite geometric positioning has become the focus of research. The development of small satellites provides a new method for obtaining repeated observations in a short time. However, compared with standard satellite images, the geometric performance of small satellite images is relatively poor, because the accuracy of small satellite positioning and attitude measurement systems is relatively low, it may have different degrees of time synchronization error, and the error cannot be eliminated by the geometric calibration process. Compared with IKONOS, WorldView-2, and other satellites, the positioning accuracy can be up to two orders of magnitude different. Therefore, it is necessary to study the geometric quality improvement of satellites with low geometric positioning accuracy.
There are many kinds of full-link errors in satellite remote sensing imaging, including satellite attitude measurement accuracy, orbit measurement accuracy, time synchronization accuracy, and camera parameter accuracy. The attitude and orbit accuracy and time synchronization accuracy are equivalent to external orientation accuracy, and camera parameter accuracy is equivalent to internal orientation accuracy. The internal and external orientation of satellites can be realized by the strict imaging model or rational function model. Among them, the rational function model is independent of sensors, has simple calculation and strong universality, and has become the mainstream model to replace the strict imaging model for satellite post-processing [2,3,4]. The rational function model generated by using the strict imaging model without control points has some systematic errors [5,6], including incomplete calibration errors and random errors in the process of the rational function model generation.
External orientation accuracy is determined by satellite attitude and orbit accuracy, including installation errors, GPS orbit determination errors, eccentricity errors, attitude determination errors, and time synchronization errors [7]. In order to eliminate these errors, various compensation models are proposed, including the offset model, the affine transformation model, and the quadratic polynomial model [8,9,10]. In general, external orientation can be corrected by a small number of control points. However, the internal orientation process is relatively complex, including satellite attitude jitter, camera distortion, CCD translation, rotation errors, and other errors, which are difficult to correct with a simple compensation model [11,12]. Most of the errors can be eliminated by on-orbit geometric calibration. For example, Wang et al. proposed a robust on-orbit geometric calibration method for both elements of interior and exterior orientation. This method has been used in a ZY1-02C panchromatic camera and ZY-3 three-line array camera successfully [13]. Jiang et al. proposed an innovative method to eliminate time synchronization errors using parallel observations of the panchromatic sensor onboard YG-12 [14]. Wang et al. proposed a geometric correction method for ZY-3 satellite images based on virtual steady-state reorientation [15]. In addition, cross-calibration [16], self-calibration [17,18,19], star-based calibration [20,21], and other methods have been proposed to improve the accuracy of satellite on-orbit calibration. However, on-orbit calibration can only calibrate system errors such as camera installation and GPS eccentricity errors, but cannot completely calibrate errors such as satellite attitude jitter and time synchronization. Moreover, the parameters of the camera will change irregularly with the change in the satellite space environment. Improper on-orbit calibration will affect the geometric positioning accuracy of the image. Therefore, it is necessary to further improve the geometric accuracy of RPC parameters generated by the strict imaging model.
In order to improve the accuracy of geometric positioning based on the rational function model, many scholars put forward various methods to improve it from different angles. In terms of RPC parameters generation, different models are proposed to solve the problem of ill-conditioned and over-parameterized features caused by highly correlated parameters. The methods include 2-norm regularization-based methods [22,23] for ill-fitting and 1-norm regularization-based methods [24] for sparse solutions. At the same time, in order to solve the problem of input errors and noises, a series of improved methods based on principal component analysis (PCA) [25,26] are proposed to reduce the influence of ill-condition and over-parameterization through noise reduction in the design matrix. This method can ensure that the generated RPC parameters are correct and better approximate to the results of the strict imaging model, but it cannot correct the errors that the strict imaging model cannot correct. Therefore, while ensuring the correctness of RPC parameters, many geometric quality improvement methods have been proposed. The correction parameters attached to RFM are the most used offset compensation methods, including shift, shift and drift, affine transformation, and second-order polynomial models [27,28]. Dong et al. proposed an RPC image-space bias model that combines object-space information to improve the positioning accuracy of TianHui-1 images [29]. Cao et al. proposed a feasible nonlinear bias compensation approach for ZiYuan-3 imagery with cubic splines to eliminate the influence of attitude oscillations on the RFM-based sensor orientation [30]. These methods can improve the geometric quality of the RFM model to a certain extent, but the nonlinear error caused by attitude oscillation or camera cannot be well-corrected. Therefore, a model to improve the internal deviation of the RFM model needs to be proposed. In addition, in the case of large geometric errors and large geometric differences between satellites in different orbits, the above method cannot be completely applicable, and a targeted algorithm should be proposed to improve the geometric accuracy.
The above methods can improve the geometric positioning accuracy, but additional parameters are added in the process of use, which cannot be compatible with different measurement systems. Therefore, the correction results need to be reflected by new RPC parameters. Some scholars proposed using batch iterative least-squares methods, incremental discrete Kalman filtering methods, sequential least-squares methods, or pseudo ground control points (GCPs) methods to recalculate RPC parameters [31,32]. The calculation of all parameters takes a lot of time, and some of them have little effect on geometric accuracy but strong correlation, so it is necessary to optimize RPC parameters. Tang et al. presented a combined adjustment approach to integrate multi-source multi-resolution satellite imagery for improved geo-positioning accuracy without the use of GCPs. When the method is implemented, only part of RPCs is modified, but there is no theoretical analysis on RPC selection, and some parameters are unnecessary [33].
In this paper, based on the evaluation and analysis of the geometrical quality of the “MN200Sar-1” satellite, an RPC model of internal and external element reorientation model is proposed to solve the problem of low geometric accuracy of the satellite. The model can eliminate nonlinear deviation caused by attitude oscillation and other factors well. At the same time, we analyze the correlation between RPCs and the influence of a single RPC on geometric quality. Based on this, we realize the optimization of RPC parameters, and realize the improvement of geometric accuracy without changing the original structure of RPCs. Therefore, the paper’s contributions are as follows:
- (1)
- Firstly, the image geometry performance of the push-broom optical satellite “MN200Sar-1” is evaluated based on the rational function model. By analyzing the data error sources, the following conclusions are drawn: due to the influence of the time synchronization error, the geometric quality of the “MN200Sar-1” satellite is not stable, the positioning errors of the same orbit data are consistent, and the positioning accuracy of different orbit images vary greatly. For different orbit images, it is necessary to add GCPs to improve the geometric performance.
- (2)
- According to the geometrical characteristics of the optical satellite “MN200Sar-1”, a satellite geometric quality improvement model based on the internal and external orientation elements is proposed. The original image is redirected by establishing the sensor rational function positioning model, external orientation model, and internal orientation model successively. After correction, the error can reach pixel-level accuracy.
- (3)
- By analyzing the relative relationship of RPCs and the influence of a single RPC on the positioning accuracy, the RPC coefficients optimization method based on the image offset and geographical dominant coefficients is realized by using the virtual control points after RFM reorientation. This method can improve the positioning accuracy without introducing additional compensation parameters and achieve accurate positioning of satellite remote sensing images based on the RFM model.
The remainder of this paper is organized as follows. Section 2 introduces the research data of this paper and evaluates its geometric quality. Based on this, the methods of this paper are proposed, including a satellite geometric quality improvement model based on an internal and external reorientation model and RPC coefficient optimization method based on image correction and geographical position dominant coefficient correction. In Section 3, the feasibility and effectiveness of our method are verified by experimental analysis. Section 4 summarizes this paper.
2. Materials and Methods
2.1. Image Geometry Performance Analysis of “MN200Sar-1” Optical Satellite
2.1.1. “MN200Sar-1” Satellite Introduction
The “MN200Sar-1” optical satellite was successfully launched on a “Long March 8” rocket from Hainan province on 27 February 2022. The satellite carries an X-band commercial SAR sensor and an intelligent optical payload for moving target detection. The optical load is composed of an optical camera and an onboard intelligent processing unit. The camera adopts panchromatic two-line array push-broom imaging, and the moving target image is collected in the push-broom scanning area. The onboard intelligent processing unit can independently complete the level 0 to 1 pre-processing in orbit, and realize the accelerated recognition of intelligent remote sensing images based on the pre-processing. The satellite realizes a new imaging mechanism that replaces strip image transmission with target and information transmission.
The “MN200Sar-1” onboard processing unit can provide real-time onboard data decoding, radiometric correction, image registration, geometric correction, sea–land segmentation, frame difference, object detection, and other functions. Among them, onboard geometric correction is realized by periodical uploading of on-orbit calibration parameters. In order to relieve the pressure of satellite–ground data transmission and improve the efficiency of data acquisition, the satellite only needs to downlink the original data with the corresponding RPCs. However, the accuracy of RPCs will be affected by the untimely uploading of calibration parameters and some random error such as attitude oscillation. Table 1 describes the parameters of the “MN200Sar-1” smart camera.

Table 1.
Description of the intelligent camera of the “MN200Sar-1” satellite.
2.1.2. Image Geometric Performance Evaluation
We collected twenty-four sets of data from the six orbits of “MN200Sar-1” since its launch. The collection period was from April to July 2022. The data were located in different regions, and the geographical range is very large. We used digital orthophoto map (DOM) data with high geometric accuracy to conduct scale-invariant feature transform (SIFT) matching with experimental data to obtain high-quality GCPs and ensure that the registration accuracy is within one pixel. By comparing the pixel errors of RPCs and control points, the geometric accuracy of the image was verified as shown in Table 2 and Figure 1.

Table 2.
Validation of image geometric accuracy.
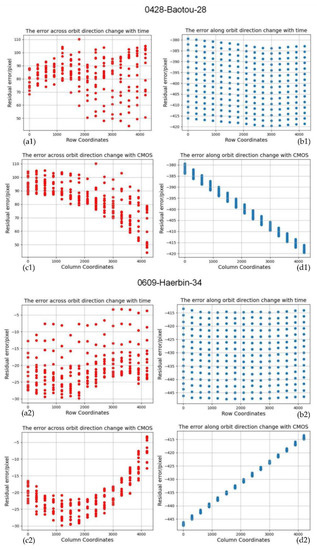
Figure 1.
The error changes with time and CMOS of different images: (a1,a2) the error across orbit direction changes with time, (b1,b2) the error along orbit direction changes with time, (c1,c2) the error across orbit direction changes with CMOS, (d1,d2) the error along orbit direction changes with CMOS. (Red in-dicates across orbit direction, blue indicates along orbit direction).
According to Table 2, we draw the following conclusions: the errors vary greatly in different orbits, and vary little in the same orbit. The maximum error can reach hundreds of pixels, the minimum is only a few pixels. According to the satellite design, the maximum error caused by side-swing, attitude stability, and other reasons will not exceed 300 m. Therefore, the above error is mainly caused by the asynchronism between attitude time, orbit time, and image time, and the error is a random error, which cannot be compensated for in geometric calibration. At the same time, the change rule of image geometric errors with time and CMOS is analyzed. With the change in time, the errors of different images vary evenly along the orbit and across the orbit. In addition, the errors change slightly across the orbit and change a lot along the orbit. With the change in CMOS, different data errors change linearly along the orbit, while the change is relatively small and irregular across the orbit. Therefore, it is not enough to use only offset compensation or affine transformation compensation for the satellite images, and the internal nonlinear errors need to be simulated.
2.1.3. Sensor Orientation Model Based on RFM
The sensor orientation model mainly includes strict imaging model and general imaging model, in which rational function model is the most commonly used. The rational function model represents the image point coordinates (R, C) as the polynomial ratio of ground coordinates (Lon, Lat, H):
where (Lonn, Latn, Hn) and (rn, cn), respectively, represent the normalized coordinates of ground point coordinates (Lon, Lat, H) and (R, C) after translation and scaling, and the value range is [−1, 1]. Each polynomial Pi (i = 1, 2, 3, 4) has a maximum power of 3, and the sum of the powers of each coordinate component of each term does not exceed 3. The RFM relates the ground coordinates of ground object points with the coordinates of image points in the form of polynomial ratios. The geometric accuracy improves with the increase in the polynomial order of the model. For flat areas, first-order RFM can meet the requirements, while for mountainous and hilly areas, third-order RFM is required. Therefore, we choose third-order RFM, which is usually composed of 78 parameters, namely, ai, bi, ci, and di (i = 0–19). Generally speaking, b0 and d0 are 1. Taking P1 as an example, the formula is expressed as:
RFM adopts regularization to improve the stability of solving each parameter in the model and reduce the data selection error caused by excessive data level differences in the calculation process. The regularization formula is expressed as:
where Lon0, Lat0, H0, R0, and C0 are the regularized translation coefficient, and LonS, LatS, HS, RS, and CS are the regularized scaling coefficient.
2.1.4. RPC Parameter Analysis
(1) RPC correlation analysis
Firstly, the correlation between RPCs is analyzed from a mathematical point of view. According to the corresponding coordinate points and RFM, functions related to RPC parameters could be established as follows:
where (r, c) and (rn, cn), respectively, represent the regularized image point coordinates of GCPs and the image point coordinates calculated by RFM. The coefficient matrix of image point k is established as follows:
The cofactor matrix is established as:
where n represents the number of image points, and Pk is the identity matrix. Therefore, the correlation coefficients cij between RPCs is defined as:
where q is the cofactor of each RPC in the cofactor matrix, and i and j are the parameters of each RPC (i, j = 0–19).
We analyze the correlation of RPCs of the “MN200Sar-1” satellite and select uniformly distributed virtual control points in multiple images to calculate the mean correlation coefficients. We make cij > 0.7 as highly correlated and cij < 0.2 as irrelevant, denoted by 0. The calculation results are shown in Table 3 and Figure 2.

Table 3.
Matrix of correlation coefficients between RPCs (only the correlation coefficients from a0 to a10 are listed here, and the detailed correlation coefficient matrix from a0 to b19 is shown in Appendix A, where bold indicates cij > 0.7).
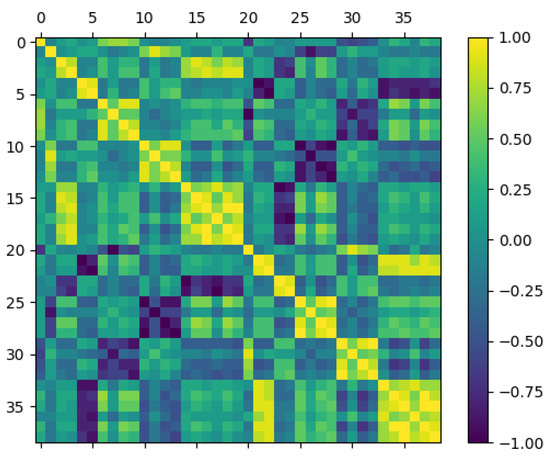
Figure 2.
Visualization of correlation coefficient matrix.
According to Table 3 and Figure 2, we can see that a0 is strongly correlated with a7, a8, and similarly, a1 is strongly correlated with a11, a12, which will inevitably lead to ill-conditioned and indeterminate forms of regular equations in the solution of least squares. In terms of polynomial order, the correlation coefficients between zero-order terms and first-order terms of RPCs are very small, but there is a strong correlation between some second-order coefficients and third-order coefficients. In addition, the correlation between a and b (c and d) is complex.
(2) Analysis of the importance of a single RPC parameter to geometric accuracy
We calculate the influence of a single RPC on the geometric accuracy, set an error of 0.01 r (r is the coefficient value) for each RPC, and calculate the difference between the image coordinates and those with 0.01 r, as shown in Figure 3. We find that different RPCs have different influences on the geometric accuracy. When the error range is 0.01 r, the first four terms of a and c have a great influence on the geometric accuracy, while the influence of other parameters on the accuracy can be ignored. At the same time, the effect of b and d, the denominator term, on the geometric accuracy, is close to zero and also negligible. Therefore, we take the parameters that have a greater impact on the geometric accuracy as the dominant coefficients, namely, the zero-order term and first-order term of RFM. By improving the accuracy of the dominant coefficients, the geometric positioning accuracy of RPCs can be rapidly and effectively improved without changing the original RPCs.
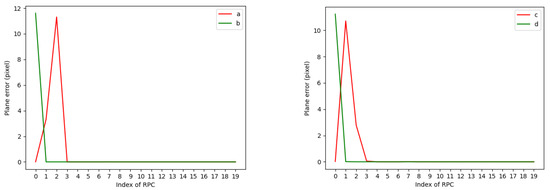
Figure 3.
Errors affected by RPCs with numerical accuracy of 0.01 r.
Based on the above analysis, we propose a geometric quality improvement model for the “MN200Sar-1” optical satellite based on internal and external element reorientation. Secondly, through the analysis of RPC parameters, the dominant coefficients which have a great influence on RPCs are determined, and the dominant coefficient and image square offset compensation is proposed to correct RPC parameters. This model can not only provide a set of additional compensation parameters for the internal and external orientation elements to improve the geometric accuracy of the original RFM model, but also provide optimized RPC parameters. The model in this paper is shown in Figure 4.
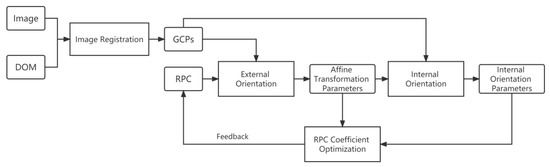
Figure 4.
Improved geometric accuracy model.
Firstly, we perform high-precision geometric registration on “MN200Sar-1” satellite remote sensing images and DOM images to obtain the GCPs. Secondly, we use the GCPs obtained and the original RPCs for external orientation, and use the affine transformation model to simulate external orientation parameters (e0, e1, e2, f0, f1, f2), as shown in Equation (9). Then, we use the external orientation parameters solved, combined with GCPs, to solve the internal orientation model, and obtain the internal orientation parameters (g0, g1, g2, g3) and (k0, k1, k2, k3), as shown in Equation (10). After the reorientation of the external and internal elements, a high-precision geometric positioning model can be obtained. In order to update RPCs, we use the reorientation positioning model to obtain the virtual GCPs, then we introduce the offset parameters (e0, f0) of the original RPCs to conduct coarse error correction, and then modify the dominant coefficients by the least-square method to obtain the new RPC model to improve the geometric positioning accuracy of the images.
2.2. Satellite Geometric Accuracy Improvement Model Based on Internal and External Reorientation
2.2.1. External Orientation Model
RFM achieves the geometric positioning of sensors by fitting strict imaging models, but the errors caused by satellite position and attitude will inevitably spread to RPC parameters. At the same time, the “MN200Sar-1” satellite contains synchronization time error, which can affect the positioning accuracy of kilometer level at most. According to the analysis, the positioning accuracy of different orbits varies greatly, and the above errors are mainly constant errors, which can be compensated for by the external orientation model.
In this paper, the image square compensation model [5,34] is adopted, and the relationship between image coordinates and ground coordinates described by RFM in Equation (1) as:
where Rr and Cr represent the truth value of GCPs, and (∆R, ∆C) represents the systematic error compensation of image points, which can be simulated by an affine transformation model. Here, because the geometric error of “MN200Sar-1” satellite is relatively large, only using the system error compensation parameter cannot compensate for the distortion well, so we choose the first-order error compensation here.
where (e0, e1, e2, f0, f1, f2) are described as affine transformation compensation parameters.
2.2.2. Internal Orientation Model
RFM can compensate for the constant error after external orientation, but for the nonlinear errors caused by camera distortion or attitude oscillations, which will cause image distortion and band registration distortion, the external orientation model cannot be corrected, so the internal orientation model should be used for nonlinear compensation.
The internal orientation model does not need to strip the errors of various internal elements and restore their true values, but only needs to restore the correct orientation of the imaging probe in the camera coordinate system. Therefore, we use the probe pointing angle model commonly used in geometric calibration to achieve internal orientation [7]. The pointing angle is a comprehensive expression of the errors of each element of interior orientation. The strict physical distortion model of a line scan camera is essentially a polynomial model, which can be fitted with a cubic polynomial, as shown in Equation (10):
where Ro and Co represent pixel coordinate values after external calibration, (g0, g1, g2, g3) and (k0, k1, k2, k3) represent polynomial coefficients, and s represents the probe number. After internal orientation, the correct orientation of the camera can be recovered and nonlinear errors can be compensated for.
Generally, the external orientation model can compensate for most of the linear errors, while the internal orientation model can compensate for the nonlinear errors caused by camera and other factors. For satellites with high positioning accuracy, the external orientation model is sufficient. For small satellites with low positioning accuracy, such as MN200Sar-1, both internal and external orientation models are needed to compensate.
2.2.3. RPC Coefficient Optimization Method Based on Image Square Correction and Geographical Location Dominant Coefficient Correction
According to the correlation of RPCs and the influence analysis of each parameter on the geometric accuracy, we take the zero-order term and first-order term of the polynomial as the dominant geographical location coefficients. Since the correlation between these terms is relatively weak, and has a great impact on the geometric accuracy, so the stability of imaging geometry can be improved while the positioning accuracy can be improved. At the same time, for the data with large geometric errors, we first introduce the image offset correction to improve RPC parameters and compensate for large linear errors. On this basis, we recalculate the dominant coefficients and fine-adjust the RPC parameters.
Firstly, the improved RPC parameters are taken as the initial values, the dominant parameters in the virtual control points are calculated by using the model after internal and external orientation, and the optimized parameters are combined with the unoptimized parameters to construct new RPC parameters. Therefore, the error equation of parameters to be optimized is constructed as follows:
where (a0, a1, a2, a3) and (c0, c1, c2, c3) are the parameters to be optimized, (ln, sn) are the virtual control point values after regularization, and (l0, s0) are the values calculated by the initial RPCs. Calculated using N control points, the error equation is abbreviated as:
Therefore, the dominant coefficients ∆ are solved by the least-square method to obtain the optimized dominant coefficients.
3. Results
Our paper tests six sets of images from Section 2. In order to verify the positioning accuracy, the DOM images with high geometric accuracy are used for registration with “MN200Sar-1” satellite remote sensing images to obtain accurate and evenly distributed control points. The GCP distribution is shown in Figure 5. The selected image size is 4500 × 4500, and each image has about 300–700 control points. Two experiments were designed to evaluate the proposed model. One is used to evaluate the accuracy of the internal and external orientation model, and the other is used to evaluate the accuracy of the model after the optimization of RPC coefficients.

Figure 5.
Distributions of GCPs in (a) image 0430-Baotou-43, (b) image 0614-Dunhuang-43.
3.1. Verification the Accuracy of Internal and External Orientation Model
In this experiment, we verify the proposed reorientation model. Compared with the offset compensation model, the affine transform compensation model, and the object–space bias compensation model, the validity and precision of the proposed model are verified. The comparison results of different methods are shown in Table 4. Taking the 0517-Weihai-50 image as an example, the error change rules of different methods are compared in Figure 6.

Table 4.
Accuracy verification of different methods (The bold indicates the result with the best accuracy index).
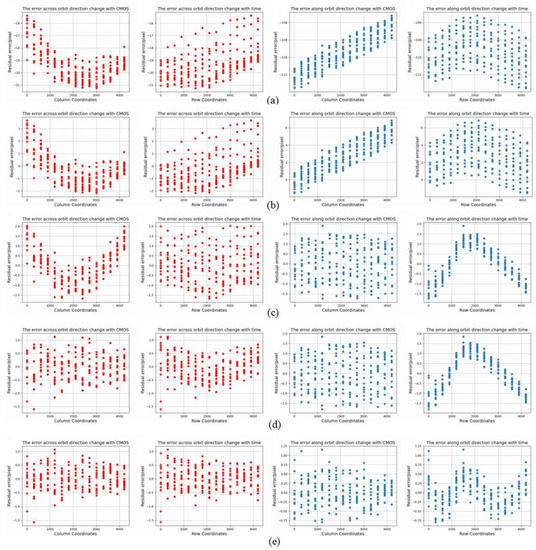
Figure 6.
The 0517-Weihai-50 image geometric error of different methods changes with time and CMOS probe: (a) no compensation, (b) offset compensation, (c) affine transform compensation, (d) object–space bias compensation, (e) the model in this paper. (Red indicates across orbit direction, blue indicates along orbit direction).
According to the comparative analysis of different methods in Table 4, the positioning accuracy of the proposed method is the highest in multiple data. When the RPCs are used for positioning, the positioning error of 0428-Baotou-28, 0517-Weihai-50, and 0614-Dunhuang-43 images can reach a maximum of 443.367 pixels, 114.976 pixels, and 324.597 pixels, respectively. It can be seen that the errors of different orbits vary greatly, so it is necessary to correct and compensate the RPCs of each orbit image separately. Comparative analysis shows that for the 0517-Weihai-50 image, offset compensation can reduce the error to 2.983 pixels, affine transform compensation can reduce it to 1.056 pixels, object–space bias compensation can reduce it to 1.002 pixels, and the proposed model can reduce it to 0.434 pixels. This is mainly because the nonlinear errors in geometric correction of RPCs are fully considered and compensated for by our model. For the 0428-Baotou-28 image, due to the large geometric error of RPCs, the model in this paper has fully compensated for it, and only part of random errors cannot be compensated for.
According to Figure 6, taking the 0517-Weihai-50 image as an example, the error change rule of different methods is analyzed. In the case of no compensation, the error is mainly distributed in the direction along the orbit, which can be up to 100 pixels, while the across-orbit direction is relatively small, only 20 pixels. After offset compensation, the error is reduced to 10 pixels, but the error distribution is the same as that without compensation. After affine transformation compensation or object–space bias compensation, the errors have nonlinear distribution along and across the orbit, so it is necessary to carry out nonlinear compensation. After the nonlinear error compensation in our method, the errors are evenly distributed and reduced to less than one pixel.
Then, we analyze the error distribution of different methods in Figure 7 to verify the correctness of the proposed method. According to the results of error distribution, the direction of error distribution is consistent before error compensation. After the offset compensation, the error distribution and error size are scattered. After compensating by the affine transformation, the error is relatively small in the center position and large in the edge position, showing a certain divergence. This is also consistent with the view discussed above, that is, after affine transformation compensation, there are still some nonlinear errors with certain regularity. However, after the compensation of our model, the error is greatly reduced and has no regularity, so the error no longer has the condition of compensation again.
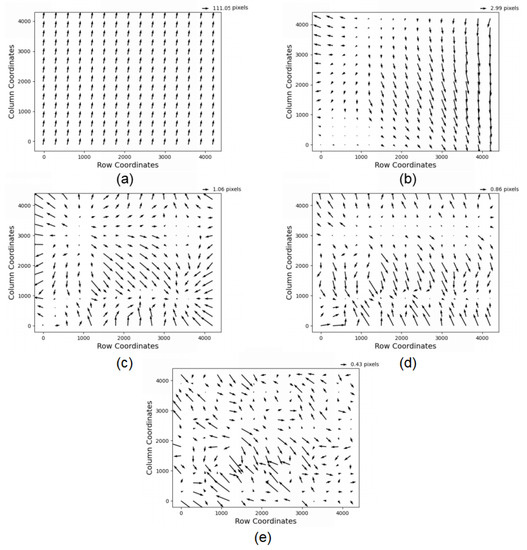
Figure 7.
Error distribution of different methods of the 0517-Weihai-50 image: (a) no compensation, (b) offset compensation, (c) affine transform compensation, (d) object–space bias compensation, (e) the model in this paper.
3.2. Verification the Accuracy of RPC Coefficient Optimization
In this experiment, we compared the accuracy of RPC parameters before and after optimization, and the statistics are shown in Table 5. Results of the original RPC model, the reorientation model, and the RPC optimization model are compared. Compared with RPCs without compensation, the geometric positioning accuracy can be greatly improved after RPC optimization, but the accuracy is slightly lower than that of the reorientation model. Therefore, the reorientation model should be used when high positioning accuracy is needed. However, for some cases that do not need high positioning accuracy, the faster RPC coefficients optimization model is used.

Table 5.
RPC coefficient optimization precision comparison.
4. Conclusions
On-orbit geometric calibration is widely used to improve the accuracy of geometric positioning, but late calibration parameters will affect the geometric correction, and then affect the generated RPC parameters. In addition, time synchronization error and attitude oscillation error cannot be compensated for by the geometric calibration method. Therefore, the geometric quality improvement model based on RPCs is extremely important.
In this paper, we propose a geometric accuracy improvement model based on RPCs, including a reorientation model of internal and external elements and an optimization method of RPCs based on geographical dominant coefficients. We make a detailed analysis of RPCs, and theoretically verify the relationship between RPCs and the influence of RPCs on geographical positioning accuracy. At the same time, the geometric calibration method is introduced to realize the reorientation of RFM, and the accuracy is improved under the condition of large geometric error. Experimental comparison results of multiple images prove the effectiveness of our model. For most images, the geometric accuracy can be improved to less than 2 pixels.
To improve geometric accuracy, we can improve advanced technical components, such as self-calibration, which will be used to reduce geometric errors. In addition, with the wide application of deep learning algorithms in registration algorithms, we can consider using deep learning models to simulate the geometric deviation of image imaging in future work, and realize the improvement of geometric accuracy.
Author Contributions
Conceptualization, Q.L and C.Z.; methodology, Q.L. and K.Z.; software, Q.L. and C.Y.; validation, Q.L. and Y.L.; writing—original draft preparation, Q.L.; writing—review and editing, Q.L. and R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC), grant number 42071444.
Acknowledgments
The authors would like to thank the anonymous reviewers and members of the editorial team for their comments and contributions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Matrix of correlation coefficients between RPCs. (bold indicates correlation coefficients > 0.7).
Table A1.
Matrix of correlation coefficients between RPCs. (bold indicates correlation coefficients > 0.7).
| a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 | a16 | a17 | a18 | a19 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b10 | b11 | b12 | b13 | b14 | b15 | b16 | b17 | b18 | b19 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a0 | 1 | ||||||||||||||||||||||||||||||||||||||
| a1 | 0 | 1 | |||||||||||||||||||||||||||||||||||||
| a2 | 0 | 0 | 1 | ||||||||||||||||||||||||||||||||||||
| a3 | 0 | 0 | 0 | 1 | |||||||||||||||||||||||||||||||||||
| a4 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||||||||||||||||||||||
| a5 | 0 | 0 | 0 | 0 | 0.9 | 1 | |||||||||||||||||||||||||||||||||
| a6 | 0.6 | 0 | 0.4 | 0.4 | 0 | 0 | 1 | ||||||||||||||||||||||||||||||||
| a7 | 0.7 | 0 | 0.1 | 0 | 0 | 0.3 | 0.5 | 1 | |||||||||||||||||||||||||||||||
| a8 | 0.7 | 0 | 0.3 | 0.4 | 0 | 0 | 0.9 | 0.5 | 1 | ||||||||||||||||||||||||||||||
| a9 | 0.6 | 0 | 0.3 | 0.4 | 0 | 0 | 0.9 | 0.5 | 0.8 | 1 | |||||||||||||||||||||||||||||
| a10 | 0 | 0.6 | 0 | 0 | 0.4 | 0.4 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||||||||||||||||
| a11 | 0 | 0.9 | 0 | 0 | 0 | 0 | 0 | −0.3 | 0 | 0 | 0.6 | 1 | |||||||||||||||||||||||||||
| a12 | 0 | 0.7 | 0 | 0 | 0.3 | 0.4 | 0 | 0 | 0 | 0 | 0.9 | 0.6 | 1 | ||||||||||||||||||||||||||
| a13 | 0 | 0.6 | 0 | 0 | 0.3 | 0.5 | 0 | 0 | 0 | 0 | 0.9 | 0.6 | 0.8 | 1 | |||||||||||||||||||||||||
| a14 | 0 | 0 | 0.7 | 0.7 | 0 | 0 | 0.3 | 0 | 0 | 0.3 | 0 | 0.3 | 0 | 0 | 1 | ||||||||||||||||||||||||
| a15 | 0 | 0 | 0.9 | 0.8 | 0 | 0 | 0.4 | 0 | 0.4 | 0.4 | −0.4 | 0 | −0.4 | −0.3 | 0.6 | 1 | |||||||||||||||||||||||
| a16 | 0 | 0 | 0.8 | 0.9 | 0 | 0 | 0.4 | 0 | 0.4 | 0.4 | −0.4 | 0 | −0.4 | 0 | 0.7 | 0.9 | 1 | ||||||||||||||||||||||
| a17 | 0 | 0 | 0.6 | 0.8 | 0 | 0 | 0.3 | 0 | 0 | 0.4 | 0 | 0.4 | 0 | 0 | 0.9 | 0.5 | 0.7 | 1 | |||||||||||||||||||||
| a18 | 0 | 0 | 0.8 | 0.9 | 0 | 0 | 0.4 | 0 | 0.5 | 0.4 | −0.4 | 0 | −0.5 | −0.3 | 0.6 | 0.9 | 1 | 0.6 | 1 | ||||||||||||||||||||
| a19 | 0 | 0 | 0.7 | 0.9 | 0 | 0 | 0.4 | 0 | 0.3 | 0.5 | 0 | 0 | –0.3 | 0 | 0.7 | 0.7 | 1 | 0.8 | 0.9 | 1 | |||||||||||||||||||
| b1 | −0.7 | 0 | 0 | 0 | 0 | 0 | −0.5 | −1 | −0.5 | −0.6 | 0 | 0.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||||||||||||||||||
| b2 | 0 | 0 | 0 | 0 | −1 | −0.8 | 0.5 | 0 | 0.5 | 0.4 | −0.4 | 0 | −0.4 | −0.3 | 0 | 0.3 | 0 | 0 | 0 | 0 | 0 | 1 | |||||||||||||||||
| b3 | 0 | 0 | 0 | 0 | −0.9 | −1 | 0.4 | 0 | 0.4 | 0.3 | −0.4 | 0 | −0.4 | −0.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9 | 1 | ||||||||||||||||
| b4 | 0 | 0 | −0.7 | −0.7 | 0 | 0 | −0.3 | 0 | −0.3 | −0.3 | 0 | 0 | 0.3 | 0 | −1 | −0.7 | −0.8 | −0.9 | −0.7 | −0.7 | 0 | −0.3 | 0 | 1 | |||||||||||||||
| b5 | 0 | 0 | −0.6 | −0.8 | 0 | 0 | −0.3 | 0 | −0.3 | −0.4 | 0 | 0 | 0 | 0 | −0.9 | −0.6 | −0.8 | −1 | −0.7 | −0.8 | 0 | 0 | 0 | 0.9 | 1 | ||||||||||||||
| b6 | 0 | −0.6 | 0.4 | 0.4 | −0.4 | −0.4 | 0 | 0 | 0 | 0 | −1 | −0.5 | −0.9 | −0.9 | 0 | 0.6 | 0.6 | 0 | 0.7 | 0.5 | 0 | 0.4 | 0.4 | −0.4 | −0.3 | 1 | |||||||||||||
| b7 | 0 | −0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.6 | −1 | −0.6 | −0.6 | 0 | 0 | 0 | −0.3 | 0 | 0 | −0.3 | 0 | 0 | 0 | 0 | 0.5 | 1 | ||||||||||||
| b8 | 0 | −0.6 | 0.5 | 0.5 | −0.3 | −0.3 | 0.3 | 0 | 0.3 | 0 | −0.9 | −0.5 | −1 | −0.8 | 0.3 | 0.7 | 0.6 | 0 | 0.7 | 0.5 | 0 | 0.4 | 0.4 | −0.5 | −0.4 | 0.9 | 0.5 | 1 | |||||||||||
| b9 | 0 | −0.6 | 0.3 | 0.3 | −0.3 | −0.4 | 0 | 0 | 0 | 0 | −1 | −0.5 | −0.9 | −1 | 0 | 0.5 | 0.5 | 0 | 0.5 | 0.3 | 0 | 0.4 | 0.4 | −0.3 | 0 | 1 | 0.6 | 0.9 | 1 | ||||||||||
| b10 | −0.5 | 0 | −0.3 | −0.3 | 0 | 0 | −0.8 | −0.6 | −0.7 | −0.9 | 0 | 0 | 0.3 | 0 | −0.4 | −0.4 | −0.4 | −0.4 | −0.4 | −0.5 | 0.6 | −0.4 | −0.4 | 0.4 | 0.4 | −0.3 | 0 | −0.3 | 0 | 1 | |||||||||
| b11 | −0.6 | 0 | 0 | 0 | 0 | −0.3 | −0.4 | −0.9 | −0.3 | −0.4 | 0 | 0.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9 | 0 | 0 | 0 | 0 | 0 | −0.4 | 0 | 0 | 0.6 | 1 | ||||||||
| b12 | −0.5 | 0 | −0.3 | −0.3 | 0.3 | 0 | −0.8 | −0.6 | −0.8 | −0.8 | 0.3 | 0 | 0.3 | 0 | −0.3 | −0.4 | −0.4 | −0.3 | −0.4 | −0.4 | 0.7 | –0.5 | –0.4 | 0.4 | 0.4 | –0.4 | 0 | –0.4 | –0.3 | 0.9 | 0.5 | 1 | |||||||
| b13 | –0.4 | 0 | 0 | –0.3 | 0 | 0 | –0.7 | –0.6 | –0.6 | –0.9 | 0 | 0 | 0 | 0 | –0.4 | –0.3 | –0.4 | –0.5 | –0.4 | –0.5 | 0.6 | –0.3 | 0 | 0.4 | 0.5 | 0 | 0 | 0 | 0 | 1 | 0.6 | 0.8 | 1 | ||||||
| b14 | 0 | 0 | 0 | 0 | –0.9 | –0.9 | 0 | 0 | 0 | 0 | –0.4 | 0 | –0.3 | –0.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9 | 0.8 | –0.3 | 0 | 0.4 | 0 | 0.3 | 0.4 | 0 | 0.3 | 0 | 0 | 1 | |||||
| b15 | 0 | 0 | 0 | 0 | –0.8 | –0.7 | 0.7 | 0 | 0.6 | 0.6 | –0.4 | 0 | –0.5 | –0.3 | 0 | 0.4 | 0.3 | 0 | 0.4 | 0 | –0.3 | 0.9 | 0.8 | –0.3 | –0.3 | 0.5 | 0 | 0.5 | 0.4 | –0.6 | 0 | –0.7 | –0.4 | 0.7 | 1 | ||||
| b16 | 0 | 0 | 0 | 0 | –0.8 | –0.8 | 0.6 | 0 | 0.5 | 0.5 | –0.5 | 0 | –0.4 | –0.5 | 0 | 0.3 | 0 | 0 | 0.3 | 0 | 0 | 0.9 | 0.9 | 0 | 0 | 0.5 | 0 | 0.4 | 0.5 | –0.5 | 0 | –0.6 | –0.3 | 0.8 | 0.9 | 1 | |||
| b17 | 0 | 0 | 0 | 0 | –0.8 | –0.9 | 0 | –0.3 | 0 | 0 | –0.4 | 0 | –0.3 | –0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 0.9 | 0 | 0 | 0.4 | 0 | 0.3 | 0.4 | 0 | 0.4 | 0 | 0 | 0.9 | 0.6 | 0.7 | 1 | ||
| b18 | 0 | 0 | 0 | 0 | –0.8 | –0.8 | 0.6 | 0 | 0.6 | 0.5 | –0.5 | 0 | –0.5 | –0.4 | 0 | 0.4 | 0.3 | 0 | 0.3 | 0 | 0 | 0.9 | 0.9 | –0.3 | 0 | 0.5 | 0 | 0.5 | 0.4 | –0.6 | 0 | –0.7 | –0.4 | 0.7 | 1 | 1 | 0.7 | 1 | |
| b19 | 0 | 0 | 0 | 0 | –0.7 | –0.9 | 0.4 | 0 | 0.4 | 0.3 | –0.5 | 0 | –0.4 | –0.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.8 | 0.9 | 0 | 0 | 0.5 | 0.3 | 0.4 | 0.5 | –0.3 | 0 | –0.4 | 0 | 0.7 | 0.8 | 1 | 0.8 | 0.9 | 1 |
References
- Tao, C.V.; Hu, Y. A Comprehensive Study of the Rational Function Model for Photogrammetric Processing. Photogramm. Eng. Remote Sens. 2001, 67, 1347–1357. [Google Scholar]
- Xiong, Z.; Zhang, Y. Bundle Adjustment with Rational Polynomial Camera Models Based on Generic Method. IEEE Trans. Geosci. Remote Sens. 2011, 49, 190–202. [Google Scholar] [CrossRef]
- Hu, Y.; Tao, C.V. Updating Solutions of the Rational Function Model Using Additional Control Information. Photogramm. Eng. Remote Sens. 2002, 68, 715–724. [Google Scholar]
- Fraser, C.S.; Dial, G.; Grodecki, J. Sensor Orientation via RPCs. ISPRS J. Photogramm. Remote Sens. 2005, 60, 182–194. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. Block Adjustment of High-Resolution Satellite Images Described by Rational Polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Toutin, T. Review article: Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.; Jiang, Y.; Zhou, P.; Zhao, Y.; Xu, Y. On-Orbit Geometric Calibration and Validation of Luojia 1-01 Night-Light Satellite. Remote Sens. 2019, 11, 264. [Google Scholar] [CrossRef]
- Hong, Z.; Tong, X.; Liu, S.; Chen, P.; Xie, H.; Jin, Y. A Comparison of the Performance of Bias-Corrected RSMs and RFMs for the Geo-Positioning of High-Resolution Satellite Stereo Imagery. Remote Sens. 2015, 7, 16815–16830. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Aguilar, F.J.; Saldaña, M.D.; Fernández, I. Geopositioning Accuracy Assessment of GeoEye-1 Panchromatic and Multispectral Imagery. ISPRS J. Photogramm. Remote Sens. 2010, 65, 218–226. [Google Scholar] [CrossRef]
- Tong, X.; Liu, S.; Weng, Q. Bias-Corrected Rational Polynomial Coefficients for High Accuracy Geo-positioning of QuickBird Stereo Imagery. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Tong, X.; Ye, Z.; Li, L.; Liu, S.; Jin, Y.; Chen, P.; Xie, H.; Zhang, S. Detection and Estimation of Along-Track Attitude Jitter from Ziyuan-3 Three-Line-Array Images Based on Back-Projection Residuals. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4272–4284. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, M.; Cheng, Y.; He, L.; Xue, L. An Improved Jitter Detection Method Based on Parallax Observation of Multispectral Sensors for Gaofen-1 02/03/04 Satellites. Remote Sens. 2019, 11, 16. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Yang, B.; Hu, F.; Zang, X. On-Orbit Geometric Calibration Model and Its Applications for High-Resolution Optical Satellite Imagery. Remote Sens. 2014, 6, 4391–4408. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, G.; Li, D.; Tang, X.; Huang, W.; Litao, L. Correction of Distortions in YG-12 High-Resolution Panchromatic Images. Photogramm. Eng. Remote Sens. 2015, 81, 25–36. [Google Scholar] [CrossRef]
- Wang, M.; Zhu, Y.; Jin, S.; Pan, J.; Zhu, Q. Correction of ZY-3 Image Distortion Caused by Satellite Jitter via Virtual Steady Reimaging Using Attitude Data. ISPRS J. Photogramm. Remote Sens. 2016, 119, 108–123. [Google Scholar] [CrossRef]
- Deng, M.; Zhang, G.; Zhao, R.; Li, S.; Li, J. Improvement of Gaofen-3 Absolute Positioning Accuracy Based on Cross-Calibration. Sensors 2017, 17, 2903. [Google Scholar] [CrossRef]
- Zhang, G.; Deng, M.; Cai, C.; Zhao, R. Geometric Self-Calibration of YaoGan-13 Images Using Multiple Overlapping Images. Sensors 2019, 19, 2367. [Google Scholar] [CrossRef]
- Jiang, Y.; Cui, Z.; Zhang, G.; Wang, J.; Xu, M.; Zhao, Y.; Xu, Y. CCD Distortion Calibration Without Accurate Ground Control Data for Pushbroom Satellites. ISPRS J. Photogramm. Remote Sens. 2018, 142, 21–26. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, Y.; Tian, Y.; He, L.; Wang, Y. A New On-Orbit Geometric Self-Calibration Approach for the High-Resolution Geostationary Optical Satellite GaoFen4. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1670–1683. [Google Scholar] [CrossRef]
- Chen, X.; Xing, F.; You, Z.; Zhong, X.; Qi, K. On-Orbit High-Accuracy Geometric Calibration for Remote Sensing Camera Based on Star Sources Observation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Wang, J.; Zhang, G. Star-Based Calibration of the Installation Between the Camera and Star Sensor of the Luojia 1-01 Satellite. Remote Sens. 2019, 11, 2081. [Google Scholar] [CrossRef]
- Wu, Y.; Ming, Y. A Fast and Robust Method of Calculating RFM Parameters for Satellite Imagery. Remote Sens. Lett. 2016, 7, 1112–1120. [Google Scholar] [CrossRef]
- Cao, J.; Fu, J. Estimation of Rational Polynomial Coefficients Based on Singular Value Decomposition. J. Appl. Remote Sens. 2018, 12, 044003. [Google Scholar]
- Long, T.; Jiao, W.; He, G. RPC Estimation via $\ell_1$-Norm-Regularized Least Squares (L1LS). IEEE Trans. Geosci. Remote Sens. 2015, 53, 4554–4567. [Google Scholar] [CrossRef]
- Naeini, A.A.; Moghaddam, S.H.A.; Sheikholeslami, M.M.; Amiri-Simkooei, A. Application of PCA Analysis and QR Decomposition to Address RFM’s Ill-Posedness. Photogramm. Eng. Remote Sens. 2020, 86, 17–21. [Google Scholar] [CrossRef]
- Gholinejad, S.; Amiri-Simkooei, A.; Alizadeh Moghaddam, S.H.; Alizadeh Naeini, A. An Automated PCA-based Approach towards Optimization of The Rational Function Model. ISPRS J. Photogramm. Remote Sens. 2020, 165, 133–139. [Google Scholar] [CrossRef]
- Liu, J.; Jia, B.; Jiang, T.; Jiang, G. Extrapolative Positioning of RPC Model of TH-1 Satellite Three-Line Imagery. Geomat. Spat. Inf. Technol. 2013, 36, 20–21+25. [Google Scholar]
- Aguilar, M.A.; Saldaña, M.D.; Aguilar, F.J. Assessing Geometric Accuracy of the Orthorectification Process from GeoEye-1 and WorldView-2 Panchromatic Images. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 427–435. [Google Scholar] [CrossRef]
- Dong, Y.; Lei, R.; Fan, D.; Gu, L.S.; Ji, S. A Novel RPC Bias Model for Improving the Positioning Accuracy of Satellite Images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 2, 35–41. [Google Scholar] [CrossRef]
- Cao, J.; Fu, J.; Yuan, X.; Gong, J. Nonlinear Bias Compensation of ZiYuan-3 Satellite Iimagery with Cubic Splines. ISPRS J. Photogramm. Remote Sens. 2017, 133, 174–185. [Google Scholar] [CrossRef]
- Cao, J.; Yuan, X. Refinement of RPCs Based on Systematic Error Compensation for Virtual Grid. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 185–189. [Google Scholar]
- Di, K.; Ma, R.; Li, R.X. Rational Functions and Potential for Rigorous Sensor Model Recovery. Photogramm. Eng. Remote Sens. 2003, 69, 33–41. [Google Scholar]
- Tang, X.; Zhang, G.; Zhu, X.; Pan, H.; Jiang, Y.; Zhou, P.; Wang, X. Triple Linear-array Image Geometry Model of ZiYuan-3 Surveying Satellite and Its Validation. Int. J. Image Data Fusion 2013, 4, 33–51. [Google Scholar] [CrossRef]
- Li, D.; Zhang, G.; Jiang, W.; Yuan, X. SPOT-5 HRS Satellite Imagery Block Adjustment Without GCPS or with Single GCP. Geomat. Inf. Sci. Wuhan Univ. 2006, 31, 377–381. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).