Quantitative Assessment of Impact of Climate Change and Human Activities on Streamflow Changes Using an Improved Three-Parameter Monthly Water Balance Model
Abstract
:1. Introduction
2. Methods
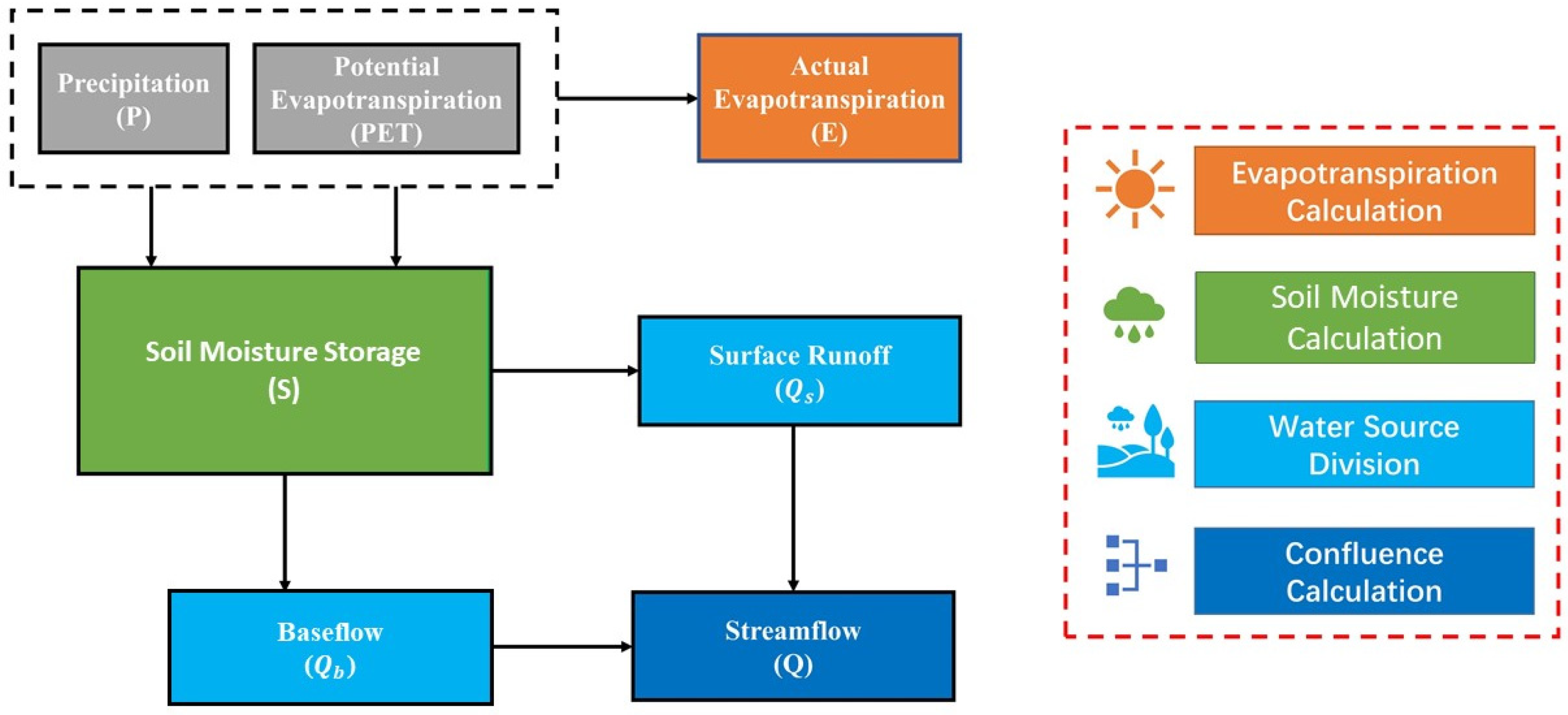
2.1. Monthly Water Balance Model
2.1.1. Three-Parameter Monthly Water Balance Model
2.1.2. Improved Three-Parameter Monthly Water Balance Model
2.1.3. Four-Parameter Monthly Water Balance Model
2.2. Performance Indicators
2.3. Assessment of Impacts of Climate Change and Human Activities on Streamflow
2.3.1. The Budyko-Based Method
2.3.2. Method of Separating Environment Variables
3. Study Area and Data Sources
3.1. Study Area
3.2. Data Sources
4. Results
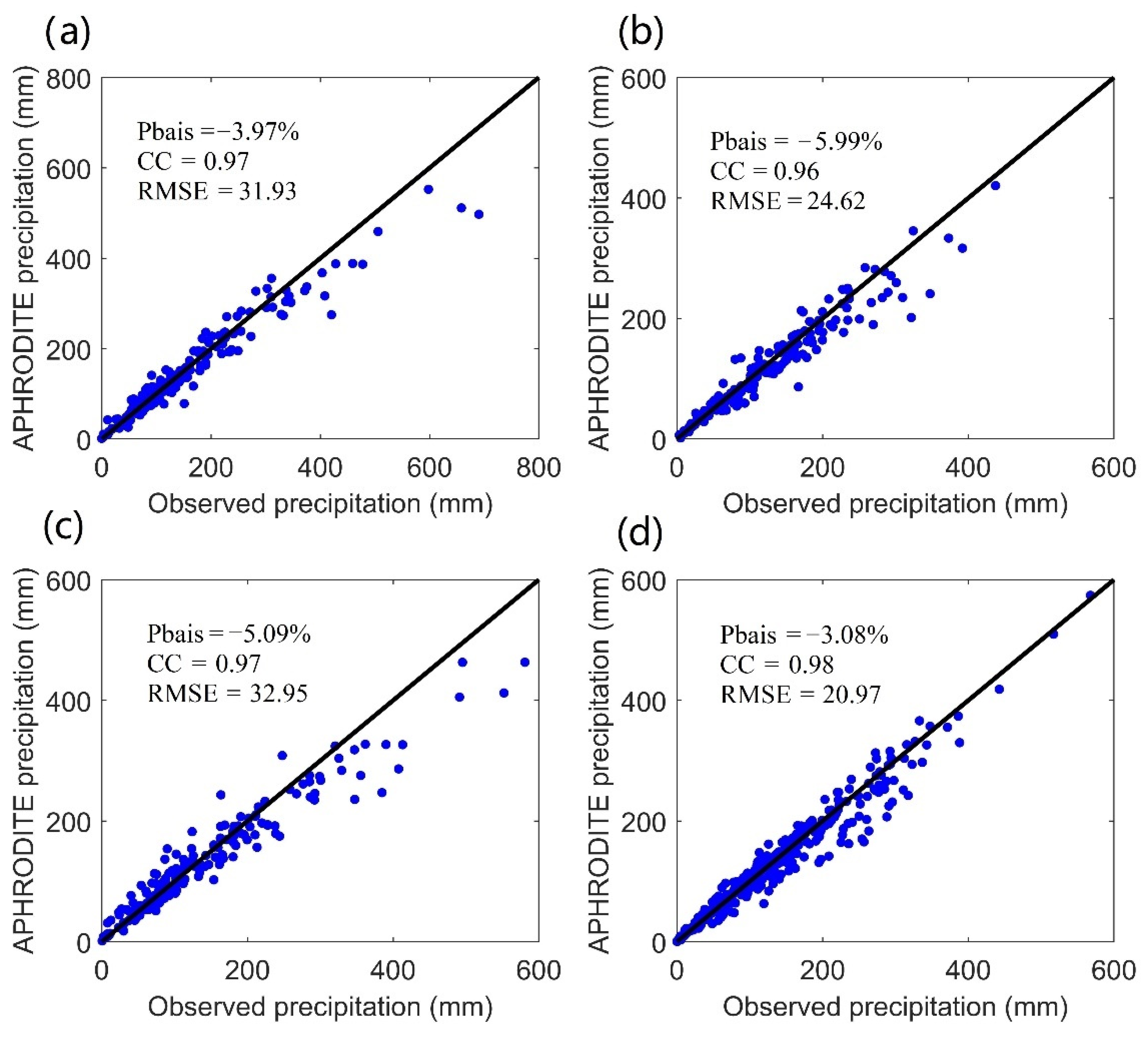
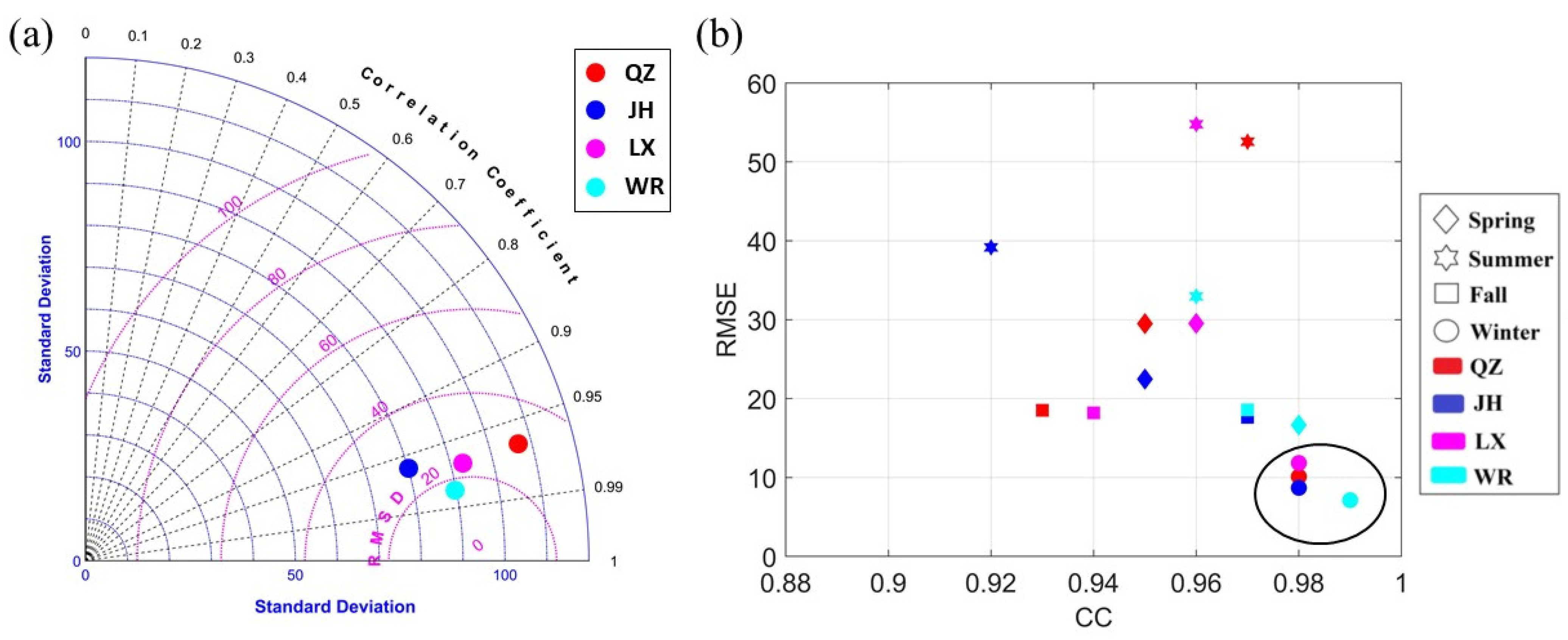
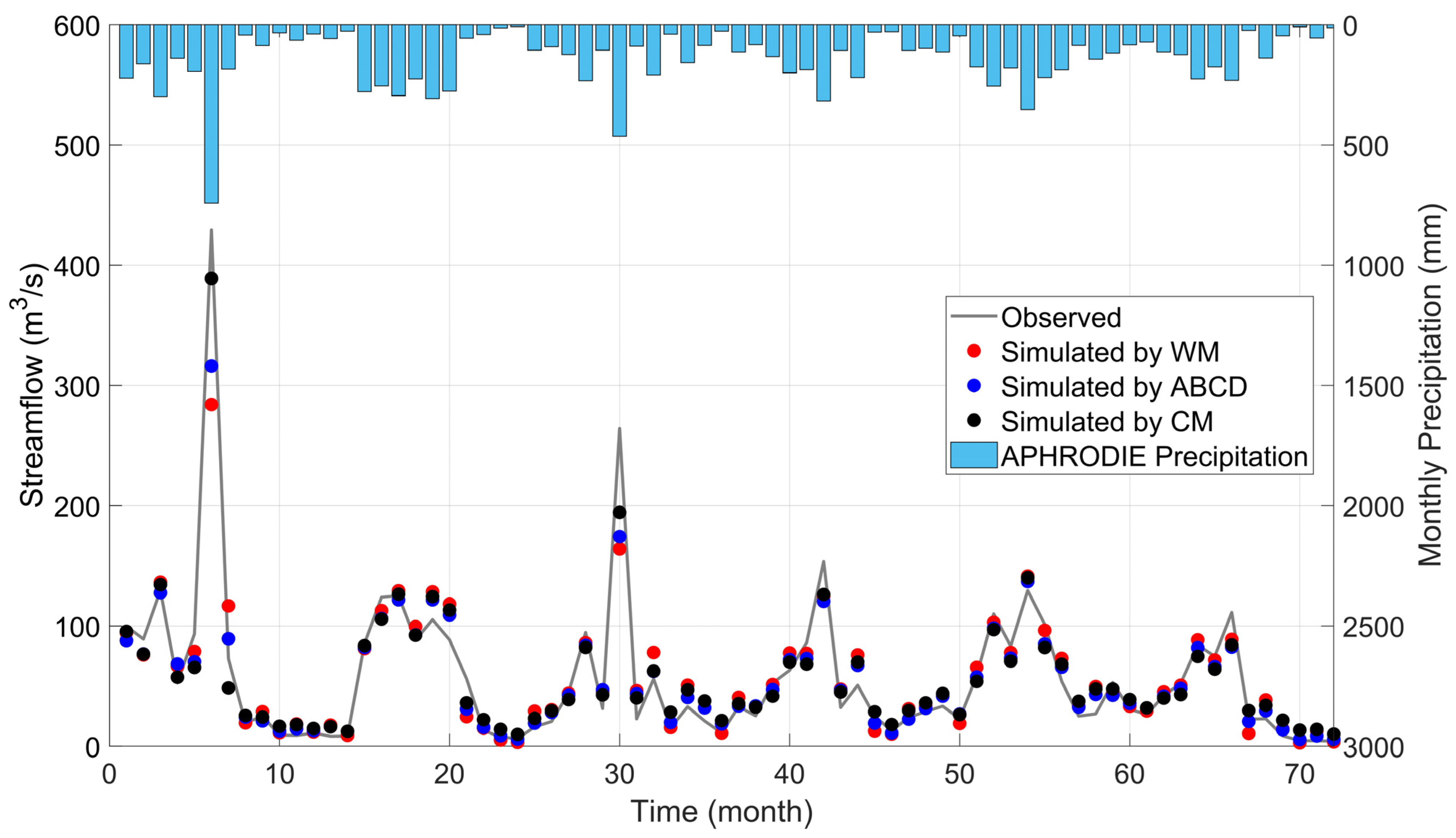
4.1. Assessment of APHRODITE Rainfall Product
4.2. Simulation Analysis of Monthly Water Balance Model
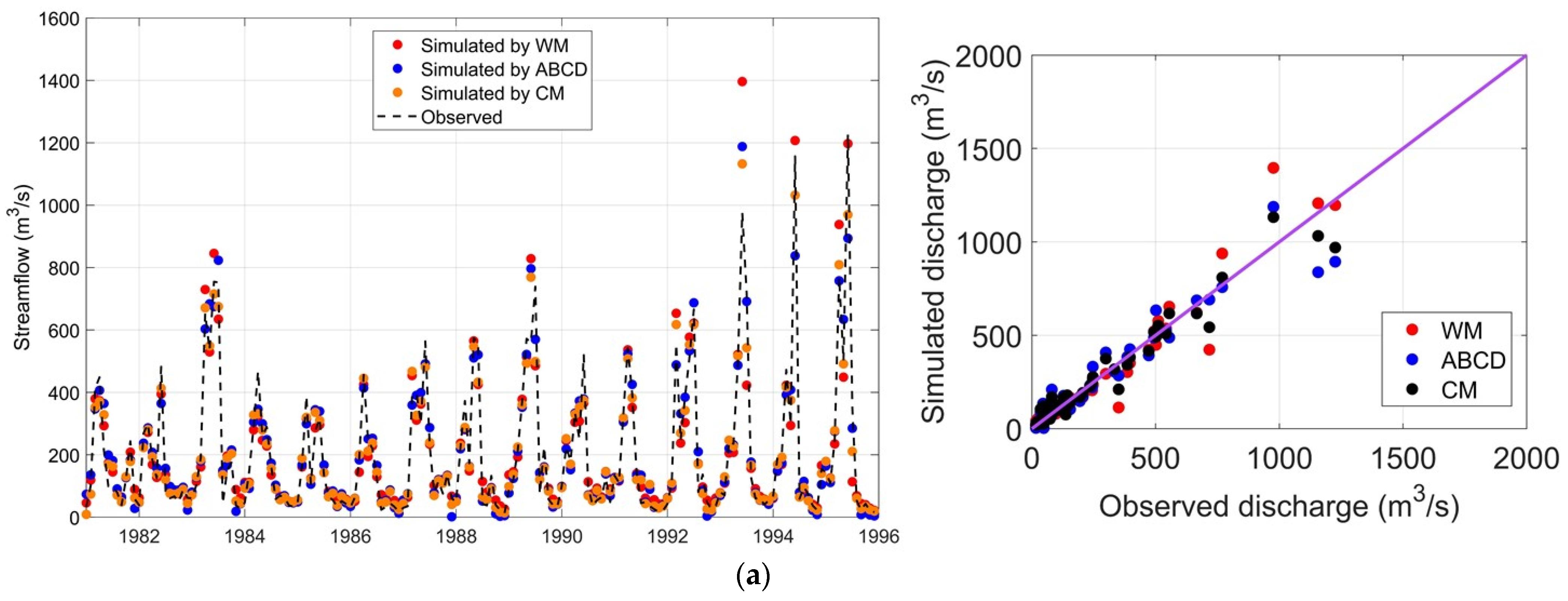
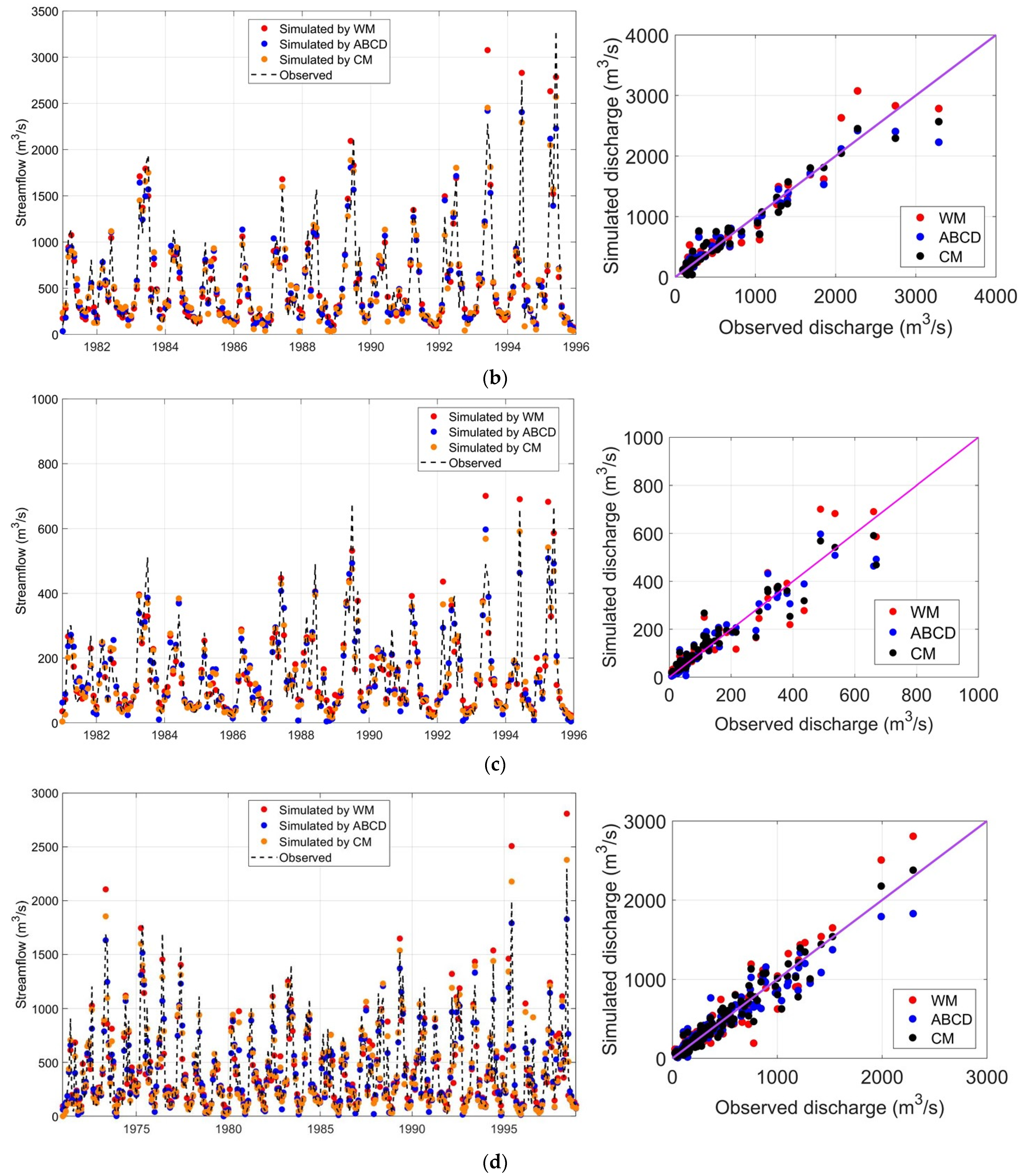
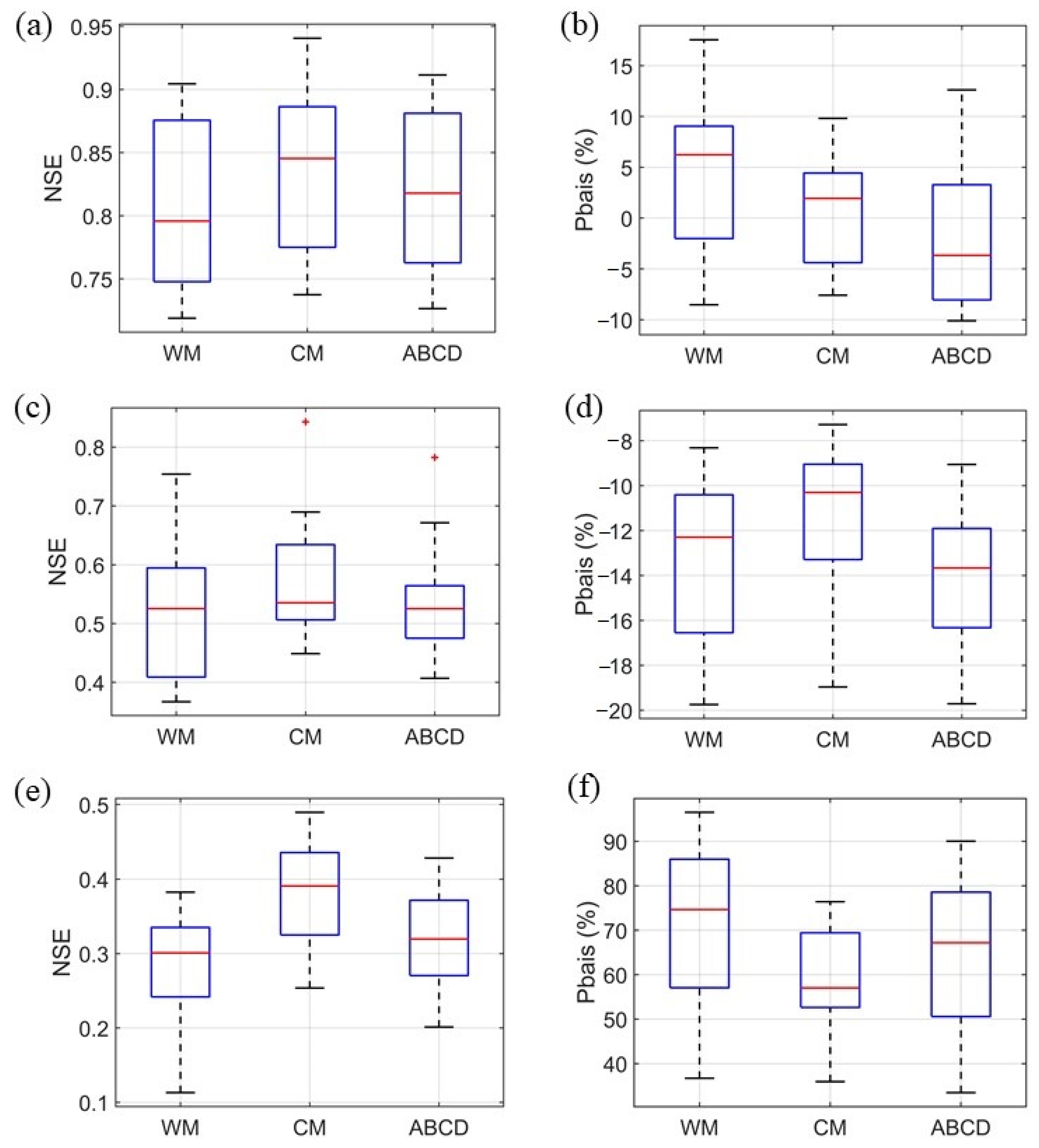
4.2.1. Simulation Results Using the Observed Rainfall
4.2.2. Simulation Results Using the APHRODITE Rainfall
4.2.3. Impacts of Climate Change and Human Activities on Streamflow Changes
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Yan, T.; Bai, J.; Lee, Z.Y.A.; Shen, Z. SWAT-simulated streamflow responses to climate variability and human activities in the Miyun Reservoir Basin by considering streamflow components. Sustainability 2018, 10, 941. [Google Scholar] [CrossRef]
- Wu, J.; Miao, C.; Zhang, X.; Yang, T.; Duan, Q. Detecting the quantitative hydrological response to changes in climate and human activities. Sci. Total Environ. 2017, 586, 328–337. [Google Scholar] [CrossRef] [PubMed]
- Grill, G.; Lehner, B.; Thieme, M.; Geenen, B.; Tickner, D.; Antonelli, F.; Babu, S.; Borrelli, P.; Cheng, L.; Crochetiere, H.; et al. Mapping the world’s free-flowing rivers. Nature 2019, 569, 215–221. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Huang, X.; Chen, H.; Godfray, H.C.J.; Wright, J.S.; Hall, J.W.; Gong, P.; Ni, S.; Qiao, S.; Huang, G.; et al. Managing nitrogen to restore water quality in China. Nature 2019, 567, 516–520. [Google Scholar] [CrossRef]
- Tang, Q. Global change hydrology: Terrestrial water cycle and global change. Sci. China Earth Sci. 2020, 63, 459–462. [Google Scholar] [CrossRef]
- Wang, X.B.; He, K.N.; Dong, Z. Effects of climate change and human activities on runoff in the Beichuan River Basin in the northeastern Tibetan Plateau, China. Catena 2019, 176, 81–93. [Google Scholar] [CrossRef]
- Zhang, H.; Meng, C.; Wang, Y.; Li, M. Comprehensive evaluation of the effects of climate change and land use and land cover change variables on runoff and sediment discharge. Sci. Total Environ. 2020, 702, 134401. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, X.; Wu, F.; Chen, B.; Liu, Y.; Yang, S.; Weng, Z. Quantitative analysis of climate change impact on Zhangye City’s economy based on the perspective of surface runoff. Ecol. Indic. 2019, 105, 645–654. [Google Scholar] [CrossRef]
- Kong, D.; Miao, C.; Wu, J.; Duan, Q. Impact assessment of climate change and human activities on net runoff in the Yellow River Basin from 1951 to 2012. Ecol. Eng. 2016, 91, 566–573. [Google Scholar] [CrossRef]
- Deng, C.; Liu, P.; Wang, D.; Wang, W. Temporal variation and scaling of parameters for a monthly hydrologic model. J. Hydrol. 2018, 558, 290–300. [Google Scholar] [CrossRef]
- Meng, S.; Xie, X.; Yu, X. Tracing temporal changes of model parameters in rainfall runoff modeling via a real-time data assimilation. Water 2016, 8, 19. [Google Scholar] [CrossRef]
- Pathiraja, S.; Marshall, L.; Sharma, A.; Moradkhani, H. Hydrologic modeling in dynamic catchments: A data assimilation approach. Water Resour. Res. 2016, 52, 3350–3372. [Google Scholar] [CrossRef]
- Wallner, M.; Haberlandt, U. Non-stationary hydrological model parameters: A framework based on SOM-B. Hydrol. Process. 2015, 29, 3145–3161. [Google Scholar] [CrossRef]
- Wang, D.; Tang, Y. A one-parameter Budyko model for water balance captures emergent behavior in darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef]
- Feng, M.; Liu, P.; Guo, S.; Shi, L.; Deng, C.; Ming, B. Deriving adaptive operating rules of hydropower reservoirs using time-varying parameters generated by the EnKF. Water Resour. Res. 2017, 53, 6885–6907. [Google Scholar] [CrossRef]
- Troin, M.; Martel, J.; Arsenault, R.; Brissette, F. Large-sample study of uncertainty of hydrological model components over North America. J. Hydrol. 2022, 609, 127766. [Google Scholar] [CrossRef]
- Rocha, J.; Carvalho-Santos, C.; Diogo, P.; Beça, P.; Keizer, J.J.; Nunes, J.P. Impacts of climate change on reservoir water availability, quality and irrigation needs in a water scarce Mediterranean region (southern Portugal). Sci. Total Environ. 2020, 736, 39477. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F. Analysis of continuous streamflow regionalization methods within a virtual setting. Hydrolog. Sci. J. 2016, 61, 2680–2693. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Wood, A.W.; Brissette, F.; Martel, J.-L. Generating ensemble streamflow forecasts: A review of methods and approaches over the past 40 years. Water Resour. Res. 2021, 57, e2020WR028392. [Google Scholar] [CrossRef]
- Mockler, E.M.; O’Loughlin, F.E.; Bruen, M. Understanding hydrological flow paths in conceptual catchment models using uncertainty and sensitivity analysis. Comput. Geosci. 2016, 90, 66–77. [Google Scholar] [CrossRef]
- Wang, F.; Huang, G.H.; Fan, Y.; Li, Y.P. Development of a disaggregated multi-level factorial hydrologic data assimilation model. J. Hydrol. 2022, 610, 127802. [Google Scholar] [CrossRef]
- Wan, Y.; Chen, J.; Xu, C.Y.; Xie, P.; Qi, W.; Li, D.; Zhang, S. Performance dependence of multi-model combination methods on hydrological model calibration strategy and ensemble size. J. Hydrol. 2021, 603, 127065. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Inter-comparison of lumped hydrological models in data-scarce watersheds using different precipitation forcing data sets: Case study of Northern Ontario, Canada. J. Hydrol. 2020, 31, 100730. [Google Scholar] [CrossRef]
- Khaniya, M.; Tachikawa, Y.; Ichikawa, Y.; Yorozu, K. Impact of assimilating dam outflow measurements to update distributed hydrological model states: Localization for improving ensemble Kalman filter performance. J. Hydrol. 2022, 608, 127651. [Google Scholar] [CrossRef]
- Remondi, F.; Kirchner, J.W.; Burlando, P.; Fatichi, S. Water flux tracking with a distributed hydrological model to quantify controls on the spatio-temporal variability of transit time distributions. Water Resour. Res. 2018, 54, 3081–3099. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Liang, K.; Liu, C. Comparison of performance of twelve monthly water balance models in different climatic catchments of China. J. Hydrol. 2015, 529, 1030–1040. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, K.; Yu, Z.; Li, Z.; Li, Q. Improving the flood prediction capability of the Xinanjiang model in ungauged nested catchments by coupling it with the geomorphologic instantaneous unit hydrograph. J. Hydrol. 2014, 517, 1035–1048. [Google Scholar] [CrossRef]
- Cheng, S.; Cheng, L.; Liu, P.; Zhang, L.; Xu, C.; Xiong, L.; Xia, J. Evaluation of baseflow modelling structure in monthly water balance models using 443 Australian catchments. J. Hydrol. 2020, 591, 125572. [Google Scholar] [CrossRef]
- Bastola, S.; Murphy, C.; Sweeney, J. The role of hydrological modelling uncertainties in climate change impact assessments of Irish river catchments. Adv. Water Resour. 2011, 34, 562–576. [Google Scholar] [CrossRef]
- Hamel, P.; Guswa, A.J.; Sahl, J.; Zhang, L.; Abebe, A. Predicting dry-season flows with a monthly rainfall-runoff model: Performance for gauged and ungauged catchments. Hydrol. Process. 2017, 31, 3844–3858. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Thornthwaite, C.W.; Mather, J.R. The Water Balance; Laboratory of Climatology, Drexel Institute of Technology: Centerton, NJ, USA, 1955; Volume 8, pp. 1–104. [Google Scholar]
- Shafii, M.; Craig, J.R.; Macrae, M.L.; English, M.C.; Schiff, S.L.; Van Cappellen, P.; Basu, N.B. Can improved flow partitioning in hydrologic models increase biogeochemical predictability? Water Resour. Res. 2019, 55, 2939–2960. [Google Scholar] [CrossRef]
- Khatami, S.; Peel, M.C.; Peterson, T.J.; Western, A.W. Equifinality and flux mapping: A new approach to model evaluation and process representation under uncertainty. Water Resour. Res. 2019, 55, 8922–8941. [Google Scholar] [CrossRef]
- Gupta, H.V.; Wagener, T.; Liu, Y. Reconciling theory with observations: Elements of a diagnostic approach to model evaluation. Hydrol. Process. 2008, 22, 3802–3813. [Google Scholar] [CrossRef]
- Thomas, H.A. Improved Methods for National Water Assessment; Center for Integrated Data Analytics Wisconsin Science Center: Washington, DC, USA, 1981. [Google Scholar]
- Makhlouf, Z.; Michel, C. A two-parameter monthly water balance model for French watersheds. J. Hydrol. 1994, 162, 299–318. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, S. A two-parameter monthly water balance model and its application. J. Hydrol. 1999, 216, 111–123. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Si, J.; Li, C.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1112. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Separating the impacts of climate change and land surface alteration on runoff reduction in the Jing River catchment of China. Catena 2016, 147, 80–86. [Google Scholar] [CrossRef]
- Omer, A.; Ma, Z.G.; Zheng, Z.Y.; Saleem, F. Natural and anthropogenic influences on the recent droughts in Yellow River Basin, China. Sci. Total Environ. 2020, 704, 135428. [Google Scholar] [CrossRef]
- Hero, M.; Booij, M.J.; Hoekstra, A.Y. Hydrological response to future land-use change and climate change in a tropical catchment. Hydrolog. Sci. J. 2018, 63, 1368–1385. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, G.; Fu, B.; Zhang, L. Explanation of climate and human impacts on sediment discharge change in Darwinian hydrology: Derivation of a differential equation. J. Hydrol. 2018, 559, 827–834. [Google Scholar] [CrossRef]
- Li, B.; Yu, Z.; Liang, Z.; Song, K. Effects of climate variations and human activities on runoff in the Zoige Alpine Wetland in the eastern edge of the Tibetan Plateau. J. Hydrol. Eng. 2014, 19, 1026–1035. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Wang, W.; Ren, D.; Zhao, Y.; Wu, X. Separating climate change and human contributions to variations in streamflow and its components using eight time-trend methods. Hydrol. Process. 2019, 33, 383–394. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, D.; Yang, H.; Sivapalan, M. Unifying catchment water balance models for different time scales through the maximum entropy production principle. Water Resour. Res. 2016, 52, 7503–7512. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Espinoza, J.C.V.; Ronchail, J.; Filho, O.C.R. Assessment of different precipitation datasets and their impacts on the water balance of the Negro River basin. J. Hydrol. 2011, 404, 304–322. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of High-resolution satellite rainfall products over complex terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhang, J.Y.; Jin, J.L.; Liu, Y.L.; He, R.M.; Bao, Z.X.; Liu, C.S.; Li, Y. Regional calibration of a water balance model for estimating stream flow in ungauged areas of the Yellow River Basin. Quat. Int. 2013, 336, 65–72. [Google Scholar] [CrossRef]
- Wilffried, B. Evaporation into the Atmosphere: Theory, History and Application; Cornell University Press: Ithaca, NY, USA, 1992; pp. 241–244. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, L.; Wang, D.; Liu, P.; Guo, S.; Xu, C.Y. Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters. J. Hydrol. 2015, 522, 326–338. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, H.; Yang, D.; Jayawardena, A.W. Quantifying the effect of vegetation change on the regional water balance within the Budyko framework. Geophys. Res. Lett. 2016, 43, 1140–1148. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: San Diego, CA, USA, 1974. [Google Scholar]
- Milly, P.C.; Dunne, K.A. Macroscale water fluxes 2. Water and energy supply control of their inter-annual variability. Water Resour. Res. 2002, 38, 241–249. [Google Scholar] [CrossRef]
- Liang, W.; Bai, D.; Wang, F.; Fu, B.; Yan, J.; Wang, S. Quantifying the impacts of climate change and ecological restoration on streamflow changes based on a Budyko hydrological model in China’s Loess Plateau. Water Resour. Res. 2015, 51, 6500–6519. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Hu, Q. An error analysis of the Budyko hypothesis for assessing the contribution of climate change to runoff. Water Resour. Res. 2014, 50, 9620–9629. [Google Scholar] [CrossRef]
- Umer, M.; Gabriel, H.F.; Haider, S.; Nusrat, A.; Shahid, M. Application of precipitation products for flood modeling of transboundary river basin: A case study of Jhelum Basin. Theor. Appl. Climatol. 2021, 143, 989–1004. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sapriza-Azuri, G.; Jodar, J.; Navarro, V.; Jan Slooten, L.; Carrera, J.; Gupta, H.V. Impacts of rainfall spatial variability on hydrogeological response. Water Resour. Res. 2015, 51, 1300–1314. [Google Scholar] [CrossRef]
- Younger, P.M.; Freer, J.E.; Beven, K.J. Detecting the effects of spatial variability of rainfall on hydrological modelling within an uncertainty analysis framework. Hydrol. Processes 2009, 23, 1988–2003. [Google Scholar] [CrossRef]
- Faiz, M.A.; Zhang, Y.; Baig, F.; Wrzesinski, D.; Naz, F. Identification and inter-comparison of appropriate long-term precipitation datasets using decision tree model and statistical matrix over China. Int. J. Climatol. 2021, 41, 5003–5021. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.W.; Hong, Y. Multi-scale evaluation of high-resolution multi-sensor blended global precipitation products over the Yangtze River. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Yang, H.; Yong, B.; Yang, X.; Fei, Y.; Ma, M. Comprehensive evaluation of multi-satellite precipitation products with a dense rain gauge network and optimally merging their simulated hydrological flows using the Bayesian model averaging method. J. Hydrol. 2012, 452–453, 213–225. [Google Scholar] [CrossRef]
- Nasseri, M.; Zahraie, B.; Ajami, N.K.; Solomatine, D.P. Monthly water balance modeling: Probabilistic, possibilistic and hybrid methods for model combination and ensemble simulation. J. Hydrol. 2014, 511, 675–691. [Google Scholar] [CrossRef]
- Liu, W.; Engel, B.A.; Feng, Q. Modelling the hydrological responses of green roofs under different substrate designs and rainfall characteristics using a simple water balance model. J. Hydrol. 2021, 602, 126786. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, H.; Wang, Y.; Zhu, Y. Assessing the impact of climate variability and human activity to streamflow variation. Hydrol. Earth Syst. Sci. 2016, 20, 1547–1560. [Google Scholar] [CrossRef]
- Greve, P.; Gudmundsson, L.; Orlowsky, B.; Seneviratne, S.I. A two-parameter Budyko function to represent conditions under which evapotranspiration exceeds precipitation. Hydrol. Earth Syst. Sci. 2019, 20, 2195–2205. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Huang, Y.; Wang, G. The complementary relationship and generation of the Budyko functions. Geophys. Res. Lett. 2015, 42, 1781–1790. [Google Scholar] [CrossRef] [Green Version]
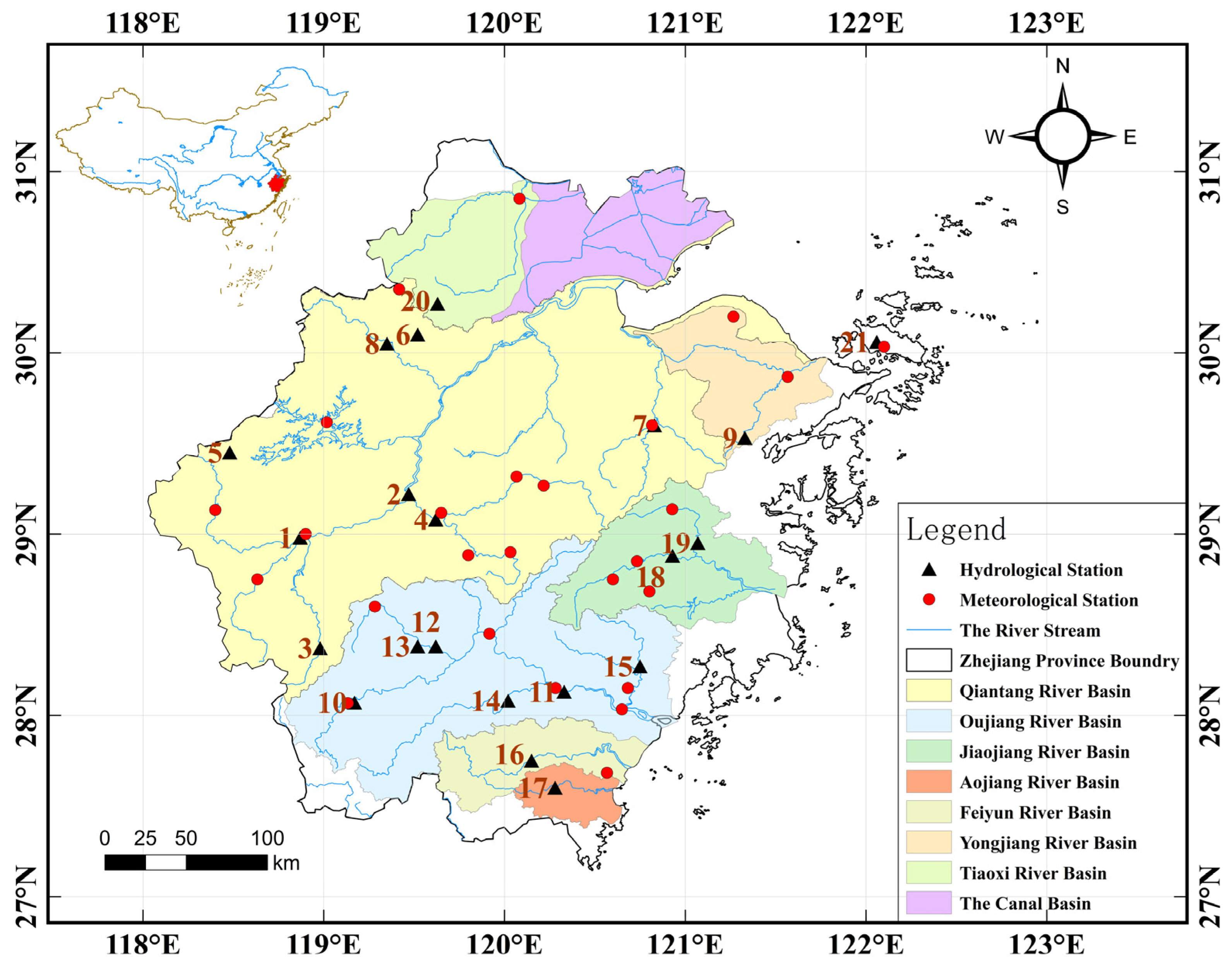
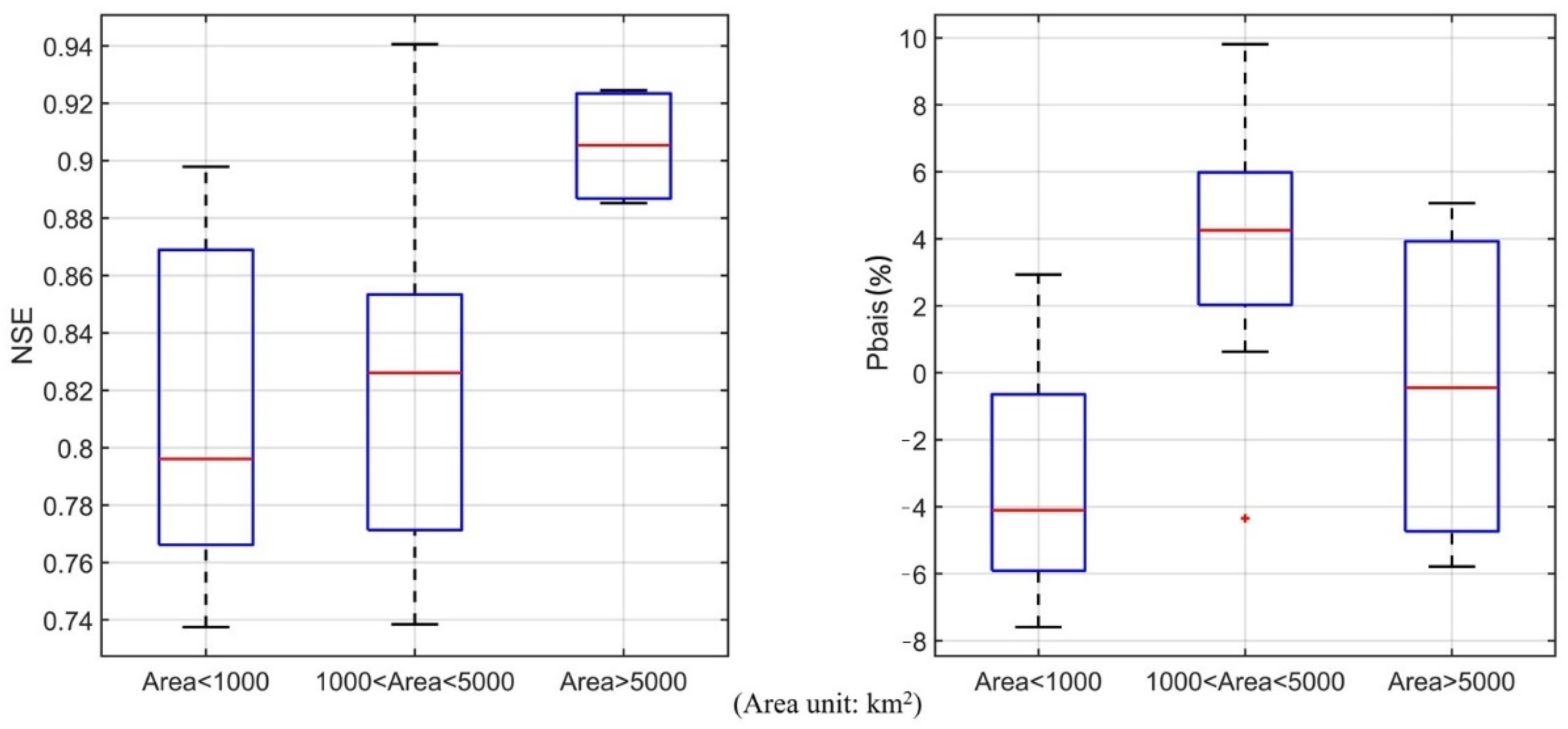
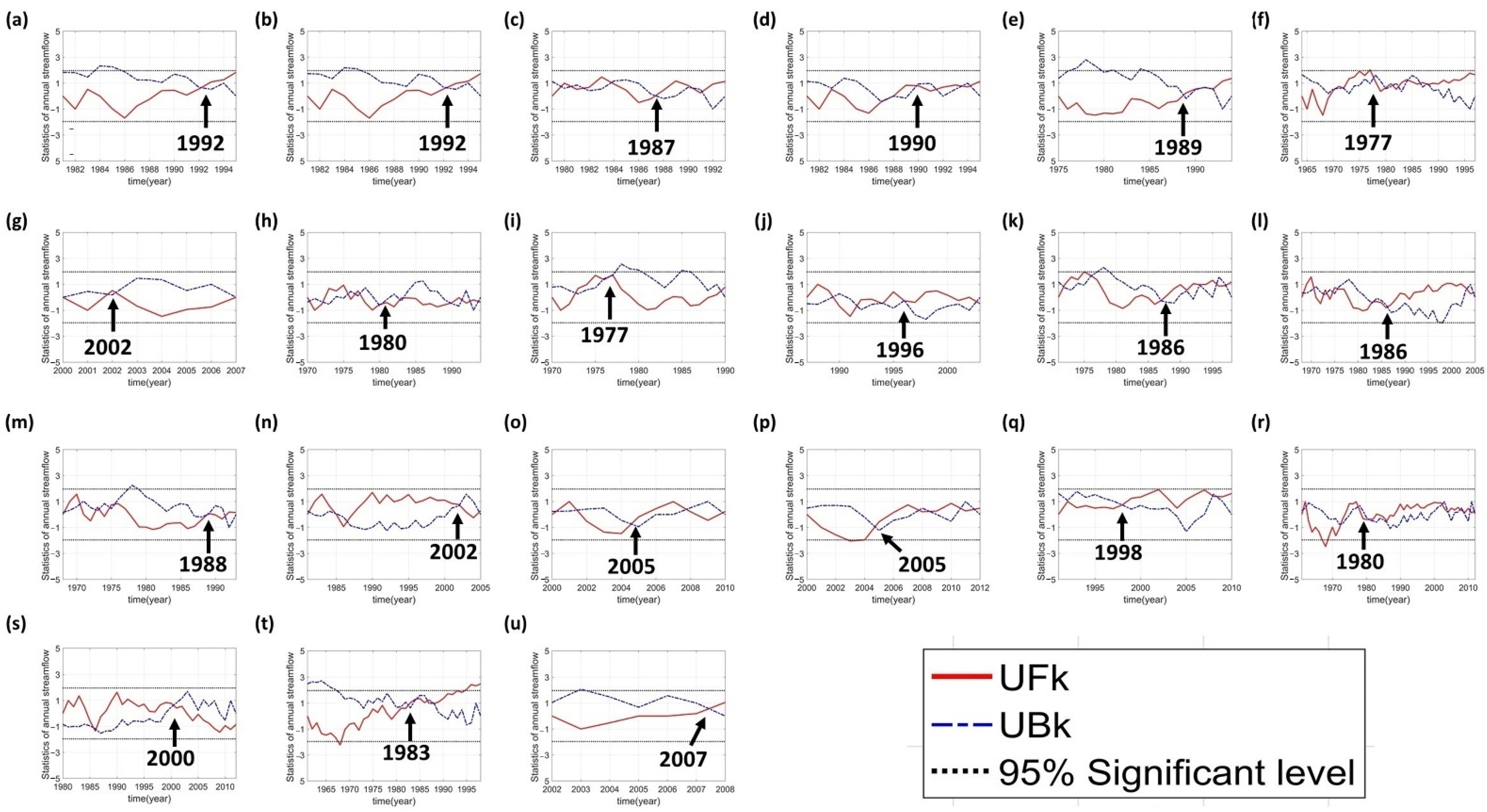

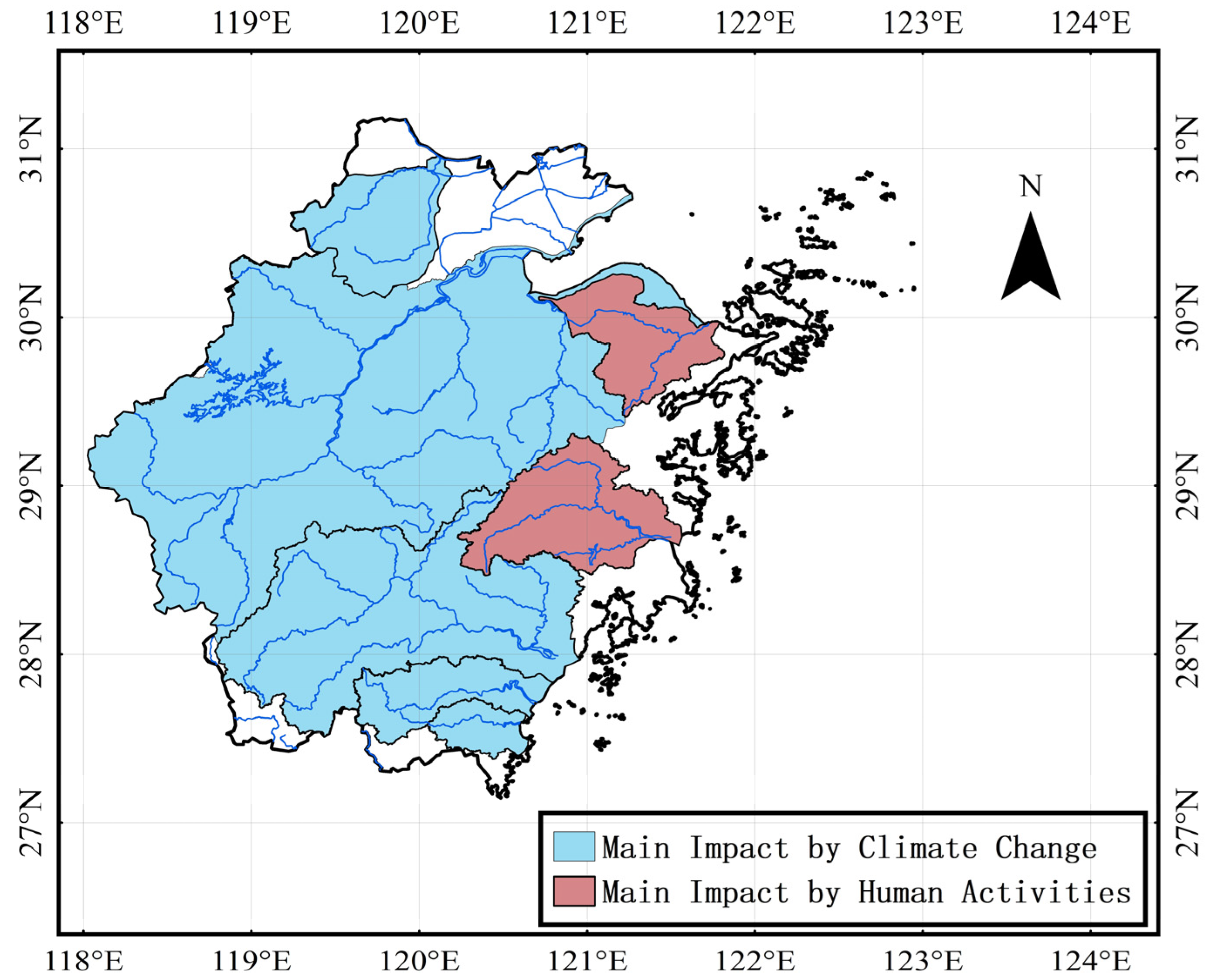
| Station Number | Station Name | River System | Period of Record | Calibration Period | Validation Period | Drainage Area (km2) |
|---|---|---|---|---|---|---|
| 1 | Quzhou (QZ) | Qiantangjiang | 1981–1995 | 1981–1990 | 1991–1995 | 5545 |
| 2 | Lanxi (LX) | Qiantangjiang | 1981–1995 | 1981–1990 | 1991–1995 | 18,204 |
| 3 | Zhonggeng (ZG) | Qiantangjiang | 1979–1993 | 1979–1988 | 1989–1993 | 610 |
| 4 | Jinhua (JH) | Qiantangjiang | 1981–1995 | 1981–1990 | 1991–1995 | 5920 |
| 5 | Zhongzhou (ZZ) | Qiantangjiang | 1975–1994 | 1975–1987 | 1988–1994 | 94 |
| 6 | Xufan (XF) | Qiantangjiang | 1964–1997 | 1964–1986 | 1987–1997 | 62 |
| 7 | Shengzhou (SZ) | Qiantangjiang | 2000–2007 | 2000–2004 | 2005–2007 | 2291 |
| 8 | Qinshandian (QSD) | Qiantangjiang | 1970–1994 | 1970–1986 | 1987–1994 | 1329 |
| 9 | Nanxikou (NXK) | Yongjiang | 1970–1990 | 1970–1983 | 1984–1990 | 126 |
| 10 | Longquan (LQ) | Oujiang | 1987–2003 | 1987–1997 | 1998–2003 | 1469 |
| 11 | Weiren (WZ) | Oujiang | 1971–1998 | 1971–1988 | 1989–1998 | 13,500 |
| 12 | Jingjukou (JJK) | Oujiang | 1968–2005 | 1968–1992 | 1993–2005 | 1880 |
| 13 | Shangbao (SB) | Oujiang | 1968–1993 | 1968–1984 | 1985–1993 | 499 |
| 14 | Baiyan (BY) | Oujiang | 1981–2005 | 1981–1997 | 1998–2005 | 3172 |
| 15 | Shizhu (SZ) | Oujiang | 2000–2010 | 2000–2006 | 2007–2010 | 1359 |
| 16 | Xuekou (XK) | Feiyunjiang | 2000–2012 | 2000–2008 | 2009–2012 | 1932 |
| 17 | Daitou (DT) | Aojiang | 1991–2010 | 1991–2004 | 2005–2010 | 338 |
| 18 | Baizhiao (BZA) | Jiaojiao | 1961–2012 | 1961–1995 | 1996–2012 | 2475 |
| 19 | Shaduan (SD) | Jiaojiao | 1980–2012 | 1980–2001 | 2002–2012 | 1482 |
| 20 | Qiaodongcun (QDC) | Tiaoxi | 1961–1998 | 1961–1985 | 1986–1998 | 242 |
| 21 | Changchunling (CCL) | Zhoushan Island | 2002–2008 | 2002–2005 | 2006–2008 | 3.9 |
| Station | WM Model | ABCD Model | CM Model | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Smax | ks | kg | a | b | c | d | k | SC | d | |
| QZ | 298.04 | 0.90 | 0.003 | 0.87 | 210.81 | 0.13 | 0.04 | 0.87 | 710.46 | 0.09 |
| LX | 538.03 | 0.65 | 0.011 | 0.81 | 205.91 | 0.37 | 0.18 | 1.07 | 1040.79 | 0.10 |
| JH | 296.92 | 0.71 | 0.001 | 0.91 | 223.25 | 0.25 | 0.12 | 0.93 | 540.19 | 0.05 |
| WR | 333.79 | 0.99 | 0.001 | 0.85 | 213.51 | 0.01 | 0.99 | 0.70 | 416.38 | 0.46 |
| Station | WM Model | ABCD Model | CM Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | Calibration | Validation | |||||||
| NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | |
| QZ | 0.90 | 2.00 | 0.91 | 2.11 | 0.91 | 2.85 | 0.92 | −1.35 | 0.92 | −0.03 | 0.96 | −1.29 |
| LX | 0.88 | 0.31 | 0.92 | 3.46 | 0.89 | −0.05 | 0.93 | −1.76 | 0.88 | −0.12 | 0.94 | −2.28 |
| JH | 0.89 | 2.11 | 0.87 | 6.93 | 0.83 | 1.39 | 0.89 | 2.08 | 0.85 | −0.09 | 0.90 | 3.20 |
| WR | 0.88 | 2.27 | 0.87 | 3.06 | 0.86 | −2.61 | 0.91 | −3.01 | 0.91 | −0.62 | 0.93 | 0.40 |
| Station | WM Model | ABCD Model | CM Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | Calibration | Validation | |||||||
| NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | NSE | Pbais(%) | |
| QZ | 0.86 | 9.26 | 0.90 | −3.57 | 0.89 | −0.29 | 0.90 | −10.11 | 0.89 | 3.19 | 0.92 | −5.78 |
| LX | 0.84 | −1.05 | 0.89 | −8.53 | 0.86 | −0.47 | 0.91 | −7.02 | 0.85 | 1.65 | 0.92 | −3.68 |
| ZG | 0.86 | 6.31 | 0.88 | −1.72 | 0.90 | −0.10 | 0.87 | −8.02 | 0.87 | 3.66 | 0.90 | −3.71 |
| JH | 0.74 | 3.21 | 0.89 | 6.64 | 0.75 | −1.16 | 0.91 | 5.26 | 0.76 | 10.96 | 0.89 | 2.79 |
| ZZ | 0.80 | 7.96 | 0.88 | −2.90 | 0.83 | −0.19 | 0.88 | −8.84 | 0.82 | 4.26 | 0.89 | −4.50 |
| XF | 0.74 | 9.05 | 0.79 | 8.05 | 0.79 | −0.19 | 0.77 | 2.62 | 0.74 | 0.27 | 0.78 | 2.93 |
| SZ | 0.69 | 3.82 | 0.73 | −6.97 | 0.77 | −0.22 | 0.75 | −4.76 | 0.71 | −4.74 | 0.75 | 2.49 |
| QSD | 0.82 | 7.39 | 0.75 | 12.96 | 0.85 | −0.42 | 0.82 | 5.54 | 0.81 | 0.95 | 0.85 | 5.52 |
| NXK | 0.76 | 9.65 | 0.75 | −1.59 | 0.76 | −0.39 | 0.75 | −4.78 | 0.78 | 5.20 | 0.76 | −5.79 |
| LQ | 0.93 | 4.67 | 0.85 | 0.22 | 0.93 | −0.20 | 0.90 | −3.67 | 0.92 | 4.86 | 0.94 | 0.63 |
| WR | 0.86 | 6.13 | 0.88 | 5.29 | 0.87 | −0.28 | 0.89 | −0.55 | 0.87 | 5.15 | 0.89 | 5.06 |
| JJK | 0.87 | 5.13 | 0.86 | 6.22 | 0.86 | −0.05 | 0.87 | 1.77 | 0.87 | 4.50 | 0.87 | 4.25 |
| SB | 0.81 | 14.38 | 0.83 | 9.15 | 0.85 | −0.51 | 0.85 | −4.19 | 0.85 | 5.40 | 0.85 | 1.94 |
| BY | 0.80 | 3.62 | 0.80 | 10.94 | 0.81 | −0.83 | 0.82 | 5.61 | 0.80 | 1.27 | 0.83 | 4.97 |
| SZ | 0.76 | 15.46 | 0.76 | 9.01 | 0.83 | −0.54 | 0.82 | 1.69 | 0.86 | 2.26 | 0.85 | 3.59 |
| XK | 0.72 | 9.35 | 0.77 | 8.63 | 0.79 | −1.43 | 0.80 | 1.39 | 0.78 | −6.25 | 0.81 | −4.35 |
| DT | 0.76 | 0.39 | 0.80 | −6.91 | 0.75 | −4.95 | 0.75 | −9.72 | 0.85 | −0.66 | 0.81 | −6.03 |
| BZA | 0.77 | 11.40 | 0.77 | 10.00 | 0.76 | −0.44 | 0.77 | 7.29 | 0.78 | 5.54 | 0.78 | 7.31 |
| SD | 0.75 | 4.49 | 0.72 | 17.55 | 0.70 | −0.07 | 0.73 | 12.62 | 0.74 | 3.96 | 0.74 | 9.81 |
| QDC | 0.74 | 11.85 | 0.73 | 2.24 | 0.80 | −0.72 | 0.75 | −8.16 | 0.78 | 5.55 | 0.74 | −3.23 |
| CCL | 0.67 | 17.81 | 0.72 | 8.89 | 0.83 | −0.71 | 0.77 | −8.80 | 0.82 | 3.04 | 0.77 | −7.59 |
| River Basin | Station | Bydyko−Based | CM | |||
|---|---|---|---|---|---|---|
| w | ηclimate (%) | ηhuman (%) | ηclimate (%) | ηhuman (%) | ||
| QTJ | QZ | 0.93 | 69.65 | 30.35 | 73.82 | 26.18 |
| LX | 1.22 | 68.15 | 31.85 | 79.89 | 20.11 | |
| ZG | 1.07 | 60.59 | 39.41 | 73.73 | 26.27 | |
| JH | 1.17 | 72.98 | −27.02 | 61.35 | −38.65 | |
| ZZ | 0.81 | 60.89 | 39.11 | 61.75 | 38.25 | |
| XF | 1.46 | 59.85 | −40.15 | 51.39 | −48.61 | |
| SZ | 1.34 | −78.78 | −21.22 | −87.39 | −12.61 | |
| QSD | 0.99 | 66.25 | −33.75 | 58.09 | −41.91 | |
| YJ | NXK | 0.50 | 22.21 | −77.79 | 25.72 | −74.28 |
| OJ | LQ | 0.84 | 95.61 | −4.39 | 60.97 | −39.03 |
| WR | 0.87 | 97.38 | −2.62 | 75.83 | −24.27 | |
| JJK | 1.12 | 85.92 | −14.08 | 76.41 | −23.59 | |
| SB | 0.77 | −57.52 | −42.48 | −79.31 | −20.69 | |
| BY | 0.70 | 79.54 | −20.45 | 75.93 | −24.07 | |
| SZ | 0.71 | 57.68 | −42.32 | 80.74 | −19.26 | |
| FYJ | XK | 0.62 | 60.06 | −39.94 | 90.96 | −9.04 |
| AJ | DT | 0.24 | 69.76 | 30.24 | 98.92 | 1.08 |
| JJ | BZA | 1.05 | −31.76 | 68.24 | −39.49 | 60.51 |
| SD | 1.18 | −36.74 | −63.26 | −8.01 | −91.99 | |
| TX | QDC | 0.91 | 51.74 | 48.26 | 76.67 | 23.33 |
| ZSI | CCL | 1.70 | 71.62 | 28.38 | 77.64 | 22.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Huang, S.; Xu, Y.-P.; Teegavarapu, R.S.V.; Guo, Y.; Xie, J.; Nie, H. Quantitative Assessment of Impact of Climate Change and Human Activities on Streamflow Changes Using an Improved Three-Parameter Monthly Water Balance Model. Remote Sens. 2022, 14, 4411. https://doi.org/10.3390/rs14174411
Chen H, Huang S, Xu Y-P, Teegavarapu RSV, Guo Y, Xie J, Nie H. Quantitative Assessment of Impact of Climate Change and Human Activities on Streamflow Changes Using an Improved Three-Parameter Monthly Water Balance Model. Remote Sensing. 2022; 14(17):4411. https://doi.org/10.3390/rs14174411
Chicago/Turabian StyleChen, Hao, Saihua Huang, Yue-Ping Xu, Ramesh S. V. Teegavarapu, Yuxue Guo, Jingkai Xie, and Hui Nie. 2022. "Quantitative Assessment of Impact of Climate Change and Human Activities on Streamflow Changes Using an Improved Three-Parameter Monthly Water Balance Model" Remote Sensing 14, no. 17: 4411. https://doi.org/10.3390/rs14174411
APA StyleChen, H., Huang, S., Xu, Y.-P., Teegavarapu, R. S. V., Guo, Y., Xie, J., & Nie, H. (2022). Quantitative Assessment of Impact of Climate Change and Human Activities on Streamflow Changes Using an Improved Three-Parameter Monthly Water Balance Model. Remote Sensing, 14(17), 4411. https://doi.org/10.3390/rs14174411







