Abstract
Morphodynamic variabilities of tidal flats (e.g., the variations of pattern, area, and topography) are a key issue in the management of coastal intertidal zones. In this study, the morphodynamic variabilities of the Lin-gang (Shanghai) tidal flat were investigated using waterlines extracted from multi-source satellite images acquired from 2013 to 2020. The waterlines were evaluated against in situ measurements. The results of our investigation indicated that the tidal flat was in a state of rapid accretion from 2015 to 2018, and in a state of erosion from 2018 to 2020. We found that the accretion of the tidal flat was most likely due to the protection of local vegetation, which prevents the sea bottom from eroding. However, storms have primarily been causing erosion since 2018. The potential mechanisms of the geomorphological variations were further analyzed using the empirical orthogonal function (EOF) method. The analysis revealed that the variation in the tidal flat was dominated by two modes. The first mode accounted for 55% of the variation, while the second mode accounted for 18%. The spatial distribution of the first mode was highly related to the artificial vegetation, indicating that the local variations in the vegetation prevented the sea bottom from eroding, which was dominant in the accretional phase from 2015 to 2018. The second model reflected the extreme meteorological events that resulted in potential changes in the tidal flat’s pattern (i.e., transitioning to an erosion phase from 2018 to 2020). The satellite-derived topographies were demonstrated to be an effective means of mapping the evolution of a meso-tidal flat.
1. Introduction
Tidal flats (also called intertidal zones or mudflats) are the coastal zone between the mean higher high water line and the lower low water line [1], and they are also important margin environments that link the oceanic and terrestrial ecosystems. Understanding the variations that occur in tidal flats is critical in fields such as coastal disaster prevention and mitigation, ecosystem management, resource development, and tourism [2,3,4]. The topography of a tidal flat can vary rapidly both temporally and spatially as the combined result of the effects of tides, waves, river flow, and meteorological events [5,6,7]. This is one of the reasons why the fundamental mechanism of tidal flat variability is difficult to determine [8]. In general, one possible method of clarifying the variations and regulation is to collect the most monitoring topography data with high temporal and spatial resolutions.
The use of frequent measurements is most convincing in studies on tidal flats or beaches. For example, Van der Werf et al. monitored the nourishment of a tidal flat every three months for five years to evaluate the effect of the sediment nourishment on mitigating the negative impacts of tidal flat erosion [9]. To quantify the multi-decade variability of Narrabeen Beach (Australia), Turner et al. analyzed cross-shore profiles from 1976 to 2016 (the topographic survey was conducted monthly); the long-term monitoring very clearly revealed how and why the beach profile changed during the 40 years [10].
With the technological development in satellite remote sensing, more optical satellite data are being used in coastal studies in recent decades, and such techniques are becoming important additions to traditional monitoring [11]. The interface between the land and water, which is defined as the shoreline [12,13], coastline [14], or waterline [15,16], can be distinguished from satellite imagery and can be extracted automatically. Based on the waterline data, many of the characteristics of a tidal flat (e.g., tidal flat pattern, profile slope, and intertidal zone topography) can be calculated [17,18,19,20]. Compared to traditional methods (e.g., real-time kinematic in situ), deriving the topography from multi-satellite optical images is much more economical and can also be conducted on wider spatial and temporal scales, providing researchers with another (maybe the only) method of studying past changes in areas of interest. Turner et al. considered that satellite remote sensing is the only source of information that complements the much more limited in situ instrumentation used for land and sea monitoring [21].
In this study, a case study of the inter-annual evolution of a tidal flat with a gentle slope (~0.0045 on the muddy flat and ~0.009 on the sandy beach) in a vigorous area of Shanghai (China) was conducted to describe the variation tendency and explore the reasons why it changed rapidly during a short period. Due to the low frequency of the field measurements (i.e., once per year (at each end of 2015–2019)), satellite images were used to extend the historical digital elevation model (DEM) data for the study area. The results are expected to reveal the main patterns of the changes that occurred in the past decade and to play an important role in coastal protection and management.
2. Methodology
2.1. Study Area
The study area (Figure 1) is situated on the artificial coast of the Lin-gang New Area of the Shanghai Free Trade Zone (hereinafter referred to as Lin-gang), and is located at the intersection of a mega estuary (the Yangtze River Estuary) and a semi-closed bay (Hangzhou Bay). The land area was reclaimed by building a seawall in 2003. The coastal vegetation includes local vegetation (Phragmites), artificial vegetation (Scirpus triqueter), and invasive vegetation (Spartina Alterniflora Loisel).
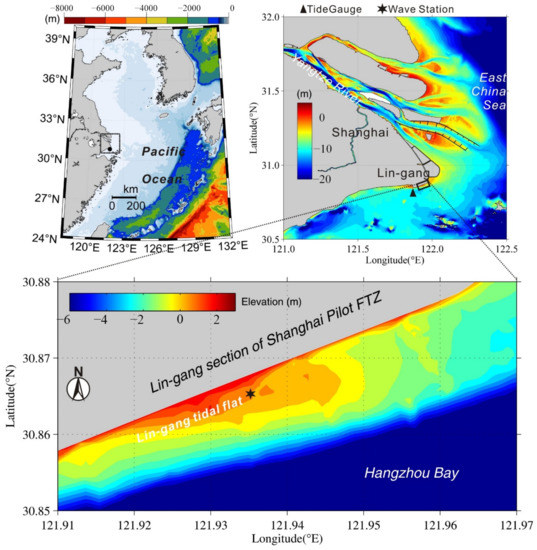
Figure 1.
The location and topography of the study area. The study area is adjacent to the Yangtze (Changjiang) River Estuary and Hangzhou Bay. The base level of the elevation datum is the local mean sea level. The triangle and star symbols represent the locations of the tide gauge and wave monitoring station, respectively.
The tidal current is characterized by reciprocal flow, and the tidal range reaches ~4.5 m during the spring tide and ~1 m during the neap tide, with a mean tidal range of 2.75 m. According to the in situ measurements, the significant wave height on the tidal flat during normal climate is less than 0.3 m. The sub-tidal currents are mainly from the Yangtze River, which carries a huge amount of suspended sediment [22,23,24]. Typhoons are typical seasonal meteorological events and may lead to extreme erosion [25]. The abundant sediment supply and strong tide and wave effects result in a dynamic tidal flat.
Figure 2 shows a satellite image of the study area and aerial photos acquired using an unmanned aerial vehicle (UAV). There is a wide muddy beach (~1 km wide in the cross-shore direction) in the intertidal zone, and the median grain size in this area is ~140 μm (fine sand). Due to the sorting processes, a sandy beach has been generated rapidly in the recent decade. Between the sandy beach and muddy tidal flat, a tidal creek has formed through erosion, and it strikes parallel to the coast. Since most of the coastal zone in Shanghai is composed of muddy tidal flats, the localized natural sandy beach is considered to be a valuable coastal resource.

Figure 2.
(A) A satellite image of the LGTF acquired on May 2021 from Google Earth and (B,C) aerial photos at low tide (the positions are shown in panel A).
It should be noted that after August 2019, the inland region adjacent to the study area was renamed the Lin-gang New Area of the Shanghai Free Trade Zone, which is expected to lead the development of Shanghai in the next few decades. According to the statistical data provided by the government, the population of Lin-gang (central region) reached ~140,000 in June 2021, which was an increase of 54.6% compared to February 2020 (http://www.pudong.gov.cn, accessed on 12 December 2021). Under the above situation, the study area is becoming a popular tourism destination (Figure 2C), which is another motivation to understand the variability in the study area.
Both the monitoring data and satellite images have revealed that the pattern of this tidal flat has changed rapidly over the last decade. Figure 3 shows the tidal flat patterns at the high and low water levels in recent years, respectively. The differences between each water level at high water level or at low water level were less than 2 cm; therefore, we can compare the satellite images at the high or low tide levels. For the high water situations, visible accretion occurred along the coast after 2014. In 2020, the area of the supratidal zone reached ~198,000 m2. For the low water situations, the tidal flat accreted in the southeastern direction from 2013 to 2017, and then the pattern shifted to the opposite direction.

Figure 3.
The satellite images acquired at the high tidal level in (A) 2014, (B) 2016, (C) 2018, and (D) 2019 and the corresponding range of the tidal levels from 2.42 m to 2.43 m (based on the mean sea level) and at the low tidal level in (E) 2013, (F) 2015, (G) 2017, and (H) 2019, and the corresponding range of the tidal levels from −1.22 m to −1.20 m.
In summary, the Lin-gang tidal flat is an important coastal resource in Shanghai. The annual satellite images reveal that the tidal flat pattern has changed a lot at both the high and low water levels. To quantify the inter-annual variability of the Lin-gang tidal flat, but limited by the low-frequency (annual) of the available profile surveys, the workflow of this study was designed as follows: (1) historical optical images taken at different tidal levels were acquired; (2) waterlines were extracted; (3) the tidal levels measured at the nearest tidal gauge were assigned to each waterline and a quarterly DEM of the tidal flat was constructed; and (4) the variations in the area were calculated, and the empirical orthogonal function (EOF) mode of the tidal flat was analyzed.
2.2. Satellite Imagery, Algorithms, and Validations
The sources of the satellite imagery, which was freely available (e.g., Landsat 7, Landsat 8, and Sentinel-2), are common and frequently reported [26]. One challenge is determining the method to extract the waterlines based on a certain algorithm when hundreds of waterlines need to be extracted. There are several open source codes for detecting waterlines automatically (e.g., CASSIE [27], CoastSat [28], OBRGIE [29], and SHOREX [30]). The workflows of these methods and software packages are similar: (1) the images are filtered (e.g., remove cloud-covered images); (2) the interface between the land and water is located using an algorithm (e.g., normalized difference water index, modified normalized difference water index [31]); (3) the tidal level is corrected (optional, depending on the study area); and (4) the time series of the waterline data is analyzed (e.g., quantifying the annual change on a decadal time scale).
The assessment of the accuracy of the waterline detection is also a key index that influences the results. Commonly, sub-pixel extraction is an acceptable method [11,32]. According to the calculations in the above references, the root mean square errors (RMSEs) of CoastSat and CASSIE are 7.2 m and 7.79 m, respectively, when they are used to analyze a similar database (i.e., Landsat and Sentinel-2). That is, these methods can study coastal variability on a long-timescale, especially when the spatial scale of the study area is much greater than the resolution of the images.
The applications of the above methods have been reported in studies of many beaches worldwide, particularly micro-tidal sandy beaches (tidal range of <2 m) [11,28,30,32,33]. For instance, Vos et al. captured the multi-timescale shoreline changes by detecting the sand/water interface in publicly available satellite images, and they assessed the shoreline variabilities of four typical sandy beaches in Europe, Australia, the USA, and New Zealand [28]. For tidal flats, the variability of the cross-shore width of the waterline is probably larger than for sandy beaches, especially in regions with large tidal ranges (i.e., macro-tidal coasts). Therefore, if the waterline and tide data are sufficient, an intertidal DEM can be constructed [15,34]. In this case, the number of waterlines at different tidal levels in a short period will affect the quality of the constructed DEM.
Based on the water-line method proposed by Mason et al. [15], two DEMs of the Western Wash (the UK, maximum tidal range of ~5 m) were described using shorelines extracted from 33 images acquired during 1992–1994, and the results were used to study the sediment transport [35]. However, limited by the number of satellite images, the time range of the waterlines was set to ~18 months. As the number of available satellite images increases, this method of extracting DEMs has been applied in many other macro-tidal zones, and the outputs are in good agreement with the measured data [36,37,38]. Furthermore, according to Mason et al., the uncertainty of the DEM’s accuracy is negligible compared to the tidal range on flatter beaches (e.g., a slope of 1/500) [15].
2.2.1. Image Extraction
The satellite images used in this study were Landsat-8 (L8), Sentinel-2 (S2), and Gaofen-1 (GF1) images, with resolutions of 30 m, 10 m, and 16 m, respectively. The duration was mainly from February 2013 to June 2021. Figure 4 shows the acquisition times of all of the available satellite images with no cloud cover and the corresponding tidal levels. The tidal levels ranged approximately from −1.5 m to 2.8 m during each year, which likely records most of the tidal flat patterns. The data were denser near the periods with the highest and lowest tidal levels due to the relatively slower tidal currents.
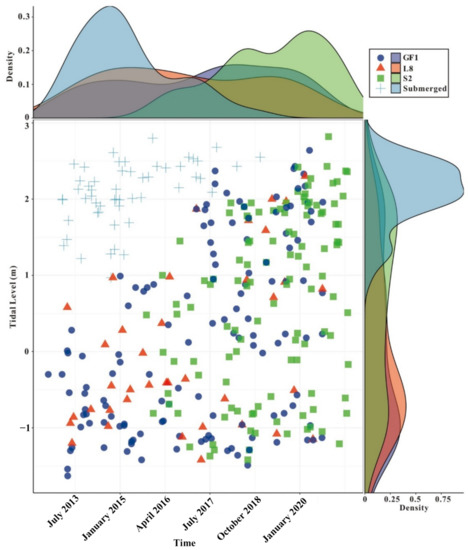
Figure 4.
The satellite image time series and the corresponding tidal levels, the top and right panels show the trends of the relative data density. GF1: Gaofen-1; L8: Landsat-8; S2: Sentinel-2; and Submerged: The entire tidal flat is submerged.
In this study, the waterlines were extracted using CoastSat, which was developed by Vos et al. as an open-source python toolkit [28]. The modified normalized difference water Index (MNDWI) was employed to distinguish the shorelines as follows:
where is a band that encompasses the reflected green light (wavelengths of S2, L8, and GF-1 are 560 nm, 530–590 nm, and 520–590 nm, respectively), and is the near-infrared radiation (wavelengths of S2, L8, and GF-1 are 842 nm, 850–880 nm and 770–890 nm, respectively). The selected extractions are shown in Figure 5.
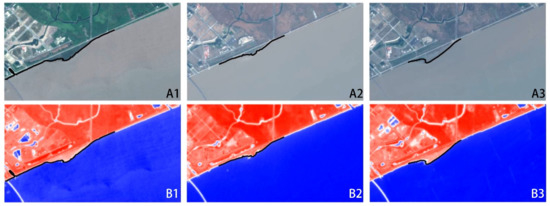
Figure 5.
The selected outputs of CoastSat. (A1–A3) are the original satellite images at three different moments; (B1–B3) are the results of MNDWI. Red and blue regions represent the land and water, respectively. The black solid lines are the waterlines calculated using this toolkit.
2.2.2. Evaluation of Waterline Detection Error
To evaluate the extraction accuracy of the above method, a UAV was employed to map the waterline. The UAV-derived waterline was compared with the results obtained from a Sentinel-2 image acquired at the same time. The drone was a DJI Phantom4 RTK Multispectral, which carried a multi-frequency global navigation satellite system (GNSS) receiver and a multispectral sensor (Figure 6). The shooting times of the UAV and satellite were 10:40 am and 10:39 am on 31 December 2020, respectively. The time difference was neglected.
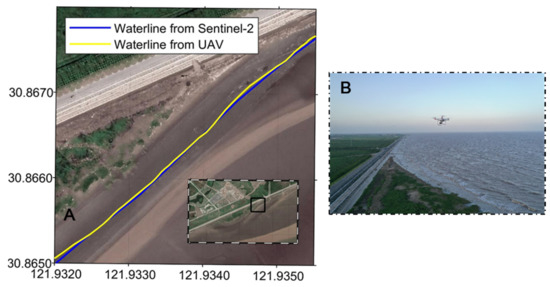
Figure 6.
(A) The waterline positions derived from the Sentinel-2 and UAV images acquired on 31 December 2020. (B) The left panel shows the photo when the drone was used for the monitoring.
The comparison of the two waterlines is shown in Figure 6A. Following Eiter and Mannila [39] and Wylie and Zhu [40], the discrete Fréchet distance (DFD) was defined as a parameter to identify the similarity of the two discrete curves:
where P and Q are polygonal curves and and are the corresponding sequences. The coupling L between P and Q is a sequence: . The of the coupling is the length of the longest link in L.
The DFD between the satellite and UAV waterlines was ~4.5 m, indicating that the waterline detection had a reliable accuracy.
2.2.3. DEM Validation
The level of accuracy achieved for the intertidal DEM depends on the accuracy of the tidal level, the local slope of the inter-tidal zone, and the resolution of the remote sensor [15]. The tidal range in the LGTF is ~4.5 m, with an average tidal flat width of ~1000 m, and thus, the average slope is ~0.0045. Therefore, if the resolutions of the satellite images range from 10 m to 30 m, the uncertainty of the topography should be 4.5–13.5 cm.
To generate the tidal flat DEM or intertidal topography, the measured tidal levels were assigned to the extracted waterlines. The waterlines from October 2018 to November 2018 were used to reconstruct the DEM of the Lin-gang tidal flat, which was then compared to the topography measured in November 2018 to evaluate the performance of the waterline-derived DEM. As shown in Figure 7, the DEM derived from the satellite data, although asynchronous, coincided well with the measured data in terms of both the tidal flat pattern and the magnitude of the topography. After interpolating onto the same grid and comparing with the measured data from 2016 to 2019, the RMSEs were 0.0563 m, 0.1248 m, 0.0887 m, and 0.0952 m, respectively. Therefore, we assumed that the change in the tidal flat in such a time interval could be neglected when investigating long-term changes.
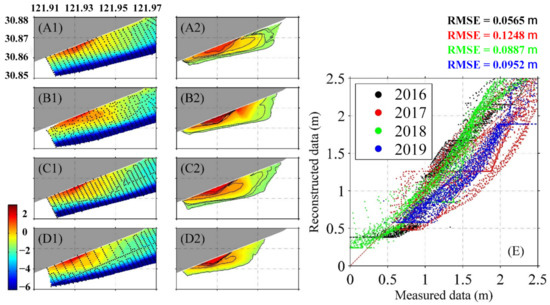
Figure 7.
(A1), (B1), (C1) and (D1) are the topography data measured in 2016, 2017, 2018, and 2019, respectively; (A2), (B2), (C2), and (D2) are the reconstructed topography of each corresponding year. The horizontal coordinates were derived from the satellite images acquired within two months, and the vertical elevations are the tidal level data from the nearest tide gauge. (E) Comparisons of the measured data and reconstructed data obtained via interpolation of the above data onto the orthogonal grids.
3. Results
3.1. General Geomorphological Changes over Time
Figure 8 presents all of the waterlines from 2013 to 2021, in which the lighter lines are closer to the current year. The western boundaries during the low tidal level only varied within a small range because there was an artificial channel, which connected to a sluice on the coast. Since the waterline positions did not contain tidal level information, we could only roughly assume that the tidal flat accreted rapidly during 2016–2020. The shorelines changed to an asymmetric pattern after 2018 for both the high and low tidal levels.
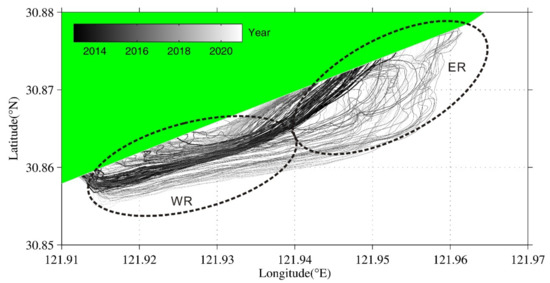
Figure 8.
All of the waterlines derived from the satellite images. The darkness and line width represent time (i.e., darker and thicker indicate older). WR and ER are the eastern and western regions of the tidal flat, respectively.
The waterlines were relatively looser in the eastern region (ER) of the entire tidal flat, which indicates that the slope in the ER was smaller than that in the western region (WR). Additionally, the waterlines in the ER did not change gradually, which may have been controlled by the more energetic wave conditions.
3.2. Relationship between Tidal Level and Tidal Flat Area
The tidal flat area (TFA) can be used as an index to quantify the potential land resources [41,42]. In this section, the area was calculated according to the plane encircled by the seawall (see Figure 2A for position) and the waterline. When the entire tidal flat was submerged, the TFA was zero.
Figure 9A presents the TFA time series at the higher and lower tidal levels relative to the mean sea level (MSL = 0 m). For a tidal level of higher than 2 m, before 2019, the seawater could cover the entire tidal flat and the corresponding area was zero. After 2019, the satellites did not capture the above situation, even when the tidal level was higher than 2.5 m. For a tidal level lower than −1 m, there was very obvious accretion from 2013 to 2019. In 2018, the largest area of the entire tidal flat (including the supratidal and intertidal zones) reached ~4 × 106 m2. After this, the TFA transitioned to the rapid reduction phase. In 2021, at a similar tidal level, the largest TFA had decreased to ~3 × 106 m2.
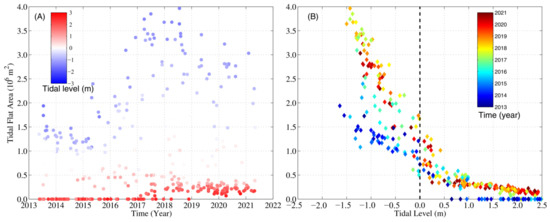
Figure 9.
Temporal variations in the tidal flat area (the envelope formed by the waterlines and seawall). (A) Variations in the tidal flat area with time. The red and blue dots represent the shorelines at the moments of the high and low tidal levels, respectively. (B) The relationship between the tidal level and the tidal flat area.
Figure 9B shows the negative relationship between the tidal levels and TFAs. The gradient was quite a bit larger under the MSL than below the MSL. The TFA exhibited the widest range (1.0–4.0 × 106 m3) with time at tidal levels of −1.5 m to −1 m, indicating that the position and slope of the edge of the LGTF changed significantly during the last decade.
3.3. Mechanisms of the Geomorphological Variations Derived via EOF Analysis
To investigate the possible spatial patterns and the corresponding temporal variabilities in the study area in recent years, EOF analysis was employed. EOF is very efficient in calculating the evolution patterns of the spatial distribution in a time series, especially in atmospheric and oceanic research [43,44]. A set of orthogonal functions can be calculated as follows:
where the left side is the original time series of DEM, and EOF(x,y)k and PC(t)k represent the spatial pattern and temporal component of each mode (k), respectively.
To guarantee enough data to reconstruct the DEM, the quarterly waterlines in the LGTF from 2015 to 2020 were considered. Figure 10 shows the domain of the EOF mode, which was statistically significant and explained 55% of the total variation. Regarding the spatial pattern, most of the regions of the tidal flat were positive, which means the tidal flat accreted or eroded simultaneously. It should also be noted that there was an opponent belt zone (NE–SW direction, parallel to the sandy beach), which coincided with the location of the tidal creek (Figure 2C). Since the bulks of the two opponent regions did not match, the sediment in this belt zone should not be the main source or sink for the rest of the regions.
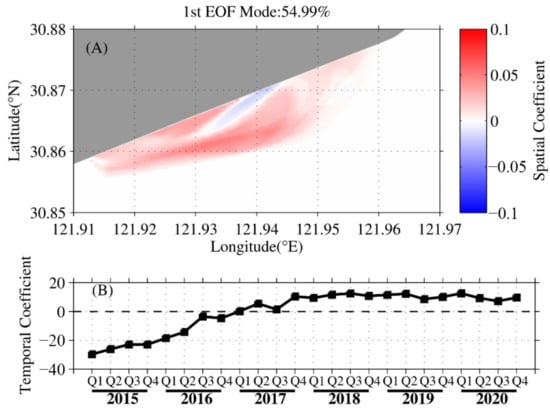
Figure 10.
(A) First EOF spatial pattern and (B) the associated temporal coefficients. Red and blue represent the opponent phases. In detail, accretion occurred in the blue regions when erosion occurred in the red regions, and vice versa. Q1, Q2, Q3, and Q4 are the four quarters of each year (the same hereinafter).
The temporal variations revealed a generally increasing trend with the seasons. In particular, the value was lowest in Q1 of 2015, increased to zero in Q3 of 2016, approached the highest value in Q4 of 2017, and then decreased slightly after 2018. The rate of change of the temporal mode was most significant during 2016 and 2017.
Considering the spatial and temporal distributions of the first EOF mode together, it was found that the entire tidal flat accreted as the tidal channel eroded in the last five years, and the fourth quarter of 2017 was the turning point at which the entire tidal flat stopped accreting rapidly. The fundamental mechanism of the first EOF mode may have been controlled by the sediment input into the LGTF or the sand fixation capacity.
The second EOF mode contributed ~18% (Figure 11). The spatial distribution indicates that the phases were opposite in the ER and WR, which may reflect the local balance of the sediment transport. In particular, after the second quarter of 2018, in the ER of the LGTF, the phase changed to erosion and lasted until the end of 2019, which led to an increase in the slope. The factors controlling the domain are discussed in the next section.
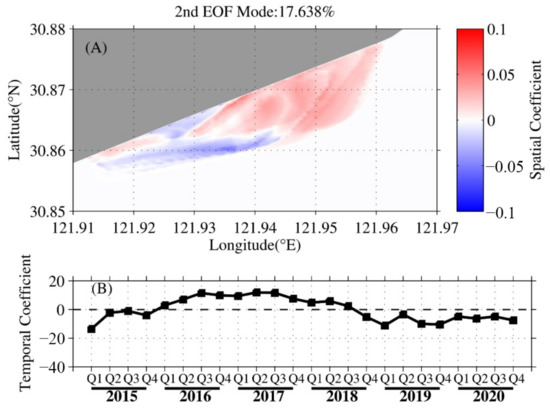
Figure 11.
(A) Second EOF spatial pattern and (B) the associated temporal coefficients.
4. Discussion
4.1. Topography Changes Based on Annual Monitoring Data
To discuss the necessity and reasonability of the above studies, the geomorphological measurements conducted at the end of each year from 2015 to 2019 were compared year by year (Figure 12). Gradual accretion occurred throughout the entire tidal flat from 2015 to 2017. After this, the LGTF transitioned to the erosion phase, mainly in the ER. The temporal trend of the geomorphological changes based on the monitoring data was consistent with the results obtained from the satellite images.
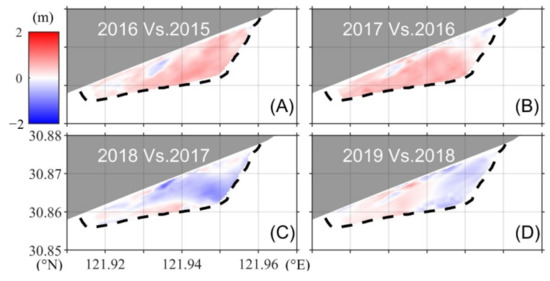
Figure 12.
(A–D) are the annual monitored changes in the topography from 2015 to 2019. The black dashed line marks the approximate location of the waterline corresponding to the lowest tidal level.
The differences between the bathymetries monitored in 2015 and 2019 are shown in Figure 13. Most of the tidal flats experienced accretion based on the comparison of the bathymetry in 2015 and 2019, but a belt region was eroded. The changing pattern is consistent with the first mode of the above EOF results, and the erosion location corresponds to the position of the tidal channel (Figure 2).
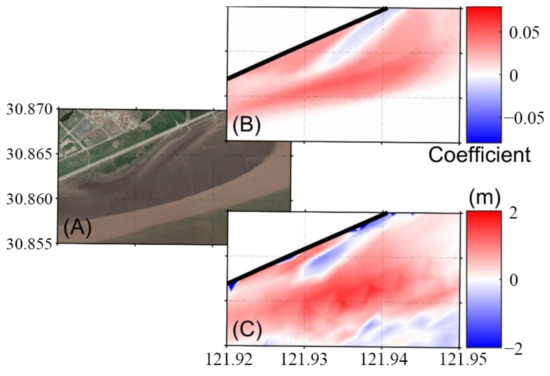
Figure 13.
(A) The satellite image. (B) The first spatial mode of the EOF results; and (C) the differences between the topography field measurements in 2015 and 2019 (2019 vs. 2015), where the red and blue represent accretion and erosion.
The satellite-derived topography provides a method to fill the gaps in the available in situ data to study the evolution of the tidal flat in the past, and to investigate the dynamic mechanism of this evolution by analyzing data with higher spatial and temporal resolutions.
4.2. What Are the Dominant Factors That Control the Variability?
Coastal vegetation plays an important role in sedimentation processes [45]. To explain the dramatic accretion (Figure 9A, Figure 10B and Figure 12A,B) that occurred from 2016 to 2017, the normalized difference vegetation index (NDVI) values in the central supratidal zone (based on the year 2020) were calculated via the algorithm provided in the Google Earth engine. The dataset employed was the Landsat 8 Top-Of-Atmosphere (TOA) dataset, and the calculation was conducted using the following equation:
where is a band that encompasses reflected red light. The NDVI results range from 1 to −1, and the place locations with higher photosynthetic activity have higher NDVI values.
Figure 14 shows the two main temporal patterns of the NDVI variations. One is the seasonal change, which exists in each profile, revealing that the NDVI is much higher during the summer due to the stronger sunlight and fresher seawater. The other is the annual change. There was a remarkable increase in the NDVI from 2016 to 2017 (Figure 14(B1,B2,C1,C2,D1,D2)), which may have been caused by artificial emergent vegetation. Because they occurred during the same period (Figure 14G), the variance in the vegetation concentration should be considered to be a significant factor affecting the nearshore accretion.
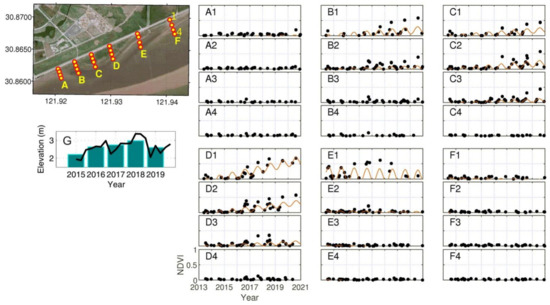
Figure 14.
(A1–F4) The temporal variations in the NDVI from 2013 to 2020. The black points represent the monitored NDVI from the satellite images, and the red lines are the harmonic modeled data. (G) The elevation variations of point (D3), black lines represent the topography derived from the reconstructed DEMs, gray bars are the annual average elevations of (D3).
Another significant response of the tidal flat topography was caused by tropical cyclones. For instance, Typhoon Mitag made landfall in Shanghai on 1 October 2019. The photographs taken before and after the typhoon revealed that obvious coastal erosion occurred and that the beach face moved westward (Figure 15). This change pattern is very similar to the spatial distribution shown in Figure 11. In addition, the typhoons that significantly influenced Shanghai are listed in Table 1. The typhoon frequencies were quite low from 2015 to 2017, and increased significantly from 2018 to 2020. In 2018, the nearest distances between three typhoon tracks and LGTF were particularly less than 50 km. Considering that LGTF turned to an eroding phase after 2018, the frequency, intensity, and track of the typhoon may play an important role. Investigating the impacts of typhoons is ongoing work.

Figure 15.
The ortho aerial photographs obtained using the DJI drone (A) on 30 September 2019 (before the typhoon) and (B) on 31 October 2019 (after the typhoon). The location is shown in Figure 2 (bottom panel). The dike shown in the right panel was buried by sediment before the typhoon occurred and is marked by the dashed line in the left panel.

Table 1.
List of the significant typhoons (nearest distance ≤ 400 km) occurred from 2015 to 2020 based on the China Meteorological Administration tropical cyclone database [46,47].
4.3. Limitation and Assumption of the Method
The water elevation associated with the detected water includes the tidal level, and wave runup (including setup and swash) [48]. Previous studies on the applications of remote sensing on the waterline extraction or coastal evolution have evaluated the effect of wave runup [49,50]. To discuss the limitation of the method employed in this study, in situ measured wave data were used to estimate the magnitude of the wave runup. The formula to calculate the wave runup is as follows [51]:
where is the beach slope; T is the wave period; H is the significant wave height; L is the wave length; is the surf similarity parameter; is the wave runup exceeded by only 2% of the waves.
Figure 16 shows the measured significant wave height (SWH) under normal and strong wind conditions. Here, we assumed that SWH takes the value of 0.3 m (which is the peak value during normal condition), so the corresponding wave period is ~3 s. The wave runup () is 0.0882 m, which is much smaller than the tidal range (~4.5 m).
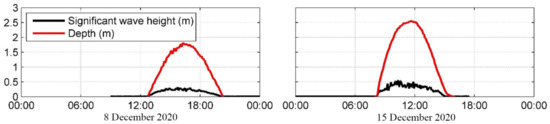
Figure 16.
The significant wave height and water depth measured during a flood–ebb tide period on 8 December 2020 (left panel) and 15 December 2020 (right panel). The wind conditions of the former and later measurements were normal condition (less than 5 m/s) and strong wind (more than 10 m/s). The location of the wave station is shown in Figure 2.
In addition, according to Ruggiero et al., the wave runup is small and increases with increasing wave height as for a gentle slope [52]. Therefore, we assumed that the wave runup could be neglected in this study.
4.4. Another Motivation for Quantifying the Variability in the Study Area
As was previously mentioned, numerous people (including residents and tourists) go down to the edge of the tidal flat during the ebb tide, which is a coastal traditional habit in China (Gan Hai in Mandarin). However, due to the gentle slope and the existence of tidal creeks, there is a threat to these people. In detail, the tide floods the lower tidal flat from the tidal creek (Figure 2). Based on this phenomenon, the potential risk should be considered, and it may be closely related to the bathymetry and pattern of the entire tidal flat. This is also currently being investigated by the authors.
5. Conclusions
This paper presented a case study of the inter-annual variability of a densely populated tidal flat on the southeast coast of Shanghai. The satellite images acquired at the same tidal levels indicated the obvious differences in the tidal flat pattern at both the nearly highest and lowest tidal levels. To quantify the variability, over 300 waterlines were detected using a publicly available satellite dataset from 2013 to 2020 and were automatically extracted. The measured water levels corresponding to the acquisition times of each satellite image were collected from the nearest tidal gauge.
The spatial patterns of the waterlines on the tidal flat in the time series exhibited significant variance. After assigning the tidal levels to the extracted waterlines, the DEMs of each quarter from 2015 to 2020 were reconstructed. The reconstructed DEMs and topographic surveys were in good agreement. The variations in the tidal flat area with time and the relationship between the tidal level and the tidal flat area revealed that the tidal flat was in a rapid accretion phase before 2018, which then changed to erosion (Figure 9). The dominant EOF mode also indicated that accretion mainly occurred from the end of 2015 to 2017, but a channel was eroded (Figure 10).
In summary, the LGTF has experienced obvious accretion during the last decade; however, during recent years from 2018 to 2021, it faces the risk of erosion. Since the study area is becoming a new tourist attraction in Shanghai, the variability of the tidal flat could increase the uncertainty of the potential risk. As such, it is necessary to evaluate how the tidal flat will change in the future.
Author Contributions
Conceptualization, R.Y. and C.Q.; Investigation, R.Y. and C.Q.; Data curation, Y.W. (Yuefeng Wang) and X.G.; Methodology, R.Y. and H.Z.; Validation, H.Z. and Y.W. (Yuefeng Wang); Writing—original draft preparation, R.Y. and H.Z.; Writing—review and editing, Y.W.(Yaping Wang) and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the foundation of the Shanghai Municipal Oceanic Bureau (Grant No. hhk202004), the Science and Technology Commission of Shanghai Municipality (Grant No. 22692193900) and the Shanghai Frontiers Science Center of ‘Full Penetration’ Far-Reaching Offshore Ocean Energy and Power (founded by the Shanghai Municipal Commission of Education).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data used in this paper can be provided by Rui Yuan (yuanrui@shmtu.edu.cn) upon request.
Acknowledgments
We thank the four anonymous reviewers for their constructive comments. Several open-source toolboxes were used in this study including CoastSat (see reference), M_map (https://www.eoas.ubc.ca/~rich/map.html, accessed on 10 June 2020), and Hiplot (https://hiplot.com.cn, accessed on 1 March 2022). We thank Ian L. Turner from the University of New South Wales for analyzing the possible use of CoastSat and UAVs to explore the evolution of this new and rapidly evolving stretch of coastline, and we thank Yongsheng Wu from the Bedford Institute of Oceanography for the insightful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dyer, K.; Christie, M.; Wright, E. The classification of intertidal mudflats. Cont. Shelf Res. 2000, 20, 1039–1060. [Google Scholar] [CrossRef]
- Sohma, A.; Sekiguchi, Y.; Yamada, H.; Sato, T.; Nakata, K. A new coastal marine ecosystem model study coupled with hydrodynamics and tidal flat ecosystem effect. Mar. Pollut. Bull. 2001, 43, 187–208. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, H.; Qiu, Z.; Fan, J. Detecting coastline change from satellite images based on beach slope estimation in a tidal flat. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 165–176. [Google Scholar] [CrossRef]
- Murray, N.; Phinn, S.; DeWitt, M.; Ferrari, R.; Johnston, R.; Lyons, M.; Clinton, N.; Thau, D.; Fuller, R. The global distribution and trajectory of tidal flats. Nature 2019, 565, 222–225. [Google Scholar] [CrossRef]
- Le Hir, P.; Roberts, W.; Cazaillet, O.; Christie, M.; Bassoullet, P.; Bacher, C. Characterization of intertidal flat hydrodynamics. Cont. Shelf Res. 2000, 20, 1433–1459. [Google Scholar] [CrossRef] [Green Version]
- Gao, S. Modeling the preservation potential of tidal flat sedimentary records, Jiangsu coast, eastern China. Cont. Shelf Res. 2009, 29, 1927–1936. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.P.; Yu, Q.; Du, Z.; Wang, Z.; Gao, S. Sand-mud tidal flat morphodynamics influenced by alongshore tidal currents. J. Geophys. Res. Oceans. 2019, 124, 3818–3836. [Google Scholar] [CrossRef] [Green Version]
- Tseng, K.; Kuo, C.; Lin, T.; Huang, Z.; Lin, Y.; Liao, W.; Chen, C. Reconstruction of time-varying tidal flat topography using optical remote sensing imageries. ISPRS J. Photogramm. 2017, 131, 92–103. [Google Scholar] [CrossRef]
- Van der Werf, J.; Reinders, J.; Van Rooijen, A.; Holzhauer, H.; Ysebaert, T. Evaluation of a tidal flat sediment nourishment as estuarine management measure. Ocean Coast. Manage. 2015, 114, 77–87. [Google Scholar] [CrossRef] [Green Version]
- Turner, I.; Harley, M.; Short, A.; Simmons, J.; Bracs, M.; Phillips, M.; Splinter, K. A multi-decade dataset of monthly beach profile surveys and inshore wave forcing at Narrabeen, Australia. Sci. Data. 2016, 3, 160024. [Google Scholar] [CrossRef] [Green Version]
- Hagenaars, G.; de Vries, S.; Luijendijk, A.; de Boer, W.; Reniers, A. On the accuracy of automated shoreline detection derived from satellite imagery: A case study of the sand motor mega-scale nourishment. Coast. Eng. 2018, 133, 113–125. [Google Scholar] [CrossRef]
- Boak, E.; Turner, I. Shoreline definition and detection: A review. J. Coastal Res. 2005, 21, 688–703. [Google Scholar] [CrossRef] [Green Version]
- Appeaning Addo, K.; Walkden, M.; Mills, J. Detection, measurement and prediction of shoreline recession in Accra, Ghana. ISPRS J. Photogramm. 2008, 63, 543–558. [Google Scholar] [CrossRef]
- Guariglia, A.; Buonamassa, A.; Losurdo, A.; Saladino, R.; Trivigno, M.; Zaccagnino, A.; Colangelo, A. A multisource approach for coastline mapping and identification of shoreline changes. Ann. Geophys. 2006, 49, 295–304. [Google Scholar] [CrossRef]
- Mason, D.; Davenport, I.; Robinson, G.; Flather, R.; McCartney, B. Construction of an inter-tidal digital elevation model by the ‘water-line’ method. Geophys. Res. Lett. 1995, 22, 3187–3190. [Google Scholar] [CrossRef]
- Ryu, J.; Won, J.; Min, K. Waterline extraction from Landsat TM data in a tidal flat: A case study in Gomso Bay, Korea. Remote Sens. Environ. 2002, 83, 442–456. [Google Scholar] [CrossRef]
- Duru, U. Shoreline change assessment using multi-temporal satellite images: A case study of Lake Sapanca, NW Turkey. Environ. Monit. Assess. 2017, 189, 385. [Google Scholar] [CrossRef]
- Hodúl, M.; Bird, S.; Knudby, A.; Chénier, R. Satellite derived photogrammetric bathymetry. ISPRS J. Photogramm. 2018, 142, 268–277. [Google Scholar] [CrossRef]
- Vos, K.; Harley, M.; Splinter, K.; Walker, A.; Turner, I. Beach slopes from satellite-derived shorelines. Geophys. Res. Lett. 2020, 47, e2020GL088365. [Google Scholar] [CrossRef]
- Nanson, R.; Bishop-Taylor, R.; Sagar, S.; Lymburner, L. Geomorphic insights into Australia’s coastal change using a national dataset derived from the multi-decadal Landsat archive. Estuar. Coast. Shelf Sci. 2022, 265, 107712. [Google Scholar] [CrossRef]
- Turner, I.; Harley, M.; Almar, R.; Bergsma, E. Satellite optical imagery in Coastal Engineering. Coast. Eng. 2021, 167, 103919. [Google Scholar] [CrossRef]
- Su, J.; Wang, K. Changjiang river plume and suspended sediment transport in Hangzhou Bay. Cont. Shelf Res. 1989, 9, 93–111. [Google Scholar]
- Xie, D. Modeling the morphodynamic response of a large tidal channel system to the large-scale embankment in the Hangzhou Bay, China. Anthr. Coasts 2018, 1, 89–100. [Google Scholar]
- Liu, Z.; Gan, J.; Wu, H.; Hu, J.; Cai, Z.; Deng, Y. Advances on Coastal and Estuarine Circulations Around the Changjiang Estuary in the Recent Decades (2000–2020). Front. Mar. Sci. 2021, 8, 43. [Google Scholar] [CrossRef]
- Dai, Z.; Fagherazzi, S.; Gao, S.; Mei, X.; Ge, Z.; Wei, W. Scaling properties of estuarine beaches. Mar. Geol. 2018, 404, 130–136. [Google Scholar] [CrossRef]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A. Shoreline Detection using Optical Remote Sensing: A Review. ISPRS Int. J. Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef] [Green Version]
- Almeida, L.; de Oliveira, I.; Lyra, R.; Dazzi, R.; Martins, V.; da Fontoura Klein, A. Coastal Analyst System from Space Imagery Engine (CASSIE): Shoreline management module. Environ. Modell. Softw. 2021, 140, 105033. [Google Scholar] [CrossRef]
- Vos, K.; Splinter, K.; Harley, M.; Simmons, J.; Turner, I. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Modell. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, X.; Hu, S.; Su, F. Extraction of Coastline in Aquaculture Coast from Multispectral Remote Sensing Images: Object-Based Region Growing Integrating Edge Detection. Remote Sens. 2013, 5, 4470–4487. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-García, E.; Palomar-Vázquez, J.; Pardo-Pascual, J.; Almonacid-Caballer, J.; Cabezas-Rabadán, C.; Gómez-Pujol, L. An efficient protocol for accurate and massive shoreline definition from mid-resolution satellite imagery. Coast. Eng. 2020, 160, 103732. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, Y.; Li, R.; Li, X. Mapping changes in coastlines and tidal flats in developing islands using the full time series of Landsat images. Remote Sens. Environ. 2020, 239, 111665. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.; Sánchez-García, E.; Almonacid-Caballer, J.; Palomar-Vázquez, J.; de los Santos, E.; Fernández-Sarría, A.; Balaguer-Beser, Á. Assessing the accuracy of automatically extracted shorelines on microtidal beaches from Landsat 7, Landsat 8 and Sentinel-2 imagery. Remote Sens. 2018, 10, 326. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Ellacuria, A.; Orfila, A.; Gómez-Pujol, L.; Simarro, G.; Obregon, N. Decoupling spatial and temporal patterns in short-term beach shoreline response to wave climate. Geomorphology 2011, 128, 199–208. [Google Scholar] [CrossRef]
- Kang, Y.; Ding, X.; Xu, F.; Zhang, C.; Ge, X. Topographic mapping on large-scale tidal flats with an iterative approach on the waterline method. Estuar. Coast. Shelf Sci. 2017, 190, 11–22. [Google Scholar] [CrossRef]
- Mason, D.; Davenport, I.; Flather, R. Interpolation of an intertidal digital elevation model from heighted shorelines: A case study in the Western Wash. Estuar. Coast. Shelf Sci. 1997, 45, 599–612. [Google Scholar] [CrossRef]
- Ryu, J.; Kim, C.; Lee, Y.; Won, J.; Chun, S.; Lee, S. Detecting the intertidal morphologic change using satellite data. Estuar. Coast. Shelf Sci. 2008, 78, 623–632. [Google Scholar] [CrossRef]
- Tong, S.; Deroin, J.; Pham, T. An optimal waterline approach for studying tidal flat morphological changes using remote sensing data: A case of the northern coast of Vietnam. Estuar. Coast. Shelf Sci. 2020, 236, 106613. [Google Scholar] [CrossRef]
- Castelle, B.; Masselink, G.; Scott, T.; Stokes, C.; Konstantinou, A.; Marieu, V.; Bujan, S. Satellite-derived shoreline detection at a high-energy meso-macrotidal beach. Geomorphology 2021, 383, 107707. [Google Scholar] [CrossRef]
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance; Tech. Report CD-TR 94/64 Information Systems Department; Technical University of Vienna: Vienna, Austria, 1994. [Google Scholar]
- Wylie, T.; Zhu, B. Intermittent Map Matching with the Discrete Fréchet Distance. arXiv 2014, arXiv:1409.2456. [Google Scholar]
- Chen, Y.; Dong, J.; Xiao, X.; Zhang, M.; Tian, B.; Zhou, Y.; Ma, Z. Land claim and loss of tidal flats in the Yangtze Estuary. Sci. Rep. 2016, 6, 24018. [Google Scholar] [CrossRef]
- Wei, W.; Tang, Z.; Dai, Z.; Lin, Y.; Ge, Z.; Gao, J. Variations in tidal flats of the Changjiang (Yangtze) Estuary during 1950s–2010s: Future crisis and policy implication. Ocean Coast. Manag. 2015, 108, 89–96. [Google Scholar] [CrossRef]
- Kawamura, R. A rotated EOF analysis of global sea surface temperature variability with interannual and interdecadal scales. J. Phys. Oceanogr. 1994, 24, 707–715. [Google Scholar] [CrossRef] [Green Version]
- Beckers, J.; Rixen, M. EOF calculations and data filling from incomplete oceanographic datasets. J. Atmos. Ocean Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Dai, Z. Tidal flat morphodynamics of the Chengjiang estuary. In Changjiang Riverine and Estuarine Hydro-Morphodynamic Processes; Springer: Singapore, 2021; pp. 171–238. [Google Scholar]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific tropical cyclone database created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Didier, D.; Bernatchez, P.; Augereau, E.; Caulet, C.; Dumont, D.; Bismuth, E.; Cormier, L.; Floc’h, F.; Delacourt, C. LiDAR Validation of a Video-Derived Beachface Topography on a Tidal Flat. Remote Sens. 2017, 9, 826. [Google Scholar] [CrossRef] [Green Version]
- Abdelhady, H.U.; Troy, C.D.; Habib, A.; Manish, R. A Simple, Fully Automated Shoreline Detection Algorithm for High-Resolution Multi-Spectral Imagery. Remote Sens. 2022, 14, 557. [Google Scholar] [CrossRef]
- Kumar, D.; Takewaka, S. Automatic Shoreline Position and Intertidal Foreshore Slope Detection from X-Band Radar Images Using Modified Temporal Waterline Method with Corrected Wave Run-up. J. Mar. Sci. Eng. 2019, 7, 45. [Google Scholar] [CrossRef] [Green Version]
- Stockdon, H.; Holman, R.; Howd, P.; Sallenger, A. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Ruggiero, P.; Holman, R.; Beach, R. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. 2004, 109, C06025. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).