Random Matrix Theory-Based Reduced-Dimension Space-Time Adaptive Processing under Finite Training Samples
Abstract
1. Introduction
2. Background
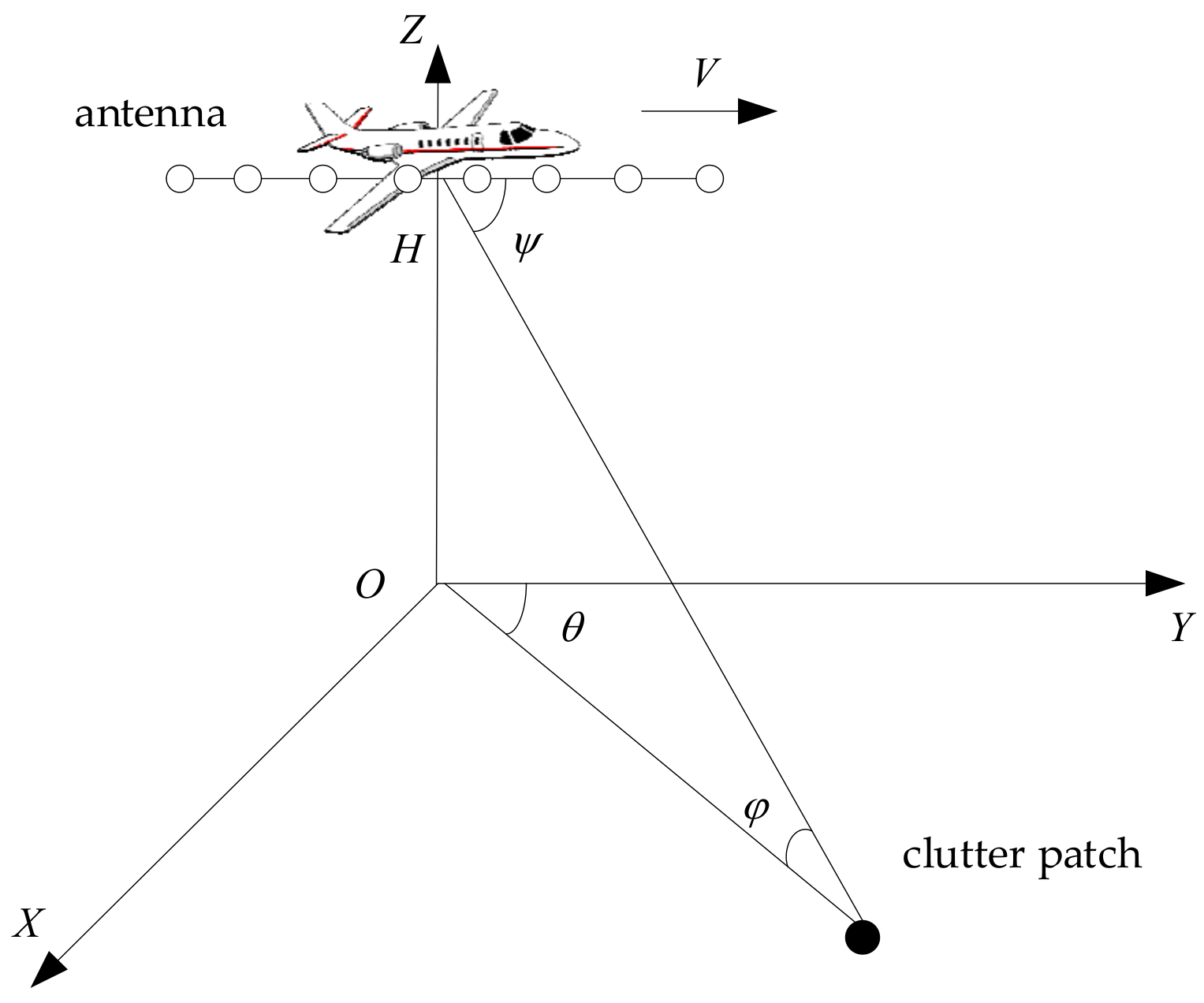
2.1. Echo Model of Airborne Radar and Optimal STAP
2.2. Sample-Based STAP and RD-STAP
2.3. Motivation by Introducing RMT in RD-STAP
3. RD-STAP Using RMT
3.1. RD-STAP Problem under the Spiked Covariance Model
3.2. Asymptotic Deterministic Equivalent and the Optimal
3.3. Obtaining Optimal Adaptive Weight Vector by Estimating
3.4. Determining the Noise Power
4. Numerical Results
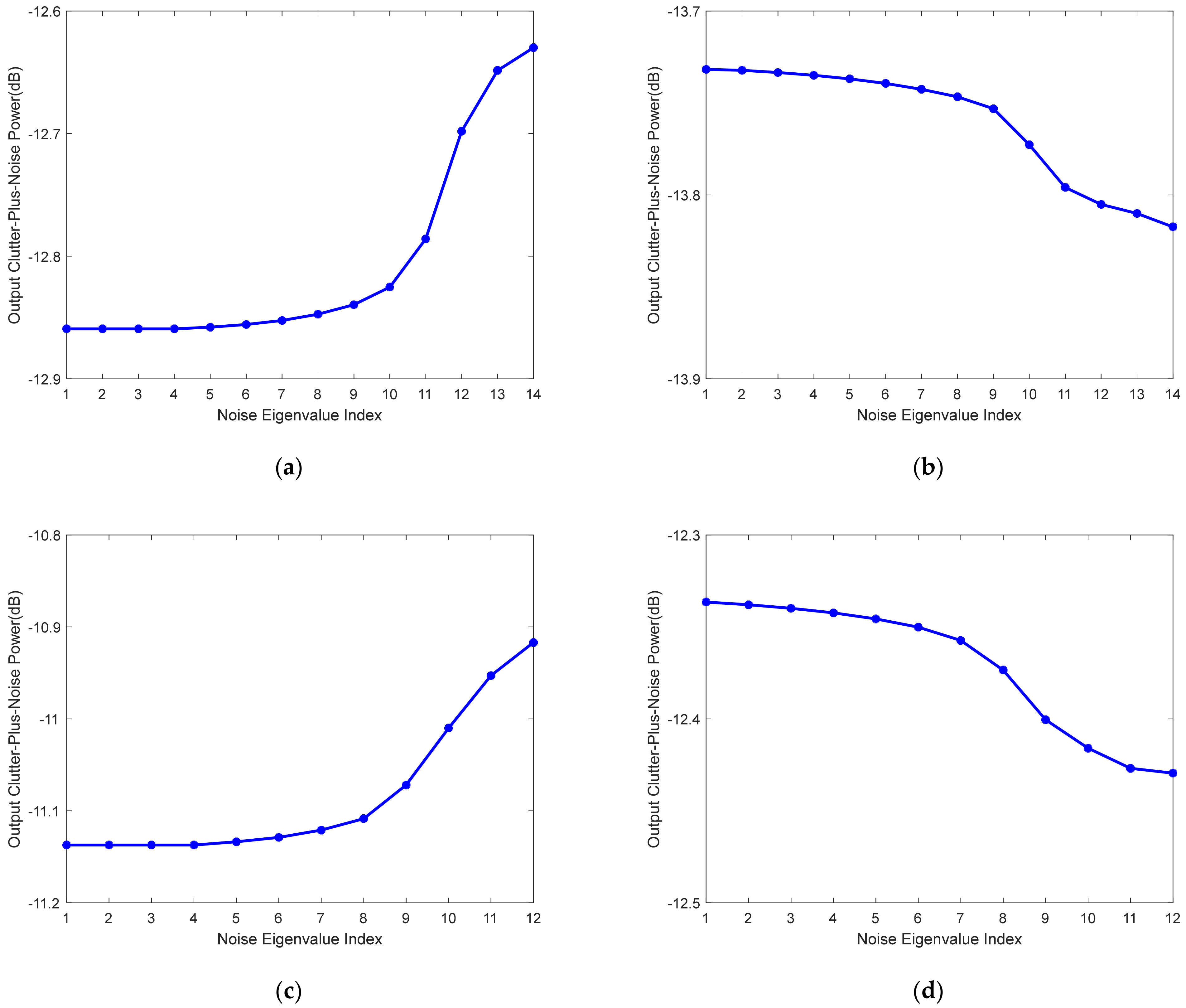
4.1. Numerical Validation on Assumption 1 and Proposition 1
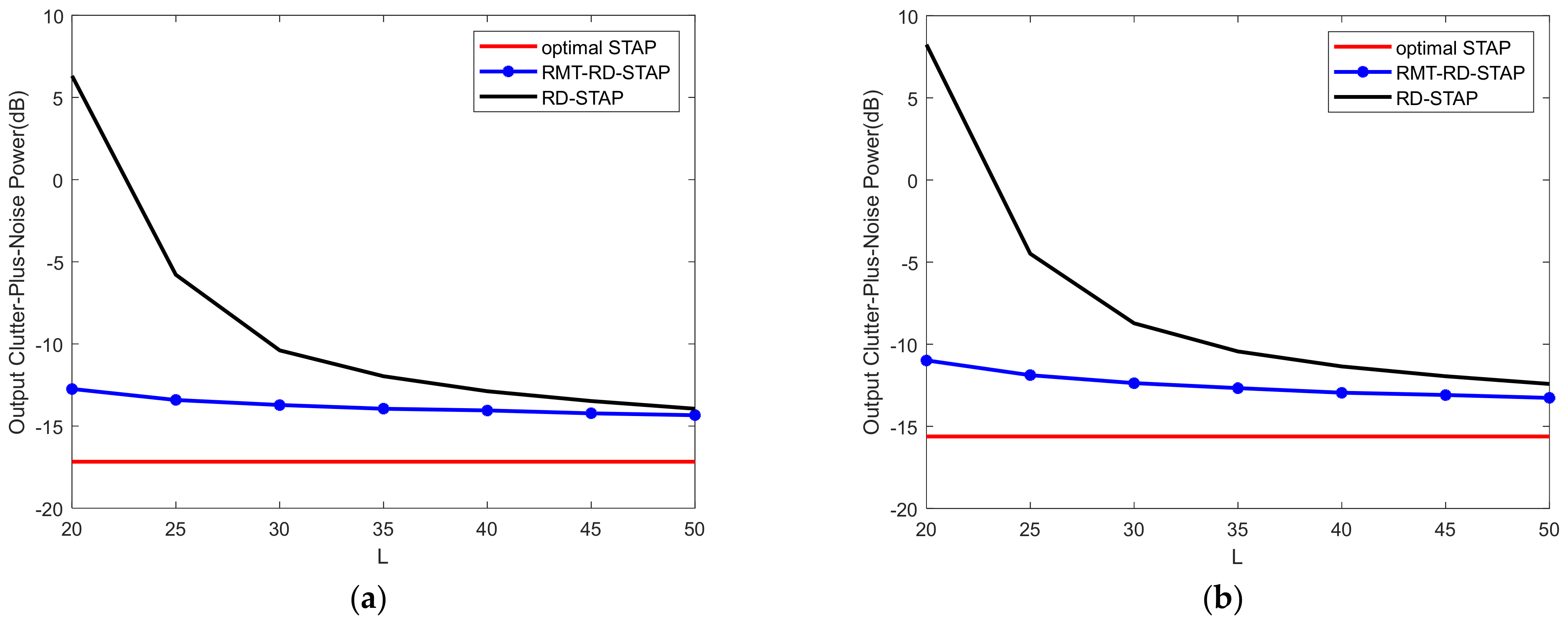
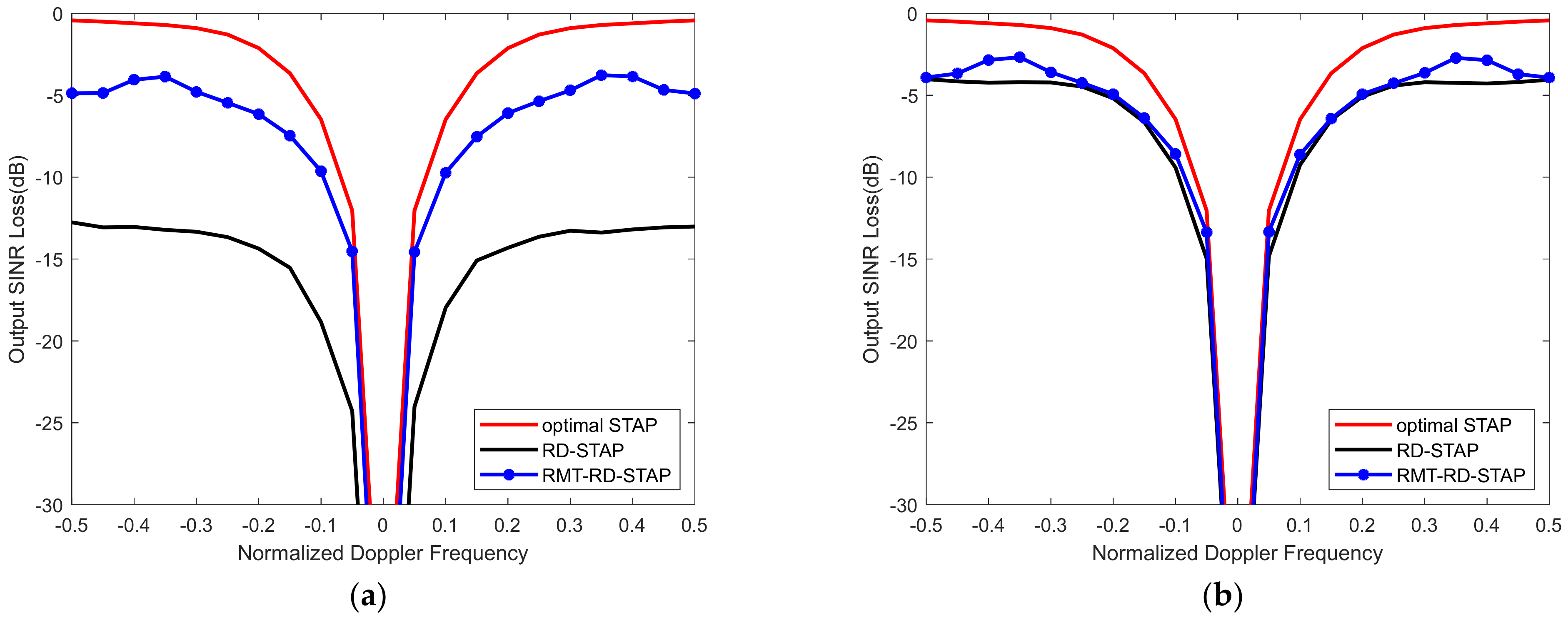
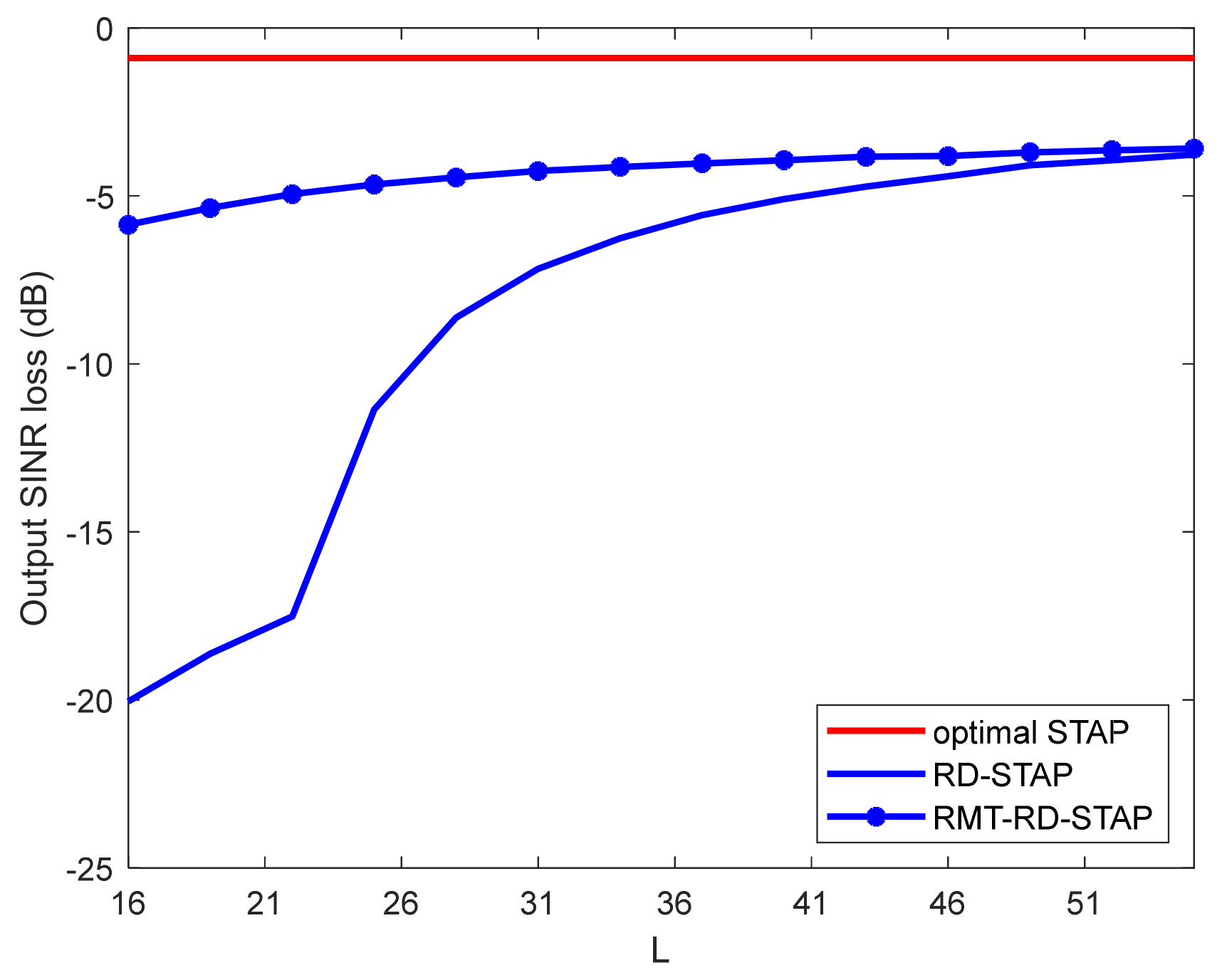
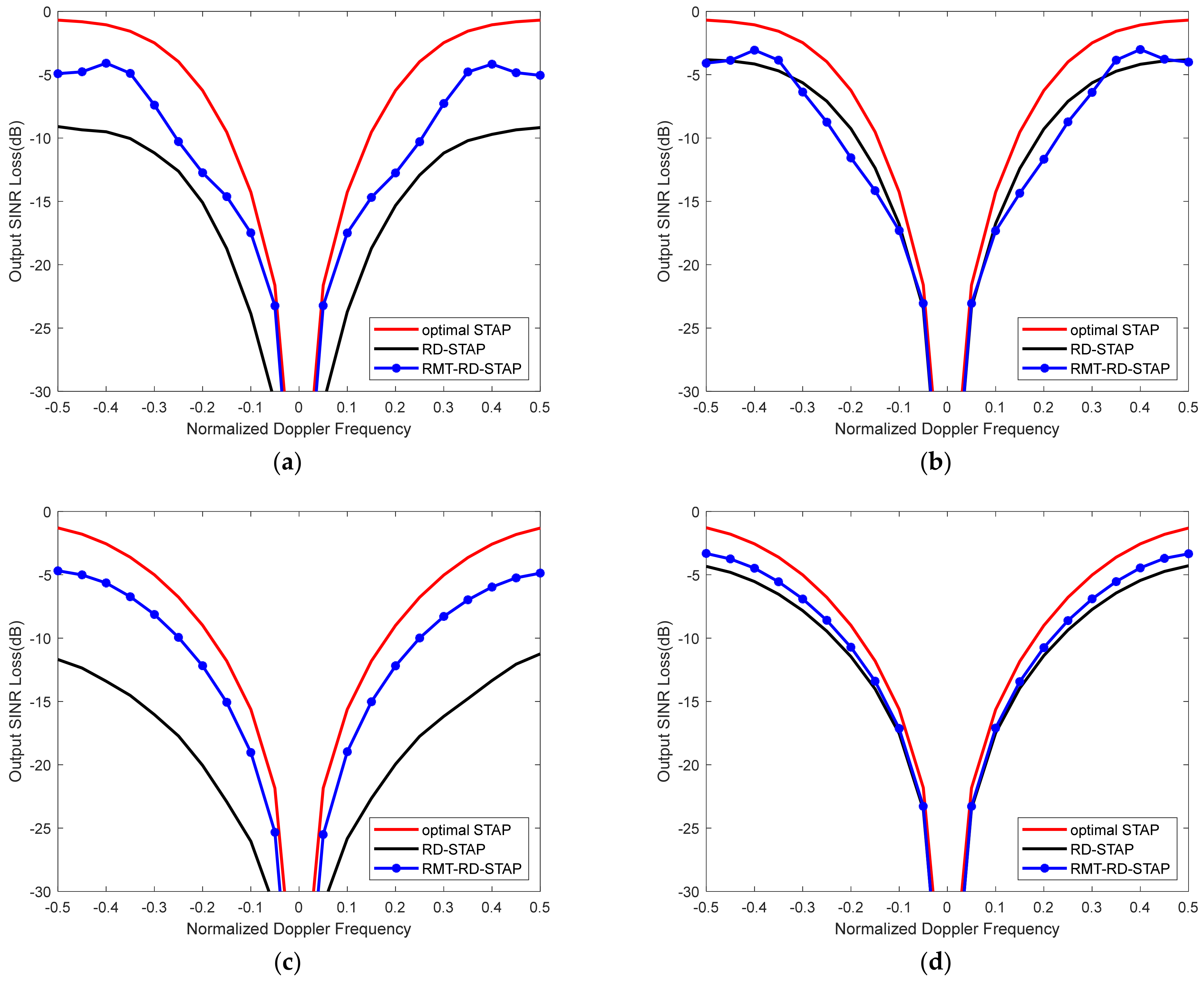
4.2. Performance Comparisons
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Brennan, L.E.; Reed, L.S. Theory of adaptive radar. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 237–252. [Google Scholar] [CrossRef]
- Ward, J. Space-Time Adaptive Processing for Airborne Radar; Technical Report 1015; MIT Lincoln Lab.: Lexington, MA, USA, 1994. [Google Scholar]
- Melvin, W.L. A STAP overview. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 19–35. [Google Scholar] [CrossRef]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid convergence rate in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 853–863. [Google Scholar] [CrossRef]
- Klemm, R. Principles of Space-Time Adaptive Processing, 3rd ed.; IET: London, UK, 2006. [Google Scholar]
- Guerci, J.R. Space-Time Adaptive Processing for Radar; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Yang, Z.; Li, X.; Wang, H.; Jiang, W. On Clutter Sparsity Analysis in Space–Time Adaptive Processing Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1214–1218. [Google Scholar] [CrossRef]
- Sen, S. Low-Rank Matrix Decomposition and Spatio-Temporal Sparse Recovery for STAP Radar. IEEE J. Sel. Top. Signal Process. 2015, 9, 1510–1523. [Google Scholar] [CrossRef]
- Yang, Z.; de Lamare, R.C.; Li, X. L1-Regularized STAP algorithms with a generalized sidelobe canceler architecture for airborne radar. IEEE Trans. Signal Process. 2012, 60, 674–686. [Google Scholar] [CrossRef]
- Zhang, W.; An, R.; He, N.; He, Z.; Li, H. Reduced dimension STAP based on sparse recovery in heterogeneous clutter environments. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 785–795. [Google Scholar] [CrossRef]
- Guerci, J.; Baranoski, E. Knowledge-aided adaptive radar at DARPA: An overview. IEEE Signal Process. Mag. 2006, 23, 41–50. [Google Scholar] [CrossRef]
- Besson, O.; Tourneret, J.-Y.; Bidon, S. Knowledge-Aided Bayesian Detection in Heterogeneous Environments. IEEE Signal Process. Lett. 2007, 14, 355–358. [Google Scholar] [CrossRef]
- Riedl, M.; Potter, L.C. Knowledge-Aided Bayesian Space-Time Adaptive Processing. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1850–1861. [Google Scholar] [CrossRef]
- Riedl, M.; Potter, L.C. Multimodel Shrinkage for Knowledge-Aided Space-Time Adaptive Processing. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2601–2610. [Google Scholar] [CrossRef]
- Duan, K.; Chen, H.; Xie, W.; Wang, Y. Deep learning for high-resolution estimation of clutter angle-Doppler spectrum in STAP. IET Radar Sonar Navig. 2022, 16, 193–207. [Google Scholar] [CrossRef]
- Zou, B.; Wang, X.; Feng, W.; Zhu, H.; Lu, F. DU-CG-STAP Method Based on Sparse Recovery and Unsupervised Learning for Airborne Radar Clutter Suppression. Remote Sens. 2022, 14, 3472. [Google Scholar] [CrossRef]
- Zhu, H.; Feng, W.; Feng, C.; Zou, B.; Lu, F. Deep Unfolding Based Space-Time Adaptive Processing Method for Airborne Rada. J. Radars 2022, 11, 1–16. [Google Scholar]
- DiPietro, R.C. Extended factored space-time processing for airborne radar systems. In Proceedings of the Conference Record of the Twenty-Sixth Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 26–28 October 1992; pp. 425–430. [Google Scholar]
- Sarkar, T.K.; Wang, H.; Park, S.; Adve, R.; Koh, J.; Kim, K.; Zhang, Y.; Wicks, M.; Brown, R. A deterministic least-squares approach to space-time adaptive processing (STAP). IEEE Trans. Antennas Propag. 2001, 49, 91–103. [Google Scholar] [CrossRef]
- Brown, R.; Schneible, R.; Wicks, M.; Wang, H.; Zhang, Y. STAP for clutter suppression with sum and difference beams. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 634–646. [Google Scholar] [CrossRef]
- Zhang, W.; He, Z.; Li, J.; Liu, H.; Sun, Y. A Method for Finding Best Channels in Beam-Space Post-Doppler Reduced-Dimension STAP. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 254–264. [Google Scholar] [CrossRef]
- Klemm, R. Adaptive airborne MTI: An auxiliary channel approach. IEE Proc. F Commun. Radar Signal Process. 1987, 134, 269–276. [Google Scholar] [CrossRef]
- Wang, H.; Cai, L. On adaptive spatial-temporal processing for airborne surveillance radar systems. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 660–670. [Google Scholar] [CrossRef]
- Karoui, N.E. Spectrum estimation for large dimensional covariance matrices using random matrix theory. Ann. Statist. 2008, 36, 2757–2790. [Google Scholar] [CrossRef]
- Daniels, R.; Kass, M.J. Shrinkage estimators for covariance matrices. Biometrics 2001, 57, 1173–1184. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Fan, Y.; Lv, J. High dimensional covariance matrix estimation using a factor model. J. Econ. 2008, 147, 186–197. [Google Scholar] [CrossRef]
- Yang, L.; McKay, M.R.; Couillet, R. High-Dimensional MVDR Beamforming: Optimized Solutions Based on Spiked Random Matrix Models. IEEE Trans. Signal Process. 2018, 66, 1933–1947. [Google Scholar] [CrossRef]
- Bai, Z.; Silverstein, J.W. Spectral Analysis of Large Dimensional Random Matrices; Springer: New York, NY, USA, 2010; Volume 20. [Google Scholar]
- Silverstein, J.; Choi, S. Analysis of the Limiting Spectral Distribution of Large Dimensional Random Matrices. J. Multivar. Anal. 1995, 54, 295–309. [Google Scholar] [CrossRef]
- Schott, J.R. Asymptotics of eigenprojections of correlation matrices with some applications in principal components analysis. Biometrika 1997, 84, 327–337. [Google Scholar] [CrossRef]
- Bai, Z.D.; Silverstein, J.W. No eigenvalues outside the support of the limiting spectral distribution of large-dimensional sample covariance matrices. Ann. Probab. 1998, 26, 316–345. [Google Scholar] [CrossRef]
- Silverstein, J. Strong Convergence of the Empirical Distribution of Eigenvalues of Large Dimensional Random Matrices. J. Multivar. Anal. 1995, 55, 331–339. [Google Scholar] [CrossRef]
- Ledoit, O.; Wolf, M. Spectrum estimation: A unified framework for covariance matrix estimation and PCA in large dimensions. J. Multivar. Anal. 2015, 139, 360–384. [Google Scholar] [CrossRef]
- Ledoit, O.; Wolf, M. Nonlinear shrinkage of the covariance matrix for portfolio selection: Markowitz meets Goldilocks. Rev. Financ. Stud. 2017, 30, 4349–4388. [Google Scholar] [CrossRef]
- Girko, V. Asymptotic behavior of eigenvalues of empirical covariance matrices. Theory Probab. Math. Stat. 1992, 44, 37–44. [Google Scholar]
- Rubio, F.; Mestre, X.; Palomar, D.P. Performance Analysis and Optimal Selection of Large Minimum Variance Portfolios Under Estimation Risk. IEEE J. Sel. Top. Signal Process. 2012, 6, 337–350. [Google Scholar] [CrossRef]
- Anderson, T.W. Asymptotic Theory for Principal Component Analysis. Ann. Math. Stat. 1963, 34, 122–148. [Google Scholar] [CrossRef]
- Gupta, R. Asymptotic theory for principal component analysis in the complex case. J. Indian Statist. Assoc. 1965, 3, 97–106. [Google Scholar]
- Marcenko, V.A.; Pastur, L.A. Distribution of Eigenvalues for Some Sets of Random Matrices. Math. USSR-Sb. 1967, 1, 457–483. [Google Scholar] [CrossRef]
- Baik, J.; Arous, G.B.; Péché, S. Phase transition of the largest eigenvalue for nonnull complex sample covariance matrices. Ann. Probab. 2005, 33, 1643–1697. [Google Scholar] [CrossRef]
- Baik, J.; Silverstein, J.W. Eigenvalues of large sample covariance matrices of spiked population models. J. Multivar. Anal. 2006, 97, 1382–1408. [Google Scholar] [CrossRef]
- Paul, D. Asymptotics of sample eigenstructure for a large dimensional spiked covariance model. Statist. Sin. 2007, 17, 1617–1642. [Google Scholar]
- Couillet, R. Robust spiked random matrices and a robust G-MUSIC estimator. J. Multivar. Anal. 2015, 140, 139–161. [Google Scholar] [CrossRef]
- Robinson, B.D.; Malinas, R.; Hero, A.O. Space-Time Adaptive Detection at Low Sample Support. IEEE Trans. Signal Process. 2021, 69, 2939–2954. [Google Scholar] [CrossRef]
- Combernoux, A.; Pascal, F.; Lesturgie, M.; Ginolhac, G. Performances of low rank detectors based on random matrix theory with application to STAP. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014; pp. 1–4. [Google Scholar]
- Pafka, S.; Kondor, I. Noisy covariance matrices and portfolio optimization II. Phys. A Stat. Mech. Its Appl. 2003, 319, 487–494. [Google Scholar] [CrossRef]
- Pafka, S.; Kondor, I. Estimated correlation matrices and portfolio optimization. Phys. A Stat. Mech. Table Its Appl. 2004, 343, 623–634. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Xie, W.; Hu, W.; Yu, W. Local degrees of freedom of airborne array radar clutter for STAP. IEEE Geosci. Remote Sens. Lett. 2009, 6, 97–101. [Google Scholar]
- Mestre, X. On the Asymptotic Behavior of the Sample Estimates of Eigenvalues and Eigenvectors of Covariance Matrices. IEEE Trans. Signal Process. 2008, 56, 5353–5368. [Google Scholar] [CrossRef]
- Mestre, X. Improved Estimation of Eigenvalues and Eigenvectors of Covariance Matrices Using Their Sample Estimates. IEEE Trans. Inf. Theory 2008, 54, 5113–5129. [Google Scholar] [CrossRef]
- Couillet, R.; Debbah, M. Random Matrix Methods for Wireless Communications; Cambridge Univ. Press: Cambridge, UK, 2011. [Google Scholar]
- Melvin, W.L.; Showman, G.A. An approach to knowledge-aided covariance estimation. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1021–1042. [Google Scholar] [CrossRef]
- Titi, G.; Marshall, D. The ARPA/NAVY Mountaintop Program: Adaptive signal processing for airborne early warning radar. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, Atlanta, GA, USA, 9 May 1996; IEEE: Piscataway Township, NJ, USA, 2002; Volume 2, pp. 1165–1168. [Google Scholar]



| Parameter | Value | Unit |
|---|---|---|
| Height | 6000 | m |
| Wavelength | 0.3 | m |
| Array number | 8 | / |
| Pulse number | 8 | / |
| PRF | 2000 | Hz |
| CNR | 30 | dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, D.; Feng, Q.; Chen, S.; Xi, F.; Liu, Z. Random Matrix Theory-Based Reduced-Dimension Space-Time Adaptive Processing under Finite Training Samples. Remote Sens. 2022, 14, 3959. https://doi.org/10.3390/rs14163959
Song D, Feng Q, Chen S, Xi F, Liu Z. Random Matrix Theory-Based Reduced-Dimension Space-Time Adaptive Processing under Finite Training Samples. Remote Sensing. 2022; 14(16):3959. https://doi.org/10.3390/rs14163959
Chicago/Turabian StyleSong, Di, Qi Feng, Shengyao Chen, Feng Xi, and Zhong Liu. 2022. "Random Matrix Theory-Based Reduced-Dimension Space-Time Adaptive Processing under Finite Training Samples" Remote Sensing 14, no. 16: 3959. https://doi.org/10.3390/rs14163959
APA StyleSong, D., Feng, Q., Chen, S., Xi, F., & Liu, Z. (2022). Random Matrix Theory-Based Reduced-Dimension Space-Time Adaptive Processing under Finite Training Samples. Remote Sensing, 14(16), 3959. https://doi.org/10.3390/rs14163959






