Marine Gravimetry and Its Improvements to Seafloor Topography Estimation in the Southwestern Coastal Area of the Baltic Sea
Abstract
:1. Introduction
2. Materials and Methods
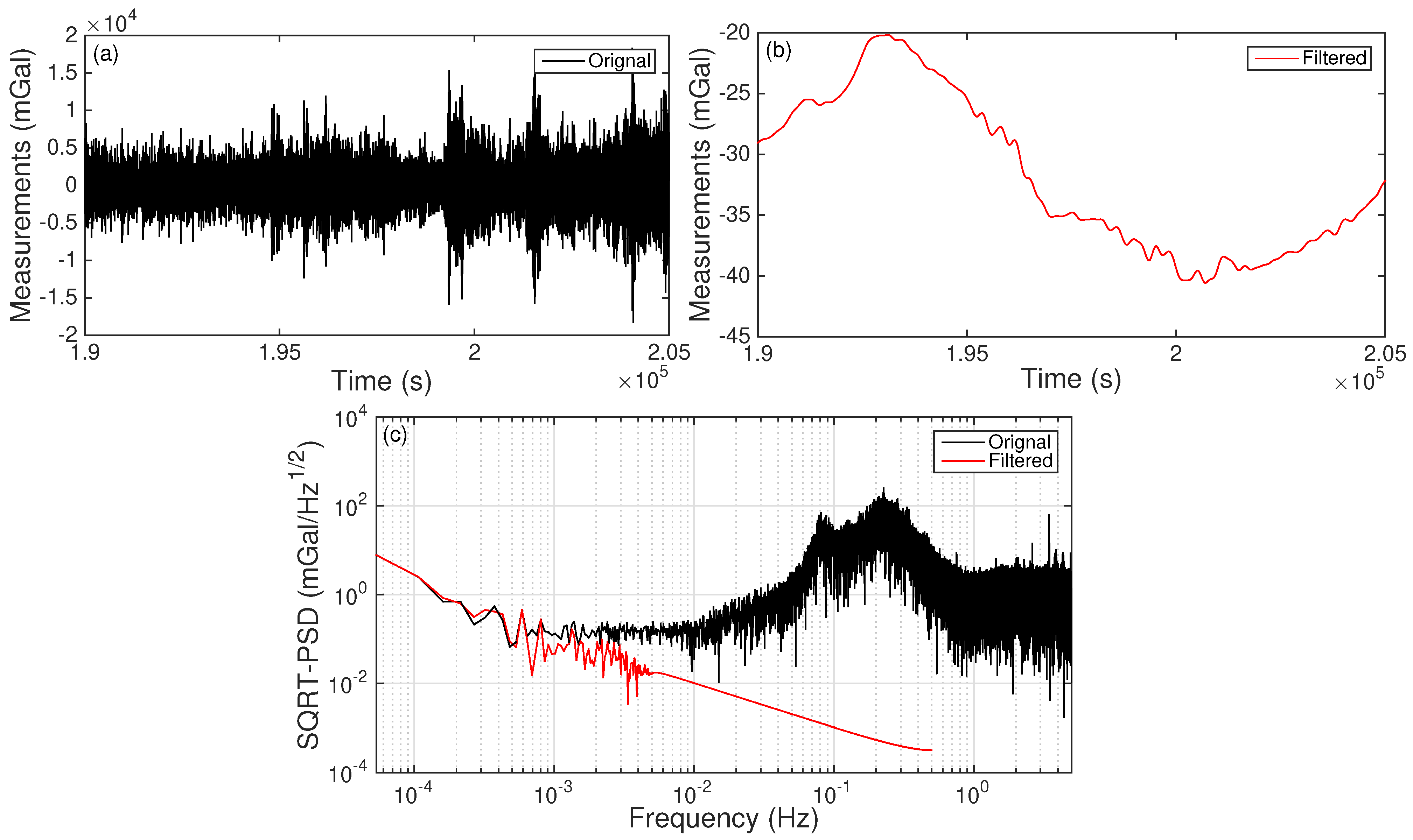
2.1. Marine Gravimetry Data Processing
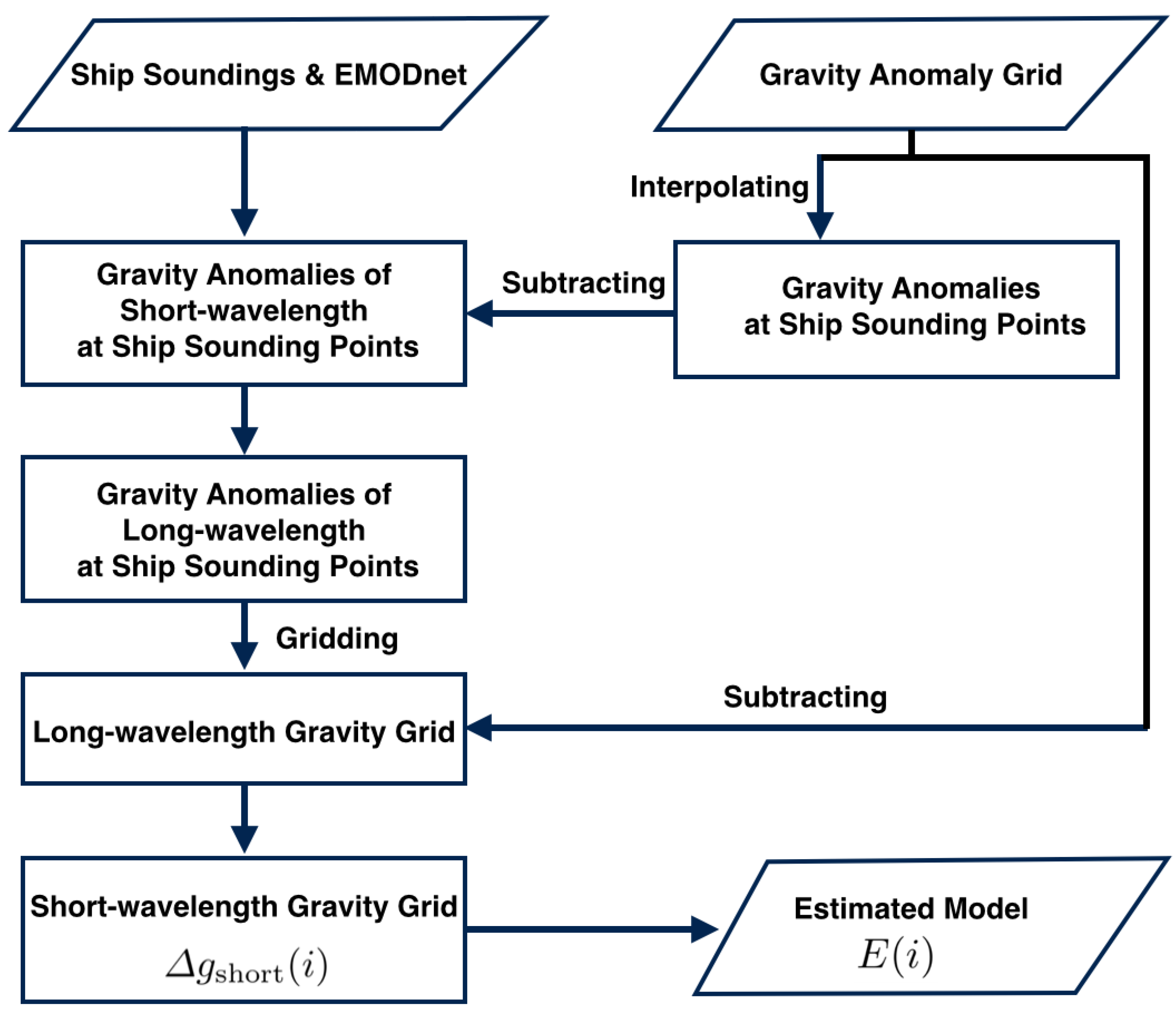
2.2. Seafloor Topography Estimation
3. Results
3.1. Marine Gravimetry Results
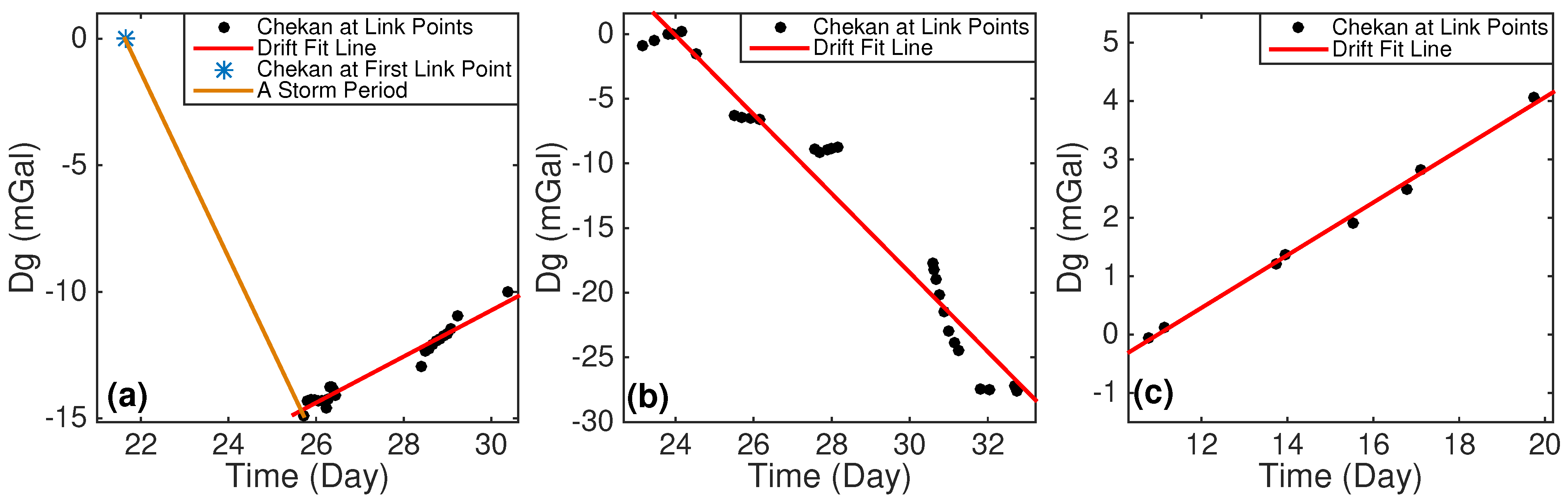
3.1.1. Drift Improvement
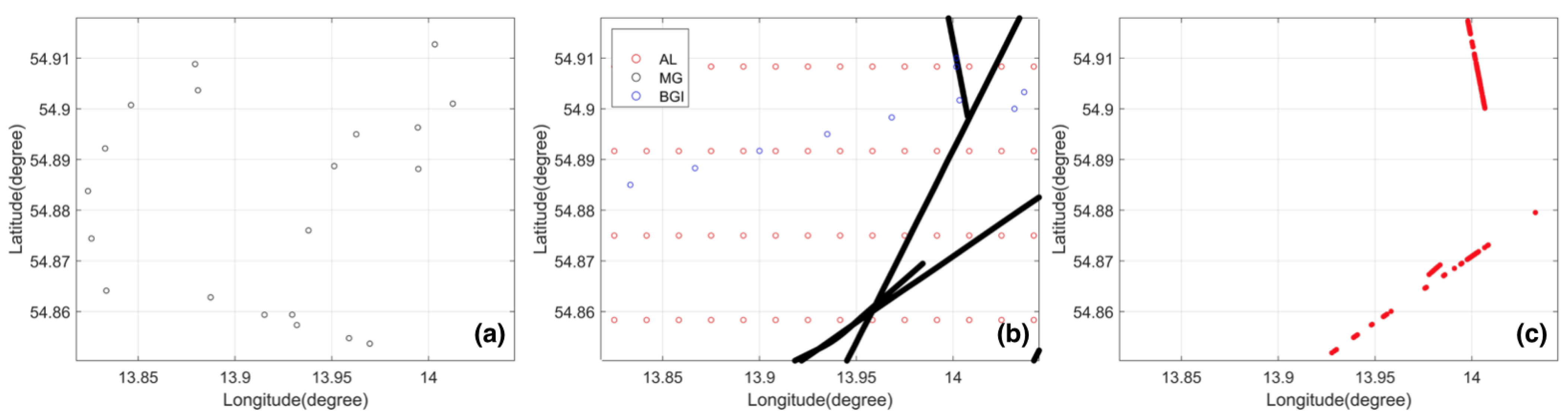
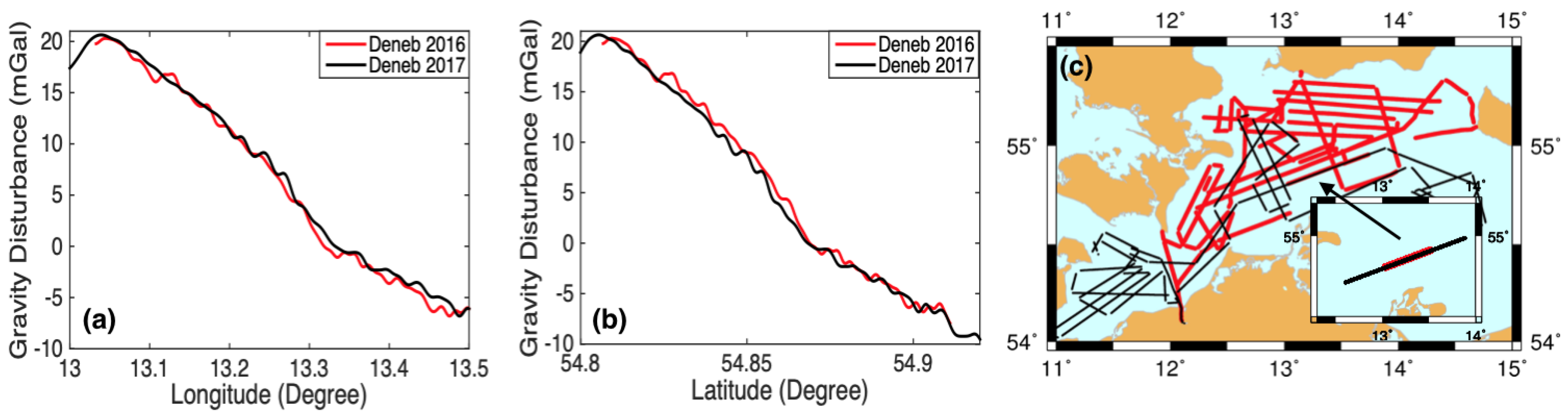
3.1.2. Tracks Checking
3.1.3. Crossover Points Checking
3.2. Seafloor Topography Estimation Results
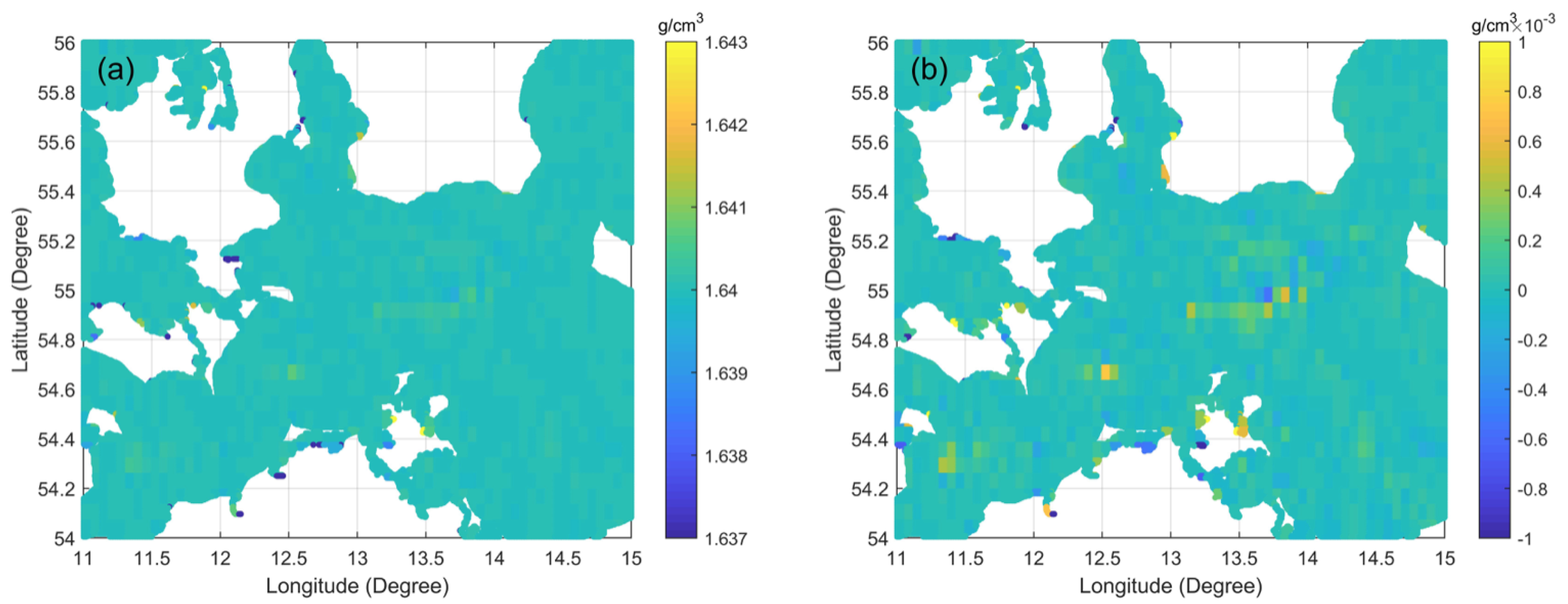
3.2.1. Checking and Combining Different Gravity Anomalies
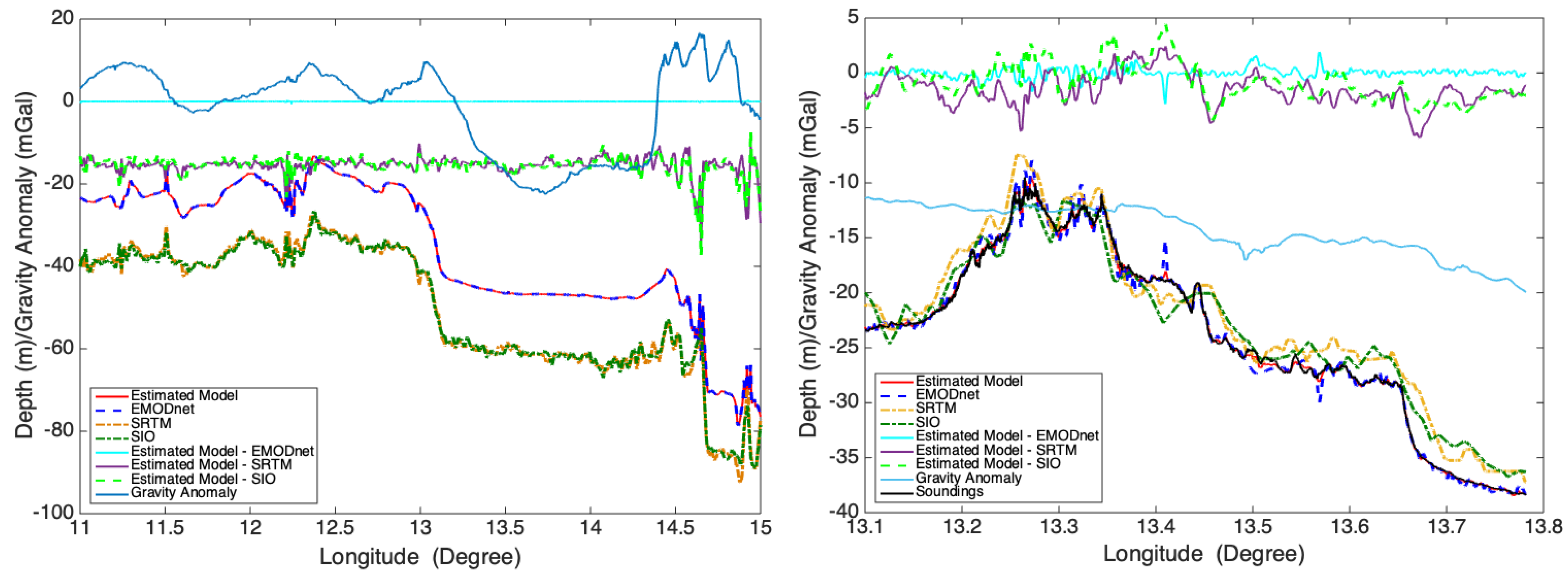
3.2.2. Checking Existing Digital Terrain Models
3.2.3. Revealing the Fine Structure of Seafloor Topography
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Min | Max | Mean | RMS | |
|---|---|---|---|---|
| Altimetry gravity | −12.67 | 1.00 | −1.79 | 3.43 |
| Combined gravity | −9.21 | 3.07 | 0.62 | 2.16 |

References
- Harff, J.; Björck, S.; Hoth, P. The Baltic Sea Basin; Springer: Berlin/Heidelberg, Germany, 2011; Volume 449. [Google Scholar]
- Dehghan, M.J.; Ardestani, V.E.; Dehghani, A. The study of crustal structures in the southwestern part of the Baltic Sea by modeling of gravity data. Arab. J. Geosci. 2021, 14, 1–16. [Google Scholar] [CrossRef]
- Xiang, X.; Wan, X.; Zhang, R.; Li, Y.; Sui, X.; Wang, W. Bathymetry inversion with the gravity-geologic method: A study of long-wavelength gravity modeling based on adaptive mesh. Mar. Geod. 2017, 40, 329–340. [Google Scholar] [CrossRef]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.; Olson, C.; Beale, J.; Wessel, P. Global bathymetry and topography at 15 arc sec: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Group, G.B.C. The GEBCO_2019 Grid—Acontinuous Terrain Model of the Global Oceans and Land; British Oceanographic Data Centre, National Oceanography Centre, NERC: Swindon, UK, 2019. [Google Scholar]
- Míguez, B.M.; Novellino, A.; Vinci, M.; Claus, S.; Calewaert, J.B.; Vallius, H.; Schmitt, T.; Pititto, A.; Giorgetti, A.; Askew, N.; et al. The European Marine Observation and Data Network (EMODnet): Visions and roles of the gateway to marine data in Europe. Front. Mar. Sci. 2019, 6, 313. [Google Scholar] [CrossRef]
- Jakobsson, M.; Stranne, C.; O’Regan, M.; Greenwood, S.L.; Gustafsson, B.; Humborg, C.; Weidner, E. Bathymetric properties of the Baltic Sea. Ocean Sci. 2019, 15, 905–924. [Google Scholar] [CrossRef]
- Hell, B.; Broman, B.; Jakobsson, L.; Jakobsson, M.; Magnusson, Å.; Wiberg, P. The use of bathymetric data in society and science: A review from the Baltic Sea. Ambio 2012, 41, 138–150. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, K.P.; Li, Y.C. What can airborne gravimetry contribute to geoid determination? J. Geophys. Res. Solid Earth 1996, 101, 17873–17881. [Google Scholar] [CrossRef]
- Li, J.; Sideris, M. Marine gravity and geoid determination by optimal combination of satellite altimetry and shipborne gravimetry data. J. Geod. 1997, 71, 209–216. [Google Scholar] [CrossRef]
- Featherstone, W. Comparison of different satellite altimeter-derived gravity anomaly grids with ship-borne gravity data around Australia. Gravity Geoid 2002, 326–331. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.566.4033&rep=rep1&type=pdf (accessed on 8 July 2022).
- Hwang, C.; Hsiao, Y.S.; Shih, H.C.; Yang, M.; Chen, K.H.; Forsberg, R.; Olesen, A.V. Geodetic and geophysical results from a Taiwan airborne gravity survey: Data reduction and accuracy assessment. J. Geophys. Res. Solid Earth 2007, 112, B04407. [Google Scholar] [CrossRef]
- Smith, D.A.; Holmes, S.A.; Li, X.; Guillaume, S.; Wang, Y.M.; Bürki, B.; Roman, D.R.; Damiani, T.M. Confirming regional 1 cm differential geoid accuracy from airborne gravimetry: The Geoid Slope Validation Survey of 2011. J. Geod. 2013, 87, 885–907. [Google Scholar] [CrossRef]
- Petrovic, S.; Barthelmes, F.; Pflug, H. Airborne and shipborne gravimetry at GFZ with emphasis on the GEOHALO project. In Proceedings of the IAG 150 Years: Proceedings of the 2013 IAG Scientific Assembly, Potsdam, Germany, 2–6 September 2013; Rizos, C., Willis, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 313–322. [Google Scholar] [CrossRef]
- Lu, B.; Barthelmes, F.; Petrovic, S.; Förste, C.; Flechtner, F.; Luo, Z.; He, K.; Li, M. Airborne gravimetry of GEOHALO mission: Data processing and gravity field modeling. J. Geophys. Res. Solid Earth 2017, 122. [Google Scholar] [CrossRef]
- Lu, B.; Barthelmes, F.; Li, M.; Förste, C.; Ince, E.S.; Petrovic, S.; Flechtner, F.; Schwabe, J.; Luo, Z.; Zhong, B.; et al. Shipborne gravimetry in the Baltic Sea: Data processing strategies, crucial findings and preliminary geoid determination tests. J. Geod. 2019, 93, 1059–1071. [Google Scholar] [CrossRef]
- Denker, H.; Roland, M. Compilation and evaluation of a consistent marine gravity data set surrounding Europe. In A Window on the Future of Geodesy; Springer: Berlin/Heidelberg, Germany, 2005; pp. 248–253. [Google Scholar]
- Hunegnaw, A.; Hipkin, R.; Edwards, J. A method of error adjustment for marine gravity with application to Mean Dynamic Topography in the northern North Atlantic. J. Geod. 2009, 83, 161. [Google Scholar] [CrossRef]
- Lequentrec-Lalancette, M.; Salaűn, C.; Bonvalot, S.; Rouxel, D.; Bruinsma, S. Exploitation of marine gravity measurements of the mediterranean in the validation of global gravity field models. In Proceedings of the International Symposium on Earth and Environmental Sciences for Future Generations, Prague, Czech Republic, 22 June–2 July 2015; Springer: Berlin/Heidelberg, Germany, 2016; pp. 63–67. [Google Scholar]
- Bell, R.E.; Watts, A.B. Evaluation of the BGM-3 sea gravity meter system onboard R/V Conrad. Geophysics 1986, 51, 1480–1493. [Google Scholar] [CrossRef]
- Ferretti, R.; Fumagalli, E.; Caccia, M.; Bruzzone, G. Seabed classification using a single beam echosounder. In Proceedings of the Oceans 2015-Genova, Genova, Italy, 18–21 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Hilgert, S.; Wagner, A.; Kiemle, L.; Fuchs, S. Investigation of echo sounding parameters for the characterisation of bottom sediments in a sub-tropical reservoir. Adv. Oceanogr. Limnol. 2016, 7, 93–105. [Google Scholar] [CrossRef]
- Blazhnov, B. Integrated mobile gravimetric system- Development and test results. In Proceedings of the 9th Saint Petersburg International Conference on Integrated Navigation Systems, St. Petersburg, Russia, 27–29 May 2002; pp. 223–232. [Google Scholar]
- Sokolov, A. High accuracy airborne gravity measurements. Methods and equipment. In Proceedings of the 18th World Congress the International Federation of Automatic Control, Milano, Italy, 28 August–2 September 2011; pp. 1889–1891. [Google Scholar]
- Harlan, R.B. Eotvos corrections for airborne gravimetry. J. Geophys. Res. 1968, 73, 4675–4679. [Google Scholar] [CrossRef]
- Jekeli, C. Inertial Navigation Systems with Geodetic Applications; Walter de Gruyter: Berlin, Germany, 2001. [Google Scholar]
- Li, M.; He, K.; Xu, T.; Lu, B. Robust adaptive filter for shipborne kinematic positioning and velocity determination during the Baltic Sea experiment. GPS Solut. 2018, 22, 81. [Google Scholar] [CrossRef]
- Childers, V.A.; Bell, R.E.; Brozena, J.M. Airborne gravimetry: An investigation of filtering. Geophysics 1999, 64, 61–69. [Google Scholar] [CrossRef]
- Akaike, H. Low pass filter design. Ann. Inst. Stat. Math. 1968, 20, 271–297. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Gold, B. Theory and Application of Digital Signal Processing; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1975; 777p. [Google Scholar]
- Zheleznyak, L. The accuracy of measurements by the CHEKAN-AM gravity system at sea. Izv. Phys. Solid Earth 2010, 46, 1000–1003. [Google Scholar] [CrossRef]
- Krasnov, A.; Sokolov, A.; Usov, S. Modern equipment and methods for gravity investigation in hard-to-reach regions. Gyroscopy Navig. 2011, 2, 178–183. [Google Scholar] [CrossRef]
- Krasnov, A.; Sokolov, A.; Elinson, L. Operational experience with the Chekan-AM gravimeters. Gyroscopy Navig. 2014, 5, 181–185. [Google Scholar] [CrossRef]
- Krasnov, A.; Sokolov, A. A modern software system of a mobile Chekan-AM gravimeter. Gyroscopy Navig. 2015, 6, 278–287. [Google Scholar] [CrossRef]
- Zheleznyak, L.; Koneshov, V.; Krasnov, A.; Sokolov, A.; Elinson, L. The results of testing the Chekan gravimeter at the Leningrad gravimetric testing area. Izv. Phys. Solid Earth 2015, 51, 315–320. [Google Scholar] [CrossRef]
- Smith, W.H.; Sandwell, D.T. Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry. J. Geophys. Res. Solid Earth 1994, 99, 21803–21824. [Google Scholar] [CrossRef]
- Smith, W.H.; Sandwell, D.T. Global sea floor topography from satellite altimetry and ship depth soundings. Science 1997, 277, 1956–1962. [Google Scholar] [CrossRef]
- Kim, J.W.; von Frese, R.R.; Lee, B.Y.; Roman, D.R.; Doh, S.J. Altimetry-derived gravity predictions of bathymetry by the gravity-geologic method. Pure Appl. Geophys. 2011, 168, 815–826. [Google Scholar] [CrossRef]
- Mingda, O.; Zhongmiao, S.; Zhenhe, Z.; Xiaogang, L. Bathymetry Prediction Based on the Admittance Theory of Gravity Anomalies. Acta Geod. Et Cartogr. Sin. 2015, 44, 1092. [Google Scholar]
- Abulaitijiang, A.; Andersen, O.B.; Sandwell, D. Improved Arctic Ocean bathymetry derived from DTU17 gravity model. Earth Space Sci. 2019, 6, 1336–1347. [Google Scholar] [CrossRef]
- Yang, J.; Luo, Z.; Tu, L. Ocean access to Zachariæ Isstrøm glacier, Northeast Greenland, revealed by OMG airborne gravity. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020281. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Li, X.; Yang, J.; Wan, X. Seafloor Topography Estimation from Gravity Anomaly and Vertical Gravity Gradient Using Nonlinear Iterative Least Square Method. Remote Sens. 2021, 13, 64. [Google Scholar] [CrossRef]
- Ibrahim, A.; Hinze, W.J. Mapping buried bedrock topography with gravity. Ground Water 1972, 10, 18–23. [Google Scholar] [CrossRef]
- Smith, W.; Wessel, P. Gridding with continuous curvature splines in tension. Geophysics 1990, 55, 293–305. [Google Scholar] [CrossRef]
- Yu-Shen, H.; Kim, J.W.; Kim, K.B.; Lee, B.Y.; Hwang, C. Bathymetry estimation using the gravity-geologic method: An investigation of density contrast predicted by the downward continuation method. TAO Terr. Atmos. Ocean. Sci. 2011, 22, 3. [Google Scholar]
- Kim, K.B.; Yun, H.S. Satellite-derived bathymetry prediction in shallow waters using the gravity-geologic method: A case study in the West Sea of Korea. KSCE J. Civ. Eng. 2018, 22, 2560–2568. [Google Scholar] [CrossRef]
- Ince, E.S.; Foerste, C.; Barthelmes, F.; Pflug, H. Ferry Gravimetry Data from the EU FAMOS project. Gfz Data Serv. 2020. [Google Scholar] [CrossRef]
- Ince, E.S.; Förste, C.; Barthelmes, F.; Pflug, H.; Li, M.; Kaminskis, J.; Neumayer, K.H.; Michalak, G. Gravity Measurements along Commercial Ferry Lines in the Baltic Sea and Their Use for Geodetic Purposes. Mar. Geod. 2020, 43, 573–602. [Google Scholar] [CrossRef]
- Sandwell, D.; Garcia, E.; Soofi, K.; Wessel, P.; Chandler, M.; Smith, W.H. Toward 1-mGal accuracy in global marine gravity from CryoSat-2, Envisat, and Jason-1. Lead. Edge 2013, 32, 892–899. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef]
- Zhang, S.; Abulaitijiang, A.; Andersen, O.B.; Sandwell, D.T.; Beale, J.R. Comparison and evaluation of high-resolution marine gravity recovery via sea surface heights or sea surface slopes. J. Geod. 2021, 95, 1–17. [Google Scholar] [CrossRef]
- Lu, B.; Xu, C.; Li, J. Combined Gravity Anomalies and Estimated Ocean Bottom Topography in the South-western Part of the Baltic Sea - (Data Sets). DANS 2021. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef]
- Tapley, B.; Ries, J.; Bettadpur, S.; Chambers, D.; Cheng, M.; Condi, F.; Gunter, B.; Kang, Z.; Nagel, P.; Pastor, R.; et al. GGM02–An improved Earth gravity field model from GRACE. J. Geod. 2005, 79, 467–478. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Eicker, A.; Kurtenbach, E.; Ilk, K.H. ITG-GRACE: Global static and temporal gravity field models from GRACE data. In System Earth via Geodetic-Geophysical Space Techniques; Springer: Berlin/Heidelberg, Germany, 2010; pp. 159–168. [Google Scholar]
- Lemoine, F.; Factor, J.; Kenyon, S. The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96; National Aeronautics and Space Administration, Goddard Space Flight Center: Greenbelt, MD, USA, 1998; Volume 206861.
- Turner, J.; Iliffe, J.; Ziebart, M.; Jones, C. Global ocean tide models: Assessment and use within a surface model of lowest astronomical tide. Mar. Geod. 2013, 36, 123–137. [Google Scholar] [CrossRef]
- Ince, E.S.; Barthelmes, F.; Reißland, S.; Elger, K.; Förste, C.; Flechtner, F.; Schuh, H. ICGEM–15 years of successful collection and distribution of global gravitational models, associated services, and future plans. Earth Syst. Sci. Data 2019, 11, 647–674. [Google Scholar] [CrossRef]
- Pail, R.; Bruinsma, S.; Migliaccio, F.; Förste, C.; Goiginger, H.; Schuh, W.D.; Höck, E.; Reguzzoni, M.; Brockmann, J.M.; Abrikosov, O.; et al. First GOCE gravity field models derived by three different approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef]
- Brockmann, J.M.; Zehentner, N.; Höck, E.; Pail, R.; Loth, I.; Mayer-Gürr, T.; Schuh, W.D. EGM_TIM_RL05: An independent geoid with centimeter accuracy purely based on the GOCE mission. Geophys. Res. Lett. 2014, 41, 8089–8099. [Google Scholar] [CrossRef]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Lemoine, J.M.; Marty, J.C.; Mulet, S.; Rio, M.H.; Bonvalot, S. ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophys. Res. Lett. 2014, 41, 7508–7514. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.; Abrikosov, O.; Lemoine, J.; Marty, J.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. Gfz Data Serv. 2014. [Google Scholar] [CrossRef]
- Fecher, T.; Pail, R.; Gruber, T.; Consortium, G. GOCO05c: A new combined gravity field model based on full normal equations and regionally varying weighting. Surv. Geophys. 2017, 38, 571–590. [Google Scholar] [CrossRef]
- Lu, B.; Luo, Z.; Zhong, B.; Zhou, H.; Flechtner, F.; Förste, C.; Barthelmes, F.; Zhou, R. The gravity field model IGGT_R1 based on the second invariant of the GOCE gravitational gradient tensor. J. Geod. 2018, 92, 561–572. [Google Scholar] [CrossRef]
- Lu, B.; Förste, C.; Barthelmes, F.; Petrovic, S.; Flechtner, F.; Luo, Z.; Zhong, B.; Zhou, H.; Wang, X.; Wu, T. Using real polar ground gravimetry data to solve the GOCE polar gap problem in satellite-only gravity field recovery. J. Geod. 2020, 94, 1–12. [Google Scholar] [CrossRef]


| Constant (Unit) | a (mGal/pixel) | b (mGal/pixel) | (pixel) | (s) |
|---|---|---|---|---|
| New value | 3.292262 | 3000 | 118.8 | |
| Previous value | 3.239682 | 3000 | 87.9 |
| Campaign | Min | Max | Mean | RMS |
|---|---|---|---|---|
| 2015 (67 points) | −1.09 | 1.37 | −0.08 | 0.48 |
| 2016 (50 points) | 0.84 | 1.73 | 0.11 | 0.55 |
| 2017 (31 points) | −0.76 | 0.52 | −0.08 | 0.32 |
| Min | Max | Mean | RMS | |
|---|---|---|---|---|
| BGI’s Marine Gravimetry—Altimetry | −14.68 | 10.71 | −1.95 | 3.71 |
| Marine Gravimetry—Altimetry, this study | −11.63 | 9.89 | −1.52 | 2.59 |
| Min | Max | Mean | RMS | |
|---|---|---|---|---|
| EMODnet—SRTM in | −52.47 | 42.59 | −0.63 | 2.59 |
| EMODnet—SIO in | −49.76 | 41.02 | −0.25 | 3.39 |
| Ship-Sounding data—SRTM | −16.71 | 16.78 | −0.70 | 1.90 |
| Ship-Sounding data—SIO | −18.01 | 16.20 | −0.51 | 2.06 |
| Ship-Sounding data—EMODnet | −12.32 | 15.44 | −0.09 | 0.73 |
| Min | Max | Mean | RMS | CORR (Unitless) | |
|---|---|---|---|---|---|
| Estimated Model-SRTM in | −55.24 | 42.58 | −0.61 | 2.65 | 0.99 |
| Estimated Model-SIO in | −43.39 | 47.92 | −0.07 | 3.67 | 0.97 |
| Estimated Model-EMODnet in | −16.70 | 22.08 | −0.00 | 0.10 | 1.00 |
| Min | Max | Mean | RMS | CORR (Unitless) | |
|---|---|---|---|---|---|
| Estimated Model | −18.32 | 9.75 | −0.06 | 0.64 | 1.00 |
| SRTM | −16.10 | 16.78 | −0.71 | 1.90 | 0.99 |
| SIO | −17.01 | 16.20 | −0.50 | 2.06 | 0.99 |
| EDMOnet | −11.97 | 15.44 | −0.09 | 0.73 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, B.; Xu, C.; Li, J.; Zhong, B.; van der Meijde, M. Marine Gravimetry and Its Improvements to Seafloor Topography Estimation in the Southwestern Coastal Area of the Baltic Sea. Remote Sens. 2022, 14, 3921. https://doi.org/10.3390/rs14163921
Lu B, Xu C, Li J, Zhong B, van der Meijde M. Marine Gravimetry and Its Improvements to Seafloor Topography Estimation in the Southwestern Coastal Area of the Baltic Sea. Remote Sensing. 2022; 14(16):3921. https://doi.org/10.3390/rs14163921
Chicago/Turabian StyleLu, Biao, Chuang Xu, Jinbo Li, Bo Zhong, and Mark van der Meijde. 2022. "Marine Gravimetry and Its Improvements to Seafloor Topography Estimation in the Southwestern Coastal Area of the Baltic Sea" Remote Sensing 14, no. 16: 3921. https://doi.org/10.3390/rs14163921
APA StyleLu, B., Xu, C., Li, J., Zhong, B., & van der Meijde, M. (2022). Marine Gravimetry and Its Improvements to Seafloor Topography Estimation in the Southwestern Coastal Area of the Baltic Sea. Remote Sensing, 14(16), 3921. https://doi.org/10.3390/rs14163921








