Evaluation of the Consistency of Three GRACE Gap-Filling Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. GRACE Products and Water Storage Estimates
2.2. Assessment Indicators
2.3. Fusion Method Based on Triple-Collocation
3. Results and Analysis
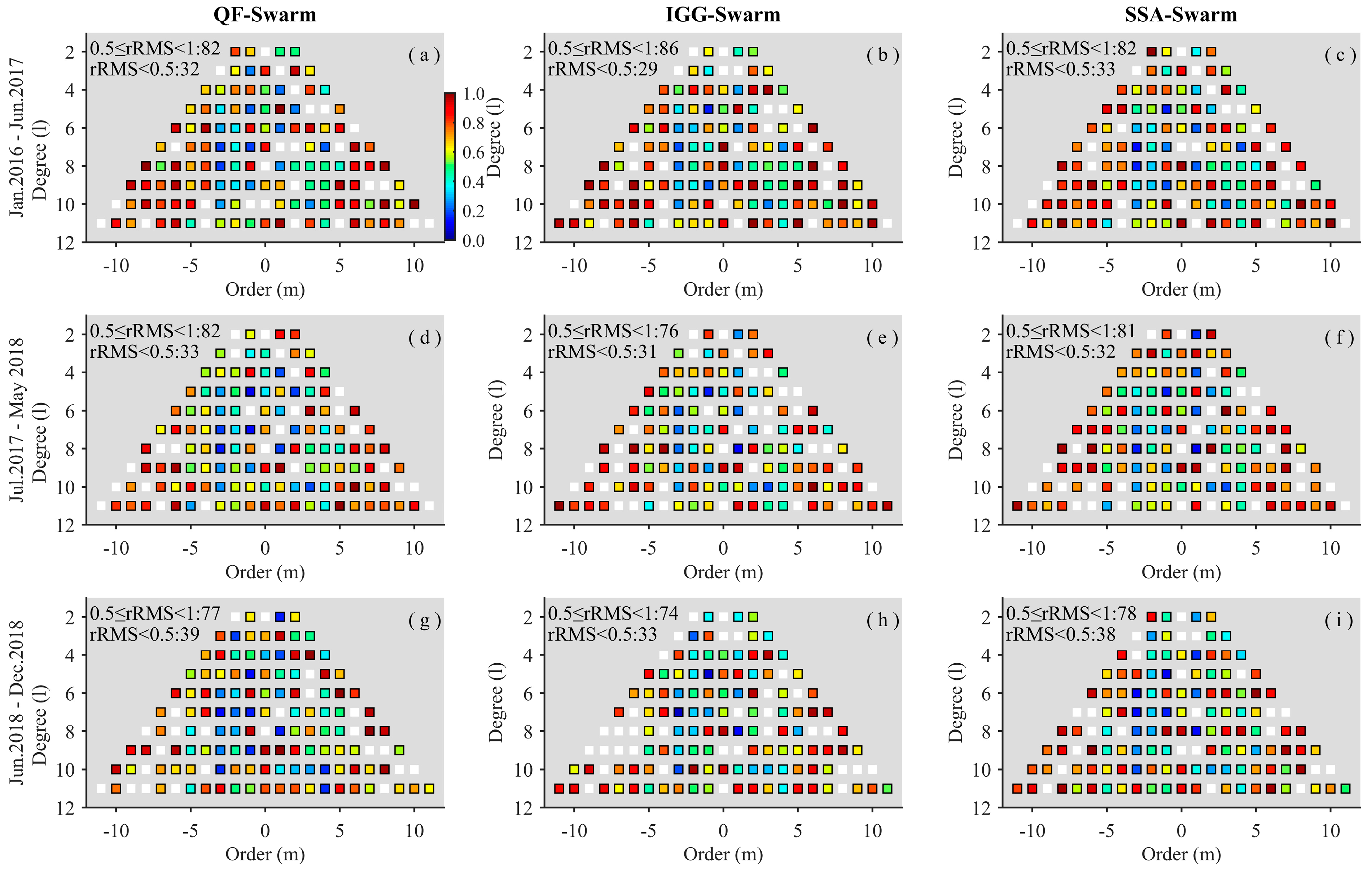
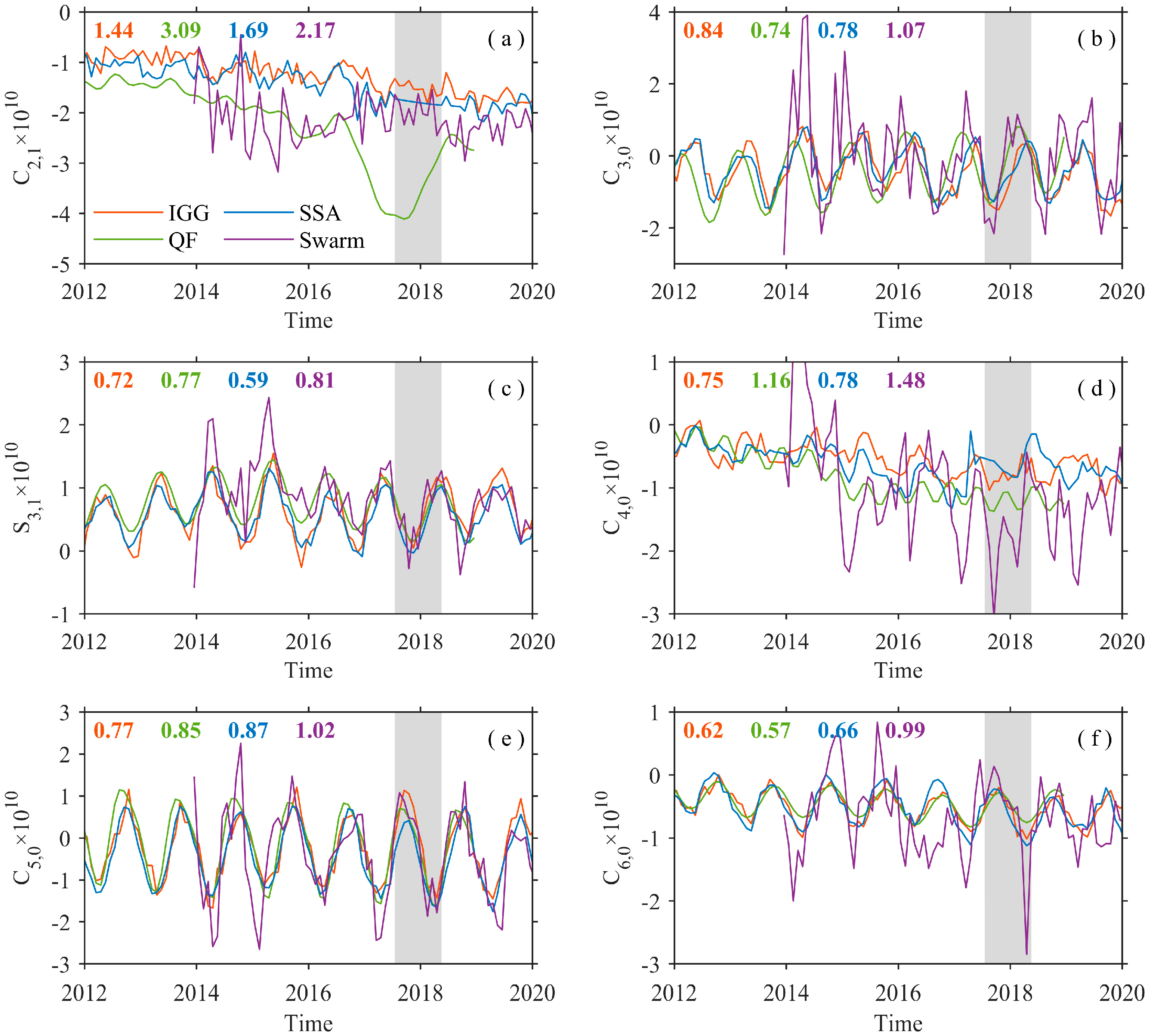
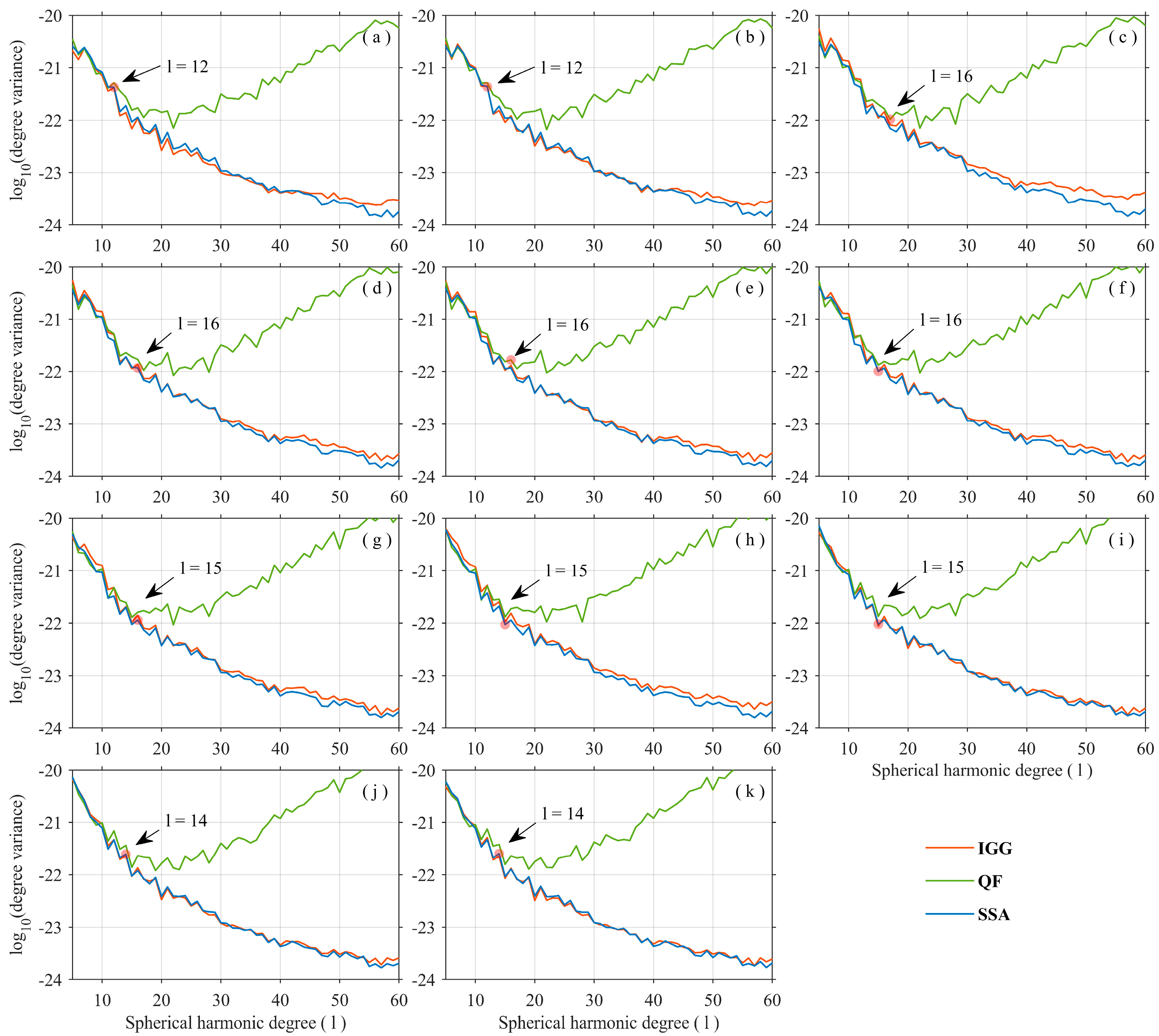
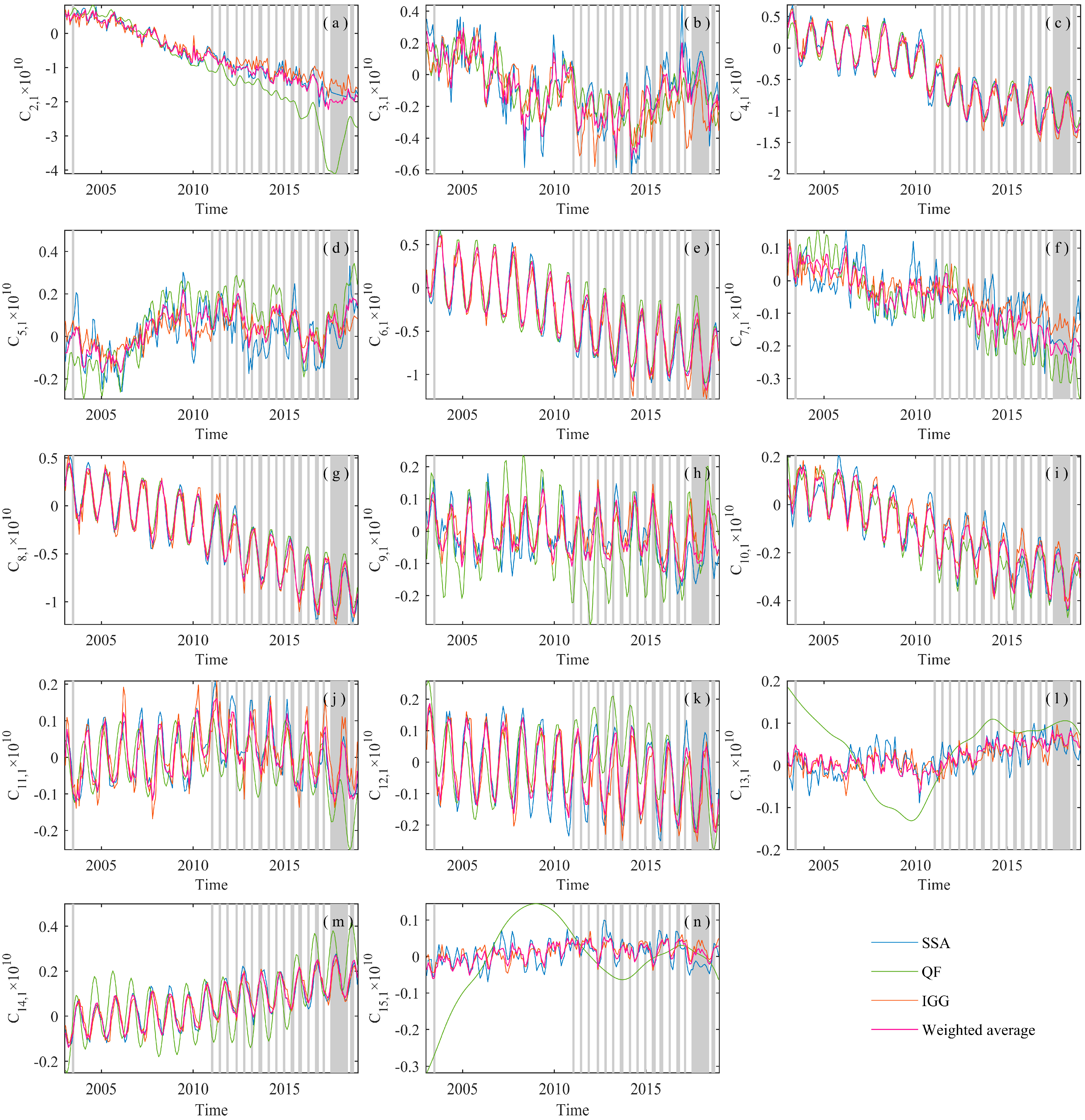
3.1. Comparative Analysis in the Spectral Domain
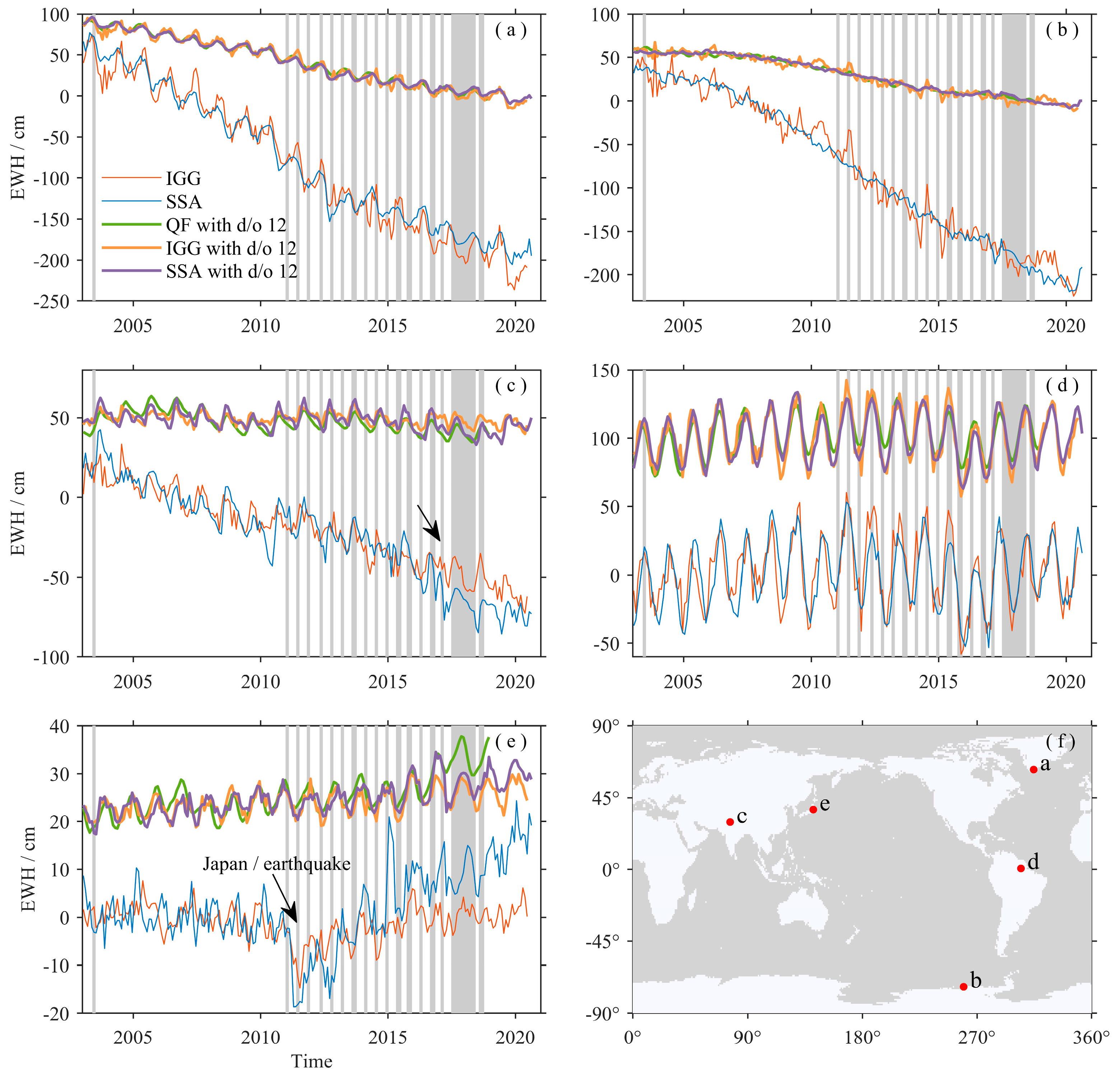
3.2. View of EWH Results of SHCs in the Space Domain
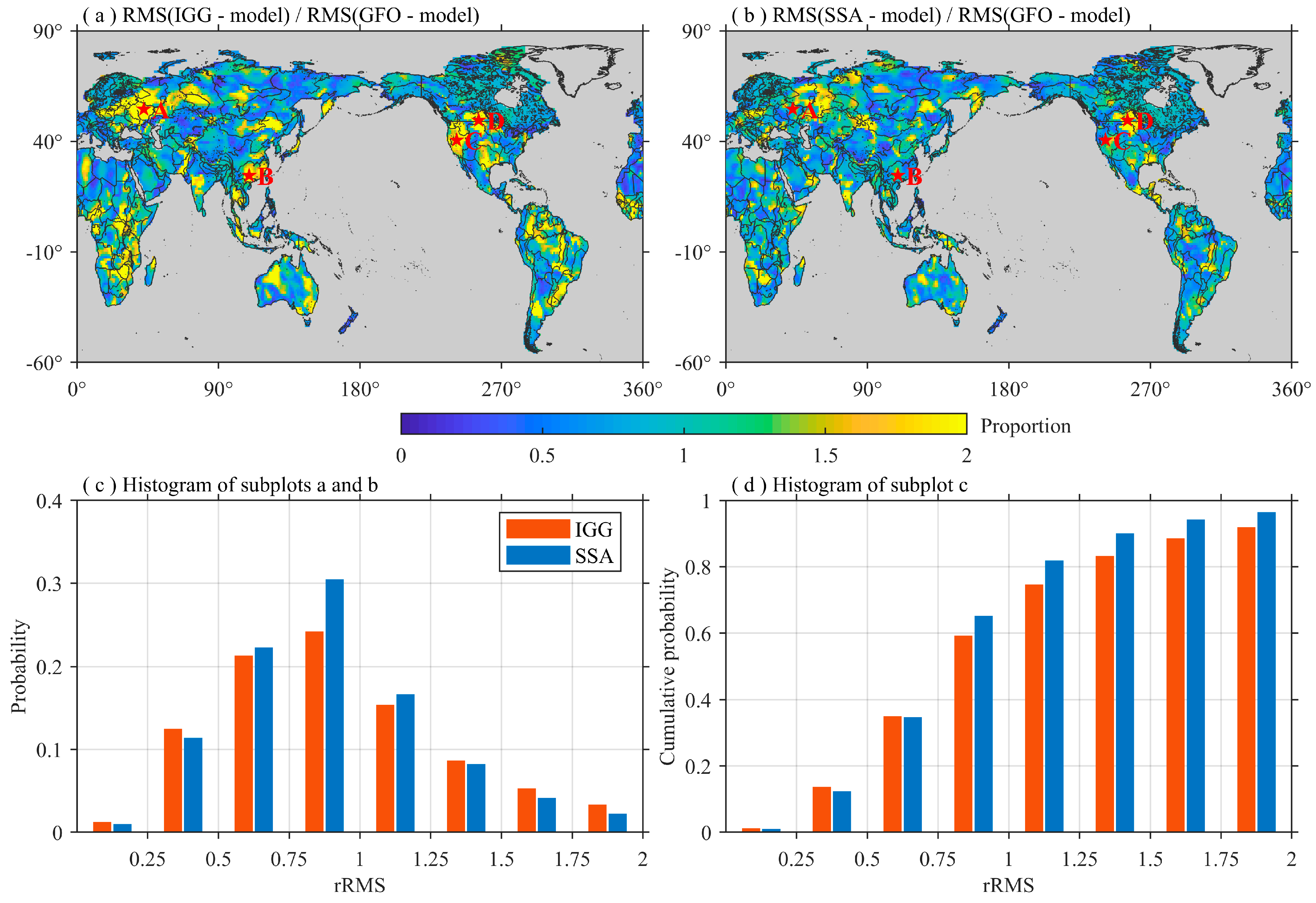
3.3. Consistency Analysis in the Spatial Domain
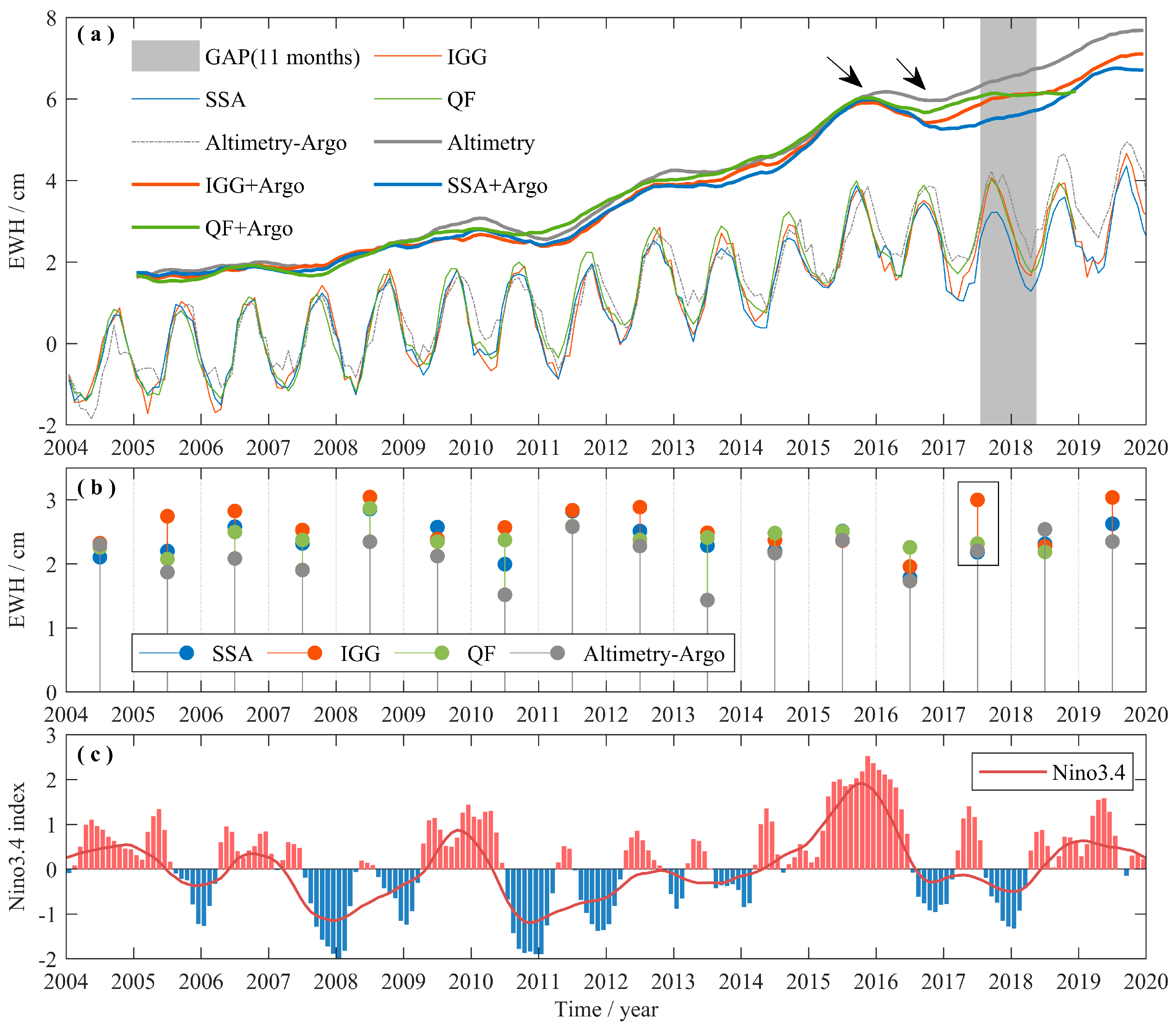
3.4. Global Mean Sea Level Change
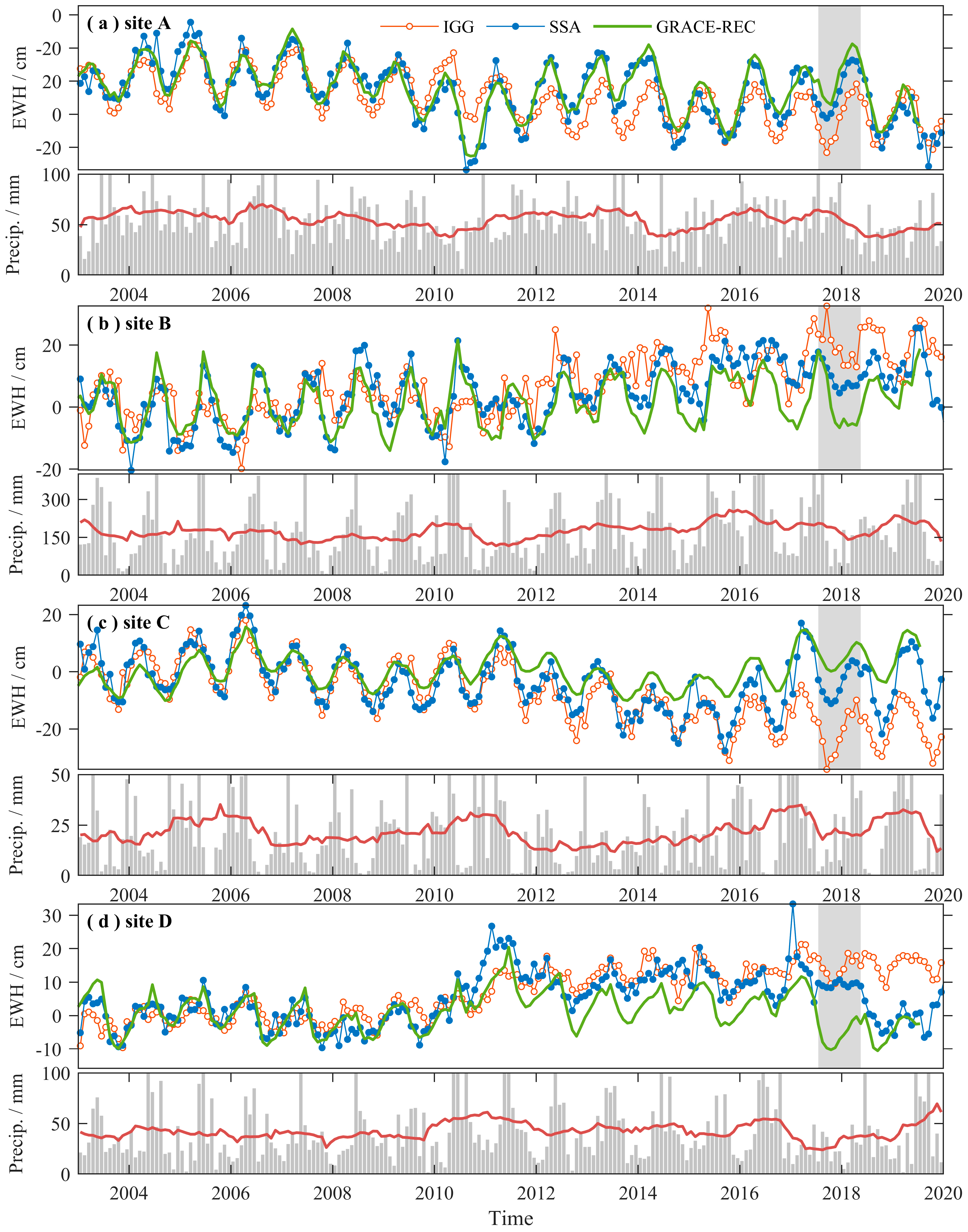
3.5. Comparison with Water Storage Model
4. Triple-Collocation Method-Based Fusion on the Gap-Filling Data
5. Discussion on Dataset Selection
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sandwell, D.T.; Smith, W.H.F. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. 1997, 102, 10039–10054. [Google Scholar] [CrossRef]
- Schwintzer, P.; Reigber, C.; Bode, A.; Kang, Z.; Zhu, S.Y.; Massmann, F.-H.; Raimondo, J.C.; Biancale, R.; Balmino, G.; Lemoine, J.M.; et al. Long-wavelength global gravity field models: GRIM4-S4, GRIM4-C4. J. Geod. 1997, 71, 189–208. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Wouters, B.; Bonin, J.A.; Chambers, D.P.; Riva, R.E.; Sasgen, I.; Wahr, J. GRACE, time-varying gravity, Earth system dynamics and climate change. Rep. Prog. Phys. 2014, 77, 116801. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Change 2019, 5, 358–369. [Google Scholar] [CrossRef]
- Chen, W.; Zhong, M.; Feng, W.; Zhong, Y.L.; Xu, H.Z. Effects of two strong ENSO events on terrestrial water storage anomalies in China from GRRACE during 2005–2017. Chin. J. Geophys. 2020, 63, 141–154. (In Chinese) [Google Scholar]
- Guo, J.; Li, W.; Chang, X.; Zhu, G.; Liu, X.; Guo, B. Terrestrial water storage changes over Xinjiang extracted by combining Gaussian filter and multichannel singular spectrum analysis from GRACE. Geophys. J. Int. 2018, 213, 397–407. [Google Scholar] [CrossRef]
- Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Sośnica, K.; et al. Laser geodetic satellites: A high-accuracy scientific tool. J. Geod. 2019, 93, 2181–2194. [Google Scholar] [CrossRef]
- Matsuo, K.; Chao, B.F.; Otsubo, T.; Heki, K. Accelerated ice mass depletion revealed by low-degree gravity field from satellite laser ranging: Greenland, 1991–2011. Geophys. Res. Lett. 2013, 40, 4662–4667. [Google Scholar] [CrossRef]
- Bloßfeld, M.; Müller, H.; Gerstl, M.; Štefka, V.; Bouman, J.; Göttl, F.; Horwath, M. Second-degree Stokes coefficients from multi-satellite SLR. J. Geod. 2015, 89, 857–871. [Google Scholar] [CrossRef]
- Sośnica, K.; Jäggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time variable Earth’s gravity field from SLR satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef]
- Weigelt, M.; Dam, T.; Jäggi, A.; Prange, L.; Tourian, M.J.; Keller, W.; Sneeuw, N. Time-variable gravity signal in Greenland revealed by high-low satellite-to-satellite tracking. J. Geophys. Res. Solid Earth 2013, 118, 3848–3859. [Google Scholar] [CrossRef]
- Wang, Z.T.; Chao, N.F. Time-variable gravity signal in Greenland revealed by SWARM high-low Satellite-to-Satellite Tracking. Chin. J. Geophys. 2014, 57, 3117–3128. (In Chinese) [Google Scholar]
- Teixeira da Encarnação, J.; Visser, P.; Arnold, D.; Bezdek, A.; Doornbos, E.; Ellmer, M.; Guo, J.; van den IJssel, J.; Iorfida, E.; Jäggi, A.; et al. Description of the multi-approach gravity field models from Swarm GPS data. Earth Syst. Sci. Data 2020, 12, 1385–1417. [Google Scholar] [CrossRef]
- Löcher, A.; Kusche, J. A hybrid approach for recovering high-resolution temporal gravity fields from satellite laser ranging. J. Geod. 2021, 95, 1–15. [Google Scholar] [CrossRef]
- Sun, A.Y.; Scanlon, B.R.; Zhang, Z.; Walling, D.; Bhanja, S.N.; Mukherjee, A.; Zhong, Z. Combining physically based modeling and deep learning for fusing GRACE satellite data: Can we learn from mismatch? Water Resour. Res. 2019, 55, 1179–1195. [Google Scholar] [CrossRef]
- Sun, Z.; Long, D.; Yang, W.; Li, X.; Pan, Y. Reconstruction of GRACE data on changes in total water storage Over the global land surface and 60 basins. Water Resour. Res. 2020, 56, e2019. [Google Scholar] [CrossRef]
- Li, F.; Kusche, J.; Rietbroek, R.; Wang, Z.; Forootan, E.; Schulze, K.; Lück, C. Comparison of data-driven techniques to reconstruct (1992–2002) and predict (2017–2018) GRACE-like gridded total water storage changes using climate inputs. Water Resour. Res. 2020, 56, e2019. [Google Scholar] [CrossRef]
- Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T. Statistical applications to downscale GRACE- derived terrestrial water storage data and to fill temporal gaps. Remote Sens. 2020, 12, 533. [Google Scholar] [CrossRef]
- Yi, S.; Sneeuw, N. Filling the data gaps within GRACE missions using Singular Spectrum Analysis. J. Geophys. Res. Solid Earth 2021, 126, e2020. [Google Scholar] [CrossRef]
- Lorenz, E. Empirical Orthogonal Functions and Statistical Weather Prediction; Science Report No. 1, Statistical Forecasting Project; M.I.T.: Cambridge, MA, USA, 1956; p. 48. [Google Scholar]
- Zotov, L.V.; Shum, C.K. Multichannel singular spectrum analysis of the gravity field data from GRACE satellites. AIP Conf. Proc. 2010, 1206, 473–479. [Google Scholar] [CrossRef]
- Zotov, L.V. Application of multichannel singular spectrum analysis to geophysical elds and astronomical images. Adv. Astron. Space Phys. 2012, 2, 82–84. [Google Scholar]
- Li, W.; Wang, W.; Zhang, C.; Wen, H.; Zhong, Y.; Zhu, Y.; Li, Z. Bridging terrestrial water storage anomaly During GRACE/GRACE-FO gap using SSA method: A case study in China. Sensors 2019, 19, 4144. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Shen, Y.; Chen, Q.; Wang, W. Bridging the gap between GRACE and GRACE follow-on monthly gravity field solutions using improved multichannel singular spectrum analysis. J. Hydrol. 2021, 594, 125972. [Google Scholar] [CrossRef]
- Weigelt, M. Time Series of Monthly Combined HLSST and SLR Gravity Field Models to Bridge the Gap between GRACE and GRACE-FO: QuantumFrontiers_HLSST_SLR_COMB2019s. GFZ Data Services; GFZ: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Mayer-Gürr, T.; Behzadpur, S.; Ellmer, M.; Kvas, A.; Klinger, B.; Strasser, S.; Zehentner, N. ITSG-Grace2018Monthly, Daily and Static Gravity Field Solutions from GRACE. GFZ Data Services; GFZ: Potsdam, Germany, 2018. [Google Scholar] [CrossRef]
- Weigelt, M.; van Dam, T.; Baur, O.; Tourian, M.; Steffen, H.; So’snica, K.; Jäggi, A.; Zehentner, N.; Mayer-Gürr, T.; Sneeuw, N. How well can the combination of hlSST and SLR replace GRACE? A discussion from the point of view of applications. In Proceedings of the GRACE Science Team Meeting, Potsdam, Germany, 29 September–2 October 2014. [Google Scholar]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated grace time-variable gravity solutions by gfz, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Cohen, J. Statistical power analysis. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Scipal, K.; Holmes, T.; Jeu, R.D.; Naeimi, V.; Wagner, W. A possible solution for the problem of estimating the error structure of global soil moisture data sets. Geophys. Res. Lett. 2008, 35, L24403. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Xiang, Z.; Hamid, M.; Hu, C. In-situ and triple-collocation based evaluations of eight global root zone soil moisture products. Remote Sens. Environ. 2021, 254, 112248. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Jiang, C.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar] [CrossRef]
- Hoareau, N.; Portabella, M.; Lin, W.; Ballabrera-Poy, J.; Turiel, A. Error characterization of sea surface salinity products using triple collocation analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5160–5168. [Google Scholar] [CrossRef]
- Lin, W.; Portabella, M.; Stoffelen, A.; Vogelzang, J.; Verhoef, A. On mesoscale analysis and ASCAT ambiguity removal. Quarterly J. R. Meteorol. Soc. 2016, 142, 1745–1756. [Google Scholar] [CrossRef]
- McColl, K.A.; Vogelzang, J.; Konings, A.G.; Entekhabi, D.; Piles, M.; Stoffelen, A. Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target. Geophys. Res. Lett. 2014, 41, 6229–6236. [Google Scholar] [CrossRef]
- Wahr, J.; Nerem, R.S.; Bettadpur, S.V. The pole tide and its effect on GRACE time-variable gravity measurements: Implications for estimates of surface mass variations. J. Geophys. Res. Solid Earth 2015, 120, 4597–4615. [Google Scholar] [CrossRef]
- Hanna, E.; Navarro, F.J.; Pattyn, F.; Domingues, C.M.; Fettweis, X.; Ivins, E.R.; Nicholls, R.J.; Ritz, C.; Smith, B.; Tulaczyk, S.; et al. Ice-sheet mass balance and climate change. Nature 2013, 498, 51–59. [Google Scholar] [CrossRef]
- Dangar, S.; Asoka, A.; Mishra, V. Causes and implications of groundwater depletion in India: A review. J. Hydrol. 2021, 596, 126103. [Google Scholar] [CrossRef]
- Ni, S.; Chen, J.; Wilson, C.R.; Li, J.; Hu, X.; Fu, R. Global Terrestrial Water Storage Changes and Connections to ENSO Events. Surv. Geophys. 2018, 39, 1–22. [Google Scholar] [CrossRef]
- Han, S.C.; Shum, C.K.; Bevis, M.; Ji, C.; Kuo, C.Y. Crustal dilatation observed by GRACE after the 2004 Sumatra-Andaman earthquake. Science 2006, 313, 658–662. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, K.; Heki, K. Coseismic gravity changes of the 2011 Tohoku-Oki earthquake from satellite gravimetry. Geophys. Res. Lett. 2011, 38, L00G12. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Geruo, A.G.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Wilson, C.; Cazenave, A.; Seo, K.-W.; Kim, J.-S. Global ocean mass change from grace and grace follow-On and altimeter and Argo measurements. Geophys. Res. Lett. 2020, 47, e2020GL090656. [Google Scholar] [CrossRef]
- Chang, L.; Sun, W.K. Progress and prospect of sea level changes of global and China nearby seas. Rev. Geophys. Planet. Phys. 2021, 52, 266–279. (In Chinese) [Google Scholar]
- Barnoud, A.; Pfeffer, J.; Guérou, A.; Frery, M.L.; Siméon, M.; Cazenave, A.; Chen, J.; Llovel, W.; Thierry, V.; Legeais, J.F.; et al. Contributions of altimetry and Argo to non-closure of the global mean sea level budget since 2016. Geophys. Res. Lett. 2021, 48, e2021GL092824. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L. GRACE-REC: A reconstruction of climate-driven water storage changes over the last century. Earth Syst. Sci. Data 2019, 11, 1153–1170. [Google Scholar] [CrossRef]
- Zhong, L.; Sośnica, K.; Weigelt, M.; Liu, B.; Zou, X. Time-Variable Gravity Field from the Combination of HLSST and SLR. Remote Sens. 2021, 13, 3491. [Google Scholar] [CrossRef]




| Data Style | Satellite | Satellite Type |
|---|---|---|
| SSA | GRACE, GRACE-FO | Gravity |
| IGG | Lageos ½, AJISAI, Starlette, Stella | Geodetic SLR |
| GRACE, GRACE-FO | Gravity | |
| QF | Champ, GRACE A/B, GOCE | Gravity |
| Swarm A, B, C | Geomagnetic | |
| TanDEM-X, TerraSAR-X, Kompsat5, Sentinel 1A, 1B, 2A, 3A | SAR | |
| SAC-C, CNOFS | Environmental monitoring | |
| Cosmic 1-6, MetOpA, MetOpB | Weather | |
| Jason 1-3 | Altimetry | |
| Lageos ½, LARES, Starlette, Stella, Larets, AJISAI, Beacon-C, Blits | Geodetic SLR |
| Types | SLR Degrees Estimated | GRACE EOFs Applied | GRACE Degrees Used in EOFs |
|---|---|---|---|
| S0+6E | None | 6 | 2–60 |
| S2+6E | 2 | 6 | 3–60 |
| S3+6E | 2–3 | 6 | 4–60 |
| S4+6E | 2–4 | 6 | 5–60 |
| S5+4E | 2–5 | 4 | 6–60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, A.; Yi, S.; Li, F.; Su, B.; Sun, G.; Liu, X. Evaluation of the Consistency of Three GRACE Gap-Filling Data. Remote Sens. 2022, 14, 3916. https://doi.org/10.3390/rs14163916
Qian A, Yi S, Li F, Su B, Sun G, Liu X. Evaluation of the Consistency of Three GRACE Gap-Filling Data. Remote Sensing. 2022; 14(16):3916. https://doi.org/10.3390/rs14163916
Chicago/Turabian StyleQian, An, Shuang Yi, Feng Li, Boli Su, Guangtong Sun, and Xiaoyang Liu. 2022. "Evaluation of the Consistency of Three GRACE Gap-Filling Data" Remote Sensing 14, no. 16: 3916. https://doi.org/10.3390/rs14163916
APA StyleQian, A., Yi, S., Li, F., Su, B., Sun, G., & Liu, X. (2022). Evaluation of the Consistency of Three GRACE Gap-Filling Data. Remote Sensing, 14(16), 3916. https://doi.org/10.3390/rs14163916








