High-Precision Population Spatialization in Metropolises Based on Ensemble Learning: A Case Study of Beijing, China
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data and Preprocessing
2.2.1. Boundary and Census Data
2.2.2. Remote Sensing Datasets
2.2.3. Point of Interest Data
2.2.4. Building Outline Data
2.2.5. Road and River Network Data
2.2.6. Community Household Registration Data
2.2.7. WorldPop Mainland China Dataset
3. Methodology
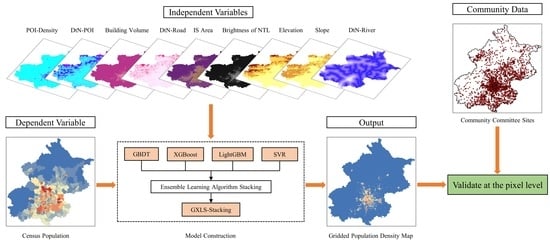
3.1. Overall Work Framework
3.2. Population Spatialization Model GXLS-Stacking
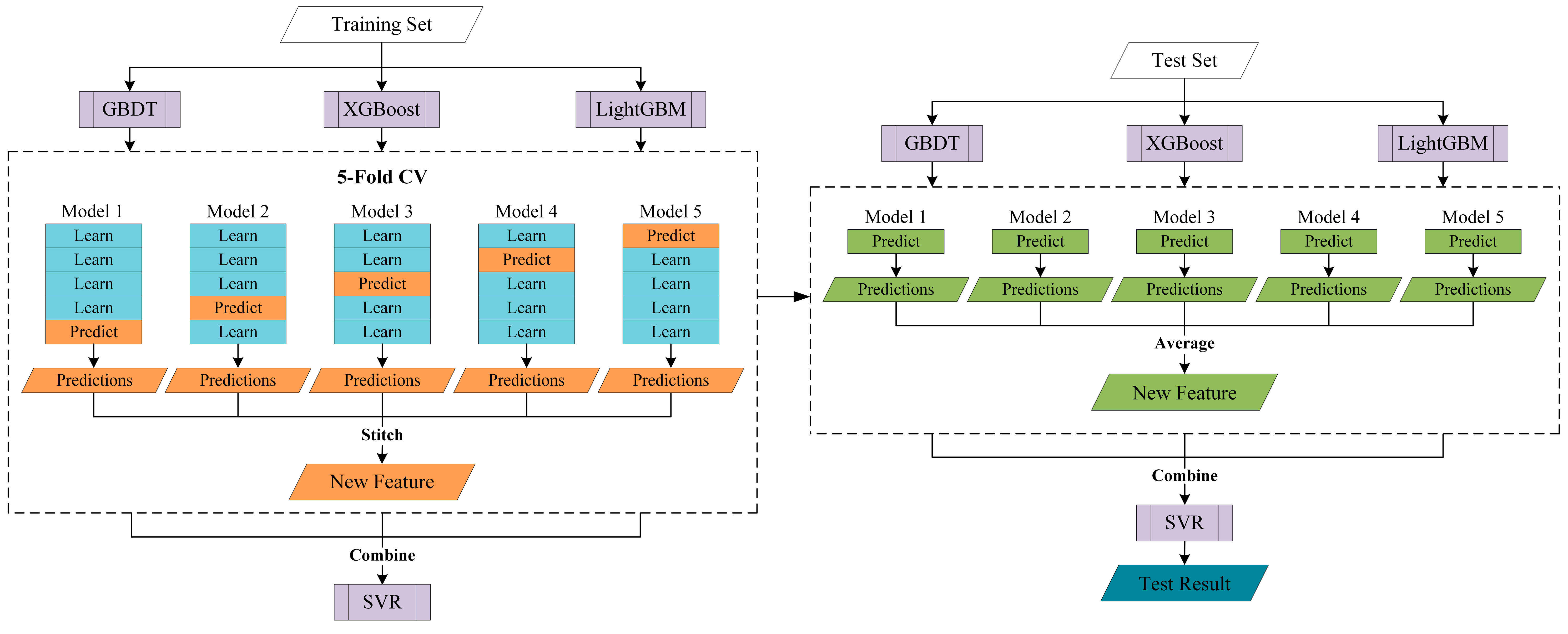
3.2.1. Stacked Generalization
3.2.2. Base Model and Meta-Model
3.2.3. Overall Model Architecture
3.3. Random Forest Model for Comparison
3.4. Evaluation Strategy and Performance Metrics
4. Results
4.1. Optimal Model Construction
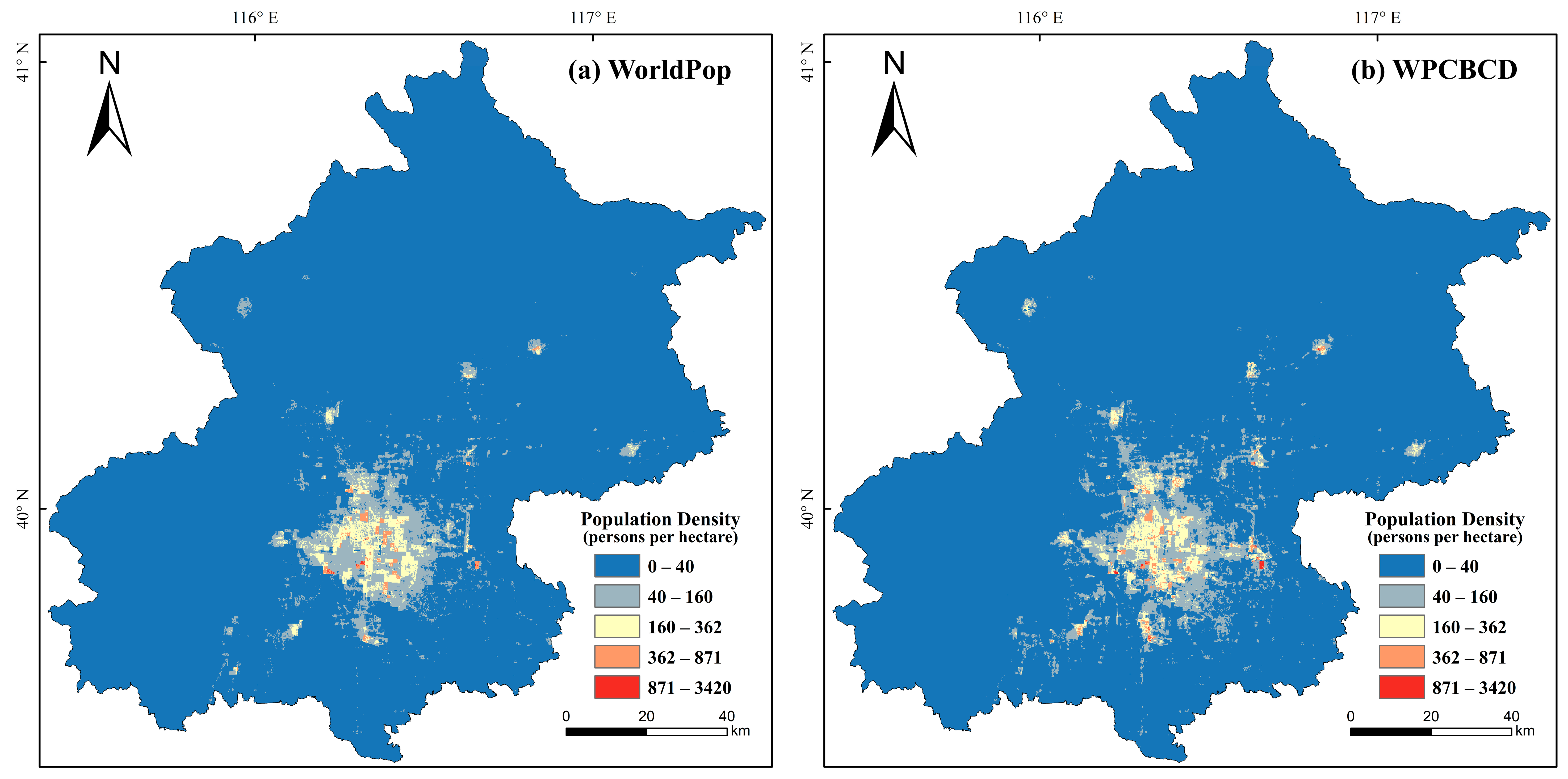
4.2. Dasymetric Population Mapping
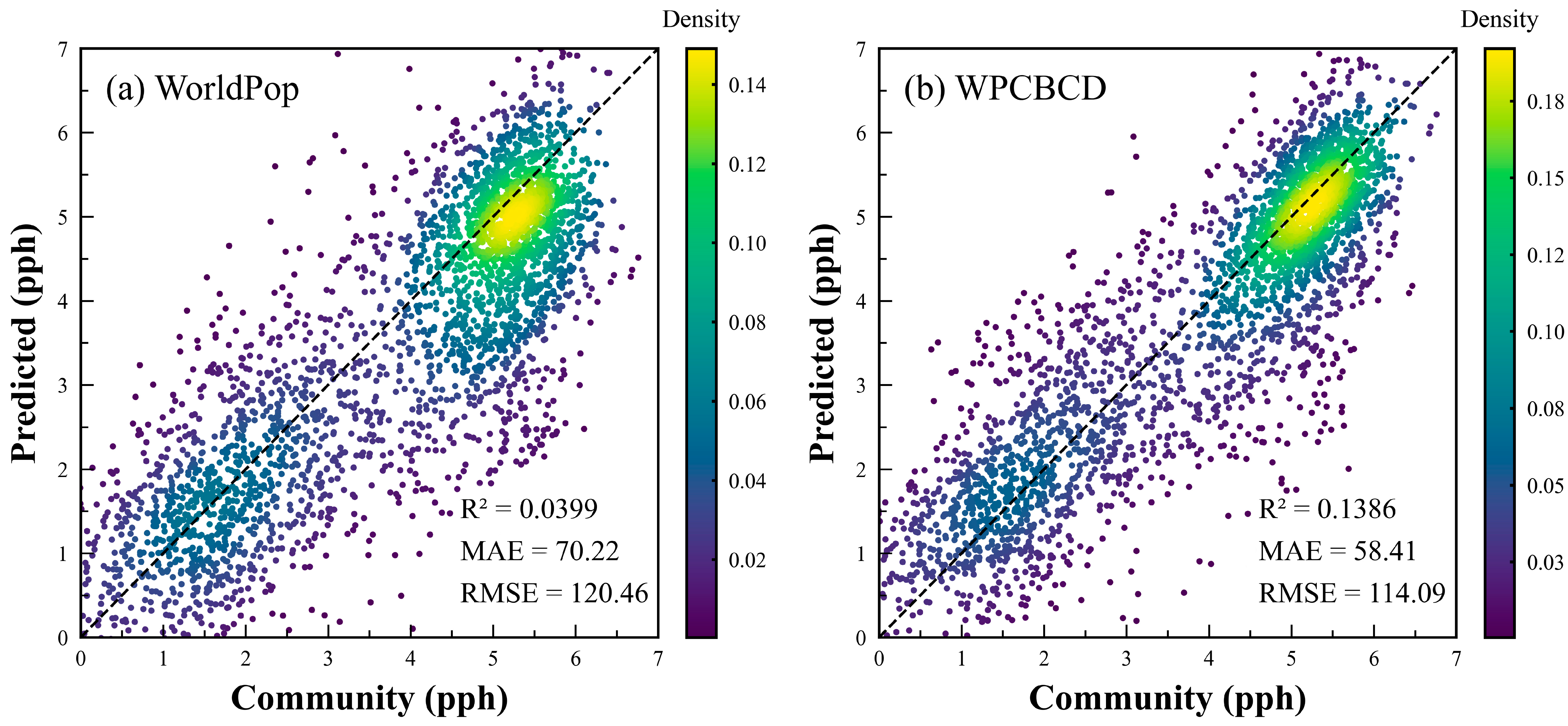
4.3. Accuracy Assessment of the Optimal Models
4.4. WorldPop Mainland China Dataset for Comparison
5. Discussion
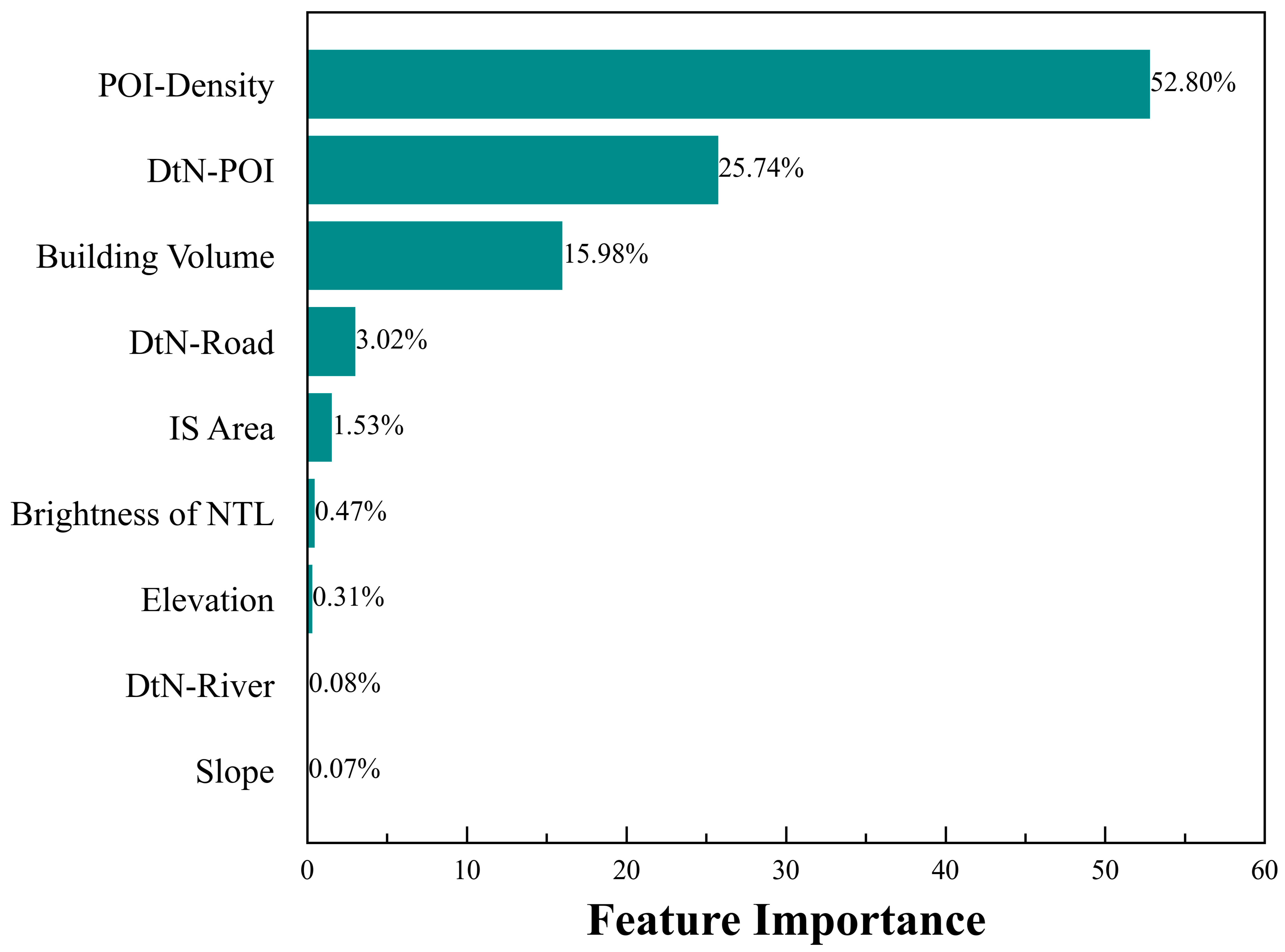
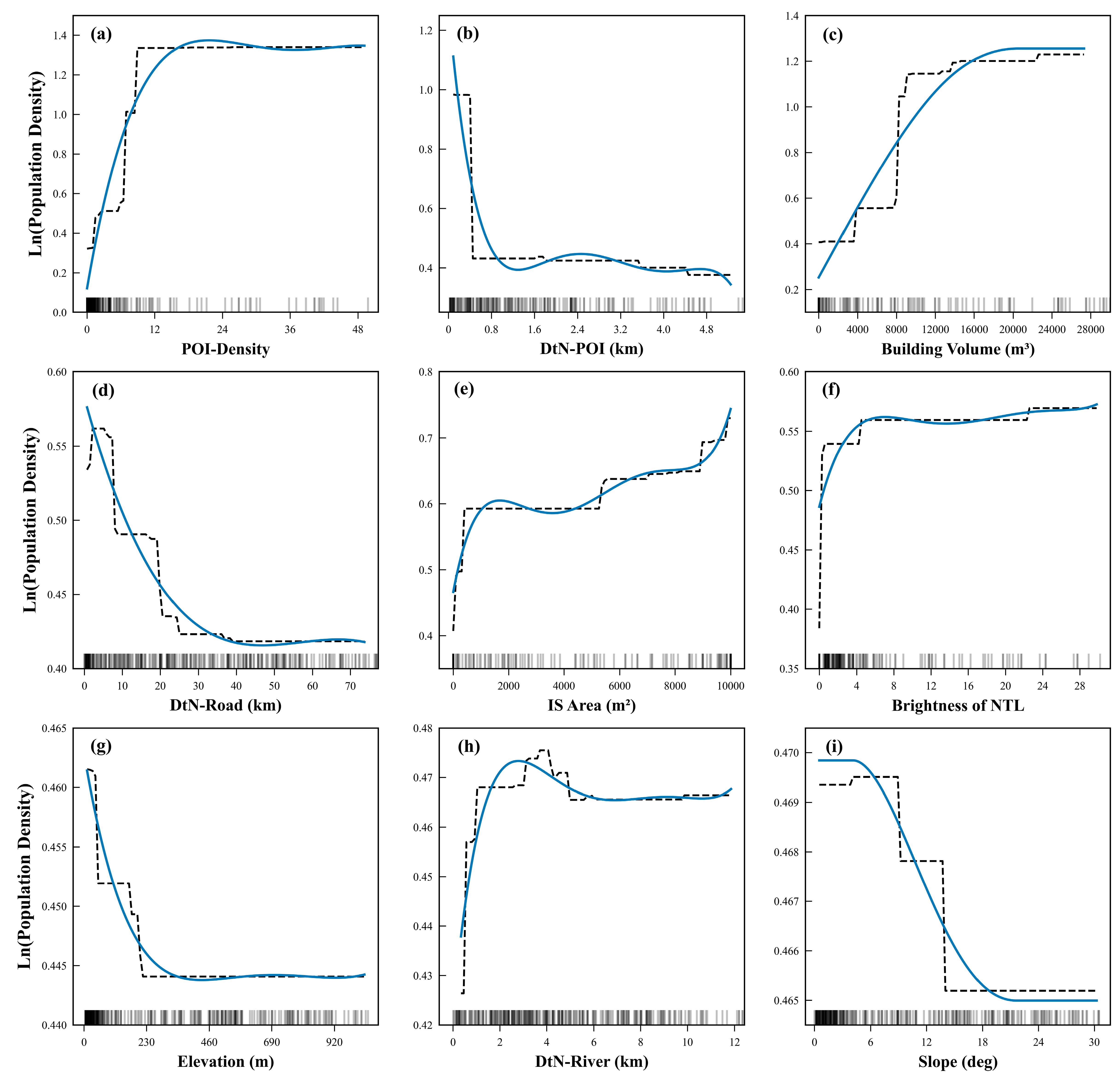
5.1. Socioeconomic Features versus Natural Environmental Features
5.2. Cons and Pros of the GXLS-Stacking Model and Future Improvement
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, P.; Wu, T.; Ge, Y.; Li, Z. Improving the accuracy of extant gridded population maps using multisource map fusion. GISci. Remote Sens. 2022, 59, 54–70. [Google Scholar] [CrossRef]
- Li, K.; Chen, Y.; Li, Y. The Random Forest-Based Method of Fine-Resolution Population Spatialization by Using the International Space Station Nighttime Photography and Social Sensing Data. Remote Sens. 2018, 10, 1650. [Google Scholar] [CrossRef] [Green Version]
- Daughton, C.G. Wastewater surveillance for population-wide COVID-19: The present and future. Sci. Total Environ. 2020, 736, 139631. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.S.; Lu, X.; Yuan, Y.; Xu, G.; Jia, J.; Christakis, N.A. Population flow drives spatio-temporal distribution of COVID-19 in China. Nature 2020, 582, 389–394. [Google Scholar] [CrossRef]
- Han, Y.; Yang, L.; Jia, K.; Li, J.; Feng, S.; Chen, W.; Zhao, W.; Pereira, P. Spatial distribution characteristics of the COVID-19 pandemic in Beijing and its relationship with environmental factors. Sci. Total Environ. 2021, 761, 144257. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Yang, M. Urban Population Distribution Mapping with Multisource Geospatial Data Based on Zonal Strategy. ISPRS Int. J. Geo-Inf. 2020, 9, 654. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W. Dasymetric mapping of urban population in China based on radiance corrected DMSP-OLS nighttime light and land cover data. Sci. Total Environ. 2018, 643, 1248–1256. [Google Scholar] [CrossRef]
- Pérez-Morales, A.; Gil-Guirado, S.; Martínez-García, V. Dasymetry Dash Flood (DDF). A method for population mapping and flood exposure assessment in touristic cities. Appl. Geogr. 2022, 142, 102683. [Google Scholar] [CrossRef]
- Tenerelli, P.; Gallego, J.F.; Ehrlich, D. Population density modelling in support of disaster risk assessment. Int. J. Disaster Risk Reduct. 2015, 13, 334–341. [Google Scholar] [CrossRef]
- Weber, E.M.; Seaman, V.Y.; Stewart, R.N.; Bird, T.J.; Tatem, A.J.; McKee, J.J.; Bhaduri, B.L.; Moehl, J.J.; Reith, A.E. Census-independent population mapping in northern Nigeria. Remote Sens. Environ. 2018, 204, 786–798. [Google Scholar] [CrossRef]
- Li, L.; Li, J.; Jiang, Z.; Zhao, L.; Zhao, P. Methods of Population Spatialization Based on the Classification Information of Buildings from China’s First National Geoinformation Survey in Urban Area: A Case Study of Wuchang District, Wuhan City, China. Sensors 2018, 18, 2558. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Li, K.; Cheng, W.; Ye, C.; Zhang, H. A Method of Population Spatialization Considering Parametric Spatial Stationarity: Case Study of the Southwestern Area of China. ISPRS Int. J. Geo-Inf. 2019, 8, 495. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, S.; Zhou, Y.; Liu, W.; Hou, Y.; Zhu, J.; Wang, F. Mapping population density in China between 1990 and 2010 using remote sensing. Remote Sens. Environ. 2018, 210, 269–281. [Google Scholar] [CrossRef]
- Jia, P.; Qiu, Y.; Gaughan, A.E. A fine-scale spatial population distribution on the High-resolution Gridded Population Surface and application in Alachua County, Florida. Appl. Geogr. 2014, 50, 99–107. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, L.; Feng, R.; Yan, J. Remote Sensing and Social Sensing Data Fusion for Fine-Resolution Population Mapping with a Multimodel Neural Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5973–5987. [Google Scholar] [CrossRef]
- Azar, D.; Engstrom, R.; Graesser, J.; Comenetz, J. Generation of fine-scale population layers using multi-resolution satellite imagery and geospatial data. Remote Sens. Environ. 2013, 130, 219–232. [Google Scholar] [CrossRef]
- Lung, T.; Lübker, T.; Ngochoch, J.K.; Schaab, G. Human population distribution modelling at regional level using very high resolution satellite imagery. Appl. Geogr. 2013, 41, 36–45. [Google Scholar] [CrossRef]
- Briggs, D.J.; Gulliver, J.; Fecht, D.; Vienneau, D.M. Dasymetric modelling of small-area population distribution using land cover and light emissions data. Remote Sens. Environ. 2007, 108, 451–466. [Google Scholar] [CrossRef]
- Chen, R.; Yan, H.; Liu, F.; Du, W.; Yang, Y. Multiple Global Population Datasets: Differences and Spatial Distribution Characteristics. ISPRS Int. J. Geo-Inf. 2020, 9, 637. [Google Scholar] [CrossRef]
- Mei, Y.; Gui, Z.; Wu, J.; Peng, D.; Li, R.; Wu, H.; Wei, Z. Population spatialization with pixel-level attribute grading by considering scale mismatch issue in regression modeling. Geo-Spat. Inf. Sci. 2022, 1–18. [Google Scholar] [CrossRef]
- Xie, Z. A Framework for Interpolating the Population Surface at the Residential-Housing-Unit Level. GISci. Remote Sens. 2013, 43, 233–251. [Google Scholar] [CrossRef]
- Langford, M. Obtaining population estimates in non-census reporting zones: An evaluation of the 3-class dasymetric method. Comput. Environ. Urban Syst. 2006, 30, 161–180. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Anselin, L.; Deichmann, U. A Framework for the Areal Interpolation of Socioeconomic Data. Environ. Plan. A Econ. Space 1993, 25, 383–397. [Google Scholar] [CrossRef]
- Bhaduri, B.; Bright, E.; Urban, C.M.L. LandScan USA: A high-resolution geospatial and temporal modeling approach for population distribution and dynamics. GeoJournal 2007, 69, 103–117. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Lam, N. Areal Interpolation—A Variant of the Traditional Spatial Problem. Geo-Processing 1980, 1, 297–312. [Google Scholar]
- Holt, J.B.; Lo, C.P.; Hodler, T.W. Dasymetric Estimation of Population Density and Areal Interpolation of Census Data. Cartogr. Geogr. Inf. Sci. 2004, 31, 103–121. [Google Scholar] [CrossRef]
- Harvey, J.T. Population estimation models based on individual TM pixels. Photogramm. Eng. Remote Sens. 2002, 68, 1181–1192. [Google Scholar]
- Lwin, K.K.; Sugiura, K.; Zettsu, K. Space–time multiple regression model for grid-based population estimation in urban areas. Int. J. Geogr. Inf. Sci. 2016, 30, 1579–1593. [Google Scholar] [CrossRef]
- Xu, Y.; Song, Y.; Cai, J.; Zhu, H. Population mapping in China with Tencent social user and remote sensing data. Appl. Geogr. 2021, 130, 102450. [Google Scholar] [CrossRef]
- Douglass, R.W.; Meyer, D.A.; Ram, M.; Rideout, D.; Song, D. High resolution population estimates from telecommunications data. EPJ Data Sci. 2015, 4, 4. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Ye, T.; Zhao, N.; Chen, Q.; Yue, W.; Qi, J.; Zeng, B.; Jia, P. Population Mapping with Multisensor Remote Sensing Images and Point-Of-Interest Data. Remote Sens. 2019, 11, 574. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liu, X.; Li, X.; Zhang, J.; Liang, Z.; Mai, K.; Zhang, Y. Mapping fine-scale population distributions at the building level by integrating multisource geospatial big data. Int. J. Geogr. Inf. Sci. 2017, 31, 1220–1244. [Google Scholar] [CrossRef]
- Zeng, C.; Zhou, Y.; Wang, S.; Yan, F.; Zhao, Q. Population spatialization in China based on night-time imagery and land use data. Int. J. Remote Sens. 2011, 32, 9599–9620. [Google Scholar] [CrossRef]
- Wu, T.; Luo, J.; Dong, W.; Gao, L.; Hu, X.; Wu, Z.; Sun, Y.; Liu, J. Disaggregating County-Level Census Data for Population Mapping Using Residential Geo-Objects with Multisource Geo-Spatial Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1189–1205. [Google Scholar] [CrossRef]
- He, M.; Xu, Y.; Li, N. Population Spatialization in Beijing City Based on Machine Learning and Multisource Remote Sensing Data. Remote Sens. 2020, 12, 1910. [Google Scholar] [CrossRef]
- Qiu, G.; Bao, Y.; Yang, X.; Wang, C.; Ye, T.; Stein, A.; Jia, P. Local Population Mapping Using a Random Forest Model Based on Remote and Social Sensing Data: A Case Study in Zhengzhou, China. Remote Sens. 2020, 12, 1618. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Zhao, M.; Hou, J.; Zhang, Y.; Gu, J. Mapping the Population Density in Mainland China Using NPP/VIIRS and Points-of-Interest Data Based on a Random Forests Model. Remote Sens. 2020, 12, 3645. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, M.; Shi, K.; Peng, Z. Estimating and Interpreting Fine-Scale Gridded Population Using Random Forest Regression and Multisource Data. ISPRS Int. J. Geo-Inf. 2020, 9, 369. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, Y.; Zhang, R.; Fu, B. China’s population spatialization based on three machine learning models. J. Clean. Prod. 2020, 256, 120644. [Google Scholar] [CrossRef]
- Czarnowski, I.; Jedrzejowicz, P. An approach to machine classification based on stacked generalization and instance selection. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 4836–4841. [Google Scholar]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Rose, S. Mortality Risk Score Prediction in an Elderly Population Using Machine Learning. Am. J. Epidemiol. 2013, 177, 443–452. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, M.H.D.M.; Dos Santos Coelho, L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Agarwal, S.; Chowdary, C.R. A-Stacking and A-Bagging: Adaptive versions of ensemble learning algorithms for spoof fingerprint detection. Expert Syst. Appl. 2020, 146, 113160. [Google Scholar] [CrossRef]
- Jia, P.; Gaughan, A.E. Dasymetric modeling: A hybrid approach using land cover and tax parcel data for mapping population in Alachua County, Florida. Appl. Geogr. 2016, 66, 100–108. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, Z.; Liu, F. Monitoring Population Evolution in China Using Time-Series DMSP/OLS Nightlight Imagery. Remote Sens. 2018, 10, 194. [Google Scholar] [CrossRef] [Green Version]
- Zandbergen, P.A.; Ignizio, D.A. Comparison of Dasymetric Mapping Techniques for Small-Area Population Estimates. Cartogr. Geogr. Inf. Sci. 2010, 37, 199–214. [Google Scholar] [CrossRef]
- Ye, T.; Zhao, N.; Yang, X.; Ouyang, Z.; Liu, X.; Chen, Q.; Hu, K.; Yue, W.; Qi, J.; Li, Z.; et al. Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model. Sci. Total Environ. 2019, 658, 936–946. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; He, J.; Yao, Y.; Zhang, J.; Liang, H.; Wang, H.; Hong, Y. Classifying urban land use by integrating remote sensing and social media data. Int. J. Geogr. Inf. Sci. 2017, 31, 1675–1696. [Google Scholar] [CrossRef]
- Lu, D.; Tian, H.; Zhou, G.; Ge, H. Regional mapping of human settlements in southeastern China with multisensor remotely sensed data. Remote Sens. Environ. 2008, 112, 3668–3679. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Gao, S.; Gong, L.; Kang, C.; Zhi, Y.; Chi, G.; Shi, L. Social Sensing: A New Approach to Understanding Our Socioeconomic Environments. Ann. Assoc. Am. Geogr. 2015, 105, 512–530. [Google Scholar] [CrossRef]
- Yao, Y.; Li, X.; Liu, X.; Liu, P.; Liang, Z.; Zhang, J.; Mai, K. Sensing spatial distribution of urban land use by integrating points-of-interest and Google Word2Vec model. Int. J. Geogr. Inf. Sci. 2017, 31, 825–848. [Google Scholar] [CrossRef]
- Bakillah, M.; Liang, S.; Mobasheri, A.; Jokar Arsanjani, J.; Zipf, A. Fine-resolution population mapping using OpenStreetMap points-of-interest. Int. J. Geogr. Inf. Sci. 2014, 28, 1940–1963. [Google Scholar] [CrossRef]
- Cai, J.; Huang, B.; Song, Y. Using multi-source geospatial big data to identify the structure of polycentric cities. Remote Sens. Environ. 2017, 202, 210–221. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Q.; Zhang, Y.; Du, X. Improving the Accuracy of Fine-Grained Population Mapping Using Population-Sensitive POIs. Remote Sens. 2019, 11, 2502. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.; Alves, A.; Rodrigues, F.; Ferreira, J.; Pereira, F.C. Mining point-of-interest data from social networks for urban land use classification and disaggregation. Comput. Environ. Urban Syst. 2015, 53, 36–46. [Google Scholar] [CrossRef] [Green Version]
- Esch, T.; Brzoska, E.; Dech, S.; Leutner, B.; Palacios-Lopez, D.; Metz-Marconcini, A.; Marconcini, M.; Roth, A.; Zeidler, J. World Settlement Footprint 3D—A first three-dimensional survey of the global building stock. Remote Sens. Environ. 2022, 270, 112877. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, H.; Lin, H.; Gamba, P.E.; Liu, X. Incorporating synthetic aperture radar and optical images to investigate the annual dynamics of anthropogenic impervious surface at large scale. Remote Sens. Environ. 2020, 242, 111757. [Google Scholar] [CrossRef]
- Wei, S.; Lin, Y.; Zhang, H.; Wan, L.; Lin, H.; Wu, Z. Estimating Chinese residential populations from analysis of impervious surfaces derived from satellite images. Int. J. Remote Sens. 2021, 42, 2303–2326. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, C.; Wang, S.; Liu, W.; Tian, Y. Estimation of Building Density with the Integrated Use of GF-1 PMS and Radarsat-2 Data. Remote Sens. 2016, 8, 969. [Google Scholar] [CrossRef] [Green Version]
- Frantz, D.; Schug, F.; Okujeni, A.; Navacchi, C.; Wagner, W.; Van der Linden, S.; Hostert, P. National-scale mapping of building height using Sentinel-1 and Sentinel-2 time series. Remote Sens. Environ. 2021, 252, 112128. [Google Scholar] [CrossRef] [PubMed]
- Gaughan, A.E.; Stevens, F.R.; Huang, Z.; Nieves, J.J.; Sorichetta, A.; Lai, S.; Ye, X.; Linard, C.; Hornby, G.M.; Hay, S.I.; et al. Spatiotemporal patterns of population in mainland China, 1990 to 2010. Sci. Data 2016, 3, 160005. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Dietz, J.B.; Bland, T.; Sutton, P.C.; Kroehl, H.W. Radiance Calibration of DMSP-OLS Low-Light Imaging Data of Human Settlements. Remote Sens. Environ. 1999, 68, 77–88. [Google Scholar] [CrossRef]
- Sutton, P.; Roberts, D.; Elvidge, C.; Baugh, K. Census from Heaven: An estimate of the global human population using night-time satellite imagery. Int. J. Remote Sens. 2010, 22, 3061–3076. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Lawrence, W.T.; Stutzer, D.C.; Elvidge, C.D. A technique for using composite DMSP/OLS “city lights” satellite data to map urban area. Remote Sens. Environ. 1997, 61, 361–370. [Google Scholar] [CrossRef]
- Cao, X.; Hu, Y.; Zhu, X.; Shi, F.; Zhuo, L.; Chen, J. A simple self-adjusting model for correcting the blooming effects in DMSP-OLS nighttime light images. Remote Sens. Environ. 2019, 224, 401–411. [Google Scholar] [CrossRef]
- Small, C.; Pozzi, F.; Elvidge, C. Spatial analysis of global urban extent from DMSP-OLS night lights. Remote Sens. Environ. 2005, 96, 277–291. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Zhizhin, M.; Ghosh, T.; Hsu, F.; Taneja, J. Annual Time Series of Global VIIRS Nighttime Lights Derived from Monthly Averages: 2012 to 2019. Remote Sens. 2021, 13, 922. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Zhao, T.; Gao, Y.; Chen, X.; Mi, J. GISD30: Global 30 m impervious-surface dynamic dataset from 1985 to 2020 using time-series Landsat imagery on the Google Earth Engine platform. Earth Syst. Sci. Data. 2022, 14, 1831–1856. [Google Scholar] [CrossRef]
- Zhong, Y.; Su, Y.; Wu, S.; Zheng, Z.; Zhao, J.; Ma, A.; Zhu, Q.; Ye, R.; Li, X.; Pellikka, P.; et al. Open-source data-driven urban land-use mapping integrating point-line-polygon semantic objects: A case study of Chinese cities. Remote Sens. Environ. 2020, 247, 111838. [Google Scholar] [CrossRef]
- Decuyper, M.; Chávez, R.O.; Lohbeck, M.; Lastra, J.A.; Tsendbazar, N.; Hackländer, J.; Herold, M.; Vågen, T. Continuous monitoring of forest change dynamics with satellite time series. Remote Sens. Environ. 2022, 269, 112829. [Google Scholar] [CrossRef]
- Dehnad, K. Density Estimation for Statistics and Data Analysis. Technometrics 2012, 29, 495. [Google Scholar] [CrossRef]
- Cao, Y.; Huang, X. A deep learning method for building height estimation using high-resolution multi-view imagery over urban areas: A case study of 42 Chinese cities. Remote Sens. Environ. 2021, 264, 112590. [Google Scholar] [CrossRef]
- Bai, Z.; Wang, J.; Wang, M.; Gao, M.; Sun, J. Accuracy Assessment of Multi-Source Gridded Population Distribution Datasets in China. Sustainability 2018, 10, 1363. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liang, S.; Zhu, Z.; Ma, H.; He, T. Soil moisture content retrieval from Landsat 8 data using ensemble learning. ISPRS J. Photogramm. 2022, 185, 32–47. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System; ACM: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; p. 30. [Google Scholar]
- Drucker, H.; Burges, C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Processing Syst. 1997, 9, 155–161. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Pavía, J.M.; Cantarino, I. Can Dasymetric Mapping Significantly Improve Population Data Reallocation in a Dense Urban Area? Geogr. Anal. 2017, 49, 155–174. [Google Scholar] [CrossRef]
- Dmowska, A.; Stepinski, T.F. A high resolution population grid for the conterminous United States: The 2010 edition. Comput. Environ. Urban Syst. 2017, 61, 13–23. [Google Scholar] [CrossRef]
- Zhuo, L.; Ichinose, T.; Zheng, J.; Chen, J.; Shi, P.J.; Li, X. Modelling the population density of China at the pixel level based on DMSP/OLS non-radiance-calibrated night-time light images. Int. J. Remote Sens. 2009, 30, 1003–1018. [Google Scholar] [CrossRef]
- Yang, X.; Yue, W.; Gao, D. Spatial improvement of human population distribution based on multi-sensor remote-sensing data: An input for exposure assessment. Int. J. Remote Sens. 2013, 34, 5569–5583. [Google Scholar] [CrossRef]
- Xu, Y.; Ho, H.C.; Knudby, A.; He, M. Comparative assessment of gridded population data sets for complex topography: A study of Southwest China. Popul. Environ. 2021, 42, 360–378. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating Census Data for Population Mapping Using Random Forests with Remotely-Sensed and Ancillary Data. PLoS ONE 2015, 10, e107042. [Google Scholar] [CrossRef] [Green Version]
- Strobl, C.; Boulesteix, A.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Janowicz, K.; Couclelis, H. Extracting urban functional regions from points of interest and human activities on location-based social networks. Trans. GIS 2017, 21, 446–467. [Google Scholar] [CrossRef]
- Alahmadi, M.; Atkinson, P.; Martin, D. Estimating the spatial distribution of the population of Riyadh, Saudi Arabia using remotely sensed built land cover and height data. Comput. Environ. Urban Syst. 2013, 41, 167–176. [Google Scholar] [CrossRef]
- Kuang, W.; Hou, Y.; Dou, Y.; Lu, D.; Yang, S. Mapping Global Urban Impervious Surface and Green Space Fractions Using Google Earth Engine. Remote Sens. 2021, 13, 4187. [Google Scholar] [CrossRef]
- Kuang, W.; Zhang, S.; Li, X.; Lu, D. A 30 m resolution dataset of China’s urban impervious surface area and green space, 2000–2018. Earth Syst. Sci. Data 2021, 13, 63–82. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y. Urban mapping using DMSP/OLS stable night-time light: A review. Int. J. Remote Sens. 2017, 38, 6030–6046. [Google Scholar] [CrossRef]
- Esch, T.; Marconcini, M.; Marmanis, D.; Zeidler, J.; Elsayed, S.; Metz, A.; Müller, A.; Dech, S. Dimensioning urbanization—An advanced procedure for characterizing human settlement properties and patterns using spatial network analysis. Appl. Geogr. 2014, 55, 212–228. [Google Scholar] [CrossRef]
- Ting, K.M.; Witten, I.H. Issues in Stacked Generalization. J. Artif. Intell. Res. 1999, 10, 271–289. [Google Scholar] [CrossRef] [Green Version]
- Anifowose, F.; Labadin, J.; Abdulraheem, A. Improving the prediction of petroleum reservoir characterization with a stacked generalization ensemble model of support vector machines. Appl. Soft Comput. 2015, 26, 483–496. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Optimization under uncertainty in the era of big data and deep learning: When machine learning meets mathematical programming. Comput. Chem. Eng. 2019, 125, 434–448. [Google Scholar] [CrossRef] [Green Version]
- Ou, J.; Liu, X.; Liu, P.; Liu, X. Evaluation of Luojia 1-01 nighttime light imagery for impervious surface detection: A comparison with NPP-VIIRS nighttime light data. Int. J. Appl. Earth Obs. 2019, 81, 1–12. [Google Scholar] [CrossRef]
- Zhuo, L.; Shi, Q.; Zhang, C.; Li, Q.; Tao, H. Identifying Building Functions from the Spatiotemporal Population Density and the Interactions of People among Buildings. ISPRS Int. J. Geo-Inf. 2019, 8, 247. [Google Scholar] [CrossRef] [Green Version]
- Kuang, W. 70 years of urban expansion across China: Trajectory, pattern, and national policies. Sci. Bull. 2020, 65, 1970–1974. [Google Scholar] [CrossRef]
- Kuang, W.; Du, G.; Lu, D.; Dou, Y.; Li, X.; Zhang, S.; Chi, W.; Dong, J.; Chen, G.; Yin, Z.; et al. Global observation of urban expansion and land-cover dynamics using satellite big-data. Sci. Bull. 2021, 66, 297–300. [Google Scholar] [CrossRef]
- Kuang, W.; Liu, J.; Tian, H.; Shi, H.; Dong, J.; Song, C.; Li, X.; Du, G.; Hou, Y.; Lu, D.; et al. Cropland redistribution to marginal lands undermines environmental sustainability. Natl. Sci. Rev. 2022, 9, nwab091. [Google Scholar] [CrossRef]





| Category | Datasets | Format | Time | Sources |
|---|---|---|---|---|
| Socioeconomic data | Point of interest | Vector (Point) | 2020 | AMap Services, China |
| Building outline | Vector (Polygon) | 2020 | Baidu Map Services, China | |
| Road network | Vector (Polyline) | 2020 | AMap Services, China | |
| Impervious surface | Raster (30 m) | 2020 | State Key Laboratory of Remote Sensing Science, China | |
| NPP-VIIRS nighttime light image | Raster (500 m) | 2020 | Earth Observation Group, USA | |
| Natural environmental data | River network | Vector (Polyline) | 2018 | Resource and Environment Science and Data Center, China |
| ASTER GDEM v3 | Raster (30 m) | 2019 | National Aeronautics and Space Administration, USA | |
| Population data | WorldPop | Raster (100 m) | 2020 | WorldPop Mainland China Dataset in 2020, UK |
| Census data | Table | 2020 | Beijing Government, China | |
| Community household registration data | Table | 2020 | Information Center of the Ministry of Civil Affairs, China | |
| Basic geographic data | Boundary maps | Vector (Polygon) | 2020 | Administration of Surveying Mapping and Geoinformation, China |
| Category | Quantity |
|---|---|
| Shopping | 187,906 |
| Enterprises | 107,055 |
| Auto Repair | 4565 |
| Auto Service | 16,522 |
| Auto Dealers | 3141 |
| Pass Facilities | 87,170 |
| Public Facility | 20,136 |
| Road Furniture | 2127 |
| Medical Service | 27,375 |
| Indoor Facilities | 99,498 |
| Daily Life Service | 143,195 |
| Tourist Attraction | 10,098 |
| Motorcycle Service | 1044 |
| Commercial House | 47,077 |
| Food and Beverages | 107,994 |
| Sports and Recreation | 28,495 |
| Transportation Service | 89,999 |
| Accommodation Service | 21,301 |
| Place Name and Address | 204,066 |
| Finance and Insurance Service | 15,285 |
| Science/Culture and Education Service | 63,618 |
| Governmental Organization and Social Group | 61,754 |
| Model Name | Ten-Fold Cross-Validation Performance Metrics | Global Optimal Hyperparameters | |||
|---|---|---|---|---|---|
| R2 | MAE | RMSE | |||
| GXLS-Stacking | 0.9687 | 0.2564 | 0.3639 | GBDT | max_depth: 3 max_features: 8 learning_rate: 0.2 n_estimators: 183 min_samples_split: 32 |
| XGBoost | n_estimators: 11 reg_lambda: 0.89 learning_rate: 0.38 gamma: 0.06 reg_alpha: 0.04 subsample: 0.7 max_depth: 8 | ||||
| LightGBM | max_depth: 5 subsample: 0.1 reg_lambda: 0.19 learning_rate: 0.1 n_estimators: 132 feature_fraction: 0.7 min_child_samples: 39 min_child_weight: 0.001 num_leaves: 6 reg_alpha: 0.39 | ||||
| SVR | gamma: 0.11C: 8 kernel: rbf | ||||
| GBDT | 0.9651 | 0.2722 | 0.3874 | min_samples_split: 32 max_depth: 3 n_estimators: 76 max_features: 19 learning_rate: 0.26 | |
| XGBoost | 0.9635 | 0.2824 | 0.3972 | gamma: 0.195 reg_alpha: 0 subsample: 1 max_depth: 5 reg_lambda: 1 n_estimators: 17 learning_rate: 0.3 min_child_weight: 1 | |
| LightGBM | 0.9658 | 0.2704 | 0.3836 | feature_fraction: 0.42 min_child_samples: 8 min_child_weight: 0.001 max_bin: 170 max_depth: 4 num_leaves: 6 reg_alpha: 0.04 subsample: 0.01 reg_lambda: 0.31 learning_rate: 0.1 n_estimators: 138 | |
| SVR | 0.9563 | 0.3049 | 0.4371 | gamma: 0.24 C: 5 kernel: rbf | |
| RF | 0.9643 | 0.2729 | 0.3920 | max_depth: 11 n_estimators: 30 max_features: 29 min_samples_split: 2 | |
| Model Name | Sum of All Pixels Values in Weight Layer | Census Population | Difference |
|---|---|---|---|
| GXLS-Stacking | 21,832,298 | 21,893,095 | −60,797 |
| GBDT | 25,122,462 | 3,229,367 | |
| XGBoost | 20,115,082 | −1,778,013 | |
| LightGBM | 22,480,540 | 587,445 | |
| SVR | 26,696,073 | 4,802,978 | |
| RF | 22,409,335 | 516,240 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, W.; Gong, A.; Zhao, Y.; Chen, S.; Ba, W.; He, Y. High-Precision Population Spatialization in Metropolises Based on Ensemble Learning: A Case Study of Beijing, China. Remote Sens. 2022, 14, 3654. https://doi.org/10.3390/rs14153654
Bao W, Gong A, Zhao Y, Chen S, Ba W, He Y. High-Precision Population Spatialization in Metropolises Based on Ensemble Learning: A Case Study of Beijing, China. Remote Sensing. 2022; 14(15):3654. https://doi.org/10.3390/rs14153654
Chicago/Turabian StyleBao, Wenxuan, Adu Gong, Yiran Zhao, Shuaiqiang Chen, Wanru Ba, and Yuan He. 2022. "High-Precision Population Spatialization in Metropolises Based on Ensemble Learning: A Case Study of Beijing, China" Remote Sensing 14, no. 15: 3654. https://doi.org/10.3390/rs14153654
APA StyleBao, W., Gong, A., Zhao, Y., Chen, S., Ba, W., & He, Y. (2022). High-Precision Population Spatialization in Metropolises Based on Ensemble Learning: A Case Study of Beijing, China. Remote Sensing, 14(15), 3654. https://doi.org/10.3390/rs14153654