Mapping Plant Species in a Former Industrial Site Using Airborne Hyperspectral and Time Series of Sentinel-2 Data Sets
Abstract
:1. Introduction
2. Materials
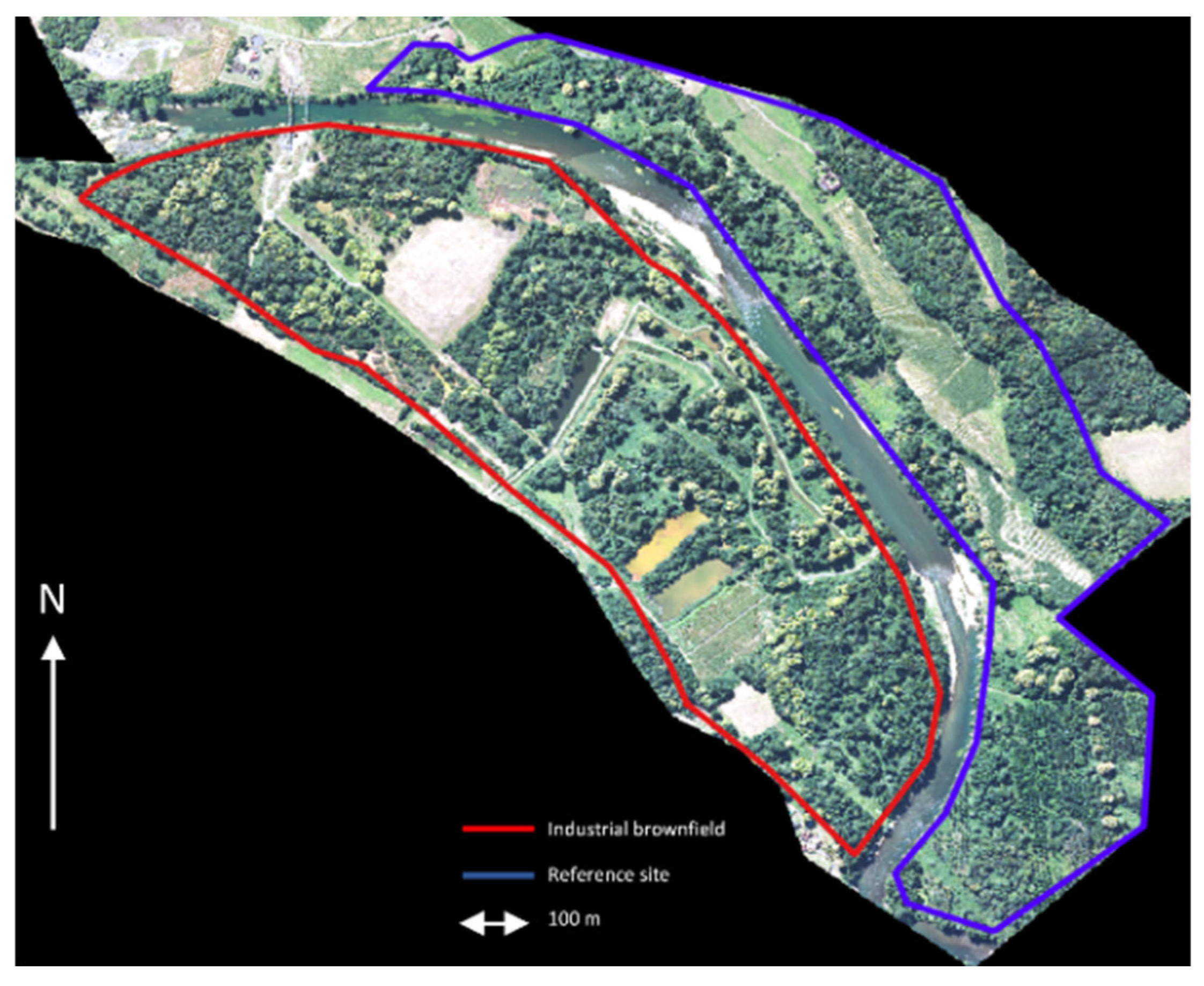
2.1. Study Site
2.2. Species Inventory
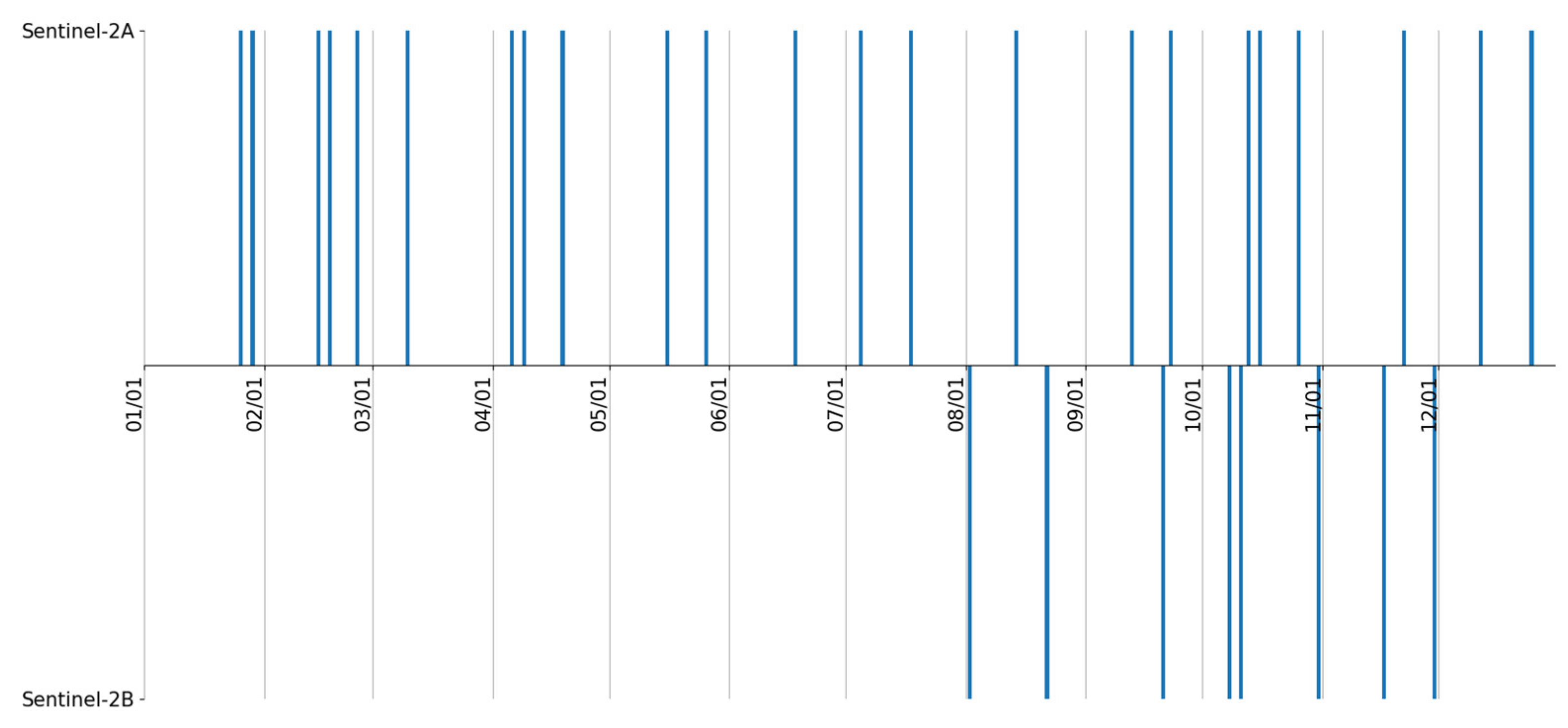
2.3. Remote Sensing Imagery
2.3.1. Hyperspectral Imagery
2.3.2. Multispectral Time Series
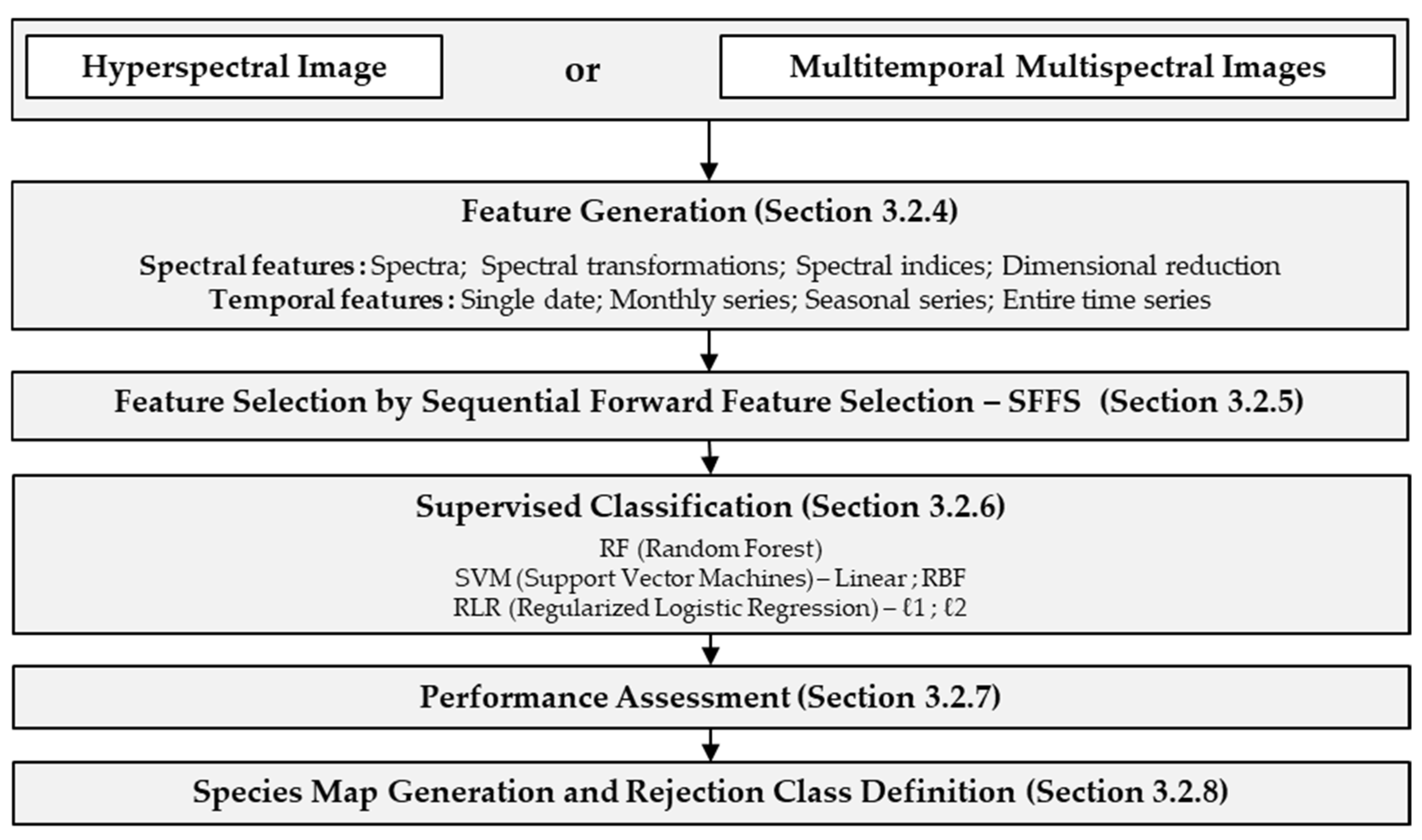
3. Method Description
3.1. Preprocessing: Non-Vegetation and Shadow Masking
3.2. Supervised Classification
3.2.1. Reference Data
3.2.2. Data Splitting Procedure
3.2.3. Classification Principle
3.2.4. Feature Generation
Spectral Features
- Reflectance spectra;
- Spectral transformations linked to absorption features [52]:
- ○
- Continuum removal;
- ○
- First derivative;
- Spectral indices related to vegetation properties and biophysical parameters [84]:
- Feature extractions [47]:
- ○
- Principal Component Analysis (PCA) [35];
- ○
- Minimal Noise Fraction (MNF), which removes the noise before applying PCA;
- ○
- Independent Component Analysis (ICA), which linearly projects the data onto a lower-dimensional space, non-orthogonal, so that the new components are as statistically independent as possible.
Temporal Features
- Monthly series: one date per month;
- Seasonal series: one date per season;
- Entire time series: all the available dates defined in Section 2.2;
- Selection of key dates by SFFS (see Section 3.2.5).
3.2.5. Feature Selection by Sequential Forward Feature Selection (SFFS)
3.2.6. Supervised Classification
Random Forest (RF)
Support Vector Machines (SVMs)
Regularized Logistic Regression (RLR)
3.2.7. Performance Assessment
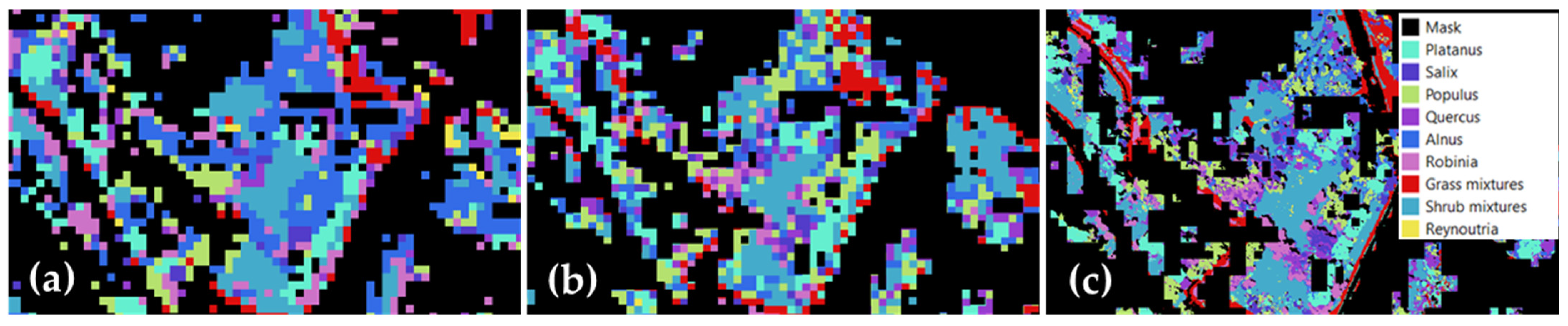
3.2.8. Species Map Generation and Rejection Class Definition
- Probability criterion: for each pixel, iterations were considered only if the differences of probability between the predicted class and the other ones were over a threshold set empirically (equal to 0.5).
- Voting criterion: the majority vote was performed. If the number of votes was under a threshold of votes (fixed empirically to 5), the pixel was rejected. Otherwise, the majority class was predicted.
3.3. Summary of Considered Scenarios
3.3.1. Classification Scenarios
Hyperspectral Classifications
Multitemporal Multispectral Classifications
3.3.2. Spatial, Spectral, and Temporal Importance Assessment
3.4. Biodiversity Assessment
- The Shannon index, based on information theory and strongly influenced by rare species [91].
- The Simpson index, which measures the probability that two individuals (here pixels) selected randomly belong to the same species and is especially sensitive to common species [91].
- Evenness metrics, such as the Pielou Equitability (ratio between Shannon index and its maximum value) and Simpson Equitability (ratio between Simpson index and its maximum value).
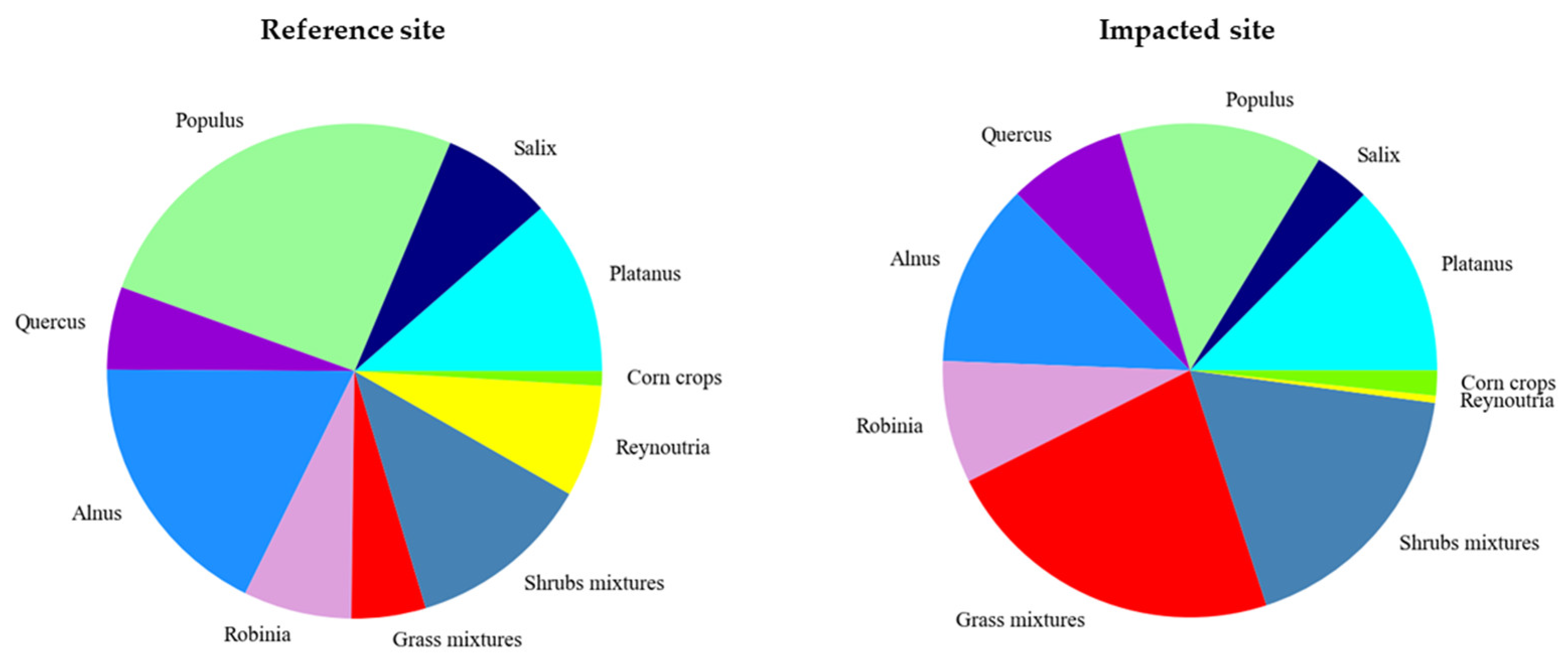
- In addition, the difference in species abundance between sites was investigated.
4. Results
4.1. Hyperspectral Classification
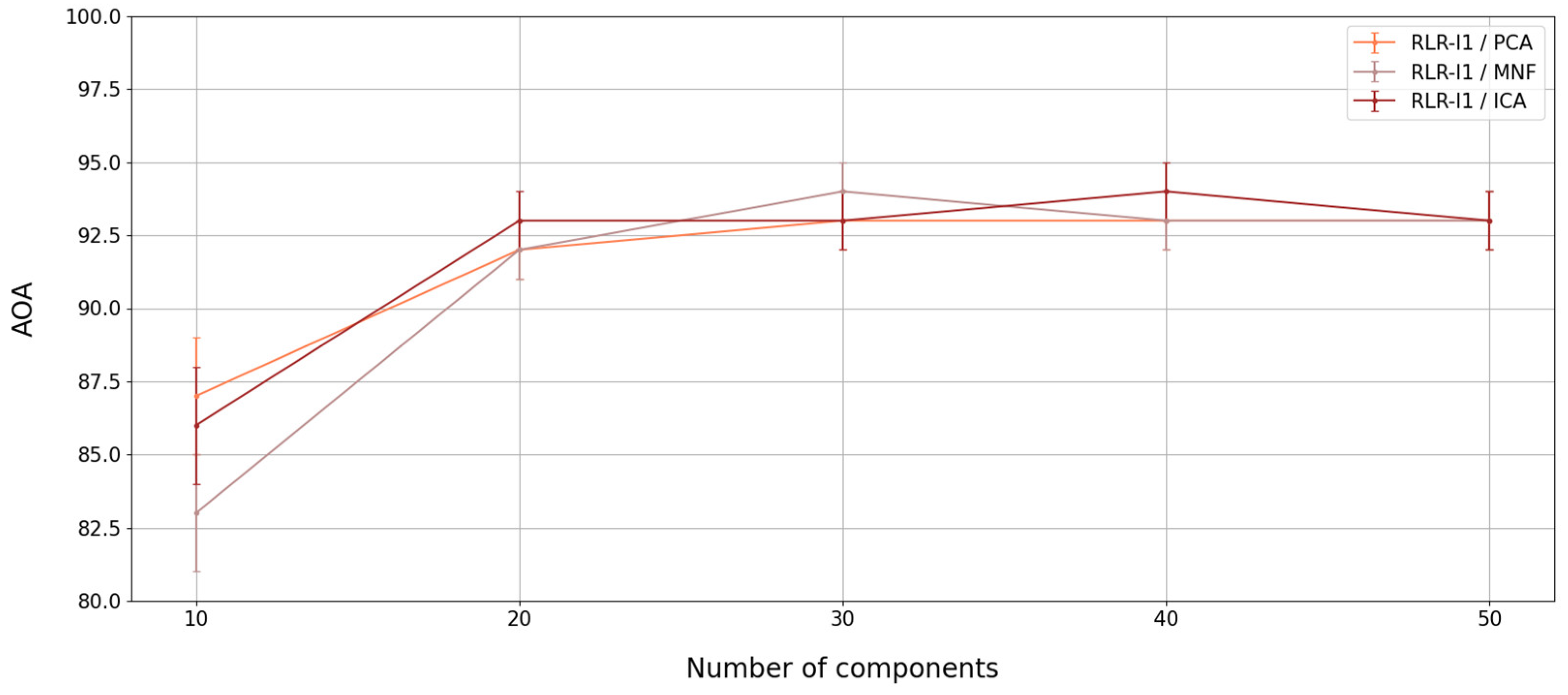
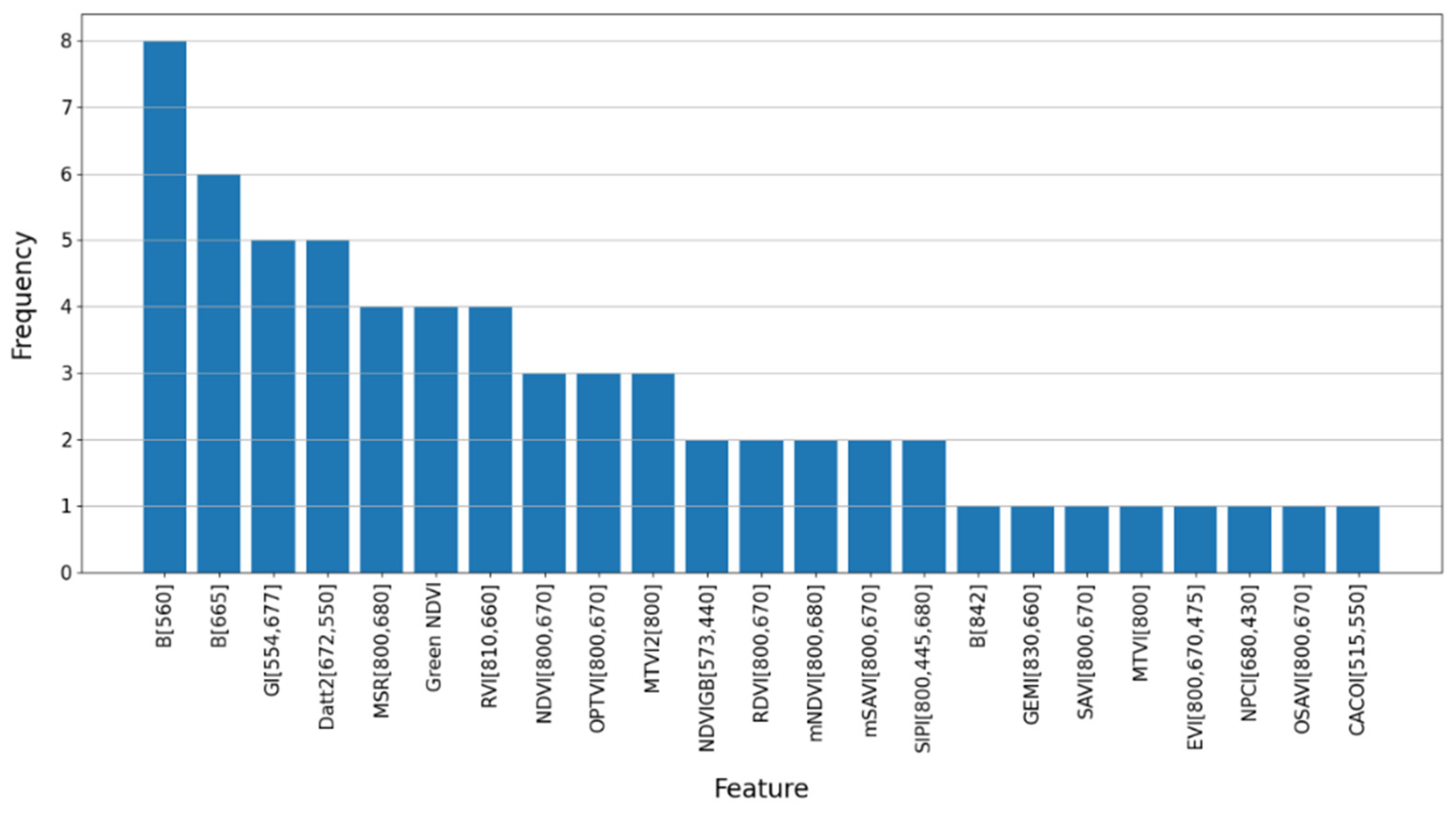
4.1.1. Feature Selection by SFFS
4.1.2. Performance Assessment
4.2. Multispectral Multitemporal Classification
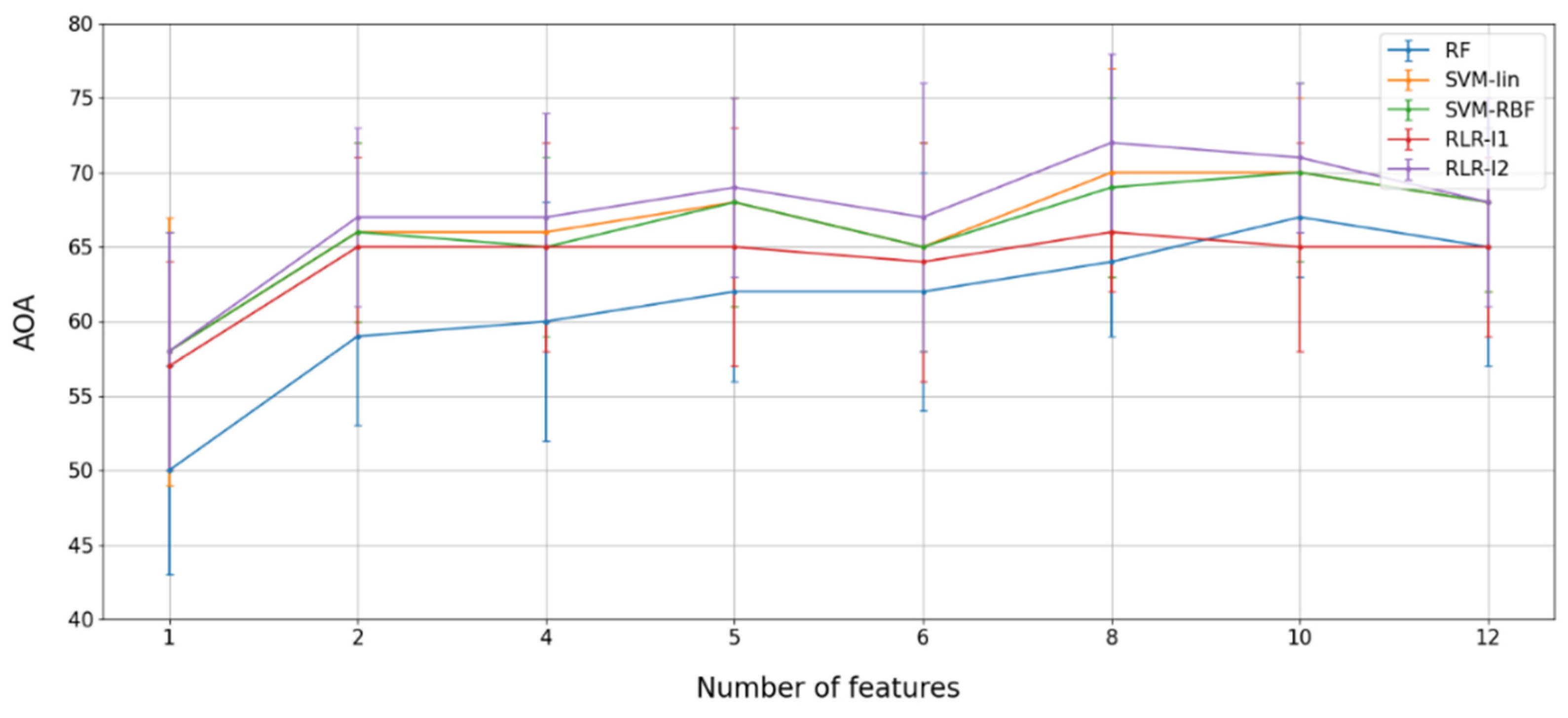
4.2.1. Feature Selection by SFFS
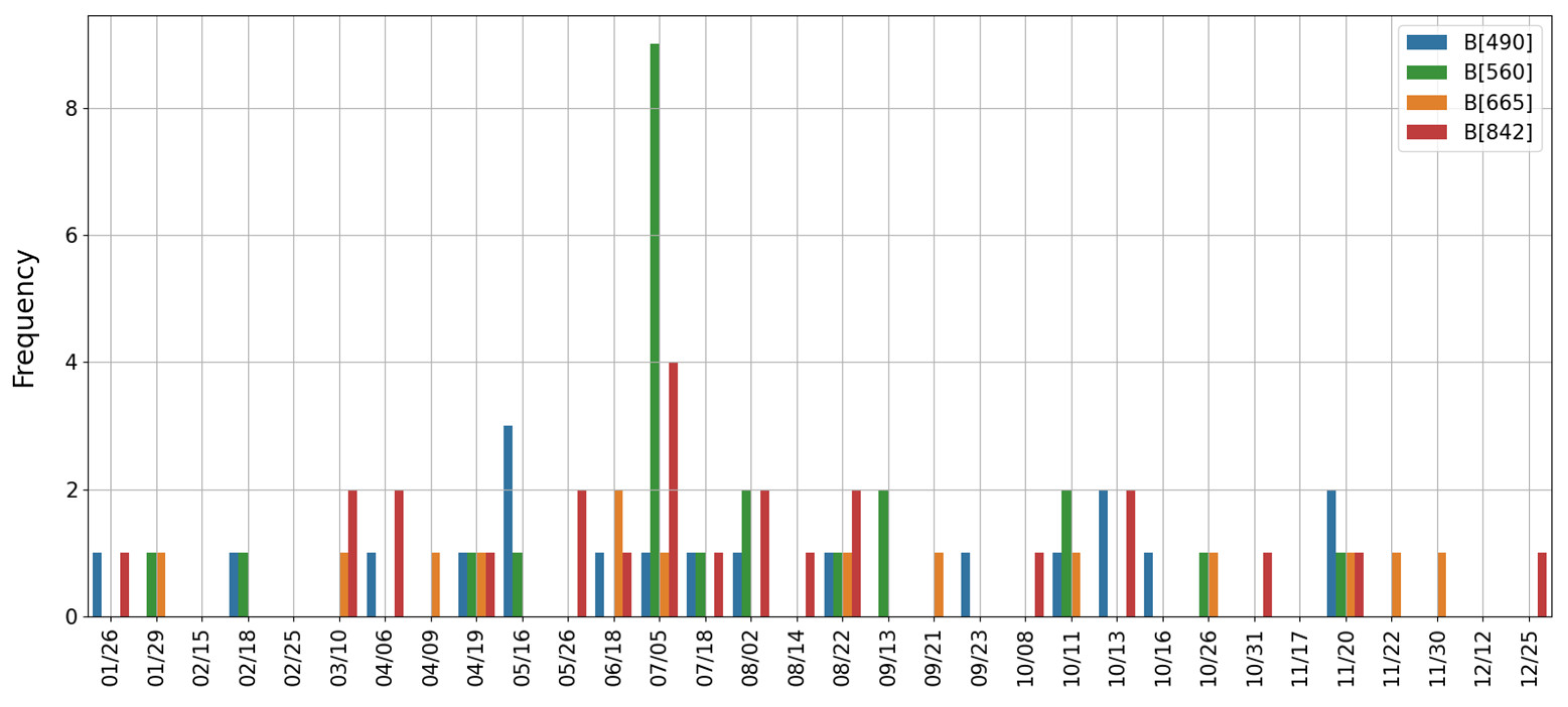
Temporal Selection
SFFS-Based Temporal Selection
4.2.2. Performance Assessment
4.3. Spatial, Spectral, and Temporal Importance Assessment
4.4. Biodiversity Assessment
5. Discussion
5.1. Supervised Classification Methodology
5.1.1. Transformations and Feature Reduction
5.1.2. Algorithm Comparison
5.1.3. Rejection Method
5.2. Classification Performance
5.2.1. Performance Comparison for Hyperspectral Image and Sentinel-2 Times Series
5.2.2. Comparison of Spectral, Spatial, and Temporal Information for Classification Improvement
5.3. Relation between Biodiversity and Anthropogenic Impacts
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ong, C.; Carrère, V.; Chabrillat, S.; Clark, R.; Hoefen, T.; Kokaly, R.; Marion, R.; Souza Filho, C.R.; Swayze, G.; Thompson, D.R. Imaging Spectroscopy for the Detection, Assessment and Monitoring of Natural and Anthropogenic Hazards. Surv. Geophys. 2019, 40, 431–470. [Google Scholar] [CrossRef] [Green Version]
- Cunningham, C.; Beazley, K.F. Changes in human population density and protected areas in terrestrial global biodiversity hotspots, 1995–2015. Land 2018, 7, 136. [Google Scholar] [CrossRef] [Green Version]
- Dietz, T.; Rosa, E.A.; York, R. Driving the human ecological footprint. Front. Ecol. Environ. 2007, 5, 13–18. [Google Scholar] [CrossRef]
- Lassalle, G. Monitoring natural and anthropogenic plant stressors by hyperspectral remote sensing: Recommendations and guidelines based on a meta-review. Sci. Total Environ. 2021, 788, 147758. [Google Scholar] [CrossRef] [PubMed]
- Holloway, J.; Mengersen, K. Statistical machine learning methods and remote sensing for sustainable development goals: A review. Remote Sens. 2018, 10, 1365. [Google Scholar] [CrossRef] [Green Version]
- Gholizadeh, A.; Kopačková, V. Detecting vegetation stress as a soil contamination proxy a review of optical proximal and remote sensing techniques. Int. J. Environ. Sci. Technol. 2019, 16, 2511–2524. [Google Scholar] [CrossRef]
- Miller, V.S.; Naeth, M.A. Hydrogel and Organic Amendments to Increase Water Retention in Anthroposols for Land Reclamation. Appl. Environ. Soil Sci. 2019, 2019, 4768091. [Google Scholar] [CrossRef]
- Obour, P.B.; Ugarte, C.M. A meta-analysis of the impact of traffic-induced compaction on soil physical properties and grain yield. Soil Tillage Res. 2021, 211, 105019. [Google Scholar] [CrossRef]
- Lwin, C.S.; Seo, B.H.; Kim, H.U.; Owens, G.; Kim, K.R. Application of soil amendments to contaminated soils for heavy metal immobilization and improved soil quality—A critical review. Soil Sci. Plant Nutr. 2018, 64, 156–167. [Google Scholar] [CrossRef]
- Lassalle, G.; Fabre, S.; Credoz, A.; Hédacq, R.; Bertoni, G.; Dubucq, D.; Elger, A. Application of PROSPECT for estimating total petroleum hydrocarbons in contaminated soils from leaf optical properties. J. Hazard. Mater. 2019, 377, 409–417. [Google Scholar] [CrossRef] [Green Version]
- Ignat, T.; De Falco, N.; Berger-Tal, R.; Rachmilevitch, S.; Karnieli, A. A novel approach for long-term spectral monitoring of desert shrubs affected by an oil spill. Environ. Pollut. 2021, 289, 117788. [Google Scholar] [CrossRef]
- Pérez-Hernández, I.; Ochoa-Gaona, S.; Adams, R.H.; Rivera-Cruz, M.C.; Pérez-Hernández, V.; Jarquín-Sánchez, A.; Geissen, V.; Martínez-Zurimendi, P. Growth of four tropical tree species in petroleum-contaminated soil and effects of crude oil contamination. Environ. Sci. Pollut. Res. 2017, 24, 1769–1783. [Google Scholar] [CrossRef]
- Matsodoum Nguemté, P.; Djumyom Wafo, G.V.; Djocgoue, P.F.; Kengne Noumsi, I.M.; Wanko Ngnien, A. Potentialities of Six Plant Species on Phytoremediation Attempts of Fuel Oil-Contaminated Soils. Water. Air. Soil Pollut. 2018, 229, 88. [Google Scholar] [CrossRef]
- Pérez-Hernández, I.; Ochoa-Gaona, S.; Adams Schroeder, R.H.; Rivera-Cruz, M.C.; Geissen, V. Tolerance of four tropical tree species to heavy petroleum contamination. Water. Air. Soil Pollut. 2013, 224, 1637. [Google Scholar] [CrossRef]
- Rola, K.; Osyczka, P.; Nobis, M.; Drozd, P. How do soil factors determine vegetation structure and species richness in post-smelting dumps? Ecol. Eng. 2015, 75, 332–342. [Google Scholar] [CrossRef]
- Válega, M.; Lillebø, A.I.; Pereira, M.E.; Duarte, A.C.; Pardal, M.A. Long-term effects of mercury in a salt marsh: Hysteresis in the distribution of vegetation following recovery from contamination. Chemosphere 2008, 71, 765–772. [Google Scholar] [CrossRef] [Green Version]
- Anawar, H.M.; Canha, N.; Santa-Regina, I.; Freitas, M.C. Adaptation, tolerance, and evolution of plant species in a pyrite mine in response to contamination level and properties of mine tailings: Sustainable rehabilitation. J. Soils Sediments 2013, 13, 730–741. [Google Scholar] [CrossRef]
- Onyia, N.N.; Balzter, H.; Berrio, J.C. Spectral diversity metrics for detecting oil pollution effect on biodiversity in the niger delta. Remote Sens. 2019, 11, 2662. [Google Scholar] [CrossRef] [Green Version]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef] [Green Version]
- Misra, G.; Cawkwell, F.; Wingler, A. Status of phenological research using sentinel-2 data: A review. Remote Sens. 2020, 12, 2760. [Google Scholar] [CrossRef]
- Transon, J.; d’Andrimont, R.; Maugnard, A.; Defourny, P. Survey of hyperspectral Earth Observation applications from space in the Sentinel-2 context. Remote Sens. 2018, 10, 157. [Google Scholar] [CrossRef] [Green Version]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced Spectral Classifiers for Hyperspectral Images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liu, M.; Liu, X.; Zhou, G. A new vegetation index based on multitemporal sentinel-2 images for discriminating heavy metal stress levels in rice. Sensors 2018, 18, 2172. [Google Scholar] [CrossRef] [Green Version]
- Lassalle, G.; Elger, A.; Credoz, A.; H’dacq, R.; Bertoni, G.; Dubucq, D.; Fabre, S. Toward quantifying oil contamination in vegetated areas using very high spatial and spectral resolution imagery. Remote Sens. 2019, 11, 2241. [Google Scholar] [CrossRef] [Green Version]
- Adamu, B.; Tansey, K.; Bradshaw, M.J. Investigating vegetation spectral reflectance for detecting hydrocarbon pipeline leaks from multispectral data. Image Signal Process. Remote Sens. XIX 2013, 8892, 889216. [Google Scholar] [CrossRef]
- Onyia, N.N.; Balzter, H.; Berrio, J.C. Detecting vegetation response to oil pollution using hyperspectral indices. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3963–3966. [Google Scholar] [CrossRef]
- Asri, N.A.M.; Sakidin, H.; Othman, M.; Matori, A.N.; Ahmad, A. Analysis of the hydrocarbon seepage detection in oil palm vegetation stress using unmanned aerial vehicle (UAV) multispectral data. AIP Conf. Proc. 2020, 2266, 050007. [Google Scholar] [CrossRef]
- Cochrane, M.A. Using vegetation reflectance variability for species level classification of hyperspectral data. Int. J. Remote Sens. 2000, 21, 2075–2087. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Coops, N.C.; Neinavaz, E.; Ali, A.; Schaepman, M.E.; Paganini, M.; Kissling, W.D.; Vihervaara, P.; Darvishzadeh, R.; Feilhauer, H.; et al. Priority list of biodiversity metrics to observe from space. Nat. Ecol. Evol. 2021, 5, 896–906. [Google Scholar] [CrossRef] [PubMed]
- Rocchini, D.; Hernández-Stefanoni, J.L.; He, K.S. Advancing species diversity estimate by remotely sensed proxies: A conceptual review. Ecol. Inform. 2015, 25, 22–28. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Müllerová, J.; Conti, L.; Malavasi, M.; Schmidtlein, S. About the link between biodiversity and spectral variation. Appl. Veg. Sci. 2022, 25, e12643. [Google Scholar] [CrossRef]
- Dian, Y.; Li, Z.; Pang, Y. Spectral and Texture Features Combined for Forest Tree species Classification with Airborne Hyperspectral Imagery. J. Indian Soc. Remote Sens. 2015, 43, 101–107. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Forster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of feature reduction algorithms for classifying tree species with hyperspectral data on three central european test sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Dabiri, Z.; Lang, S. Comparison of independent component analysis, principal component analysis, and minimum noise fraction transformation for tree species classification using APEX hyperspectral imagery. ISPRS Int. J. Geo-Inf. 2018, 7, 488. [Google Scholar] [CrossRef] [Green Version]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Dalponte, M.; Ørka, H.O.; Gobakken, T.; Gianelle, D.; Næsset, E. Tree species classification in boreal forests with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
- Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree species classification using hyperspectral imagery: A comparison of two classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; de Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Burai, P.; Deák, B.; Valkó, O.; Tomor, T. Classification of herbaceous vegetation using airborne hyperspectral imagery. Remote Sens. 2015, 7, 2046–2066. [Google Scholar] [CrossRef] [Green Version]
- Burai, P.; Lövei, G.; Lénárt, C.; Nagy, I.; Enyedi, E. Mapping aquatic vegetation of the Rakamaz-Tiszanagyfalui Nagy-Morotva using hyperspectral imagery. Landsc. Environ. 2010, 4, 1–10. [Google Scholar]
- Hill, R.A.; Wilson, A.K.; George, M.; Hinsley, S.A. Mapping tree species in temperate deciduous woodland using time-series multi-spectral data. Appl. Veg. Sci. 2010, 13, 86–99. [Google Scholar] [CrossRef]
- Guidici, D.; Clark, M.L. One-dimensional convolutional neural network land-cover classification of multi-seasonal hyperspectral imagery in the San Francisco Bay Area, California. Remote Sens. 2017, 9, 629. [Google Scholar] [CrossRef] [Green Version]
- Clark, M.L.; Buck-Diaz, J.; Evens, J. Mapping of forest alliances with simulated multi-seasonal hyperspectral satellite imagery. Remote Sens. Environ. 2018, 210, 490–507. [Google Scholar] [CrossRef]
- Grigorieva, O.; Brovkina, O.; Saidov, A. An original method for tree species classification using multitemporal multispectral and hyperspectral satellite data. Silva Fenn. 2020, 54, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine learning based hyperspectral image analysis: A survey. arXiv 2018, arXiv:1802.08701v2. [Google Scholar]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Zhang, J.; Rivard, B.; Sánchez-Azofeifa, A.; Castro-Esau, K. Intra- and inter-class spectral variability of tropical tree species at La Selva, Costa Rica: Implications for species identification using HYDICE imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Kochb, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Lim, J.; Kim, K.M.; Jin, R. Tree species classification using hyperion and sentinel-2 data with machine learning in South Korea and China. ISPRS Int. J. Geo-Inf. 2019, 8, 150. [Google Scholar] [CrossRef] [Green Version]
- Erudel, T.; Fabre, S.; Houet, T.; Mazier, F.; Briottet, X. Criteria Comparison for Classifying Peatland Vegetation Types Using In Situ Hyperspectral Measurements. Remote Sens. 2017, 9, 748. [Google Scholar] [CrossRef] [Green Version]
- Macintyre, P.; van Niekerk, A.; Mucina, L. Efficacy of multi-season Sentinel-2 imagery for compositional vegetation classification. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101980. [Google Scholar] [CrossRef]
- Hennessy, A.; Clarke, K.; Lewis, M. Hyperspectral Classification of Plants: A Review of Waveband Selection Generalisability. Remote Sens. 2020, 12, 113. [Google Scholar] [CrossRef] [Green Version]
- Ghiyamat, A.; Shafri, H.Z.M.; Mahdiraji, G.A.; Shariff, A.R.M.; Mansor, S. Hyperspectral discrimination of tree species with different classifications using single- and multiple-endmember. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 177–191. [Google Scholar] [CrossRef]
- Hughes, G.F. On the Mean Accuracy of Statistical Pattern Recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef] [Green Version]
- Hameed, S.S.; Petinrin, O.O.; Hashi, A.O.; Saeed, F. Filter-wrapper combination and embedded feature selection for gene expression data. Int. J. Adv. Soft Comput. Its Appl. 2018, 10, 90–105. [Google Scholar]
- Dumont, J.; Hirvonen, T.; Heikkinen, V.; Mistretta, M.; Granlund, L.; Himanen, K.; Fauch, L.; Porali, I.; Hiltunen, J.; Keski-Saari, S.; et al. Thermal and hyperspectral imaging for Norway spruce (Picea abies) seeds screening. Comput. Electron. Agric. 2015, 116, 118–124. [Google Scholar] [CrossRef]
- Pant, P.; Heikkinen, V.; Korpela, I.; Hauta-Kasari, M.; Tokola, T. Logistic regression-based spectral band selection for tree species classification: Effects of spatial scale and balance in training samples. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1604–1608. [Google Scholar] [CrossRef]
- Gimenez, R.; Lassalle, G.; Hédacq, R.; Elger, A.; Dubucq, D.; Credoz, A.; Jennet, C.; Fabre, S. Exploitation of Spectral and Temporal Information for Mapping Plant Species in a Former Industrial Site. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLIII-B3-2, 559–566. [Google Scholar] [CrossRef]
- Torabzadeh, H.; Leiterer, R.; Hueni, A.; Schaepman, M.E.; Morsdorf, F. Tree species classification in a temperate mixed forest using a combination of imaging spectroscopy and airborne laser scanning. Agric. For. Meteorol. 2019, 279, 107744. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z. Object-based vegetation mapping in the kissimmee river watershed using hymap data and machine learning techniques. Wetlands 2013, 33, 233–244. [Google Scholar] [CrossRef]
- Hycza, T.; Stereńczak, K.; Bałazy, R. Potential use of hyperspectral data to classify forest tree species. N. Z. J. For. Sci. 2018, 48, 18. [Google Scholar] [CrossRef]
- Condessa, F.; Bioucas-Dias, J.; Kovacevic, J. Supervised hyperspectral image classification with rejection. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2600–2603. [Google Scholar] [CrossRef]
- Aval, J. Automatic Mapping of Urban Tree Species Based on Multi-Source Remotely Sensed Data. Ph.D. Thesis, Université de Toulouse, Toulouse, France, 2018. [Google Scholar]
- Lassalle, G.; Fabre, S.; Credoz, A.; Hédacq, R.; Dubucq, D.; Elger, A. Mapping leaf metal content over industrial brownfields using airborne hyperspectral imaging and optimized vegetation indices. Sci. Rep. 2021, 11, 2. [Google Scholar] [CrossRef]
- BD ORTHO® IGN Website. Available online: https://geoservices.ign.fr/bdortho (accessed on 2 February 2022).
- Brigot, G.; Colin-Koeniguer, E.; Plyer, A.; Janez, F. Adaptation and Evaluation of an Optical Flow Method Applied to Coregistration of Forest Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2923–2939. [Google Scholar] [CrossRef] [Green Version]
- Theia. Produits à Valeur Ajoutée et al. Gorithmes pour les Surfaces Continentales. Available online: https://www.theia-land.fr/ (accessed on 13 January 2022).
- Fabre, S.; Gimenez, R.; Elger, A.; Rivière, T. Unsupervised Monitoring Vegetation after the Closure of an ore Processing Site with Multi-temporal Optical Remote Sensing. Sensors 2020, 20, 4800. [Google Scholar] [CrossRef]
- Waqar, M.M.; Mirza, J.F.; Mumtaz, R.; Hussain, E. Development of new indices for extraction of built-up area & bare soil from landsat data. Open Access Sci. Rep. 2012, 1, 4. [Google Scholar]
- Valdiviezo-N, J.C.; Téllez-Quiñones, A.; Salazar-Garibay, A.; López-Caloca, A.A. Built-up index methods and their applications for urban extraction from Sentinel 2A satellite data: Discussion. JOSA A 2018, 35, 35–44. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Ling, F.; Wang, Q.; Li, W.; Li, X. Water bodies’ mapping from Sentinel-2 imagery with Modified Normalized Difference Water Index at 10-m spatial resolution produced by sharpening the swir band. Remote Sens. 2016, 8, 354. [Google Scholar] [CrossRef] [Green Version]
- Rasul, A.; Balzter, H.; Ibrahim, G.R.F.; Hameed, H.M.; Wheeler, J.; Adamu, B.; Ibrahim, S.; Najmaddin, P.M. Applying built-up and bare-soil indices from Landsat 8 to cities in dry climates. Land 2018, 7, 81. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Pearson, R.L.; Miller, L.D. Remote mapping of standing crop biomass for estimation of the productivity of the shortgrass prairie. In Proceedings of the Eighth International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 2–6 October 1972; Willow Run Laboratories, Environmental Research Institute of Michigan: Ann Arbor, MI, USA, 1972; p. 1355. [Google Scholar]
- Nagao, M.; Matsuyama, T.; Ikeda, Y. Region extraction and shape analysis in aerial photographs. Comput. Graph. Image Process. 1979, 10, 195–223. [Google Scholar] [CrossRef]
- Smith, P.; Reid, D.B.; Environment, C.; Palo, L.; Alto, P.; Smith, P.L. NOBUYUKI OTSU.-1979-A Tlreshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 20, 62–66. [Google Scholar]
- Vluymans, S. Learning from imbalanced data. Stud. Comput. Intell. 2019, 807, 81–110. [Google Scholar] [CrossRef]
- Baldeck, C.A.; Asner, G.P. Improving remote species identification through efficient training data collection. Remote Sens. 2014, 6, 2682–2698. [Google Scholar] [CrossRef] [Green Version]
- Karasiak, N.; Dejoux, J.F.; Monteil, C.; Sheeren, D. Spatial dependence between training and test sets: Another pitfall of classification accuracy assessment in remote sensing. Mach. Learn. 2022, 111, 2715–2740. [Google Scholar] [CrossRef]
- Karasiak, N.; Dejoux, J.F.; Fauvel, M.; Willm, J.; Monteil, C.; Sheeren, D. Statistical stability and spatial instability in mapping forest tree species by comparing 9 years of satellite image time series. Remote Sens. 2019, 11, 2512. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef] [Green Version]
- Erudel, T. Caractérisation de la Biodiversité Végétale et des Impacts Anthropiques en Milieu Montagneux par Télédétection: Apport des Données Aéroportées à Très haute Résolution Spatiale et Spectrale. Ph.D. Thesis, Onera-Geode Labex DRIIHM, Toulouse, France, 2018. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; Volume 1, p. 2. [Google Scholar]
- Stehman, S.V.; Czaplewski, R.L. Design and Analysis for Thematic Map Accuracy Assessment—An application of satellite imagery. Remote Sens. Environ. 1998, 64, 331–344. [Google Scholar] [CrossRef]
- Peet, R.K. The measurement of species diversity. Annu. Rev. Ecol. Syst. 1974, 5, 285–307. [Google Scholar] [CrossRef]
- Fedor, P.; Zvaríková, M. Biodiversity indices. Encycl. Ecol. 2019, 2, 337–346. [Google Scholar]
- Wang, R.; Gamon, J.A.; Cavender-Bares, J.; Townsend, P.A.; Zygielbaum, A.I. The spatial sensitivity of the spectral diversity-biodiversity relationship: An experimental test in a prairie grassland. Ecol. Appl. 2018, 28, 541–556. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Huang, J.; Ao, Z.; Lao, D.; Xin, Q. Deep learning approaches for the mapping of tree species diversity in a tropical wetland using airborne LiDAR and high-spatial-resolution remote sensing images. Forests 2019, 10, 1047. [Google Scholar] [CrossRef] [Green Version]
- Cui, L.; Zuo, X.; Dou, Z.; Huang, Y.; Zhao, X.; Zhai, X.; Lei, Y.; Li, J.; Pan, X.; Li, W. Plant identification of Beijing Hanshiqiao wetland based on hyperspectral data. Spectrosc. Lett. 2021, 54, 381–394. [Google Scholar] [CrossRef]
- Immitzer, M.; Neuwirth, M.; Böck, S.; Brenner, H.; Vuolo, F.; Atzberger, C. Optimal input features for tree species classification in Central Europe based on multi-temporal Sentinel-2 data. Remote Sens. 2019, 11, 2599. [Google Scholar] [CrossRef] [Green Version]
- Grabska, E.; Hostert, P.; Pflugmacher, D.; Ostapowicz, K. Forest stand species mapping using the sentinel-2 time series. Remote Sens. 2019, 11, 1197. [Google Scholar] [CrossRef] [Green Version]
- Koerich, A.L. Rejection strategies for handwritten word recognition. In Proceedings of the Ninth International Workshop on Frontiers in Handwriting Recognition, Kokubunji, Japan, 26–29 October 2004; pp. 479–484. [Google Scholar] [CrossRef] [Green Version]
- Denisova, A.; Kavelenova, L.; Korchikov, E.; Prokhorova, N.; Terentyeva, D.; Fedoseev, V. Tree species classification for clarification of forest inventory data using Sentinel-2 images. In Proceedings of the Seventh International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2019), Paphos, Cyprus, 18–21 March 2019; Volume 1117408, p. 3. [Google Scholar] [CrossRef]
- Bolyn, C.; Michez, A.; Gaucher, P.; Lejeune, P.; Bonnet, S. Forest mapping and species composition using supervised per pixel classification of Sentinel-2 imagery. Biotechnol. Agron. Soc. Environ. 2018, 22, 16. [Google Scholar] [CrossRef]
- Persson, M.; Lindberg, E.; Reese, H. Tree species classification with multi-temporal Sentinel-2 data. Remote Sens. 2018, 10, 1794. [Google Scholar] [CrossRef] [Green Version]
- Kluczek, M.; Zagajewski, B.; Kycko, M. Airborne HySpex Hyperspectral Versus Multitemporal Sentinel-2 Images for Mountain Plant Communities Mapping. Remote Sens. 2022, 14, 1209. [Google Scholar] [CrossRef]
- Clark, M.L. Comparison of multi-seasonal Landsat 8, Sentinel-2 and hyperspectral images for mapping forest alliances in Northern California. ISPRS J. Photogramm. Remote Sens. 2020, 159, 26–40. [Google Scholar] [CrossRef]
- Briottet, X.; Asner, G.P.; Bajjouk, T.; Carrère, V.; Chabrillat, S.; Chami, M.; Chanussot, J.; Dekker, A.; Delacourt, C.; Feret, J.-B. European hyperspectral explorer: Hypex-2. Monitoring anthropogenic influences in critical zones. In Proceedings of the 10. EARSeL SIG Imaging Spectroscopy Workshop, Zurich, Switzerland, 19–21 April 2017. 11p. [Google Scholar]
- Briottet, X.; Marion, R.; Carrere, V.; Jacquemoud, S.; Chevrel, S.; Prastault, P.; D’oria, M.; Gilouppe, P.; Hosford, S.; Lubac, B. HYPXIM: A new hyperspectral sensor combining science/defence applications. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Galeazzi, C.; Sacchetti, A.; Cisbani, A.; Babini, G. The PRISMA program. In Proceedings of the IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 4, pp. IV-105–IV-108. [Google Scholar]
- Stuffler, T.; Kaufmann, C.; Hofer, S.; Förster, K.P.; Schreier, G.; Mueller, A.; Eckardt, A.; Bach, H.; Penné, B.; Benz, U. The EnMAP hyperspectral imager—An advanced optical payload for future applications in Earth observation programmes. Acta Astronaut. 2007, 61, 115–120. [Google Scholar] [CrossRef]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the NASA Hyperspectral InfraRed Imager (HyspIRI) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Ibrahimpašić, J.; Jogić, V.; Toromanović, M.; Džaferović, A.; Makić, H.; Dedić, S. Japanese Knotweed (Reynoutria japonica) as a Phytoremediator of Heavy Metals. J. Agric. Food Environ. Sci. 2020, 74, 45–53. [Google Scholar] [CrossRef]
- Steingräber, L.F.; Ludolphy, C.; Metz, J.; Germershausen, L.; Kierdorf, H.; Kierdorf, U. Heavy metal concentrations in floodplain soils of the Innerste River and in leaves of wild blackberries (Rubus fruticosus L. agg.) growing within and outside the floodplain: The legacy of historical mining activities in the Harz Mountains (Germany). Environ. Sci. Pollut. Res. 2022, 29, 22469–22482. [Google Scholar] [CrossRef]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M.; et al. Remotely sensed spectral heterogeneity as a proxy of species diversity: Recent advances and open challenges. Ecol. Inform. 2010, 5, 318–329. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Gamon, J.A.; Zygielbaum, A.I.; Wang, R.; Schweiger, A.K.; Cavender-Bares, J. Remote sensing of biodiversity: Soil correction and data dimension reduction methods improve assessment of α-diversity (species richness) in prairie ecosystems. Remote Sens. Environ. 2018, 206, 240–253. [Google Scholar] [CrossRef]
- Knauer, U.; von Rekowski, C.S.; Stecklina, M.; Krokotsch, T.; Minh, T.P.; Hauffe, V.; Kilias, D.; Ehrhardt, I.; Sagischewski, H.; Chmara, S.; et al. Tree species classification based on hybrid ensembles of a convolutional neural network (CNN) and random forest classifiers. Remote Sens. 2019, 11, 2788. [Google Scholar] [CrossRef] [Green Version]







| Genus/Assemblage of Genera | Species | Tree Crowns or Sample Units (Sample Unit: Homogeneous Area Manually Delineated) (n) |
|---|---|---|
| Platanus | sp. | 28 |
| Salix | cinerea, babylonica | 42 |
| Populus | nigra, alba | 35 |
| Quercus | pubescens, robur | 37 |
| Fraxinus | excelsior | 17 |
| Acer | campestre | 7 |
| Alnus | glutinosa | 61 |
| Ulmus | minor | 5 |
| Robinia | pseudoacacia | 46 |
| Castanea | sativa. | 1 |
| Juglans | nigra, regia | 3 |
| Corylus | avellana | 18 |
| Reynoutria | japonica | 21 |
| Shrub mixtures | Rubus fruticosus, Cornus sanguinea, Buddleja davidii | 30 |
| Grass mixtures | Mix of various grasses and dicots | 15 |
| Genus/Assemblage of Genera | HySpex Image | Sentinel-2 VNIR |
|---|---|---|
| Platanus * | 4183 | 21 |
| Salix * | 1512 | 21 |
| Populus * | 2251 | 22 |
| Quercus * | 2936 | 20 |
| Fraxinus | 931 | 9 |
| Acer | 403 | 0 |
| Alnus * | 1588 | 20 |
| Ulmus | 305 | 0 |
| Robinia * | 1536 | 20 |
| Castanea | 107 | 0 |
| Juglans | 140 | 0 |
| Corylus | 40 | 0 |
| Reynoutria * | 1533 | 22 |
| Shrub mixtures * | 1944 | 19 |
| Feature Combination Selected by SFFS | Spectral Feature |
|---|---|
| Spectral reflectance | Spectral reflectance |
| +Spectral indices | First derivative |
| Continuum removal | |
| +PCA components | PCA components |
| +MNF components | MNF components |
| +ICA components | ICA components |
| Feature Combination Selected by SFFS | Spectral Feature |
|---|---|
| Spectral reflectance + Spectral indices | Spectral reflectance |
| First derivative | |
| Continuum removal | |
| PCA components | |
| MNF components | |
| ICA components |
| Spatial Resolution | 10-m | 1-m | ||
| Spectral Resolution | VNIR (HS) | VNIR + SWIR (HS) | VNIR (HS) | VNIR (S2) |
| Algorithm | Reflectance Spectra | First Derivative | Continuum Removal |
|---|---|---|---|
| RF | 83 ± 2% | 89 ± 1% | 83 ± 3% |
| SVM—linear | 93 ± 1% | 90 ± 1% | 86 ± 4% |
| SVM—RBF | 93 ± 1% | 89 ± 2% | 85 ± 4% |
| RLR—ℓ1 | 94 ± 1% | 91 ± 2% | 90 ± 2% |
| RLR—ℓ2 | 93 ± 1% | 90 ± 2% | 88 ± 3% |
| Algorithm | Seasonal 4 Dates | Monthly 12 Dates | All Dates 32 Dates | SFFS Selection 11 Dates |
|---|---|---|---|---|
| RF | 56 ± 8% | 59 ± 5% | 61 ± 6% | 60 ± 6% |
| SVM—linear | 58 ± 8% | 62 ± 6% | 67 ± 6% | 64 ± 5% |
| SVM—RBF | 57 ± 9% | 62 ± 4% | 64 ± 6% | 67 ± 5% |
| RLR—ℓ1 | 58 ± 5% | 61 ± 6% | 66 ± 6% | 61 ± 6% |
| RLR—ℓ2 | 59 ± 5% | 64 ± 4% | 67 ± 5% | 64 ± 4% |
| Sentinel-2 Time Series | Simulated Sentinel-2 VNIR Bands Derived from HS Image | Spatial Resampled HS Image | HS Image | |||
|---|---|---|---|---|---|---|
| Algorithm | MS VNIR (All Dates) | HS 4-Bands VNIR 1 m | HS VNIR 10 m | HS VNIR SWIR 10 m | HS VNIR 1 m | HS VNIR SWIR 1 m |
| RF | 61 ± 6% | 72 ± 2% | 51 ±5% | 50 ± 6% | 80 ± 3% | 83 ± 2% |
| SVM—linear | 67 ± 6% | 68 ± 3% | 61 ± 8% | 62 ± 6% | 91 ± 1% | 93 ± 1% |
| SVM—RBF | 64 ± 4% | 70 ± 3% | 60 ± 6% | 60 ± 4% | 91 ± 1% | 93 ± 1% |
| RLR—ℓ1 | 66 ± 6% | 64 ± 3% | 69 ± 5% | 74 ± 4% | 93 ± 1% | 94 ± 1% |
| RLR—ℓ2 | 67 ± 5% | 65 ± 2% | 64 ± 10% | 64 ± 11% | 91 ± 2% | 93 ± 1% |
| Shannon | Simpson | Pielou Equitability | Simpson Equitability | |
|---|---|---|---|---|
| Reference site | 3.0 | 0.15 | 0.90 | 0.94 |
| Impacted site | 2.95 | 0.14 | 0.89 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gimenez, R.; Lassalle, G.; Elger, A.; Dubucq, D.; Credoz, A.; Fabre, S. Mapping Plant Species in a Former Industrial Site Using Airborne Hyperspectral and Time Series of Sentinel-2 Data Sets. Remote Sens. 2022, 14, 3633. https://doi.org/10.3390/rs14153633
Gimenez R, Lassalle G, Elger A, Dubucq D, Credoz A, Fabre S. Mapping Plant Species in a Former Industrial Site Using Airborne Hyperspectral and Time Series of Sentinel-2 Data Sets. Remote Sensing. 2022; 14(15):3633. https://doi.org/10.3390/rs14153633
Chicago/Turabian StyleGimenez, Rollin, Guillaume Lassalle, Arnaud Elger, Dominique Dubucq, Anthony Credoz, and Sophie Fabre. 2022. "Mapping Plant Species in a Former Industrial Site Using Airborne Hyperspectral and Time Series of Sentinel-2 Data Sets" Remote Sensing 14, no. 15: 3633. https://doi.org/10.3390/rs14153633
APA StyleGimenez, R., Lassalle, G., Elger, A., Dubucq, D., Credoz, A., & Fabre, S. (2022). Mapping Plant Species in a Former Industrial Site Using Airborne Hyperspectral and Time Series of Sentinel-2 Data Sets. Remote Sensing, 14(15), 3633. https://doi.org/10.3390/rs14153633






