Total Carbon Content Assessed by UAS Near-Infrared Imagery as a New Fire Severity Metric
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Sample Collection
2.2. Sample Treatments and Measurements
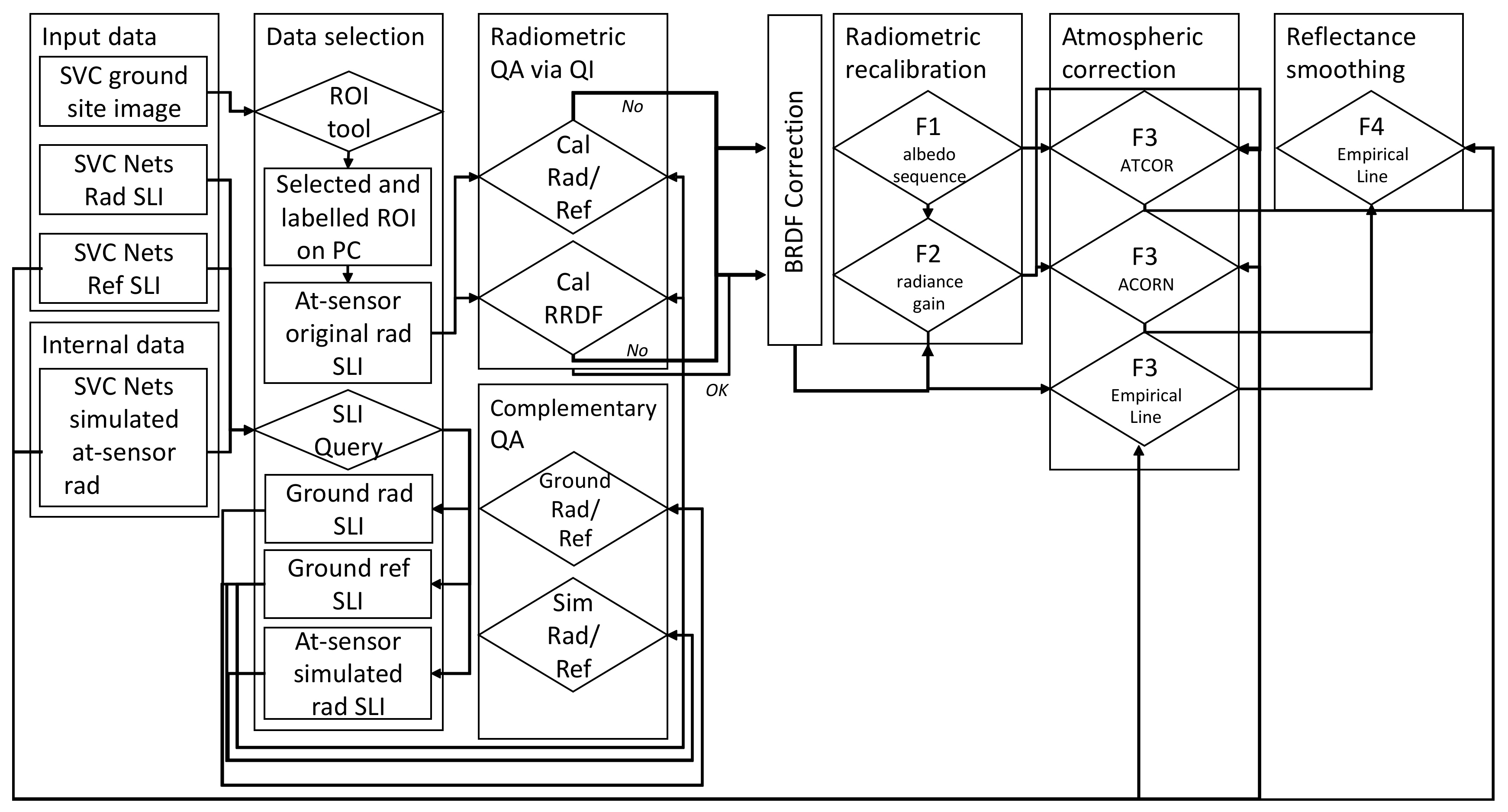
2.3. Spectral and Imagery Data Pre-Processing
- (1)
- Radiometric quality indicators—the first step is dependent on a selected region of interest by the operator. This step is performed on the UAS-based orthophoto and projected on the reconstructed pout cloud.
- (2)
- BRDF correction—following the recommendations reported by [64], prior to submitting the imagery data to the radiometric recalibration (F1 stage), the BRDF effect must be estimated and reduced. This essential stage was included in the modified scheme of the SVC method to provide more realistic at-sensor radiance data. Once the point/pixel/surface is facing the sensor (in nadir), the calculated angle is equal to 90°. The angle decries when the point/pixel/surface is tilted then its radiance is scattered and reflected in an off-nadir way. The calculated ground target depression angle is used to correct solar information (azimuth and zenith), which is calculated by a given date, time, and geographic location at a central given coordinate. The corresponding solar information is used to retrieve the BRDF correction coefficients (Rcorr) for the SVC calibration nets target [64]. The calculated coefficients are further applied for the full scanned scene, the full point cloud data.
- (3)
- The SVC correction-the at-sensor radiance is converted into accurate reflectance by applying four stages: normalization of the albedo sequence (F1) inspected by QIs, radiometric calibration gain using the net ground-truth reflectance (F2), applying a model-based atmospheric correction (F3) using ATCOR5 model, ACORN and empirical line method, and spectral polishing using the net ground0truth reflectance (F4). The SVC scheme is guided by the QIs scores. Well-calibrated sensors can proceed directly to stages F3 and F4. When the Rad/Ref holds a theoretical sequence but the RRDF indicator gives an indistinct result, the F2 stage should be applied before stages F3 and F4. Finally, when both Rad/Ref and RRDF indicators generate indistinctly, the full SVC correction chain is necessary, i.e., F1 and F2 until both parameters (Rad/Ref and RRDF).
2.4. Data Processing and Analysis
2.4.1. Spectral Model for TC Content
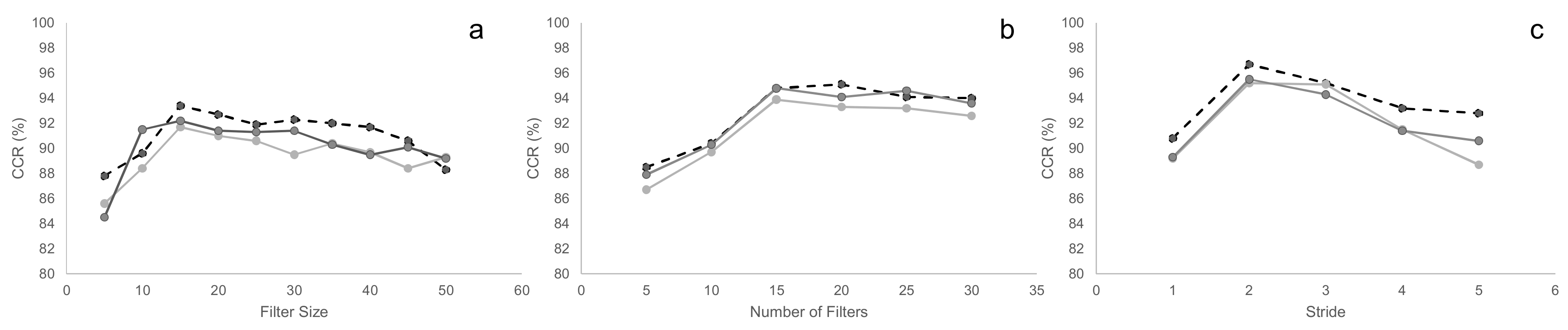
2.4.2. Partial Least Squares Discriminant Analysis and Machine Learning for TC Content
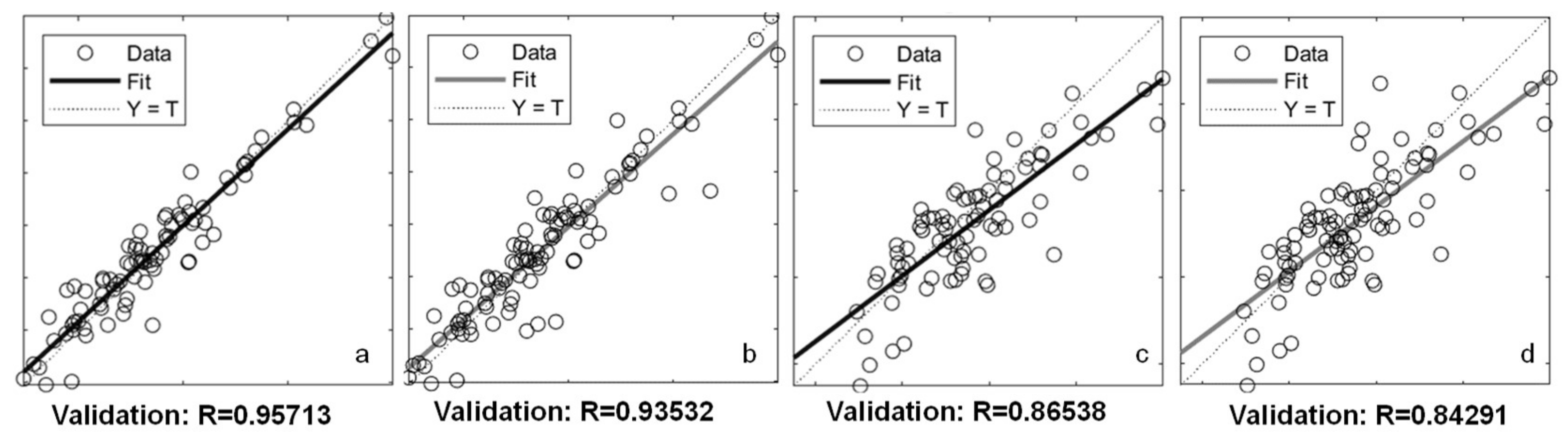
2.5. Validation and Verification
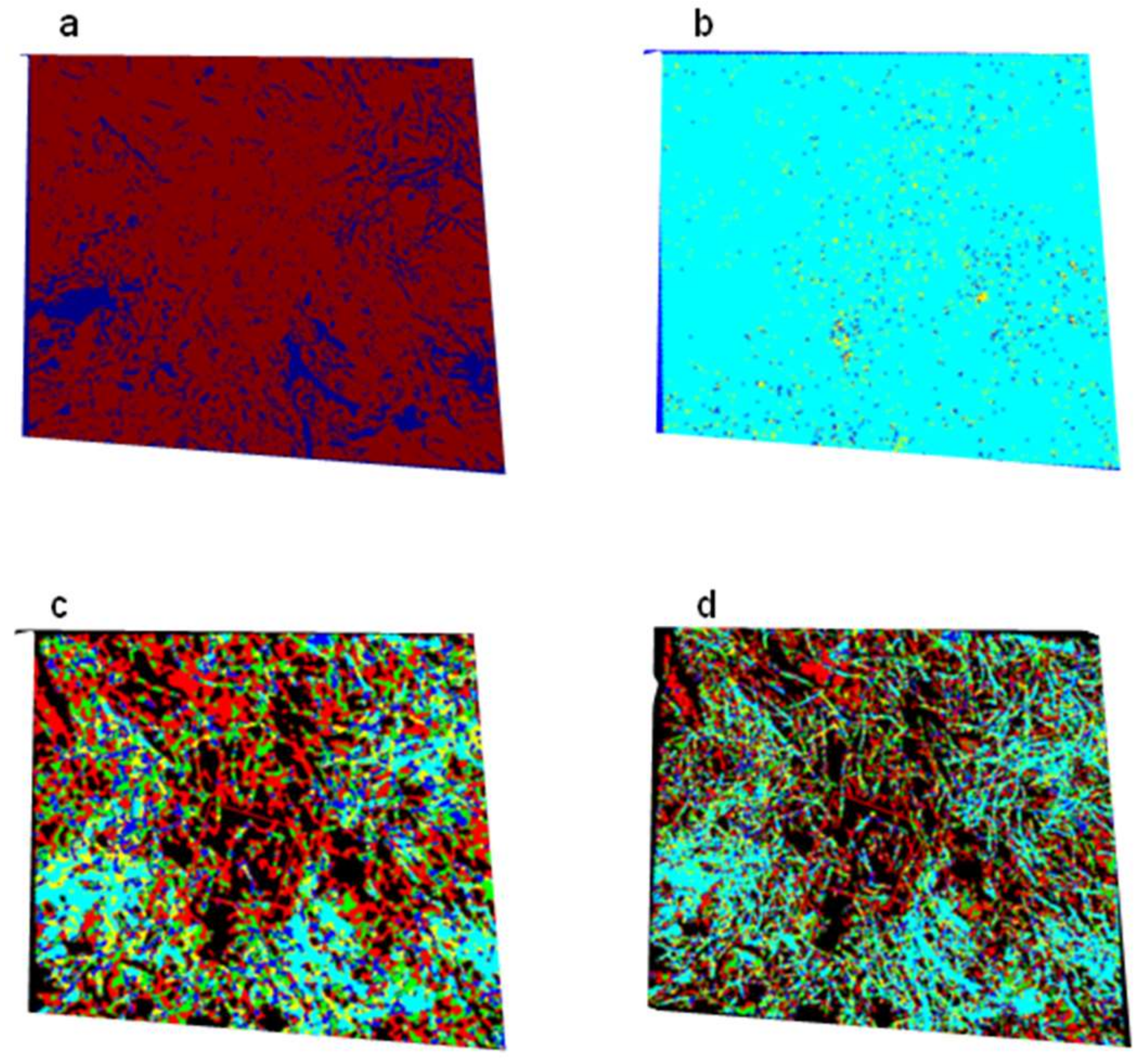
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bento-Gonçalves, A.; Vieira, A.; Úbeda, X.; Martin, D. Fire and soils: Key concepts and recent advances. Geoderma 2012, 191, 3–13. [Google Scholar] [CrossRef]
- Úbeda, X.; Pereira, P.; Outeiro, L.; Martin, D.A. Effects of fire temperature on the physical and chemical characteristics of the ash from two plots of cork oak (Quercus suber). Land Degrad. Dev. 2009, 20, 589–608. [Google Scholar] [CrossRef] [Green Version]
- Pereira, P.; Úbeda, X.; Martin, D.A. Fire severity effects on ash chemical composition and water-extractable elements. Geoderma 2012, 191, 105–114. [Google Scholar] [CrossRef]
- Thomaz, E.L. Ash physical characteristics affects differently soil hydrology and erosion subprocesses. Land Degrad. Dev. 2018, 29, 690–700. [Google Scholar] [CrossRef]
- Bodí, M.B.; Martin, D.A.; Balfour, V.N.; Santín, C.; Doerr, S.H.; Pereira, P.; Cerdà, A.; Mataix-Solera, J. Wildland fire ash: Production, composition and eco-hydro-geomorphic effects. Earth-Sci. Rev. 2014, 130, 103–127. [Google Scholar] [CrossRef]
- Santín, C.; Doerr, S.H.; Preston, C.M.; González-Rodríguez, G. Pyrogenic organic matter production from wildfires: A missing sink in the global carbon cycle. Glob. Chang. Biol. 2015, 21, 1621–1633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Vanha-Majamaa, I.; Lilja, S.; Ryömä, R.; Kotiaho, J.S.; Laaka-Lindberg, S.; Lindberg, H.; Puttonen, P.; Tamminen, P.; Toivanen, T.; Kuuluvainen, T. Rehabilitating boreal forest structure and species composition in Finland through logging, dead wood creation and fire: The EVO experiment. For. Ecol. Manag. 2007, 250, 77–88. [Google Scholar] [CrossRef]
- Giovannini, A. The interest elasticity of savings in developing countries: The existing evidence. World Dev. 1983, 11, 601–607. [Google Scholar] [CrossRef]
- Badía, D.; Martí, C. Plant ash and heat intensity effects on chemicaland physical properties of two contrasting soils. Arid. Land Res. Manag. 2003, 17, 23–41. [Google Scholar] [CrossRef]
- Mataix-Solera, J.; Cerdà, A.; Arcenegui, V.; Jordán, A.; Zavala, L.M. Fire effects on soil aggregation: A review. Earth-Sci. Rev. 2011, 109, 44–60. [Google Scholar] [CrossRef]
- Wondafrash, T.T.; Sancho, I.M.; Miguel, V.G.; Serrano, R.E. Relationship between soil color and temperature in the surface horizon of Mediterranean soils: A laboratory study. Soil Sci. 2005, 170, 495–503. [Google Scholar] [CrossRef]
- Granged, A.J.; Jordán, A.; Zavala, L.M.; Muñoz-Rojas, M.; Mataix-Solera, J. Short-term effects of experimental fire for a soil under eucalyptus forest (SE Australia). Geoderma 2011, 167, 125–134. [Google Scholar] [CrossRef]
- Munsell Colour Company. Munsell Soil Color Charts; Munsell Color Co.: Baltimore, MD, USA, 1975. [Google Scholar]
- Handbook of Near-Infrared Analysis; Burns, D.A.; Ciurczak, E.W. (Eds.) CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Brook, A.; Wittenberg, L. Ash-soil interface: Mineralogical composition and physical structure. Sci. Total Environ. 2016, 572, 1403–1413. [Google Scholar] [CrossRef] [PubMed]
- Skvaril, J.; Kyprianidis, K.G.; Dahlquist, E. Applications of near-infrared spectroscopy (NIRS) in biomass energy conversion processes: A review. Appl. Spectrosc. Rev. 2017, 52, 675–728. [Google Scholar] [CrossRef]
- Nuzzo, A.; Buurman, P.; Cozzolino, V.; Spaccini, R.; Piccolo, A. Infrared spectra of soil organic matter under a primary vegetation sequence. Chem. Biol. Technol. Agric. 2020, 7, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Reeves, J.B.; Smith, D.B. The potential of mid-and near-infrared diffuse reflectance spectroscopy for determining major-and trace-element concentrations in soils from a geochemical survey of North America. Appl. Geochem. 2009, 24, 1472–1481. [Google Scholar] [CrossRef]
- Paerl, H.W.; Scott, J.T. Throwing fuel on the fire: Synergistic effects of excessive nitrogen inputs and global warming on harmful algal blooms. Environ. Sci. Technol. 2010, 44, 7756–7758. [Google Scholar] [CrossRef]
- Santín, C.; Doerr, S.H.; Shakesby, R.A.; Bryant, R.; Sheridan, G.J.; Lane, P.N.; Smith, H.G.; Bell, T.L. Carbon loads, forms and sequestration potential within ash deposits produced by wildfire: New insights from the 2009 ‘Black Saturday’ fires, Australia. Eur. J. For. Res. 2012, 131, 1245–1253. [Google Scholar] [CrossRef]
- Almendros, G.; Knicker, H.; González-Vila, F.J. Rearrangement of carbon and nitrogen forms in peat after progressive thermal oxidation as determined by solid-state 13C-and 15N-NMR spectroscopy. Org. Geochem. 2003, 34, 1559–1568. [Google Scholar] [CrossRef]
- Knicker, H. Pyrogenic organic matter in soil: Its origin and occurrence, its chemistry and survival in soil environments. Quat. Int. 2011, 243, 251–263. [Google Scholar] [CrossRef]
- Baldock, J.A.; Smernik, R.J. Chemical composition and bioavailability of thermally altered Pinus resinosa (Red pine) wood. Org. Geochem. 2002, 33, 1093–1109. [Google Scholar] [CrossRef]
- Miesel, J.; Reiner, A.; Ewell, C.; Maestrini, B.; Dickinson, M. Quantifying changes in total and pyrogenic carbon stocks across fire severity gradients using active wildfire incidents. Front. Earth Sci. 2018, 6, 41. [Google Scholar] [CrossRef] [Green Version]
- Morgan, P.; Keane, R.E.; Dillon, G.K.; Jain, T.B.; Hudak, A.T.; Karau, E.C.; Sikkink, P.G.; Holden, Z.A.; Strand, E.K. Challenges of assessing fire and burn severity using field measures, remote sensing and modelling. Int. J. Wildland Fire 2014, 23, 1045–1060. [Google Scholar] [CrossRef] [Green Version]
- Roberts, D.A.; Paul, N.A.; Dworjanyn, S.A.; Bird, M.I.; de Nys, R. Biochar from commercially cultivated seaweed for soil amelioration. Sci. Rep. 2015, 5, 9665. [Google Scholar] [CrossRef] [Green Version]
- Santín, C.; Doerr, S.H.; Kane, E.S.; Masiello, C.A.; Ohlson, M.; de la Rosa, J.M.; Preston, C.M.; Dittmar, T. Towards a global assessment of pyrogenic carbon from vegetation fires. Glob. Chang. Biol. 2016, 22, 76–91. [Google Scholar] [CrossRef]
- Masiello, C.A. New directions in black carbon organic geochemistry. Mar. Chem. 2004, 92, 201–213. [Google Scholar] [CrossRef]
- Bird, M.I.; Wynn, J.G.; Saiz, G.; Wurster, C.M.; McBeath, A. The pyrogenic carbon cycle. Annu. Rev. Earth Planet. Sci. 2015, 43, 273–298. [Google Scholar] [CrossRef]
- Chafer, C.J.; Noonan, M.; Macnaught, E. The post-fire measurement of fire severity and intensity in the Christmas 2001 Sydney wildfires. Int. J. Wildland Fire 2004, 13, 227–240. [Google Scholar] [CrossRef]
- Robichaud, P.R.; Lewis, S.A.; Laes, D.Y.; Hudak, A.T.; Kokaly, R.F.; Zamudio, J.A. Postfire soil burn severity mapping with hyperspectral image unmixing. Remote Sens. Environ. 2007, 108, 467–480. [Google Scholar] [CrossRef] [Green Version]
- Verbyla, D.L.; Kasischke, E.S.; Hoy, E.E. Seasonal and topographic effects on estimating fire severity from Landsat TM/ETM+ data. Int. J. Wildland Fire 2008, 17, 527–534. [Google Scholar] [CrossRef]
- Russell-Smith, J.; Cook, G.D.; Cooke, P.M.; Edwards, A.C.; Lendrum, M.; Meyer, C.P.; Whitehead, P.J. Managing fire regimes in north Australian savannas: Applying Aboriginal approaches to contemporary global problems. Front. Ecol. Environ. 2013, 11 (Suppl. S1), e55–e63. [Google Scholar] [CrossRef] [Green Version]
- Marino, E.; Guillén-Climent, M.; Ranz Vega, P.; Tomé, J. Fire severity mapping in Garajonay National Park: Comparison between spectral indices. Flamma Madr. Spain 2016, 7, 22–28. [Google Scholar]
- Lutes, D.C.; Keane, R.E.; Caratti, J.F.; Key, C.H.; Benson, N.C.; Sutherland, S.; Gangi, L.J. FIREMON: Fire Effects Monitoring and Inventory System; General Technical Report RMRS-GTR-164; Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; p. 164. [Google Scholar]
- Jain, T.B.; Pilliod, D.S.; Graham, R.T.; Lentile, L.B.; Sandquist, J.E. Index for characterizing post-fire soil environments in temperate coniferous forests. Forests 2012, 3, 445–466. [Google Scholar] [CrossRef] [Green Version]
- Soverel, N.O.; Perrakis, D.D.; Coops, N.C. Estimating burn severity from Landsat dNBR and RdNBR indices across western Canada. Remote Sens. Environ. 2010, 114, 1896–1909. [Google Scholar] [CrossRef]
- Mitsopoulos, I.; Chrysafi, I.; Bountis, D.; Mallinis, G. Assessment of factors driving high fire severity potential and classification in a Mediterranean pine ecosystem. J. Environ. Manag. 2019, 235, 266–275. [Google Scholar] [CrossRef] [PubMed]
- Caselles, V.; Lopez Garcia, M.J.; Melia, J.; Perez Cueva, A.J. Analysis of the heat-island effect of the city of Valencia, Spain, through air temperature transects and NOAA satellite data. Theor. Appl. Climatol. 1991, 43, 195–203. [Google Scholar] [CrossRef]
- García-Llamas, P.; Suarez-Seoane, S.; Fernández-Guisuraga, J.M.; Fernández-García, V.; Fernández-Manso, A.; Quintano, C.; Taboada, A.; Marcos, E.; Calvo, L. Evaluation and comparison of Landsat 8, Sentinel-2 and Deimos-1 remote sensing indices for assessing burn severity in Mediterranean fire-prone ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 137–144. [Google Scholar] [CrossRef]
- Fernández-Guisuraga, J.M.; Suárez-Seoane, S.; Calvo, L. Modeling Pinus pinaster forest structure after a large wildfire using remote sensing data at high spatial resolution. For. Ecol. Manag. 2019, 446, 257–271. [Google Scholar] [CrossRef]
- Kolden, C.A.; Smith, A.M.; Abatzoglou, J.T. Limitations and utilisation of Monitoring Trends in Burn Severity products for assessing wildfire severity in the USA. Int. J. Wildland Fire 2015, 24, 1023–1028. [Google Scholar] [CrossRef]
- Wittenberg, L.; van der Wal, H.; Keesstra, S.; Tessler, N. Post-fire management treatment effects on soil properties and burned area restoration in a wildland-urban interface, Haifa Fire case study. Sci. Total Environ. 2020, 716, 135190. [Google Scholar] [CrossRef]
- Halofsky, J.E.; Hibbs, D.E. Controls on early post-fire woody plant colonization in riparian areas. For. Ecol. Manag. 2009, 258, 1350–1358. [Google Scholar] [CrossRef]
- Picotte, J.J.; Robertson, K. Timing constraints on remote sensing of wildland fire burned area in the southeastern US. Remote Sens. 2011, 3, 1680–1690. [Google Scholar] [CrossRef] [Green Version]
- Lydersen, J.M.; Collins, B.M.; Miller, J.D.; Fry, D.L.; Stephens, S.L. Relating fire-caused change in forest structure to remotely sensed estimates of fire severity. Fire Ecol. 2016, 12, 99–116. [Google Scholar] [CrossRef]
- Gibson, R.; Danaher, T.; Hehir, W.; Collins, L. A remote sensing approach to mapping fire severity in south-eastern Australia using sentinel 2 and random forest. Remote Sens. Environ. 2020, 240, 111702. [Google Scholar] [CrossRef]
- Cortenbach, J.; Williams, R.; Madurapperuma, B. Determining Fire Severity of the Santa Rosa, CA 2017 Fire. IdeaFest Interdiscip. J. Creat. Work. Res. Humboldt State Univ. 2019, 3, 8. [Google Scholar]
- Chu, T.; Guo, X. Remote sensing techniques in monitoring post-fire effects and patterns of forest recovery in boreal forest regions: A review. Remote Sens. 2013, 6, 470–520. [Google Scholar] [CrossRef] [Green Version]
- Maier, S.W.; Russell-Smith, J. Measuring and monitoring of contemporary fire regimes in Australia using satellite remote sensing. In Flammable Australia: Fire Regimes, Biodiversity and Ecosystems in a Changing World; CSIRO Publishing: Clayton, Australia, 2012; pp. 79–95. [Google Scholar]
- Gupta, V.; Reinke, K.J.; Jones, S.D.; Wallace, L.; Holden, L. Assessing metrics for estimating fire induced change in the forest understorey structure using terrestrial laser scanning. Remote Sens. 2015, 7, 8180–8201. [Google Scholar] [CrossRef] [Green Version]
- McKenna, P.; Erskine, P.D.; Lechner, A.M.; Phinn, S. Measuring fire severity using UAV imagery in semi-arid central Queensland, Australia. Int. J. Remote Sens. 2017, 38, 4244–4264. [Google Scholar] [CrossRef]
- Burnett, J.D.; Wing, M.G. A low-cost near-infrared digital camera for fire detection and monitoring. Int. J. Remote Sens. 2018, 39, 741–753. [Google Scholar] [CrossRef]
- Fraser, R.H.; Van der Sluijs, J.; Hall, R.J. Calibrating satellite-based indices of burn severity from UAV-derived metrics of a burned boreal forest in NWT, Canada. Remote Sens. 2017, 9, 279. [Google Scholar] [CrossRef] [Green Version]
- Simpson, C.C.; Sharples, J.J.; Evans, J.P. Sensitivity of atypical lateral fire spread to wind and slope. Geophys. Res. Lett. 2016, 43, 1744–1751. [Google Scholar] [CrossRef]
- Qian, G.; Yang, X.; Dong, S.; Zhou, J.; Sun, Y.; Xu, Y.; Liu, Q. Stabilization of chromium-bearing electroplating sludge with MSWI fly ash-based Friedel matrices. J. Hazard. Mater. 2009, 165, 955–960. [Google Scholar] [CrossRef]
- Hogue, B.A.; Inglett, P.W. Nutrient release from combustion residues of two contrasting herbaceous vegetation types. Sci. Total Environ. 2012, 431, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Singh, B.; Fang, Y.; Johnston, C.T. A Fourier-transform infrared study of biochar aging in soils. Soil Sci. Soc. Am. J. 2016, 80, 613. [Google Scholar] [CrossRef]
- Brook, A.; Dor, E.B. Supervised vicarious calibration (SVC) of hyperspectral remote-sensing data. Remote Sens. Environ. 2011, 115, 1543–1555. [Google Scholar] [CrossRef]
- Tmušić, G.; Manfreda, S.; Aasen, H.; James, M.R.; Gonçalves, G.; Ben-Dor, E.; Brook, A.; Polinova, M.; Arranz, J.J.; Mészáros, J.; et al. Current practices in UAS-based environmental monitoring. Remote Sens. 2020, 12, 1001. [Google Scholar] [CrossRef] [Green Version]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Rossel, R.V.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by vis—NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar] [CrossRef]
- Brook, A.; Polinova, M.; Ben-Dor, E. Fine tuning of the SVC method for airborne hyperspectral sensors: The BRDF correction of the calibration nets targets. Remote Sens. Environ. 2018, 204, 861–871. [Google Scholar] [CrossRef]
- Nault, J.R.; Preston, C.M.; Trofymow, J.T.; Fyles, J.; Kozak, L.; Siltanen, M.; Titus, B. Applicability of diffuse reflectance Fourier transform infrared spectroscopy to the chemical analysis of decomposing foliar litter in Canadian forests. Soil Sci. 2009, 174, 130–142. [Google Scholar] [CrossRef]
- Brook, A.; Wittenberg, L.; Kopel, D.; Polinova, M.; Roberts, D.; Ichoku, C.; Shtober-Zisu, N. Structural heterogeneity of vegetation fire ash. Land Degrad. Dev. 2018, 29, 2208–2221. [Google Scholar] [CrossRef]
- Singh, A.K.; Rai, A.; Singh, N. Effect of long term land use systems on fractions of glomalin and soil organic carbon in the Indo-Gangetic plain. Geoderma 2016, 277, 41–50. [Google Scholar] [CrossRef]
- Francioso, O.; Sanchez-Cortes, S.; Bonora, S.; Roldán, M.L.; Certini, G. Structural characterization of charcoal size-fractions from a burnt Pinus pinea forest by FT-IR, Raman and surface-enhanced Raman spectroscopies. J. Mol. Struct. 2011, 994, 155–162. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, PMLR, Virtual Event, 13–18 July 2020; Volume 37, pp. 448–456. [Google Scholar]
- Chuvieco, E.; Martin, M.P.; Palacios, A. Assessment of different spectral indices in the red-near-infrared spectral domain for burned land discrimination. Int. J. Remote Sens. 2002, 23, 5103–5110. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Dietz, J.B. Expert system-based mineral mapping in northern Death Valley, California/Nevada, using the airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sens. Environ. 1993, 44, 309–336. [Google Scholar] [CrossRef]
- Meddens, A.J.; Kolden, C.A.; Lutz, J.A. Detecting unburned areas within wildfire perimeters using Landsat and ancillary data across the northwestern United States. Remote Sens. Environ. 2016, 186, 275–285. [Google Scholar] [CrossRef]
- Collins, L.; Griffioen, P.; Newell, G.; Mellor, A. The utility of Random Forests for wildfire severity mapping. Remote Sens. Environ. 2018, 216, 374–384. [Google Scholar] [CrossRef]
- Monaco, S.; Greco, S.; Farasin, A.; Colomba, L.; Apiletti, D.; Garza, P.; Cerquitelli, T.; Baralis, E. Attention to Fires: Multi-Channel Deep Learning Models for Wildfire Severity Prediction. Appl. Sci. 2021, 11, 11060. [Google Scholar] [CrossRef]
- Farasin, A.; Colomba, L.; Garza, P. Double-step u-net: A deep learning-based approach for the estimation of wildfire damage severity through sentinel-2 satellite data. Appl. Sci. 2020, 10, 4332. [Google Scholar] [CrossRef]





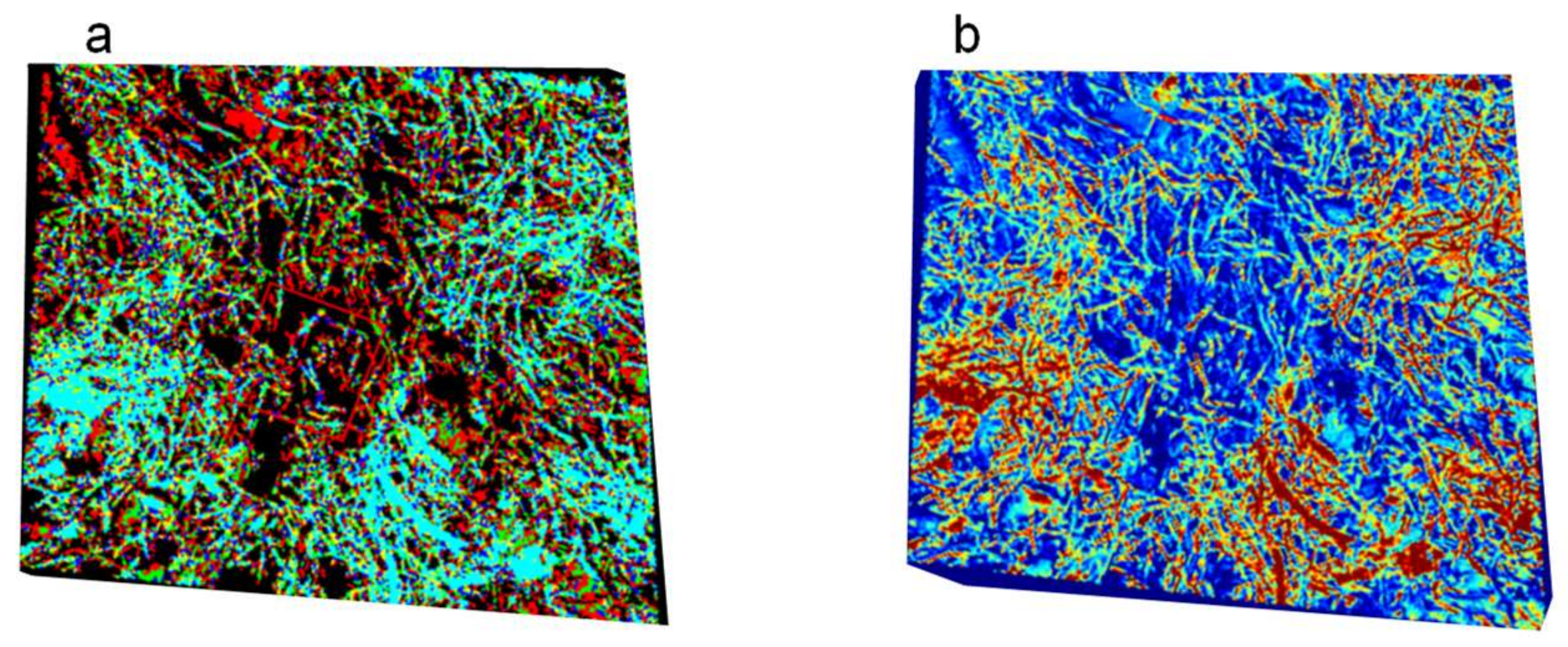
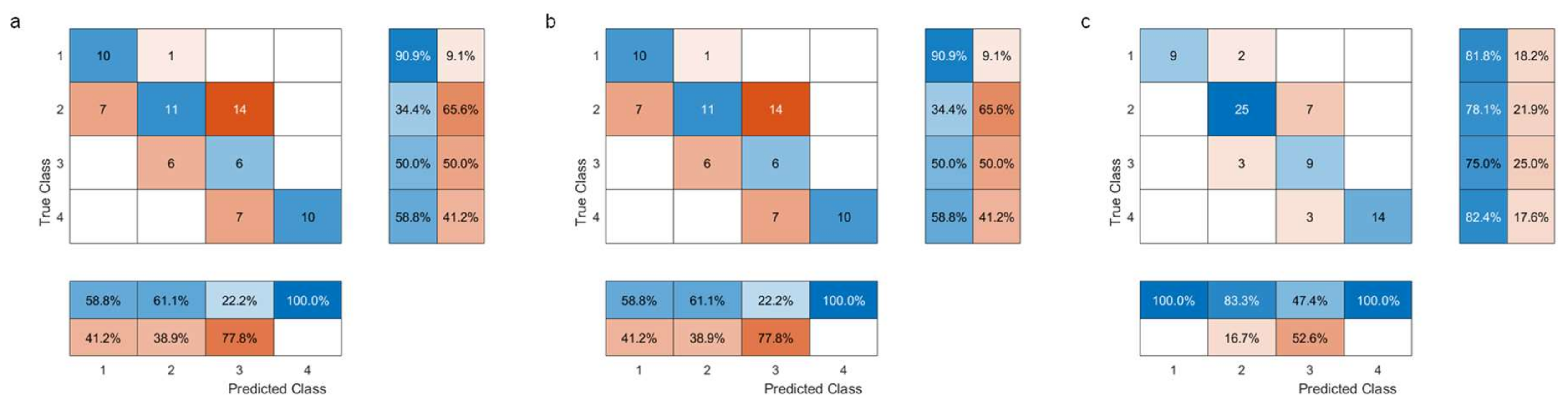
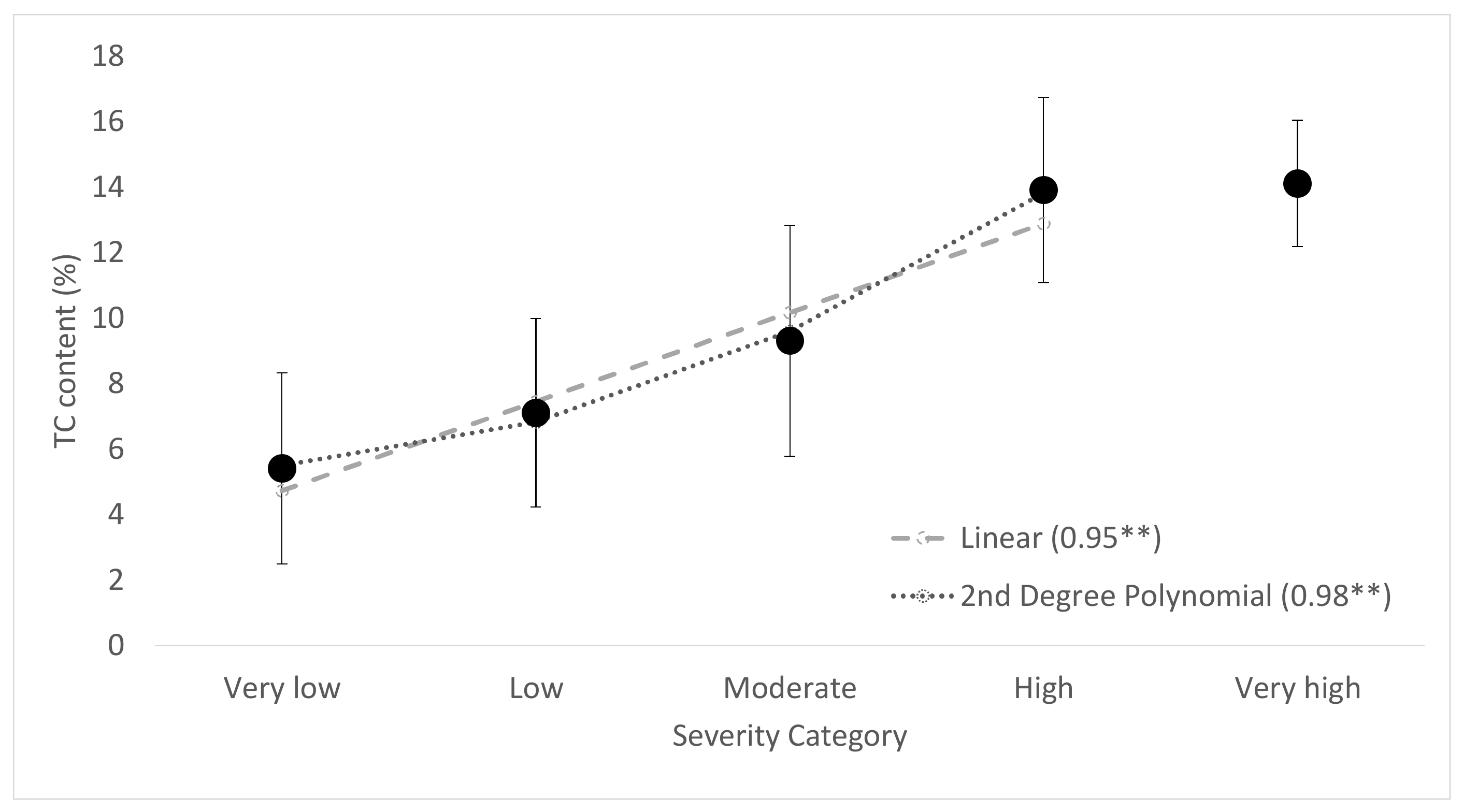

| Laboratory Dataset | Controlled Field Experiment Dataset | Urban Wildfire Dataset | |
|---|---|---|---|
| Location | 3 unburnt plots (20 m2). Location Mt. Carmel (32°43′16.3″N 35°00′15.8″E). | Isolated 2 × 2 m area burned by an open fire without interference and without combustion accelerators. Location near the University of Haifa (32°45′28.0″N 35°01′27.0″E). | Site size 550 × 150 m; Before the fire, more than 70% of the site was covered by vegetation and more than 50% of the vegetation was trees. Location Haifa (32°46′54.3″N 34°59′56.7″E). |
| Event Description | The experiment took place in July 2017. Air temperature 26 °C, average wind speed 2 m/s, soil temperature 46 °C, litter temperature 38 °C. | In November 2016 following a typically hot dry summer and unusually dry autumn, a wave of fires hit Israel. There were more than 170 wildfire events. The fire suppression activities in Haifa took nearly 24 h. The total burned area was 13 ha. | |
| Sample Collection | Samples were collected using a circular sampling ring and leaves, twigs, soil, and fine fuel were placed in separate bags. | Multiple subsamples at evenly spaced intervals along a transect radiating from a centroid were collected and composited. | Samples were collected on November 26th from an almost fully burned site. The top-ash samples (at a depth of 1–3 cm) were collected along a transect radiating from a centroid at the site. |
| Sample Description | The vegetation is broadly classified as a Mediterranean forest and the predominant species are P. halepensis and P. lentiscus. OM1 is herbaceous (n = 50) OM2 is a mixed sample of leaves and twigs of P. lentiscus, C. salviifolius, and herbaceous vegetation at a size of approximately 5–7 cm (n = 50) OM3 is the needles of P. halepensis (n = 50) OM4 is the leaves of P. lentiscus (n = 50) OM5 is the twigs of P. halepensis (n = 50) OM6 is the twigs of P. lentiscus (n = 50). | The vegetation is mainly composed of annual herbaceous species partially covered by the needles and branches of P. halepensis. Note that the summer months are very dry. | The natural vegetation is composed of Pinus halepensis, Quercus spp. and Pistacia spp. Pinus halepensis and Quercus spp. have relatively short time-to-ignition and long flame duration, relegating them to the class of extremely flammable vegetation. |
| LVs | RMSE | MAE | R2 | ||
|---|---|---|---|---|---|
| Spectrometer | Reflectance | 15 | 0.08 | 0.07 | 0.989 |
| RedEdge-MX Micasense camera | DN | 5 | 1.32 | 1.11 | 0.594 |
| SVC without BRDF correction | 4 | 1.18 | 0.92 | 0.874 | |
| SVC with BRDF correction | 4 | 0.41 | 0.32 | 0.923 | |
| DJI Phantom4 RGB camera | DN | 3 | 1.50 | 1.43 | 0.588 |
| SVC without BRDF correction | 3 | 1.21 | 1.13 | 0.752 | |
| SVC with BRDF correction | 3 | 0.98 | 0.84 | 0.855 |
| Validation | Test | ||||||
|---|---|---|---|---|---|---|---|
| Dataset | Laboratory | Controlled Field Experiment | Urban Wildfire | Laboratory | Controlled Field Experiment | Urban Wildfire | |
| Spectrometer | Reflectance | 98.12 | 99.84 | 96.39 | 99.14 | 96.72 | 94.92 |
| RedEdge-MX Micasense camera | DN | 59.42 | 59.86 | 59.73 | 57.81 | 57.29 | 58.11 |
| SVC without BRDF | 93.67 | 87.67 | 64.55 | 92.18 | 81.44 | 63.91 | |
| SVC with BRDF | 95.94 | 92.45 | 91.16 | 91.78 | 90.84 | 89.57 | |
| DJI Phantom4 RGB camera | DN | 58.77 | 49.06 | 47.82 | 49.94 | 49.27 | 40.81 |
| SVC without BRDF | 80.73 | 78.59 | 69.61 | 79.68 | 73.64 | 66.21 | |
| SVC with BRDF | 87.52 | 83.61 | 70.63 | 88.42 | 85.31 | 72.09 | |
| Lowest RMSEP for Bayesian Regularization | Lowest RMSEP for Levenberg–Marquardt | Test | ||||
|---|---|---|---|---|---|---|
| Dataset | Laboratory | Controlled Field Experiment | Urban Wildfire | |||
| Spectrometer | Reflectance | 0.06 | 0.08 | 98.28 | 98.3 | 96.2 |
| RedEdge-MX Micasense camera | DN | 1.2 | 1.35 | 64.31 | 61.38 | 53.65 |
| SVC without BRDF correction | 0.98 | 1.2 | 88.29 | 87.67 | 79.62 | |
| SVC with BRDF correction | 0.26 | 0.96 | 92.11 | 90.52 | 91.48 | |
| DJI Phantom4 RGB camera | DN | 1.5 | 2.4 | 66.72 | 41.27 | 43.84 |
| SVC without BRDF correction | 1.8 | 2.1 | 82.91 | 81.49 | 81.43 | |
| SVC with BRDF correction | 1.3 | 1.9 | 84.28 | 83.17 | 82.67 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brook, A.; Hamzi, S.; Roberts, D.; Ichoku, C.; Shtober-Zisu, N.; Wittenberg, L. Total Carbon Content Assessed by UAS Near-Infrared Imagery as a New Fire Severity Metric. Remote Sens. 2022, 14, 3632. https://doi.org/10.3390/rs14153632
Brook A, Hamzi S, Roberts D, Ichoku C, Shtober-Zisu N, Wittenberg L. Total Carbon Content Assessed by UAS Near-Infrared Imagery as a New Fire Severity Metric. Remote Sensing. 2022; 14(15):3632. https://doi.org/10.3390/rs14153632
Chicago/Turabian StyleBrook, Anna, Seham Hamzi, Dar Roberts, Charles Ichoku, Nurit Shtober-Zisu, and Lea Wittenberg. 2022. "Total Carbon Content Assessed by UAS Near-Infrared Imagery as a New Fire Severity Metric" Remote Sensing 14, no. 15: 3632. https://doi.org/10.3390/rs14153632
APA StyleBrook, A., Hamzi, S., Roberts, D., Ichoku, C., Shtober-Zisu, N., & Wittenberg, L. (2022). Total Carbon Content Assessed by UAS Near-Infrared Imagery as a New Fire Severity Metric. Remote Sensing, 14(15), 3632. https://doi.org/10.3390/rs14153632









