A Local and Nonlocal Feature Interaction Network for Pansharpening
Abstract
:1. Introduction
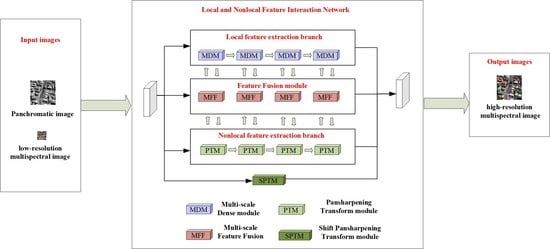
- A novel local and nonlocal feature interaction network is proposed to solve the pansharpening problem. In the LNFIN, an MDM is designed for extracting local features from images, and a Transformer structure-based PTM is introduced for learning nonlocal dependence in images.
- We propose an FIM to interact with the local and nonlocal features obtained by the CNN and Transformer branches. In the feature-extraction stage, local and nonlocal features are fused and returned to the respective branches to enhance the representational capability of the features.
- An SPTM based on the PTM is proposed to further enhance the spatial representation of features. The SPTM learns the spatial texture information of PAN image patches into MS images patches to obtain high-quality HRMS images.
2. Proposed Methods
2.1. Multiscale Dense Module for Local Feature Extraction
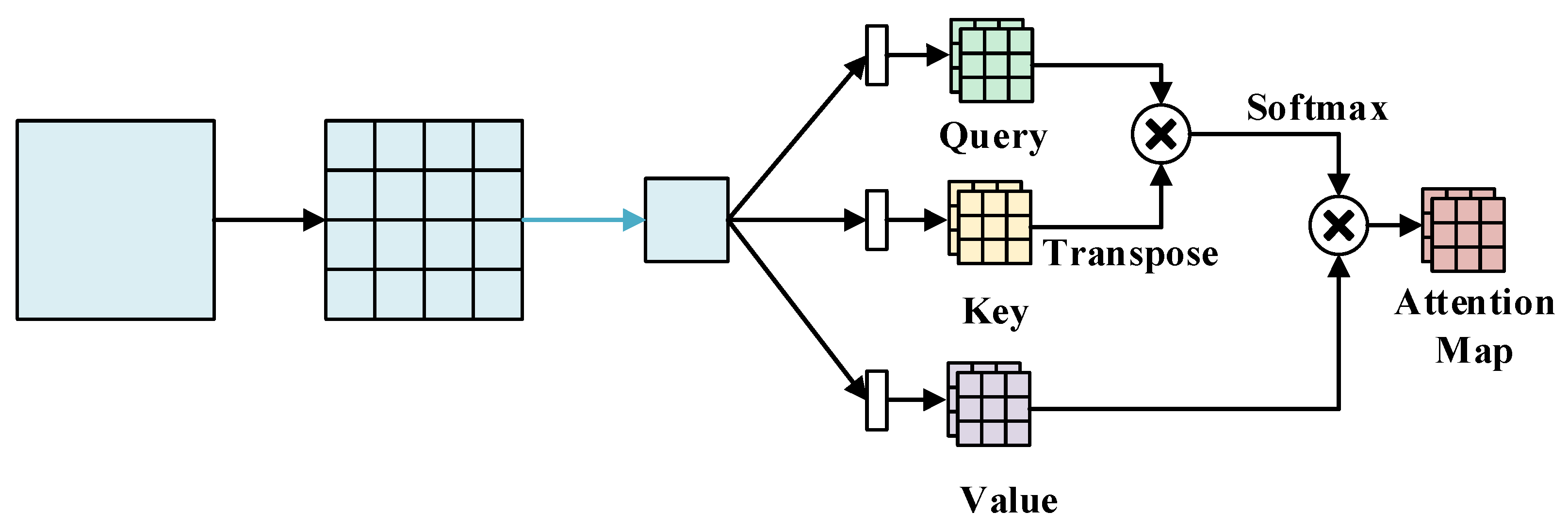
2.2. Pansharpening Transformer Module for Nonlocal Feature Extraction
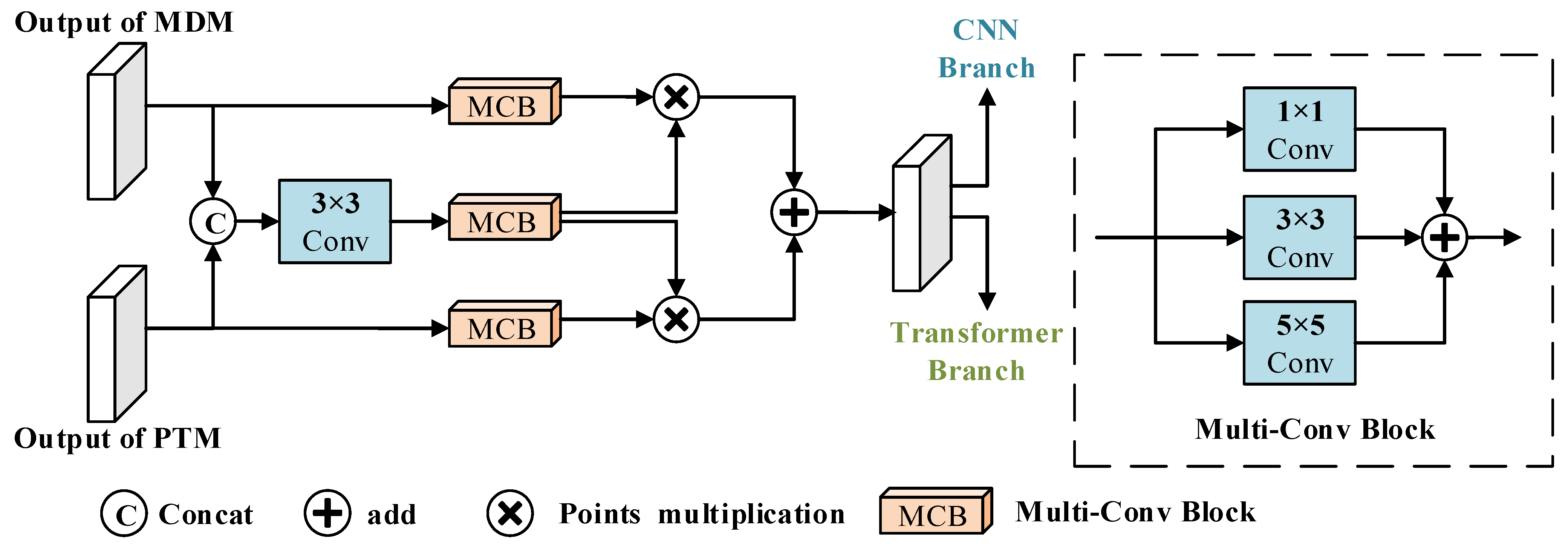
2.3. Feature Interaction Module
2.4. Shift Pansharpening Transformer Module for Texture Features
2.5. Loss
3. Experiments
3.1. Datasets
3.2. Comparison Methods
3.3. Quantitative Evaluation Indices
3.4. Ablation Experiments
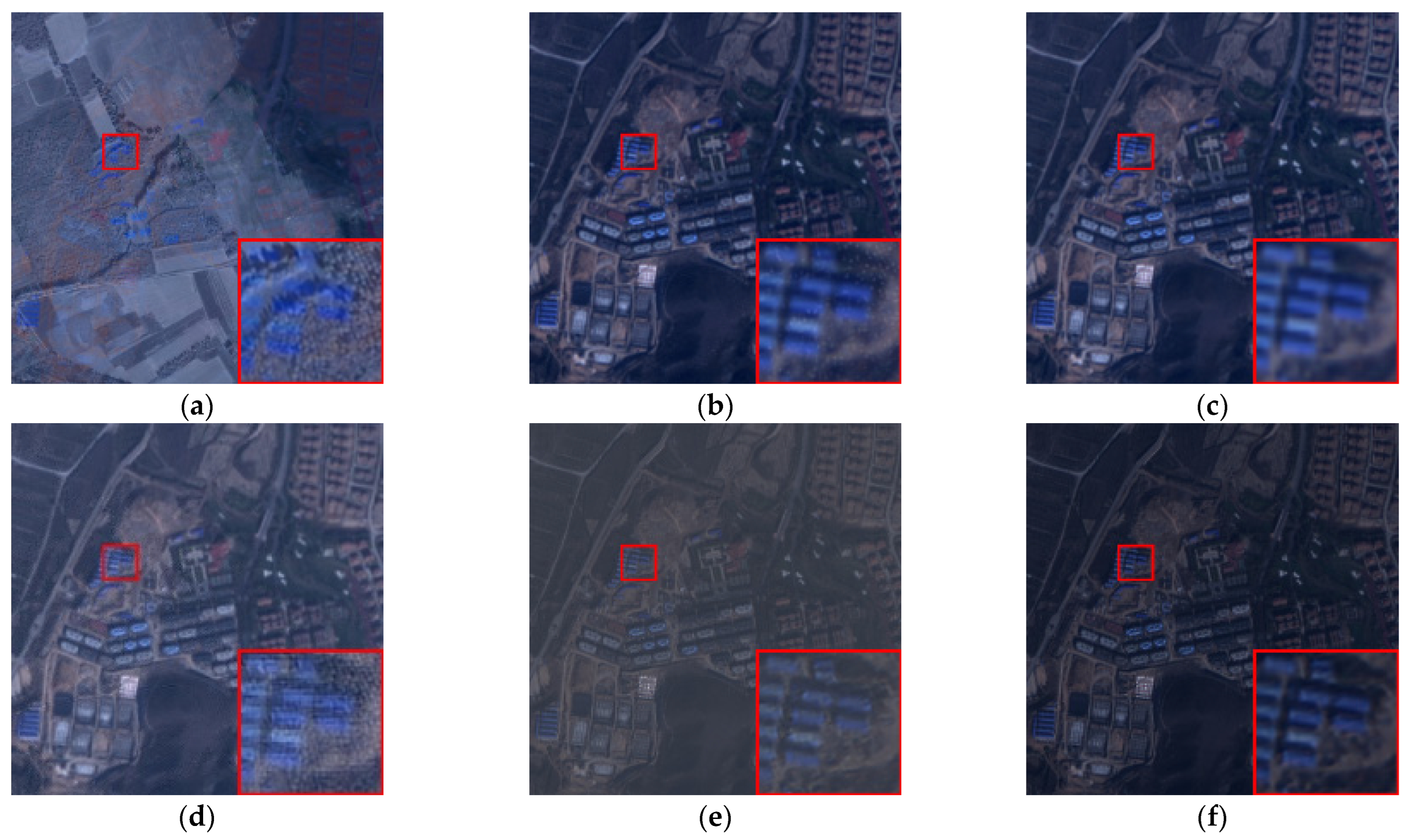
3.5. Simulation Experiments
3.6. Real Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ye, Q.; Li, D.; Fu, L.; Zhang, Z.; Yang, W. Non-Peaked Discriminant Analysis for Data Representation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3818–3832. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Li, Z.; Ye, Q.; Yin, H.; Liu, Q.; Chen, X.; Fan, X.; Yang, W.; Yang, G. Learning Robust Discriminant Subspace Based on Joint L2,p- and L2,s-Norm Distance Metrics. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 130–144. [Google Scholar] [CrossRef] [PubMed]
- He, C.X.; Sun, L.; Huang, W.; Zhang, J.W.; Zheng, Y.H.; Jeon, B. TSLRLN: Tensor subspace low-rank learning with non-local prior for hyperspectral image mixed denoising. Signal Process 2021, 184, 108060. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral-Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Ye, Q.; Huang, P.; Zhang, Z.; Zheng, Y.; Fu, L.; Yang, W. Multiview Learning with Robust Double-Sided Twin SVM. IEEE Trans. Cybern. 2021, 1–14. [Google Scholar] [CrossRef]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Kwarteng, P.; Chavez, A. Extracting spectral contrast in Landsat Thematic Mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 339–348. [Google Scholar]
- Choi, J.; Yu, K.; Kim, Y. A new adaptive component-substitution-based satellite image fusion by using partial replacement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 295–309. [Google Scholar] [CrossRef]
- Ghassemian, H. A review of remote sensing image fusion methods. Inf. Fusion 2016, 32, 75–89. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE Pan Sharpening of Very High Resolution Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving Component Substitution Pansharpening Through Multivariate Regression of MS +Pan Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J. A Critical Comparison Among Pansharpening Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full Scale Regression-Based Injection Coefficients for Panchromatic Sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef]
- Lee, J.; Lee, C. Fast and Efficient Panchromatic Sharpening. IEEE Trans. Geosci. Remote Sens. 2010, 48, 155–163. [Google Scholar]
- Vivone, G.; Alparone, L.; Garzelli, A.; Lolli, S. Fast reproducible pansharpening based on instrument and acquisition modeling: AWLP revisited. Remote Sens. 2019, 11, 2315. [Google Scholar] [CrossRef] [Green Version]
- Ballester, C.; Caselles, V.; Igual, L.; Verdera, J.; Rougé, B. A variational model for P + XS image fusion. Int. J. Comput. Vis. 2006, 69, 43–58. [Google Scholar] [CrossRef]
- Vivone, G.; Simões, M.; Dalla Mura, M.; Restaino, R.; Bioucas-Dias, J.M.; Licciardi, G.A.; Chanussot, J. Pansharpening based on semiblind deconvolution. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1997–2010. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z. A practical pan-sharpening method with wavelet transform and sparse representation. In Proceedings of the IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 22–23 October 2013. [Google Scholar]
- Zeng, D.; Hu, Y.; Huang, Y.; Xu, Z.; Ding, X. Pan-sharpening with structural consistency and ℓ1/2 gradient prior. Remote Sens. Lett. 2016, 7, 1170–1179. [Google Scholar] [CrossRef]
- Fu, X.; Lin, Z.; Huang, Y.; Ding, X. A variational pan-sharpening with local gradient constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Convolution Structure Sparse Coding for Fusion of Panchromatic and Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1117–1130. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Chica-Olmo, M.; Atkinson, P.M. Downscaling cokriging for image sharpening. Remote Sens. Environ. 2006, 102, 86–98. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Shi, W.; Atkinson, P.M. Area-to-point regression kriging for pan-sharpening. ISPRS J. Photogramm. Remote Sens. 2016, 114, 151–165. [Google Scholar] [CrossRef]
- Zhang, Y.; Atkinson, P.M.; Ling, F. Object-based area-to-point regression kriging for pansharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 8599–8614. [Google Scholar] [CrossRef]
- He, L.; Zhu, J.; Li, J.; Plaza, A.; Chanussot, J.; Li, B. HyperPNN: Hyperspectral pansharpening via spectrally predictive convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 3092–3100. [Google Scholar] [CrossRef]
- He, L.; Zhu, J.; Li, J.; Meng, D.; Chanussot, J.; Plaza, A. Spectral-fidelity convolutional neural Networks for hyperspectral pansharpening. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 5898–5914. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, H.; Huang, S.; Tu, W. Pansharpening based on joint-guided detail extraction. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 389–401. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, L.; Zhang, G.; Bi, H.; Dalla Mura, M.; Chanussot, J. Superresolution land cover mapping based on pixel-, subpixel-, and superpixel-scale spatial dependence with pansharpening Technique. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 4082–4098. [Google Scholar] [CrossRef]
- He, L.; Rao, Y.; Li, J.; Chanussot, J.; Plaza, A.; Zhu, J.; Li, B. Pansharpening via detail injection based convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 1188–1204. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zheng, Y.; Jeon, B. Pansharpening via subpixel convolutional residual network. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 10303–10313. [Google Scholar] [CrossRef]
- Zhong, X.; Qian, Y.; Liu, H.; Chen, L.; Wan, Y.; Gao, L.; Liu, J. Attention_FPNet: Two-branch remote sensing image pansharpening network based on attention feature fusion. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 11879–11891. [Google Scholar] [CrossRef]
- Luo, S.; Zhou, S.; Feng, Y.; Xie, J. Pansharpening via unsupervised convolutional neural networks. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 4295–4310. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masi, G.; Cozzolino, D.; Verdoliva, L. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Fu, X.; Hu, Y.; Huang, Y.; Ding, X.; Paisley, J. PanNet: A deep network architecture for pan-sharpening. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5449–5457. [Google Scholar]
- Ma, J.; Yu, W.; Chen, C.; Liang, P.; Guo, X.; Jiang, J. Pan-GAN: An unsupervised pan-sharpening method for remote sensing image fusion. Inf. Fusion 2020, 62, 110–120. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, Z.; Liu, H. MSDRN: Pansharpening of Multispectral Images via Multi-Scale Deep Residual Network. Remote Sens. 2021, 13, 1200. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, L.J.; Zhang, T.J. SSconv: Explicit Spectral-to-Spatial Convolution for Pansharpening. In Proceedings of the 29th ACM International Conference on Multimedia, Chengdu, China, 20–24 October 2021; pp. 4472–4480. [Google Scholar]
- Deng, L.J.; Vivone, G.; Jin, C. Detail Injection-Based Deep Convolutional Neural Networks for Pansharpening. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6995–7010. [Google Scholar] [CrossRef]
- Yang, Z.; Fu, X.; Liu, A.; Zha, Z.J. Progressive Pan-Sharpening via Cross-Scale Collaboration Networks. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhou, M.; Yan, K.; Huang, J.; Yang, Z.; Fu, X.; Zhao, F. Mutual Information-Driven Pan-Sharpening. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–20 June 2022; pp. 1798–1808. [Google Scholar]
- Zhou, M.; Fu, X.; Huang, J.; Zhao, F.; Liu, A.; Wang, R. Effective Pan-Sharpening with Transformer and Invertible Neural Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Yang, F.; Yang, H.; Fu, J.; Lu, H.; Guo, B. Learning texture transformer network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 14–19 June 2020; pp. 5791–5800. [Google Scholar]
- Nithin, G.R.; Kumar, N.; Kakani, R.; Venkateswaran, N.; Garg, A.; Gupta, U.K. Pansformers: Transformer-Based Self-Attention Network for Pansharpening. TechRxiv, 2021; preprint. [Google Scholar] [CrossRef]
- Guan, P.; Lam, E.Y. Multistage dual-attention guided fusion network for hyperspectral pansharpening. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Proceedings of the Summaries 3rd Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; pp. 147–149. [Google Scholar]
- Khademi, G.; Ghassemian, H. A multi-objective component-substitution-based pansharpening. In Proceedings of the 3rd International Conference on Pattern Recognition and Image Analysis (IPRIA), Shahrekord, Iran, 19–20 April 2017; pp. 248–252. [Google Scholar]
- Liu, X.; Liu, Q.; Wang, Y. Remote sensing image fusion based on two-stream fusion network. Inf. Fusion 2020, 55, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef] [Green Version]









| Dataset | Resolution of PAN Image (m) | Resolution of MS Images (m) | Size of Original PAN Image | Size of Original MS Images |
|---|---|---|---|---|
| QuickBird | 0.61 | 2.44 | 16,251 × 16,004 | 4063 × 4001 |
| GaoFen-2 | 1 | 4 | 18,192 × 18,000 | 4548 × 4500 |
| WorldView-2 | 0.5 | 1.8 | 16,384 × 16,384 | 4096 × 4096 |
| Dataset | Number of Training Set | Number of Validation Set | Size of PAN Image | Size of MS Images |
|---|---|---|---|---|
| QuickBird | 2184 | 546 | 64 × 64 | 16 × 16 |
| GaoFen-2 | 2776 | 694 | 64 × 64 | 16 × 16 |
| WorldView-2 | 1600 | 400 | 64 × 64 | 16 × 16 |
| Method | Strategies | Quantitative Evaluation Indices | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MDM | PTM | FIM | SPTM | SAM | ERGAS | CC | Q | Q2n | |
| 1 | √ | 2.7990 | 2.6087 | 0.9595 | 0.9572 | 0.9244 | |||
| 2 | √ | 2.8086 | 2.6079 | 0.9557 | 0.9588 | 0.9211 | |||
| 3 | √ | √ | 2.1781 | 2.3784 | 0.9597 | 0.9655 | 0.9352 | ||
| 4 | √ | √ | √ | 1.7254 | 1.9555 | 0.9623 | 0.9755 | 0.9379 | |
| 5 | √ | √ | √ | √ | 1.3489 | 1.8224 | 0.9833 | 0.9865 | 0.9415 |
| Method | SAM | ERGAS | CC | Q | Q2n |
|---|---|---|---|---|---|
| IHS | 4.6574 | 2.6945 | 0.9141 | 0.9137 | 0.6521 |
| HPF | 4.5232 | 2.7628 | 0.9022 | 0.9134 | 0.6617 |
| PRACS | 2.7181 | 1.8431 | 0.9668 | 0.9640 | 0.7682 |
| Wavelet | 4.2887 | 3.4220 | 0.8771 | 0.9068 | 0.6884 |
| PNN | 2.6906 | 1.7205 | 0.9687 | 0.9635 | 0.8718 |
| FusionNet | 1.7285 | 1.2036 | 0.9840 | 0.9497 | 0.9172 |
| Pansformers | 1.6894 | 1.1287 | 0.9836 | 0.9670 | 0.9255 |
| Proposed | 1.5890 | 1.0796 | 0.9846 | 0.9679 | 0.9282 |
| Method | SAM | ERGAS | CC | Q | Q2n |
|---|---|---|---|---|---|
| IHS | 2.6436 | 3.9945 | 0.8835 | 0.9612 | 0.6714 |
| HPF | 2.6185 | 3.6253 | 0.9121 | 0.9659 | 0.7325 |
| PRACS | 2.9328 | 3.7703 | 0.9042 | 0.9592 | 0.7258 |
| Wavelet | 2.8180 | 3.9006 | 0.8957 | 0.9608 | 0.6826 |
| PNN | 2.1865 | 2.3352 | 0.9419 | 0.9618 | 0.9215 |
| FusionNet | 1.8154 | 2.2297 | 0.9553 | 0.9750 | 0.9350 |
| Pansformers | 1.8515 | 1.9600 | 0.9767 | 0.9743 | 0.9393 |
| Proposed | 1.3489 | 1.8224 | 0.9833 | 0.9865 | 0.9415 |
| Method | SAM | ERGAS | CC | Q | Q2n |
|---|---|---|---|---|---|
| IHS | 4.7252 | 3.5953 | 0.9577 | 0.9343 | 0.8487 |
| HPF | 4.7003 | 3.7872 | 0.9458 | 0.9278 | 0.7992 |
| PRACS | 4.6301 | 3.1958 | 0.9587 | 0.9356 | 0.8706 |
| Wavelet | 5.5041 | 3.7325 | 0.9500 | 0.9211 | 0.8417 |
| PNN | 3.7531 | 2.9329 | 0.9708 | 0.9563 | 0.9007 |
| FusionNet | 2.6965 | 1.9571 | 0.9849 | 0.9703 | 0.9559 |
| Pansformers | 2.6740 | 2.3796 | 0.9785 | 0.9730 | 0.9613 |
| Proposed | 2.6520 | 1.7409 | 0.9866 | 0.9786 | 0.9651 |
| QuickBird | GaoFen-2 | WorldView-2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | QNR | Dλ | DS | QNR | Dλ | DS | QNR | Dλ | DS |
| IHS | 0.8278 | 0.0899 | 0.0904 | 0.8939 | 0.0314 | 0.0871 | 0.8893 | 0.0267 | 0.0855 |
| HPF | 0.8505 | 0.0416 | 0.1126 | 0.8856 | 0.0128 | 0.1029 | 0.8479 | 0.0580 | 0.0999 |
| PRACS | 0.8463 | 0.0472 | 0.1118 | 0.8247 | 0.0032 | 0.1725 | 0.8852 | 0.0326 | 0.0850 |
| Wavelet | 0.5479 | 0.3132 | 0.2023 | 0.8757 | 0.0046 | 0.1201 | 0.8257 | 0.1149 | 0.0628 |
| PNN | 0.9235 | 0.0405 | 0.0375 | 0.9061 | 0.0103 | 0.0843 | 0.8587 | 0.0355 | 0.0785 |
| FusionNet | 0.9399 | 0.0268 | 0.0342 | 0.9136 | 0.0073 | 0.0795 | 0.9202 | 0.0271 | 0.0541 |
| Pansformers | 0.9476 | 0.0172 | 0.0357 | 0.9222 | 0.0082 | 0.0701 | 0.9325 | 0.0299 | 0.0386 |
| Proposed | 0.9592 | 0.0088 | 0.0321 | 0.9303 | 0.0014 | 0.0683 | 0.9539 | 0.0258 | 0.0207 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, J.; Qu, J.; Sun, L.; Huang, W.; Chen, Q. A Local and Nonlocal Feature Interaction Network for Pansharpening. Remote Sens. 2022, 14, 3743. https://doi.org/10.3390/rs14153743
Yin J, Qu J, Sun L, Huang W, Chen Q. A Local and Nonlocal Feature Interaction Network for Pansharpening. Remote Sensing. 2022; 14(15):3743. https://doi.org/10.3390/rs14153743
Chicago/Turabian StyleYin, Junru, Jiantao Qu, Le Sun, Wei Huang, and Qiqiang Chen. 2022. "A Local and Nonlocal Feature Interaction Network for Pansharpening" Remote Sensing 14, no. 15: 3743. https://doi.org/10.3390/rs14153743
APA StyleYin, J., Qu, J., Sun, L., Huang, W., & Chen, Q. (2022). A Local and Nonlocal Feature Interaction Network for Pansharpening. Remote Sensing, 14(15), 3743. https://doi.org/10.3390/rs14153743