A Comprehensive Machine Learning Study to Classify Precipitation Type over Land from Global Precipitation Measurement Microwave Imager (GPM-GMI) Measurements
Abstract
:1. Introduction
2. Data, Models, and Methodology
2.1. Data and Preprocessing
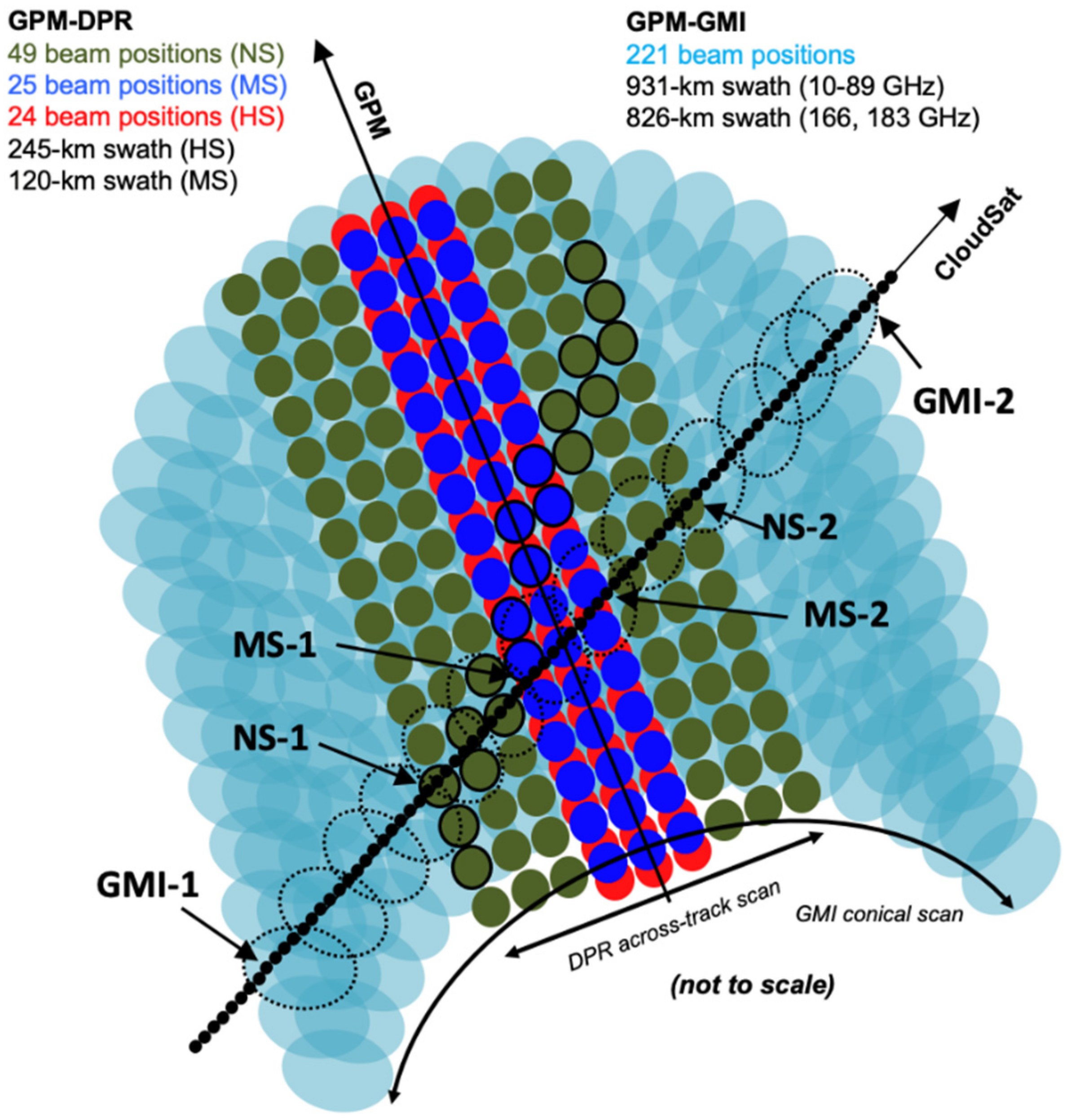
2.2. Data Augmentation
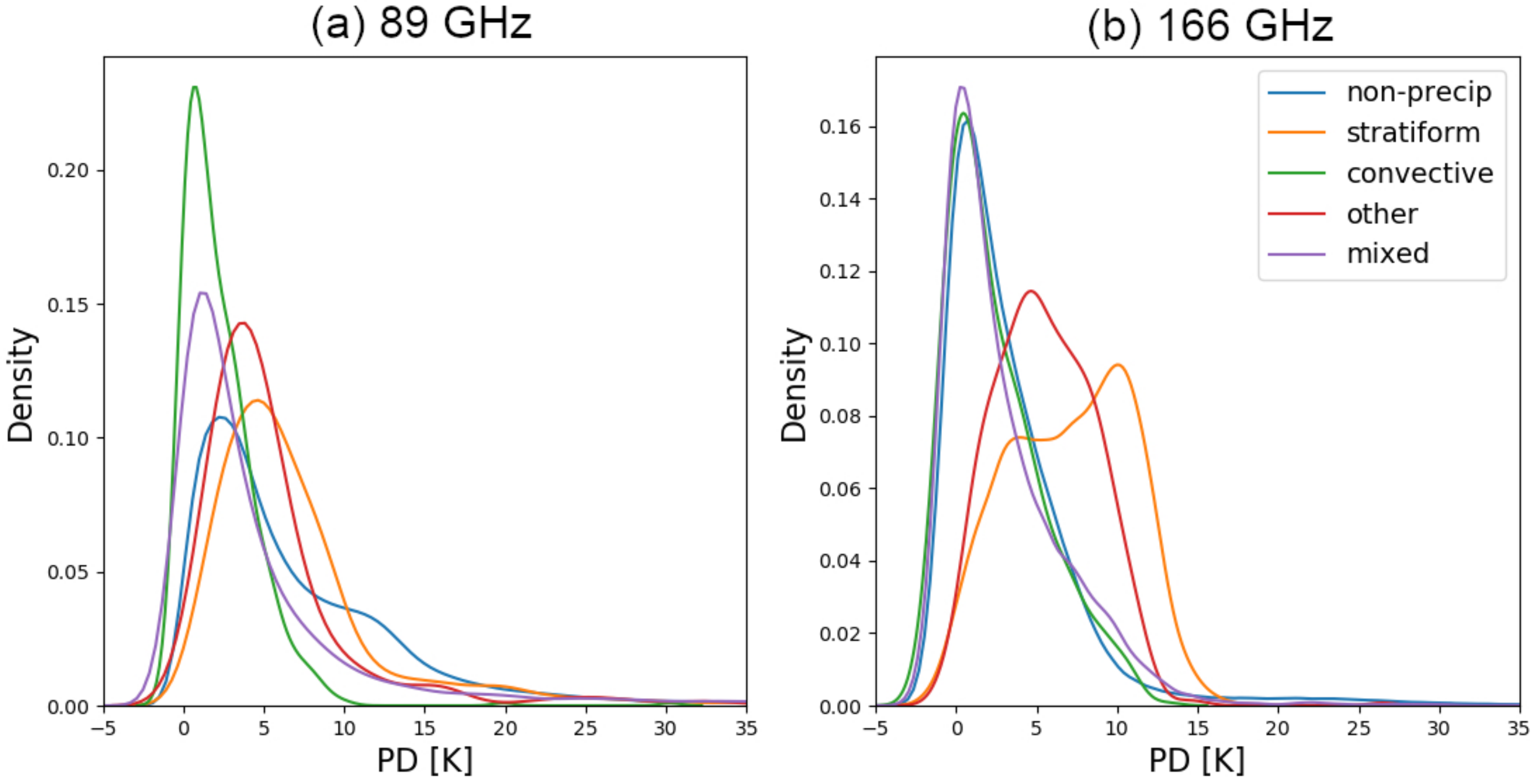
2.2.1. Polarization Differences
2.2.2. Surface Emissivity
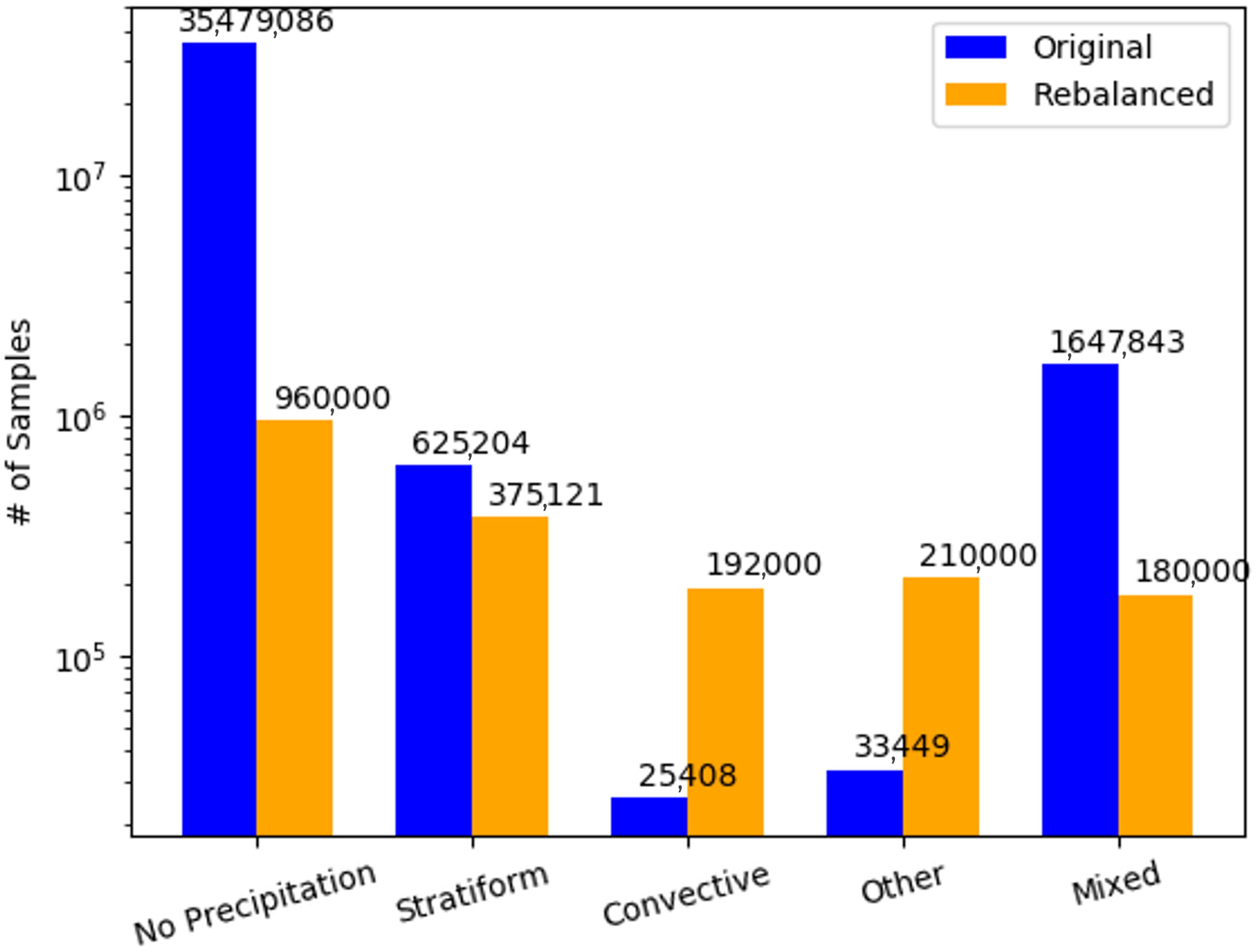
2.2.3. Sample Balancing
2.3. Machine Learning Models
3. Results
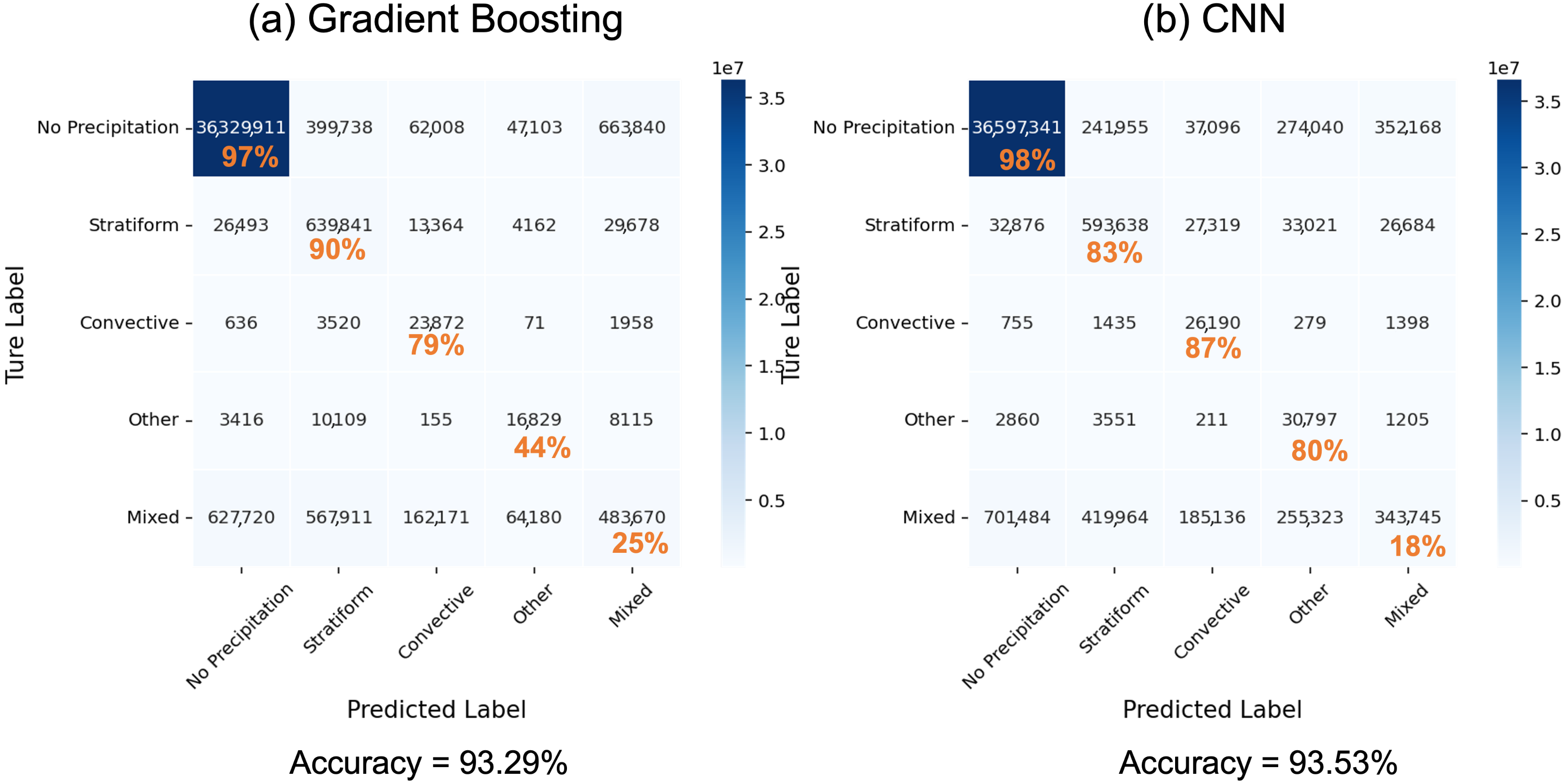
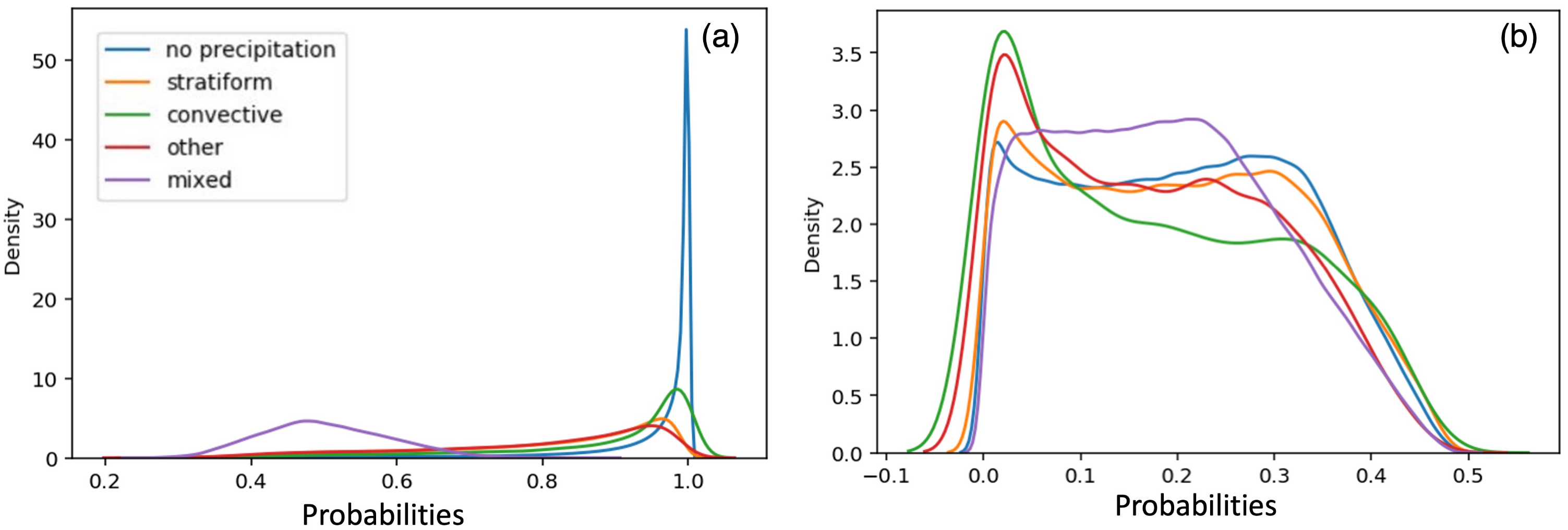
3.1. Prediction Accuracy
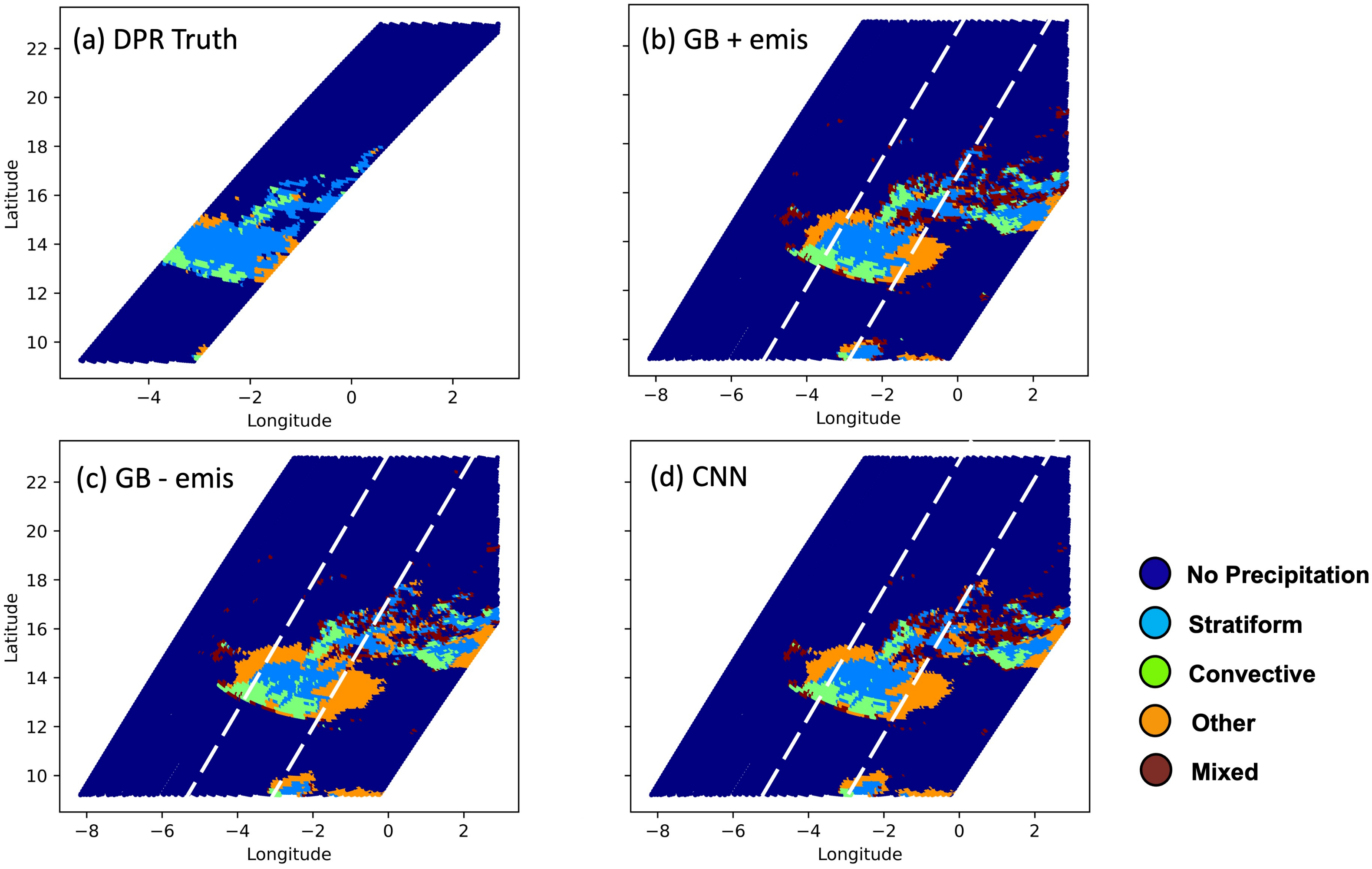
3.2. Sensitivity to Surface Emissivity
3.3. Rank of Importance and Corresponding Physics Mechanisms
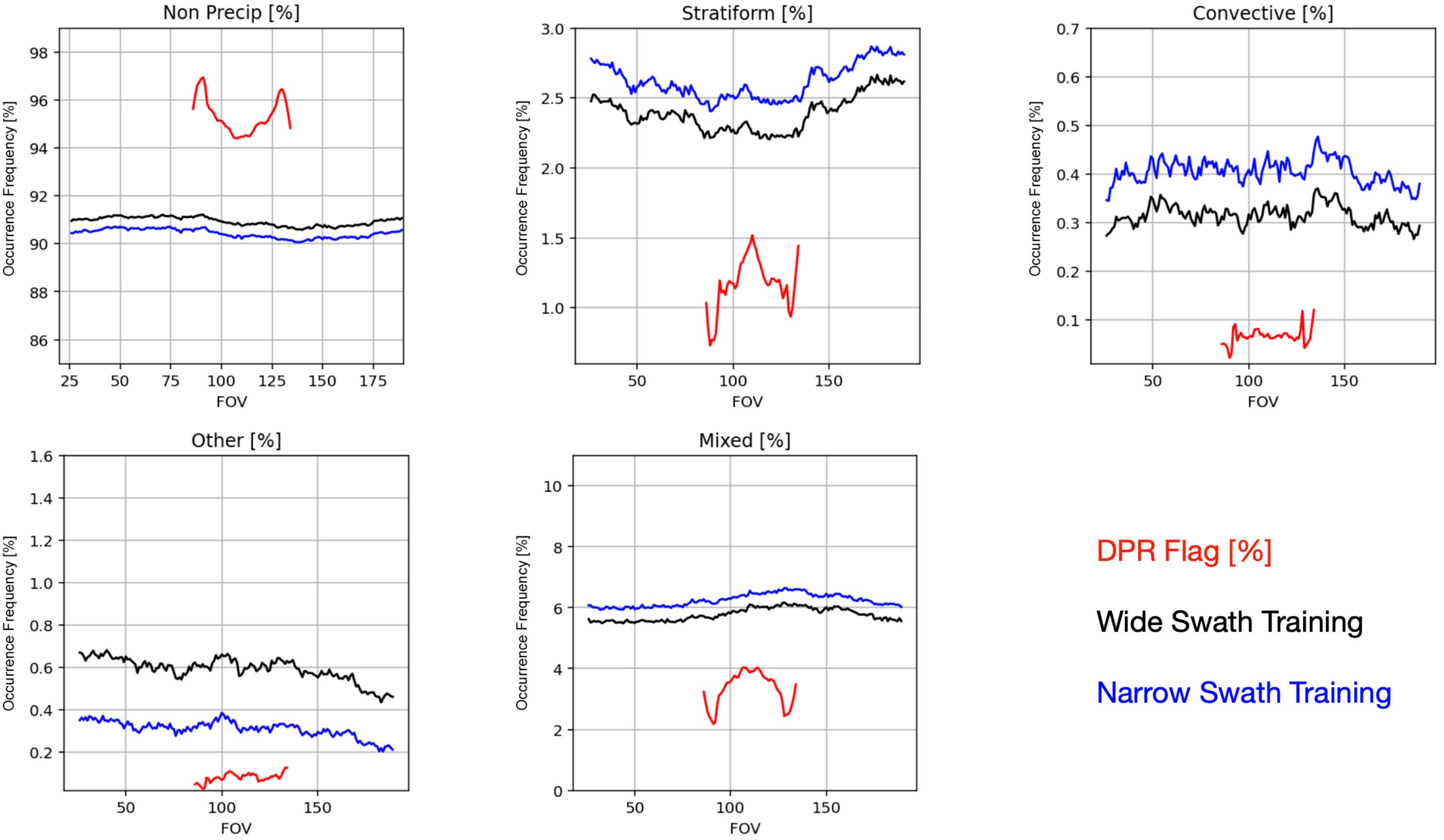
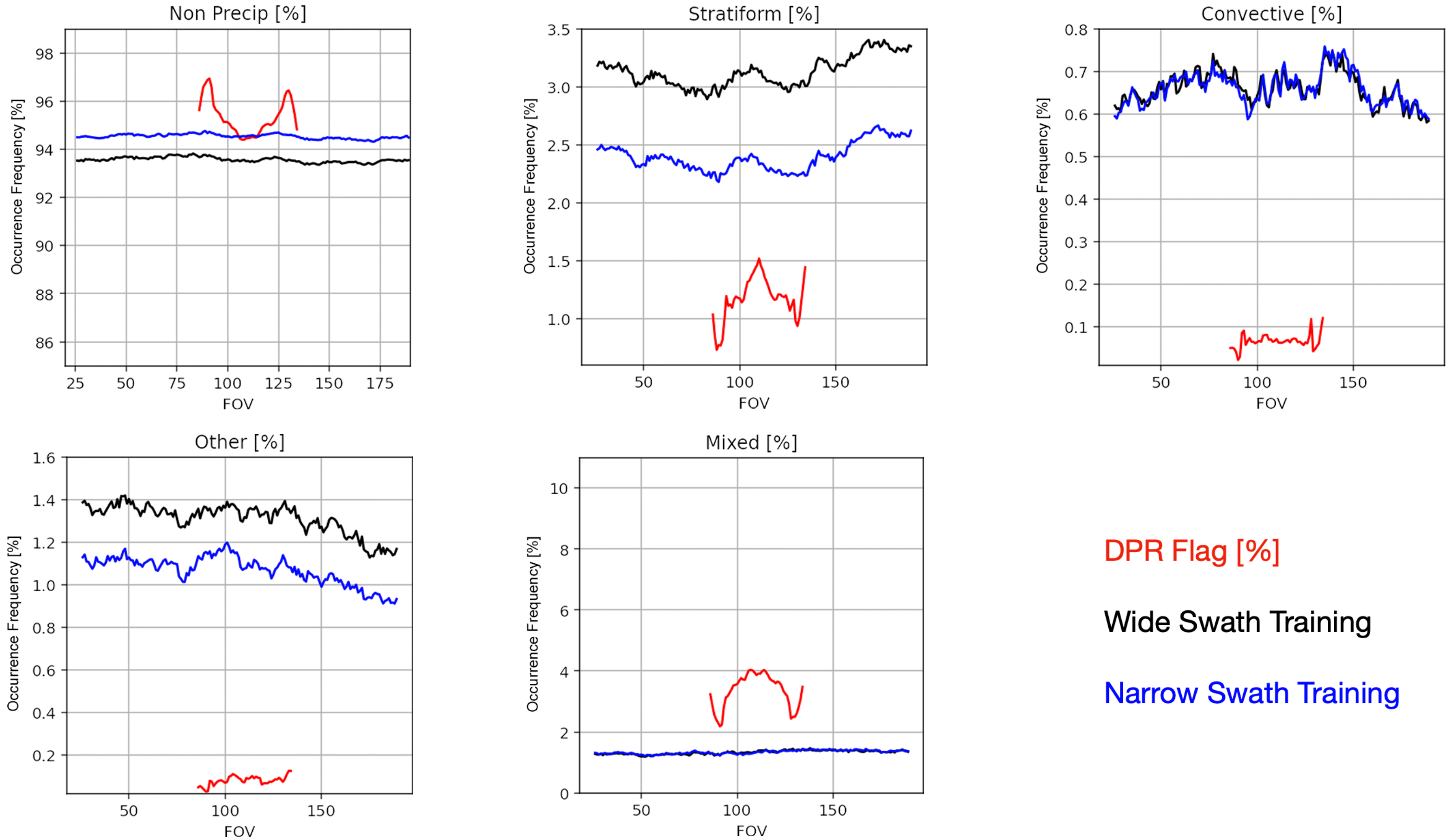
3.4. View-Angle Dependency
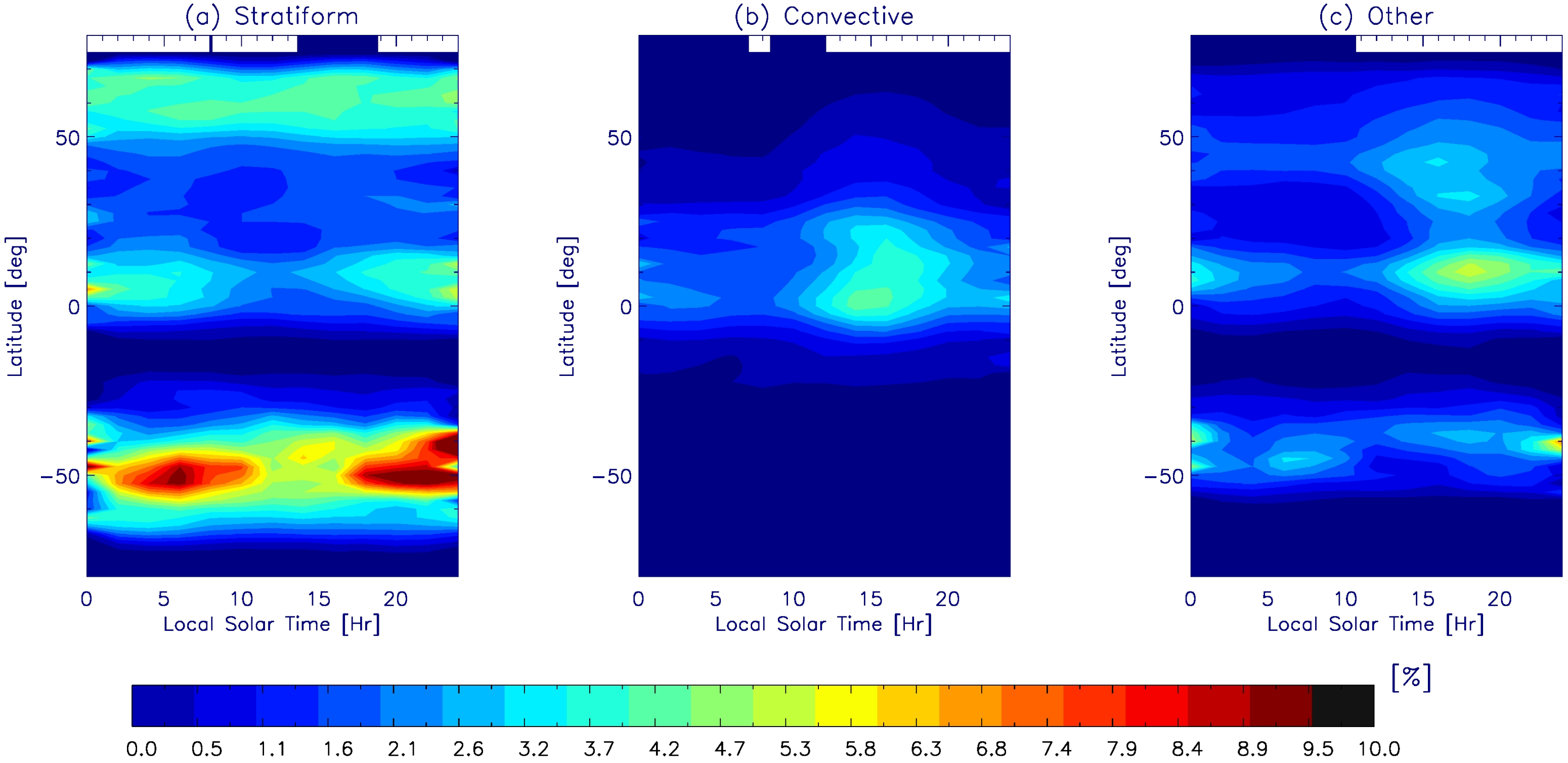
4. Application of GMI-Only Prediction on Weather and Climate Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Smith, E.A. Convective–Stratiform Precipitation Variability at Seasonal Scale from 8 Yr of TRMM Observations: Implications for Multiple Modes of Diurnal Variability. J. Clim. 2008, 21, 4087–4114. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Akella, S.; Coy, L.; Cullather, R.; Draper, C.; Gelaro, R.; Kovach, R.; Liu, Q.; Molod, A.; Norris, P.; et al. MERRA-2: Initial Evaluation of the Climate. Available online: https://gmao.gsfc.nasa.gov/pubs/docs/Bosilovich803.pdf (accessed on 4 May 2022).
- Yuan, W.; Yu, R.; Zhang, M.; Lin, W.; Li, J.; Fu, Y. Diurnal cycle of summer precipitation over subtropical East Asia in CAM5. J. Clim. 2013, 26, 3159–3172. [Google Scholar] [CrossRef]
- Liao, L.; Meneghini, R. GPM DPR Retrievals: Algorithm, Evaluation, and Validation. Remote Sens. 2022, 14, 843. [Google Scholar] [CrossRef]
- Seto, S.; Iguchi, T.; Meneghini, R.; Awaka, J.; Kubota, T.; Masaki, T.; Takahashi, N. The Precipitation Rate Retrieval Algorithms for the GPM Dual-frequency Precipitation Radar. J. Meteorol. Soc. Jpn. 2021, 99, 205–237. [Google Scholar] [CrossRef]
- Petković, V.; Kummerow, C.D.; Randel, D.L.; Pierce, J.R.; Kodros, J.K. Improving the Quality of Heavy Precipitation Estimates from Satellite Passive Microwave Rainfall Retrievals. J. Hydrometeorol. 2018, 19, 69–85. [Google Scholar] [CrossRef]
- Henderson, D.S.; Kummerow, C.D.; Marks, D.A.; Berg, W. A Regime-Based Evaluation of TRMM Oceanic Precipitation Biases. J. Atmos. Ocean. Technol. 2017, 34, 2613–2635. [Google Scholar] [CrossRef]
- Olson, W.S.; Hong, Y.; Kummerow, C.D.; Turk, J. A Texture-Polarization Method for Estimating Convective–Stratiform Precipitation Area Coverage from Passive Microwave Radiometer Data. J. Appl. Meteorol. 2001, 40, 1577–1591. [Google Scholar] [CrossRef] [Green Version]
- Islam, T.; Srivastava, P.K.; Dai, Q.; Gupta, M.; Jaafar, W. Stratiform/convective rain delineation for TRMM microwave imager. ScienceDirect 2015, 133, 25–35. [Google Scholar] [CrossRef]
- Hong, Y.; Kummerow, C.D.; Olson, W.S. Separation of convective and stratiform precipitation using microwave brightness temperature. J. Appl. Meteorol. Clim. 1999, 38, 1195–1213. [Google Scholar] [CrossRef] [Green Version]
- Orescanin, M.; Petković, V.; Powell, S.W.; Marsh, B.R.; Heslin, S.C. Bayesian deep learning for passive microwave precipitation type detection. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, C.; Platnick, S.; Meyer, K.; Zhang, Z.; Zhou, Y. A machine-learning-based cloud detection and thermodynamic-phase classification algorithm using passive spectral observations. Atmos. Meas. Tech. 2020, 13, 2257–2277. [Google Scholar] [CrossRef]
- Robbins, D.; Poulsen, C.; Siems, S.; Proud, S. Improving discrimination between clouds and optically thick aerosol plumes in geostationary satellite data. Atmos. Meas. Tech. Discuss. 2022, 15, 3031–3051. [Google Scholar] [CrossRef]
- Gong, J.; Wang, C.; Wu, D.L.; Barahona, D.; Tian, B.; Ding, L. A GCM-Oriented and Artificial Intelligence Based Passive Microwave Diurnal Ice/Snow Cloud Retrieval Product using CloudSat/CALIPSO as the Baseline. Atmos. Chem. Phys. 2022, 2021, A14B-07. [Google Scholar]
- Upadhyaya, S.A.; Kirstetter, P.-E.; Kuligowski, R.J.; Gourley, J.J.; Grams, H.M. Classifying precipitation from GEOS satellite observations: Prognostic model. Q. J. R. Meteorol. Soc. 2021, 147, 3394–3409. [Google Scholar] [CrossRef]
- Upadhyaya, S.A.; Kirstetter, P.-E.; Kuligowski, R.J.; Searls, M. Classifying precipitation from GEO satellite observations: Diagnostic model. Q. J. R. Meteorol. Soc. 2021, 147, 3318–3334. [Google Scholar] [CrossRef]
- Petkovic, V.; Orescanin, M.; Kirstetter, P.; Kummerow, C.; Ferraro, R. Enhancing PMW Satellite Precipitation Estimation: Detecting Convective Class. J. Atmos. Ocean. Technol. 2019, 36, 2349–2363. [Google Scholar] [CrossRef]
- Iguchi, T.; Seto, S.; Meneghini, R.; Yoshida, N.; Awaka, J.; Kubota, T. GPM/DPR Level-2 Algorithm Theoretical Basis Document, Version 06 Updates. 2018. Available online: https://gpm.nasa.gov/sites/default/files/2019-05/ATBD_DPR_201811_with_Appendix3b.pdf (accessed on 4 May 2022).
- Awaka, J.; Iguchi, T.; Okamoto, K.T. Early results on rain type classification by the Tropical Rainfall Measuring Mission (TRMM) precipitation radar. In Proceedings of the 8th URSI Commission F Triennial Open Symposium, Aveiro, Portugal, 22–25 September 1998; pp. 143–146. [Google Scholar]
- Awaka, J.; Iguchi, T.; Okamoto, K. TRMM PR standard algorithm 2A23 and its performance on bright band detection. J. Meteorol. Soc. 2009, 87, 31–52. [Google Scholar] [CrossRef] [Green Version]
- GPM Intercalibration (X-CAL) Working Group. Algorithm Theoretical Basis Document (ATBD), NASA Global Precipitation Measurement (GPM) Level 1C Algorithms (Version 1.6). 2016. Available online: https://gpm.nasa.gov/sites/default/files/2020-05/L1C_ATBD_v1.6_V04_0.pdf (accessed on 4 May 2022).
- Turk, F.J.; Ringerud, S.E.; Camplani, A.; Casella, D.; Chase, R.J.; Ebtehaj, A.; Gong, J.; Kulie, M.; Liu, G.; Milani, L.; et al. Applications of a CloudSat-TRMM and CloudSat-GPM Satellite Coincidence Dataset. Remote Sens. 2021, 87, 2264. [Google Scholar] [CrossRef]
- Suzuki, K.; Kamamoto, R.; Nakagawa, K.; Nonaka, M.; Shinoda, T.; Ohigashi, T.; Minami, Y.; Kubo, M.; Kaneko, Y. Ground Validation of GPM DPR Precipitation Type Classification Algorithm by Precipitation Particle Measurements in Winter. SOLA 2019, 15, 94–98. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirchengast, G.; Goodrich, D.C.; Wolff, D.B. Evaluation of Global Precipitation Measurement Rainfall Estimates against Three Dense Gauge Networks. J. Hydrometeorol. 2018, 19, 517–532. [Google Scholar] [CrossRef]
- Grecu, M.; Bolvin, D.; Heymsfield, G.M.; Lang, S.E.; Olson, W.S. Improved parameterization of precipitation fluxes in the GPM combined algorithm to mitigate ground clutter effects. In Proceedings of the AGU Fall Meeting, New Orleans, LA, USA, 13–17 December 2021; Available online: https://agu.confex.com/agu/fm21/meetingapp.cgi/Paper/953816 (accessed on 4 May 2022).
- Grecu, M.; Olson, W.S.; Munchak, S.J.; Ringerud, S.; Liao, L.; Haddad, Z.; Kelley, B.L.; McLaughlin, S.F. The GPM Combined Algorithm. J. Atmos. Ocean. Technol. 2016, 33, 2225–2245. [Google Scholar] [CrossRef]
- Munchak, S.J.; Ringerud, S.; Brucker, L.; You, Y.; de Gelis, I.; Prigent, C. An Active–Passive Microwave Land Surface Database From GPM. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6224–6242. [Google Scholar] [CrossRef]
- Gong, J.; Wu, D.L. Microphysical properties of frozen particles inferred from Global Precipitation Measurement (GPM) Microwave Imager (GMI) polarimetric measurements. Atmos. Chem. Phys. 2017, 17, 2741–2757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gong, J.; Zeng, X.; Wu, D.L.; Munchak, S.J.; Li, X.; Kneifel, S.; Ori, D.; Liao, L.; Barahona, D. Linkage among ice crystal microphysics, mesoscale dynamics, and cloud and precipitation structures revealed by collocated microwave radiometer and multifrequency radar observations. Atmos. Chem. Phys. 2020, 20, 12633–12653. [Google Scholar] [CrossRef]
- Prigent, C. Precipitation retrieval from space: An overview. C. R. Geosci. 2010, 342, 380–389. [Google Scholar] [CrossRef]
- Aires, F.; Prigent, C.; Bernardo, F.; Jiménez, C.; Saunders, R.; Brunel, P. A tool to estimate land-surface emissivities at microwave frequencies (TELSEM) for use in numerical weather prediction. Q. J. R. Meteorol. Soc. 2011, 137, 690–699. [Google Scholar] [CrossRef] [Green Version]
- Japkowicz, N.; Stephen, S. The class imbalance problem: A systematic study. Intell. Data Anal. 2002, 6, 429–449. [Google Scholar] [CrossRef]
- Menardi, G.; Torelli, N. Training and assessing classification rules with imbalanced data. Data Min. Knowl. Discov. 2014, 28, 92–122. [Google Scholar] [CrossRef]
- Breiman, L. Random forest. Mach. Learn. 2001, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Branco, P.; Torgo, L.; Ribeiro, R.P. A survey of predictive modeling on imbalanced domain. ACM Comput. Surv. 2016, 49, 1–50. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision? In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017.
- Ortiz, P.; Orescanin, M.; Petković, V.; Powell, S.W.; Marsh, B. Decomposing Satellite-Based Classification Uncertainties in Large Earth Science Datasets. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Skofronick-Jackson, G.M.; Wang, J.R.; Heymsfield, G.M.; Hood, R.; Manning, W.; Meneghini, R.; Weinman, J.A. Combined Radiometer-Radar Microphysical Profile Estimations with Emphasis on High Frequency Brightness Temperature Observations. J. Appl. Meteorol. 2003, 42, 476–487. [Google Scholar] [CrossRef] [Green Version]
- O’Dell, C.W.; Wentz, F.; Bennartz, R. Cloud Liquid Water Path from Satellite-Based Passive Microwave Observations: A New Climatology over the Global Ocean. J. Clim. 2008, 21, 1721–1739. [Google Scholar] [CrossRef]
- Choi, Y.; Shin, D.-B.; Kim, J.; Joh, M. Passive Microwave Precipitation Retrieval Algorithm With A Priori Databases of Various Cloud Microphysics Schemes: Tropical Cyclone Applications. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2366–2382. [Google Scholar] [CrossRef]
- Awaka, J.; Le, M.; Brodzik, S.; Kubota, T.; Masaki, T.; Chandrasekar, V.; Iguchi, T. Improvements of rain type classification algorithms for a full scan mode of GPM Dual-frequency Precipitation Radar. J. Meteorol. Soc. Jpn. 2021, 99, 1253–1270. [Google Scholar] [CrossRef]
- Gao, J.; Tang, G.; Hong, Y. Similarities and Improvements of GPM Dual-Frequency Precipitation Radar (DPR) upon TRMM Precipitation Radar (PR) in Global Precipitation Rate Estimation, Type Classification and Vertical Profiling. Remote Sens. 2017, 9, 1142. [Google Scholar] [CrossRef] [Green Version]
- Alexander, S.P.; McFarquhar, G.M.; Marchand, R.; Protat, A.; Vignon, É.; Mace, G.G.; Klekociuk, A.R. Klekociuk: Mixed-Phase Clouds and Precipitation in Southern Ocean Cyclones and Cloud Systems Observed Poleward of 64°S by Ship-Based Cloud Radar and Lidar. J. Geophys. Res. Atmos. 2021, 126, e2020JD033626. [Google Scholar] [CrossRef]
- Mace, G.G.; Protat, A.; Benson, S. Mixed-Phase Clouds Over the Southern Ocean as Observed From Satellite and Surface Based Lidar and Radar. J. Geophys. Res. Atmos. 2021, 126, e2021JD034569. [Google Scholar] [CrossRef]
- Lang, F.; Huang, Y.; Siems, S.T.; Manton, M.J. Evidence of a Diurnal Cycle in Precipitation over the Southern Ocean as Observed at Macquarie Island. Atmosphere 2020, 11, 181. [Google Scholar] [CrossRef] [Green Version]
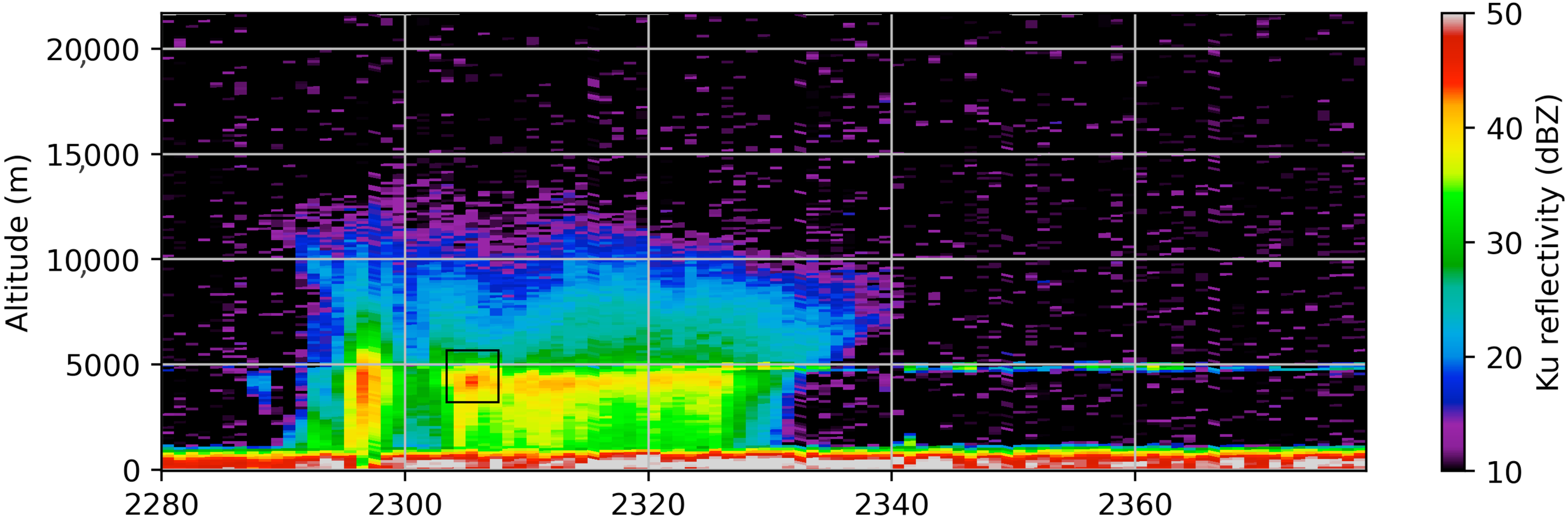
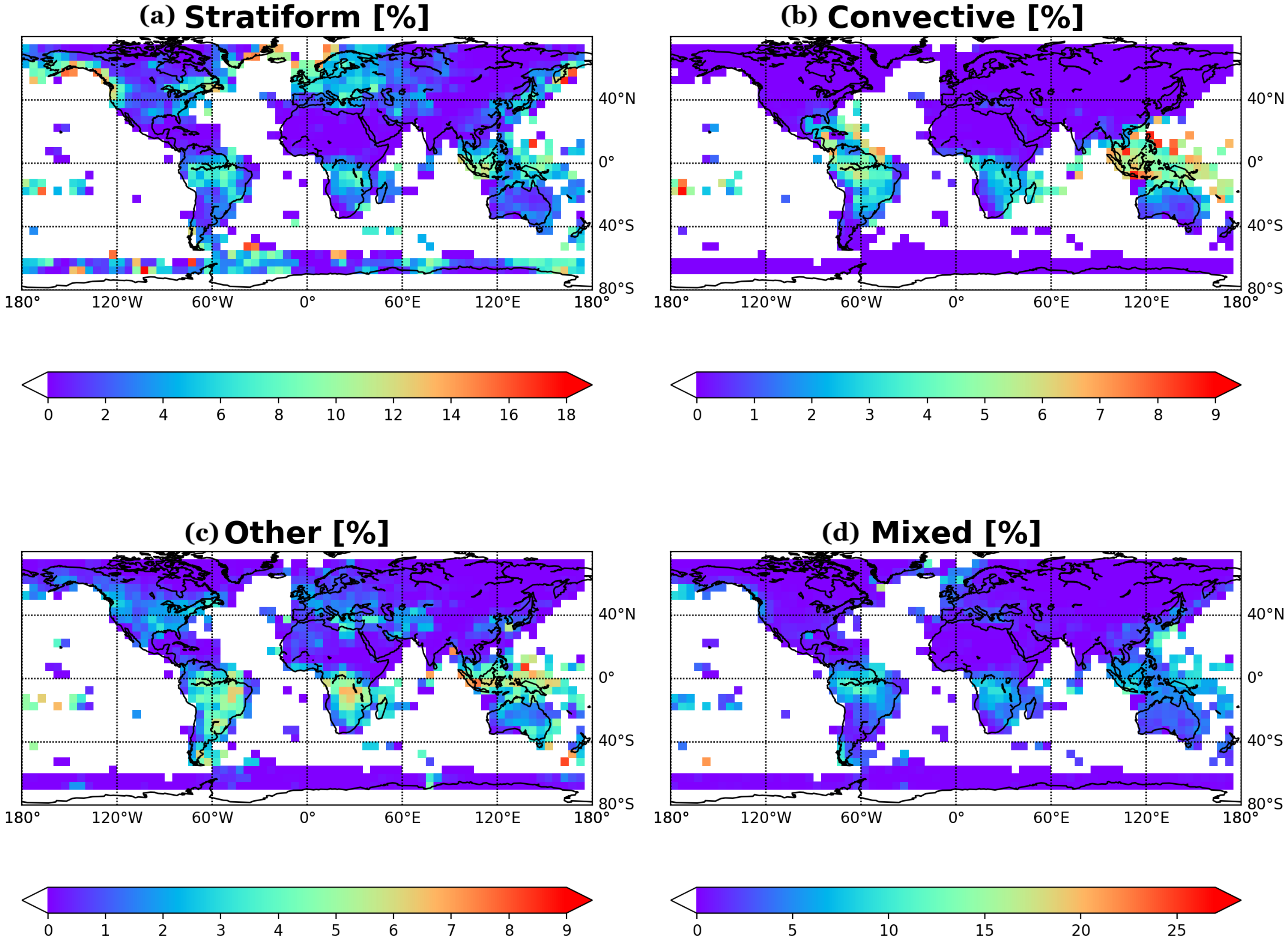
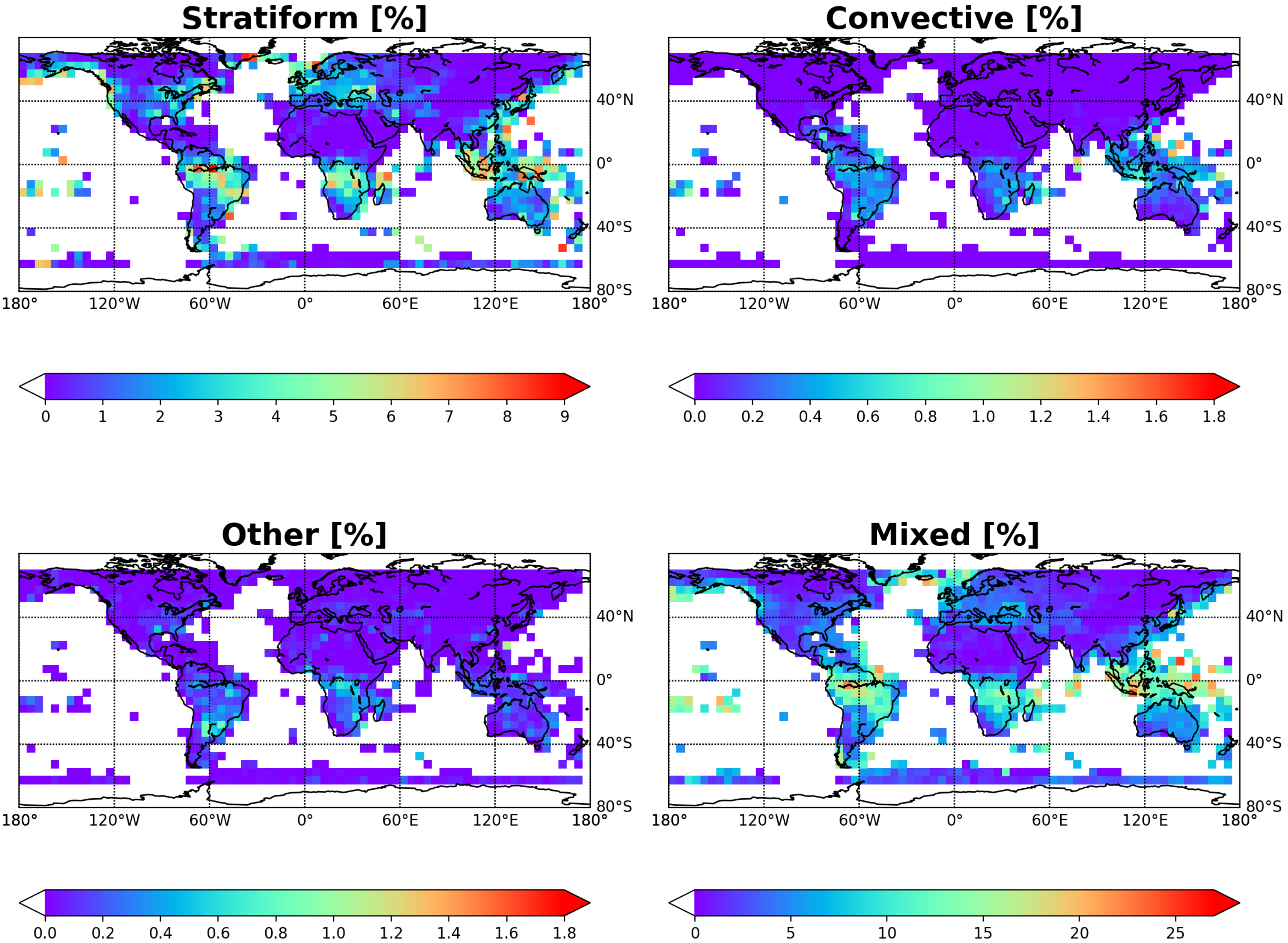
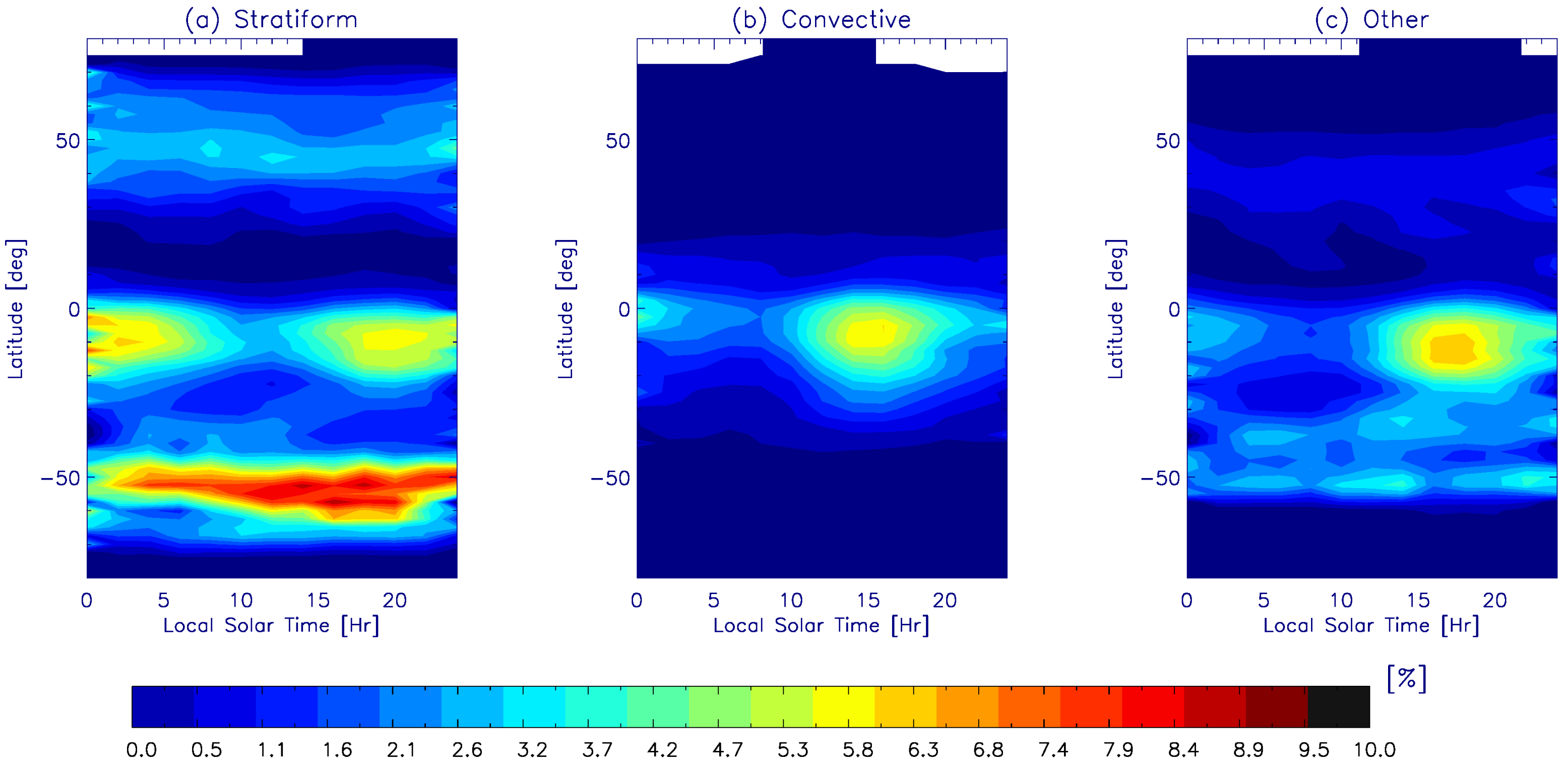
| Feature | Name | No. of Variables | Channel Info | Data Source | Note |
|---|---|---|---|---|---|
| Tc | GMI brightness temperature | 13 | 10V, 10H, 18V, 18H, 23, 36V, 36H, 89V, 89H, 166V, 166H, 183/3, and 183/7 GHz | L1-CR Observation | Ref. [21] |
| * PD | GMI polarization difference | 5 | 10, 18, 36, 89 and 166 GHz | L1-CR Observation | Ref. [28] |
| ** Emis | Surface Emissivity | 13 | Same as 1st row | Retrieval | Ref. [27] |
| CLWP | Cloud liquid water path | 1 | MERRA-2 | Auxiliary | |
| TWC | Total column water vapor | 1 | MERRA-2 | Auxiliary | |
| T2m | 2meter Temperature | 1 | MERRA-2 | Auxiliary | |
| Lat/Lon | Latitude/ Longitude | 2 | L1-CR Observation | Rounded to integer | |
| Month | Month of the year | 1 |
| Classifier | Overall Accuracy (%) | AUC Score |
|---|---|---|
| Support Vector Machine (SVM) | 91.15 | N/A |
| Logistic Regression (LR) | 76.07 | 0.8995 |
| Gradient Boosting (GB) | 93.31 | 0.9672 |
| Random Forest (RF) | 89.99 | 0.9594 |
| Neural Network (NN) | 93.56 | 0.9661 |
| Convolutional Neural Network (CNN) | 93.53 | 0.9678 |
| Classifier | Non-Precip (%) | Stratiform (%) | Convective (%) | Other (%) | Mixed (%) | Overall Accuracy (%) | ECE Score |
|---|---|---|---|---|---|---|---|
| GB + emis | 97 | 90 | 79 | 44 | 25 | 93.29 | 0.557 |
| GB − emis | 97 | 87 | 83 | 76 | 20 | 92.78 | 0.554 |
| RF + emis | 92 | 85 | 74 | 43 | 45 | 89.99 | 0.547 |
| RF − emis | 94 | 86 | 73 | 66 | 36 | 91.29 | 0.553 |
| CNN + emis | 98 | 83 | 87 | 80 | 18 | 93.53 | 0.555 |
| CNN − emis | 97 | 86 | 86 | 80 | 15 | 92.68 | – |
| Feature Importance Rank | GB + emis | RF + emis | GB − emis | RF − emis |
|---|---|---|---|---|
| 1 | CLWP | TWV | ||
| 2 | ||||
| 3 | CLWP | |||
| 4 | ||||
| 5 | CLWP | |||
| 6 | CLWP | TWV | ||
| 7 | TWV | |||
| 8 | TWV | |||
| 9 | Ts | |||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, S.; Wang, Y.; Gong, J.; Ding, L.; Munchak, S.J.; Wang, C.; Wu, D.L.; Liao, L.; Olson, W.S.; Barahona, D.O. A Comprehensive Machine Learning Study to Classify Precipitation Type over Land from Global Precipitation Measurement Microwave Imager (GPM-GMI) Measurements. Remote Sens. 2022, 14, 3631. https://doi.org/10.3390/rs14153631
Das S, Wang Y, Gong J, Ding L, Munchak SJ, Wang C, Wu DL, Liao L, Olson WS, Barahona DO. A Comprehensive Machine Learning Study to Classify Precipitation Type over Land from Global Precipitation Measurement Microwave Imager (GPM-GMI) Measurements. Remote Sensing. 2022; 14(15):3631. https://doi.org/10.3390/rs14153631
Chicago/Turabian StyleDas, Spandan, Yiding Wang, Jie Gong, Leah Ding, Stephen J. Munchak, Chenxi Wang, Dong L. Wu, Liang Liao, William S. Olson, and Donifan O. Barahona. 2022. "A Comprehensive Machine Learning Study to Classify Precipitation Type over Land from Global Precipitation Measurement Microwave Imager (GPM-GMI) Measurements" Remote Sensing 14, no. 15: 3631. https://doi.org/10.3390/rs14153631
APA StyleDas, S., Wang, Y., Gong, J., Ding, L., Munchak, S. J., Wang, C., Wu, D. L., Liao, L., Olson, W. S., & Barahona, D. O. (2022). A Comprehensive Machine Learning Study to Classify Precipitation Type over Land from Global Precipitation Measurement Microwave Imager (GPM-GMI) Measurements. Remote Sensing, 14(15), 3631. https://doi.org/10.3390/rs14153631






