Multiscale Assimilation of Sentinel and Landsat Data for Soil Moisture and Leaf Area Index Predictions Using an Ensemble-Kalman-Filter-Based Assimilation Approach in a Heterogeneous Ecosystem
Abstract
:1. Introduction
2. Materials and Methods
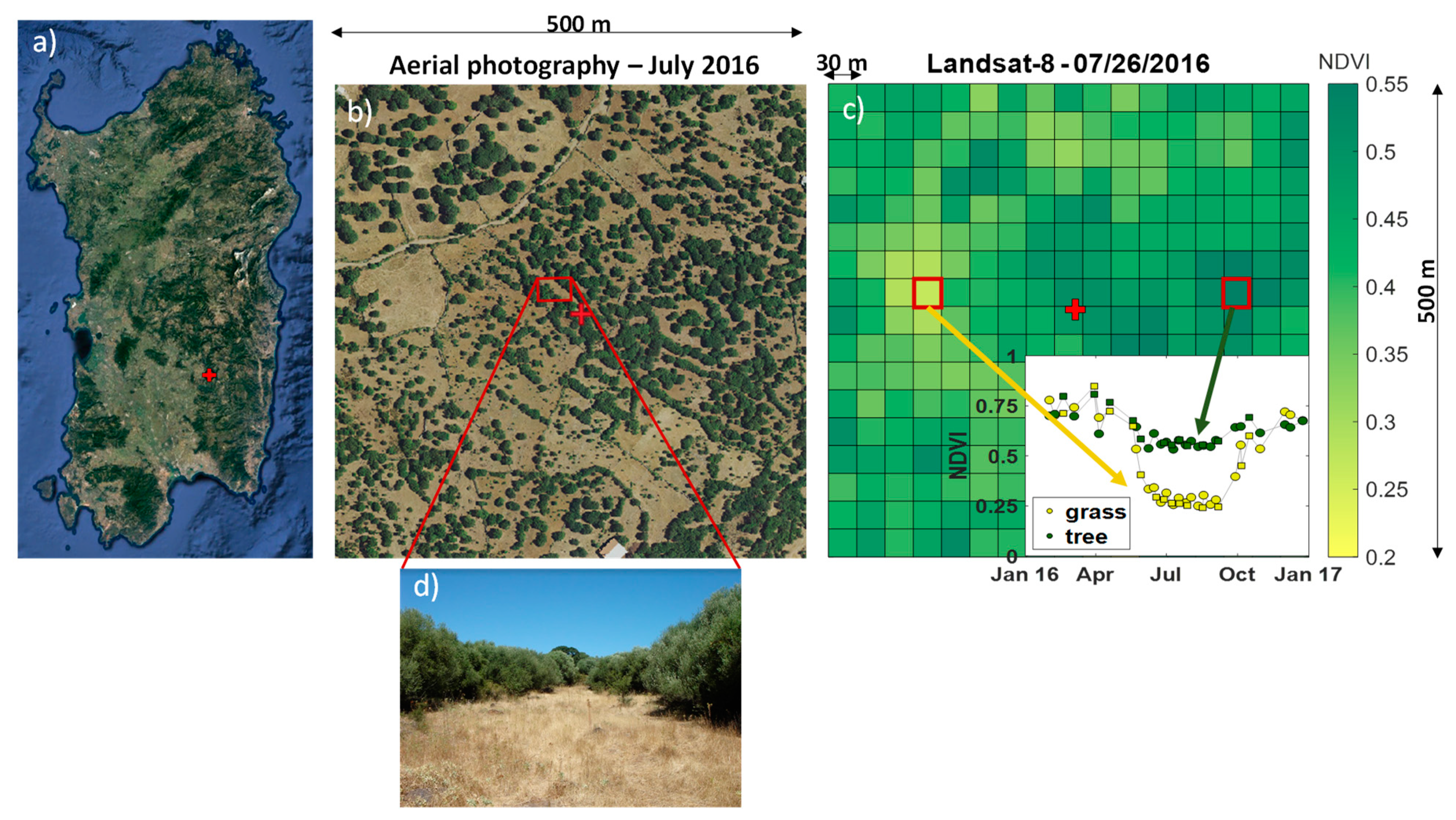
2.1. Case Study
2.1.1. Field Data
2.1.2. Remote Sensing Data
2.2. The Proposed Assimilation Approach
2.2.1. Optical Remote Sensing Data for LAI Estimate
2.2.2. Radar Images for Soil Moisture Retrieval
2.2.3. The Ecohydrological Model
2.2.4. The Land Surface Model
| Equations | Source |
|---|---|
| Drainage | [11] |
| Canopy resistance | [69] |
f3 = 1 − ω log(VPD) | [74] |
| Sensible heat flux , where CH the heat transfer coefficient | [14] |
| Net radiation , with shortwave incoming ration, Rswin; longwave incoming ration, Rlwin, estimated based on Equation 6 in Brutsaert (1982); α—albedo; ε—emissivity; σ—the Stefan–Boltzmann constant | [14] |
| Soil heat flux G = Rn − H − LE | [14] |
| Surface temperature , where T2 is the mean Ts value over one day, τ, and CT is the soil thermal coefficient | [14] |
| Ecophysiological Term | Equations | Source |
|---|---|---|
| Photosynthesis | [76] | |
| Allocation | For the tree cover: | [14] |
| For grass cover: | [14] | |
| Respiration | Maintenance and growth respirations of biomass components: | [77] |
| with Tm = mean daily temperature | [76] | |
where R10 is the reference respiration rate at 10 °C and QN is the soil respiration sensitivity to temperature | [57] | |
| Senescence | [14,77] | |
| Litterfall | [14,77] |
| Parameter | Description | Value | |
|---|---|---|---|
| Grass | Tree | ||
| LSM–VDM parameters | |||
| rs,min [s m−1] | Minimum stomatal resistance | 100 | 300 |
| Tmin [°K] | Minimum temperature | 272.15 | 272.15 |
| Topt [°K] | Optimal temperature | 295.15 | 285.15 |
| Tmax [°K] | Maximum temperature | 313.15 | 318.15 |
| θwp [-] | Wilting point | 0.08 | 0.04 |
| θlim, [-] | Limiting soil moisture for vegetation | 0.20 | 0.17 |
| ω [KPa−1] | Slope of the f3 relation | 0.6 | 0.6 |
| Only VDM parameters | |||
| cl [m2 gDM−1] | Specific leaf areas of the green biomass in growing season | 0.01 | 0.005 |
| cd [m2 gDM−1] | Specific leaf areas of the dead biomass | 0.01 | 0.003 |
| ke [-] | PAR extinction coefficient | 0.5 | 0.5 |
| ξa [-] | Parameter controlling allocation to leaves | 0.6 | 0.55 |
| ξs [-] | Parameter controlling allocation to stem | - | 0.1 |
| ξr [-] | Parameter controlling allocation to roots | 0.4 | 0.35 |
| Ω [-] | Allocation parameter | 0.8 | 0.8 |
| ma [d−1] | Maintenance respiration coefficients for aboveground biomass | 0.032 | 0.001 |
| ga [-] | Growth respiration coefficients for aboveground biomass | 0.28 | 0.69 |
| mr [d−1] | Maintenance respiration coefficients for root biomass | 0.007 | 0.002 |
| gr [-] | Growth respiration coefficients for root biomass | 0.1 | 0.1 |
| Q10 [-] | Temperature coefficient in the respiration process | 2.45 | 2.42 |
| da [d−1] | Death rate of aboveground biomass | 0.05 | 0.0045 |
| dr [d−1] | Death rate of root biomass | 0.003 | 0.005 |
| ka [d−1] | Rate of standing biomass pushed down | 0.05 | 0.35 |
| Only LSM parameters | |||
| zom,v [m] | Vegetation momentum roughness length | 0.05 | 0.5 |
| zov,v [m] | Vegetation water vapor roughness length | zom/7.4 | zom/2.5 |
| zom,bs [m] | Bare soil momentum roughness length | 0.015 | |
| zov,bs [m] | Bare soil water vapor roughness length | zom/10 | |
| θs [-] | Saturated soil moisture | 0.53 | |
| b [-] | Slope of the retention curve | 8 | |
| ks [m/s] | Saturated hydraulic conductivity | 5 × 10−6 | |
| |ψs| [m] | Air entry suction head | 0.79 | |
| drz [m] | Root zone depth | 0.19 | |
2.2.5. The Vegetation Dynamic Model
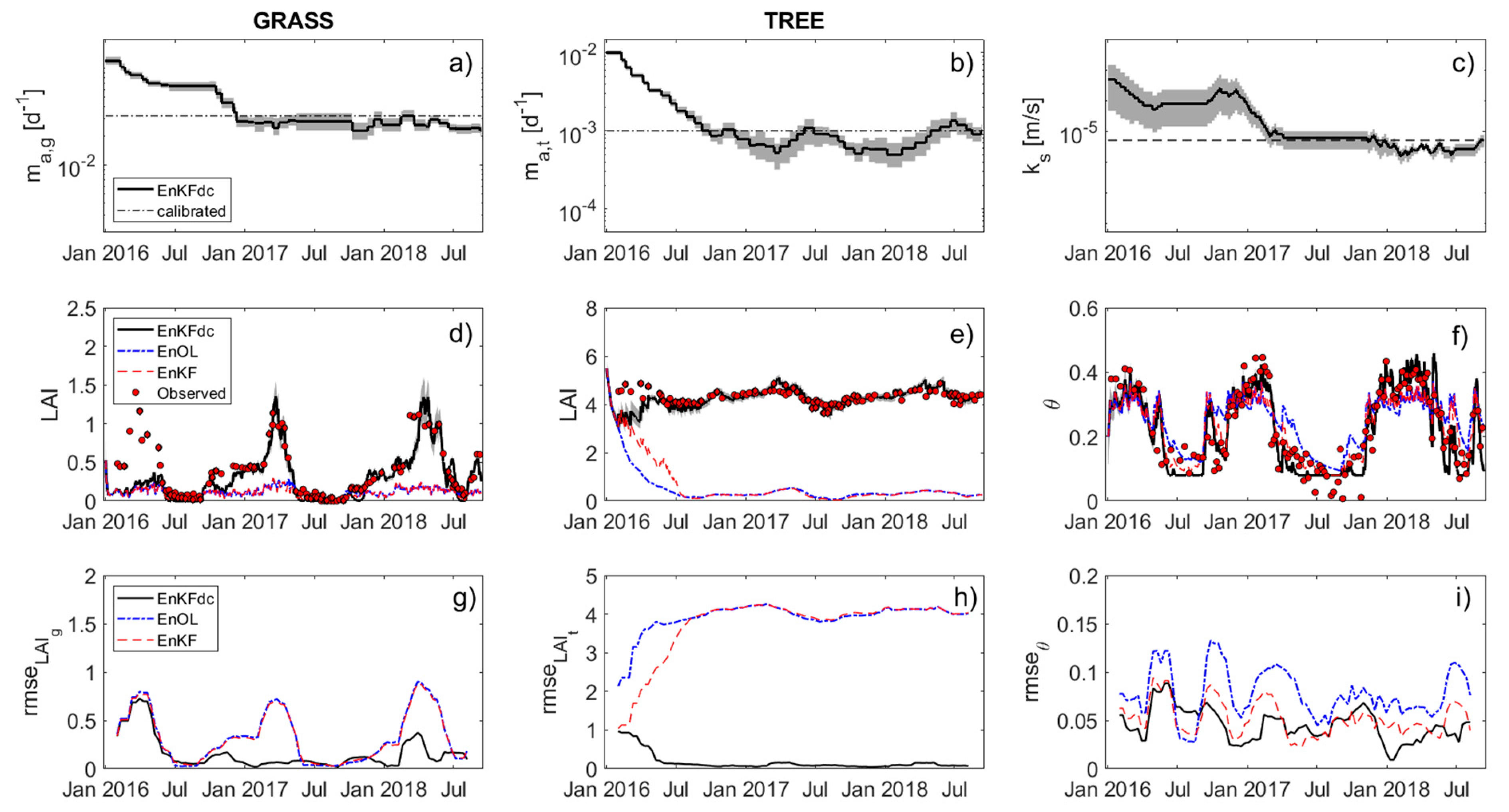
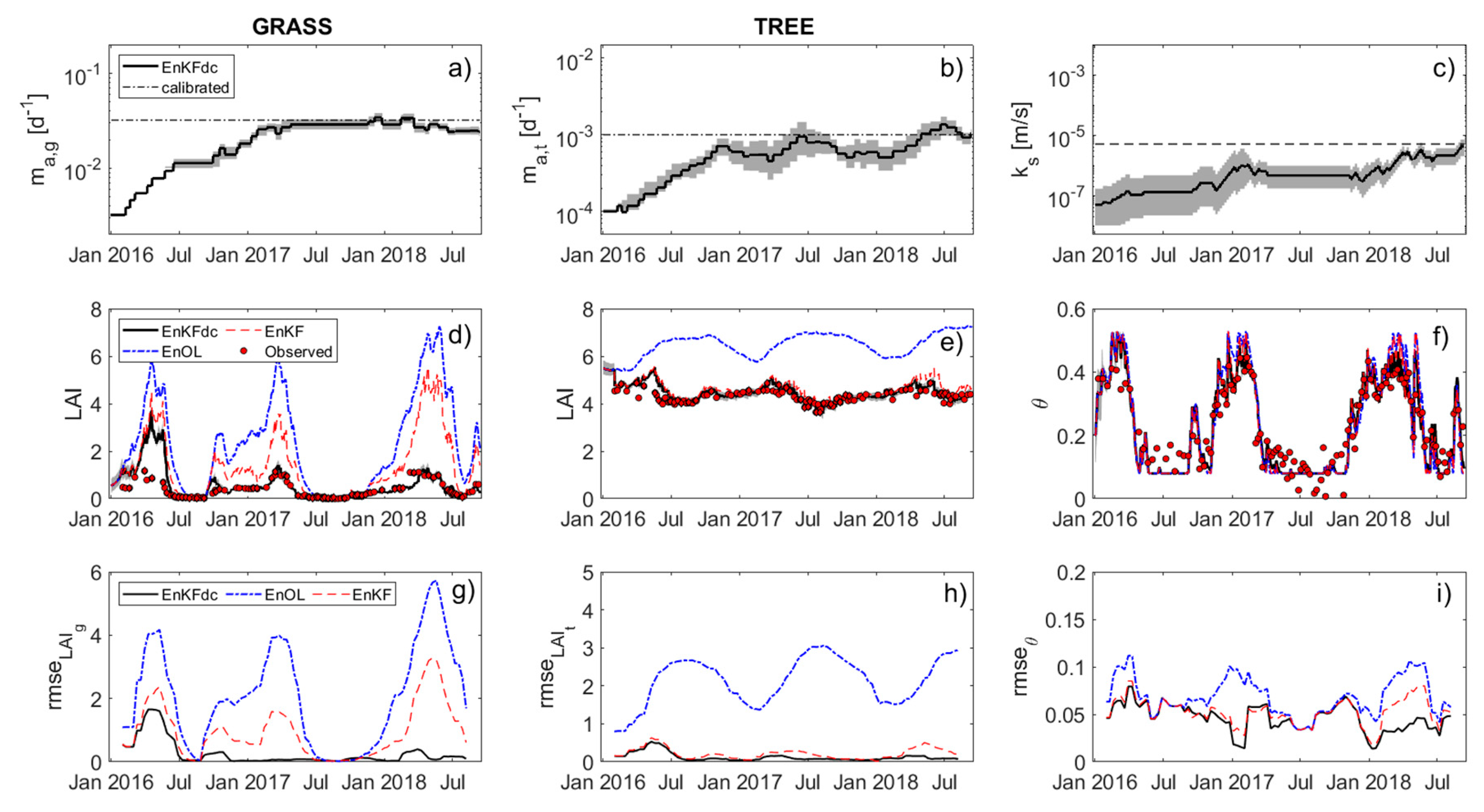
2.2.6. The Ensemble Kalman Filter
2.2.7. The Updating of Model Parameters through the Assimilation
2.2.8. The Multiscale Assimilation Approach
- A land surface model that predicts the ensemble of soil moisture states through (5) at the half-hourly timescale (Δt1);
- A vegetation dynamic model that predicts the ensembles of grass and tree LAI through (8) and (12) at a daily timescale (Δt2);
- EnKF filters of the ε observations (4), which are available every 6 days on average (Δt3); these account for moderate LSM errors and provide optimal updates of the ensemble of through (15) to arrive at ;
- EnKF filters of the NDVI remote data (1) of grass and trees, available over the weekly timescale on average (Δt4), which optimally update the ensembles of of grass and trees through (15) to arrive at ;
- An ensemble of the key LSM parameter, , which is updated through (16) over the weekly timescale (Δt5);
- Finally, the ensembles of grass and trees that are updated through (19) at > weekly (e.g., 3 weeks) timescale (Δt6).
2.2.9. Application of the Assimilation Approach to the Case Study
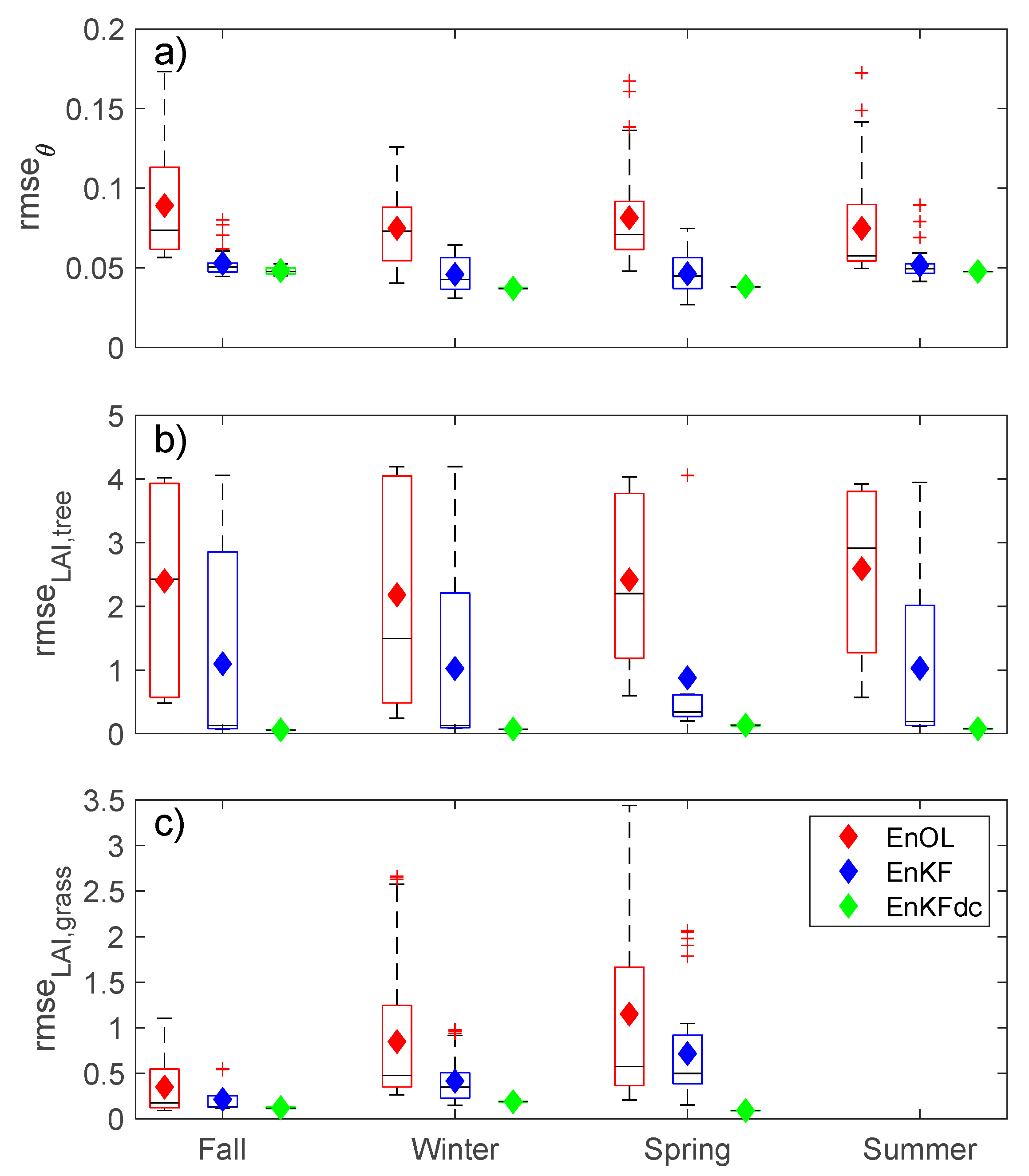
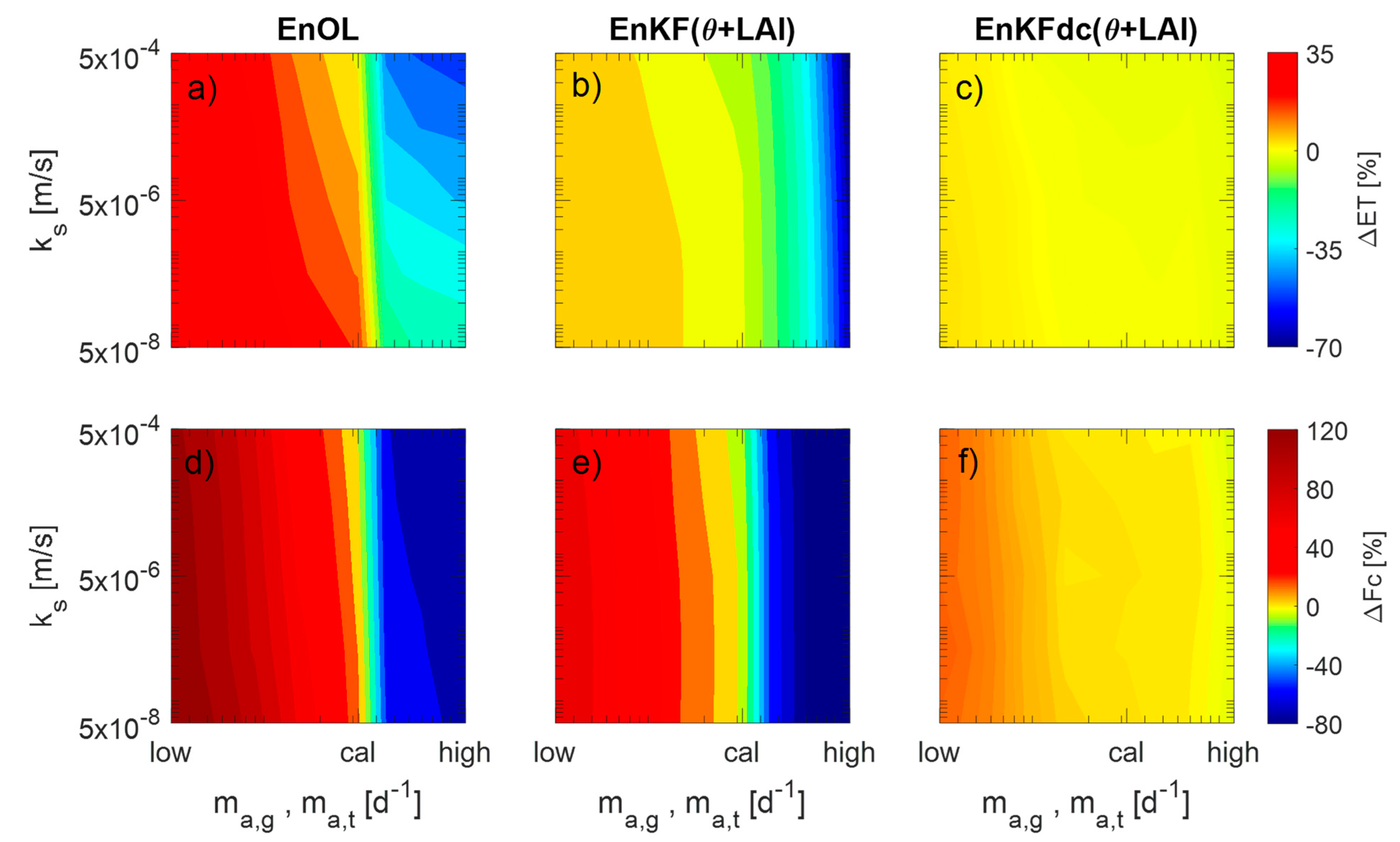
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Huang, S.; Ding, J.L.; Zou, J.; Liu, B.H.; Zhang, J.Y.; Chen, W.Q. Soil Moisture Retrival Based on Sentinel-1 Imagery under Sparse Vegetation Coverage. Sensors 2019, 19, 589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santi, E.; Paloscia, S.; Pettinato, S.; Brocca, L.; Ciabatta, L.; Entekhabi, D. On the synergy of SMAP, AMSR2 AND SENTINEL-1 for retrieving soil moisture. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 114–123. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Amini, J. Towards an object-based multi-scale soil moisture product using coupled Sentinel-1 and Sentinel-2 data. Remote Sens. Lett. 2019, 10, 619–628. [Google Scholar] [CrossRef]
- Hill, T.C.; Quaife, T.; Williams, M. A data assimilation method for using low-resolution Earth observation data in heterogeneous ecosystems. J. Geophys. Res. 2011, 116, D08117. [Google Scholar] [CrossRef] [Green Version]
- Montaldo, N.; Corona, R.; Curreli, M.; Sirigu, S.; Piroddi, L.; Oren, R. Rock water as a key resource for patchy ecosystems on shallow soils: Digging deep tree clumps subsidize surrounding surficial grass. Earth’s Future 2021, 9, e2020EF001870. [Google Scholar] [CrossRef]
- Detto, M.; Montaldo, N.; Albertson, J.D.; Mancini, M.; Katul, G. Soil moisture and vegetation controls on evapotranspiration in a heterogeneous Mediterranean ecosystem on Sardinia, Italy. Water Resour. Res. 2006, 42, 16. [Google Scholar] [CrossRef]
- Axelsson, C.R.; Hanan, N.P. Patterns in woody vegetation structure across African savannas. Biogeosciences 2017, 14, 3239–3252. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.S.; Lin, L.B.; Wu, S.Y.; Deng, K.A.K.; Petropoulos, G.P. Surface soil moisture retrievals over partially vegetated areas from the synergy of Sentinel-1 and Landsat 8 data using a modified water-cloud model. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 76–85. [Google Scholar] [CrossRef]
- Ngadze, F.; Mpakairi, K.S.; Kavhu, B.; Ndaimani, H.; Maremba, M.S. Exploring the utility of Sentinel-2 MSI and Landsat 8 OLI in burned area mapping for a heterogeneous savannah landscape. PLoS ONE 2020, 15, e0232962. [Google Scholar] [CrossRef]
- Cayrol, P.; Chehbouni, A.; Kergoat, L.; Dedieu, G.; Mordelet, P.; Nouvellon, Y. Grassland modeling and monitoring with SPOT-4 VEGETATION instrument during the 1997–1999 SALSA experiment. Agric. For. Meteorol. 2000, 105, 91–115. [Google Scholar] [CrossRef]
- Albertson, J.D.; Kiely, G. On the structure of soil moisture time series in the context of Land Surface Models. J. Hydrol. 2001, 243, 101–119. [Google Scholar] [CrossRef]
- Montaldo, N.; Albertson, J.D.; Mancini, M.; Kiely, G. Robust simulation of root zone soil moisture with assimilation of surface soil moisture data. Water Resour. Res. 2001, 37, 2889–2900. [Google Scholar] [CrossRef] [Green Version]
- Arora, V.K. Simulating energy and carbon fluxes over winter wheat using coupled land surface and terrestrial ecosystem models. Agr. For. Meteorol. 2003, 118, 21–47. [Google Scholar] [CrossRef]
- Montaldo, N.; Albertson, J.D.; Mancini, M. Vegetation dynamics and soil water balance in a water-limited Mediterranean ecosystem on Sardinia, Italy. Hydrol. Earth Syst. Sci. 2008, 12, 1257–1271. [Google Scholar] [CrossRef] [Green Version]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef] [Green Version]
- Bousbih, S.; Zribi, M.; El Hajj, M.; Baghdadi, N.; Lili-Chabaane, Z.; Gao, Q.; Fanise, P. Soil moisture and irrigation mapping in A semi-arid region, based on the synergetic use of Sentinel-1 and Sentinel-2 data. Remote Sens. 2018, 10, 1953. [Google Scholar] [CrossRef] [Green Version]
- Urban, M.; Berger, C.; Mudau, T.E.; Heckel, K.; Truckenbrodt, J.; Odipo, V.O.; Smit, I.P.J.; Schmullius, C. Surface Moisture and Vegetation Cover Analysis for Drought Monitoring in the Southern Kruger National Park Using Sentinel-1, Sentinel-2, and Landsat-8. Remote Sens. 2018, 10, 1482. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Verrelst, J.; Camp-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties-A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Li, X.; Mao, F.; Du, H.; Zhou, G.; Xu, X.; Han, N.; Sun, S.; Gao, G.; Chen, L. Assimilating leaf area index of three typical types of subtropical forest in China from MODIS time series data based on the integrated ensemble Kalman filter and PROSAIL model. ISPRS J. Photogramm. Remote Sens. 2017, 126, 68–78. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Altese, E.; Bolognani, O.; Mancini, M.; Troch, P.A. Retrieving soil moisture over bare soil from ERS 1 synthetic aperture radar data: Sensitivity analysis based on a theoretical surface scattering model and field data. Water Resour. Res. 1996, 32, 653–661. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Dunbar, R.S.; Chaubell, M.J.; Colliander, A.; Yueh, S.; Jagdhuber, T.; Chen, F.; Crow, W.; O’Neill, P.E.; et al. The SMAP and Copernicus Sentinel 1A/B microwave active-passive high resolution surface soil moisture product. Remote Sens. Environ. 2019, 233, 17. [Google Scholar] [CrossRef]
- Brocca, L.; Morbidelli, R.; Melone, F.; Moramarco, T. Soil moisture spatial variability in experimental areas of central Italy. J. Hydrol. 2007, 333, 356–373. [Google Scholar] [CrossRef]
- Merheb, M.; Moussa, R.; Abdallah, C.; Colin, F.; Perrin, C.; Baghdadi, N. Hydrological response characteristics of Mediterranean catchments at different time scales: A meta-analysis. Hydrol. Sci. J. 2016, 61, 2520–2539. [Google Scholar] [CrossRef] [Green Version]
- Prakash, R.; Singh, D.; Pathak, N.P. A Fusion Approach to Retrieve Soil Moisture with SAR and Optical Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 196–206. [Google Scholar] [CrossRef]
- Shi, J.; Du, Y.; Du, J.; Jiang, L.; Chai, L.; Mao, K.; Xu, P.; Ni, W.; Xiong, C.; Liu, Q.; et al. Progresses on microwave remote sensing of land surface parameters. Sci. China Earth Sci. 2012, 55, 1052–1078. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; Lili-Chabaane, Z.; Baghdadi, N.; El Hajj, M.; Gao, Q.; Mougenot, B. Potential of Sentinel-1 Radar Data for the Assessment of Soil and Cereal Cover Parameters. Sensors 2017, 17, 2617. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Xing, M.; He, B.; Wang, J.; Shang, J.; Huang, X.; Xu, M. Estimating Soil Moisture over Winter Wheat Fields during Growing Season Using RADARSAT-2 Data. Remote Sens. 2022, 14, 2232. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Advances in soil moisture retrieval from synthetic aperture radar and hydrological applications. J. Hydrol. 2013, 476, 460–489. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Belaud, G.; Cheviron, B.; Courault, D.; Charron, F. Soil moisture retrieval over irrigated grassland using X-band SAR data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef] [Green Version]
- Montaldo, N.; Fois, L.; Corona, R. Soil Moisture Estimates in a Grass Field Using Sentinel-1 Radar Data and an Assimilation Approach. Remote Sens. 2021, 13, 3293. [Google Scholar] [CrossRef]
- Dubois, P.C.; Vanzyl, J.; Engman, T. Measuring Soil-Moisture with Imaging Radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef] [Green Version]
- Wigneron, J.P.; Olioso, A.; Calvet, J.C.; Bertuzzi, P. Estimating root zone soil moisture from surface soil moisture data and soil-vegetation-atmosphere transfer modeling. Water Resour. Res. 1999, 35, 3735–3745. [Google Scholar] [CrossRef]
- Hoeben, R.; Troch, P.A. Assimilation of active microwave observation data for soil moisture profile estimation. Water Resour. Res. 2000, 36, 2805–2819. [Google Scholar] [CrossRef] [Green Version]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. One-dimensional soil moisture profile retrieval by assimilation of near-surface observations: A comparison of retrieval algorithms. Adv. Water Resour. 2001, 24, 631–650. [Google Scholar] [CrossRef] [Green Version]
- Montaldo, N.; Albertson, J.D.; Mancini, M. Dynamic calibration with an ensemble kalman filter based data assimilation approach for root-zone moisture predictions. J. Hydrometeorol. 2007, 8, 910–921. [Google Scholar] [CrossRef]
- Reichle, R.H.; Walker, J.P.; Koster, R.D.; Houser, P.R. Extended versus ensemble Kalman filtering for land data assimilation. J. Hydrometeorol. 2002, 3, 728–740. [Google Scholar] [CrossRef]
- Evensen, G. Sequential Data Assimilation with A Nonlinear Quasi-Geostrophic Model Using Monte-Carlo Methods To Forecast Error Statistics. J. Geophys. Res.Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Dunne, S.; Entekhabi, D. An ensemble-based reanalysis approach to land data assimilation. Water Resour. Res. 2005, 41, 18. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.V.; Mocko, M.D.; Wang, S.; Peters-Lidard, C.D.; Borak, J. Assimilation of remotely sensed leaf area index into the Noah-MP land surface model: Impacts on water and carbon fluxes and states over the continental United States. J. Hydrometeorol. 2019, 20, 1359–1377. [Google Scholar] [CrossRef]
- Ling, X.L.; Fu, C.B.; Yang, Z.L.; Guo, W.D. Comparison of different sequential assimilation algorithms for satellite-derived leaf area index using the Data Assimilation Research Testbed (version Lanai). Geosci. Model Dev. 2019, 12, 3119–3133. [Google Scholar] [CrossRef] [Green Version]
- Albergel, C.; Zheng, Y.; Bonan, B.; Dutra, E.; Rodríguez-Fernández, N.; Munier, S.; Calvet, J.C. Data assimilation for continuous global assessment of severe conditions over terrestrial surfaces. Hydrol. Earth Syst. Sci. 2020, 24, 4291–4316. [Google Scholar] [CrossRef]
- Bonan, B.; Albergel, C.; Zheng, Y.; Barbu, A.L.; Fairbairn, D.; Munier, S.; Calvet, J.C. An ensemble square root filter for the joint assimilation of surface soil moisture and leaf area index within the Land Data Assimilation System LDAS-Monde: Application over the Euro-Mediterranean region. Hydrol. Earth Syst. Sci. 2020, 24, 325–347. [Google Scholar] [CrossRef] [Green Version]
- Rahman, A.; Maggioni, V.; Zhang, X.; Houser, P.; Sauer, T.; Mocko, D.M. The Joint Assimilation of Remotely Sensed Leaf Area Index and Surface Soil Moisture into a Land Surface Model. Remote Sens. 2022, 14, 437. [Google Scholar] [CrossRef]
- Pan, H.Z.; Chen, Z.X.; de Wit, A.; Ren, J.Q. Joint Assimilation of Leaf Area Index and Soil Moisture from Sentinel-1 and Sentinel-2 Data into the WOFOST Model for Winter Wheat Yield Estimation. Sensors 2019, 19, 3161. [Google Scholar] [CrossRef] [Green Version]
- Zhuo, W.; Huang, J.X.; Li, L.; Zhang, X.D.; Ma, H.Y.; Gao, X.R.; Huang, H.; Xu, B.D.; Xiao, X.M. Assimilating Soil Moisture Retrieved from Sentinel-1 and Sentinel-2 Data into WOFOST Model to Improve Winter Wheat Yield Estimation. Remote Sens. 2019, 11, 1618. [Google Scholar] [CrossRef] [Green Version]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state-parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef] [Green Version]
- Nie, S.; Zhu, J.; Luo, Y. Simultaneous estimation of land surface scheme states and parameters using the ensemble Kalman filter: Identical twin experiments. Hydrol. Earth Syst. Sci. 2011, 15, 2437–2457. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Hendricks Franssen, H.J.; Han, X.; Vrugt, J.A.; Vereecken, H. State and parameter estimation of two land surface models using the ensemble Kalman filter and the particle filter. Hydrol. Earth Syst. Sci. 2017, 21, 4927–4958. [Google Scholar] [CrossRef] [Green Version]
- Lü, H.; Yu, Z.; Horton, R.; Zhu, Y.; Wang, Z.; Hao, Z.; Xiang, L. Multi-scale assimilation of root zone soil water predictions. Hydrol. Processes 2011, 25, 3158–3172. [Google Scholar] [CrossRef]
- Lü, H.; Yu, Z.; Zhu, Y.; Drake, S.; Hao, Z.; Sudicky, E.A. Dual state-parameter estimation of root zone soil moisture by optimal parameter estimation and extended Kalman filter data assimilation. Adv. Water Resour. 2011, 34, 395–406. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Improved prediction of unsaturated hydraulic conductivity with the Mualem-van Genuchten model. Soil Sci. Soc. Am. J. 2000, 64, 843–851. [Google Scholar] [CrossRef] [Green Version]
- Montaldo, N.; Mancini, M.; Rosso, R. Flood hydrograph attenuation induced by a reservoir system: Analysis with a distributed rainfall-runoff model. Hydrol. Processes 2004, 18, 545–563. [Google Scholar] [CrossRef]
- Montaldo, N.; Gaspa, A. Multi Scale Assimilation of NDVI data for Leaf Area Index Predictions in an Heterogeneous Mediterranean Ecosystem. Agric. For. Meteorol. 2022; submitted. [Google Scholar]
- Montaldo, N.; Corona, R.; Albertson, J.D. On the separate effects of soil and land cover on Mediterranean ecohydrology: Two contrasting case studies in Sardinia, Italy. Water Resour. Res. 2013, 49, 1123–1136. [Google Scholar] [CrossRef]
- Montaldo, N.; Curreli, M.; Corona, R.; Oren, R. Fixed and variable components of evapotranspiration in a Mediterranean wild-olive-grass landscape mosaic. Agric. For. Meteorol. 2020, 280, 107769. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Change Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.K.; Prasad, T.S.; Vijayan, D. Relationship between LAI and NDVI for IRS LISS and Landsat TM bands. Adv. Space Res. 2000, 26, 1047–1050. [Google Scholar] [CrossRef]
- Potithep, S.; Nasahara, N.K.; Muraoka, H.; Nagai, S.; Suzuki, R. What is the actual relationship between LAI and VI in a deciduous broadleaf forest. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 609–614. [Google Scholar]
- Amazirh, A.; Merlin, O.; Er-Raki, S.; Gao, Q.; Rivalland, V.; Malbeteau, Y.; Khabba, S.; Escorihuela, M.J. Retrieving surface soil moisture at high spatio-temporal resolution from a synergy between Sentinel-1 radar and Landsat thermal data: A study case over bare soil. Remote Sens. Environ. 2018, 211, 321–337. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Musial, J.; Malinska, A.; Budzynska, M.; Gurdak, R.; Kiryla, W.; Bartold, M.; Grzybowski, P. Soil Moisture in the Biebrza Wetlands Retrieved from Sentinel-1 Imagery. Remote Sens. 2018, 10, 1979. [Google Scholar] [CrossRef] [Green Version]
- Capodici, F.; Maltese, A.; Ciraolo, G.; La Loggia, G.; D’Urso, G. Coupling two radar backscattering models to assess soil roughness and surface water content at farm scale. Hydrol. Sci. J. 2013, 58, 1677–1689. [Google Scholar] [CrossRef] [Green Version]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef] [Green Version]
- Montaldo, N.; Albertson, J.D. On the use of the force–restore SVAT model formulation for stratified soils. J. Hydrometeorol. 2001, 2, 571–578. [Google Scholar] [CrossRef]
- Noihlan, J.; Planton, S. A Simple parameterization of Land Sur- face Processes for Meteorological Models. Mon. Weather. Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W. Evaporation into the Atmosphere; Kluwer Academic Publications: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. T. Roy. Soc. B 1976, 273, 593–610. [Google Scholar]
- Parlange, M.B.; Albertson, J.D.; Eichinger, W.E.; Cahill, A.T.; Jackson, T.J. Evaporation: Use of fast response turbulence sensors, raman lidar and passive microwave remote sensing. In Vadose Zone Hydrology: Cutting Across Disciplines; Parlange, M.B., Hopmans, J.W., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 260–278. [Google Scholar]
- Novick, K.A.; Stoy, P.C.; Katul, G.G.; Ellsworth, D.S.; Siqueira, M.B.S.; Juang, J.; Oren, R. Carbon dioxide and water vapor exchange in a warm temperate grassland. Oecologia 2004, 138, 259–274. [Google Scholar] [CrossRef] [PubMed]
- Ruehr, N.K.; Buckmann, N. Soil respiration fluxes in a temperate mixed forest: Seasonality and temperature sensitivities differ among microbial and root–rhizosphere respiration. Tree Physiol. 2009, 30, 165–176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Larcher, W. Physiological Plant Ecology, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Montaldo, N.; Rondena, R.; Albertson, J.D.; Mancini, M. Parsimonious modeling of vegetation dynamics for ecohydrologic studies of water-limited ecosystems. Water Resour. Res. 2005, 41, 16. [Google Scholar] [CrossRef]
- Nouvellon, Y.; Rambal, S.; Lo Seen, D.; Moran, M.S.; Lhomme, J.P.; Begue, A.; Chehbouni, A.G.; Kerr, Y. Modelling of daily fluxes of water and carbon from shortgrass steppes. Agric. For. Meteorol. 2000, 100, 137–153. [Google Scholar] [CrossRef]
- Hanson, J.D.; Skiles, J.W.; Parton, W.J. A multi-species model for rangeland plant communities. Ecol. Modell. 1988, 44, 89–123. [Google Scholar] [CrossRef]
- Crow, W.T.; Wood, E.F. The assimilation of remotely sensed soil brightness temperature imagery into a land surface model using Ensemble Kalman filtering: A case study based on ESTAR measurements during SGP97. Adv. Water Resour. 2003, 26, 137–149. [Google Scholar] [CrossRef]
- Margulis, S.A.; McLaughlin, D.; Entekhabi, D.; Dunne, S. Land data assimilation and estimation of soil moisture using measurements from the Southern Great Plains 1997 Field Experiment. Water Resour. Res. 2002, 38, 18. [Google Scholar] [CrossRef]
- Montaldo, N.; Albertson, J.D. Multi-scale assimilation of surface soil moisture data for robust root zone moisture predictions. Adv. Water Resour. 2003, 26, 33–44. [Google Scholar] [CrossRef]
- Chavez, P.S. Image-based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Lumaret, R.; Ouazzani, N. Ancient wild olives in Mediterranean forests. Nature 2001, 413, 700. [Google Scholar] [CrossRef]
- Terral, J.F.; Alonso, N.; Capdevila, R.B.I.; Chatti, N.; Fabre, L.; Fiorentino, G.; Alibert, P. Historical biogeography of olive domestication (Olea europaea L.) as revealed by geometrical morphometry applied to biological and archaeological material. J. Biogeogr. 2004, 31, 63–77. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration analysis of SAR signals in the C and L bands for wheat, maize, and grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef] [Green Version]
- Benninga, H.J.F.; van der Velde, R.; Su, Z. Sentinel-1 soil moisture content and its uncertainty over sparsely vegetated fields. J. Hydrol. X 2020, 9, 100066. [Google Scholar] [CrossRef]
- Schönbrodt-Stitt, S.; Ahmadian, N.; Kurtenbach, M.; Conrad, C.; Romano, N.; Bogena, H.R.; Nasta, P. Statistical exploration of Sentinel-1 data, terrain parameters, and in-situ data for estimating the near-surface soil moisture in a mediterranean agroecosystem. Front. Water 2021, 3, 75. [Google Scholar] [CrossRef]
- Dee, D.P. Bias and data assimilation. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2005, 131, 3323–3343. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Weerts, A.H.; Clark, M.; Hendricks Franssen, H.J.; Kumar, S.; Moradkhani, H.; Restrepo, P. Advancing data assimilation in operational hydrologic forecasting: Progresses, challenges, and emerging opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D.D.; Xu, L.; Kiang, N. How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak-grass savanna and an annual grassland. Agric. Forest. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Iturbe, I. Ecohydrology: A hydrologic perspective of climate-soil-vegetation dynamics. Water Resour. Res. 2000, 36, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Kurc, S.A.; Small, E.E. Dynamics of evapotranspiration in semiarid grassland and shrubland ecosystems during the summer monsoon season, central New Mexico. Water Resour. Res. 2004, 40, W09305. [Google Scholar] [CrossRef]
- Montaldo, N.; Toninelli, V.; Albertson, J.D.; Mancini, M.; Troch, P.A. The effect of background hydrometeorological conditions on the sensitivity of evapotranspiration to model parameters: Analysis with measurements from an Italian alpine catchment. Hydrol. Earth Syst. Sci. 2003, 7, 848–861. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montaldo, N.; Gaspa, A.; Corona, R. Multiscale Assimilation of Sentinel and Landsat Data for Soil Moisture and Leaf Area Index Predictions Using an Ensemble-Kalman-Filter-Based Assimilation Approach in a Heterogeneous Ecosystem. Remote Sens. 2022, 14, 3458. https://doi.org/10.3390/rs14143458
Montaldo N, Gaspa A, Corona R. Multiscale Assimilation of Sentinel and Landsat Data for Soil Moisture and Leaf Area Index Predictions Using an Ensemble-Kalman-Filter-Based Assimilation Approach in a Heterogeneous Ecosystem. Remote Sensing. 2022; 14(14):3458. https://doi.org/10.3390/rs14143458
Chicago/Turabian StyleMontaldo, Nicola, Andrea Gaspa, and Roberto Corona. 2022. "Multiscale Assimilation of Sentinel and Landsat Data for Soil Moisture and Leaf Area Index Predictions Using an Ensemble-Kalman-Filter-Based Assimilation Approach in a Heterogeneous Ecosystem" Remote Sensing 14, no. 14: 3458. https://doi.org/10.3390/rs14143458
APA StyleMontaldo, N., Gaspa, A., & Corona, R. (2022). Multiscale Assimilation of Sentinel and Landsat Data for Soil Moisture and Leaf Area Index Predictions Using an Ensemble-Kalman-Filter-Based Assimilation Approach in a Heterogeneous Ecosystem. Remote Sensing, 14(14), 3458. https://doi.org/10.3390/rs14143458






