GNSSseg, a Statistical Method for the Segmentation of Daily GNSS IWV Time Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model
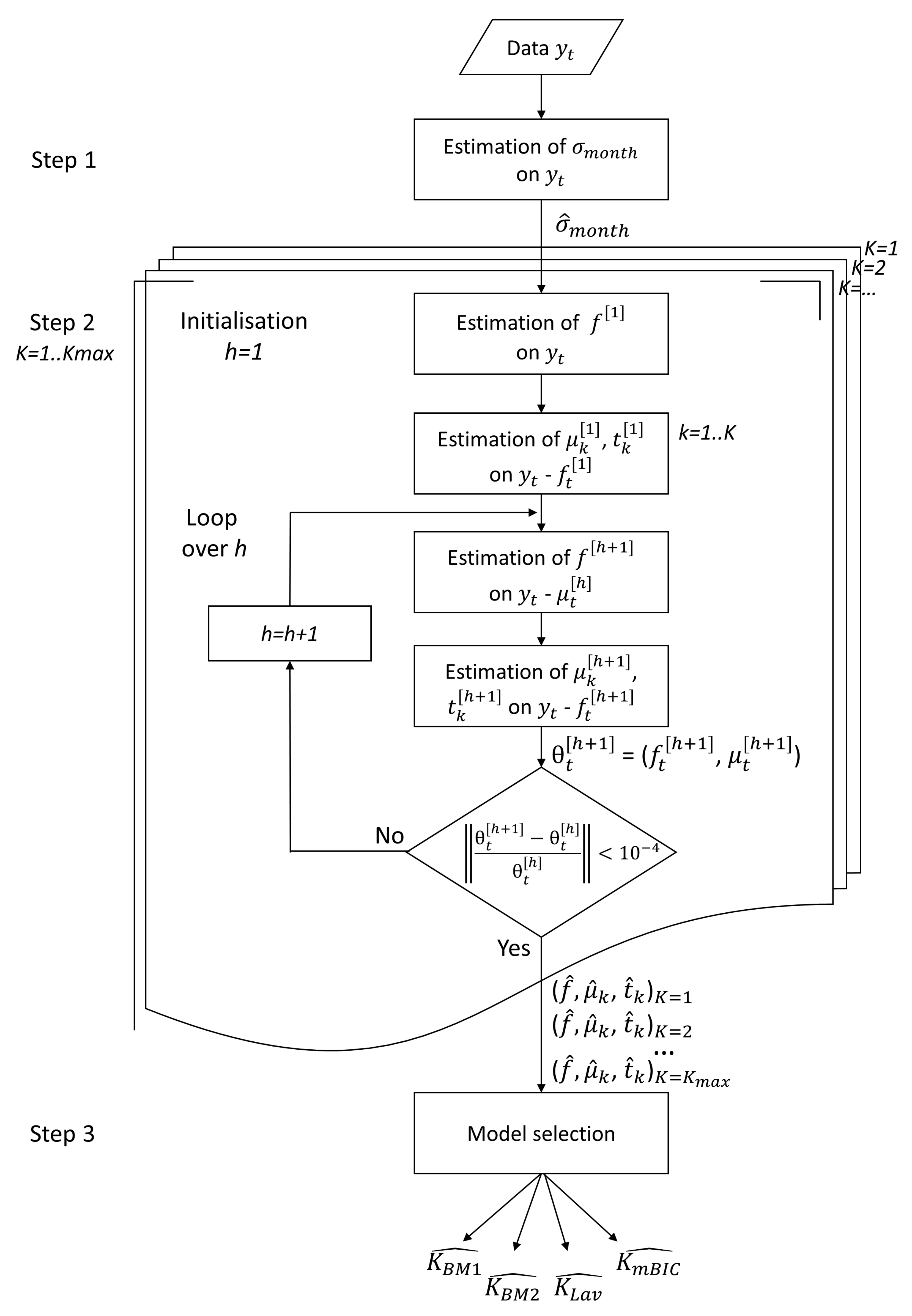
2.2. Inference
- Step 1
- Estimation of . The classical sample variance estimator cannot be used here because of the presence of change points in the series. Following Bock et al. [8], we use instead the Qn estimator proposed by Rousseeuw and Croux [32], applied to the differentiated series . The differentiation acts to center the series, except at the change point positions, which can be seen as outliers. Because the Qn estimator is not sensitive to outliers, the resulting variance estimator has low bias and high efficiency. The estimated variance is denoted . We propose to estimate the variance parameters before we start the iterative procedure (Step 2). This choice was made after testing the alternative version in which the variance parameters are updated at each iteration of the iterative procedure. In the alternative version, the variance estimates were slightly more accurate but at the severe cost of slowing down the convergence, with no significant benefit in the segmentation results. Thus, we opted for the estimation of the variance parameters before the iterative procedure. Note that the presence of the function f in our model has little impact on the resulting variance estimation because it is a smoothly varying function (see below).
- Step 2
- Estimation of f, t, and . These parameters are estimated iteratively for a given K, where the variances are estimated in Step 1. The estimates are obtained by maximizing the log-likelihood given by Equation (2), which is equivalent to minimizing the following squared sum of residuals, , in a least-squares sense:At iteration :
- (a)
- The estimator of f results in a weighted least-squares estimator with weights on . For our application, we follow [39] and represent f as a Fourier series of order 4, which accounts for annual, semi-annual, ter-annual, and quarter-annual periodicities in the signal:where is the angular frequency of period and L is the mean length of the year ( days when time t is expressed in days). The estimated function is denoted .
- (b)
- The segmentation parameters are estimated based on . We obtainandwhere is the set of all the possible partitions of the grid in K segments. This turns into a classical segmentation problem for which DP applies.
The final estimators are denoted , , and . - Step 3
- Choice of K. This is the most delicate and difficult problem. We use three penalized least-squares-based criteria since the segmentation is conducted with ‘known’ variances. The model selection strategy consists in selecting K as follows:where is defined by (3). We recall the three considered criteria:
- Lav
- BM
- mBIC
- the modified version of the classical BIC criterion derived in the segmentation framework by [36], which is a BIC-based criterion with the integration of a penalty term depending on the segment lengths.
2.3. Procedure Settings and R Packages
2.3.1. Maximal Number of Segments,
2.3.2. Iterative Procedure of Step 2
2.3.3. Time Complexity
2.3.4. R Packages
2.4. Simulation Study
3. Results
3.1. Data, Metadata, Outlier Detection, and Validation Procedures
3.2. General Results
3.3. Examples of Special Cases
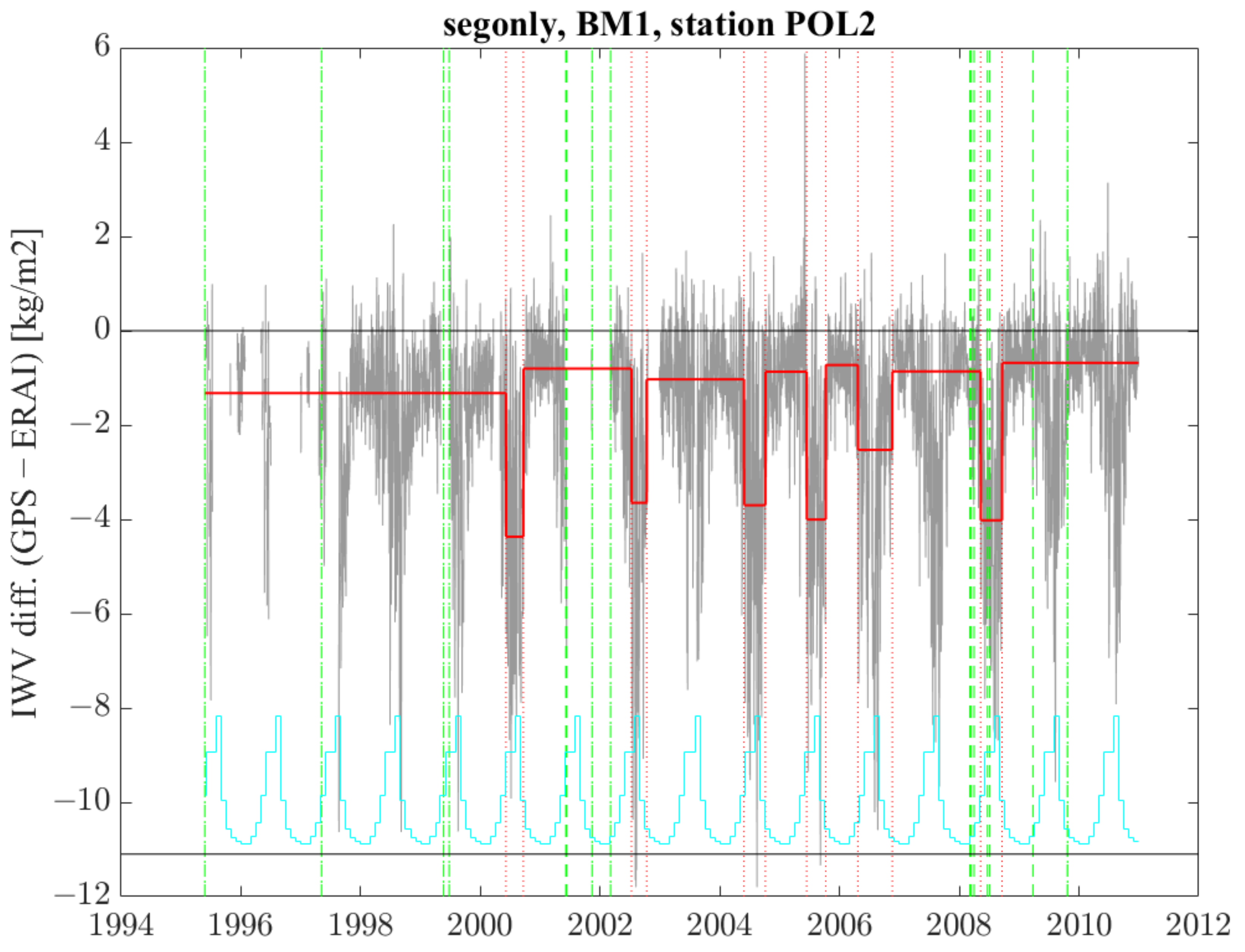
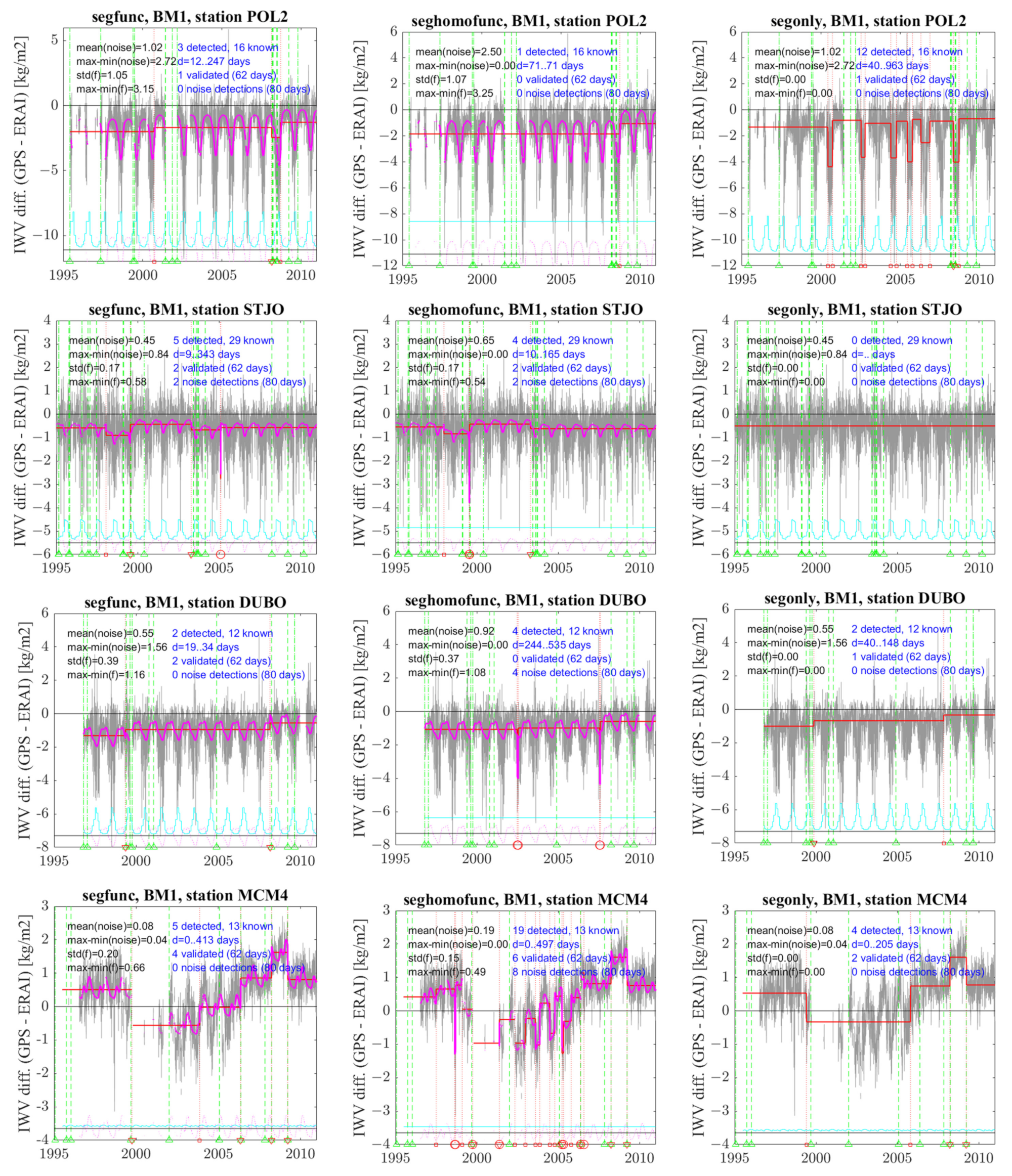
- In the case of POL2, variants segfunc, segonly, and seghomofunc detect 3, 12, and 1 change point(s), respectively. The signal shows a strong periodic variation, which is well fitted with segfunc and seghomofunc but is erroneously captured by the segmentation with segonly. Variant segfunc has one validated change point (23 February 2008), while segonly has no validation, although it detects 12 change points. Variant seghomofunc detects only one change point, which is located 72 days from the nearest known change point and is thus not validated, but it coincides with one of the three detections found by segfunc. The detection of this change point is made difficult because it is located in a month with strong noise.
- In the case of STJO, variants segfunc and seghomofunc detect five and four change points, respectively, with two similar validated change points (at 20 July 1999 and 18 April 2003) and one cluster of two outliers each. The two clusters are not at the same positions, but both are associated with a significant change in mean before/after and their outliers are thus replaced with one single change point at mid-range by the screening procedure. Variant segonly gives no detection in this case. This is due to the ‘Big Jump’ heuristic, as discussed in the section above.
- In the case of DUBO, variants segfunc and segonly detect two change points at almost the same position. Both are located close to known changes and are validated with segfunc, but only one is validated with segonly. Variant seghomofunc has two clusters of two outliers and no validation. Both clusters are associated with significant changes in mean before/after and thus two change points remain after screening. The second one is close to a change point detected by the other variants.
- Finally, for MCM4, the signal has very marked inhomogeneities in the form of several abrupt changes in the mean but also large oscillations between 2000 and 2005. The abrupt changes are well captured by segfunc, which detects five change points, among which four are validated. The non-stationary oscillations are only partly modeled by the periodic function. This is a special case where the functional model does not well capture the full signal. This result advocates for a future improvement of the modeling of the functional part. Variant segonly works quite well too and leads to almost the same detections as segfunc, but only two change points are validated. Variant seghomofunc, on the other hand, significantly overestimates the number of change points in order to fit the non-stationary oscillations. It also contains several outliers. This variant has six validated change points, with two additional ones compared to segfunc, but this may be by chance because the total number of change points is quite large.
3.4. Semi-Automatic Selection of Change Points
- (1)
- Is there any one criterion that performs well and could be used systematically?
- (2)
- Is the solution with the smallest number of change points a better choice?
- (3)
- Is the solution selected by more than one criterion a better choice?
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Segmentation Results for 120 GNSS Stations
| Name | Date | Flag | Name | Date | Flag | Name | Date | Flag |
|---|---|---|---|---|---|---|---|---|
| algo | 12 December 2008 | RC | gode | 06 August 1998 | U | mcm4 | 18 May 2006 | R |
| algo | 26 March 2009 | PC | gope | 26 April 1996 | U | mcm4 | 31 March 2008 | P |
| alic | 31 July 1999 | RC | gope | 24 July 2000 | RADGT | mcm4 | 26 March 2009 | P |
| alic | 20 April 2006 | UC | gope | 01 January 2002 | UGTL | mdo1 | 24 December 2001 | UC |
| ankr | 24 November 2000 | RAL | gope | 18 January 2005 | UL | mdo1 | 18 April 2004 | UC |
| ankr | 06 May 2008 | RADGTL | guam | 26 April 2000 | RGT | medi | 27 March 1999 | UC |
| areq | 28 January 2000 | RC | guam | 19 September 2004 | U | medi | 27 June 2004 | UC |
| areq | 23 April 2001 | UC | hers | 01 January 1998 | RAGTC | medi | 14 May 2006 | UC |
| areq | 20 August 2004 | U | hers | 10 September 2000 | UC | monp | 22 March 2000 | AD |
| azu1 | 12 February 2008 | RC | hob2 | 16 August 1999 | RGTL | nlib | 11 August 1998 | U |
| azu1 | 03 October 2008 | RC | hob2 | 02 April 2002 | RL | nlib | 12 March 2003 | U |
| azu1 | 20 July 2010 | R | hob2 | 04 October 2005 | RTL | nlib | 15 November 2009 | U |
| blyt | 14 May 1998 | R | holb | 02 January 2002 | RGTC | onsa | 02 February 1999 | RAD |
| bor1 | 24 June 2003 | UT | holb | 15 November 2005 | UC | penc | 22 January 2001 | UC |
| bor1 | 26 March 2009 | P | holb | 06 March 2009 | RTC | penc | 08 December 2003 | RTC |
| braz | 05 November 2005 | T | holp | 19 November 1997 | R | pert | 12 June 1996 | R |
| brmu | 01 October 1997 | R | hrao | 26 April 2000 | RGTC | pert | 06 June 2001 | RA |
| brus | 09 June 2006 | UC | hrao | 02 August 2004 | UC | pert | 18 August 2006 | U |
| brus | 26 October 2008 | UC | hrao | 23 February 2006 | AGT | pin1 | 28 February 2001 | AD |
| cagl | 11 July 2001 | RAGT | iisc | 02 May 2004 | UC | pots | 15 January 1996 | R |
| cas1 | 27 January 1996 | RC | iisc | 22 July 2006 | UC | pots | 19 August 1999 | RGT |
| cas1 | 27 November 1997 | UC | irkt | 17 April 1998 | UL | pots | 15 April 2009 | A |
| cas1 | 05 February 2000 | RT | irkt | 17 June 2003 | UL | quin | 13 November 2002 | RA |
| cas1 | 31 March 2008 | P | karr | 22 August 2006 | U | reyk | 13 June 2003 | A |
| cas1 | 02 December 2008 | RPT | kely | 14 September 2001 | RADL | reyk | 31 March 2008 | P |
| ccjm | 24 February 2001 | RA | kely | 11 November 2006 | UL | reyk | 26 March 2009 | P |
| cedu | 10 September 1997 | RA | kely | 17 December 2009 | UL | rock | 10 June 1999 | RT |
| cfag | 06 May 1997 | UL | kerg | 31 March 1999 | RA | sant | 02 November 1999 | RC |
| cfag | 21 January 2008 | UL | kerg | 14 November 2002 | UGT | sant | 14 December 2000 | RC |
| chat | 28 March 2002 | RUC | kiru | 01 December 2004 | U | shao | 08 February 2003 | U |
| chat | 31 March 2008 | PC | kit3 | 31 March 2008 | P | sio3 | 12 April 2000 | AD |
| chil | 30 May 1995 | AD | kokb | 23 July 1999 | R | sni1 | 19 December 2000 | AD |
| clar | 12 September 1996 | R | kokb | 21 July 2001 | U | stjo | 23 January 1998 | UC |
| coco | 04 September 1998 | RGT | kokb | 06 December 2006 | U | stjo | 29 July 1999 | RC |
| coco | 09 August 2003 | UL | kosg | 07 December 1996 | U | svtl | 23 October 2008 | RADT |
| coco | 13 January 2007 | UL | kosg | 28 February 1999 | R | syog | 08 February 2000 | RT |
| coso | 09 November 2000 | U | kosg | 27 November 2000 | !RGT | syog | 25 January 2007 | RGT |
| crfp | 12 November 1997 | RC | kosg | 29 September 2009 | U | syog | 31 March 2008 | P |
| crfp | 27 May 2002 | UC | kour | 30 July 1999 | R | syog | 26 March 2009 | P |
| crfp | 07 September 2005 | UC | kour | 21 November 2000 | U | tow2 | 29 August 1998 | U |
| cro1 | 30 September 1999 | R | kour | 30 September 2004 | R | tow2 | 01 November 2003 | U |
| cro1 | 04 August 2005 | RAD | kour | 13 December 2009 | U | tow2 | 14 February 2006 | RT |
| darw | 21 June 1998 | UT | lama | 06 October 2000 | AD | trak | 04 August 1995 | AD |
| darw | 23 December 2003 | UC | lbch | 01 September 1998 | U | trak | 05 February 2004 | U |
| darw | 03 November 2005 | UC | lbch | 05 February 2004 | U | uclu | 16 May 2003 | UC |
| dav1 | 14 March 2002 | UC | long | 04 April 1995 | RA | uclu | 04 May 2007 | RACT |
| dav1 | 27 January 2003 | UC | long | 05 September 1996 | R | usud | 05 October 2000 | RT |
| dav1 | 31 March 2008 | P | long | 25 March 2001 | U | vill | 18 July 2000 | R |
| dav1 | 31 January 2009 | P | long | 02 January 2007 | U | vill | 03 December 2004 | R |
| dav1 | 04 May 2010 | R | lpgs | 02 May 2003 | U | vndp | 17 March 1996 | R |
| dgar | 15 November 2006 | U | lpgs | 30 August 2006 | ? | wes2 | 05 February 1998 | R |
| dhlg | 23 December 1999 | R | mac1 | 04 January 2001 | R | wes2 | 26 July 2000 | RA |
| drao | 08 October 1999 | RGT | madr | 18 August 1999 | R | wes2 | 29 June 2001 | RA |
| dubo | 04 October 1999 | RAD | madr | 07 November 2004 | U | wlsn | 18 August 1997 | U |
| dubo | 31 March 2008 | P | mas1 | 14 August 1999 | R | wlsn | 11 January 2000 | U |
| ebre | 23 February 1999 | U | mas1 | 30 March 2006 | U | wlsn | 29 March 2006 | U |
| ebre | 16 November 2005 | RT | mate | 25 September 2001 | R | wslr | 29 March 2000 | RAD |
| fair | 03 June 1999 | RTC | maw1 | 07 November 1997 | U | wtzr | 30 June 2009 | R |
| fair | 15 April 2000 | RTC | maw1 | 22 August 1999 | R | wuhn | 08 June 2000 | RAD |
| fale | 04 September 1998 | UC | maw1 | 07 December 2004 | RT | wuhn | 18 September 2006 | U |
| fale | 01 June 2001 | UC | maw1 | 04 May 2010 | R | yell | 22 August 1996 | A |
| flin | 21 September 1999 | AD | mcm4 | 07 September 1999 | R | |||
| flin | 03 January 2008 | P | mcm4 | 13 November 2003 | UGT |
References
- Trenberth, K.E.; Jones, P.D.; Ambenje, P.; Bojariu, R.; Easterling, D.; Klein Tank, A.; Parker, D.; Rahimzadeh, F.; Renwick, J.A.; Rusticucci, M.; et al. Observations. Surface and Atmospheric Climate Change. In IPCC Fourth Assessment Report: Climate Change 2007; Working Group I: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2007; Chapter 3; pp. 235–336. [Google Scholar]
- Held, I.M.; Soden, B.J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 2000, 25, 445–475. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, T.; Elgered, G. Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Bock, O.; Willis, P.; Lacarra, M.; Bosser, P. An inter-comparison of zenith tropospheric delays derived from DORIS and GPS data. Adv. Space Res. 2010, 46, 1408–1447. [Google Scholar] [CrossRef]
- Vey, S.; Dietrich, R.; Fritsche, M.; Rülke, A.; Steigenberger, P.; Rothacher, M. On the homogeneity and interpretation of precipitable water time series derived from global GPS observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Parracho, A.C.; Bock, O.; Bastin, S. Global IWV trends and variability in atmospheric reanalyses and GPS observations. Atmos. Chem. Phys. 2018, 18, 16213–16237. [Google Scholar] [CrossRef] [Green Version]
- Ning, T.; Wickert, J.; Deng, Z.; Heise, S.; Dick, G.; Vey, S.; Schöne, T. Homogenized Time Series of the Atmospheric Water Vapor Content Obtained from the GNSS Reprocessed Data. J. Clim. 2016, 29, 2443–2456. [Google Scholar] [CrossRef]
- Bock, O.; Collilieux, X.; Guillamon, F.; Lebarbier, E.; Pascal, C. A breakpoint detection in the mean model with heterogeneous variance on fixed time intervals. Stat. Comput. 2020, 30, 195–207. [Google Scholar] [CrossRef] [Green Version]
- Van Malderen, R.; Pottiaux, E.; Klos, A.; Domonkos, P.; Elias, M.; Ning, T.; Bock, O.; Guijarro, J.; Alshawaf, F.; Hoseini, M.; et al. Homogenizing GPS Integrated Water Vapor Time Series: Benchmarking Break Detection Methods on Synthetic Data Sets. Earth Space Sci. 2020, 7, e2020EA001121. [Google Scholar] [CrossRef] [Green Version]
- Jones, P.D.; Raper, S.C.B.; Bradley, R.S.; Diaz, H.F.; Kellyo, P.M.; Wigley, T.M.L. Northern Hemisphere Surface Air Temperature Variations: 1851–1984. J. Clim. Appl. Meteorol. 1986, 25, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Easterling, D.; Peterson, T. A new method for detecting undocumented discontinuities in climatological time series. Int. J. Climatol. 1995, 15, 369–377. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. J. R. Meteorol. Soc. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Caussinus, H.; Mestre, O. Detection and correction of artificial shifts in climate series. J. R. Stat. Soc. Ser. Appl. Stat. 2004, 53, 405–425. [Google Scholar] [CrossRef]
- Menne, M.J.; Williams, C.N. Detection of Undocumented Changepoints Using Multiple Test Statistics and Composite Reference Series. J. Clim. 2005, 18, 4271–4286. [Google Scholar] [CrossRef]
- Szentimrey, T. Development of MASH homogenization procedure for daily data. In Proceedings of the Fifth Seminar for Homogenization and Quality Control in Climatological Databases, Budapest, Hungary, 29 May–2 June 2006; WMO/TD- No. 1493, WCDMP- No. 71. pp. 123–130. [Google Scholar]
- Reeves, J.; Chen, J.; Wang, X.L.; Lund, R.; Lu, Q.Q. A Review and Comparison of Changepoint Detection Techniques for Climate Data. J. Appl. Meteorol. Climatol. 2007, 46, 900–915. [Google Scholar] [CrossRef]
- Costa, A.C.; Soares, A. Homogenization of Climate Data: Review and New Perspectives Using Geostatistics. Math. Geosci. 2009, 41, 291–305. [Google Scholar] [CrossRef]
- Venema, V.K.C.; Mestre, O.; Aguilar, E.; Auer, I.; Guijarro, J.A.; Domonkos, P.; Vertacnik, G.; Szentimrey, T.; Stepanek, P.; Zahradnicek, P.; et al. Benchmarking homogenization algorithms for monthly data. Clim. Past 2012, 8, 89–115. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Lund, R.; Lee, T.C.M. An MDL approach to the climate segmentation problem. Ann. Appl. Stat. 2010, 4, 299–319. [Google Scholar] [CrossRef] [Green Version]
- Lund, R.; Wang, X.L.; Lu, Q.Q.; Reeves, J.; Gallagher, C.; Feng, Y. Changepoint Detection in Periodic and Autocorrelated Time Series. J. Clim. 2007, 20, 5178–5190. [Google Scholar] [CrossRef] [Green Version]
- Jones, J.; Guerova, G.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; Bock, O.; Pacione, R.; van Malderen, R. Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate: COST Action ES1206 Final Action Dissemination Report; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. Segmentation of the mean of heteroscedastic data via cross-validation. Stat. Comput. 2010, 21, 613–632. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Bock, O.; Parracho, A. Consistency and representativeness of integrated water vapour from ground-based GPS observations and ERA-Interim reanalysis. Atmos. Chem. Phys. 2019, 19, 9453–9468. [Google Scholar] [CrossRef] [Green Version]
- Auger, I.E.; Lawrence, C.E. Algorithms for the optimal identification of segment neighborhoods. Bull. Math. Biol. 1989, 51, 39–54. [Google Scholar] [CrossRef]
- Killick, R.; Fearnhead, P.; Eckley, I.A. Optimal Detection of Changepoints with a Linear Computational Cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar] [CrossRef]
- Rigaill, G. A pruned dynamic programming algorithm to recover the best segmentations with 1 to Kmax change-points. J. Société Française Stat. 2015, 156, 180–205. [Google Scholar]
- Maidstone, R.; Hocking, T.; Rigaill, G.; Fearnhead, P. On Optimal Multiple Changepoint Algorithms for Large Data. Stat. Comput. 2017, 27, 519–533. [Google Scholar] [CrossRef] [Green Version]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Picard, F.; Robin, S.; Lavielle, M.; Vaisse, C.; Daudin, J.J. A statistical approach for array CGH data analysis. BMC Bioinform. 2005, 6, 27. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Lund, R. Multiple Changepoint Detection via Genetic Algorithms. J. Clim. 2012, 25, 674–686. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Croux, C. Alternatives to the Median Absolute Deviation. J. Am. Stat. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- Bertin, K.; Collilieux, X.; Lebarbier, E.; Meza, C. Semi-parametric segmentation of multiple series using a DP-Lasso strategy. J. Stat. Comput. Simul. 2017, 87, 1255–1268. [Google Scholar] [CrossRef]
- Lebarbier, E. Detecting Multiple Change-Points in the Mean of Gaussian Process by Model Selection. Signal Process. 2005, 85, 717–736. [Google Scholar] [CrossRef] [Green Version]
- Lavielle, M. Using penalized contrasts for the change-point problem. Signal Process. 2005, 85, 1501–1510. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.R.; Siegmund, D.O. A Modified Bayes Information Criterion with Applications to the Analysis of Comparative Genomic Hybridization Data. Biometrics 2007, 63, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Truong, C.; Oudre, L.; Vayatis, N. Selective review of offline change point detection methods. Signal Process. 2020, 167, 107299. [Google Scholar] [CrossRef] [Green Version]
- Gazeaux, J.; Lebarbier, E.; Collilieux, X.; Métivier, L. Joint segmentation of multiple GPS coordinate series. J. Société Française Stat. 2015, 156, 163–179. [Google Scholar]
- Weatherhead, E.C.; Reinsel, G.C.; Tiao, G.C.; Meng, X.; Choi, D.; Cheang, W.; Keller, T.; DeLuisi, J.; Wuebbles, D.J.; Kerr, J.B.; et al. Factors affecting the detection of trends: Statistical considerations and applications to environmental data. JGR Atmos. 1998, 103, 17149–17161. [Google Scholar] [CrossRef]
- Birgé, L.; Massart, P. Gaussian model selection. J. Eur. Math. Soc. 2001, 3, 203–268. [Google Scholar] [CrossRef] [Green Version]
- Arlot, S.; Massart, P. Data-driven calibration of penalties for least-squares regression. J. Mach. Learn. Res. 2009, 10, 245–279. [Google Scholar]
- Varadhan, R.; Roland, C. Simple and globally convergent methods for accelerating the convergence of any EM algorithm. Scand. J. Stat. 2008, 35, 335–353. [Google Scholar] [CrossRef]
- Hocking, T.D.; Rigaill, G.; Fearnhead, P.; Bourque, G. Generalized Functional Pruning Optimal Partitioning (GFPOP) for Constrained Changepoint Detection in Genomic Data. arXiv 2018, arXiv:1810.00117. [Google Scholar] [CrossRef]
- Bock, O. GPS Data: Daily and Monthly Reprocessed IWV Data from 120 Global GPS Stations, Version 1.2. 2016. Available online: https://observations.ipsl.fr/espri/metadata/global_gps_iwv_v1.2.html (accessed on 12 June 2022).
- Byun, S.H.; Bar-Sever, Y.E. A new type of troposphere zenith path delay product of the international GNSS service. J. Geod. 2009, 83, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M.; et al. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Solid Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef] [Green Version]
- Hewaarachchi, A.P.; Li, Y.; Lund, R.; Rennie, J. Homogenization of Daily Temperature Data. J. Clim. 2017, 30, 985–999. [Google Scholar] [CrossRef]
- Lebarbier, É. Discussion on “Minimal penalties and the slope heuristic: A survey” by Sylvain Arlot. J. Société Française Stat. 2019, 160, 140–149. [Google Scholar]
- Estey, L.; Meertens, C. TEQC: The Multi-Purpose Toolkit for GPS/GLONASS Data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Ardia, D.; Dufays, A.; Criado, C.O. Frequentist and Bayesian Change-Point Models: A Missing Link. SSRN Electron. J. 2019. [Google Scholar] [CrossRef]
- Chakar, S.; Lebarbier, E.; Lévy-Leduc, C.; Robin, S. A robust approach for estimating change-points in the mean of an AR(1) process. Bernoulli 2017, 23, 1408–1447. [Google Scholar] [CrossRef]

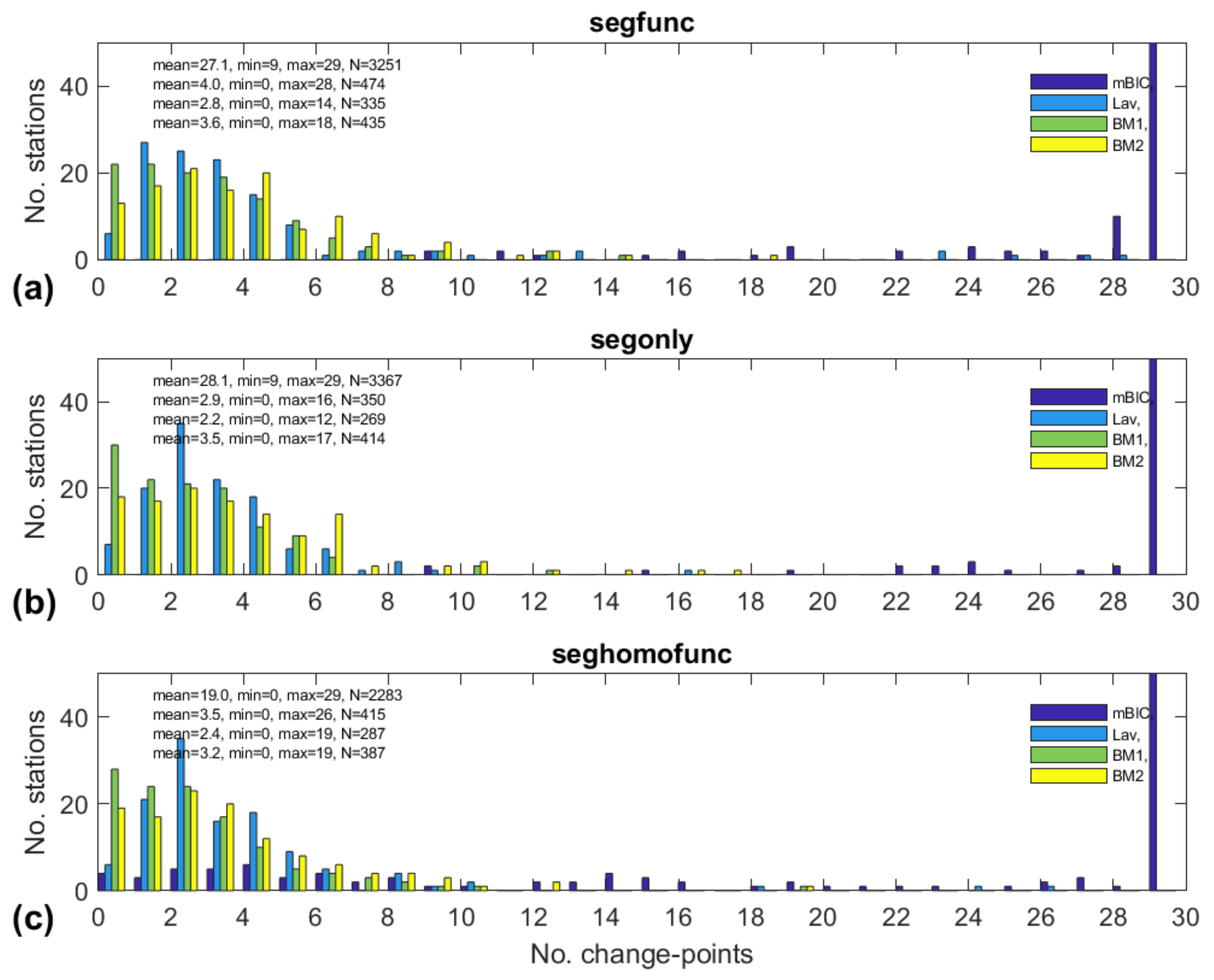
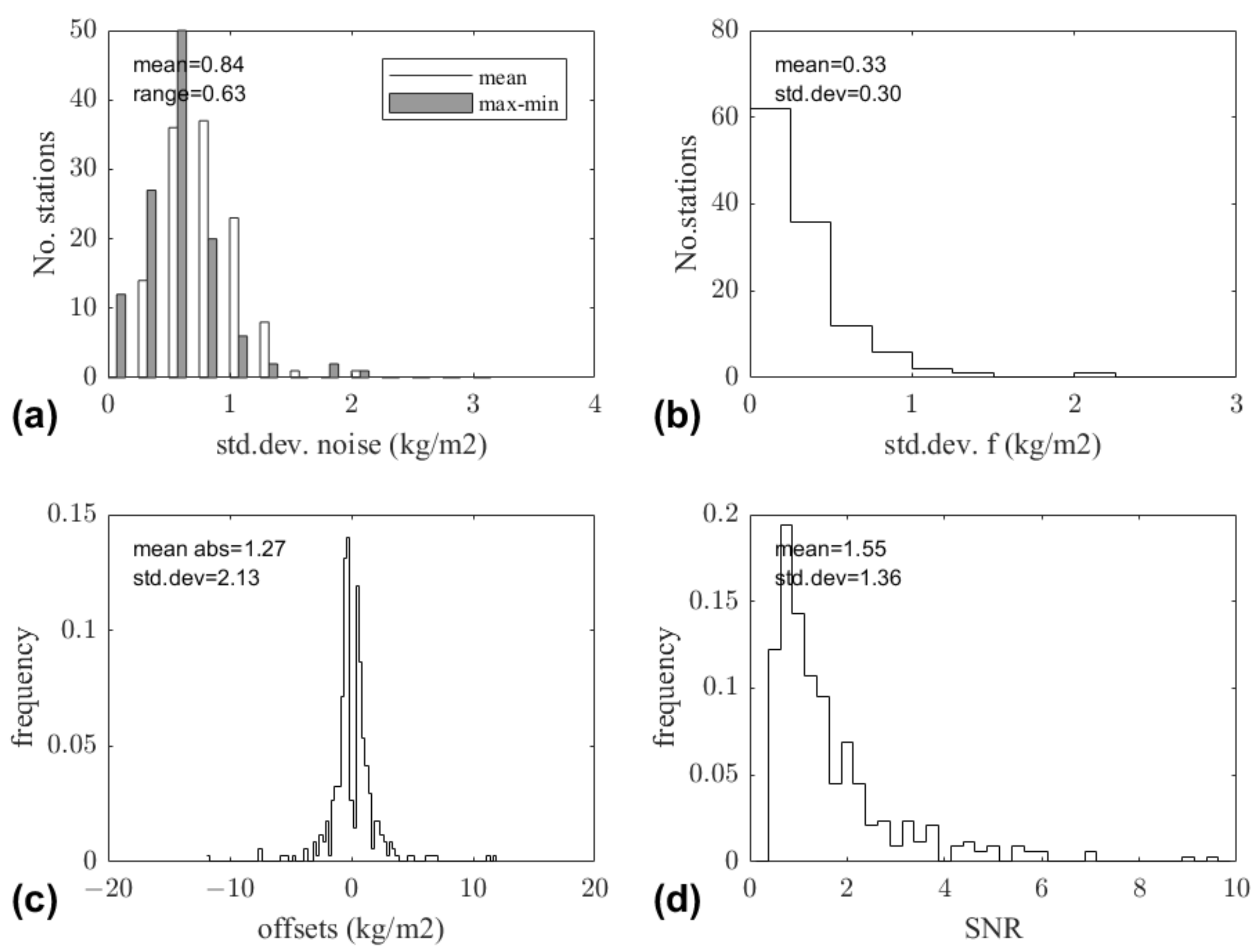
| Before Screening | After Screening | ||||||
|---|---|---|---|---|---|---|---|
| Detections | Outliers | Validations | Detections | Validations | |||
| Variant (a) segfunc | |||||||
| mBIC | 3251 | 2714 | 415 | 13% | 1270 | 263 | 21% |
| Lav | 474 | 194 | 108 | 23% | 341 | 102 | 30% |
| BM1 | 335 | 70 | 93 | 28% | 292 | 93 | 32% |
| BM2 | 435 | 113 | 107 | 25% | 370 | 105 | 28% |
| Variant (b) segonly | |||||||
| mBIC | 3367 | 2123 | 538 | 16% | 1865 | 393 | 21% |
| Lav | 350 | 54 | 87 | 25% | 316 | 85 | 27% |
| BM1 | 269 | 28 | 76 | 28% | 253 | 74 | 29% |
| BM2 | 414 | 66 | 98 | 24% | 378 | 94 | 25% |
| Variant (c) seghomofunc | |||||||
| mBIC | 2283 | 1941 | 278 | 12% | 678 | 180 | 27% |
| Lav | 415 | 212 | 86 | 21% | 249 | 75 | 30% |
| BM1 | 287 | 75 | 86 | 30% | 242 | 83 | 34% |
| BM2 | 387 | 142 | 101 | 26% | 295 | 96 | 33% |
| Before Screening | After Screening | |||
|---|---|---|---|---|
| Median | iqr | Median | iqr | |
| Variant (a) segfonc | ||||
| mBIC | 221 | 430 | 205 | 399 |
| Lav | 190 | 390 | 149 | 358 |
| BM1 | 168 | 361 | 150 | 358 |
| BM2 | 171 | 352 | 158 | 337 |
| Variant (b) segonly | ||||
| mBIC | 219 | 414 | 224 | 417 |
| Lav | 183 | 418 | 175 | 425 |
| BM1 | 163 | 341 | 157 | 337 |
| BM2 | 193 | 348 | 188 | 350 |
| Variant (c) seghomofunc | ||||
| mBIC | 225 | 423 | 178 | 376 |
| Lav | 190 | 370 | 155 | 340 |
| BM1 | 129 | 320 | 132 | 336 |
| BM2 | 153 | 354 | 138 | 333 |
| Before | After | Accepted | Validated (Metadata) | Validated (+TEQC) | |
|---|---|---|---|---|---|
| BM1 | 335 | 292 | 168 (57%) | 99 (58.9%) | 105 (62.5%) |
| BM2 | 435 | 370 | 166 (45%) | 99 (59.6%) | 105 (63.3%) |
| Lav | 474 | 341 | 175 (51%) | 103 (58.9%) | 109 (62.3%) |
| total | 187 | 110 (58.8%) | 116 (62.0%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quarello, A.; Bock, O.; Lebarbier, E. GNSSseg, a Statistical Method for the Segmentation of Daily GNSS IWV Time Series. Remote Sens. 2022, 14, 3379. https://doi.org/10.3390/rs14143379
Quarello A, Bock O, Lebarbier E. GNSSseg, a Statistical Method for the Segmentation of Daily GNSS IWV Time Series. Remote Sensing. 2022; 14(14):3379. https://doi.org/10.3390/rs14143379
Chicago/Turabian StyleQuarello, Annarosa, Olivier Bock, and Emilie Lebarbier. 2022. "GNSSseg, a Statistical Method for the Segmentation of Daily GNSS IWV Time Series" Remote Sensing 14, no. 14: 3379. https://doi.org/10.3390/rs14143379
APA StyleQuarello, A., Bock, O., & Lebarbier, E. (2022). GNSSseg, a Statistical Method for the Segmentation of Daily GNSS IWV Time Series. Remote Sensing, 14(14), 3379. https://doi.org/10.3390/rs14143379






