Inferring 2D Local Surface-Deformation Velocities Based on PSI Analysis of Sentinel-1 Data: A Case Study of Öræfajökull, Iceland

Abstract

Two-dimensional deformation estimates derived from Persistent Scatterer Interferometric (PSI) analysis of Synthetic Aperture Radar (SAR) data can improve the characterisation of spatially and temporally varying deformation processes of Earth’s surface. In this study, we examine the applicability of Persistent Scatterer (PS) Line-Of-Sight (LOS) estimates in providing two-dimensional deformation information, focusing on the retrieval of the local surface-movement processes. Two Sentinel-1 image stacks, ascending and descending, acquired from 2015 to 2018, were analysed based on a single master interferometric approach. First, Interferometric SAR (InSAR) deformation signals were corrected for divergent plate spreading and the Glacial Isostatic Adjustment (GIA) signals. To constrain errors due to rasterisation and interpolation of the pointwise deformation estimates, we applied a vector-based decomposition approach to solve the system of linear equations, resulting in 2D vertical and horizontal surface-deformation velocities at the PSs. We propose, herein, a two-step decomposition procedure that incorporates the Projected Local Incidence Angle (PLIA) to solve for the potential slope-deformation velocity. Our derived 2D velocities reveal spatially detailed movement patterns of the active Svínafellsjökull slope, which agree well with the independent GPS time-series measurements available for this area.

1. Introduction

Satellite-based Interferometric Synthetic Aperture Radar (InSAR) has been proven to be a valuable tool for detecting subtle deformation of the ground surface at a high spatial resolution, covering large areas, under favourable conditions, with up to sub-centimetre precision [1,2,3,4]. A more advanced technique, Multi-temporal InSAR (MTI), has further improved InSAR’s applicability in detecting deformation and estimating displacement rates associated with earthquakes or volcanic activity [5,6,7]; slope instabilities and slow landslide displacements [8,9,10,11]; anthropogenically induced subsidence [12,13,14]; and monitoring critical infrastructures such as buildings and dams [15,16,17]. Despite promising results in some cases, accurate mapping and monitoring of deformation processes in mountainous environments by means of MTI is still challenging. Constraints are mainly encountered because of Synthetic Aperture Radar (SAR) geometric distortions, e.g., layover and shadow, which reduce SAR-to-target visibility and, therefore, the density of usable Persistent Scatterer (PS). In addition, signal decorrelation occurs due to changes in vegetation cover or fast surface-movements [3,18].

The launches of the Copernicus Sentinel-1 (S-1) radar satellites in 2014 (Sentinel-1A) and 2016 (Sentinel-1B) [19,20] and the provision of a ready-to-use software toolbox, i.e., the SentiNel Application Platform (SNAP) [21,22], have provided the user community with unprecedented SAR data quality and tools allowing deformation studies at low cost. Technically, Sentinel-1 marks a new era, wherein deformation phenomena can be actively observed on a spatially detailed grid (~10 m), with high temporal frequencies (every 6 days) and in two dimensions (2D), wherever both ascending and descending acquisitions are available. Despite the availability of S-1 data in most areas, the applicability and interpretation of MTI-based Line-Of-Sight (LOS) deformation estimates, particularly the 2D characterisation of deformation evolution processes in high relief areas, still need to be researched [23]. Several case studies have applied MTI for hot-spot mapping, landslide characterisation, slope failure prediction, and landslide inventory updating [10,14,23,24,25,26,27,28,29]. While research on the continuous, semi-automatic monitoring of slow-moving landslides has been emerging, studies that examine the applicability of 2D decomposition algorithms in areas governed by complex deformation processes are still underrepresented.

Persistent Scatterer Interferometry (PSI) is known as a subcategory of MTI processing. The PSI technique [2,5,30,31] applied in this study relies on the single–master approach, meaning all radar images are co-registered with reference to their master image to form a time-series of interferograms. Only resolution elements (i.e., PS) exhibiting phase stability and a high signal-to-noise ratio (SNR) over the study period are selected and integrated into the PSI analysis. The derivation of LOS deformation estimates is, therefore, possible only on sparse grids of PSs. The Stanford Method for Persistent Scatterers (StaMPS) was selected for this study because it does not require any a priori assumption of the temporal model of deformation. It allows for the extraction of deformation signals that are not necessarily linear with time, e.g., slope deformation related to slow-moving landslides [5,32].

Several studies were carried out to quantify deformation fields in Iceland, with or without applying PSI. Based on countrywide GNSS measurement campaigns (1993, 2004), crustal deformation fields characterising Glacial Isostatic Adjustment (GIA) and plate-spreading velocities were modelled [33]. This work indicated that GIA and plate-spreading movements are major contributors to crustal deformation processes and should not be ignored when interpreting local deformation in Iceland. PSI analysis was previously applied to ERS and Envisat data to derive LOS deformation rates. The study concluded the detected regional uplift trend to be deformation primarily induced by GIA [34]. Recently, PSI analyses of S-1 data (2015–2018) were carried out to derive 2D velocity fields and used to update existing GIA and plate tectonic velocity models [35]. The results indicated the existence of local deformation residuals, interpreted as deformation induced by subsurface rheology variations.

Theoretically, the retrieval of 3D motion vectors (i.e., east, north, and vertical components) from three independent InSAR LOS measurements is possible, provided that multi-geometry data with a satellite inclination of about 60°/120° covering the same area are available. The N-S component is known to be the most difficult to determine using data from near-polar orbiting satellites [36,37]. The decomposition of LOS measurements from Sentinel-1 ascending and descending data into a 2D motion vector is crucial for the accurate quantification of 2D deformation fields in this study, mainly for two reasons. First, disregarding the quantification of the horizontal movement, when it is present, would lead to the misinterpretation of the vertical movement. The interpretation error depends on the magnitude of the horizontal movement and steepness of the incidence angle. Second, due to its system configurations, the S-1 LOS measurement is more sensitive to horizontal motion and less sensitive to vertical motion when compared to ERS and TerraSAR-X missions (also known as decomposition sensitivity, cf. Appendix A,

Table A1. Comparison of decomposition sensitivity (unit vector) for the InSAR LOS estimate from former and current SAR missions (cf. Equation (2) or (3)). All values are estimated at mid-swath incidence angle.

Mission	Incidence Angle (Mid-Range)	East (E)	North (N)	Up (U)
Sentinel-1 (A)	37°	−0.58	−0.16	0.80
Sentinel-1 (D)	37°	0.59	−0.10	0.80
Sentinel-1 (A) 1	43.4°	−0.68	−0.11	0.73
Sentinel-1 (D) 2	38.7°	0.61	−0.12	0.78
TerraSAR-X (D)	32°	0.53	−0.05	0.85
ERS-1/2 (D)	23°	0.37	−0.14	0.92

^1,2 parameters from Öræfajökull image subset analysed in this case study.

for further detail).

This research aims to investigate the applicability of the full-resolution, two-dimensional LOS deformation estimates, derived from a state-of-the-art workflow that combines PSI analysis of S-1 data with a vector-based decomposition approach to infer local deformation information, focusing on inclined terrain. We propose a new two-step decomposition procedure that allows for the isolation of the deformation signal of interest; it incorporates the Project Local Incidence Angle (PLIA) instead of the classical Ellipsoid Incidence Angle (EIA), to directly retrieve the slope-deformation velocity. We test and demonstrate the usability of the proposed algorithm to infer 2D movements in the geomorphologically dynamic Öræfajökull area in Iceland.

In the subsequent sections, the terms “deformation” and “surface movement” (mm) are used interchangeably to describe the estimated surface deformation (mm) from a time-series of interferograms. The terms “deformation rate”, “surface-deformation velocity”, and “motion rate” can be interchangeably used to define the mean velocity (mm/y) as derived over the entire period of an InSAR stack.

2. Materials and Methods

2.1. Study Area

Iceland is traversed by the Mid-Atlantic-Ridge, which forms the plate boundary zone between the North American and Eurasian tectonic plates. Our study area is located west of the Öræfajökull stratovolcano, in the southern part of the Vatnajökull National Park in southeastern Iceland (Figure 1). The Öræfajökull massif is composed of basaltic and silicic rocks (lava flows, hyaloclastite, and intrusions) as well as sedimentary rocks [38]. This area is influenced by the rapid retreat of the Vatnajökull (Vat) glacier, the largest and most voluminous Icelandic glacier, which causes significant isostatic uplift. This uplift—coupled with the steep relief, the large amount of unconsolidated debris, glacial erosion, the thawing of permafrost, and high precipitation—make the Öræfajökull area highly susceptible to slope instability, resulting in landslides and debris flows (e.g., [39,40]). Geodetically, GPS measurement campaigns have been carried out and time-series data from continuous GPS (cGPS) stations across Iceland have been used to quantify the surface deformation due to Glacial Isostatic Adjustment (GIA) and plate-spreading processes at the regional scale [33,41]. Such regional deformation signals characterised by slow, steady movements can usually be well constrained by PSI. Surface deformation induced by seismic events, earthquakes, and volcanic deflation or inflation, depending on its magnitude and duration, also affect the overall deformation field in this area.

2.2. Data

Sentinel-1 radar imagery from the European Copernicus programme (Single-Look Complex (SLC) product, Interferometric Wide (IW) mode) spanning the period from spring 2015 to autumn 2018, for both ascending (A118) and descending (D111) passes, were acquired for the PSI. Only radar data acquired from May to October were considered, to avoid snow-covered areas as much as possible. High- to medium-resolution digital elevation models (DEMs), i.e., the ArcticDEM [42] and TanDEM-X DEM [43] and their derived products, were used for interferometric processing, data analysis and visualisation. Three-dimensional (3D) time-series deformation information at several GPS stations, kindly made available by the Icelandic Meteorological Office (IMO), was used for calibration and validation purposes.

Table 1. Data and ancillary data used for the analysis.

Data	Resolution (m)	Description
Sentinel-1 SAR	2.3 × 14.1 1	Orbit: Ascending (A118) Acquisition time: 29/05/2015–10/09/2018 No. of ifgs 3: 28 Incidence angle (EIA): 41.2°–45.6° Heading: 350.6°
Sentinel-1 SAR	2.3 × 14.1 2	Orbit: Descending (D111) Acquisition time: 17/05/2015–04/10/2018 No. of ifgs: 25 Incidence angle (EIA): 36.0°–41.5° Heading: 191.0°
Arctic-DEM	2	Derived from stereo–optical imagery acquired during 2012–2017
Tandem-X DEM	20	Derived from radar imagery acquired during 2011–2015
GPS deformation time-series 4 SKFC 5 SVIN SVIE		Observation period: July 2015–October 2018 July 2018–October 2018 July 2018–October 2018

^1,2 Pixel spacing rg × az m; ³ interferograms; ⁴ kindly made available by the Icelandic Meteorological Office (IMO); ⁵ GPS station name.

summarises the data and ancillary data used in this study.

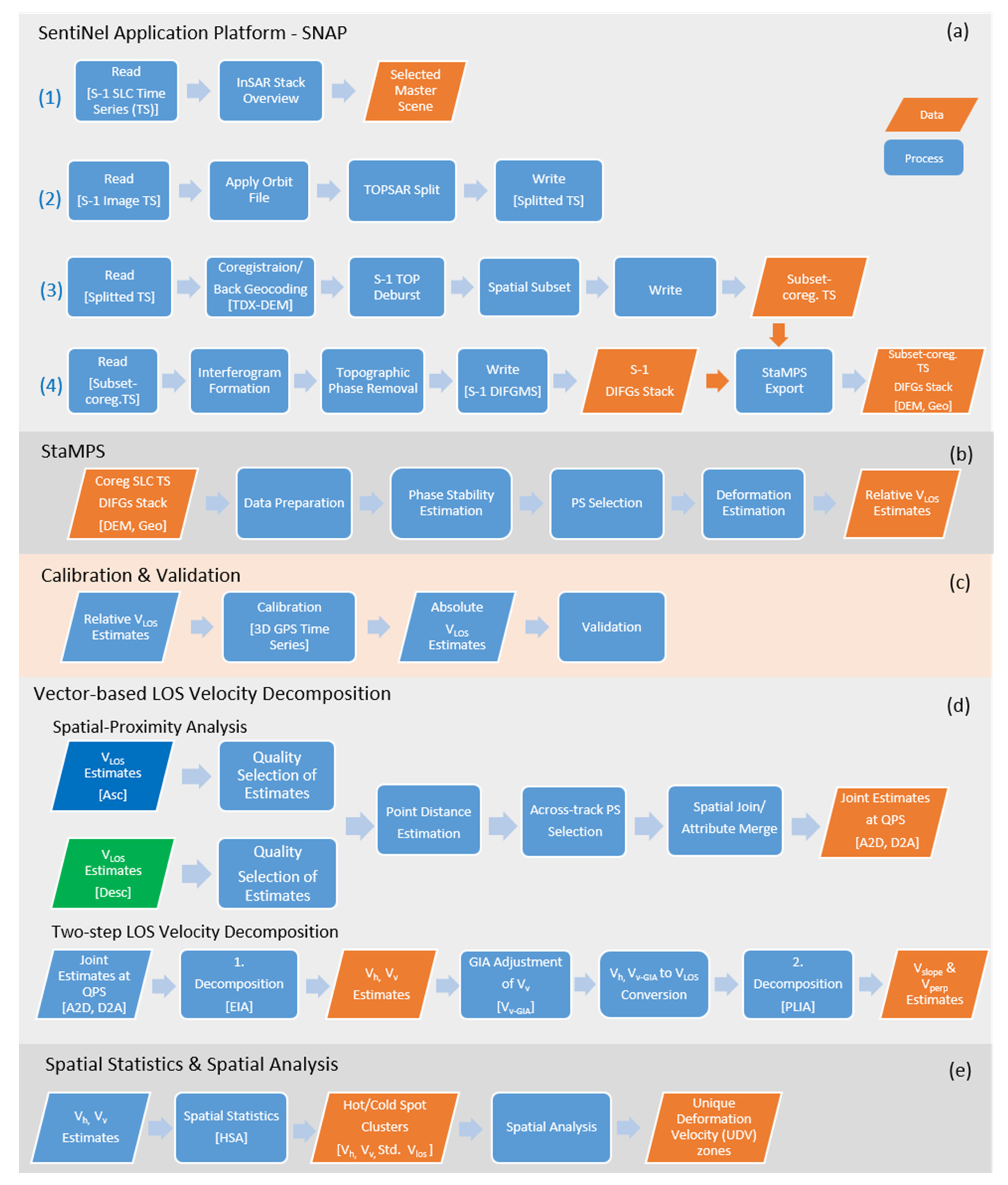
2.3. Methods

The overall processing, validation and analysis workflow consists of five main components: (1) Terrain Observation with Progressive Scans SAR (TOPSAR) pre-processing and InSAR processing [21,44]; (2) PSI analysis with StaMPS; (3) calibration and validation of LOS estimates; (4) vector-based LOS velocity decomposition, including spatial-proximity analysis and a two-step decomposition procedure of LOS deformation vectors into 2D vertical and horizontal deformation velocities; and (5) spatial statistics and spatial analysis to infer the 2D local deformation velocities (cf. Figure 2).

For simplicity, we divided dedicated pre-processing procedures for TOPSAR data and the generic interferometric processing within SNAP [22,45] into four processing steps. The InSAR stack overview was used to determine the optimal master scenes that minimise the overall signal decorrelation for each S-1 image time-series (ts in Figure 2a). In general, the scene that lay in the middle of the study period was selected. Apply orbit file and TOPSAR Split involve satellite orbit correction and the splitting up of SAR images into smaller parts (subswath and burst) according to the area of interest (AoI). Then S-1 split time-series were coregistered (back geocoding) based on their selected master scene and spatial subset. This step requires elevation information of the scene to preserve geolocational accuracy. In our case, the Tandem-X DEM was used. Next, interferogram formation and topographic phase removal were required to generate differential interferograms (DIFGs). Finally, during the StaMPS export, we prepared interferogram stacks (DIFGs stack and co-registered S-1 time series) and associated parameters in compatible formats for further PSI analysis in StaMPS.

PSI was performed using the StaMPS [46] open-source software packages. The main outcome of this analysis is known as the relative deformation rate or mean velocity estimate in the LOS direction. The conceptual basis of the PSI analysis using StaMPS is briefly described in Section 2.3.1. The detailed implementation steps are beyond the scope of this paper and can be found in the StaMPS manual [47]. Calibration and validation of the PS-based estimation results are described in Section “Calibration and Validation of LOS Estimates”.

To constrain propagating errors due to rasterisation and interpolation of the pointwise LOS estimates, the vector-based approach of spatial-proximity analysis described in [48] was implemented. The goals of the analysis were to ensure that LOS estimates of quality PSs (hereafter, QPSs) were exploited, and suitable neighbouring PSs in across-track data were identified. Once neighbouring PSs were identified, the attributes of the centred PS (for example, ascending) and its across-track surrounding PSs (descending) were spatially joined and made available for 2D decomposition. Thus, we can derive 2D deformation velocities at all QPSs available from both ascending (A) and descending (D) data. The proposed algorithm increases the spatial density of measurement points as well as preserving the reliability of the pointwise 2D velocity estimates compared to the rasterised 2D estimates [48]. A schematic representation of the overall processing and analysis workflows is shown in Figure 2.

2.3.1. PSI Analysis for Deriving LOS Deformation Estimates

The wrapped phase (${\psi }_{x,i}$) at pixel x in the topographically corrected ith interferogram (the DIFG) is affected by multiple phase contributions and can be written as the wrapped sum of five phase terms [5]

$${\psi }_{x,i}=W\left\{{\varphi }_{D,x,i}+{\varphi }_{A,x,i}+\mathsf{\Delta }{\varphi }_{O,x,i}+\mathsf{\Delta }{\varphi }_{\theta ,x,i}+{\varphi }_{N,x,i}\right\}$$

(1)

where ${\varphi }_{D,x,i}$ is the phase change due to surface movement in the LOS; ${\varphi }_{A,x,i}$ is the phase due to the difference in atmospheric phase delay during the two acquisitions; $\mathsf{\Delta }{\varphi }_{O,x,i}$ is the phase due to orbit inaccuracies; $\mathsf{\Delta }{\varphi }_{\theta ,x,i}$ is the residual phase due to look-angle (DEM) error; ${\varphi }_{N,x,i}$ is the phase noise due to scattering variability, thermal noise, processing errors, etc.; and $W\{·\}$ is the wrapping operator. The first three terms in Equation (1) are spatially correlated. The fourth term is partially spatially correlated. Since we are interested in the first term $({\varphi }_{D,x,i})$, the deformation, the other terms must be estimated and subtracted from the wrapped phase.

In practice, the following four PS processing tasks are transformed into eight operational steps (steps 1 to 8) within the StaMPS environment, which can be automatically implemented at once, or step-by-step (cf. Figure 2b) [47]. These include:

• Data Preparation, which involves selection of the initial PS Candidates (PSC) and processed-area subsetting (patches).
• Phase Stability Estimation, which includes phase noise estimation for each PSC in every interferogram. Gamma (${\gamma }_x),$ a coherence-like measure, is used to express the phase noise level of a PSC and its possibility to become a PS.
• PS Selection, which determines whether a PSC will be a PS based on their phase noise estimates. Only PSCs with persistent phase stability for the entire period were selected.
• Displacement/Deformation Estimation, which involves deformation signal isolation at PS pixel. This is achieved by unwrapping phase values and by subtracting various unwanted terms.

We applied the suggested (default) processing parameters to derive LOS deformation-rate estimates (aka Mean LOS Velocity (MLV) in StaMPS) of the PSs. We estimated deformation rates with respect to the selected reference point (SKFC), whose available GPS deformation time-series measurements coincided with the InSAR analysis period, i.e., May 2015 to October 2018, for MLV estimation (cf. Table 1).

Calibration and Validation of LOS Estimates

In principle, a SAR sensor can measure only the path length difference in one dimension, i.e., in its LOS (slant range) direction. That is, a three-dimensional (3D) deformation vector ($d$) with its components in East ($d_E$), North ($d_N$), and Up ($d_U$) is projected in the LOS direction ($d_{los}$). The LOS deformation vector ($d_{los}$) can be expressed in relation to its 3D components as [49]:

$$d_{los}=\left[\begin{array}{ccc}-\sin \theta \cos \alpha & \sin \theta \sin \alpha & \cos \theta \end{array}\right]\left[\begin{array}{c}{d}_E\\ d_N\\ d_U\end{array}\right]$$

(2)

where θ is the incidence angle and α denotes the satellite’s orbit heading (azimuth) measured positive clockwise from the north. Since we are interested in the surface-movement velocity ($v)$, we replace $d_{los}$ in Equation (2) with $v_{los}$; the same expression is valid [3,50] and can be written as Equation (3).

$$v_{los}=\left[\begin{array}{ccc}-\sin \theta \cos \alpha & \sin \theta \sin \alpha & \cos \theta \end{array}\right]\left[\begin{array}{c}{v}_E\\ v_N\\ v_U\end{array}\right]$$

(3)

Relative LOS estimates as a result of PSI in StaMPS require calibration before further analysis. Based on 3D displacement time-series measurements ($d_E$, $d_N$, $d_U$) and linear regression analysis, the mean velocities ($v_E,v_N,v_U$) of the SKFC reference point were derived using Equations (2) and (3). Using S-1 parameters, we derived the LOS velocities of SKFC for the ascending and descending InSAR stacks. We then used the obtained LOS estimates ($v_{los})$ of SKFC to calibrate other relative PS LOS measurements globally, leading to absolute LOS measurements at all PSs.

Validation of the PS MLV estimates was carried out based on the available GPS displacement time-series observations from three reference stations, corresponding to the InSAR time span (cf. Table 1). Using SAR parameters, i.e., incidence angle, azimuth heading, and linear regression analysis, 3D GPS velocities were projected into the LOS direction and used for validation (cf. Equations (2) and (3)). MLV estimates of PSs located within a maximum distance of 250 m with a slope aspect similar to the reference GPS stations were selected for validation purposes.

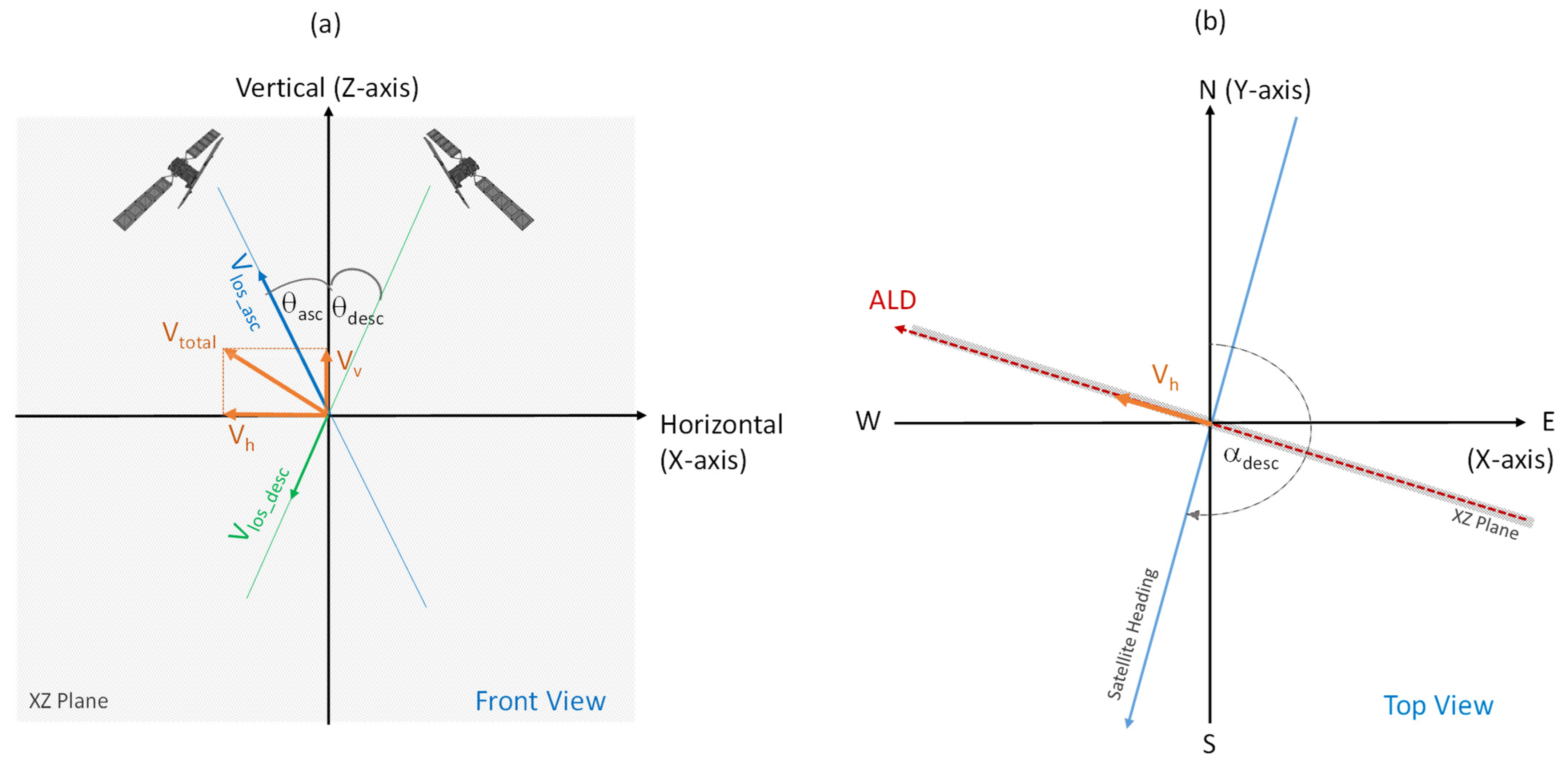
2.3.2. Decomposition of LOS Deformation Rate Estimates

The vector-based velocity decomposition started with quality PS estimate selection, followed by a spatial-proximity analysis. The proposed two-step vector decomposition was then executed to accommodate GIA-like signal removal and, finally, to obtain the potential “slope-deformation velocity”.

Spatial-Proximity Analysis

Two criteria were used to filter good quality PS (QPS) estimates. The standard deviation of $v_{los}$ implies the degree of linearity of the movement, and the layover-shadow mask implies that the PS pixels are affected by geometric distortions. Since the remaining number of PSs on the mountainous slopes should be sufficient and the nonlinear movement of PS is of interest, standard deviation thresholding (percentile 95) and layover-shadow-mask buffering of 100 m were applied to select quality estimates.

The derivation of location-based $V_v$ and $V_h$ at PS started with spatial-proximity analysis. Different spatial search radii between 100 and 300 m (with 50 m steps) were tested to find the optimal distance that balances the number of detectable across-track PSs and the computational time for 2D decomposition at PSs. We executed the searches twice, from ascending to descending (A2D) and descending to ascending (D2A) PSs, to make 2D decomposition possible at all PSs. Once across-track PSs were identified, all their attributes were spatially merged and the pointwise computation of 2D velocity parameters was performed (cf. Equations (4)–(6)).

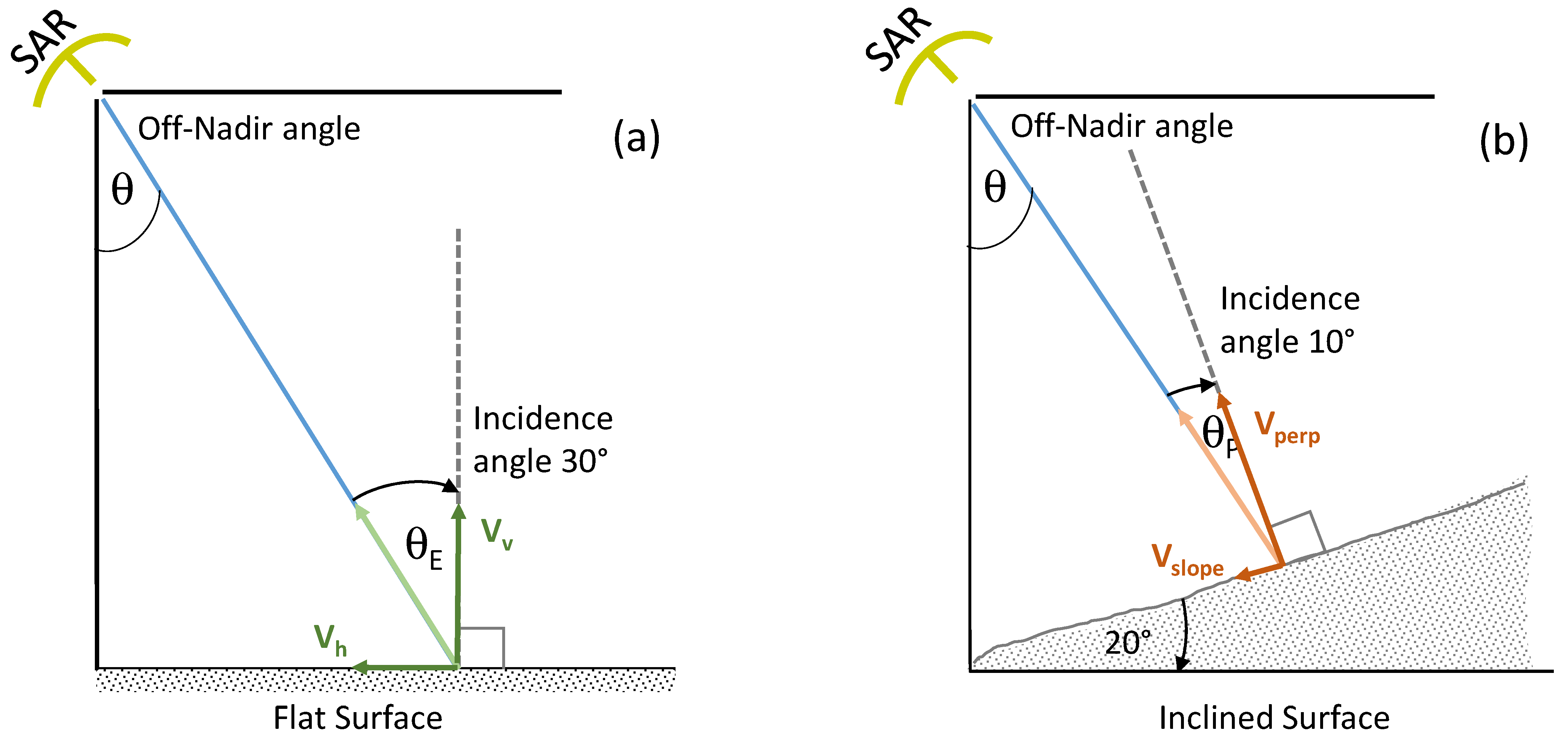
Two-Step LOS Velocity Decomposition

A SAR sensor can measure only the path length difference in one dimension in the LOS direction. If three independent InSAR measurements from different viewing geometries are available, one can solve for three deformation components [36,37]. In this study, we derived the LOS deformation velocities based on two independent InSAR passes; thus, only 2D velocity retrieval was possible.

Having LOS velocity estimates from ascending $\left(V_{los\_asc}\right)$ and descending $\left(V_{los\_desc}\right)$ passes coupled with satellite geometrical parameters, we started the first vector decomposition and retrieved deformation velocities in 2D—namely, vertical, $V_v$, and horizontal, $V_h$, velocities at individual QPS using [51] (cf. Figure 3):

$$\left[\begin{array}{c}{V}_{los\_asc}\\ V_{los\_desc}\end{array}\right]=\left[\begin{array}{cc}\cos {\theta }_{E\_asc}& \sin {\theta }_{E\_asc}/cos\mathsf{\Delta }\alpha \\ \cos {\theta }_{E\_desc}& \sin {\theta }_{E\_desc}\end{array}\right]\left[\begin{array}{c}{V}_v\\ V_h\end{array}\right]$$

(4)

where $\mathsf{\Delta }\alpha$ denotes the difference between ascending and descending satellite headings. The linear equation shown in Equation (4) has no redundancy, and therefore, it is not possible to derive the estimation error. The parameters of interest at individual PS, $V_v$, and $V_h$ can then be solved via linear equation system inversion.

The major vertical uplift trend in the AoI detectable by InSAR could be considered as a mixture of GIA and the seasonal deformation signal, hereafter, GIA-SS. We inferred the GIA-SS magnitude based on the literature [52] and the median of the decomposed vertical velocities. After major vertical-deformation-velocity removal, the residual vertical $V_{v\_res}$ and horizontal components $V_h$ can be inversely modelled to obtain two residual LOS vectors, namely, $V_{los\_asc\_res}$ and $V_{los\_desc\_res}$ (cf. Equation (5)). These residual vectors act as inputs for the second vector decomposition. The potential slope-deformation velocity $V_{slope}$ and the velocity perpendicular to the slope surface—hereafter, $V_{perp}$—are the main results of this step (cf. Equation (6) and Figure 4).

$$\left[\begin{array}{c}{V}_{los\_asc\_res}\\ V_{los\_desc\_res}\end{array}\right]=\left[\begin{array}{cc}\cos {\theta }_{asc}& \sin {\theta }_{asc}/\cos \mathsf{\Delta }\alpha \\ \cos {\theta }_{desc}& \sin {\theta }_{desc}\end{array}\right]\left[\begin{array}{c}{V}_{v\_res}\\ V_h\end{array}\right]$$

(5)

$$\left[\begin{array}{c}{V}_{los\_asc\_res}\\ V_{los\_desc\_res}\end{array}\right]=\left[\begin{array}{cc}\cos {\theta }_{P_{asc}}& \sin {\theta }_{P_{asc}}/\cos \mathsf{\Delta }\alpha \\ \cos {\theta }_{P_{desc}}& \sin {\theta }_{P_{desc}}\end{array}\right]\left[\begin{array}{c}{V}_{perp}\\ V_{slope}\end{array}\right]$$

(6)

2.3.3. Inferring the Local Deformation Fields Based on the PS-Based Estimates

Based on the reliable two-dimensional deformation estimates of QPSs and the MLV standard deviation, we further investigated their spatial distribution statistically, aiming to derive significant 2D deformation clusters. We then spatially analysed those deformation clusters based on two and three PS-based deformation parameters, resulting in nine and twenty-seven Unique Deformation Velocity (UDV) zones, respectively. To demonstrate the applicability of the detailed surface-deformation zoning results, we attempted to relate zonal attributes to possible deformation behaviours to interpret and better understand the motion processes that have taken place in the Öræfajökull area.

We recall the notion of previous studies stating that the magnitude of the GIA and the seasonal deformation signals in its vertical component (GIA-SS) are closely dependent on the distance to the ice caps and to the centre of Iceland [34,35]. Seasonal deformation is primarily contributed by glacial-mass balance and snow-load changes in glaciated and non-glaciated areas, respectively [53].

The Getis-Ord Gi* Hot-Spot Analysis (HSA), as implemented in the ArcGIS spatial statistics tool [54], was applied to evaluate the spatial relationship between a pointwise estimate and its neighbourhood. HSA assesses the randomness of the value of a parameter, i.e., velocity at a point feature, in relation to its neighbouring points. Thus, significant clusters of high values (Hot Spot), low values (Cold Spot), or insignificant clusters (randomness is dominant) can be identified at different confidence levels (99%, 95%, and 90%), and meaningful movement patterns can be derived.

From the spatial analysis (Combinatorial Or) between the $std.V_{los}$ and the 1D surface-movement rates, either the $V_v$ or $V_h$ parameter led to nine UDV zones in the AoI. Relying on the resulting unique zoning, we attempted to interpret the mixed deformation signals, i.e., the vertical component.

In practice, local surface-deformation zoning was achieved based on the following implementation steps:

• The Calculate Distance Band tool was used to initially investigate the neighbourhood of PS estimates, i.e., the relationship between the number of neighbouring PS points and the spatial distance between them was assessed. By inputting the expected number of neighbouring points, required for an arbitrary PS, the average, the minimum and the maximum distance bands were estimated. The average distance in which one obtains a sufficient number of PSs (>30), was then used for HSA.
• Hot-Spot Analysis was applied to evaluate the spatial distribution of three relevant deformation parameters ($V_v,V_h,std.V_{los}$) based on two spatial relationship concepts, the Inverse Distance Weighted (IDW) and the Fixed Distance Band (FDB), at different spatial scales. By increasing the FDB distance from 100, 250, and 500 to 1000 m, Hot-Spot and Cold-Spot clusters in the AoI, ranging from fine (local) to coarser scales, were mapped.
• The inputs for the spatial analysis were three rasterised deformation clusters from the HSA. To ensure high quality of the results, we selected three clusters (Hot Spot, Cold Spot, and not significant) with the highest confidence level (99%) of each parameter, resulting in nine distinct surface-deformation zones from each analysis.

3. Results

3.1. PS LOS Deformation-Rate Estimates

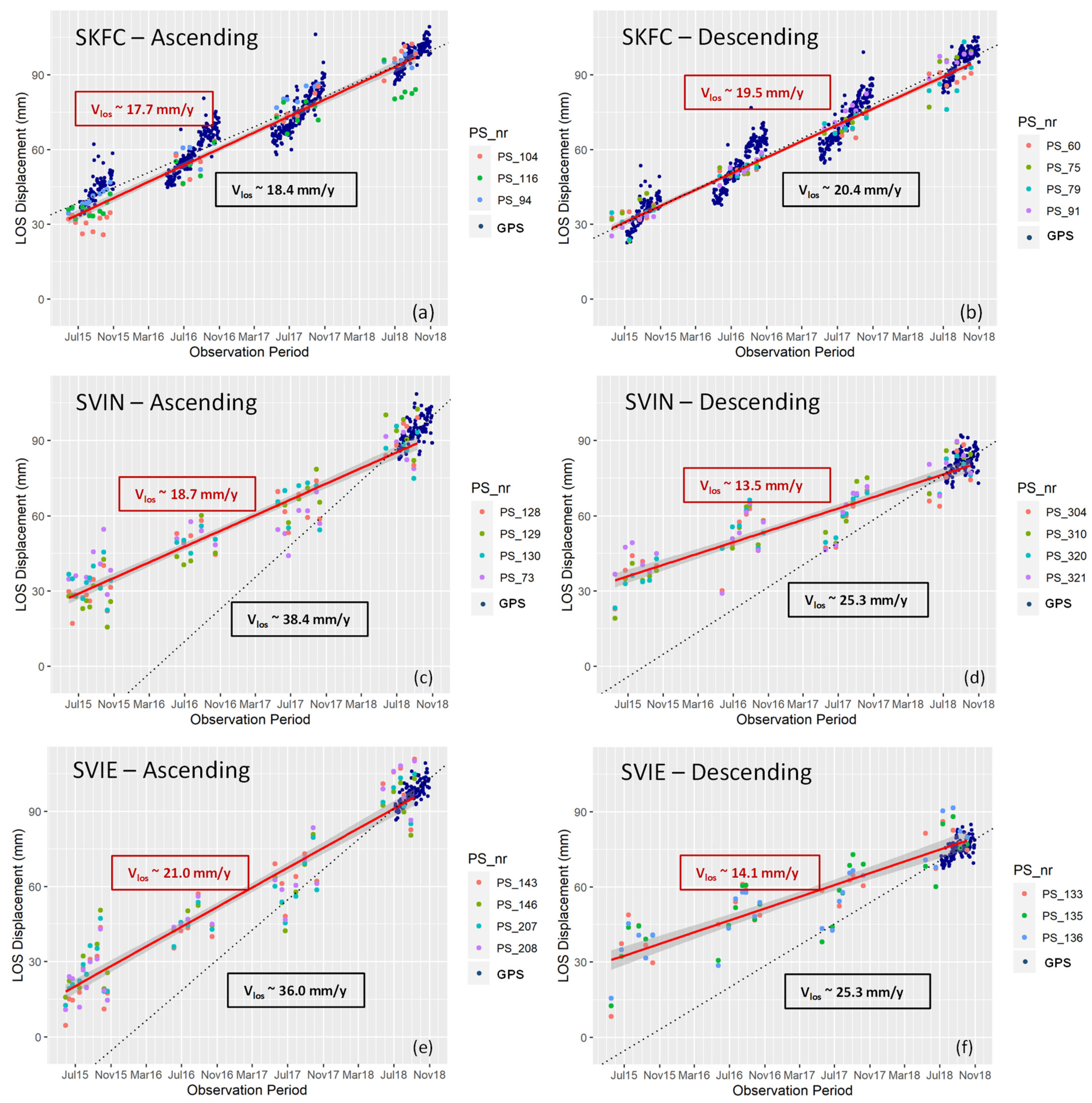
The resulting LOS deformation-rate estimates based on the PSI analysis are shown in Figure 5. The statistics are summarised in

Table 2. Statistical descriptions of relative and calibrated mean LOS velocity ($V_{los}$ ) estimates, with PS density obtained from PSI analysis of ascending (A) and descending (D) data.

Pass/Orbit	Master Scene (# of ifg)	Nr. of PS (PS/km2)	$\begin{array}{c}\mathbf{Relative}{\mathit{V}}_{\mathit{l}\mathit{o}\mathit{s}}(\mathbf{mm}/\mathbf{y})\\ \mathbf{Min}.\mathbf{to}\mathbf{Max}.\\ \left(\mathbf{Median}\right)\end{array}$	$\begin{array}{c}\mathbf{Calibrated}{\mathit{V}}_{\mathit{l}\mathit{o}\mathit{s}}\\ \mathbf{Min}.\mathbf{to}\mathbf{Max}.\\ \left(\mathbf{Median}\right)\end{array}$	$\begin{array}{c}\mathit{s}\mathit{t}\mathit{d}{.}^1{\mathit{V}}_{\mathit{l}\mathit{o}\mathit{s}}(\mathbf{mm}/\mathbf{y})\\ \mathbf{Min}.\mathbf{to}\mathbf{Max}.\\ \left(\mathbf{Median}\right)\end{array}$
A118	27/08/2016 (28 ifgs)	214,061 (~460)	−8.1 to +17.9 (0.3)	10.3 to 36.3 (18.7)	0.3 to 2.6 (0.9)
D111	26/09/2016 (25 ifgs)	228,335 (~480)	−13.7 to +13.6 (0.6)	6.7 to 34.0 (21.1)	0.3 to 2.7 (1.0)

¹ standard deviation.

. A large number of PSs could be identified in both ascending (A) and descending (D) interferogram stacks, which correspond to a PS density of more than 450 PS/km²; this is comparable to dense urban areas. During 2015–2018, the median of relative LOS velocities (relative $V_{los}$) of both A and D data are slightly higher than zero (about +0.3 and +0.6 mm/y for A and D, respectively) with respect to the reference point (0 mm/y).

Calibrated $V_{los}$ values of the GPS time-series at the SKFC reference point obtained from Equation (3) for the A and D data are 18.4 mm/y ($\theta =44.3,\alpha =350.6$) and 20.4 mm/y ($\theta =39.8,\alpha =191.0$), respectively. These absolute LOS velocities of SKFC were used to calibrate other estimates linearly, resulting in the calibrated velocity shown in Table 2. Note that the horizontal plate-spreading signal was preliminarily estimated and removed from 3D GPS measurements prior to the calibration. Therefore, our calibrated LOS velocity estimates do not contain deformation signals subjected to plate spreading.

The median values of uncertainties ($std.V_{los})$ of the LOS estimates are approximately 1 mm/y for both tracks. Precisely, ascending data have slightly lower $std.V_{los}$, which is likely due to the greater number of interferograms used in the PSI.

The initial visual interpretation of the relative LOS estimates of both A and D data in Figure 5a,b indicates that PSs with cold colour tones (light green to blue) have moved towards the satellite (positive velocity). PSs with warm colour tones (yellow to red) have moved away from the satellite (negative velocity) during this time span, relative to the reference point.

The interpretation also indicated remarkable areas with extreme colour differences—i.e., blue in A and orange in D data (Figure 5e,f), corresponding to positive and negative LOS velocities, respectively—observed on the slopes south of Svínafellsjökull and southwest of the Virkisjökull and Falljökull outlet glaciers (areas surrounded by white rectangle, cf. Figure 5). This occurrence can be explained using Figure 3a: when the ascending $V_{los}$ is positive and descending $V_{los}$ is negative, the horizontal component ($V_h)$ of the resulting motion vector ($V_{total})$ should be significantly present during our observation period. However, when the horizontal component is not significant, the resulting LOS vectors projected between the two LOS vectors can be either positive or negative.

The standard deviation of LOS deformation-rate estimates ($std.V_{los}$) informs us about the degree of nonlinearity (NL) of the movement, i.e., how much an individual velocity (of an interferogram) deviated from the mean velocity during the observed period, expressed in mm/y. The larger the value, the more a PS has deformed nonlinearly with time. The estimated standard deviation ranges from 0.3 to 2.6 or 2.7 mm/y for our ascending and descending data. The $Std.V_{los}$ estimates shown in Figure 5c,d indicate clearly that PSs located at the margin of the glaciers (orange/red points) deformed in a nonlinear fashion compared to PSs located further away from the glaciers.

Validation of PS LOS Deformation-Rate Estimates

Comparisons between the GPS LOS deformation and the calibrated LOS deformation time-series (hereafter, absolute LOS velocity—$V_{los}$) of the selected PSs surrounding three GPS stations (SKFC, SVIN, SVIE) over the SAR observation period are shown in Figure 6. The PS $V_{los}$ estimate represented by the red lines in Figure 6a–f is the least square estimate of the LOS deformation velocities from all selected PSs (3–4 PSs per station). The GPS LOS deformation rate, represented by the black dotted lines in Figure 6a–f, was derived from the best available GPS time series. GPS measurement outliers were omitted during the GPS LOS velocity estimation. The uncertainties ($s_N$,$s_E$, $s_U$) of the GPS deformation time-series measurements are 2–3 mm for $d_N$, 2 mm for $d_E$, and 6–8 mm for $d_U$.

A comparison of the results indicates lower PS LOS velocity estimates (flatter slope of the red line) than the reference GPS deformation velocity (black dotted line) at the SVIN and SVIE stations. One of the reasons for PS underestimation is the usage of the LOS velocity of the reference point (SKFC), averaged over 4 years for the overall LOS estimate calibration. Whether this value is an optimal calibration value depends on the similarity of the deformation behaviour of a particular location compared to the reference point. Additionally, the $std.V_{los}$ values indicate that PSs in the vicinity of SKFC deformed more linearly with time (lower $std.V_{los}$ value) than PSs near the SVIN and SVIE locations (cf. $std.V_{los}$ in

Table 3. Summary of statistics of 3D GPS time-series measurements at three reference points available for the InSAR period, with comparison between GPS $V_{los}$ and PS $V_{los}$ (cf. Figure 6), and the standard deviations of the selected PS deformation estimates used for validation.

Station (# GPS Obs.)	GPS dN 1/sN 2 (mm)	GPS dE/sE (mm)	GPS dU/sU (mm)	Data	$\begin{array}{c}\mathbf{GPS}{\mathit{V}}_{\mathit{l}\mathit{o}\mathit{s}}{}^3/\\ \mathbf{PS}{\mathit{V}}_{\mathit{l}\mathit{o}\mathit{s}}\end{array}$	$\begin{array}{c}\mathit{S}\mathit{t}\mathit{d}.{\mathit{V}}_{\mathit{l}\mathit{o}\mathit{s}}{}^4\mathbf{PS}\\ \mathbf{Min}.\mathbf{Max}.\\ (\mathbf{mm}/\mathbf{y})\end{array}$
SKFC (550)	−13.0/2.6	6.1/2.1	45.8/8.0	A D	18.4/19.7 20.4/19.5	0.5–1.0 0.4–1.1
SVIN (109)	−2.8/2.1	−2.4/1.8	9.3/6.8	A D	38.4/18.7 25.3/13.5	1.1–1.4 1.1–1.4
SVIE (107)	−3.0/2.0	−2.1/1.7	7.7/6.3	A D	36.0/21.0 25.3/14.1	1.4–1.6 1.6–1.8

¹ Mean of deformation measurements (d) in N, E, and U directions averaged over the GPS observation period; ² average one sigma uncertainty (s) of GPS measurements in N, E, and U directions of the same period; ³ derived GPS LOS deformation velocity using satellite geometries; and ⁴ range of $std.V_{los}$ of the selected PSs visualised in Figure 6.

). As such, the difference in $std.V_{los}$ implies a difference in movement behaviours and is one of the factors affecting these deviations, ranging from approximately −10 to −20 mm/y, from the reference GPS $V_{los}$ estimates.

3.2. Two-Dimensional Decomposed Deformation Velocities

Applying quality criteria selection and layover-shadow-mask buffering to all $V_{los}$ estimates from both A and D data resulted in about 7% of PSs being eliminated; the remaining 93% were considered quality PSs (QPSs). We also observed that isolated PSs on the glaciers were almost 100% removed (cf. Figure 7a–d). The selected thresholds proved to be feasible, since PS clusters on the slopes and at the edge of the glaciers remained, while isolated PSs on glaciers were eliminated.

With an average PS density of more than 350 QPS/km², and considering the spatial-proximity tests, we decided to use the shortest search radius of 100 m to achieve a reasonable computing time. For the selected search distance of 100 m, the average number of across-track PSs in the proximity is 17, and the minimum is 1 for A and D data (for details, cf.

Table 4. Statistics of vertical $V_v$ and horizontal velocities $V_h$, $V_{v\_res}$, $V_{perp}$, and $V_{slope}$ as a result of the first and the second vector-based decompositions of A2D, D2A and a combination of both A2D and D2A (cf. Figure 7 and Figure 8).

Dataset	QPS 2 Density PS/km2	# Across-Track 3 PSs Min. to Max. (Mean)	$\begin{array}{c}{\mathit{V}}_{\mathit{v}}\\ \mathbf{Min}.\mathbf{to}\mathbf{Max}.\\ \left(\mathbf{Median}\right)\\ \mathbf{mm}/\mathbf{y}\end{array}$	$\begin{array}{c}{\mathit{V}}_{\mathit{h}}\\ \mathbf{Min}.\mathbf{to}\mathbf{Max}.\\ \left(\mathbf{Median}\right)\\ \mathbf{mm}/\mathbf{y}\end{array}$
A2D	~396	1–47 (17)	−18.9 to 37.7 (26.7)	−15.2 to 10.5 (1.2)
D2A	~360	1–39 (17)	−17.2 to 37.1 (26.7)	−14.4 to 9.5 (1.0)
Combined 1 1st decomposition	~757		−17.2 to 37.7 (26.7)	−15.2 to 10.5 (1.1)
Combined (after GIA-SS removal)	~757		$V_{v\_res}$ −7.8 to 12.7 (1.7)	$V_h$ −15.2 to 10.5 (1.1)
Combined 2nd decomposition	~757		$V_{perp}$ −8.1 to 17.7 (1.8)	$V_{slope}$ −15.3 to 10.6 (1.1)

¹ Combination of A2D and D2A point estimates; ² quality PS; ³ descending data are the across-track for ascending data and vice versa.

). This means that $V_v$ and $V_h$ can be estimated for all QPSs surrounded by at least one across-track PS.

The two-dimensional horizontal $V_h$ and vertical velocity $V_v$ as a result of the first $V_{los}$ vector decomposition (cf. Equation (4)) are presented in Figure 7a–d. Our estimated $V_v$ fields indicate lower vertical velocities at the Svínafellsheiði (SvH) slope and the slope south of Skaftafellsjökull compared to the slopes that lie between the Skeiðarárjökull and Skaftafellsjökull glaciers. The estimated $V_h$ fields reveal that the entire Svínafellsheiði slope and the slope southwest of Virkisjökull and Falljökull predominantly displaced towards the west (negative $V_h$) at a magnitude of more than 10 mm/y (orange and red PSs). This supports our initial interpretation in Section 3.1 concerning the horizontal velocity. Other slopes (next to Skeiðarárjökull, Morsárjökull, and Skaftafellsjökull glaciers) indicate a mixture of horizontal movements that move partially towards the east or the west (blue or yellow, Figure 7c,d).

We applied quantile data classification to visualise the $std.V_{los}$ (Figure 7e,f and Figure 8), with the aim of assigning an equal number of QPSs to each class, represented by individual colours. The fourth quantile classification divides the total QPS into an equal number of PSs (approximately 25%). Likewise, the sixth quantile classification divides the total QPSs into approximately 16.7%. Thus, the median of the parameter of interest and extremely deforming QPSs with their corresponding values can be spatially located and determined. The $std.V_{los}$ distribution patterns in Figure 7e,f and Figure 8c indicate that 25% of QPSs located in the low-lying areas deform more linearly (blue QPSs have a $std.V_{los}$ ranges from ~0.3–0.8 mm/y), while 25% of QPSs along the margin of the glaciers (red QPSs) tend to deform nonlinearly ($std.V_{los}$ higher than ~1.1 mm/y).

The A2D and D2A estimates were spatially combined, leading to almost double the number of robust measurement points (QPS density). The major vertical uplift trend, the GIA-SS, was inferred based on the median of the decomposed vertical velocities (median $V_v$ 26.7 mm/y estimated from more than 350,000 PSs), from the literature [52], and from the fact that our calibrated LOS velocity at SKFC is an underestimate (cf. Figure 6). The constant rate of 25 mm/y was subtracted from $V_v$, resulting in $V_{v\_res}$ being used for the second decomposition.

The results in Figure 8 are visualised based on quantile data classification. Here, we divided $V_v$, $V_h$, $V_{perp}$, and $V_{slope}$ into six classes (~16.7% QPS per class). Hence, we can constrain the most dynamic locations in terms of the maximum and minimum motion rates based on our estimates. These dynamic QPSs (blue or red coloured) constitute only a small part of the total QPSs (max. 16.7%). Figure 8a shows that approximately one-third of the QPSs in our AoI are dominated by high vertical velocities (dark blue and dark green QPSs). Another one-third of the QPSs are potentially affected by other deformation processes, dominated by their horizontal component, i.e., red and orange QPSs showing negative vertical velocities (Figure 8b). We found that the maximum vertical velocities are clustered on the mountain slopes between Skeiðarárjökull and Morsárjökull, and parts of these slopes also show strong movement in the east direction (upper white rectangle in Figure 8a,b). The minimum vertical velocities were grouped into two clusters: one on the slopes surrounding Svínafellsjökull and the other in the low-lying areas lower than 200 m a.s.l. The highest horizontal motion rates are clustered on the southwest slope of the Virkisjökull and Falljökul outlet glaciers and the south slope of Svínafellsjökull, indicating movement westward. Figure 8d,e illustrate $V_{perp}$ and $V_{slope}$ results, respectively, obtained from the second vector decomposition. The $V_{slope}$ estimates are almost identical to the $V_h$ estimates, since the horizontal component has not been adjusted after the first decomposition step and its magnitude is small (cf. Table 4). Only a constant GIA-SS velocity of 25 mm/y was removed from the vertical component, giving $V_{v\_res}$ as input for the second vector decomposition. The $V_{perp}$, estimated from the residual vertical velocities $V_{v\_res}$ and $V_h$, shown in Figure 8d, additionally revealed movements in the direction perpendicular to the slope surface (blue) at the Svínafellsheiði slope and the slope southwest of Virkisjökull and Falljökull, which were not detectable during the first vector decomposition (cf. Figure 8a).

3.3. Derived Two-Dimensional Local Deformation Fields

3.3.1. Hot-Spot Analysis (HSA) Results

Applying Hot-Spot Analysis to the PS-based deformation estimates resulted in the identified clusters of high values (“Hot Spot”, presented in red), clusters of low values (“Cold Spot”, presented in blue), as well as clusters of “not significant” values (presented in grey) in Figure 9. The IDW approach provides a smoother transition between “Hot Spot”, “Cold Spot”, and “not significant” clusters than the FDB. This is because the FDB does not consider PSs lying outside the defined distance band, whereas IDW does. We adapted HSA results based on FDB = 100 m for two reasons: (1) our $V_v$ and $V_h$ estimates are derived based on 100 m spatial proximity, and (2) results from “calculate distance band” indicate an average number of neighbouring QPSs of 48 at FDB = 100 m, which is statistically significant. HSA enables us to statistically classify our AoI into three sub-areas based on the deformation parameter under consideration ($V_v$ or $V_h$ or $std.V_{los}$). For example, the analysis results differentiate dynamic zones affected by uplift or subsidence from stable zones. Similarly, the HSA of $std.V_{los}$ allows us to differentiate highly nonlinear deforming areas from more linear deforming areas.

3.3.2. Interpretation of the Local Deformation Fields

Based on the HSA zones (100 m grid) with their mean velocities, we integrated the HSA results with two-dimensional pointwise estimates from PSI (~750 PS/km²), leading to spatially detailed surface-deformation velocity maps at the local scale, as shown in Figure 10. In Figure 10a–h, clusters with low values are outlined in blue, and clusters with high values are outlined in red.

The derived 2D deformation estimates resulting from the first vector decomposition indicate the minimum $V_v$ (+17.2 mm/y) at the Svínafellsheiði slope and low $V_v$ at the slope south of the Skaftafellsjökull, respectively (blue triangles and brown-shaded PSs in Figure 10b). PSs with the minimum $V_h$ (−15.2 mm/y) and relatively low $V_h$ were found at the slope southwest of the Virkisjökull and Falljökull glaciers and the Svínafellsheiði slope, respectively (blue triangles and orange-shaded PSs in Figure 10d). The obtained negative horizontal velocities at PSs indicate movement towards the off-west direction (Figure 10c,d), which agree well with independent GPS deformation observations at the SVIN and SVIE reference points in the area (cf. Table 3).

Two velocity components, $V_{perp}$ and $V_{slope}$, were obtained from the second vector decomposition (Figure 10f,h). The terrain slope southwest of Virkisjökull and Falljökul shows low $V_v$ (slightly higher than the assumed GIA-SS = 25 mm/y) and minimum horizontal movement (yellow–light-brown-shaded PSs in Figure 10b and blue triangles in Figure 10d, respectively). After removing the assumed GIA from $V_v$, the positive residual velocity remained, resulting in positive $V_{perp}$, and PSs differentiated themselves from the neighbourhood as Hot Spots (PS surrounded by white oval in Figure 10e,f). It should be noted that without applying the second decomposition, areas of different deformation behaviours, such as in this example, could not be detected.

The estimated two-dimensional deformation velocities from the second vector decomposition also suggest that the Svínafellsheiði terrain slope slightly moves perpendicular to the slope surface (mean $V_{perp}$ +0.4 mm/y, Figure 10e) and in the downslope direction (min $V_{slope}$ −2.8 mm/y, Figure 10g). During our observation period, the magnitude of the estimated horizontal movement in the off-west direction seems significant, as it suppresses the vertical component. Our results also indicate that surface deformation around Svínafellsheiði behaves differently compared to the mountain slopes east of Skeiðarárjökull, which move towards the off-east direction (lower white rectangle compared to the upper white rectangle in Figure 8d,e).

Spatial analysis of the rasterised velocity clusters ($V_v$ and $V_h$) with $std.V_{los}$, as shown in Figure 9 leads to detailed categorisation of movement behaviours and the unique deformation velocity zones, characterised by different degrees of NL and movement directions in the AoI (cf. Figure 11).

Our results indicate a decrease in $V_v$ from west to east of the AoI, i.e., changing from Hot Spot (mean $V_v$ = 29.7 mm/y) to Cold Spot (mean $V_v$ = 25.3 mm/y). This approximately corresponds to the increase in the distance from the centre of the ice cap (Figure 10a and Figure 11b). The closer a PS is to the ice cap, the higher its $V_v$. An integrated interpretation of $V_v$ and $std.V_{los}$ shows that PSs at higher altitudes deform more in the NL fashion than in low-lying areas (Figure 11b). Likewise, integrated interpretation of $V_h$ and $std.V_{los}$ reveals that the areas lying approximately west of the Skaftafellsheiði slope deform towards the east, whereas areas to its east deform towards the west (Figure 11d). The PSs lying between 100 and 200 m a.s.l. do not indicate a significant horizontal movement pattern (cluster with random $V_h$, grey in Figure 11d).

Joint interpretation of the deformation attributes further shows that the mountain slopes north and south of Svínafellsjökull, including the terrain slope southwest of Virkisjökull and Falljökull, behave similarly (Figure 11a–d). Their deformation behaviours are characterised by low $V_v$, high NL, and horizontal movement towards the west, i.e., the cream-shaded areas in Figure 11a and the green-shaded areas in Figure 11c. Since the horizontal plate-spreading deformation was initially removed before the decomposition, the residual horizontal velocity, whose mean $V_h$ ranges from +2.5 to 2.8 mm/y (Figure 10c and Figure 11d), could be subjected to the horizontal component of seasonal deformation.

4. Discussion

MLV estimates derived from PSI analysis to quantitatively describe ongoing, two-dimensional deformation velocities in the Öræfajökull area show discrepancies ranging from ~2 to more than 10 mm/y when compared to independent GPS time-series measurements available for the same period (Figure 6). These deviations can be attributed to several factors. First, the use of the known velocity of the reference point (SKFC) to calibrate the relative PS LOS deformation-rate estimates globally led to underestimations of PS LOS velocities at SVIE and SVIN. The lower $std.V_{los}$ value, which implies more linearity of the deformation of the reference point SKFC when compared to SVIE and SVIN, could be used to justify such discrepancies (cf. Figure 6c–f and Table 3). In addition, when the surface-deformation processes under consideration vary substantially in space and time, as in our case study, it is unlikely that an optimal calibrated velocity that fits all local deformation models can be found. This led to increasing deviations at PSs, where their deformation behaviours differ significantly from those of SKFC.

Second, only the 2018 annual GPS deformation rates of SVIN and SVIE were available for validation with the InSAR LOS velocity estimates, which have an acquisition time-span from 2015 to 2018. The difference in both measurement time spans could affect the validation accuracy. The obtained maximum uncertainty of QPS LOS estimates, or the standard deviation of the MLV, is approximately 2 mm/y.

Compared to previous studies that employed either 1D LOS displacement information [34] or 2D rasterised deformation estimates at a coarser scale for wide-area deformation mapping [35], we exploited the full potential of Sentinel-1 data for the derivation of 2D deformation estimates at full resolution based on a vector-based decomposition approach. Unlike raster-based algorithms, the applied workflow utilises LOS point estimates to derive 2D deformation velocities. The approach preserves the original point estimate accuracy and the subsequent 2D estimate accuracy as the processing errors are minimised. Rasterisation and interpolation of the velocity parameters were applied only in the final steps, spatial statistics and spatial analysis. With a PS density of 750 PS/km² and an average of 17 neighbouring QPSs (100 m search distance) used for the decomposition, our final product, the unique deformation velocity (UDV), represents the most detailed PS-based deformation zoning at its highest resolution and accuracy. For further quantitative assessment, the focal statistics of two-dimensional PS velocity estimates derived from A2D and D2A decompositions could be examined.

Our proposal to exploit the PLIA instead of the EIA in the two-step vector decomposition first allows for the isolation of deformation signals of interest. In our case, the assumed constant vertical deformation rate (GIA-SS) was subtracted, leaving the 2D residual components to be decomposed in the next step (Equation (5)). Second, the algorithm makes the direct derivation of $V_{slope}$ and $V_{perp}$ from 2D $V_{los}$ measurements possible, which is particularly beneficial and unbiased for the derivation of surface-deformation information over both flat and inclined terrain. It should be noted that the $V_h$ and $V_{slope}$ value ranges are almost identical (Figure 8b,d). This is due to the fact that after the removal of the unwanted signals, plate spreading and GIA-SS, the magnitudes of the residual velocities are relatively small (Equation (6)).

Considering the challenges encountered in this study, such as the complex deformation signal in its vertical component, and the acquisition time of the SAR imagery analysed (May–October scenes), it is not possible to isolate the GIA from the semi-annual seasonal signal relying only on PSI. Since both signals were detected as uplift trends (positive $V_v$) during the observation period, we could only estimate the mixture of vertical deformation signals, i.e., the GIA-SS. In future, instead of removing the constant GIA-SS from the $V_{los}$ before entering the second decomposition, possibilities for improving the GIA-SS spatial model, e.g., using $std.V_{los},$ should be investigated.

Integrated spatial analysis enables us to consider co-existing attributes based on two or three deformation parameters—i.e., $V_v$ and $std.V_{los}$ (Figure 11a); $V_h$ and $std.V_{los}$ (Figure 11c); and $V_v,V_h\mathrm{and}std.V_{los}$ (Figure 12b)—simultaneously. Depending on the number of parameters under consideration, two or three parameters, the analysis led to 9 to 27 UDV classes that describe the diversity of the geomorphological dynamics around Öræfajökull.

The combined interpretation of HSA results of $std.V_{los}$ values and the elevation contours in Figure 12a indicates that PSs surrounded by a glacier or located at the margin of the outlet glaciers (red cluster) at higher altitudes (approximately 400 m–1000 m a.s.l.) deform more nonlinearly with time, with an average $std.V_{los}$ value of ~1.2 mm/y. QPSs located further away from glaciers in low-lying areas (blue cluster, located between 100 m and 400 m a.s.l.) deform more linearly with time. The average $std.V_{los}$ for this class is ~0.7 mm/y. QPSs with medium-nonlinearity deformation (grey cluster) have an average $std.V_{los}$ of 0.9 mm/y. Using the fourth quantile classification for data visualisation further confirms that the high nonlinearly deforming (high NL) or linearly deforming (low NL) QPSs constitute smaller parts of the entire QPS, namely, 25% for each class (Figure 8c and Figure 12a). The medium nonlinearly (medium NL) deforming QPSs comprise the largest part, i.e., 50% of the all QPSs. We can observe that on most of the mountain slopes, only PSs located below 1000 m a.s.l. could be detected in all of the interferograms and used for PSI, because these PSs were not covered by snow during the warmer months’ SAR acquisitions. Based on this PS detectability finding, we propose 1000 m as the Equilibrium Line Altitude (ELA) for glaciers in the study area, which is consistent with the existing reference elevation [55]. In addition, we observed high $std.V_{los}$ values (high NL) at QPSs located at high elevations (approximately 600–1000 m a.s.l.) when compared to the $std.V_{los}$ of QPSs at lower altitudes (Figure 8c and Figure 12a). This implies that QPSs located at higher altitudes, right below the ELA in the ablative zone, deform in a more nonlinear fashion than QPSs located at a lower altitude, further away from the ELA. If we assume the surface uplift due to GIA to be linearly constant over time, the nonlinear deformation component inferred from the $std.V_{los}$ could be subjected to glacial-mass balance or snow-load changes, the main contribution to seasonal deformation in the area. Our findings are consistent with those of a previous study [53].

The combined interpretation of spatial analysis results provides detailed deformation information for Öræfajökull as follows: First, we observed heterogeneous two-dimensional deformation patterns at the ends of glacier tongues at low elevations (e.g., 200 m a.s.l.). There is no indication of a specific movement pattern in either the vertical or horizontal component in these areas (random $V_v$ and/or random $V_h$). Such heterogeneity can be observed at Skeiðarárjökull, Skaftafellsjökull, and Svínafellsjökull glacier termini (Figure 12b). Second, the $V_v$ HSA clustering (Figure 11b) clearly defines the $V_v$ transition zone located at the mountain slope northwest of Skaftafellsjökull. Likewise, the $V_h$ HSA clustering (Figure 11d) indicates a $V_h$ transition zone located at the same mountain slope. Localisation of the transition zone could be used to update the deformation inventory in the area.

Previous studies have suggested that the magnitude of GIA and the seasonal deformation signals (GIA-SS) are related to the distance to the Vatnajökull ice cap. Following this statement, the GIA-SS-induced $V_v$ values of any arbitrary PSs located at the same Euclidean distance from the centre of Vatnajökull should be similar when only GIA-SS and no other coexisting deformation processes have taken place. Our investigations at points a and b, however, result in $V_v$ magnitudes of 31.0 and 27.7 mm/y respectively (upper white dashed line in Figure 12b). Both points are located ~38 km away from the centre of Vatnajökull at approximately 800 m a.s.l. In addition, a larger $V_v$ difference is observed between points c and d. The estimated $V_v$ of point c is ~30.0 and of point d is ~25.3 mm/y, and they have the same Euclidean distance (50 km from Vatnajökull, cf. lower white dashed line in Figure 12b). Coupling $V_v$ with the estimated $V_h$, we, therefore, interpret the overall 2D deformation field around point d (compared to point c) to be affected not only by the vertical motion (GIA-SS) but also by the more intense off-west horizontal motion. Likewise, the similar $V_v$ magnitudes of points a and c, despite a Euclidean distance discrepancy of more than 10 km, cannot be satisfactorily explained by the aforementioned statement. In general, the 2D deformation fields around Öræfajökull during our observation period were affected by diverse, coexisting deformation processes at both the regional and local scales. The regional vertical deformation signal (GIA-SS-like signal) is dominant in the west of the AoI. Moving to the east, closer to the Öræfajökull volcano, the 2D deformation field is dominated by stronger horizontal motion, suppressing vertical motion.

5. Conclusions

In this study, we demonstrated the applicability of two-dimensional deformation estimates derived from the PSI of Sentinel-1 data, focusing on improved understanding of local deformation processes. Based on the vector-based LOS velocity decomposition approach, we derived high spatial resolution (PS density of 750 PS/km²) and more precise motion information (QPS LOS velocity uncertainty better than 2 mm/y) than those previously achieved by other geodetic measurements. The diversity and nonlinearity of the ground-surface-motion processes make direct exploitation of the absolute MLV estimate less effective. However, we demonstrate that by analysing QPSs’ local spatial statistics (Hot Spot Analysis) in relation to their neighbours, statistically relevant QPSs can be grouped into meaningful clusters and used to describe local deformation trends, i.e., Hot Spots, Cold Spots, and not significant (random) clusters. The combined spatial analysis of three QPS-based parameters, $V_v$, $V_h$, and $std.V_{los}$, enables us to infer up to 27 UDV classes that characterise and reveal the diversity of the deformation behaviours around Öræfajökull.

Our PS-based raster product, the UDV clusters, provides the most detailed (100 m grid) reliable deformation categorisation to date. The UDV zones provide us with more insight into the classification of ongoing deformation processes. We infer that local deformation fields west of Öræfajökull are dominated by high vertical motion in the west and by horizontal motion in the east. The approximate horizontal motion rate of −2.8 mm/y and low vertical motion rate of +25.3 mm/y describe the surface motion behaviours at Svínafellsheiði and the southwest slope of the Virkisjökull and Falljökull glaciers during the study period. Knowing the approximate location of $V_v$ and $V_h$ cluster boundaries and the mixture of random vertical and horizontal motion zones dominating at the north slope of Skaftafellsjökull, we infer this area to be the deformation transition zone.

For the first time, we introduce and demonstrate the results of a two-step vector decomposition that integrates the PLIA parameter in its implementation. We found that the concept is particularly beneficial for case studies where the isolation of two-dimensional deformation components is necessary and/or the surface motion of the inclined surface and slope-deformation rates are in focus.

In this study, we have demonstrated the potential use of the PS-based high-resolution 2D deformation products derived from the proposed workflow for improving the characterisation of the local deformation fields, determining the motion transitioning zone, and confirming the glacial ELA. Although the pointwise accuracy of the 2D PS estimate derived from this study is not as high as that of the geodetic measurement, PSI analysis of Sentinel-1 data has proved to be one of the most applicable techniques for the derivation of highly precise, two-dimensional surface-deformation information, complementary to traditional cost and time-intensive techniques.