A Study of Simulation of the Urban Space 3D Temperature Field at a Community Scale Based on High-Resolution Remote Sensing and CFD
Abstract
:1. Introduction
2. Study Area
3. Materials and Methodology
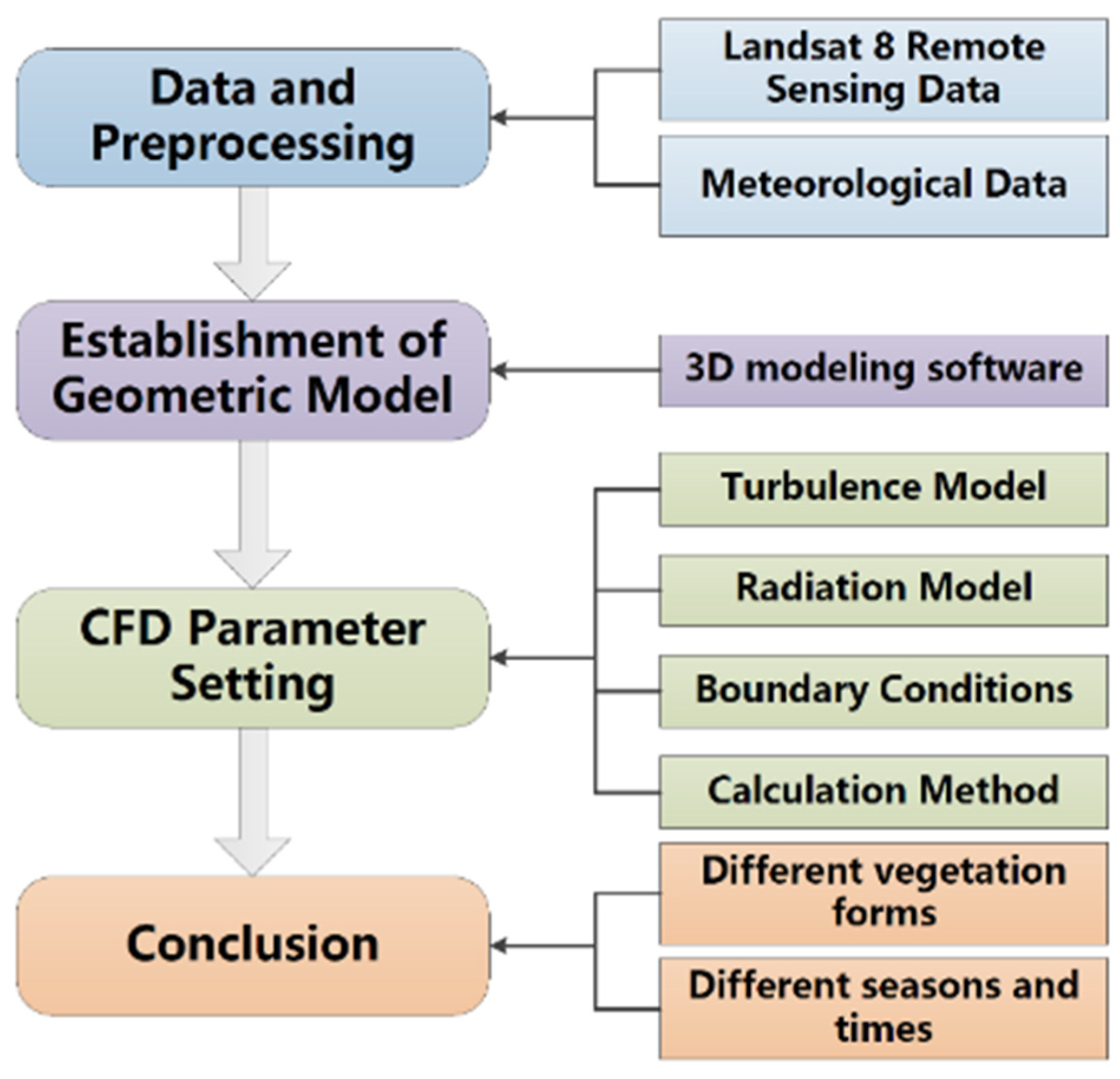
3.1. Materials and Their Processing
3.1.1. 3D Model Building Based on Remotely Sensed Dataset
3.1.2. Definition of Materials
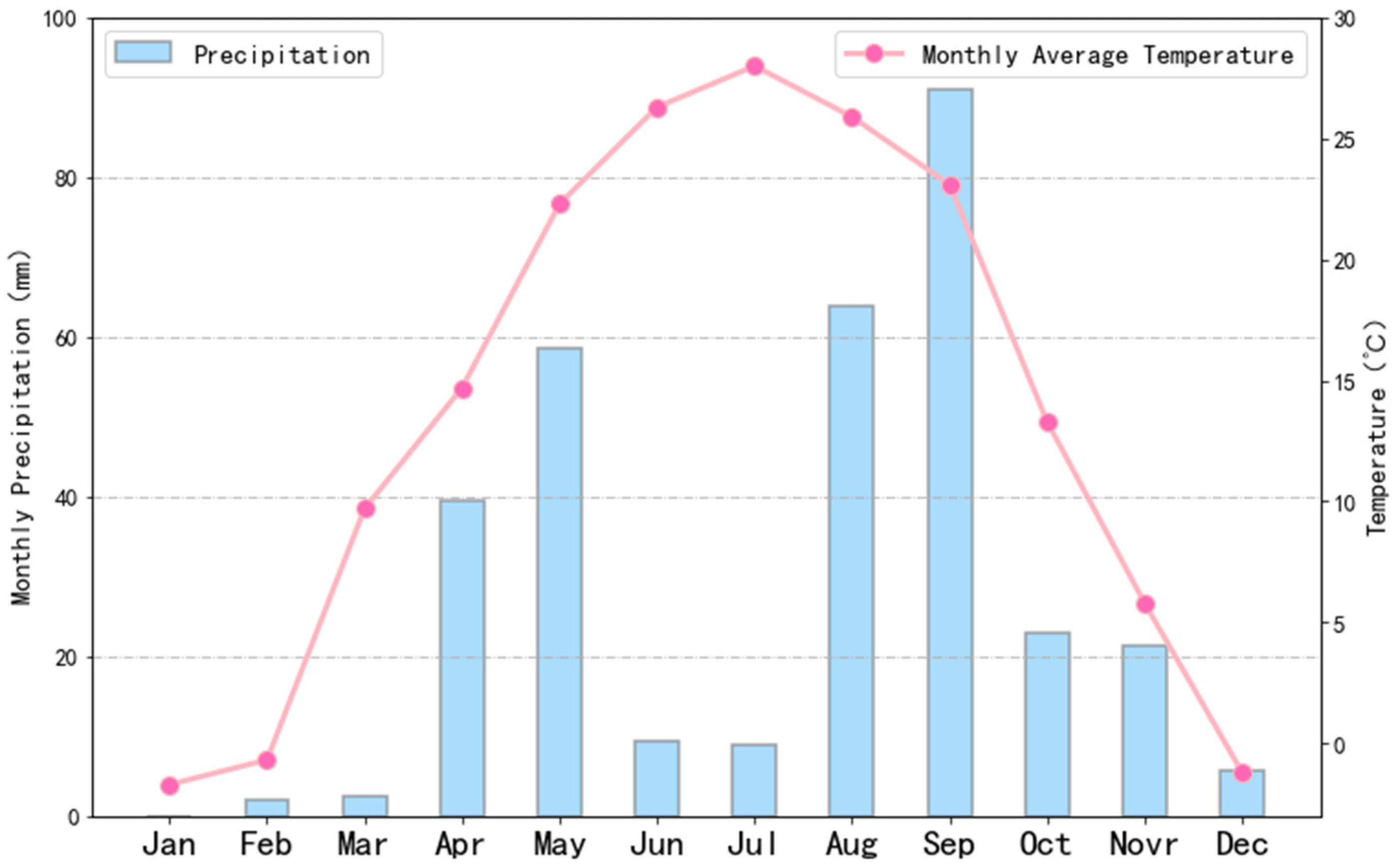
3.1.3. Meteorological Dataset
3.2. CFD Modeling Principle
3.2.1. CFD Turbulence Governing Equations
- ρ
- is the fluid density (unit is m3/s);
- t
- is time (unit is s);
- v
- is the speed vector (unit is m/s);
- p
- is the pressure on the infinite element (unit is N);
- τ
- is the viscous stress (unit is N);
- F
- is the volume (unit is m3);
- Cp
- is the thermal capacitance (unit is kJ·kg/°C);
- T
- is the temperature (unit is °C);
- k
- is the coefficient of heat conductivity (unit is W·m2/K);
- ST
- is the viscous dissipation term;
- ϕ
- is the flux variant;
- Γ
- is the general diffusion coefficient;
- S
- is the general source term.
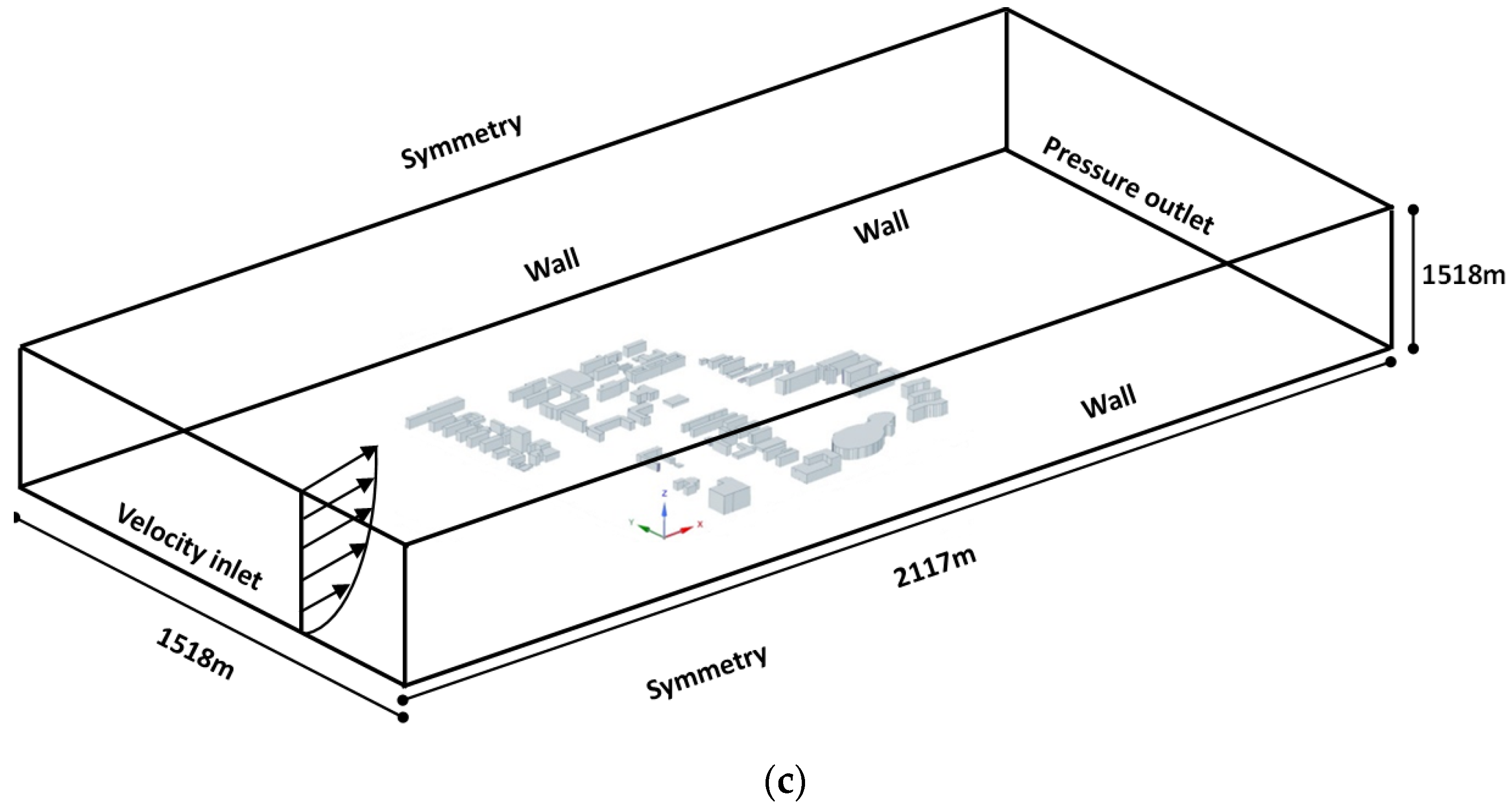
3.2.2. Mesh Division and Boundary Condition Parameter Settings
3.2.3. Calculation and Setting of Wind Speed Profile
3.2.4. Simplification and Setting of Vegetation Porous Media Model
- ρa (kg/m3) is the density of air;
- Cd is the drag coefficient;
- LAD is the leaf area density;
- ui is the local speed in the i-direction;
- u is the magnitude of the local speed;
- Rn,vol (W/m3) is the volumetric net radiation;
- Qconv (W/m2) is the heat flux;
- LEv (J/kg) is the amount of latent heat released by leaves;
- Sk is the sink term of the turbulence kinetic energy equation;
- Sε is the sink term of the turbulent dissipation.
4. Results and Discussion
4.1. Simulation of 3D Urban Spatial Surface and Air Temperatures
4.1.1. Influence of Vegetation Morphology Layout on Temperature
4.1.2. Influence of Vegetation Morphology Layout on Wind Speed
4.1.3. Distribution Characteristics of Wind and Heat Environment during Daytime and Nighttime in Four Seasons
- (A)
- Distribution characteristics and analysis of wind and heat environment for daytime in four seasons
- (B)
- Distribution characteristics and analysis of wind and heat environment for night time in four seasons
4.2. Simulation of Urban Wind and Heat Environment and Research on Its Distribution Characteristics at a Community Scale
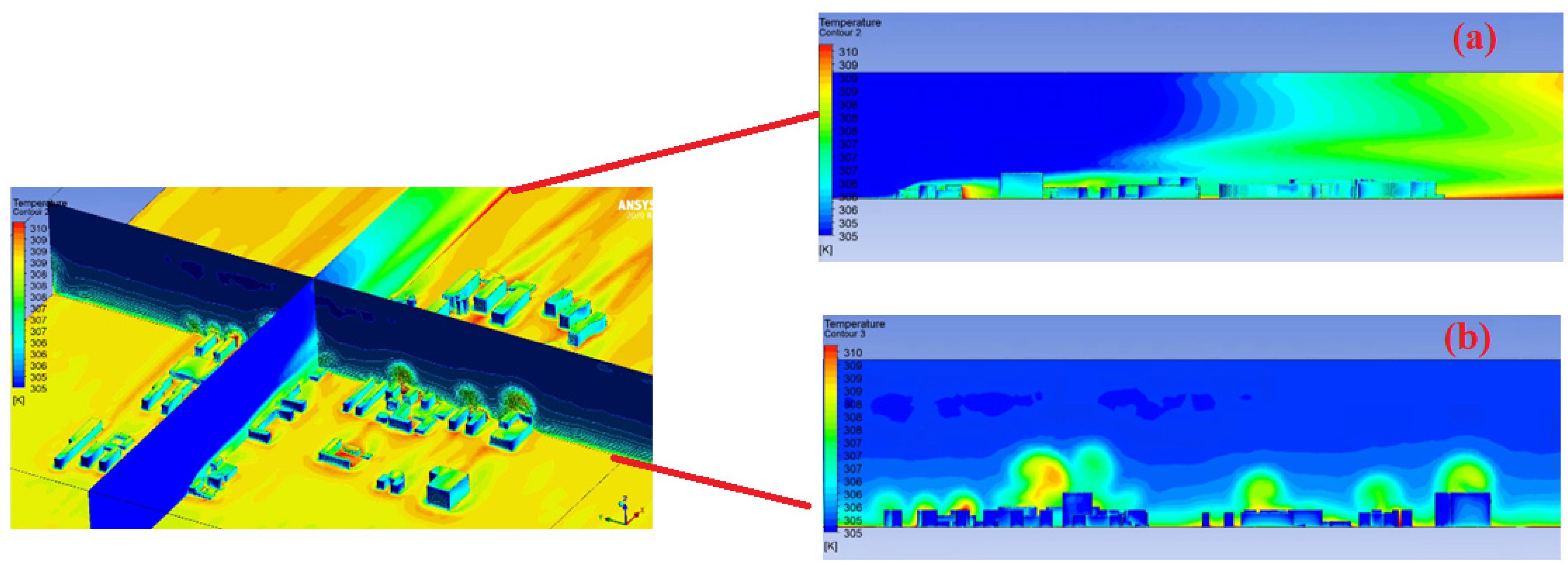
4.2.1. Distribution Characteristics and Influencing Factors of Spatial Wind and Heat Environment at a Community Scale during the Daytime
4.2.2. Distribution Characteristics and Influencing Factors of Spatial Wind and Heat Environment at the Community Scale at Nighttime
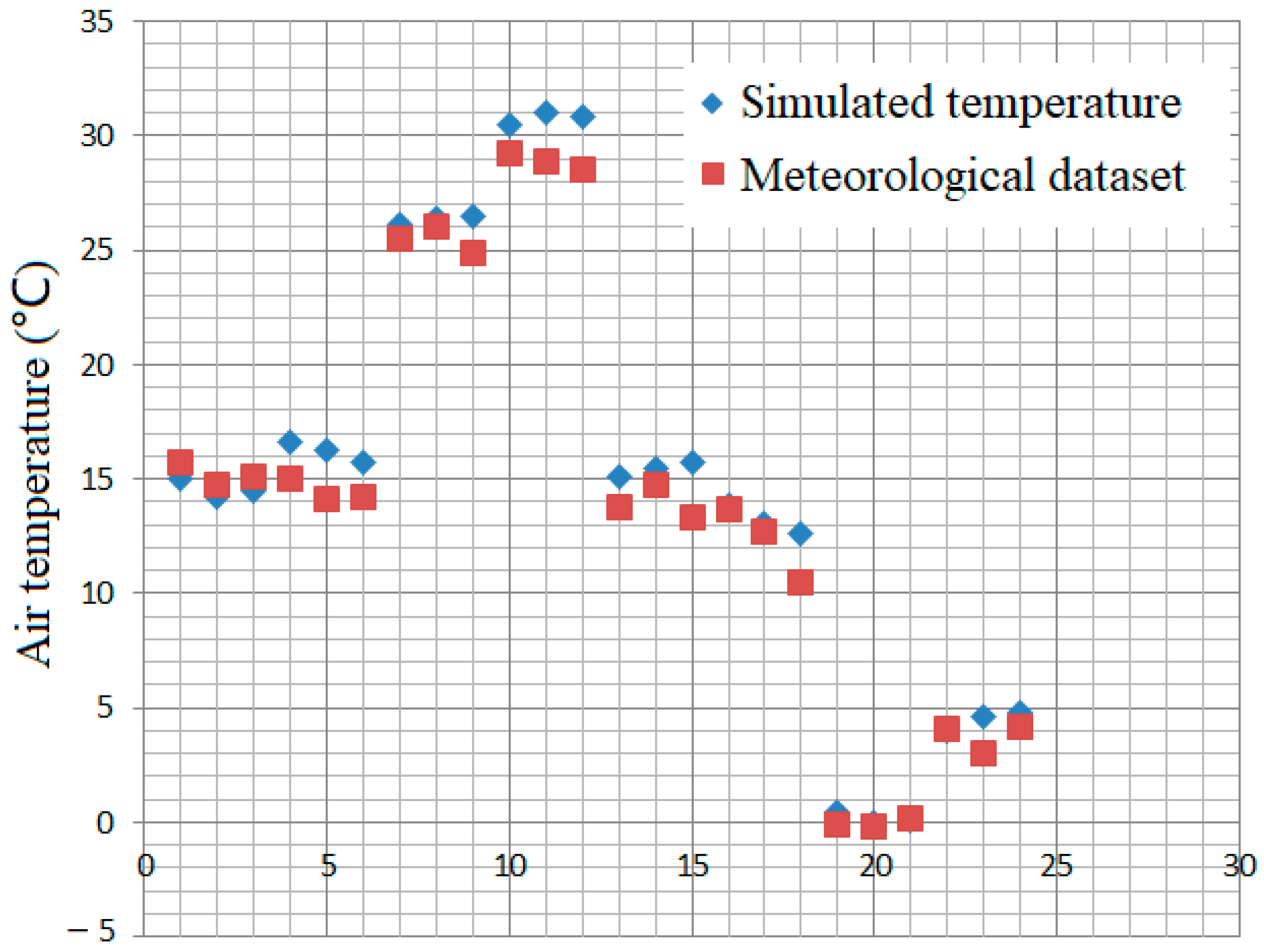
4.3. Thermal Environment Simulation Validation Based on Meteorological Station Observation Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, K.; Yu, Z. Comparative and Combinative Study of Urban Heat island in Wuhan City with Remote Sensing and CFD Simulation. Sensors 2008, 8, 6692–6703. [Google Scholar] [CrossRef]
- Radhi, H.; Fikry, F.; Sharples, S. Impacts of urbanisation on the thermal behaviour of new built up environments: A scoping study of the urban heat island in Bahrain. Landsc. Urban Plan. 2013, 113, 47–61. [Google Scholar] [CrossRef]
- Dimoudi, A.; Zoras, S.; Kantzioura, A.; Stogiannou, X.; Kosmopoulos, P.; Pallas, C. Use of cool materials and other bioclimatic interventions in outdoor places in order to mitigate the urban heat island in a medium size city in Greece. Sustain. Cities Soc. 2014, 13, 89–96. [Google Scholar] [CrossRef]
- Takahashi, K.; Yoshida, H.; Tanaka, Y.; Aotake, N.; Wang, F. Measurement of thermal environment in Kyoto city and its prediction by CFD simulation. Energy Build. 2004, 36, 771–779. [Google Scholar] [CrossRef]
- Huo, H.; Chen, F.; Geng, X.; Tao, J.; Liu, Z.; Zhang, W.; Leng, P. Simulation of the Urban Space Thermal Environment Based on Computational Fluid Dynamics: A Comprehensive Review. Sensors 2021, 21, 6898. [Google Scholar] [CrossRef]
- Wong, K.; Paddon, A.; Jimenez, A. Review of World Urban Heat Islands: Many Linked to Increased Mortality. J. Energy Resour. Technol. 2013, 135, 022101. [Google Scholar] [CrossRef]
- Fan, H.; Sailor, D. Modeling the impacts of anthropogenic heating on the urban climate of Philadelphia: A comparison of implementations in two PBL schemes. Atmos. Environ. 2005, 39, 73–84. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, X.; Qian, J. Research progress on the thermal environment of the urban surfaces. Acta Ecol. Sin. 2018, 38, 1134–1147. [Google Scholar]
- Sobrino, J.A.; Raissouni, N.; Li, Z.L. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Wu, P.; Duan, S.; Zhan, W.; Ma, X.; Wu, Y. Spatiotemporal reconstruction of land surface temperature derived from fengyun geostationary satellite data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4531–4543. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Li, H.; Göttsche, F.M.; Wu, H.; Zhao, W.; Leng, P.; Zhang, X.; Coll, C. Validation of Collection 6 MODIS land surface temperature product using in situ measurements. Remote Sens. Environ. 2019, 225, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Qian, Y.; Wang, N.; Li, K.; Wu, H.; Duan, S.; Liu, Y.; Ma, L.; Gao, C.; Qiu, S.; Tang, L.; et al. Retrieval of surface temperature and emissivity from ground-based time-series thermal infrared data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 284–292. [Google Scholar] [CrossRef]
- Radhi, H.; Sharples, S.; Assem, E. Impact of urban heat islands on the thermal comfort and cooling energy demand of artificial islands—A case study of AMWAJ Islands in Bahrain. Sustain. Cities Soc. 2015, 19, 310–318. [Google Scholar] [CrossRef]
- Huang, J.-M.; Chen, L.-C. A Numerical Study on Mitigation Strategies of Urban Heat Islands in a Tropical Megacity: A Case Study in Kaohsiung City, Taiwan. Sustainability 2020, 12, 3952. [Google Scholar] [CrossRef]
- Kubilay, A.; Derome, D.; Carmeliet, J. Coupled numerical simulations of cooling potential due to evaporation in a street canyon and an urban public square. J. Phys. Conf. Ser. 2019, 1343, 012016. [Google Scholar] [CrossRef]
- Hsieh, C.-M.; Huang, H.-C. Mitigating urban heat islands: A method to identify potential wind corridor for cooling and ventilation. Comput. Environ. Urban Syst. 2016, 57, 130–143. [Google Scholar] [CrossRef]
- Tominaga, Y.; Sato, Y.; Sadohara, S. CFD simulations of the effect of evaporative cooling from water bodies in a micro-scale urban environment: Validation and application studies. Sustain. Cities Soc. 2015, 19, 259–270. [Google Scholar] [CrossRef]
- Toparlar, Y.; Blocken, B.; Maiheu, B.; van Heijst, G. A review on the CFD analysis of urban microclimate. Renew. Sustain. Energy Rev. 2017, 80, 1613–1640. [Google Scholar] [CrossRef]
- Albatayneh, A.; Alterman, D.; Page, A. Adaptation the use of CFD modelling for building thermal simulation. In Proceedings of the 2018 International Conference on Software Engineering and Information Management, Casablanca, Morocco, 4–6 January 2018; pp. 68–72. [Google Scholar]
- Antoniou, N.; Montazeri, H.; Neophytou, M.; Blocken, B. CFD simulation of urban microclimate: Validation using high-resolution field measurements. Sci. Total Environ. 2019, 695, 133743. [Google Scholar] [CrossRef]
- Ashie, Y.; Kono, T. Urban-scale CFD analysis in support of a climate-sensitive design for the Tokyo Bay area. Int. J. Clim. 2010, 31, 174–188. [Google Scholar] [CrossRef]
- Chang, S.; Jiang, Q.; Zhao, Y. Integrating CFD and GIS into the development of urban ventilation corridors: A case study in Changchun City, China. Sustainability 2018, 10, 1814. [Google Scholar] [CrossRef] [Green Version]
- Du, H.; Cai, Y.; Zhou, F.; Jiang, H.; Jiang, W.; Xu, Y. Urban blue-green space planning based on thermal environment simulation: A case study of Shanghai, China. Ecol. Indic. 2019, 106, 105501. [Google Scholar] [CrossRef]
- Piroozmand, P.; Mussetti, G.; Allegrini, J.; Mohammadi, M.H.; Akrami, E.; Carmeliet, J. Coupled CFD framework with mesoscale urban climate model: Application to microscale urban flows with weak synoptic forcing. J. Wind. Eng. Ind. Aerodyn. 2020, 197, 104059. [Google Scholar] [CrossRef]
- van Hooff, T.; Blocken, B.; Tominaga, Y. On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments. Build. Environ. 2017, 114, 148–165. [Google Scholar] [CrossRef]
- Fatima, S.F.; Chaudhry, H.N. Steady-state CFD modelling and experimental analysis of the local microclimate in Dubai (UAE). Sustain. Build. 2017, 2, 5. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhan, Y.; Yu, T.; Ren, X. Urban green effects on land surface temperature caused by surface characteristics: A case study of summer Beijing metropolitan region. Infrared Phys. Technol. 2017, 86, 35–43. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Okaze, T.; Sato, T.; Nemoto, M.; Motoyoshi, H.; Nakai, S.; Tsutsumi, T.; Otsuki, M.; Uamatsu, T.; et al. Development of a system for predicting snow distribution in built-up environments: Combining a mesoscale meteorological model and a CFD model. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 460–468. [Google Scholar] [CrossRef]
- Antoniou, N.; Montazeri, H.; Wigo, H.; Neophytou, M.K.-A.; Blocken, B.; Sandberg, M. CFD and wind-tunnel analysis of outdoor ventilation in a real compact heterogeneous urban area: Evaluation using “air delay”. Build. Environ. 2017, 126, 355–372. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F. Approaches to study Urban Heat Island—Abilities and limitations. Build. Environ. 2010, 45, 2192–2201. [Google Scholar] [CrossRef]
- Gülten, A.; Aksoy, U.T.; Öztop, H.F. Influence of trees on heat island potential in an urban canyon. Sustain. Cities Soc. 2016, 26, 407–418. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Hou, C.; Hou, J.; Kang, Q.; Meng, X.; Wei, D.; Liu, Z.; Zhang, L. Research on urban park design combined with the urban ventilation system. Energy Procedia 2018, 152, 1133–1138. [Google Scholar] [CrossRef]
- Vuckovic, M.; Maleki, A.; Mahdavi, A. Strategies for Development and Improvement of the Urban Fabric: A Vienna Case Study. Climate 2018, 6, 7. [Google Scholar] [CrossRef] [Green Version]
- Santamouris, M.; Haddad, S.; Saliari, M.; Vasilakopoulou, K.; Synnefa, A.; Paolini, R.; Ulpiani, G.; Garshasbi, S.; Fiorito, F. On the energy impact of urban heat island in Sydney: Climate and energy potential of mitigation technologies. Energy Build. 2018, 166, 154–164. [Google Scholar] [CrossRef]
- Akbari, H.; Cartalis, C.; Kolokotsa, D.; Muscio, A.; Pisello, A.L.; Rossi, F.; Santamouris, M.; Synnefa, A.; Wong, N.H.; Zinzi, M. Local climate change and urban heat island mitigation techniques—The state of the art. J. Civ. Eng. Manag. 2016, 22, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Chatzinikolaou, E.; Chalkias, C.; Dimopoulou, E. Urban microclimate improvement using ENVI-MET climate model. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 69–76. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Jia, S.; Han, R.; Liu, Y.; Lu, X.; Zhang, H. RS and GIS supported urban LULC and UHI change simulation and assessment. J. Sens. 2020, 2020, 5863164. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, S.; Cheng, H.; Li, F. Spatio-temporal evolution of urban thermal environment and its driving factors: Case study of Nanjing, China. PLoS ONE 2021, 16, e0246011. [Google Scholar] [CrossRef]
- Grifoni, R.C.; Caprari, G.; Graziano, E.M. Combinative Study of Urban Heat Island in Ascoli Piceno City with Remote Sensing and CFD Simulation—Climate Change and Urban Health Resilience—CCUHRE Project. Sustainability 2022, 14, 688. [Google Scholar] [CrossRef]
- Hedquist, B.C.; Di Sabatino, S.; Fernando, H.J.; Leo, L.S.; Brazel, A.J. Results from the Phoenix Arizona urban heat island experiment. In Proceedings of the Seventh International Conference on Urban Climate, Yokohama, Japan, 29 June–3 July 2009; Volume 29. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Krishnamoorthy, G. A computationally efficient P1 radiation model for modern combustion systems utilizing pre-conditioned conjugate gradient methods. Appl. Therm. Eng. 2017, 119, 197–206. [Google Scholar] [CrossRef] [Green Version]
- Barbason, M.; Reiter, S. Coupling building energy simulation and computational fluid dynamics: Application to a two-storey house in a temperate climate. Build. Environ. 2014, 75, 30–39. [Google Scholar] [CrossRef]
- Buratti, C.; Palladino, D.; Moretti, E.; Di Palma, R. Development and optimization of a new ventilated brick wall: CFD analysis and experimental validation. Energy Build. 2018, 168, 284–297. [Google Scholar] [CrossRef]
- Gromke, C.; Blocken, B.; Janssen, W.; Merema, B.; van Hooff, T.; Timmermans, H. CFD analysis of transpirational cooling by vegetation: Case study for specific meteorological conditions during a heat wave in Arnhem, Netherlands. Build. Environ. 2015, 83, 11–26. [Google Scholar] [CrossRef]
- Montazeri, H.; Blocken, B.; Derome, D.; Carmeliet, J.; Hensen, J.L. CFD analysis of forced convective heat transfer coefficients at windward building facades: Influence of building geometry. J. Wind Eng. Ind. Aerodyn. 2015, 146, 102–116. [Google Scholar] [CrossRef] [Green Version]
- Toparlar, Y.; Blocken, B.; Vos, P.; van Heijst, G.; Janssen, W.; van Hooff, T.; Montazeri, H.; Timmermans, H. CFD simulation and validation of urban microclimate: A case study for Bergpolder Zuid, Rotterdam. Build. Environ. 2015, 83, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Toparlar, Y.; Blocken, B.; Maiheu, B.; van Heijst, G. Impact of urban microclimate on summertime building cooling demand: A parametric analysis for Antwerp, Belgium. Appl. Energy 2018, 228, 852–872. [Google Scholar] [CrossRef]
- Dimitris, F.; Catherine, B.; Aris, T.; Thomas, B.; Constantinos, K. CFD study of thermal comfort in urban area. Energy Environ. Eng. 2017, 5, 8–18. [Google Scholar] [CrossRef]





| Material Type | Density kg/m3 | Specific Heat Capacity J/kg*K | Thermal Conductivity W/(m2*k) | Absorption Coefficient | Albedo % |
|---|---|---|---|---|---|
| Building | 400 | 837 | 1.056 | 0.5 | 0.5 |
| Road | 2300 | 924.9 | 2.3 | 0.8 | 0.2 |
| Water | 993.7 | 417.8 | 0.632 | 0.8 | 0.25 |
| Date | Time (Hours) | Air Temperature (°C) | Average Wind Direction at 1 m Height in 10 min (°) | Average Wind Speed at 1 m Height in 10 min (m/s) |
|---|---|---|---|---|
| 19 January | 01 | 0.1 | 46 | 2.6 |
| 13 | 3.9 | 306 | 1.9 | |
| 19 April | 01 | 14.9 | 201 | 1.7 |
| 13 | 14.6 | 234 | 1.0 | |
| 18 July | 01 | 25.8 | 38 | 0.8 |
| 13 | 29.2 | 126 | 1.4 | |
| 20 October | 01 | 15.6 | 27 | 0.9 |
| 13 | 12.8 | 211 | 0.8 |
| Parameters | Method | ||
|---|---|---|---|
| Discretization method | Finite volume method | ||
| Flow field numerical calculation method | Separate solution method | ||
| Solver type | Pressure-based implicit solver | ||
| Near-wall treatment method | Standard wall function method | ||
| Coupling solution of pressure and velocity | SIMPLE algorithm | ||
| Spatial difference format | Second order upwind | ||
| Boundary Condition | Corresponding Model Location | Specific Type | |
| Inlet | Entrance to the flow field | Wind inlet | |
| Outlet | Outlet of the flow field | Pressure outlet | |
| Building | Architecture | Non-slip wall | |
| Ground | Surface | Non-slip wall | |
| Grass | Grassland | Porous media | |
| Sky | Top of the flow field | Symmetry boundaries | |
| Height (m) | Dotted Shape | Ribbon Shape | Polyline Shape | Arc Shape |
|---|---|---|---|---|
| 0 (Surface) |  |  |  | 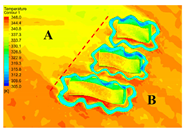 |
| 2 | 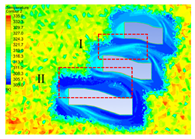 | 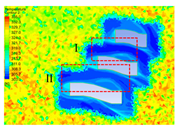 | 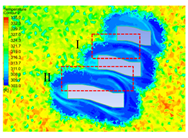 |  |
| 5 |  |  |  |  |
| 10 |  |  |  |  |
| 20 |  |  |  |  |
| Height (m) | Dotted Shape | Ribbon Shape | Polyline Shape | Arc Shape |
|---|---|---|---|---|
| 2 | 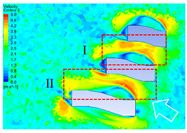 | 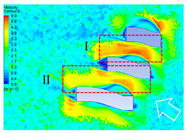 |  | 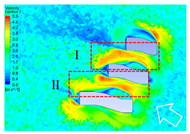 |
| 5 | 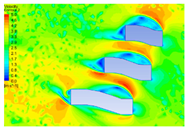 |  | 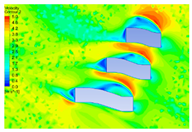 |  |
| 10 | 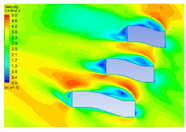 | 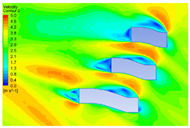 |  | 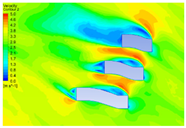 |
| 20 | 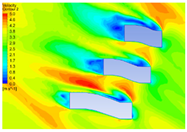 | 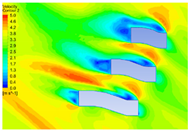 | 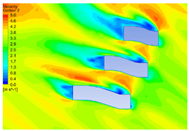 | 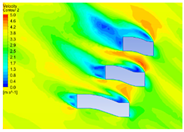 |
| Height (m) | April | July | October | January |
|---|---|---|---|---|
| 0 (Surface) |  | 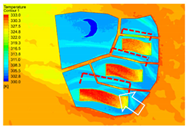 | 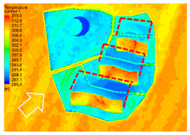 | 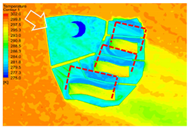 |
| 2 |  |  |  |  |
| 5 |  |  |  |  |
| 10 |  | 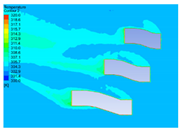 |  |  |
| 20 |  |  |  |  |
| Height (m) | April | July | October | January |
|---|---|---|---|---|
| 2 | 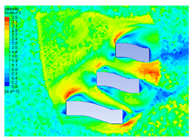 | 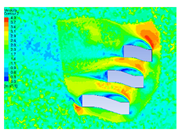 |  | 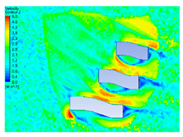 |
| 5 | 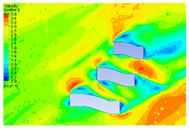 | 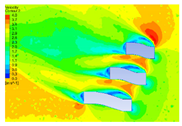 | 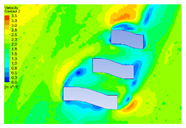 |  |
| 10 | 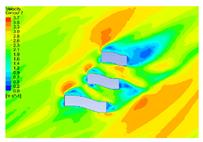 | 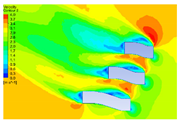 | 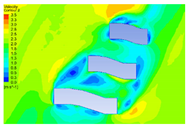 |  |
| 20 | 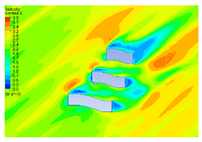 | 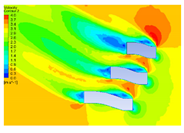 | 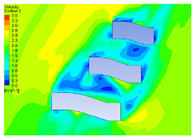 | 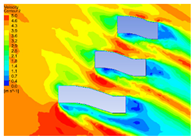 |
| Height (m) | April | July | October | January |
|---|---|---|---|---|
| 0 (Surface) |  |  |  | 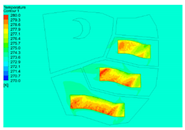 |
| 2 |  |  |  | 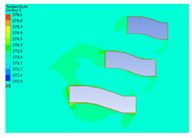 |
| 5 |  |  |  |  |
| 10 |  |  |  |  |
| 20 |  |  |  |  |
| Height (m) | April | July | October | January |
|---|---|---|---|---|
| 2 | 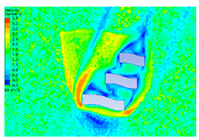 | 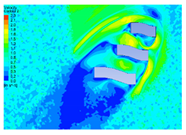 |  | 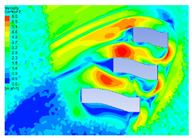 |
| 5 |  | 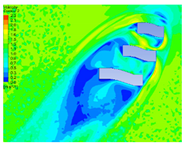 | 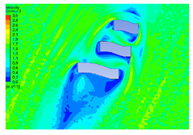 |  |
| 10 | 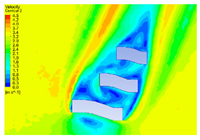 | 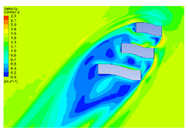 |  | 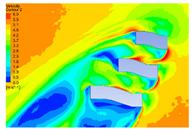 |
| 20 | 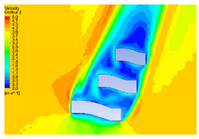 |  | 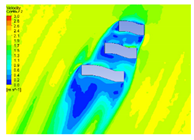 | 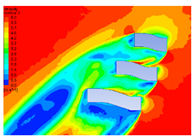 |
| Height (m) | Temperature (°C) | Wind Field (m/s) | Wind Pressure (Pa) |
|---|---|---|---|
| 2 | 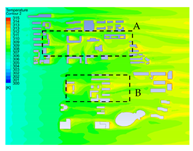 |  |  |
| 5 | 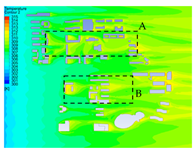 | 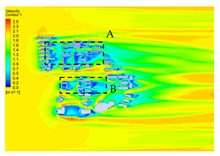 |  |
| 10 |  |  |  |
| 20 | 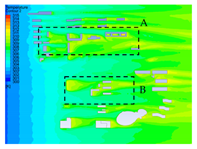 |  |  |
| Height (m) | Temperature (°C) | Wind Field (m/s) | Wind Pressure (Pa) |
|---|---|---|---|
| 2 |  | 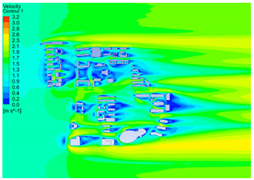 | 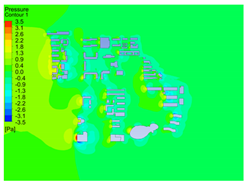 |
| 5 |  | 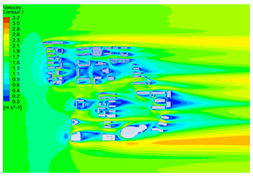 |  |
| 10 |  |  |  |
| 20 |  |  | 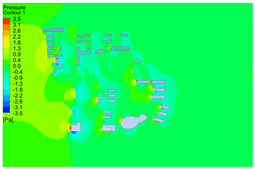 |
| Time | Season | 1st Group | 2nd Group | 3rd Group | Seasonal RMSE | Day and Night RMSE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simulation | Meteorological Data | Δt | Simulation | Meteorological Data | Δt | Simulation | Meteorological Data | Δt | ||||
| Daytime | Spring | 16.70 | 15.00 | 1.70 | 16.30 | 14.10 | 2.20 | 15.80 | 14.20 | 1.60 | 2.009 | 1.578 |
| Summer | 30.60 | 29.20 | 1.40 | 31.10 | 28.90 | 2.20 | 30.90 | 28.50 | 2.40 | 2.396 | ||
| Autumn | 13.90 | 13.70 | 0.20 | 13.10 | 12.70 | 0.40 | 12.70 | 10.50 | 2.20 | 1.053 | ||
| Winter | 4.10 | 4.10 | 0.00 | 4.70 | 3.00 | 1.70 | 4.90 | 4.20 | 0.70 | 0.853 | ||
| Nighttime | Spring | 15.10 | 15.70 | −0.60 | 14.30 | 14.70 | −0.40 | 14.60 | 15.10 | −0.50 | 0.399 | 0.872 |
| Summer | 26.20 | 25.50 | 0.70 | 26.50 | 26.00 | 0.50 | 26.60 | 24.90 | 1.70 | 0.989 | ||
| Autumn | 15.20 | 13.80 | 1.40 | 15.50 | 14.70 | 0.80 | 15.80 | 13.30 | 2.50 | 1.781 | ||
| Winter | 0.50 | −0.10 | 0.60 | 0.10 | −0.20 | 0.30 | 0.20 | 0.20 | 0.00 | 0.321 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, H.; Chen, F. A Study of Simulation of the Urban Space 3D Temperature Field at a Community Scale Based on High-Resolution Remote Sensing and CFD. Remote Sens. 2022, 14, 3174. https://doi.org/10.3390/rs14133174
Huo H, Chen F. A Study of Simulation of the Urban Space 3D Temperature Field at a Community Scale Based on High-Resolution Remote Sensing and CFD. Remote Sensing. 2022; 14(13):3174. https://doi.org/10.3390/rs14133174
Chicago/Turabian StyleHuo, Hongyuan, and Fei Chen. 2022. "A Study of Simulation of the Urban Space 3D Temperature Field at a Community Scale Based on High-Resolution Remote Sensing and CFD" Remote Sensing 14, no. 13: 3174. https://doi.org/10.3390/rs14133174
APA StyleHuo, H., & Chen, F. (2022). A Study of Simulation of the Urban Space 3D Temperature Field at a Community Scale Based on High-Resolution Remote Sensing and CFD. Remote Sensing, 14(13), 3174. https://doi.org/10.3390/rs14133174






