Improving the SSH Retrieval Precision of Spaceborne GNSS-R Based on a New Grid Search Multihidden Layer Neural Network Feature Optimization Method
Abstract
:1. Introduction
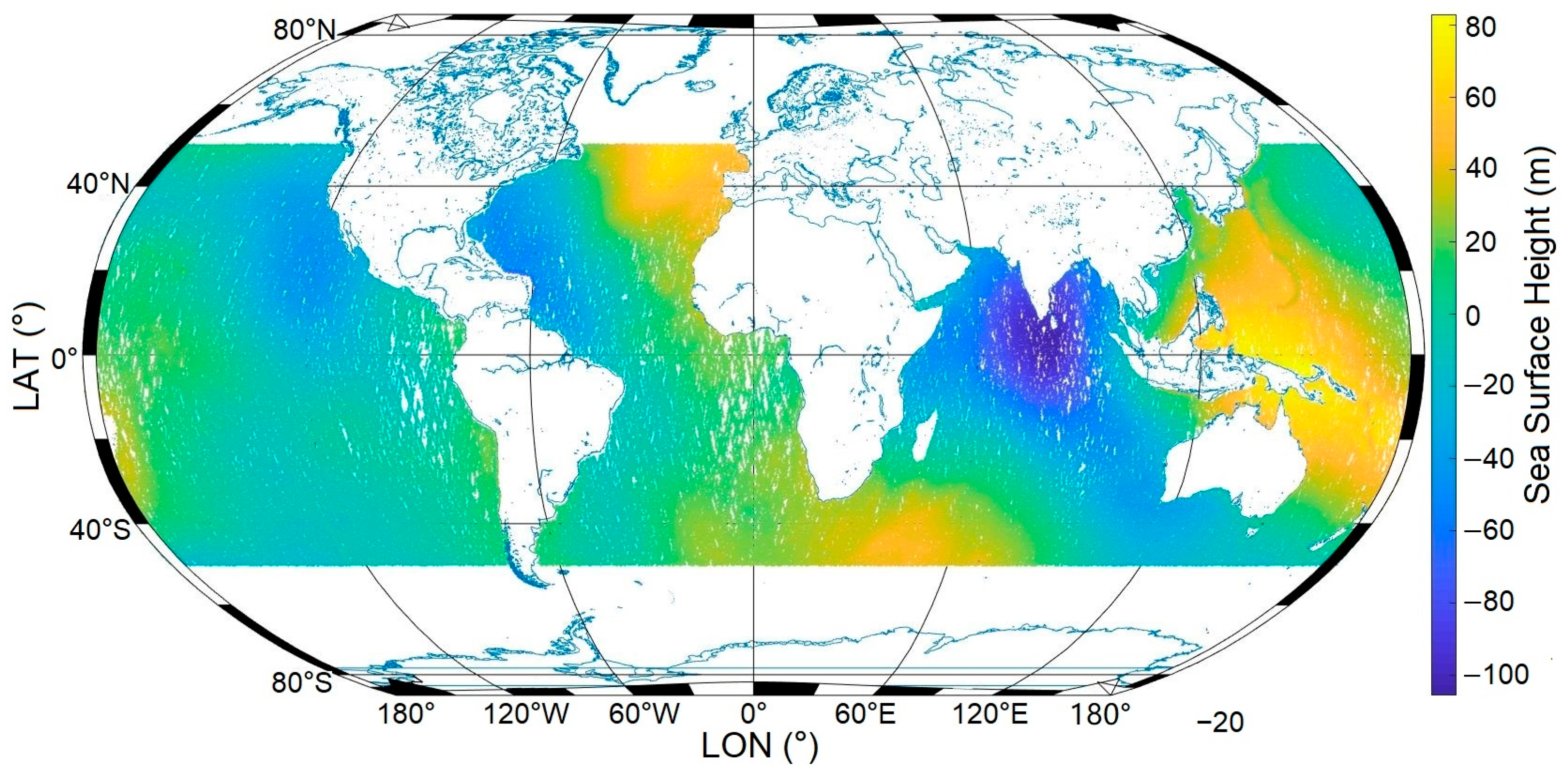
2. Materials and Data Filtering
2.1. Datasets
2.2. Data Quality Control
2.3. Data Matching
3. Methods
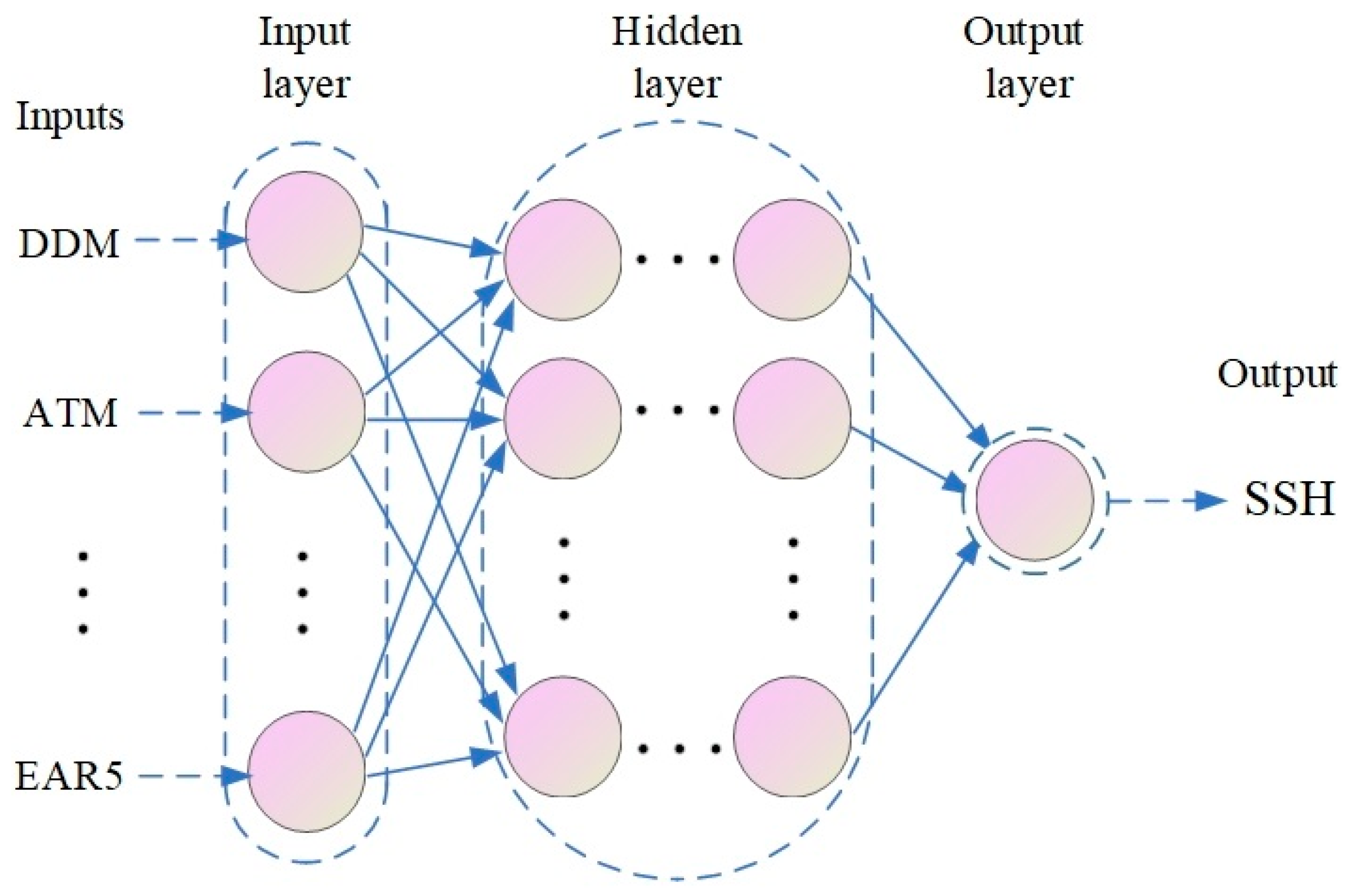
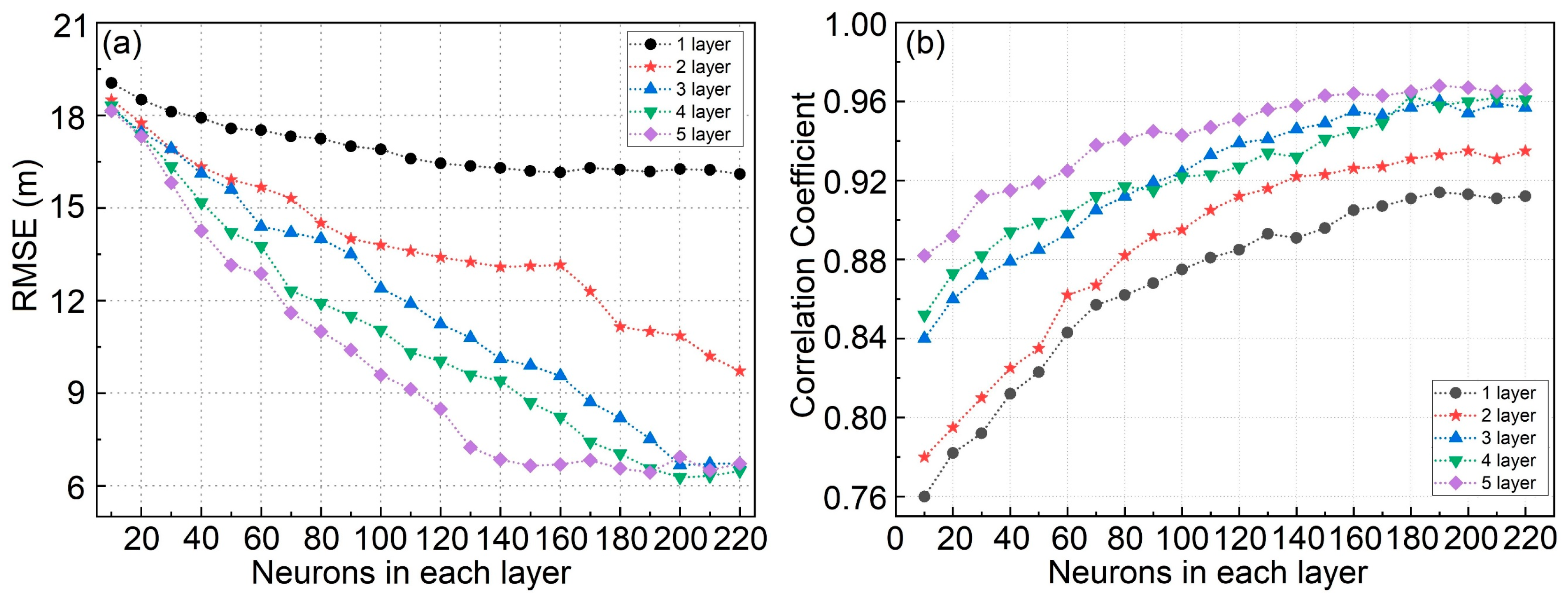
3.1. Determining the GSMHLFO Configuration
3.1.1. Basic Settings
3.1.2. Cross-Validation and Hyperparameter Optimization
3.2. Feature Engineering
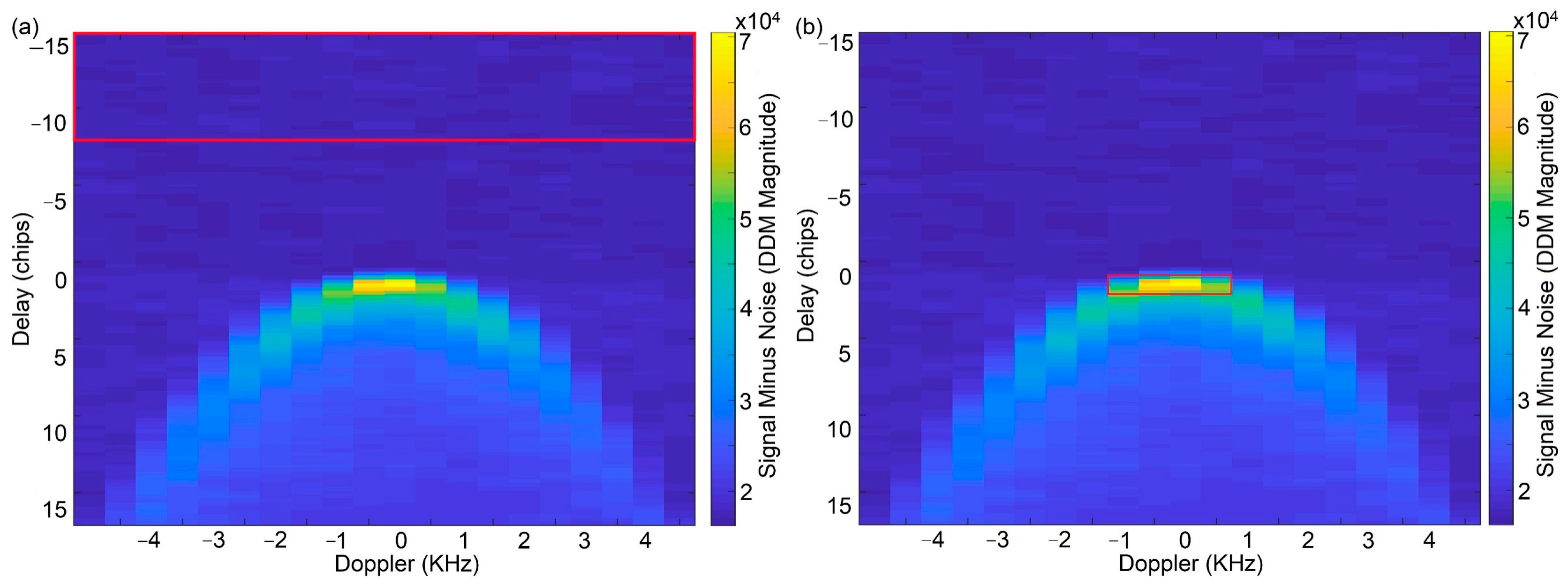
3.2.1. Feature Construction
3.2.2. Feature Sensitivity Analysis
- Set 1: DW
- Set 2: IDW
- Set 3: IDW and ELE
- Set 4: IDW and SNR
- Set 5: IDW, ELE, and SNR
- Set 6: IDW, ELE, SNR, and ATM
- Set 7: IDW, ELE, SNR, and EAR5
- Set 8: IDW, ELE, SNR, ATM, and EAR5
- Set 9: IDW, ELE, SNR, ATM, EAR5, and LES
- Set 10: IDW, ELE, SNR, ATM, EAR5, and PCP
- Set 11: IDW, ELE, SNR, ATM, EAR5, and PFD
- Set 12: IDW, ELE, SNR, ATM, EAR5, and PCP70
- Set 13: DDMA, ELE, SNR, ATM, EAR5, and PCP
- Set 14: IDW, ELE, SNR, ATM, EAR5, LES, PCP, and DDMA
4. Results
4.1. Analysis of SSH Retrieval Results
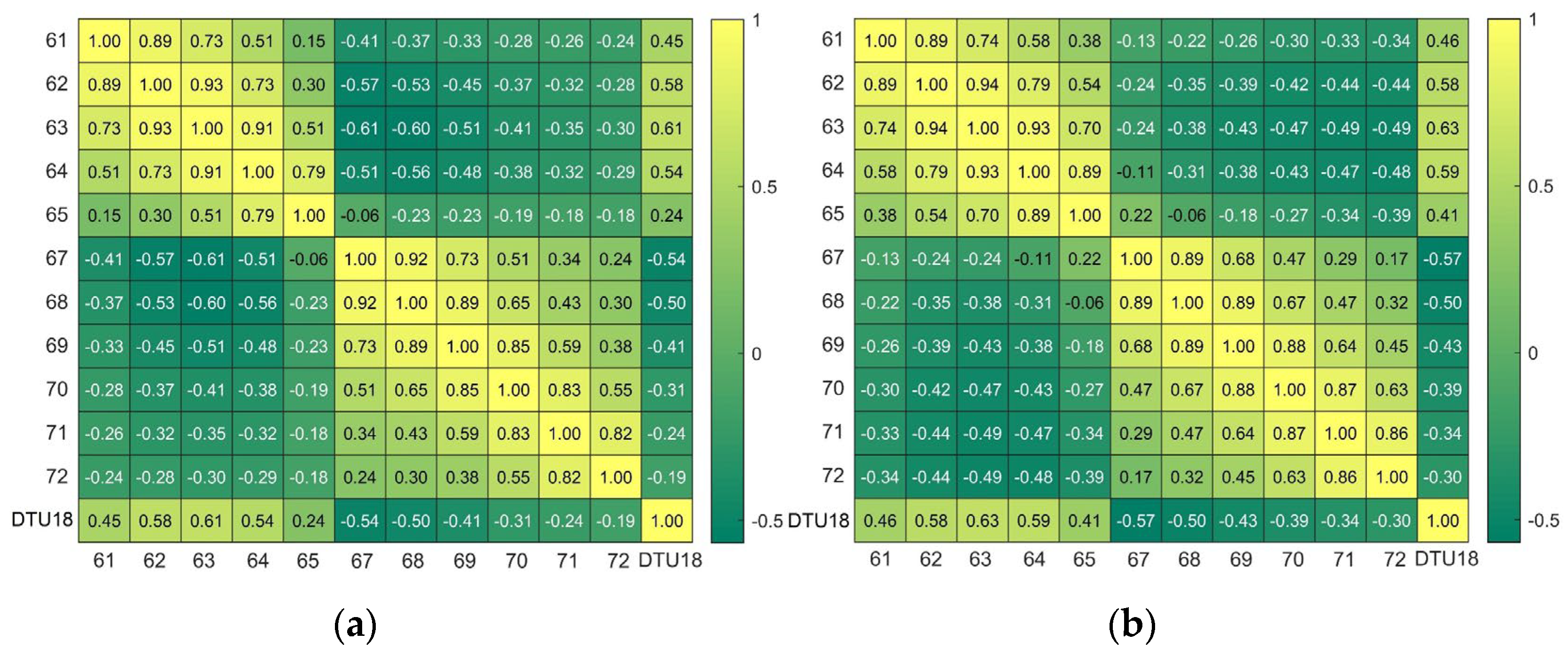
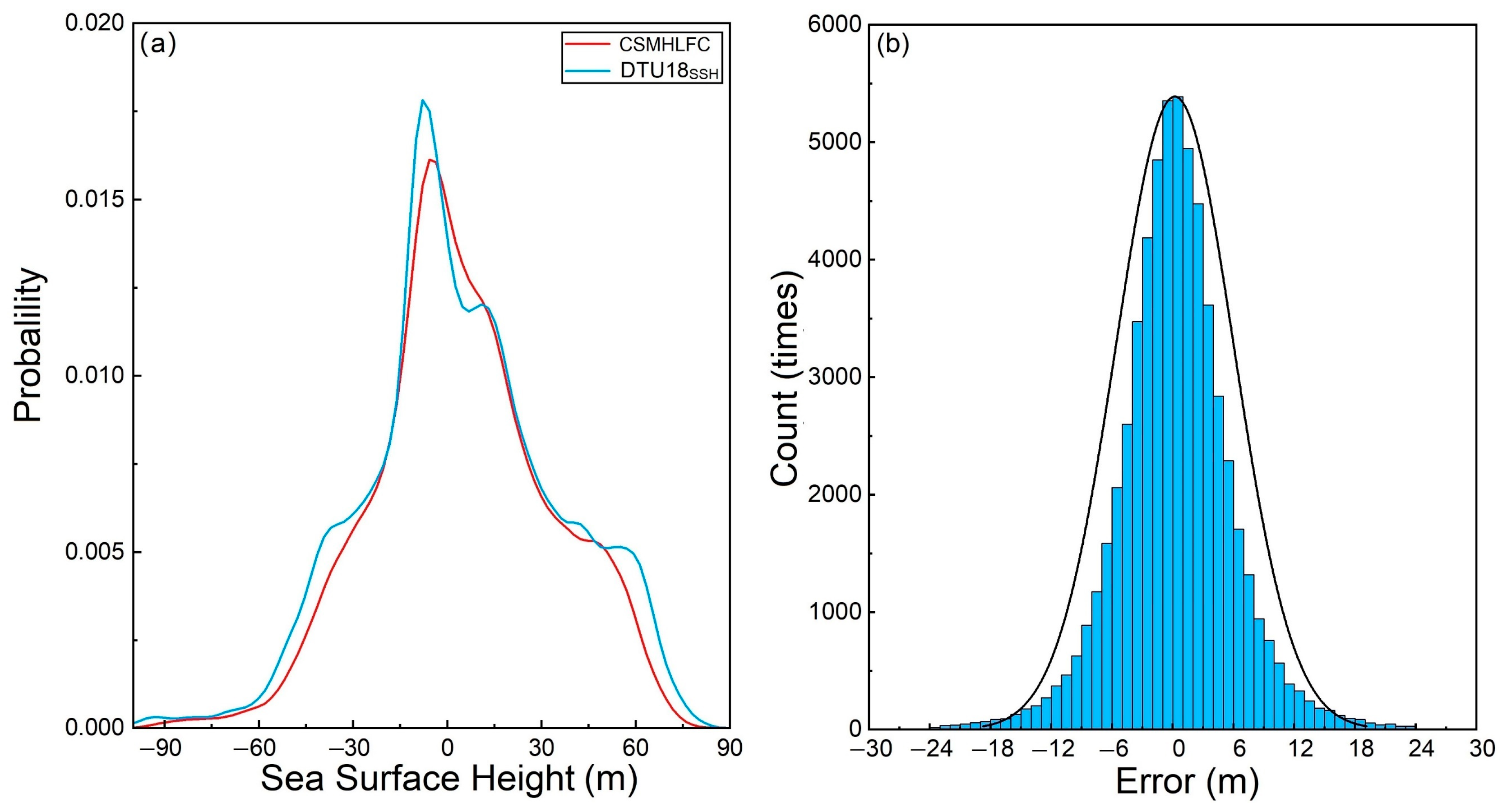
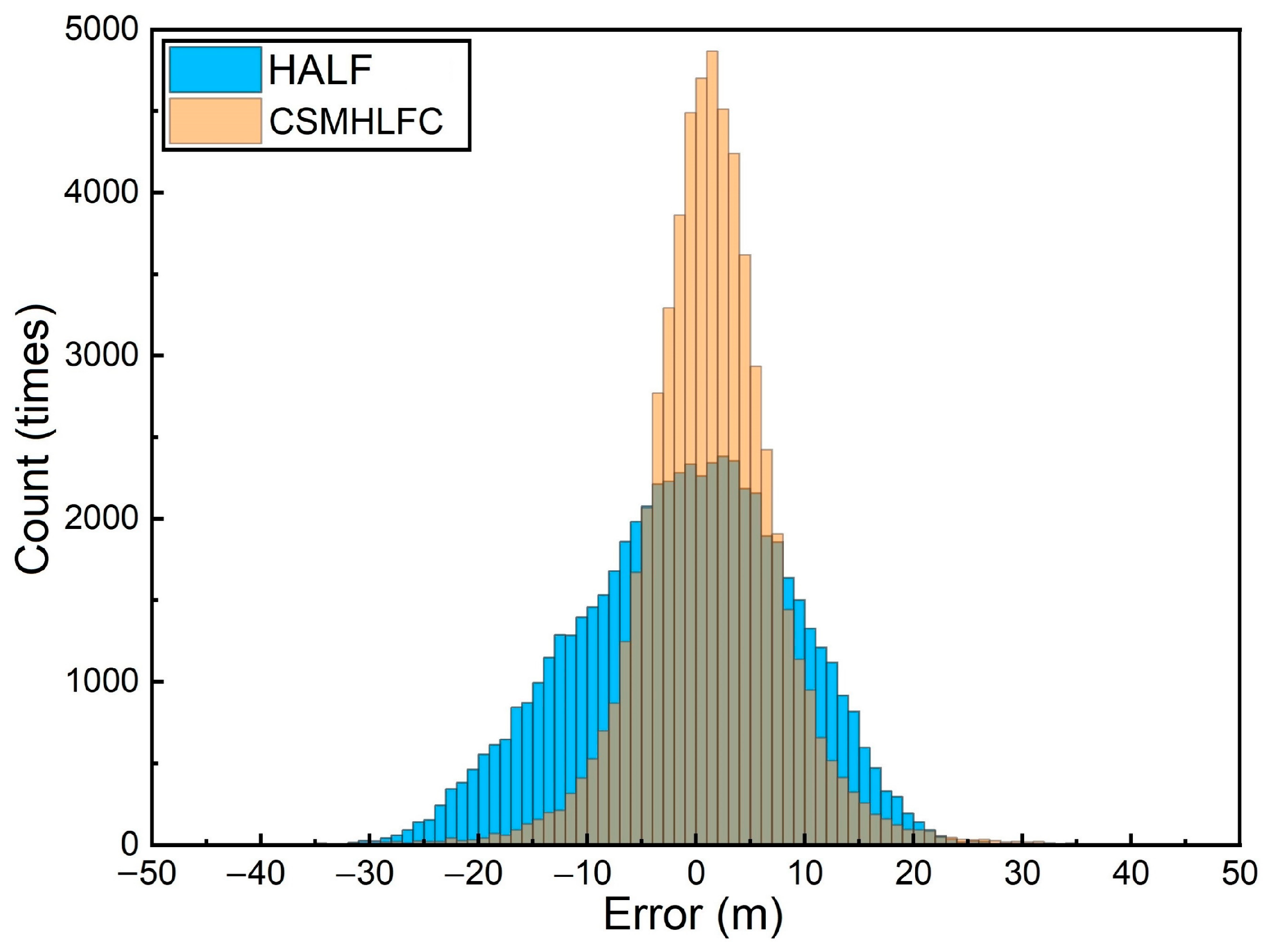
4.2. Evaluation of SSH Retrieval Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Xu, H.; Yang, L.; Song, Q.; Ma, C. Cross-calibrations of the HY-2B altimeter using Jason-3 satellite during the period of April 2019–September 2020. Front. Earth Sci. 2021, 9, 215–231. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Wu, F.; Kang, G.; Sun, X.; Wang, Q. Relationship Between Altimetric Quality and Along-Track Spatial Resolution for iGNSS-R Sea Surface Altimetry: Example for the Airborne Experiment. Front. Earth Sci. 2021, 9, 213–222. [Google Scholar] [CrossRef]
- Wu, F.; Zheng, W.; Liu, Z. Quantifying GNSS-R Delay Sea State Bias and Predicting Its Variation Based on Ship-Borne Observations in China’s Seas. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Cui, Z.; Zheng, W.; Wu, F.; Li, X.; Zhu, C.; Liu, Z.; Ma, X. Improving GNSS-R Sea Surface Altimetry Precision Based on the Novel Dual Circularly Polarized Phased Array Antenna Model. Remote Sens. 2021, 13, 2974. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Wu, F.; Cui, Z.; Kang, G. A Necessary Model to Quantify the Scanning Loss Effect in Spaceborne iGNSS-R Ocean Altimetry. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1619–1627. [Google Scholar] [CrossRef]
- D’Addio, S.; Martín-Neira, M.; Bisceglie, M.d.; Galdi, C.; Alemany, F.M. GNSS-R altimeter based on doppler multi-looking. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1452–1460. [Google Scholar] [CrossRef]
- Wu, F.; Zheng, W.; Li, Z.; Liu, Z. Improving the GNSS-R specular reflection point positioning accuracy using the gravity field normal projection reflection reference surface combination correction method. Remote Sens. 2019, 11, 33. [Google Scholar] [CrossRef] [Green Version]
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- He, Y.; Gao, F.; Xu, T.; Meng, X.; Wang, N. Coastal altimetry using interferometric phase from GEO satellite in quasi-zenith satellite system. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martín-Neira, M.; Fabra, F.; Nogués-Correig, O.; Ribó, S.; Kainulainen, J.; Camps, A.; Addio, S.D. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, W.; Wu, F.; Xu, A.; Zhu, H.; Liu, Z. A new GNSS-R altimetry algorithm based on machine learning fusion model and feature optimization to improve the precision of sea surface height retrieval. Front. Earth Sci. 2021, 9, 123–135. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, W.; Wu, F.; Liu, Z. Improving the iGNSS-R Ocean Altimetric Precision Based on the Coherent Integration Time Optimization Model. Remote Sensing 2021, 13, 4715. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. Global ocean altimetry with GNSS reflections from TechDemoSat-1. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4088–4097. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Assessment of spaceborne GNSS-R ocean altimetry performance using CYGNSS mission raw data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 238–250. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Zuffada, C.; Loria, E.; O’Brien, A.; Haines, B. Improved GNSS-R ocean surface altimetry with CYGNSS in the seas of indonesia. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6071–6087. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Wu, F.; Kang, G.; Li, Z.; Wang, Q.; Cui, Z. Increasing the Number of Sea Surface Reflected Signals Received by GNSS-Reflectometry Altimetry Satellite Using the Nadir Antenna Observation Capability Optimization Method. Remote Sens. 2019, 11, 2473. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Zheng, W.; Liu, Z.; Sun, X. Improving the Specular Point Positioning Accuracy of Ship-borne GNSS-R Observations in China’s Seas based on a new Instantaneous Sea Reflection Surface Model. Front. Earth Sci. 2021, 9, 112–122. [Google Scholar] [CrossRef]
- Li, Z.; Zuffada, C.; Lowe, S.T.; Lee, T.; Zlotnicki, V. Analysis of GNSS-R altimetry for mapping ocean mesoscale sea surface heights using high-resolution model simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4631–4642. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Martin-Neira, M. Revisiting the GNSS-R waveform statistics and its impact on altimetric retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2854–2871. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef] [Green Version]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Yang, X. Sea surface wind speed retrieval from the first chinese GNSS-R mission: Technique and preliminary results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Wan, W.; Chen, X.; Zhu, S.; Hong, Y. Spaceborne GNSS-R observation of global lake level: First results from the TechDemoSat-1 mission. Remote Sens. 2019, 11, 1438. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, J.; Clarizia, M.P.; Santi, E. Wind speed estimation from CYGNSS using artificial neural networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 708–716. [Google Scholar] [CrossRef]
- Li, X.; Yang, D.; Yang, J.; Zheng, G.; Han, G.; Nan, Y.; Li, W. Analysis of coastal wind speed retrieval from CYGNSS mission using artificial neural network. Remote Sens. Environ. 2021, 260, 112454–112466. [Google Scholar] [CrossRef]
- Liu, Y.; Collett, I.; Morton, Y.J. Application of neural network to GNSS-R wind speed retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Chu, X.; He, J.; Song, H.; Qi, Y.; Sun, Y.; Bai, W.; Li, W.; Wu, Q. Multimodal deep learning for heterogeneous GNSS-R data fusion and ocean wind speed retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5971–5981. [Google Scholar] [CrossRef]
- Luo, L.; Bai, W.; Sun, Y.; Xia, J. GNSS-R sea surface wind speed inversion based on tree model machine learning method. Chin. J. Space Sci. 2020, 40, 595–601. [Google Scholar] [CrossRef]
- Jia, Y.; Jin, S.; Savi, P.; Gao, Y.; Tang, J.; Chen, Y.; Li, W. GNSS-R soil moisture retrieval based on a XGboost machine learning aided method: Performance and validation. Remote Sens. 2019, 11, 1655. [Google Scholar] [CrossRef] [Green Version]
- Yan, Q.; Huang, W. Sea ice sensing from GNSS-R data using convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1510–1514. [Google Scholar] [CrossRef]
- Wu, F.; Zheng, W.; Li, Z.; Liu, Z. Improving the positioning accuracy of satellite-borne GNSS-R specular reflection point on sea surface based on the ocean tidal correction positioning method. Remote Sens. 2019, 11, 1626. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Guo, J.; Niu, Y.; Zhu, C.; Li, Z. Mean sea surface model over the sea of Japan determined from multi-satellite altimeter data and tide gauge records. Remote Sens. 2020, 12, 4168. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef] [Green Version]
- Wessel, P.; Smith, W. A global self-consistent, hierarchical, high-resolution shoreline. J. Geophys. Res. 1996, 101, 8741–8743. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y. Research on Spaceborne Multimode GNSS Reflectometry Sea Wind Sensing Signal Processing; National Space Science Center, Chinese Academy of Sciences: Beijing, China, 2021. [Google Scholar]
- Hu, C.; Benson, C.; Park, H.; Camps, A.; Rizos, C. Detecting targets above the earth’s surface using GNSS-R delay doppler maps: Results from TDS-1. Remote Sens. 2019, 11, 2327. [Google Scholar] [CrossRef] [Green Version]
- Garrison, J.L. A statistical model and simulator for ocean-reflected GNSS signals. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6007–6019. [Google Scholar] [CrossRef]
- Liu, L.; Sun, Y.; Bai, W.; Luo, L. The inversion of sea surface wind speed in GNSS-R base on the model fusion of data mining. Geomat. Inf. Sci. Wuhan Univ. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Jung, Y. Multiple predicting K-fold cross-validation for model selection. J. Nonparametric Stat. 2018, 30, 197–215. [Google Scholar] [CrossRef]
- Lavalle, S.M.; Branicky, M.S.; Lindemann, S.R. On the Relationship between Classical Grid Search and Probabilistic Roadmaps. Int. J. Rob. Res. 2004, 23, 673–692. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Wind speed retrieval algorithm for the cyclone global navigation satellite system (CYGNSS) mission. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4419–4432. [Google Scholar] [CrossRef]
- Rodgers, J.L.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R minimum variance wind speed estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2008, 83, 263–275. [Google Scholar] [CrossRef]
- Yan, Z.; Zheng, W.; Wu, F.; Wang, C.; Zhu, H.; Xu, A. Correction of Atmospheric Delay Error of Airborne and Spaceborne GNSS-R Sea Surface Altimetry. Front. Earth Sci. 2022, 10, 223–234. [Google Scholar] [CrossRef]
- Leandro, R.; Santos, M.; Langley, R.B. UNB neutral atmosphere models: Development and performance. In Proceedings of the National Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 18–20 January 2006; pp. 564–573. [Google Scholar] [CrossRef] [Green Version]
- Mashburn, J.R. Analysis of GNSS-R Observations for Altimetry and Characterization of Earth Surfaces; University of Colorado: Boulder, CO, USA, 2018. [Google Scholar]




| Variable Name | Description |
|---|---|
| DDM | Delay-Doppler Map |
| SpecularPointLat | Specular point latitude |
| SpecularPointLon | Specular point longitude |
| SPIncidenceAngle | Specular point incidence angle |
| AntennaGainTowardsSpecularPoint | Antenna Gain |
| DDMSNRAtPeakSingleDDM | Signal-to-Noise Ratio |
| Set | The First Experiment | The Second Experiment | The Third Experiment | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAD (m) | RMSE (m) | PCC | MAD (m) | RMSE (m) | PCC | MAD (m) | RMSE (m) | PCC | |
| Set 1 | 13.66 | 18.28 | 0.81 | 13.47 | 18.15 | 0.81 | 13.52 | 18.09 | 0.81 |
| Set 2 | 11.90 | 17.05 | 0.85 | 11.73 | 16.95 | 0.85 | 11.82 | 16.83 | 0.85 |
| Set 3 | 11.40 | 16.43 | 0.87 | 11.47 | 16.52 | 0.87 | 11.40 | 16.40 | 0.87 |
| Set 4 | 11.65 | 16.66 | 0.87 | 11.59 | 16.62 | 0.87 | 11.66 | 16.9 | 0.87 |
| Set 5 | 8.72 | 12.16 | 0.91 | 8.65 | 12.04 | 0.91 | 8.59 | 11.57 | 0.91 |
| Set 6 | 5.54 | 7.79 | 0.97 | 5.67 | 7.85 | 0.97 | 5.59 | 7.82 | 0.97 |
| Set 7 | 6.89 | 9.60 | 0.95 | 6.75 | 9.49 | 0.95 | 6.83 | 9.62 | 0.95 |
| Set 8 | 4.86 | 6.96 | 0.97 | 4.82 | 6.90 | 0.97 | 4.85 | 6.96 | 0.97 |
| Set 9 | 4.78 | 6.73 | 0.98 | 4.75 | 6.69 | 0.98 | 4.71 | 6.65 | 0.98 |
| Set 10 | 4.73 | 6.67 | 0.97 | 4.76 | 6.71 | 0.97 | 4.75 | 6.69 | 0.97 |
| Set 11 | 5.09 | 7.16 | 0.97 | 5.05 | 7.14 | 0.97 | 5.01 | 7.12 | 0.97 |
| Set 12 | 5.15 | 7.21 | 0.97 | 5.11 | 7.18 | 0.97 | 5.09 | 7.15 | 0.97 |
| Set 13 | 5.02 | 7.30 | 0.97 | 5.05 | 7.26 | 0.97 | 4.97 | 7.10 | 0.97 |
| Set 14 | 4.23 | 5.94 | 0.98 | 4.32 | 6.05 | 0.98 | 4.18 | 5.91 | 0.98 |
| Errors | Correction Method |
|---|---|
| Ionospheric delay | GIM |
| Tropospheric delay | UNB3m |
| Antenna baseline | Metadata |
| GPS orbit error | IGS Ephemeris |
| TDS-1 orbit error | Metadata |
| Delay error | Reflected Signal Geometry |
| TDS-1 data bias | Metadata |
| Tracking error noise | HALF |
| MAD (m) | RMSE (m) | PCC | |
|---|---|---|---|
| HALF | 6.30 | 7.92 | 0.89 |
| GSMHLFO | 4.23 | 5.94 | 0.97 |
| Improve (%) | 32.86 | 25.00 | 8.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zheng, W.; Wu, F.; Zhu, H.; Xu, A.; Shen, Y.; Zhao, Y. Improving the SSH Retrieval Precision of Spaceborne GNSS-R Based on a New Grid Search Multihidden Layer Neural Network Feature Optimization Method. Remote Sens. 2022, 14, 3161. https://doi.org/10.3390/rs14133161
Wang Q, Zheng W, Wu F, Zhu H, Xu A, Shen Y, Zhao Y. Improving the SSH Retrieval Precision of Spaceborne GNSS-R Based on a New Grid Search Multihidden Layer Neural Network Feature Optimization Method. Remote Sensing. 2022; 14(13):3161. https://doi.org/10.3390/rs14133161
Chicago/Turabian StyleWang, Qiang, Wei Zheng, Fan Wu, Huizhong Zhu, Aigong Xu, Yifan Shen, and Yelong Zhao. 2022. "Improving the SSH Retrieval Precision of Spaceborne GNSS-R Based on a New Grid Search Multihidden Layer Neural Network Feature Optimization Method" Remote Sensing 14, no. 13: 3161. https://doi.org/10.3390/rs14133161
APA StyleWang, Q., Zheng, W., Wu, F., Zhu, H., Xu, A., Shen, Y., & Zhao, Y. (2022). Improving the SSH Retrieval Precision of Spaceborne GNSS-R Based on a New Grid Search Multihidden Layer Neural Network Feature Optimization Method. Remote Sensing, 14(13), 3161. https://doi.org/10.3390/rs14133161







