Multi-Crop Classification Using Feature Selection-Coupled Machine Learning Classifiers Based on Spectral, Textural and Environmental Features
Abstract
:1. Introduction
2. Study Region and Dataset
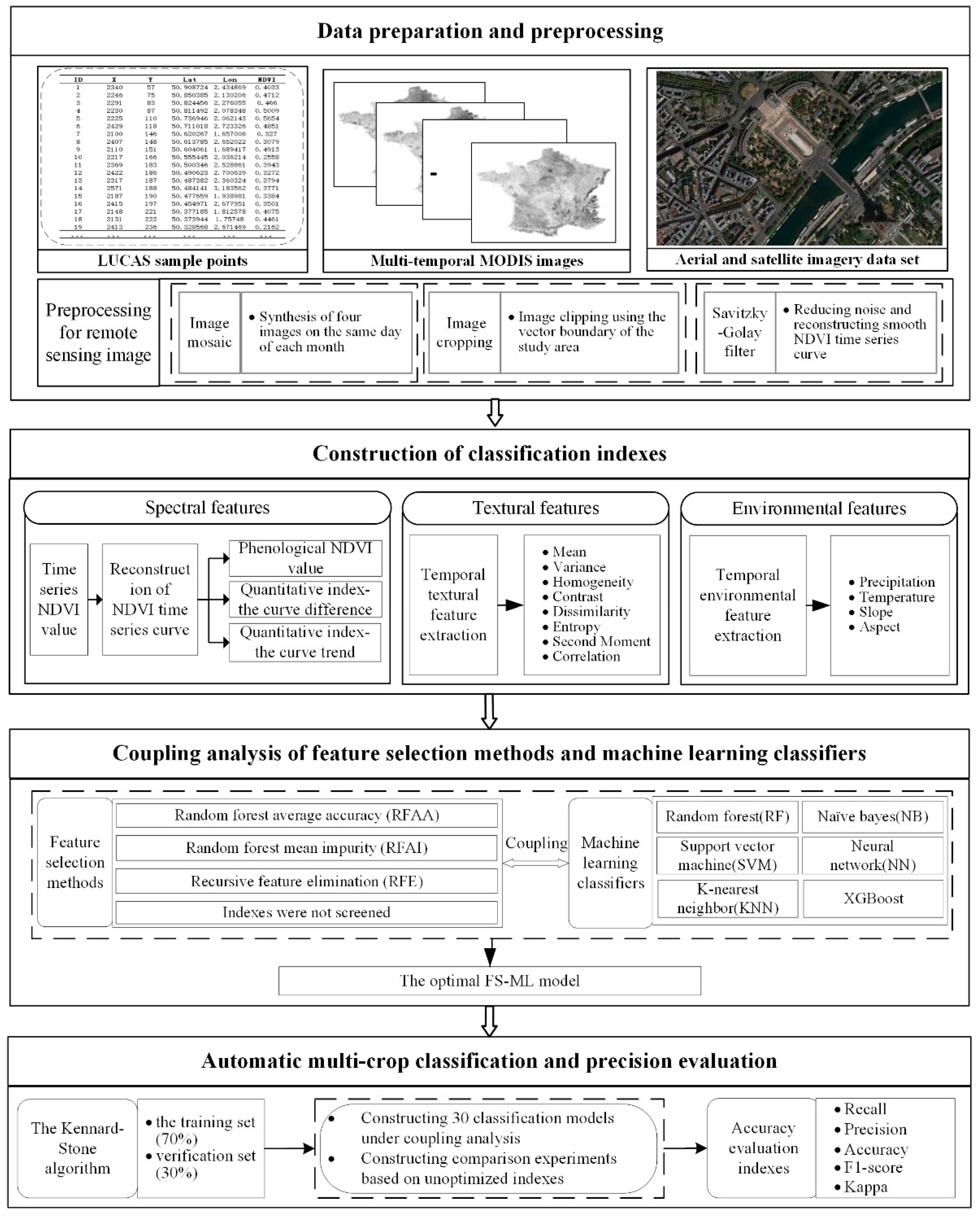
2.1. Data Acquisition and Analysis in Study Region
2.1.1. Data Source
2.1.2. Crop Phenology Information
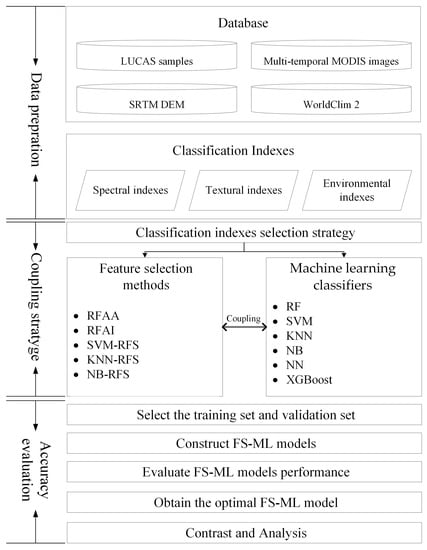
3. Methodology
3.1. Construction of Classification Indexes
3.1.1. Construction of Spectral Indexes
3.1.2. Construction of Textural Indexes
3.1.3. Construction of Environmental Indexes
3.2. Coupling Strategy Based on Feature Selection Methods and Machine Learning Classifiers
3.2.1. Feature Selection Methods
3.2.2. Machine Learning Classifiers
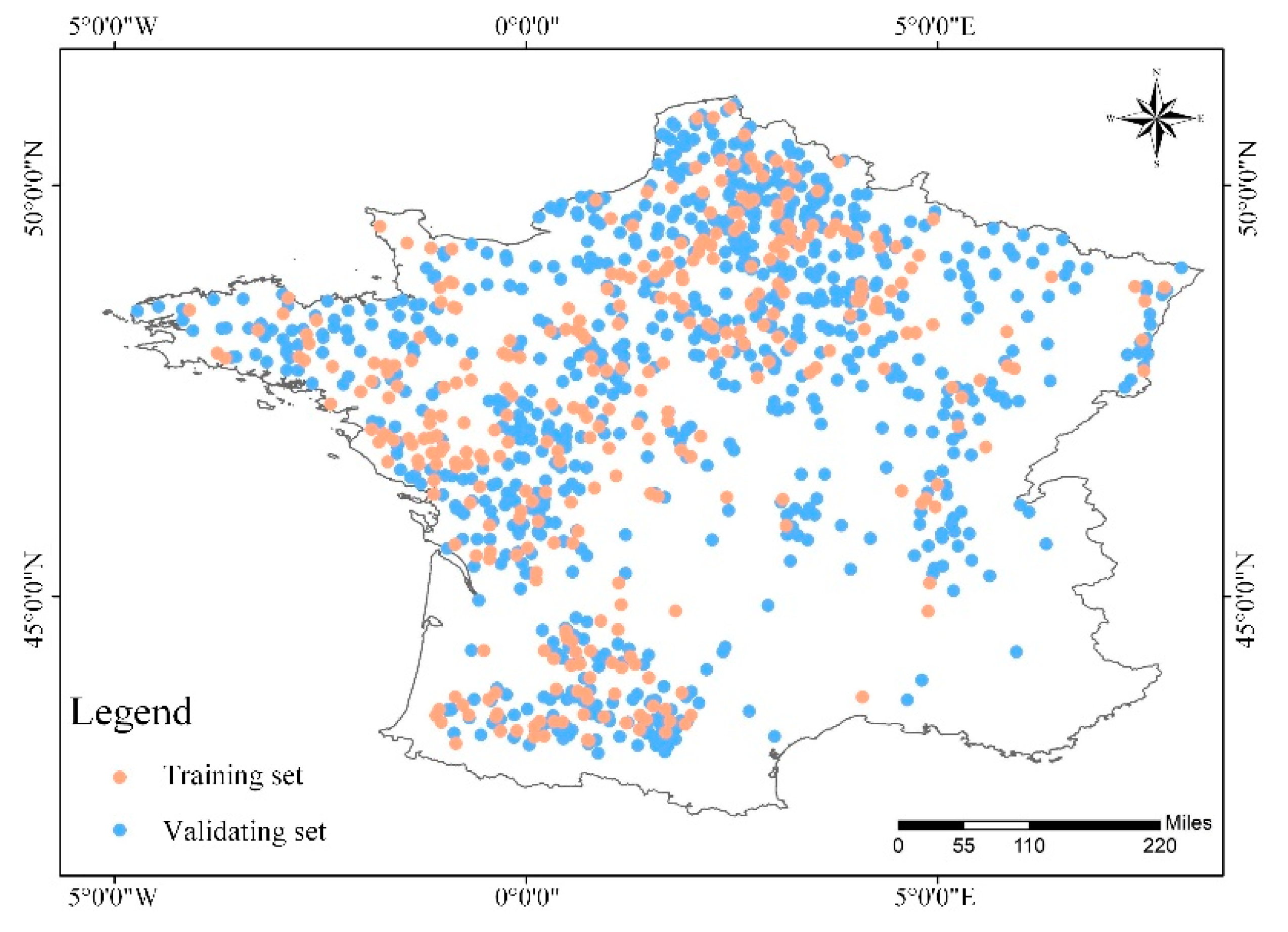
3.3. Construction of Training Set and Validation Set
3.4. Accuracy Evaluation
4. Results and Discussion
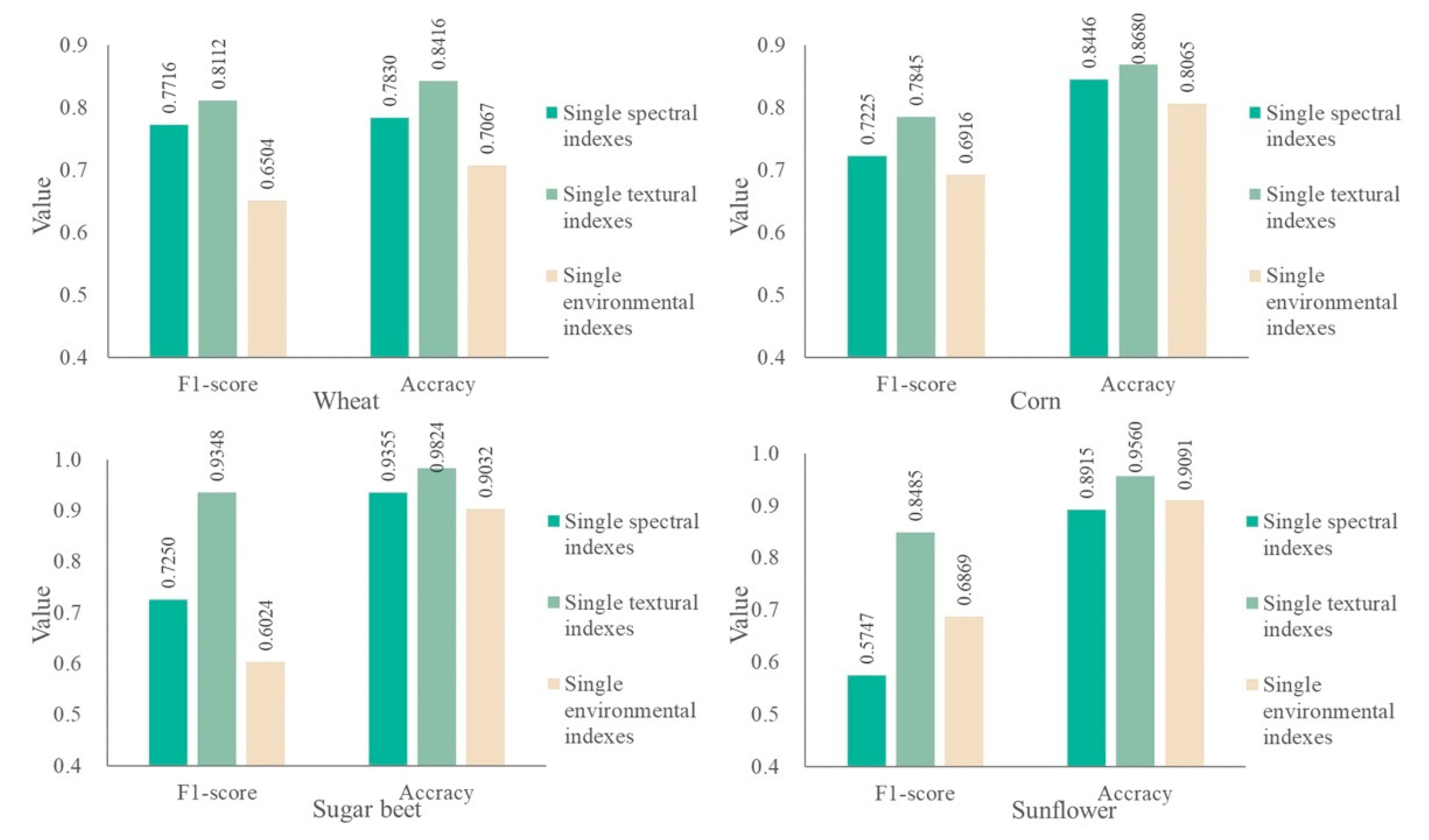
4.1. Classification Indexes
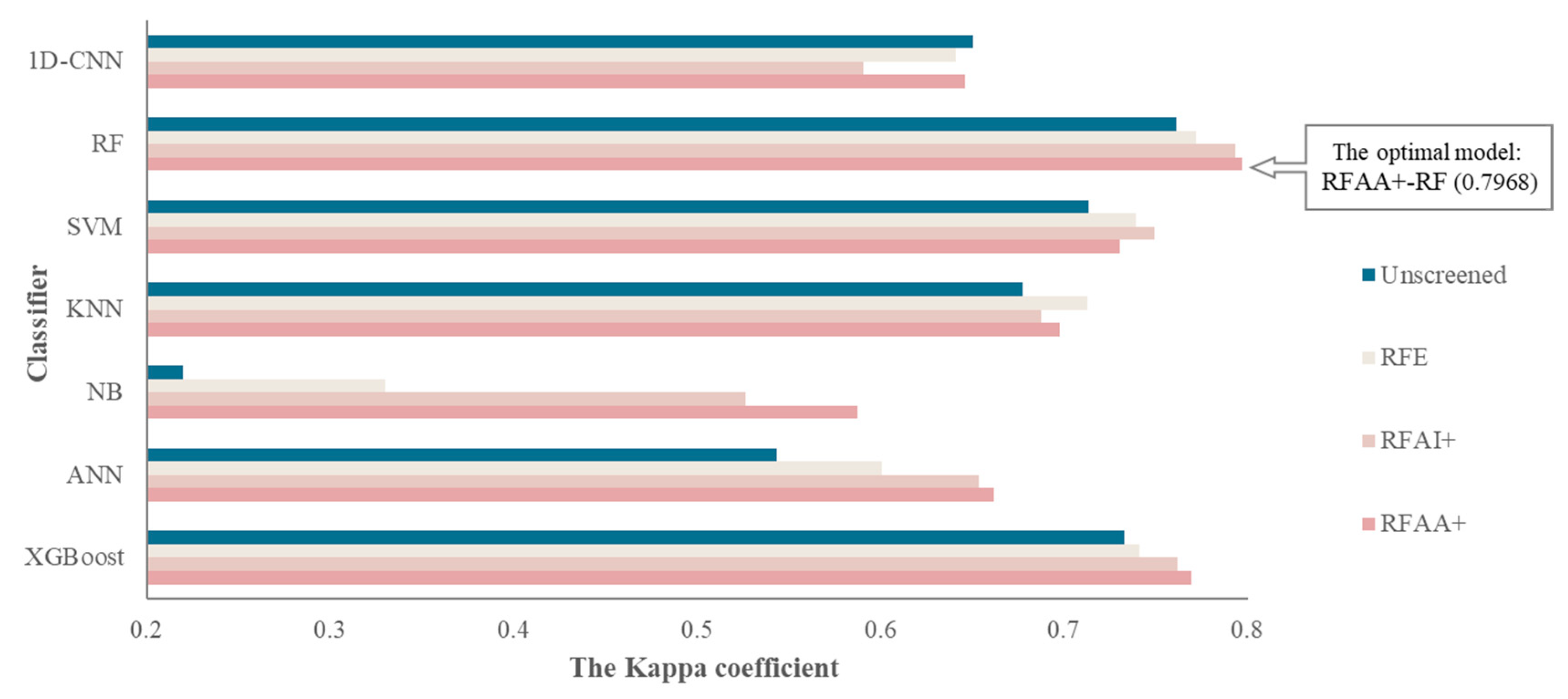
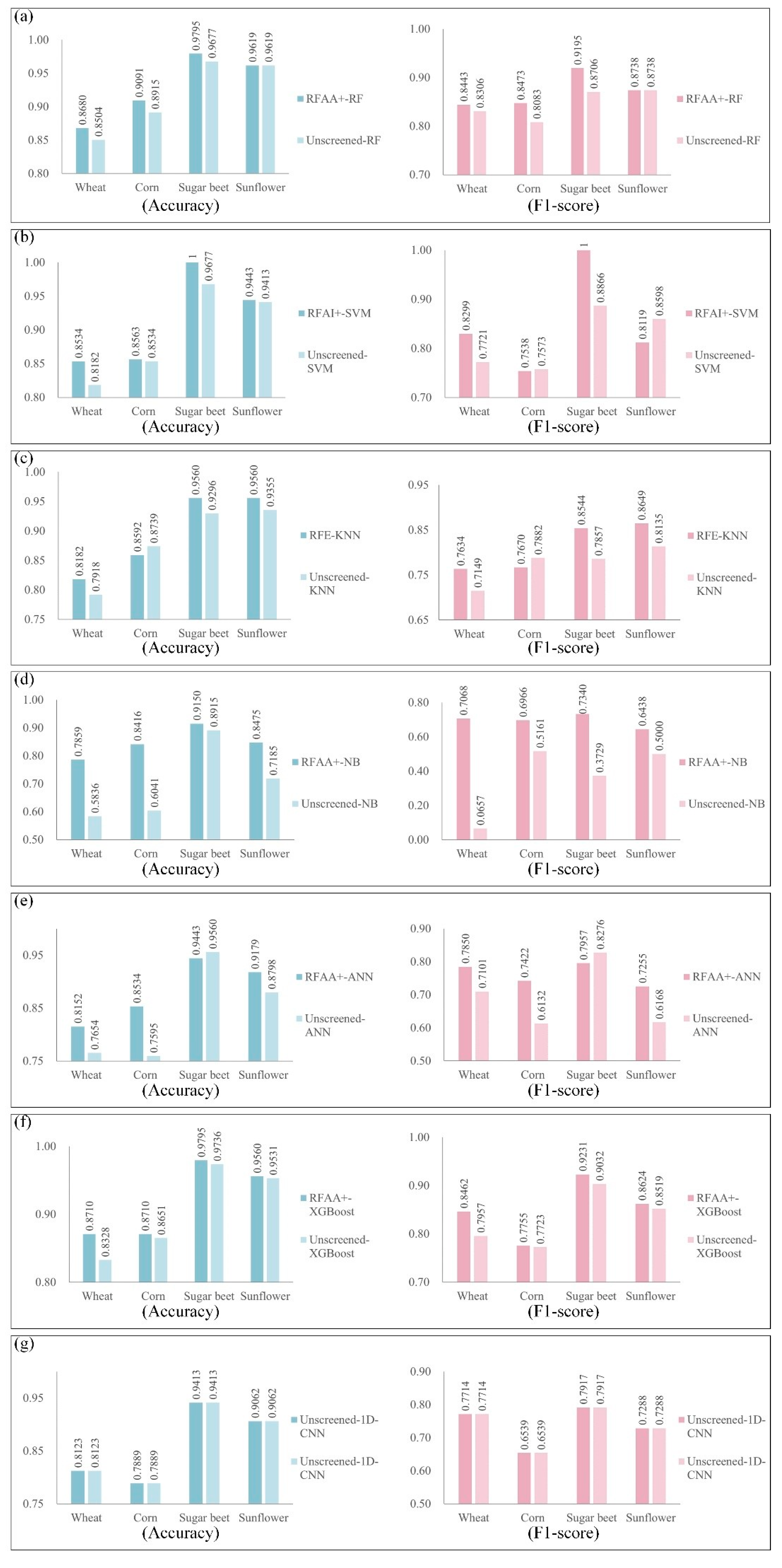
4.2. Results of the Coupling Classification Models
4.3. Comparative Results of the Coupling Classification Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Y.B.; Chen, Z.-X.; Yu, T.; Huang, X.-Z.; Gu, X.-F. Agricultural remote sensing big data: Management and applications. J. Integr. Agric. 2018, 17, 1915–1931. [Google Scholar] [CrossRef]
- Dharumarajan, S.; Hegde, R. Digital mapping of soil texture classes using Random Forest classification algorithm. Soil Use Manag. 2020, 38, 135–149. [Google Scholar] [CrossRef]
- Yu, P.; Fennell, S.; Chen, Y.; Liu, H.; Xu, L.; Pan, J.; Bai, S.; Gu, S. Positive impacts of farmland fragmentation on agricultural production efficiency in Qilu Lake watershed: Implications for appropriate scale management. Land Use Policy 2022, 117, 106108. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Peng, J.; Wang, S.; Seifert, C.; Wardlow, B.; Li, Z. A high-performance and in-season classification system of field-level crop types using time-series Landsat data and a machine learning approach. Remote Sens. Environ. 2018, 210, 35–47. [Google Scholar] [CrossRef]
- Martos, V.; Ahmad, A.; Cartujo, P.; Ordoñez, J. Ensuring Agricultural Sustainability through Remote Sensing in the Era of Agriculture 5.0. Appl. Sci. 2021, 11, 5911. [Google Scholar] [CrossRef]
- Li, S.; Li, F.; Gao, M.; Li, Z.; Leng, P.; Duan, S.; Ren, J. A New Method for Winter Wheat Mapping Based on Spectral Reconstruction Technology. Remote Sens. 2021, 13, 1810. [Google Scholar] [CrossRef]
- Jiang, M.; Xin, L.; Li, X.; Tan, M.; Wang, R. Decreasing Rice Cropping Intensity in Southern China from 1990 to 2015. Remote Sens. 2018, 11, 35. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Yu, P.; Chen, Y.; Chen, Z. Spatiotemporal dynamics of rice–crayfish field in Mid-China and its socioeconomic benefits on rural revitalisation. Appl. Geogr. 2022, 139, 102636. [Google Scholar] [CrossRef]
- Nizalapur, V.; Vyas, A. Texture Analysis for Land Use Land Cover (Lulc) Classification in Parts of Ahmedabad, Gujarat. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B3-2, 275–279. [Google Scholar] [CrossRef]
- Girolamo-Neto, C.D.; Sato, L.Y.; Sanches, I.D.; Silva, I.C.O.; Rocha, J.C.S.; Almeida, C.A. Object Based Image Analysis And Texture Features For Pasture Classification In Brazilian Savannah. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-3-2020, 453–460. [Google Scholar] [CrossRef]
- Raja, S.P.; Sawicka, B.; Stamenkovic, Z.; Mariammal, G. Crop Prediction Based on Characteristics of the Agricultural Environment Using Various Feature Selection Techniques and Classifiers. IEEE Access 2022, 10, 23625–23641. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, L.; Huang, C.; Wang, N.; Wang, S.; Peng, M.; Zhang, X.; Tong, Q. Crop classification based on the spectrotemporal signature derived from vegetation indices and accumulated temperature. Int. J. Digit. Earth 2022, 1–27. [Google Scholar] [CrossRef]
- Xu, F.; Li, Z.; Zhang, S.; Huang, N.; Quan, Z.; Zhang, W.; Liu, X.; Jiang, X.; Pan, J.; Prishchepov, A. Mapping Winter Wheat with Combinations of Temporally Aggregated Sentinel-2 and Landsat-8 Data in Shandong Province, China. Remote Sens. 2020, 12, 2065. [Google Scholar] [CrossRef]
- Lebrini, Y.; Boudhar, A.; Hadria, R.; Lionboui, H.; Elmansouri, L.; Arrach, R.; Ceccato, P.; Benabdelouahab, T. Identifying Agricultural Systems Using SVM Classification Approach Based on Phenological Metrics in a Semi-arid Region of Morocco. Earth Syst. Environ. 2019, 3, 277–288. [Google Scholar] [CrossRef]
- Jiang, F.; Smith, A.R.; Kutia, M.; Wang, G.; Liu, H.; Sun, H. A Modified KNN Method for Mapping the Leaf Area Index in Arid and Semi-Arid Areas of China. Remote Sens. 2020, 12, 1884. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, X.; Lawes, R.; Dunkerley, D.; Zhang, H. Comparison of machine learning algorithms for classification of LiDAR points for characterization of canola canopy structure. Int. J. Remote Sens. 2019, 40, 5973–5991. [Google Scholar] [CrossRef]
- Ganesan, M.; Andavar, S.; Raj, R.S.P. Prediction of Land Suitability for Crop Cultivation Using Classification Techniques. Braz. Arch. Biol. Technol. 2021, 64. [Google Scholar] [CrossRef]
- Loggenberg, K.; Strever, A.; Greyling, B.; Poona, N. Modelling Water Stress in a Shiraz Vineyard Using Hyperspectral Imaging and Machine Learning. Remote Sens. 2018, 10, 202. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Feng, Q.; Gong, J.; Zhou, J.; Liang, J.; Li, Y. Winter wheat mapping using a random forest classifier combined with multi-temporal and multi-sensor data. Int. J. Digit. Earth 2017, 11, 783–802. [Google Scholar] [CrossRef]
- Saini, R.; Ghosh, S.K. Crop classification in a heterogeneous agricultural environment using ensemble classifiers and single-date Sentinel-2A imagery. Geocarto Int. 2019, 36, 2141–2159. [Google Scholar] [CrossRef]
- Prins, A.J.; Van Niekerk, A. Crop type mapping using LiDAR, Sentinel-2 and aerial imagery with machine learning algorithms. Geo-Spatial Inf. Sci. 2020, 24, 215–227. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal Convolutional Neural Network for the Classification of Satellite Image Time Series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Coltin, B.; McMichael, S.; Smith, T.; Fong, T. Automatic boosted flood mapping from satellite data. Int. J. Remote Sens. 2016, 37, 993–1015. [Google Scholar] [CrossRef] [Green Version]
- Reyes, A.K.; Caicedo, J.C.; Camargo, J.E. Fine-tuning Deep Convolutional Networks for Plant Recognition. CLEF 2015, 1391, 467–475. [Google Scholar]
- Mahdianpari, M.; Mohammadimanesh, F.; McNairn, H.; Davidson, A.; Rezaee, M.; Salehi, B.; Homayouni, S. Mid-season Crop Classification Using Dual-, Compact-, and Full-Polarization in Preparation for the Radarsat Constellation Mission (RCM). Remote Sens. 2019, 11, 1582. [Google Scholar] [CrossRef] [Green Version]
- Tayebi, M.; Rosas, J.F.; Mendes, W.; Poppiel, R.; Ostovari, Y.; Ruiz, L.; dos Santos, N.; Cerri, C.; Silva, S.; Curi, N.; et al. Drivers of Organic Carbon Stocks in Different LULC History and along Soil Depth for a 30 Years Image Time Series. Remote Sens. 2021, 13, 2223. [Google Scholar] [CrossRef]
- Nasrallah, A.; Baghdadi, N.; El Hajj, M.; Darwish, T.; Belhouchette, H.; Faour, G.; Darwich, S.; Mhawej, M. Sentinel-1 Data for Winter Wheat Phenology Monitoring and Mapping. Remote Sens. 2019, 11, 2228. [Google Scholar] [CrossRef] [Green Version]
- Demarez, V.; Helen, F.; Marais-Sicre, C.; Baup, F. In-Season Mapping of Irrigated Crops Using Landsat 8 and Sentinel-1 Time Series. Remote Sens. 2019, 11, 118. [Google Scholar] [CrossRef] [Green Version]
- Sicre, C.M.; Inglada, J.; Fieuzal, R.; Baup, F.; Valero, S.; Cros, J.; Huc, M.; Demarez, V. Early Detection of Summer Crops Using High Spatial Resolution Optical Image Time Series. Remote Sens. 2016, 8, 591. [Google Scholar] [CrossRef] [Green Version]
- Veloso, A.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Planells, M.; Dejoux, J.-F.; Ceschia, E. Understanding the temporal behavior of crops using Sentinel-1 and Sentinel-2-like data for agricultural applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
- Manfron, G.; Delmotte, S.; Busetto, L.; Hossard, L.; Ranghetti, L.; Brivio, P.A.; Boschetti, M. Estimating inter-annual variability in winter wheat sowing dates from satellite time series in Camargue, France. Int. J. Appl. earth Obs. Geoinf. ITC J. 2017, 57, 190–201. [Google Scholar] [CrossRef]
- van der Meero, F.; Bakker, W. Cross correlogram spectral matching: Application to surface mineralogical mapping by using AVIRIS data from Cuprite, Nevada. Remote Sens. Environ. 1997, 61, 371–382. [Google Scholar] [CrossRef]
- Guo, Y.; Qing-sheng, l.; Liu Gao, H.; Huang, c. Research on extraction of planting information of major crops based on MODIS time-series NDVI. J. Nat. Resour. 2017, 32, 1808–1818. [Google Scholar]
- Sanz, H.; Valim, C.; Vegas, E.; Oller, J.M.; Reverter, F. SVM-RFE: Selection and visualization of the most relevant features through non-linear kernels. BMC Bioinform. 2018, 19, 432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kwak, G.-H.; Park, N.-W. Impact of Texture Information on Crop Classification with Machine Learning and UAV Images. Appl. Sci. 2019, 9, 643. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Yang, C.; Wang, X.-M. Landslide susceptibility assessment using feature selection-based machine learning models. Geomech. Eng. 2021, 25, 1. [Google Scholar] [CrossRef]
- Thanh Noi, P.; Kappas, M. Comparison of Random Forest, k-Nearest Neighbor, and Support Vector Machine Classifiers for Land Cover Classification Using Sentinel-2 Imagery. Sensors 2018, 18, 18. [Google Scholar] [CrossRef] [Green Version]
- Setyaningsih, E.R.; Listiowarni, I. Categorization of exam questions based on bloom taxonomy using naïve bayes and laplace smoothing. In Proceedings of the 2021 3rd East Indonesia Conference on Computer and Information Technology (EIConCIT), Surabaya, Indonesia, 9–11 April 2021; pp. 330–333. [Google Scholar]
- Beck, M.W. NeuralNetTools: Visualization and Analysis Tools for Neural Networks. J. Stat. Softw. 2018, 85, 1–20. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery Data Mining 2016, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Wolff, E. Very High Resolution Object-Based Land Use–Land Cover Urban Classification Using Extreme Gradient Boosting. IEEE Geosci. Remote Sens. Lett. 2018, 15, 607–611. [Google Scholar] [CrossRef] [Green Version]
- Alghamdi, M.; Al-Mallah, M.; Keteyian, S.; Brawner, C.; Ehrman, J.; Sakr, S. Predicting diabetes mellitus using SMOTE and ensemble machine learning approach: The Henry Ford ExercIse Testing (FIT) project. PLoS ONE 2017, 12, e0179805. [Google Scholar] [CrossRef]
- Andrada, M.F.; Vega-Hissi, E.G.; Estrada, M.R.; Martinez, J.C.G. Impact assessment of the rational selection of training and test sets on the predictive ability of QSAR models. SAR QSAR Environ. Res. 2017, 28, 1011–1023. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, H.; Wu, W.; Zhan, L.; Wei, J. Mapping Rice Paddy Based on Machine Learning with Sentinel-2 Multi-Temporal Data: Model Comparison and Transferability. Remote Sens. 2020, 12, 1620. [Google Scholar] [CrossRef]
- Song, I.; Kim, S. AVILNet: A New Pliable Network with a Novel Metric for Small-Object Segmentation and Detection in Infrared Images. Remote Sens. 2021, 13, 555. [Google Scholar] [CrossRef]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Kim, S.-H.; Geem, Z.W.; Han, G.-T. Hyperparameter Optimization Method Based on Harmony Search Algorithm to Improve Performance of 1D CNN Human Respiration Pattern Recognition System. Sensors 2020, 20, 3697. [Google Scholar] [CrossRef]



| Indicator | Calculation Formula | Meanings |
|---|---|---|
| Similarity between sample i and crop type j in NDVI index, j = {wheat, corn, sugar beet, and sunflower}. | ||
| Difference between sample i and crop type j in NDVI index, j = {wheat, corn, sugar beet, and sunflower}. |
| Indicator | Textural Index |
|---|---|
| Indicator | Meanings |
|---|---|
| Slope | Degree of surface inclination |
| Aspect | Orientation of the topographic slope |
| Average annual precipitation | |
| Average annual temperature |
| Wheat | Corn | Sugar Beet | Sunflower | |
|---|---|---|---|---|
| The training set | 338 | 240 | 100 | 117 |
| The validation set | 146 | 104 | 43 | 48 |
| RFAA+ | RFAI+ | RFE |
|---|---|---|
| (4) | ||
| Index Set | Feature Selection Method | Classifier | ||||||
|---|---|---|---|---|---|---|---|---|
| RF | SVM | KNN | NB | NN | XGBoost | 1D-CNN | ||
| Single spectral indexes | RFAA+ | 0.5922 | 0.53 | 0.5286 | 0.4606 | 0.5088 | 0.5463 | 0.5392 |
| RFAI+ | 0.5806 | 0.5146 | 0.5285 | 0.4581 | 0.5138 | 0.5582 | 0.5498 | |
| RFE | 0.5498 | 0.5126 | 0.5676 | 0.4325 | 0.4977 | 0.5385 | 0.5414 | |
| Unscreened | 0.5230 | 0.4900 | 0.5232 | 0.4202 | 0.4902 | 0.5378 | 0.5680 | |
| RF | SVM | KNN | NB | NN | XGBoost | 1D-CNN | ||
| Single textural indexes | RFAA+ | 0.7467 | 0.6700 | 0.6445 | 0.4606 | 0.6161 | 0.6924 | 0.6027 |
| RFAI+ | 0.7314 | 0.6736 | 0.6504 | 0.2850 | 0.6079 | 0.669 | 0.5830 | |
| RFE | 0.7189 | 0.6742 | 0.6023 | 0.1682 | 0.5959 | 0.6755 | 0.5964 | |
| Unscreened | 0.7062 | 0.6425 | 0.5377 | 0.1416 | 0.5484 | 0.6387 | 0.6373 | |
| RF | SVM | KNN | NB | NN | XGBoost | 1D-CNN | ||
| Single environmental indexes | RFAA+ | 0.5113 | 0.5078 | 0.5087 | 0.3242 | 0.4528 | 0.4529 | 0.4290 |
| RFAI+ | 0.5220 | 0.4979 | 0.4319 | 0.3205 | 0.4492 | 0.4420 | 0.3536 | |
| RFE | 0.5003 | 0.4609 | 0.4658 | 0.2914 | 0.4362 | 0.4505 | 0.4129 | |
| Unscreened | 0.5081 | 0.4514 | 0.4371 | 0.2871 | 0.4172 | 0.4485 | 0.4312 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Peng, P.; Chen, Y.; Wang, X. Multi-Crop Classification Using Feature Selection-Coupled Machine Learning Classifiers Based on Spectral, Textural and Environmental Features. Remote Sens. 2022, 14, 3153. https://doi.org/10.3390/rs14133153
He S, Peng P, Chen Y, Wang X. Multi-Crop Classification Using Feature Selection-Coupled Machine Learning Classifiers Based on Spectral, Textural and Environmental Features. Remote Sensing. 2022; 14(13):3153. https://doi.org/10.3390/rs14133153
Chicago/Turabian StyleHe, Shan, Peng Peng, Yiyun Chen, and Xiaomi Wang. 2022. "Multi-Crop Classification Using Feature Selection-Coupled Machine Learning Classifiers Based on Spectral, Textural and Environmental Features" Remote Sensing 14, no. 13: 3153. https://doi.org/10.3390/rs14133153
APA StyleHe, S., Peng, P., Chen, Y., & Wang, X. (2022). Multi-Crop Classification Using Feature Selection-Coupled Machine Learning Classifiers Based on Spectral, Textural and Environmental Features. Remote Sensing, 14(13), 3153. https://doi.org/10.3390/rs14133153