Dual Receiver EGNOS+SDCM Positioning with C1C and C1W Pseudo-Range Measurements
Abstract
:1. Introduction
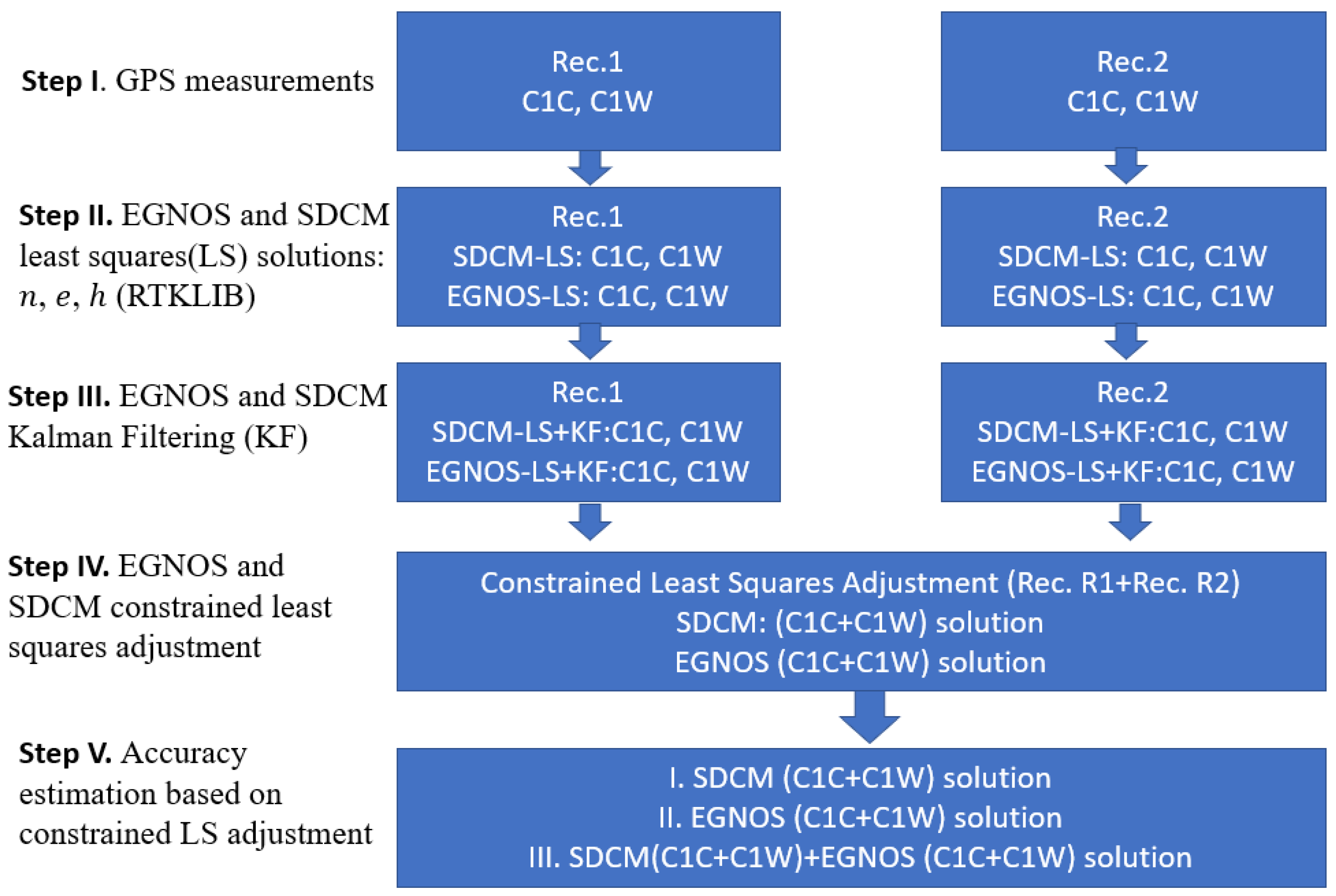
- I.
- Taking measurements with C1C and C1W codes using two independent GPS receivers.
- II.
- A determination of the EGNOS and SDCM autonomous position for single measurement epochs, for C1C and C1W code solutions, using the least squares method.
- III.
- The use of Kalman filtering to smoothen the coordinates obtained in step II.
- IV.
- Using a forced equation with a known 3D distance between two GNSS receivers.
- V.
- Conducting an accuracy analysis of the obtained coordinates using the least squares covariance matrix adjustment solution.
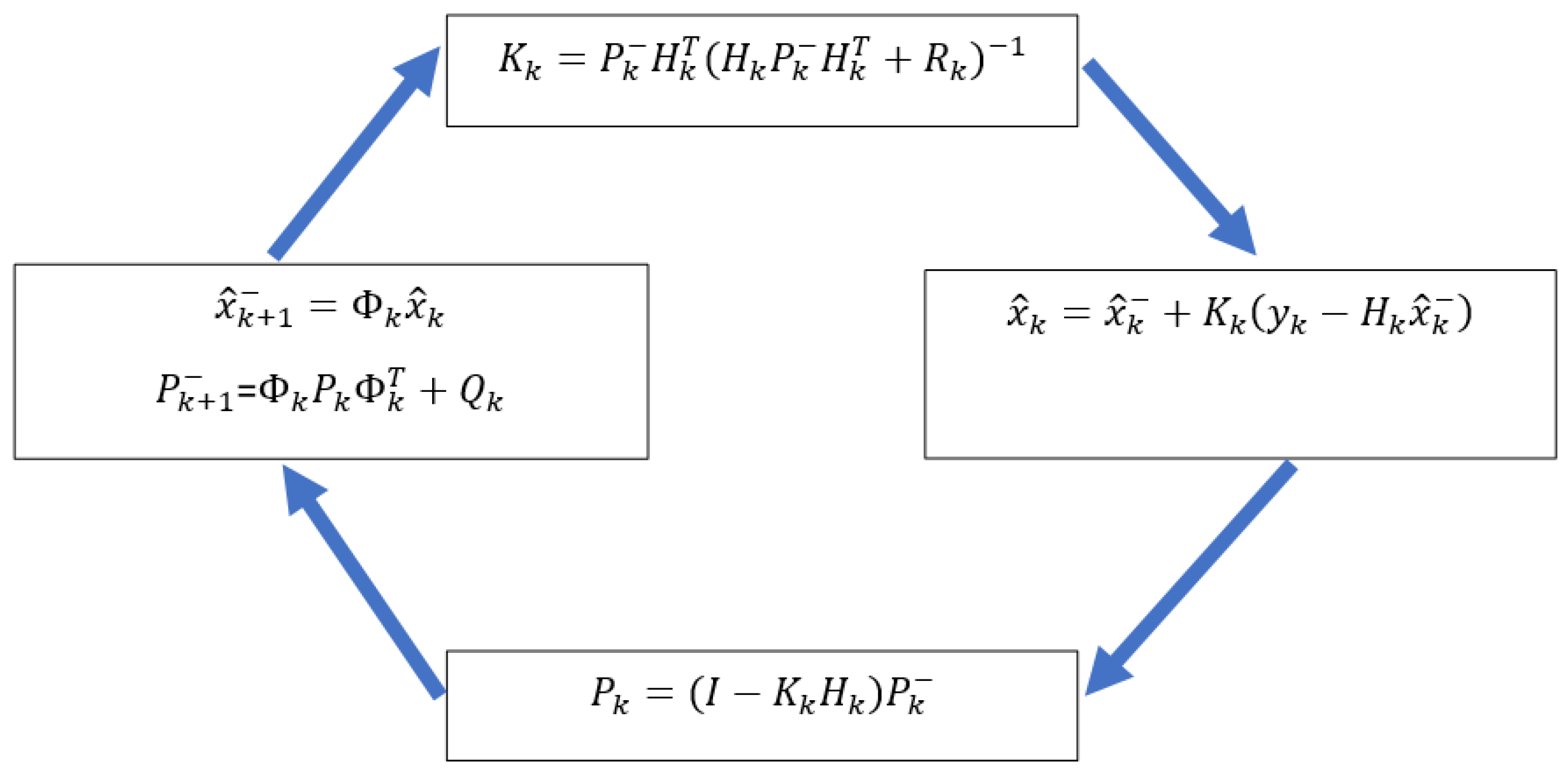
2. Kalman Filtering in SBAS Positioning
3. Mathematic Model of Dual Receiver in SBAS Positioning
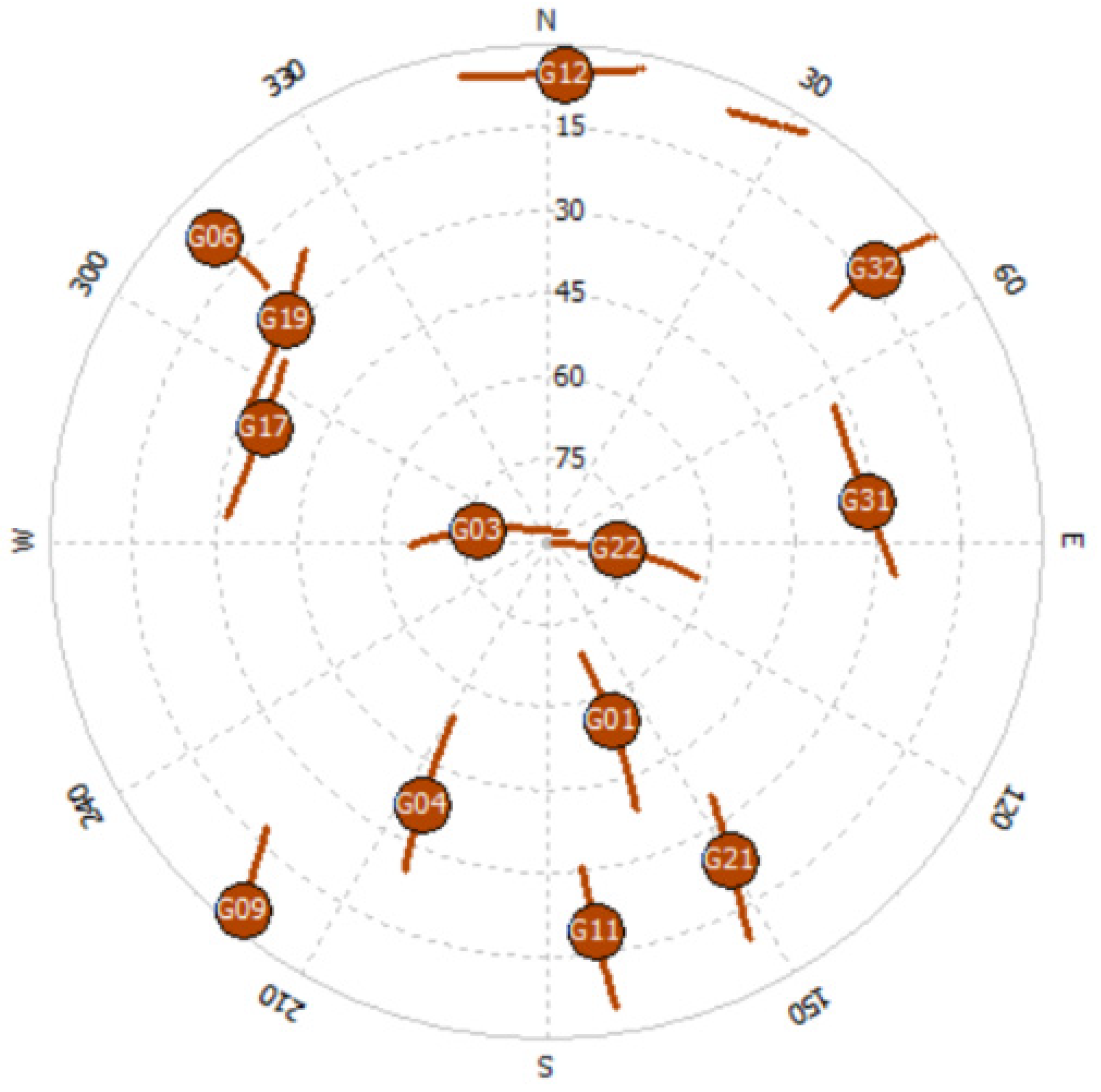
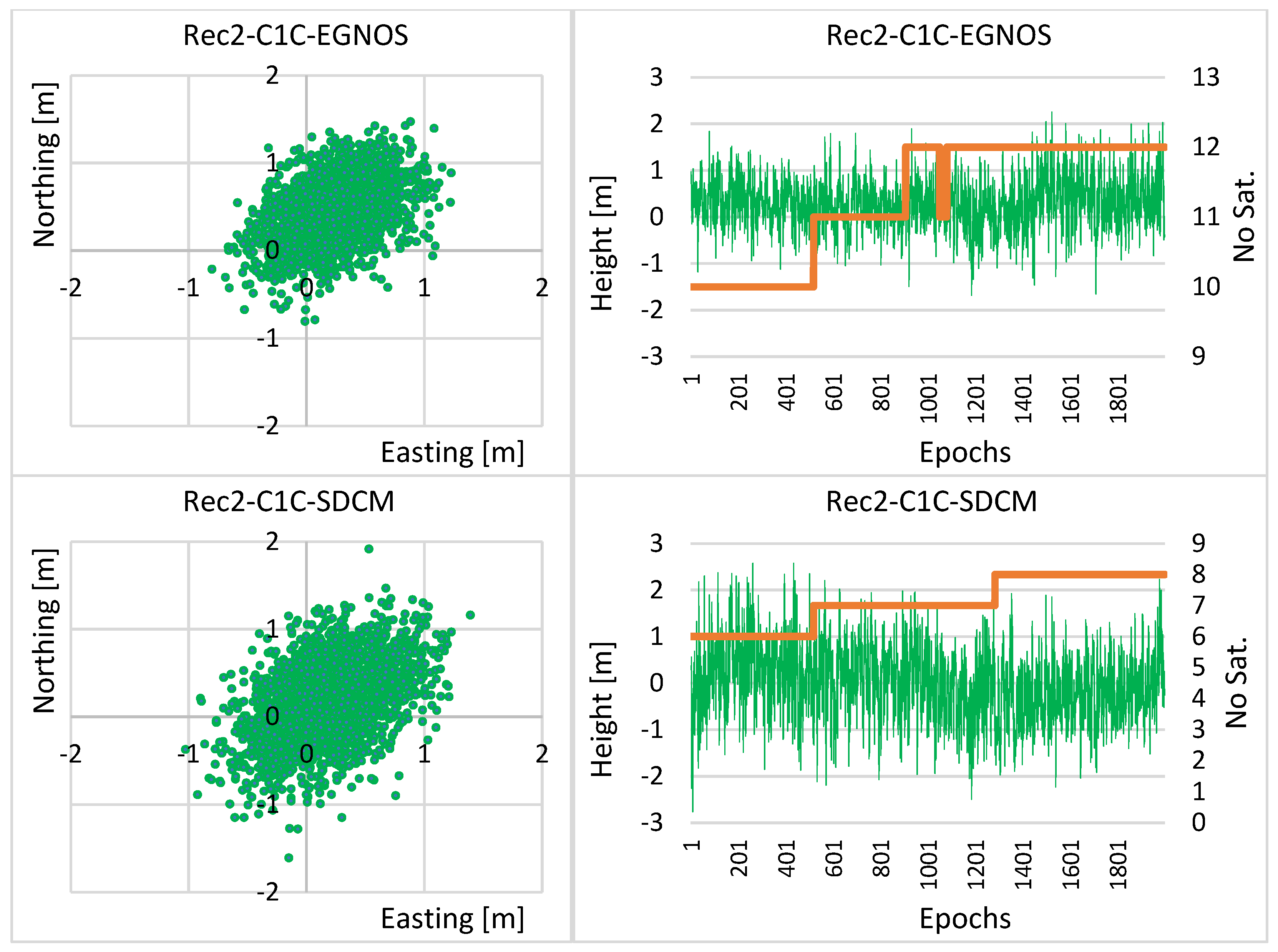
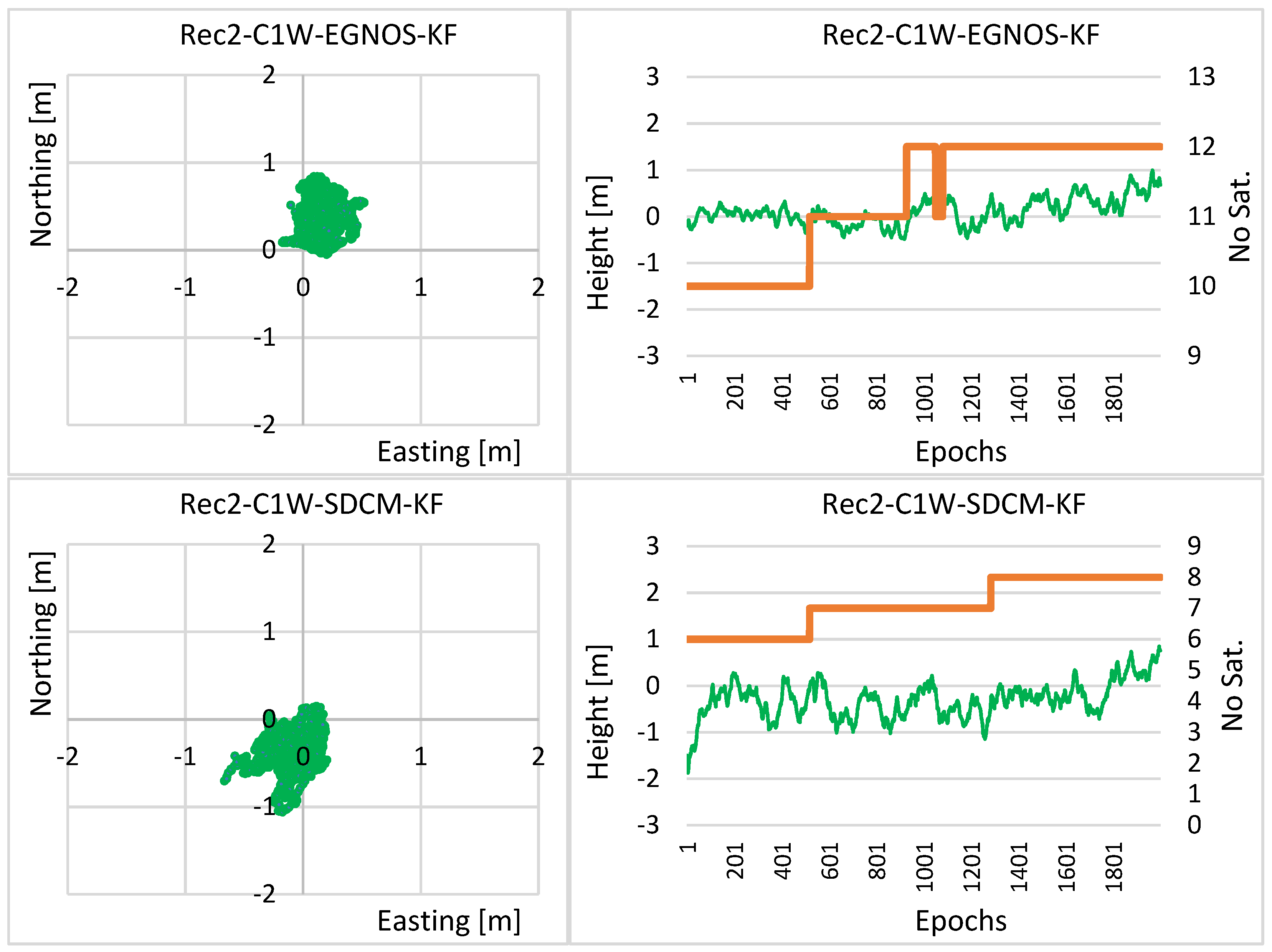
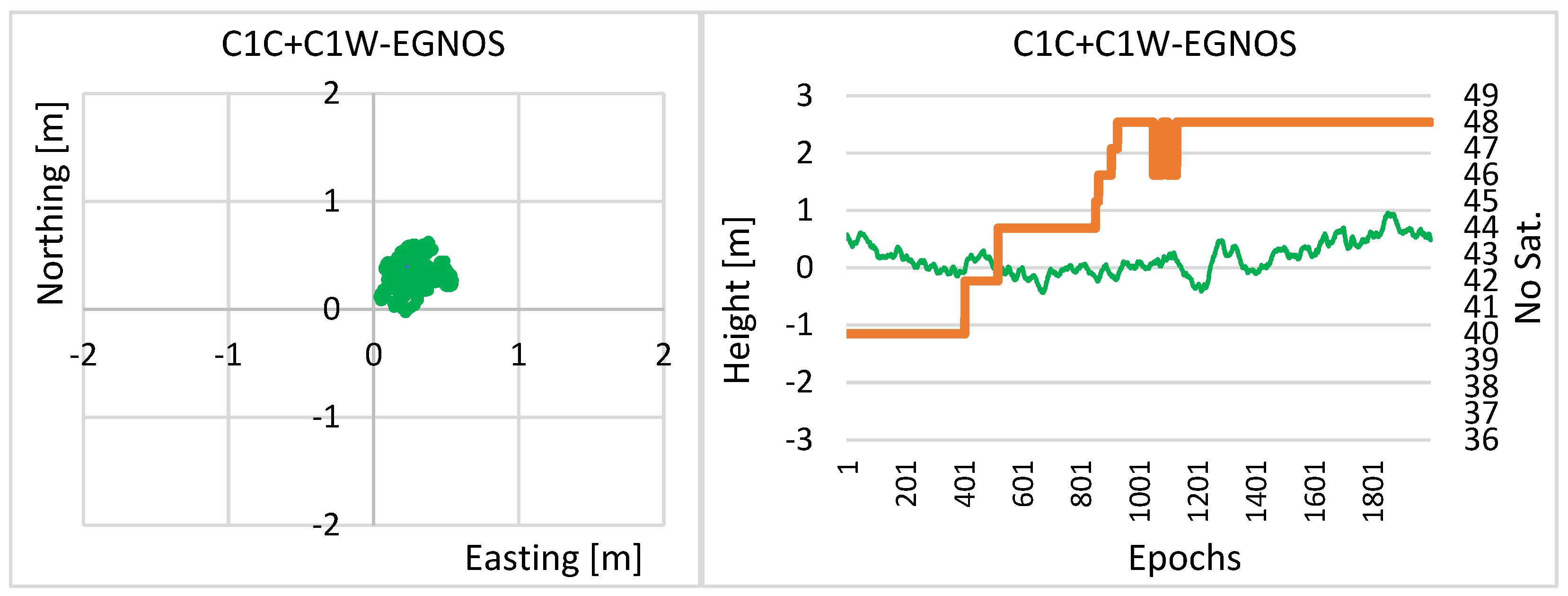
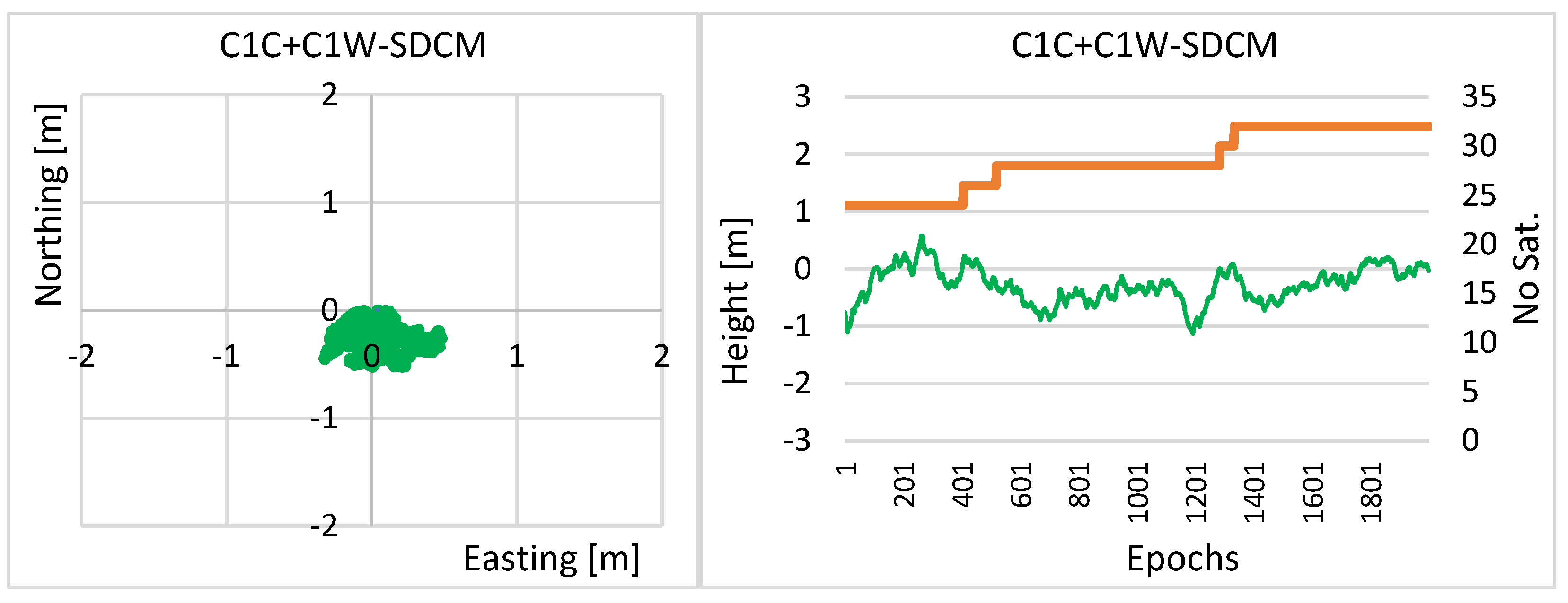
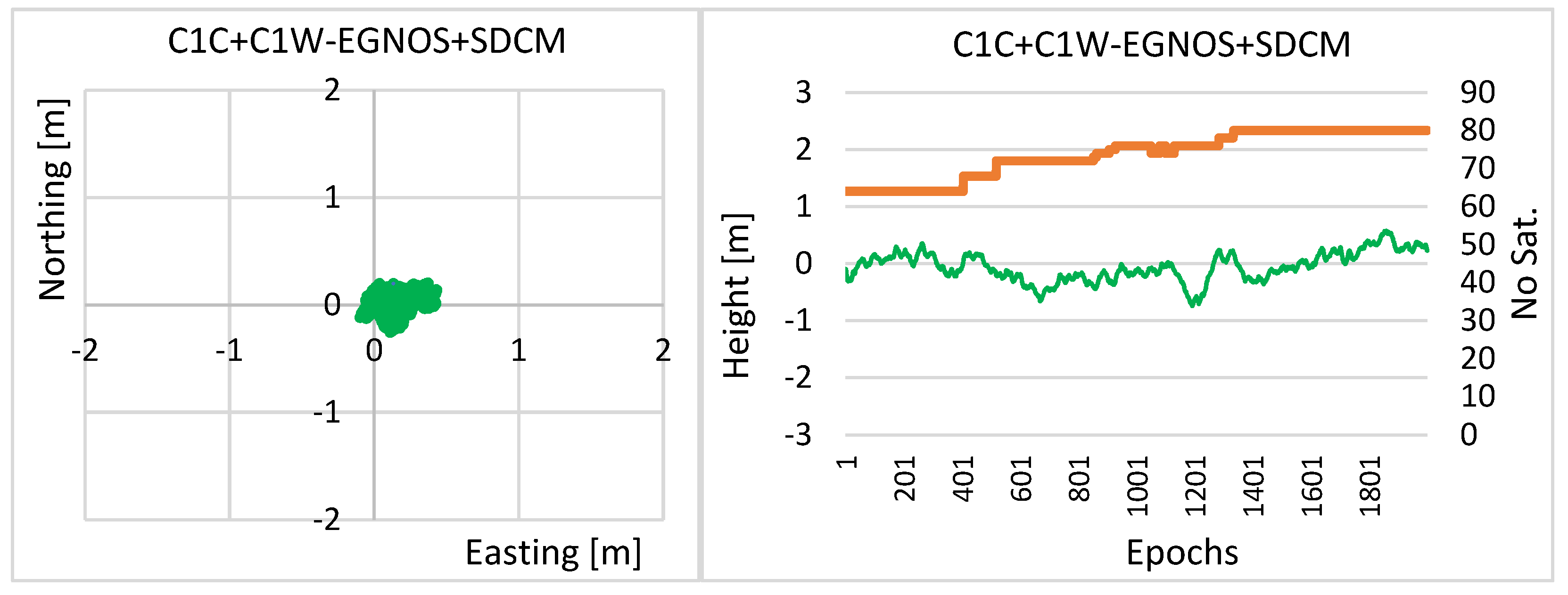
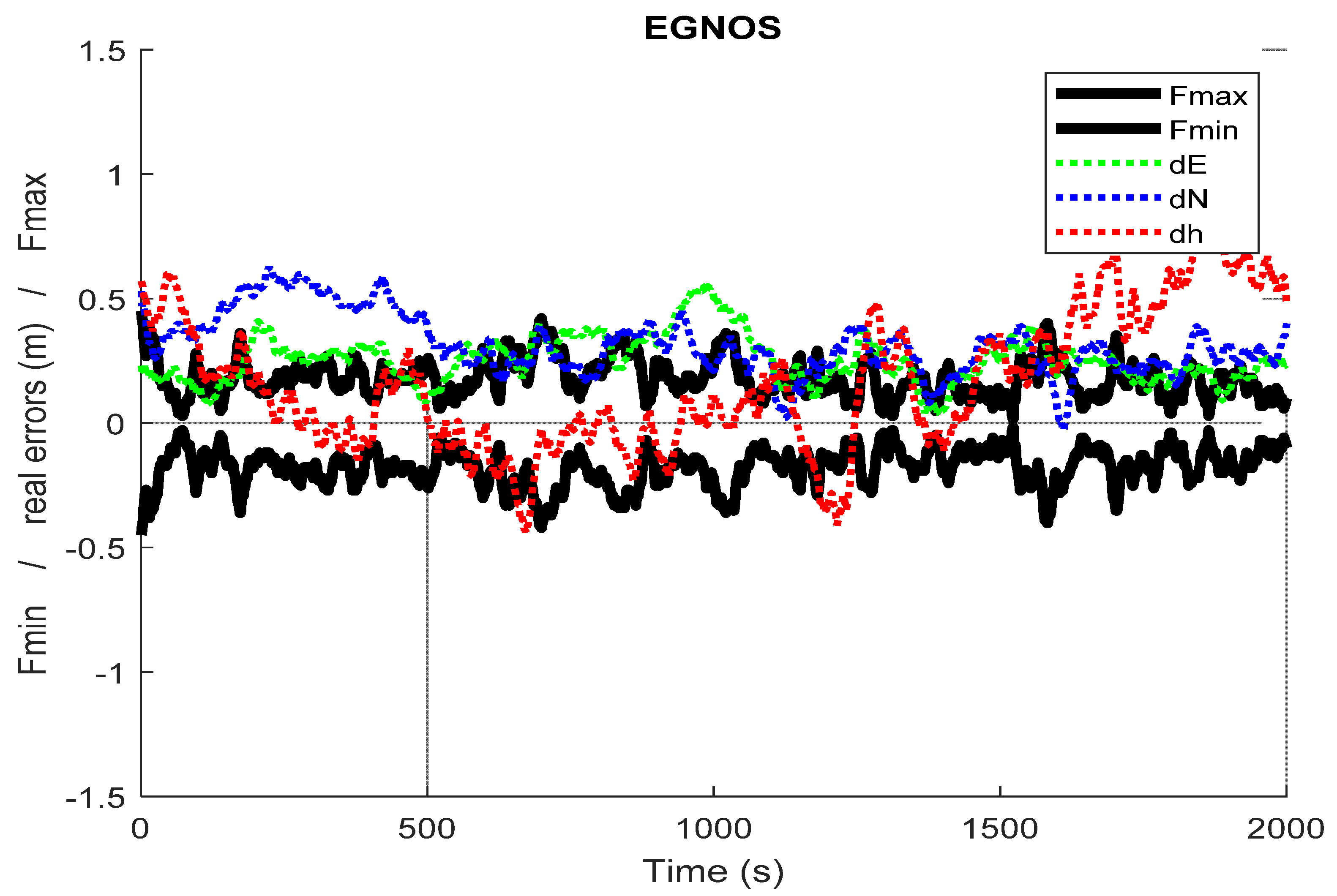
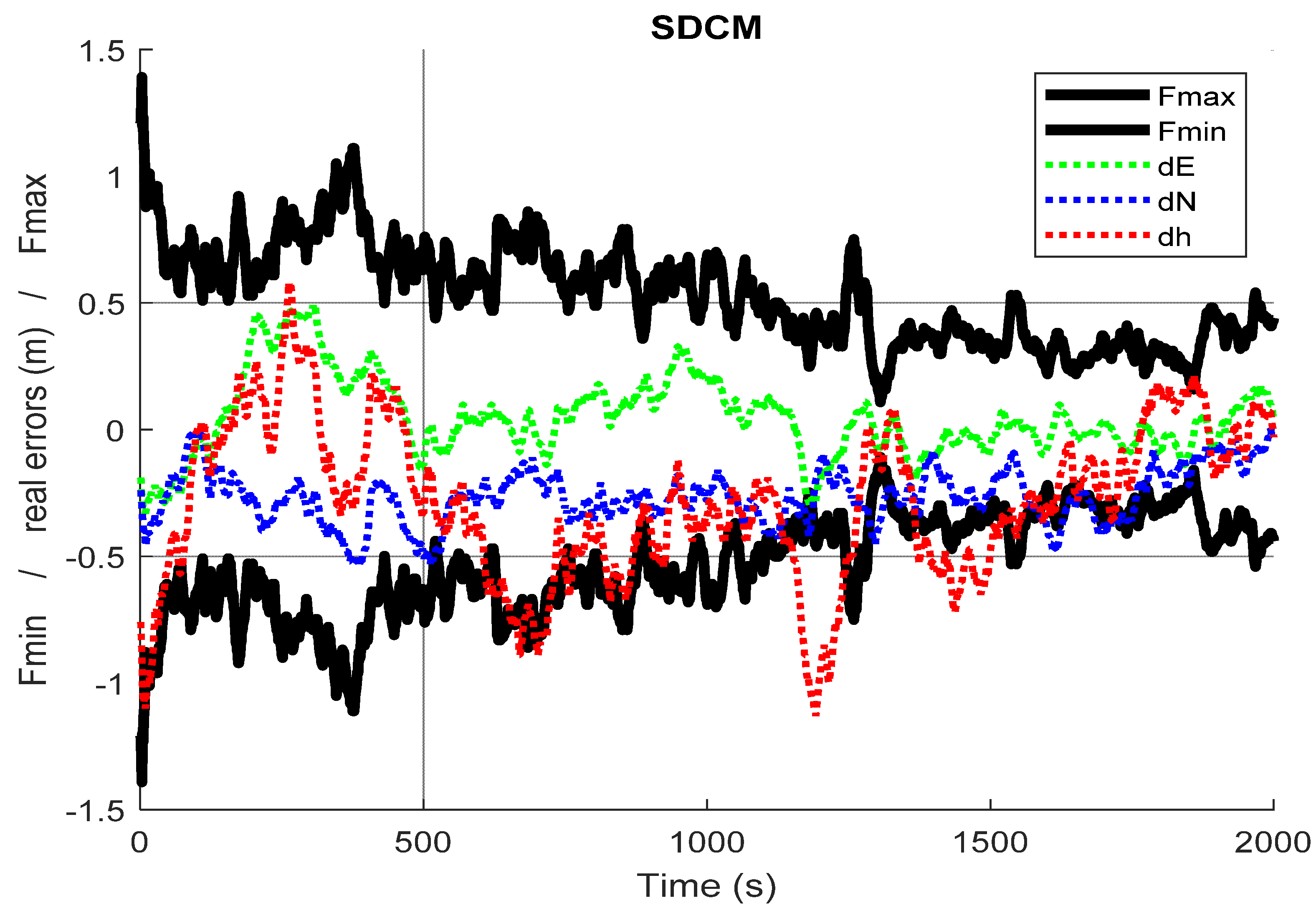
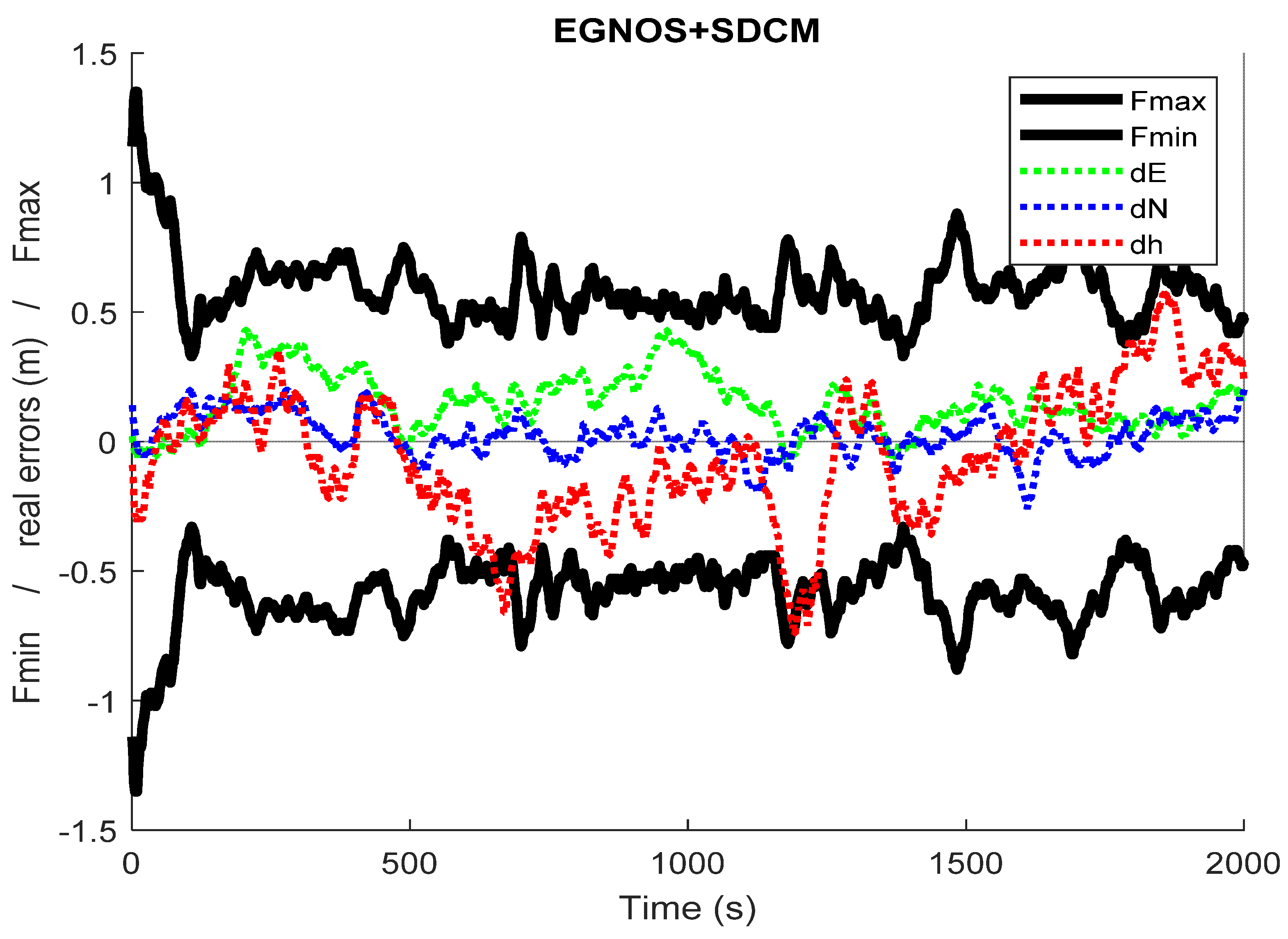
4. Experimental Test and Results
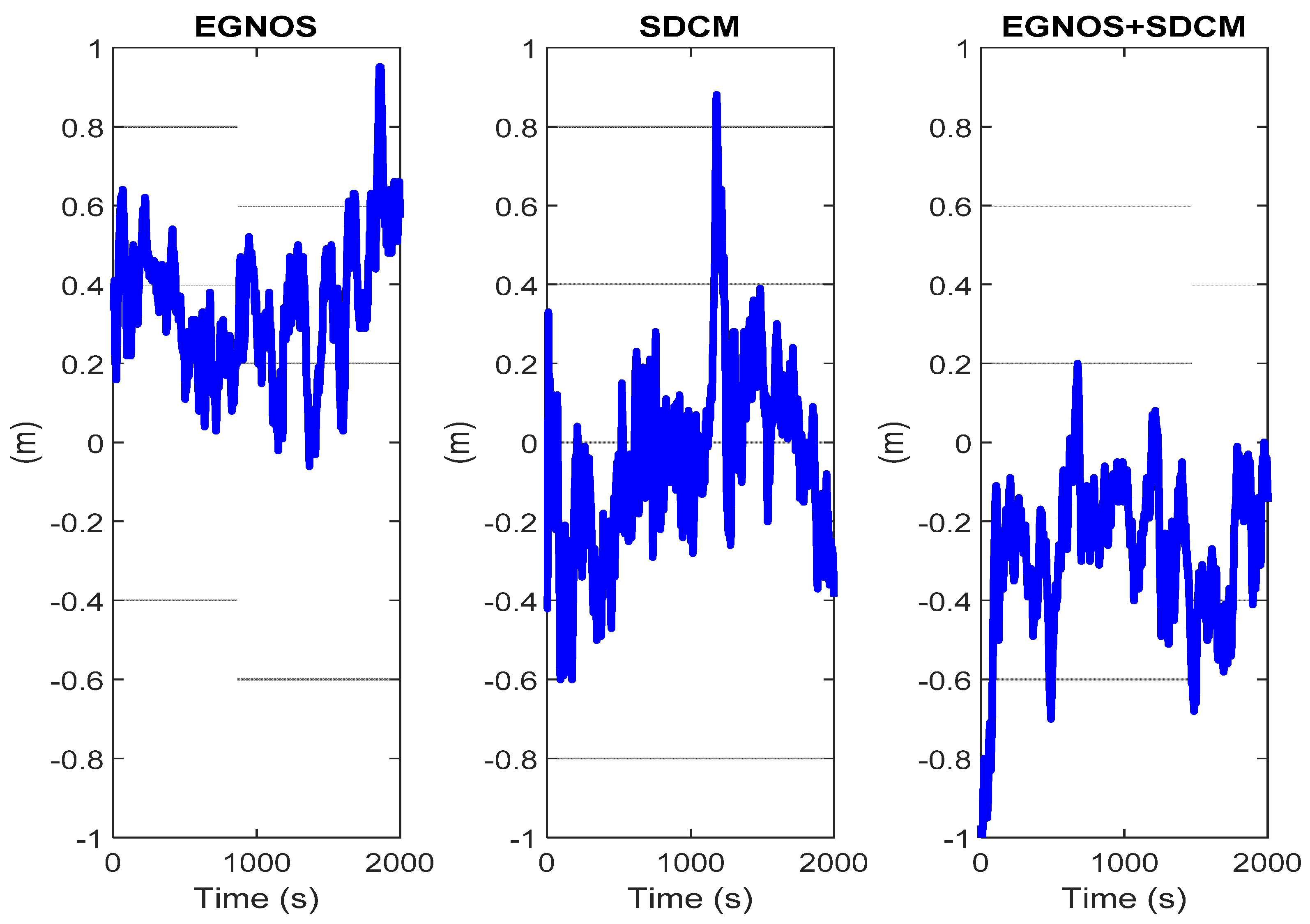
5. Accuracy Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wubbena, G.; Bagge, A.; Seeber, G.; Boder, V.; Hankemeier, P. Reducing Distance Dependent Errors for Real-Time Precise DGPS Applications by Establishing Reference Station Networks. In Proceedings of the 9th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1996), Kansas City, MO, USA, 17–20 September 1996; pp. 1845–1852. [Google Scholar]
- Weng, D.; Ji, S.; Lu, Y.; Chen, W.; Li, L. Improving DGNSS Performance through the Use of Network RTK Corrections. Remote Sens. 2021, 13, 1621. [Google Scholar] [CrossRef]
- Bakuła, M.; Pelc-Mieczkowska, R.; Walawski, M. Reliable and redundant RTK positioning for applications in hard observational conditions. Artif. Satell. 2012, 47, 23–33. [Google Scholar] [CrossRef]
- Bakuła, M.; Przestrzelski, P.; Kaźmierczak, R. Reliable Technology of Centimeter GPS/GLONASS Surveying in Forest Environments. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1029–1038. [Google Scholar] [CrossRef]
- Hernandez-Pajares, M.; Zornoza, J.M.J.; Subirana, J.S.; Farnworth, R.; Soley, S. EGNOS test bed ionospheric corrections under the October and November 2003 storms. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2283–2293. [Google Scholar] [CrossRef]
- Sieradzki, R.; Paziewski, J. Towards a reliable ionospheric polar patch climatology with ground-based GNSS. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5802614. [Google Scholar] [CrossRef]
- Gao, J. Integration of GPS with remote sensing and GIS: Reality and prospect. Photogramm. Eng. Remote Sens. 2002, 68, 447–454. [Google Scholar]
- Lin, Y.C.; Manish, R.; Bullock, D.; Habib, A. Comparative Analysis of Different Mobile LiDAR Mapping Systems for Ditch Line Characterization. Remote Sens. 2021, 13, 2485. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Gao, Z.; Niu, X.; El-Sheimy, N. Tight fusion of a monocular camera, MEMS-IMU, and single-frequency multi-GNSS RTK for precise navigation in GNSS-challenged environments. Remote Sens. 2019, 11, 610. [Google Scholar] [CrossRef] [Green Version]
- Bar, Y.; Consoli, A.; Realini, E.; Caldera, S.; Mazzoni, A.; Crespi, M. Consumer GNSS chipsets-based, dual-frequency receivers as enablers of precise navigation and dense networks. Meas. Sci. Technol. 2019, 30, 044007. [Google Scholar]
- Grayson, B.; Penna, N.T.; Mills, J.P.; Grant, D.S. GPS precise point positioning for UAV photogrammetry. Photogramm. Rec. 2018, 33, 427–447. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Xu, T.; Nie, W.; Xu, G. A new algorithm for a multi-baseline solution based on the equivalence principle. Meas. Sci. Technol. 2022, 32, 015015. [Google Scholar] [CrossRef]
- Krasuski, K.; Ciećko, A.; Bakuła, M.; Wierzbicki, D. New strategy for improving the accuracy of aircraft positioning based on GPS SPP solution. Sensors 2022, 20, 4921. [Google Scholar] [CrossRef] [PubMed]
- Krasuski, K.; Wierzbicki, D. Application the SBAS/EGNOS Corrections in UAV Positioning. Energies 2021, 14, 739. [Google Scholar] [CrossRef]
- Ciećko, A.; Bakuła, M.; Grunwald, G.; Ćwiklak, J. Examination of Multi-Receiver GPS/EGNOS Positioning with Kalman Filtering and Validation Based on CORS Stations. Sensors 2020, 20, 2732. [Google Scholar] [CrossRef]
- Paziewski, J. Precise GNSS single epoch positioning with multiple receiver configuration for medium-length baselines: Methodology and performance analysis. Meas. Sci. Technol. 2015, 26, 035002. [Google Scholar] [CrossRef]
- Wilk, W.; Koc, W.; Specht, C.; Skibicki, J.; Judek, S.; Karwowski, K.; Chrostowski, P.; Szmagliński, J.; Dąbrowski, P.; Czaplewski, K.; et al. Innovative mobile method to determine railway track axis position in global coordinate system using position measurements performed with GNSS and fixed base of the measuring vehicle. Measurement 2021, 175, 109016. [Google Scholar] [CrossRef]
- Li, M.; He, K.; Xu, T.; Lu, B. Robust adaptive filter for shipborne kinematic positioning and velocity determination during the Baltic Sea experiment. GPS Solut. 2018, 22, 81. [Google Scholar] [CrossRef]
- Gao, F.; Xu, T.; Wang, N.; He, Y.; Luo, B. A shipborne experiment using a dual-antenna reflectometry system for GPS/BDS code delay measurements. J. Geod. 2020, 94, 88. [Google Scholar] [CrossRef]
- Hong, C.K.; Park, C.H.; Han, J.H.; Kwon, J.H. Medium to long range kinematic GPS positioning with position-velocity-acceleration model using multiple reference stations. Sensors 2015, 15, 16895–16909. [Google Scholar] [CrossRef]
- Wang, J.; Xu, T.; Nie, W.; Xu, G. GPS/BDS RTK Positioning Based on Equivalence Principle Using Multiple Reference Stations. Remote Sens. 2020, 12, 3178. [Google Scholar] [CrossRef]
- Wang, J.; Xu, T.; Nie, W.; Xu, G. A simplified processing algorithm for multi-baseline RTK positioning in urban environments. Measurement 2021, 179, 109446. [Google Scholar] [CrossRef]
- Bakuła, M.; Kaźmierczak, R. Technology of rapid and ultrarapid static GPS/GLONASS surveying in urban environments. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics) IEEE, Gdansk, Poland, 22–25 June 2017; pp. 336–342. [Google Scholar]
- Bakuła, M. Constrained and network multi-receiver single-epoch RTK positioning. Surv. Rev. 2020, 52, 289–298. [Google Scholar] [CrossRef]
- Loh, R.; Wullschleger, V.; Elrod, B.; Lage, M.; Haas, F. The US Wide-Area Augmentation System (WAAS). Navigation 1995, 42, 435–465. [Google Scholar] [CrossRef]
- Walter, T.; Kee, C.; Chao, Y.C.; Tsai, Y.J.; Peled, U.; Ceva, J.; Barrows, A.K.; Abbott, E.; Powell, D.; Enge, P.; et al. Flight Trials of the Wide Area Augmentation System (WAAS). In Proceedings of the ION GPS-94 7th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Palace Convention Center, Salt Lake City, UT, USA, 20–23 September 1994; pp. 1537–1546. [Google Scholar]
- Bolstad, P.; Jenks, A.; Berkin, J.; Horne, K.; Reading, W.H. A comparison of autonomous, WAAS, real-time, and post-processed global positioning systems (GPS) accuracies in northern forests. North J. Appl. For. 2005, 22, 5–11. [Google Scholar] [CrossRef] [Green Version]
- Radio Technical Committee for Aeronautics (RTCA). Minimum Operational Performance Standards for Airborne Equipment Using Global Positioning System/Wide Area Augmentation System; Doc. DO-229D, with Change 1, 2013; Radio Technical Committee for Aeronautics (RTCA): Washington, DC, USA, 2006. [Google Scholar]
- Shimamura, A. MSAS (MTSAT satellite-based augmentation system) project status. Air Space Eur. 1999, 2, 63–67. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, Y.; Tang, C.; Chen, J.; Zhao, L.; Zhou, S.; Hu, X.; Tian, Q.; Yang, Y. Pseudorange Bias Analysis and Preliminary Service Performance Evaluation of BDSBA. Remote Sens. 2021, 13, 4815. [Google Scholar] [CrossRef]
- Choy, S.; Kuckartz, J.; Dempster, A.G.; Rizos, C.; Higgins, M. GNSS satellite-based augmentation systems for Australia. GPS Solut. 2017, 21, 835–848. [Google Scholar] [CrossRef]
- European GNSS Agency (GSA). EGNOS Open Service (OS) Service Definition Document (v. 2.3); The European GNSS Agency: Prague, Czech Republic, 2017.
- Averin, S.; Dvorkin, V.; Karutin, S.; Kurshin, V.; Urlichich, U.; Klimov, V. Russian System for Differential Correction and Monitoring: A Concept and Results of the First Phase of Development. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; pp. 2103–2110. [Google Scholar]
- Averin, S.V.; Dvorkin, V.V.; Karutin, V.S.N.; Sergey, N. Russian System for Differential Correction and Monitoring: A Concept, Present Status, And Prospects For Future. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 3037–3044. [Google Scholar]
- Ali, K.; Pini, M.; Dovis, F. Measured performance of the application of EGNOS in the road traffic sector. GPS Solut. 2012, 16, 135–145. [Google Scholar] [CrossRef]
- Skórkowski, A.; Topór-Kamiński, T. Analysis of EGNOS-augmented GPS receiver positioning accuracy. Acta Phys. Pol. 2012, 122, 821–824. [Google Scholar] [CrossRef]
- Konin, V.; Shyshkov, F. Extending the reach of SBAS. Some aspects of EGNOS performance in Ukraine. Inside GNSS 2015, 1, 50–54. [Google Scholar]
- Grunwald, G.; Bakuła, M.; Ciećko, A. Study of EGNOS accuracy and integrity in eastern Poland. Aeronaut. J. 2016, 120, 1275–1290. [Google Scholar] [CrossRef]
- Grunwald, G.; Bakuła, M.; Ciećko, A.; Kaźmierczak, R. Examination of GPS/EGNOS integrity in north-eastern Poland. IET Radar Sonar Navig. 2016, 10, 114–121. [Google Scholar] [CrossRef]
- Specht, C.; Pawelski, J.; Smolarek, L.; Specht, M.; Dąbrowski, P.S. Assessment of the positioning accuracy of DGPS and EGNOS systems in the Bay of Gdansk using maritime dynamic measurements. J. Navig. 2019, 72, 575–587. [Google Scholar] [CrossRef] [Green Version]
- GSA. EGNOS Safety of Life (SoL) Service Definition Document (v. 3.3); The European GNSS Agency: Prague, Czech Republic, 2019.
- Krasuski, K. Application of the GPS/EGNOS solution for the precise positioning of an aircraft vehicle. Sci. J. Sil. Univ. Technol. Ser. Transp. 2017, 96, 81–93. [Google Scholar] [CrossRef]
- Krasuski, K.; Ciećko, A.; Grunwald, G.; Wierzbicki, D. Assessment of velocity accuracy of aircraft in the dynamic tests using GNSS sensors. Facta Univ. Ser. Mech. Eng. 2020, 18, 301–313. [Google Scholar] [CrossRef]
- Kirschenstein, M.; Krasuski, K.; Goś, A. Methods of precise aircraft positioning in the GPS system with an application of the troposphere correction. Sci. J. Sil. Univ. Technol. 2020, 109, 73–84. [Google Scholar] [CrossRef]
- Krasuski, K.; Wierzbicki, D. Monitoring aircraft position using EGNOS data for the SBAS APV approach to the landing procedure. Sensors 2020, 20, 1945. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.; Park, B.; So, H.; Jang, J.; Seo, S.; Park, J.; Bu, S.; Lee, C. Analysis on the multi-constellation SBAS performance of SDCM in Korea. J. Position. Navig. Timing 2016, 5, 181–191. [Google Scholar] [CrossRef]
- Park, K.W.; Cho, M.; Park, C. An efficient positioning method for multi-GNSS with multi-SBAS. J. Position. Navig. Timing 2018, 7, 245–253. [Google Scholar]
- Park, K.W.; Park, J.I.; Park, C. Efficient methods of utilizing multi-SBAS corrections in multi-GNSS positioning. Sensors 2020, 20, 256. [Google Scholar] [CrossRef] [Green Version]
- Krasuski, K.; Wierzbicki, D.; Bakuła, M. Improvement of UAV Positioning Performance Based on EGNOS+SDCM Solution. Remote Sens. 2021, 13, 2597. [Google Scholar] [CrossRef]
- Weng, D.; Chen, W. SBAS enhancement using an independent monitor station in a local area. GPS Solut. 2019, 23, 12. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, Z.; Liu, Z.; Tang, X.; Ou, G. SBAS performance improvement with a new under sampled ionosphere threat model based on relative coverage metric. J. Atmos. Sol.-Terr. Phys. 2020, 198, 105178. [Google Scholar] [CrossRef]
- Romero, I. RINEX The Receiver Independent Exchange Format Version 3.05. ESA/ESOC/Navigation Support Office. 2020. Available online: https://files.igs.org/pub/data/format/rinex305.pdf (accessed on 1 May 2022).
- Kaplan, E. Understanding GPS/GNSS: Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Takasu, T. RTKLIB ver. 2.4.2 Manual, RTKLIB: An Open Source Program, Package for GNSS Positioning. 2013. Available online: http://www.rtklib.com/prog/manual_2.4.2.pdf (accessed on 10 February 2022).
- Minkler, G.; Minkler, J. Theory and Applications of Kalman Filtering; Magellan Book Company: Bamberg, Germany, 1993. [Google Scholar]
- Brown, R.G.; Hwang, P.Y. Introduction to Random Signals and Applied Kalman Filtering: With MATLAB Exercises and Solutions; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Kayton, M.; Fried, W.R. Avionics Navigation Systems; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Baran, L.W. Teoretyczne Podstawy Opracowania Wyników Pomiarów Geodezyjnych; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1999. [Google Scholar]
- Wiśniewski, Z. Rachunek Wyrównawczy w Geodezji (Z Przykładami); Wydawnictwo UWM: Olsztyn, Poland, 2005. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps. Navig. J. Inst. Navig. 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, C.; Odolinski, R.; Liu, T. Functional model modification of precise point positioning considering the time-varying code biases of a receiver. Satell. Navig. 2021, 2, 11. [Google Scholar] [CrossRef]


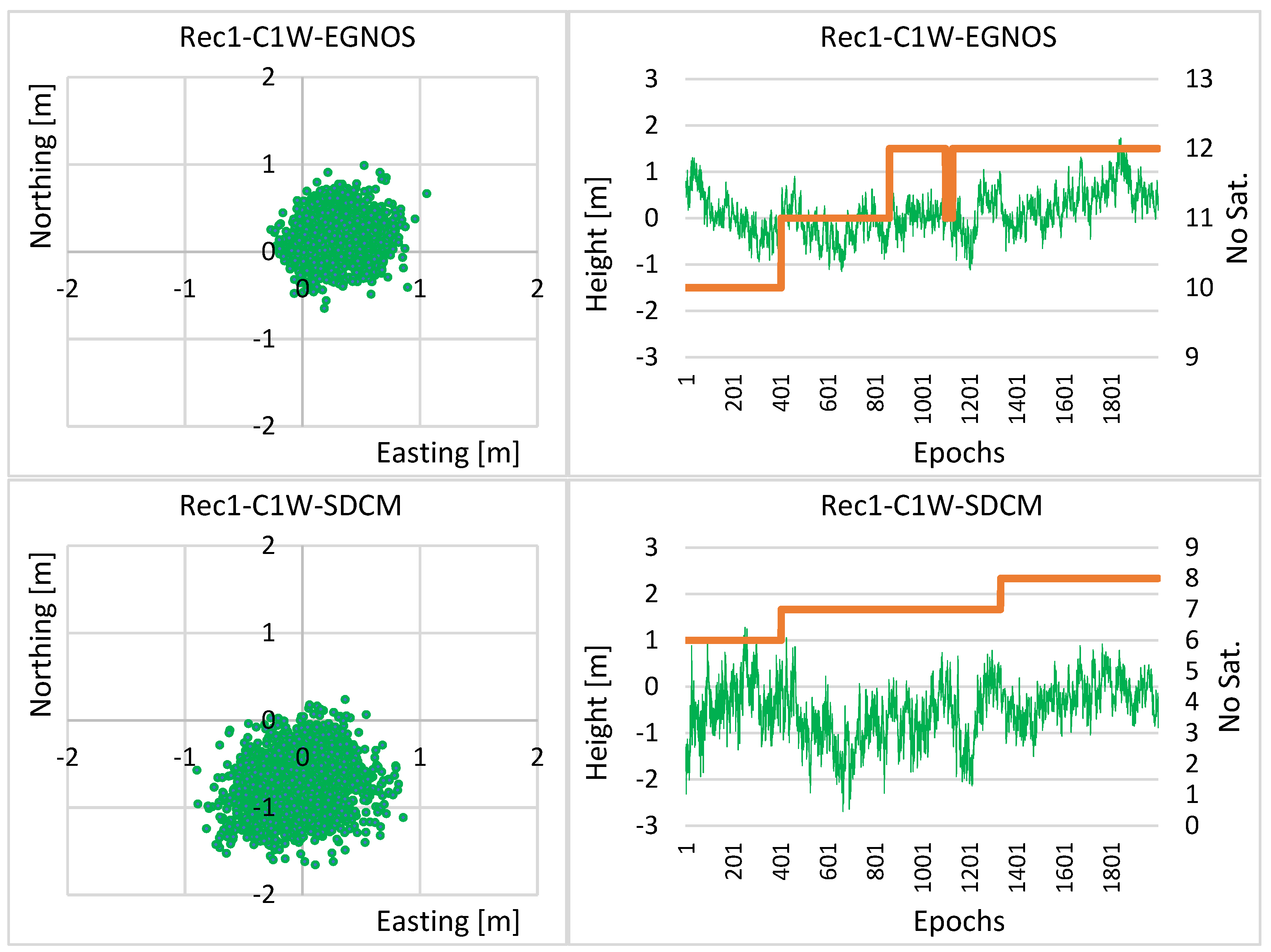
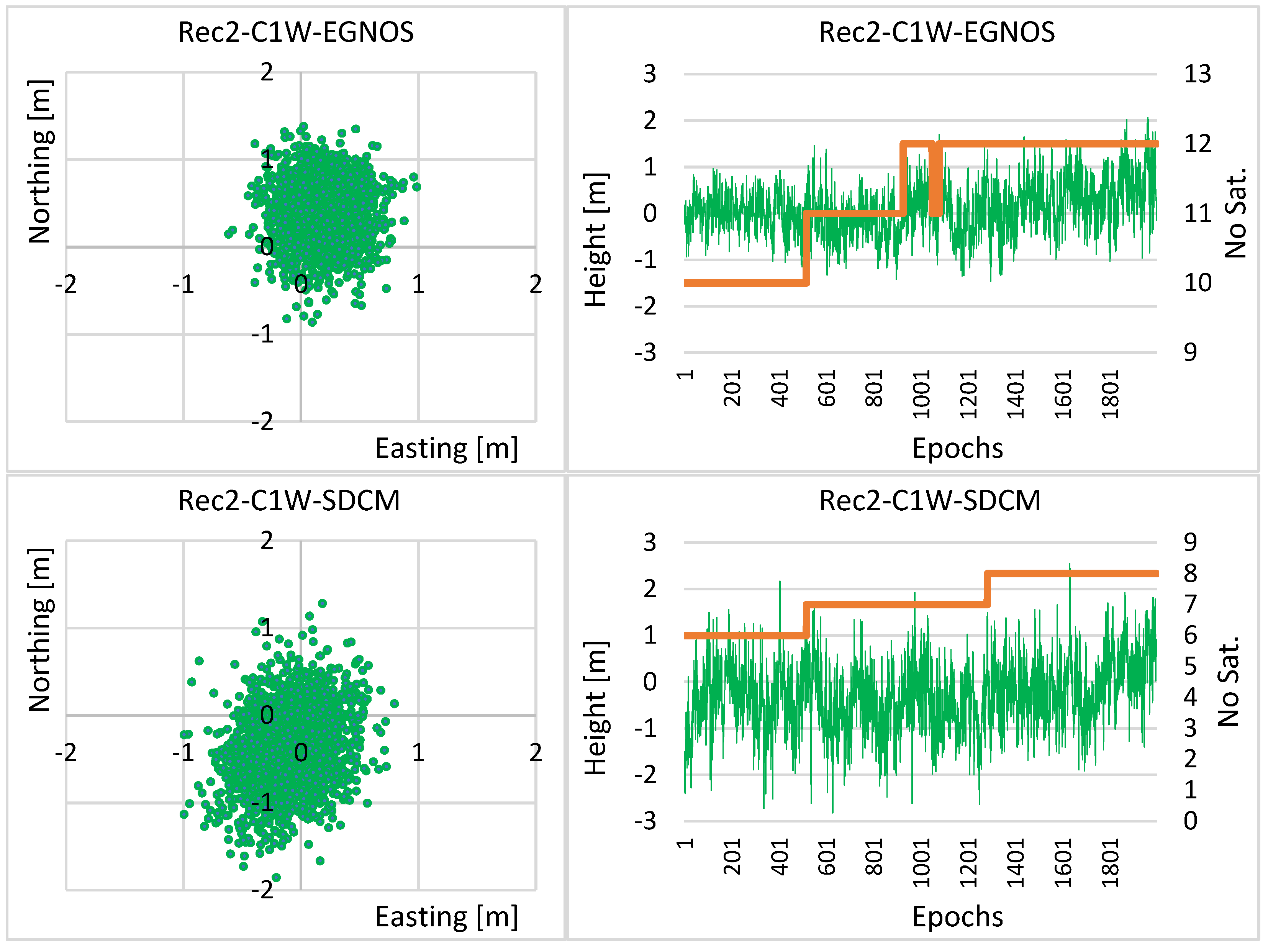
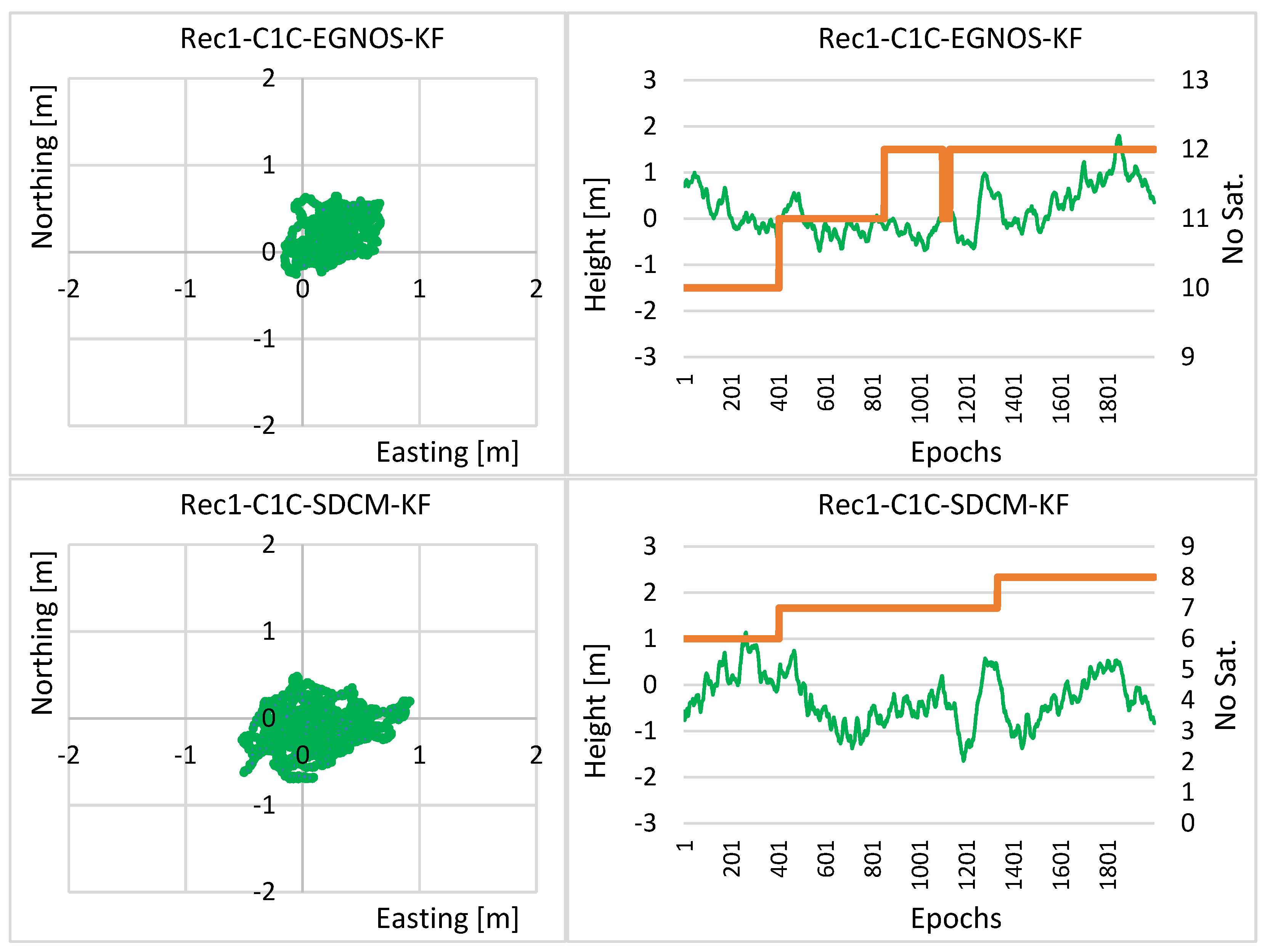

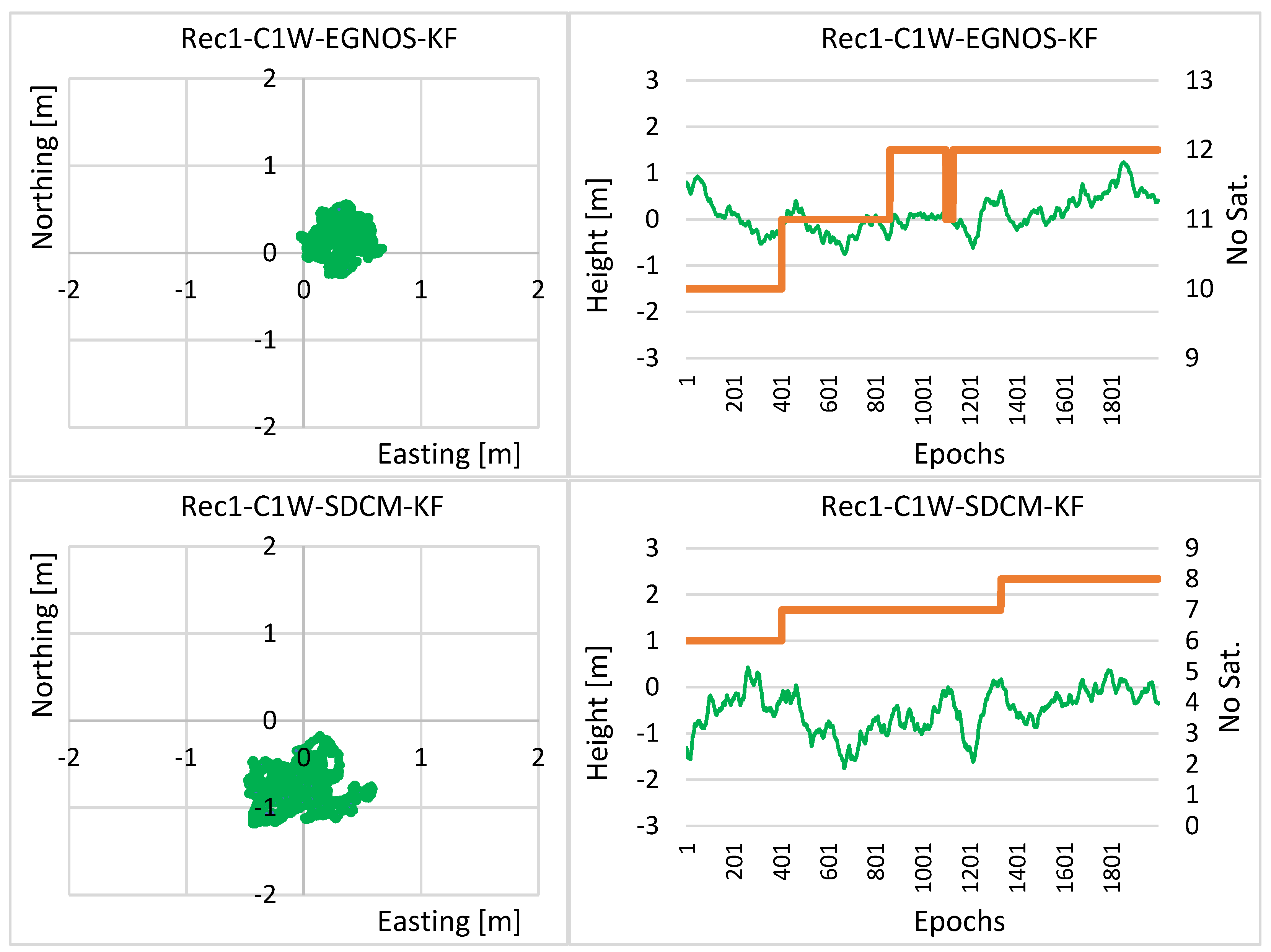
| LS | LS | LS | |
|---|---|---|---|
(m) | (m) | (m) | |
| R1-C1C-EGNOS | 0.28 | 0.30 | 0.65 |
| R1-C1C-SDCM | 0.41 | 0.38 | 0.79 |
| R2-C1C-EGNOS | 0.33 | 0.54 | 0.62 |
| R2-C1C-SDCM | 0.38 | 0.45 | 0.82 |
| R1-C1W-EGNOS | 0.21 | 0.23 | 0.48 |
| R1-C1W-SDCM | 0.29 | 0.31 | 0.62 |
| R2-C1W-EGNOS | 0.22 | 0.34 | 0.55 |
| R2-C1W-SDCM | 0.27 | 0.42 | 0.77 |
| LS+KF | LS+KF | LS+KF | ||||
|---|---|---|---|---|---|---|
(m) | dRMS (%) | (m) | dRMS (%) | (m) | dRMS (%) | |
| R1-C1C-EGNOS | 0.16 | 42 | 0.18 | 40 | 0.50 | 23 |
| R1-C1C-SDCM | 0.29 | 29 | 0.21 | 45 | 0.55 | 30 |
| R2-C1C-EGNOS | 0.18 | 45 | 0.20 | 63 | 0.17 | 72 |
| R2-C1C-SDCM | 0.18 | 52 | 0.15 | 67 | 0.32 | 61 |
| R1-C1W-EGNOS | 0.16 | 23 | 0.16 | 30 | 0.39 | 19 |
| R1-C1W-SDCM | 0.23 | 21 | 0.21 | 32 | 0.46 | 26 |
| R2-C1W-EGNOS | 0.11 | 50 | 0.19 | 44 | 0.28 | 49 |
| R2-C1W-SDCM | 0.14 | 48 | 0.18 | 57 | 0.39 | 49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakuła, M.; Krasuski, K.; Dawidowicz, K. Dual Receiver EGNOS+SDCM Positioning with C1C and C1W Pseudo-Range Measurements. Remote Sens. 2022, 14, 3152. https://doi.org/10.3390/rs14133152
Bakuła M, Krasuski K, Dawidowicz K. Dual Receiver EGNOS+SDCM Positioning with C1C and C1W Pseudo-Range Measurements. Remote Sensing. 2022; 14(13):3152. https://doi.org/10.3390/rs14133152
Chicago/Turabian StyleBakuła, Mieczysław, Kamil Krasuski, and Karol Dawidowicz. 2022. "Dual Receiver EGNOS+SDCM Positioning with C1C and C1W Pseudo-Range Measurements" Remote Sensing 14, no. 13: 3152. https://doi.org/10.3390/rs14133152
APA StyleBakuła, M., Krasuski, K., & Dawidowicz, K. (2022). Dual Receiver EGNOS+SDCM Positioning with C1C and C1W Pseudo-Range Measurements. Remote Sensing, 14(13), 3152. https://doi.org/10.3390/rs14133152