A Spherical “Earth–Ionosphere” Model for Deep Resource Exploration Using Artificial ELF-EM Field
Abstract
:1. Introduction
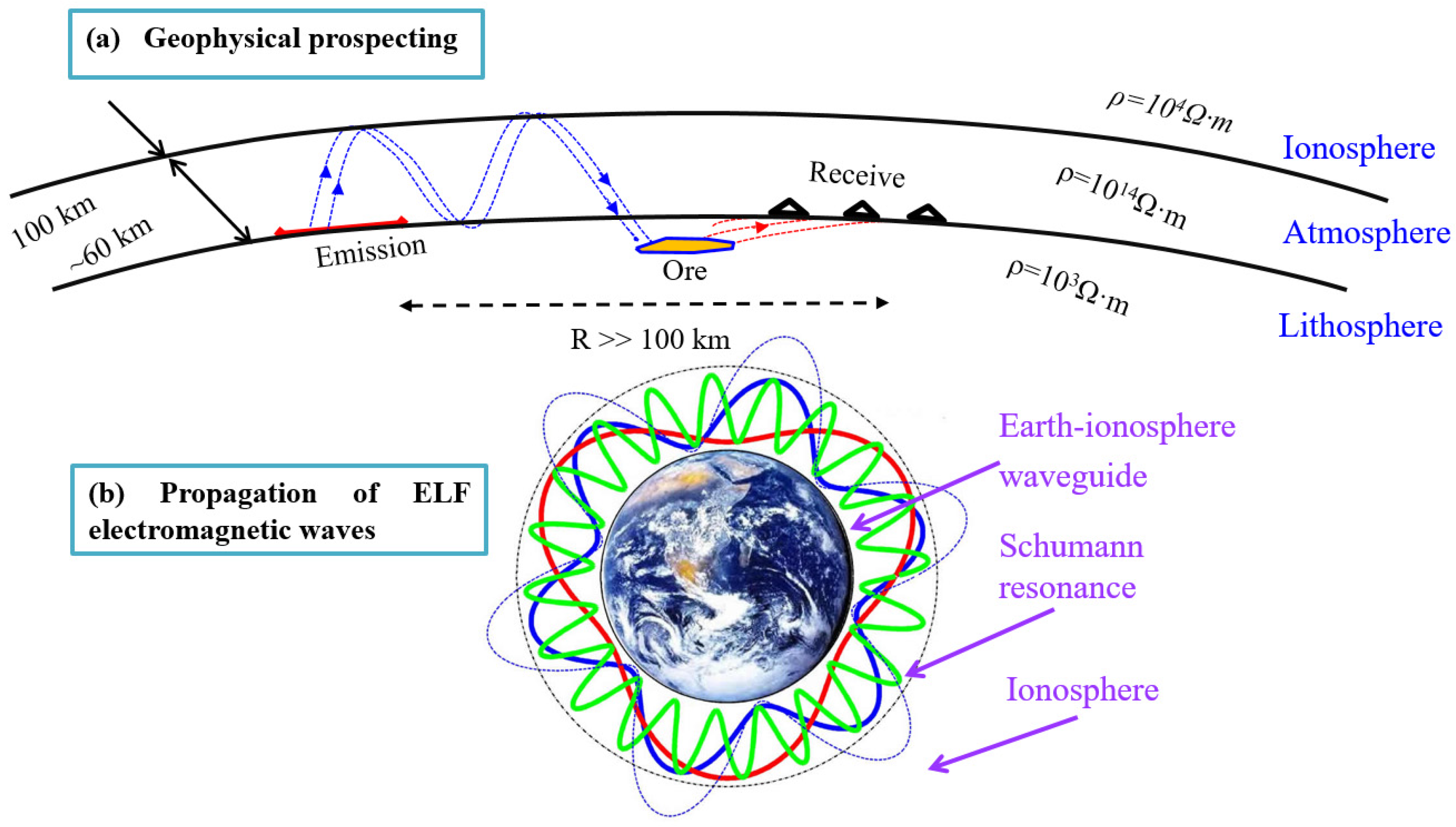
2. Description of the Method
2.1. Spherical Earth–Ionosphere Model
2.2. Debye Potentials
2.3. Determination of Coefficients
3. Convergence of Spherical Harmonic Series
4. Verification
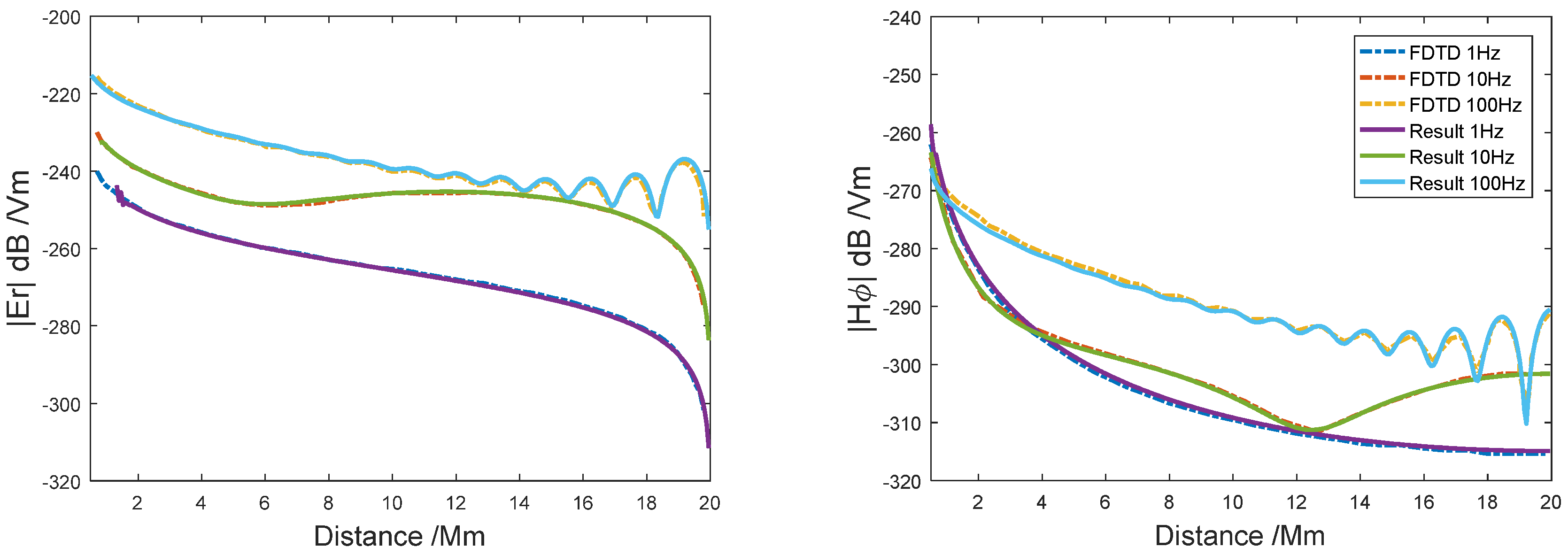
4.1. Comparison with FDTD
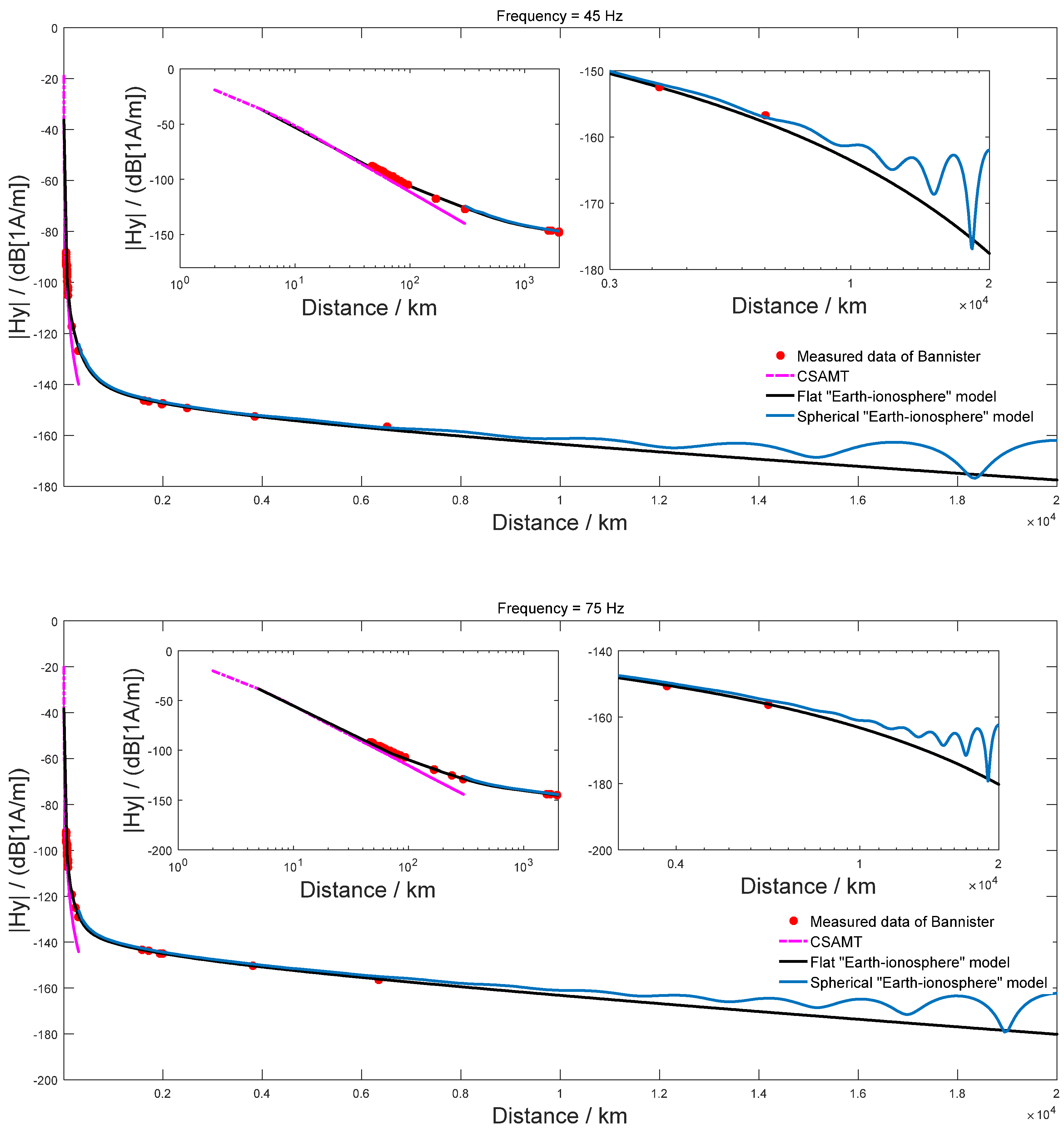
4.2. Comparison of CSAMT and WEM Methods
5. Numerical Simulations
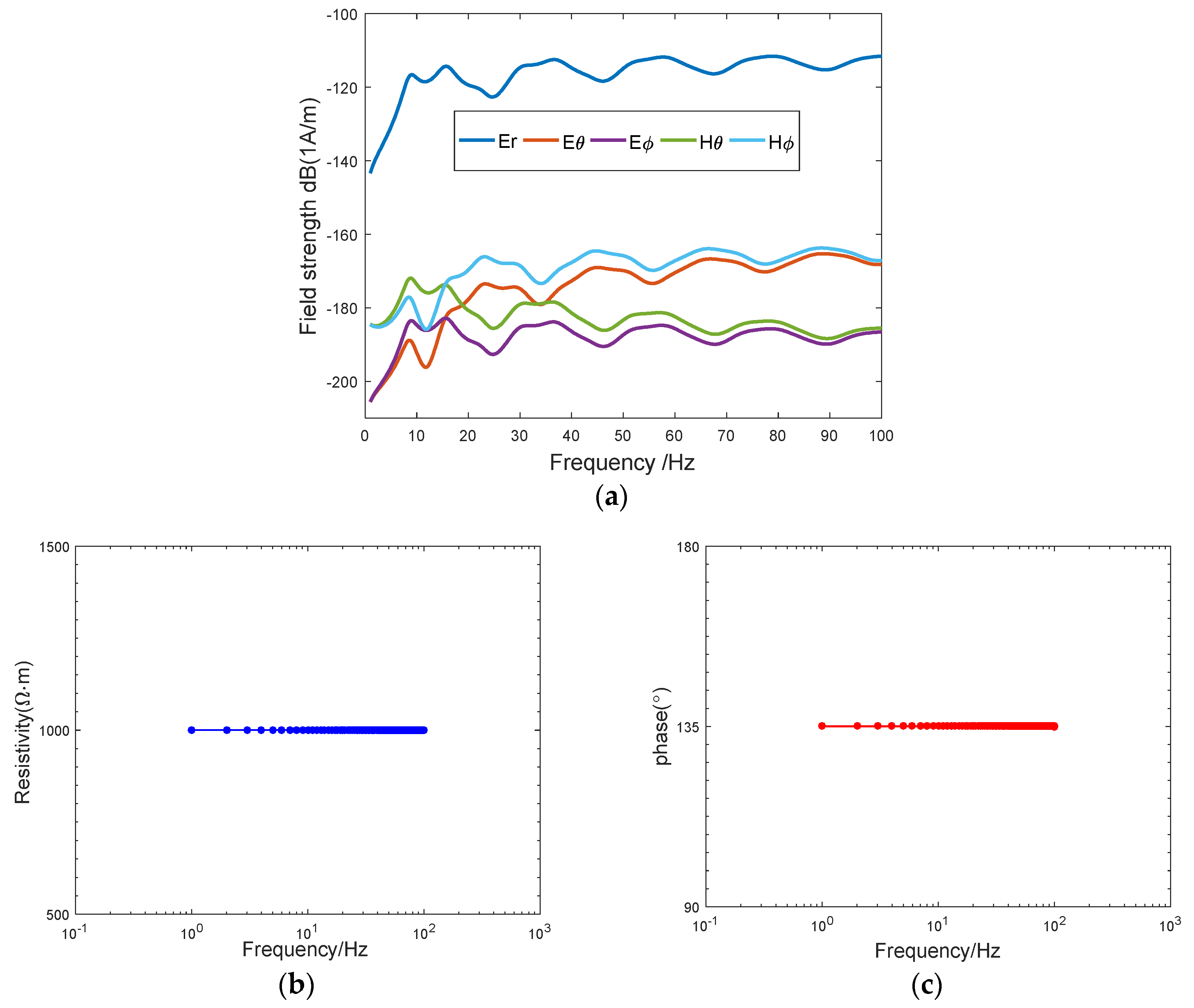
5.1. Response of a Homogeneous Earth
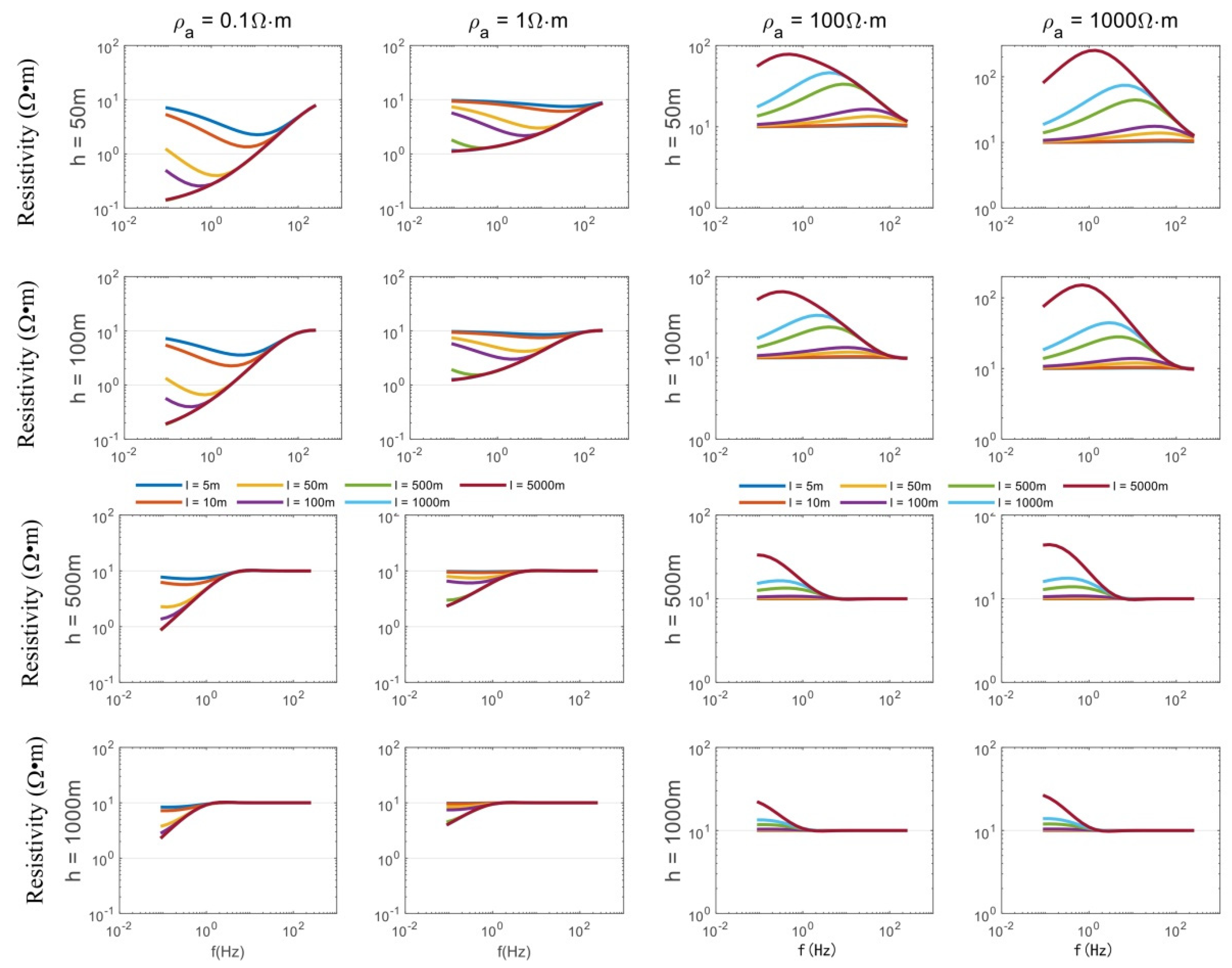
5.2. Sensitivity to a Thin Resistive Target
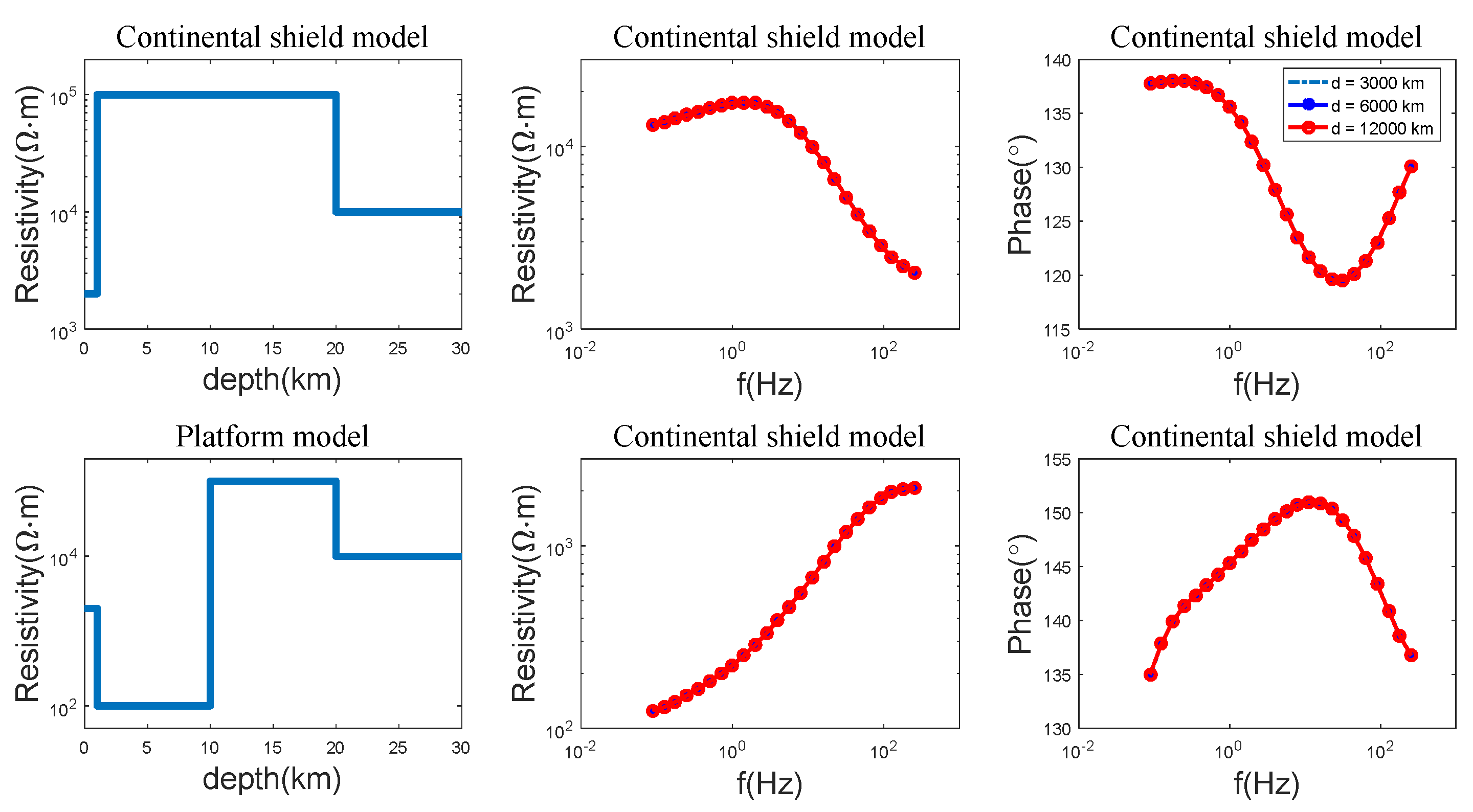
5.3. Forward Modeling of the Stratified Ground
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Zhdanov, M.S. Geophysical Electromagnetic Theory and Methods; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Holzer, R.; Deal, O. Low audio-frequency electromagnetic signals of natural origin. Nature 1956, 177, 536–537. [Google Scholar] [CrossRef]
- Lanzerotti, L.; Chave, A.; Sayres, C.; Medford, L.; Maclennan, C. Large-scale electric field measurements on the Earth’s surface: A review. J. Geophys. Res. Planets 1993, 98, 23525–23534. [Google Scholar] [CrossRef]
- Dong, H.; Wei, W.; Jin, S.; Ye, G.; Jones, A.G.; Zhang, L.; Jing, J.e.; Xie, C.; Yin, Y. Shaping the Surface Deformation of Central and South Tibetan Plateau: Insights from Magnetotelluric Array Data. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019206. [Google Scholar] [CrossRef]
- Yu, N.; Unsworth, M.; Wang, X.; Li, D.; Wang, E.; Li, R.; Hu, Y.; Cai, X. New Insights into Crustal and Mantle Flow Beneath the Red River Fault Zone and Adjacent Areas on the Southern Margin of the Tibetan Plateau Revealed by a 3-D Magnetotelluric Study. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019396. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; Bannister, P.R. Reception of ELF signals at antipodal distances. Radio Sci. 1998, 33, 83–88. [Google Scholar] [CrossRef] [Green Version]
- Velikhov, E.; Zhamaletdinov, A.; Shevtsov, A.; Tokarev, A.; Kononov, Y.M.; Pesin, L.; Kadyshevich, G.; Pertel, M.; Veshchev, A. Deep electromagnetic studies with the use of powerful ELF radio installations. Izv. Phys. Solid Earth C/C Fiz. Zemli-Ross. Akad. Nauk. 1998, 34, 615–632. [Google Scholar]
- Zhamaletdinov, A.; Shevtsov, A.; Korotkova, T.; Kopytenko, Y.A.; Ismagilov, V.; Petrishev, M.; Efimov, B.; Barannik, M.; Kolobov, V.; Prokopchuk, P. Deep electromagnetic sounding of the lithosphere in the Eastern Baltic (Fennoscandian) shield with high-power controlled sources and industrial power transmission lines (FENICS experiment). Izv. Phys. Solid Earth 2011, 47, 2–22. [Google Scholar] [CrossRef]
- Bernstein, S.L.; Burrows, M.L.; Evans, J.E.; Griffiths, A.; McNeill, D.; Niessen, C.; Richer, I.; White, D.; Willim, D. Long-range communications at extremely low frequencies. Proc. IEEE 1974, 62, 292–312. [Google Scholar] [CrossRef]
- Mosayebidorcheh, T.; Hosseinibalam, F.; Hassanzadeh, S. Analytical solution of electromagnetic radiation by a vertical electric dipole inside the earth and the effect of atmospheric electrical conductivity inhomogeneity. Adv. Space Res. 2017, 60, 1949–1957. [Google Scholar] [CrossRef]
- Wait, J.R. Electromagnetic Waves in Stratified Media, 2nd ed.; Pergamon Press: New York, NY, USA, 1970; Volume 3. [Google Scholar]
- Galejs, J. Terrestrial Propagation of Long Electromagnetic Waves: International Series of Monographs in Electromagnetic Waves; Elsevier: Amsterdam, The Netherlands, 2013; Volume 16. [Google Scholar]
- Bannister, P.R.; Wolkoff, E.A.; Katan, J.R.; Williams, F. FarFarnal series of monographs in elecpagation measurements, 14 March to 9 April 1971. Radio Sci. 1973, 8, 623–631. [Google Scholar] [CrossRef]
- Casey, J.P. Extremely Low Frequency (ELF) Propagation Formulas for Dipole Sources Radiating in a Spherical Earth-Ionosphere Waveguide; Naval Undersea Warfare Center: Newport, RI, USA, 2002. [Google Scholar]
- Pan, W.; Li, K. Propagation of SLF/ELF Electromagnetic Waves; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lu, H.; Yang, J.; Li, Q.; Hao, S.; Guo, F.; Wu, J.; Chen, J.; Ma, G.; Xu, T. ELF/VLF communication experiment by modulated heating of ionospheric auroral electrojet at EISCAT. IEEE Trans. Antennas Propag. 2020, 69, 2267–2273. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model–An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Nemec, F.; Santolik, O.; Parrot, M. Decrease of intensity of ELF/VLF waves observed in the upper ionosphere close to earthquakes: A statistical study. J. Geophys. Res. Atmos. 2009, 114, A04303. [Google Scholar] [CrossRef]
- Asada, T.; Baba, H.; Kawazoe, M.; Sugiura, M. An attempt to delineate very low frequency electromagnetic signals associated with earthquakes. Earth Planets Space 2001, 53, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Zhamaletdinov, A.; Velikhov, E.; Shevtsov, A.; Kolobov, V.; Skorokhodov, A.; Ivonin, V.; Barannik, M.; Korotkova, T. Deep Electrical Conductivity of the Archaean Blocks of Kola Peninsula in the Light of the Results of Murman-2018 Experiment: A Review. Izv. Phys. Solid Earth 2021, 57, 61–83. [Google Scholar] [CrossRef]
- Di, Q.; Xue, G.; Fu, C.; Wang, R. An alternative tool to controlled-source audio-frequency magnetotellurics method for prospecting deeply buried ore deposits. Sci. Bull. 2020, 65, 611–615. [Google Scholar] [CrossRef] [Green Version]
- Qu, X.; Xue, B.; Fang, G. The propagation model and characteristics for extremely low frequency electromagnetic wave in Earth-ionosphere system and its application in geophysics prospecting. J. Electromagn. Waves Appl. 2018, 32, 319–331. [Google Scholar] [CrossRef]
- Cao, M.; Tan, H.; Wang, K. 3D LBFGS inversion of controlled source extremely low frequency electromagnetic data. Appl. Geophys. 2016, 13, 689–700. [Google Scholar] [CrossRef]
- Li, D.; Di, Q.; Wang, M.; Nobes, D. ‘Earth–ionosphere’mode controlled source electromagnetic method. Geophys. J. Int. 2015, 202, 1848–1858. [Google Scholar] [CrossRef]
- Chandrasekhar, E. Regional electromagnetic induction studies using long period geomagnetic variations. In The Earth’s Magnetic Interior; Springer: Berlin/Heidelberg, Germany, 2011; pp. 31–42. [Google Scholar]
- Barrick, D.E. Exact ULF/ELF dipole field strengths in the Earth-ionosphere cavity over the Schumann resonance region: Idealized boundaries. Radio Sci. 1999, 34, 209–227. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, R.; Geng, J.; Liang, X. Exact SLF/ELF underground HED field strengths in earth-ionosphere cavity and Schumann resonance. IEEE Trans. Antennas Propag. 2011, 59, 3031–3039. [Google Scholar] [CrossRef]
- Cummer, S.A. Modeling electromagnetic propagation in the Earth-ionosphere waveguide. IEEE Trans. Antennas Propag. 2000, 48, 1420–1429. [Google Scholar] [CrossRef] [Green Version]
- Simpson, J.J. Current and future applications of 3-D global earth-ionosphere models based on the full-vector Maxwell’s equations FDTD method. Surv. Geophys. 2009, 30, 105–130. [Google Scholar] [CrossRef]
- Di, Q.; Fu, C.; Xue, G.; Wang, M.; An, Z.; Wang, R.; Wang, Z.; Lei, D.; Zhuo, X. Insight into skywave theory and breakthrough applications in resource exploration. Natl. Sci. Rev. 2021, 8, nwab046. [Google Scholar] [CrossRef]
- Fu, C.; Di, Q.; Xu, C.; Wang, M. Electromagnetic fields for different type sources with effect of the ionosphere. Chin. J. Geophys. 2012, 55, 3958–3968. [Google Scholar]
- Di, Q.; Wang, M.; Fu, C.; Li, D.; XU, C.; Zhuo, X. Study on the Propagation Characteristics of Electromagnetic Waves in the “Earth-Ionosphere” Mode; Science Press: Beijing, China, 2013. [Google Scholar]
- Li, D.; Xie, W.; Di, Q.; Wang, M. Forward modeling for “earth-ionosphere” mode electromagnetic field. J. Cent. South Univ. 2016, 23, 2305–2313. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, X. Electromagnetic fields excited by the horizontal electrical dipole on the surface of the ionosphere-homogeneous earth model. Chin. J. Geophys. 2010, 53, 2497–2506. [Google Scholar]
- Zhang, L. Research on Response of Full-Field Wiress Electromagnetic Method and 3D Intergral Equation Forward Modeling; Chinese Academy of Sciences: Beijing, China, 2021. [Google Scholar]
- Chave, A.D.; Cox, C.S. Controlled electromagnetic sources for measuring electrical conductivity beneath the oceans: 1. Forward problem and model study. J. Geophys. Res. Solid Earth 1982, 87, 5327–5338. [Google Scholar] [CrossRef]
- Xu, J.; Nie, Z. Scattering response of electromagnetic waves by multilayered spheres. Chin. J. Geophys. 1998, 865–876. [Google Scholar]
- Zheng, F.; Di, Q. Propagation of ELF electromagnetic waves over a curved stratified ground and its application in geophysical prospecting. IEEE Access 2021, 9, 145563–145572. [Google Scholar] [CrossRef]
- Ladutenko, K.; Pal, U.; Rivera, A.; Peña-Rodríguez, O. Mie calculation of electromagnetic near-field for a multilayered sphere. Comput. Phys. Commun. 2017, 214, 225–230. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, R.; Geng, J. Fast Convergence Algorithm for Earthquake Prediction Using SLF/ELF Horizontal Electric Dipole during Day and Night and Schumann Resonance. Wirel. Pers. Commun. 2012, 67, 149–163. [Google Scholar] [CrossRef]
- Li, R.; Jiang, H.; Ren, K.F. Debye series for light scattering by a multilayered sphere. Appl. Opt. 2006, 45, 1260–1270. [Google Scholar] [CrossRef] [PubMed]
- Kinayman, N.; Aksun, M. Comparative study of acceleration techniques for integrals and series in electromagnetic problems. Radio Sci. 1995, 30, 1713–1722. [Google Scholar] [CrossRef] [Green Version]
- Zheng, F.; Di, Q.; Yun, Z.; Gao, Y. Convergence Acceleration of Infinite Series Involving the Product of Riccati–Bessel Function and Its Application for the Electromagnetic Field: Using the Continued Fraction Expansion Method. Appl. Comput. Electromagn. Soc. J. 2021, 36, 1518–1525. [Google Scholar]
- Dong, H.; Yan, Y.; Li, Q. FDTD Simulation of SLF\ELF Fields Excited by Horizontal Electric Dipoles in Inhomogeneous Earth-Ionospheric Waveguides. Chin. J. Radio Sci. 2010, 25, 276–280. [Google Scholar] [CrossRef]
- Zheng, F.; Di, Q.; Gao, Y.; Fu, C. Frequency response characteristics of WEM in seafloor. Chin. J. Geophys. 2021, 64, 2170–2183. [Google Scholar]
- Unsworth, M. New developments in conventional hydrocarbon exploration with electromagnetic methods. CSEG Rec. 2005, 30, 34–38. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, F.; Di, Q.; Fu, C. A Spherical “Earth–Ionosphere” Model for Deep Resource Exploration Using Artificial ELF-EM Field. Remote Sens. 2022, 14, 3088. https://doi.org/10.3390/rs14133088
Zheng F, Di Q, Fu C. A Spherical “Earth–Ionosphere” Model for Deep Resource Exploration Using Artificial ELF-EM Field. Remote Sensing. 2022; 14(13):3088. https://doi.org/10.3390/rs14133088
Chicago/Turabian StyleZheng, Fanghua, Qingyun Di, and Changmin Fu. 2022. "A Spherical “Earth–Ionosphere” Model for Deep Resource Exploration Using Artificial ELF-EM Field" Remote Sensing 14, no. 13: 3088. https://doi.org/10.3390/rs14133088
APA StyleZheng, F., Di, Q., & Fu, C. (2022). A Spherical “Earth–Ionosphere” Model for Deep Resource Exploration Using Artificial ELF-EM Field. Remote Sensing, 14(13), 3088. https://doi.org/10.3390/rs14133088





