Performance of Multi-GNSS in the Asia-Pacific Region: Signal Quality, Broadcast Ephemeris and Precise Point Positioning (PPP)

Abstract

Since BeiDou Navigation Satellite System (BDS) and Japan’s Quasi-Zenith Satellite System (QZSS) have more visible satellites in the Asia-Pacific region, and navigation satellites of Global Positioning System (GPS), Galileo satellite navigation system (Galileo), and GLONASS satellite navigation system (GLONASS) are uniformly distributed globally, the service level of multi-mode Global Navigation Satellite System (GNSS) in the Asia-Pacific region should represent the best service capability. Based on the observation data of 10 Multi-GNSS Experiment (MGEX) stations, broadcast ephemeris and precision ephemeris from 13 to 19 October 2021, this paper comprehensively evaluated the service capability of multi-GNSS in the Asia-Pacific region from three aspects of observation data quality, broadcast ephemeris performance, and precision positioning level. The results show that: (1) the carrier-to-noise-density ratio (C/N0) quality of the GPS and Galileo is the best, followed by BDS and GLONASS, and QZSS is the worst. GPS, BDS-2, GLONASS, and QZSS pseudorange multipath values range from 0 to 0.6 m, while Galileo system and BDS-3 pseudorange multipath values range from 0 to 0.8 m. (2) In terms of broadcast ephemeris accuracy, BDS-3 broadcast ephemeris has the best orbit, and the three-dimensional (3D) Root Mean Square (RMS) is 0.21 m; BDS-2 was the worst, with a 3D RMS of 1.99 m. The broadcast ephemeris orbits of GPS, Galileo, QZSS, and GLONASS have 3D RMS of 0.60 m, 0.62 m, 0.83 m, and 1.27 m, respectively. For broadcast ephemeris clock offset: Galileo has the best performance, 0.61 ns, GLONASS is the worst, standard deviation (STD) is 3.10 ns, GPS, QZSS, BDS-3 and BDS-2 are 0.65 ns, 0.75 ns, and 1.72 ns, respectively. For signal-in-space ranging errors (SISRE), the SISRE results of GPS and Galileo systems are the best, fluctuating in the range of 0 m–2 m, followed by QZSS, BDS-3, Galileo, and BDS-2. (3) GPS, BDS, GLONASS, Galileo, GPS/QZSS, and BDS/QZSS were used for positioning experiments. In static PPP, the convergence time and positioning accuracy of GPS show the best performance. The positioning accuracy of GPS/QZSS and BDS/QZSS is improved compared with that of GPS and BDS. In terms of kinematic PPP, the convergence time and positioning accuracy of GPS/QZSS and BDS/QZSS are improved compared with that of GPS and BDS. In addition to GLONASS and Galileo systems, the other combinations outperformed 3 cm, 3 cm, and 5 cm in the east, north, and up directions.

1. Introduction

The accurate positioning, navigation, and timing (PNT) services can be provided by the Global Navigation Satellite System (GNSS), and it has been widely used in many areas such as agriculture [1], weather monitoring [2], time and frequency transfer [3], and disaster monitoring [4]. As of the end of April 2022, there are about 120 GNSS satellites, including GPS, GLONASS, Galileo, BDS-2, BDS-3, and QZSS systems, which can provide PNT services to users around the world [5,6,7]. The available satellites, frequency, and PRN for each system are listed in

Table 1. Available satellites of each system at the end of April 2022.

System	Satellite Types	Signals	Number of Satellites	PRN
GPS	IIR	L1C/A, L1/L2	1	G13 G20 G22 G16 G21 G19 G02 G17 G31 G12 G15 G25 G07
	IIF	L1C/A, L2C, L5	11	G01 G24 G27 G30 G06 G09 G03 G26 G08 G10 G32
	III	L1C/A, L2C, L5	5	G04 G11 G14 G18 G23
BDS-2	GEO	B1I, B2I, B3I	5	C01 C02 C03 C04 C05
	IGSO	B1I, B2I, B3I	7	C06 C07 C08 C09 C10 C13 C16
	MEO	B1I, B2I, B3I	3	C11 C12 C14
BDS-3	MEO	B1I, B3I, B1C, B2a, B2b	24	C19 C20 C21 C22 C23 C24 C25 C26 C27 C28 C29 C30 C32 C33 C34 C35 C36 C37 C41 C42 C43 C44 C45 C46
	IGSO	B1I, B3I, B1C, B2a, B2b	3	C38 C39 C40
GLONASS	GLONASS-M	G1C, G2C	20	R01 R02 R03 R04 R05 R06 R07 R08 R10 R12 R13 R14 R15 R16 R18 R19 R20 R22 R23 R24
	GLONASS-M+	G1C, G2C, L3	2	R17 R21
	GLONASS-K1	G1C, G2C, L3	2	R09 R11
Galileo	IOV	E1, E5a/b/ab	4	E11 E12 E19 E20
	FOC	E1, E5a/b/ab, E6	22	E01 E02 E03 E04 E05 E07 E08 E09 E10 E13 E14 E15 E18 E22 E24 E26 E27 E30 E31 E33 E34 E36
QZSS	GEO	L1C/A, L1C, L2C, L5	1	J07
	QZO	L1C/A, L1C, L2C, L5	3	J01 J02 J03

. For GNSS, the observation data quality on the receiver side directly determines the result of precise data processing at the GNSS server and user end. The positioning performance at the GNSS user side plays a key role in the quality of GNSS service, and the broadcast ephemeris directly affects the performance of real-time navigation and positioning. The stations located in the Asia-Pacific region can receive the signals broadcasted by five navigation satellite systems at the same time. Therefore, it is worthy to investigate and evaluate the performance of GNSS observation data quality, broadcast ephemeris, and positioning performance in the Asia-Pacific region.

For the observation data quality of GNSS: the BDS-3 satellites signals were evaluated by Zhang et al.; the B1I/B2I/B3I signals of the BDS-2 satellites, L1/L2/L5 of the GPS Block IIF satellites, and E1/E5a/E5b of the Galileo satellites are also evaluated for comparison in their study [8]. The observation data quality of the BDS-3 signal was studied and analyzed by Yang et al. [9]. The signal quality of BDS-2 and BDS-3 satellites was evaluated by Yan et al. [10]. The observation data quality and positioning performance of BDS/QZSS satellites were studied by Bu et al. [11]. The data quality of BDS/GPS/GLONASS satellites was investigated by Zuo et al. [12]. The signal quality of Galileo/BDS/GPS satellites was evaluated by Tian et al. [13]. It can be seen that previous studies about signal quality mainly focus on single and dual systems; the investigation and comparison of observation data quality among five GNSS systems in Asia-Pacific regions are limited and still needs further study.

In the context of GNSS broadcast ephemeris accuracy assessment, the GPS/GLONASS/BDS/Galileo/QZSS broadcast ephemeris was evaluated by Montenbruck et al. [14], but the BDS-3 satellite constellation had not been built at that time. After the BDS-3 satellites were launched, their broadcast ephemeris orbit and clock offset accuracy were evaluated by many scholars [15,16], and the comparison of broadcast ephemeris orbit and clock offset accuracy between BDS-2 and BDS-3 was also conducted [17]. However, with the modernization of GNSS satellites, the performance of broadcast ephemeris orbit and clock offset accuracy of five GNSS systems satellites is still unknown and unrevealed, it is urgent to conduct a comprehensive evaluation and comparison of the broadcast ephemeris performance for five GNSS systems satellites.

In terms of multi-GNSS positioning, the contribution of QZSS to the single-frequency PPP of GPS/BDS/GLONASS/Galileo satellites was studied by Hong et al. [18]. The positioning performance of BDS/QZSS in the Asia-Pacific region was evaluated by Bu et al. [11]. The precise positioning performance of QZSS and GPS in the Asia-Pacific region was investigated by Li [19]. The positioning performance of BDS-2/BDS-3 in the Asia-Pacific region was analyzed by Cao et al. [20]. It can be seen that the previous studies about PPP in the Asia-Pacific region are mainly focused on single or dual systems, while the PPP performance of multi-GNSS in the Asia-Pacific region is still limited.

In this contribution, multi-GNSS (GPS/GLONASS/Galileo/BDS-2/BDS-3/QZSS) observation data quality, broadcast ephemeris orbit, and clock offset performance and PPP performance in the Asia-Pacific region are investigated in detail. Based on the observation data from 10 Asia-Pacific MGEX stations, multi-GNSS broadcast ephemeris and precise satellite orbit and clock offset products, the observation data quality, broadcast ephemeris orbit, clock offset performance, and PPP performance in the Asia-Pacific region are evaluated and compared from DOY 283 to 289, in 2021. This paper is organized as follows: after this introduction, the observation data quality of five GNSS systems from 10 stations located in the Asia-Pacific region are investigated and analyzed in terms of carrier-to-noise-density ratio(C/N0) and pseudorange multipath in Section 2. The accuracy of the broadcast ephemeris orbit and clock offset and signal-in-space ranging errors (SISRE) of the five systems is investigated, evaluated, and compared in Section 3. The static and kinematic PPP performance of five GNSS systems in the Asia-Pacific region is evaluated and compared from convergence time and positioning accuracy in Section 4. Finally, the conclusions are presented in Section 5.

2. Data Quality

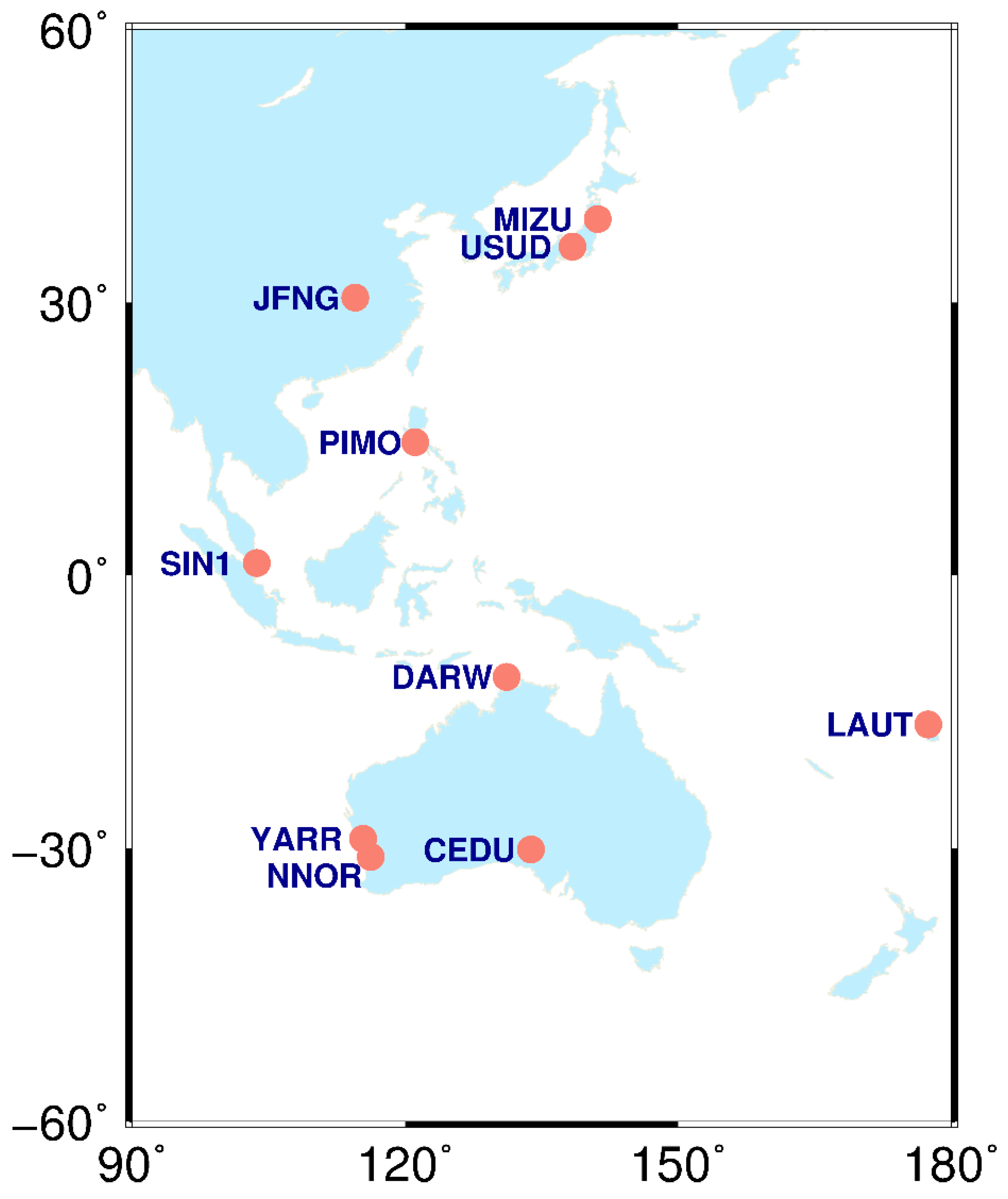
The observation data of 10 stations (CEDU, DARW, JFNG, MIZU, NNOR, PIMO, SIN1, USUD, YARR) from the MGEX network located in the Asia-Pacific region from day of year (DOY) 283 to 289 in 2021 are applied. The distribution of these stations is shown in Figure 1, and the latitude, longitude, receiver type, and antenna type of each station are listed in

Table 2. Receiver information.

	Longitude	Latitude	Receiver Type	Antenna Type
CEDU	133.81	−30.13	SEPT POLARX5	AOAD/M_T
DARW	131.13	−11.16	SEPT POLARX5	JAVRINGANT_DM
JFNG	114.49	30.52	TRIMBLE ALLOY	TRM59800.00
LAUT	177.45	−16.39	SEPT POLARX5	JAVRINGANT_DM
MIZU	141.13	39.14	SEPT POLARX5	SEPCHOKE_B3E6
NNOR	116.19	−30.95	SEPT POLARX5TR	SEPCHOKE_B3E6
PIMO	121.08	14.64	JAVAD TRE_G3TH DELTA4.1.01	ASH701945C_M
SIN1	103.68	1.34	TRIMBLE NETR9	LEIAR25.R3
USUD	138.36	36.13	SEPT POLARX5	AOAD/M_T
YARR	115.35	−28.95	SEPT POLARX5	LEIAT504
CEDU	133.81	−30.13	SEPT POLARX5	AOAD/M_T
DARW	131.13	−11.16	SEPT POLARX5	JAVRINGANT_DM

. These 10 stations are evenly distributed in different latitudes and longitudes around the Asia-Pacific region, and all frequencies of GPS, BDS-2, BDS-3, GLONASS, Galileo, and QZSS satellites can be received by these stations, which can better reflect the observation data quality and positioning performance of multi-GNSS in the Asia-Pacific region. The observation data quality was studied in the Asia-Pacific region in terms of two indicators: C/N0 and pseudorange multipath, in which the C/N0 can reflect the ability of the signal strength from satellite to receiver, whereas the impact of the satellite signal due to ground interference on the receiver can be reflected in pseudorange multipath. The C/N0 and pseudorange multipath are important indicators in the observation data quality assessment, and their performance directly affects the performance of PNT services.

2.1. Carrier-to-Noise-Density Ratio

The C/N0 is the ratio of the carrier signal to noise, which can reflect the signal strength of GNSS observations on the receiver side. The larger the C/N0, the smaller the noise and the better the signal quality, and vice versa. The C/N0 of every satellite at each epoch can be directly obtained from the observation files. In this study, the relationship between the C/N0 and the elevation of the GNSS satellite signal is investigated and analyzed. When obtaining the C/N0, the sampling interval of the observation data is set as 30 s and the elevation mask is set to 0°. All C/N0 values within 5 degrees of elevation angle are grouped into one group, and then the average of C/N0 within each group of elevation angle is calculated [21].

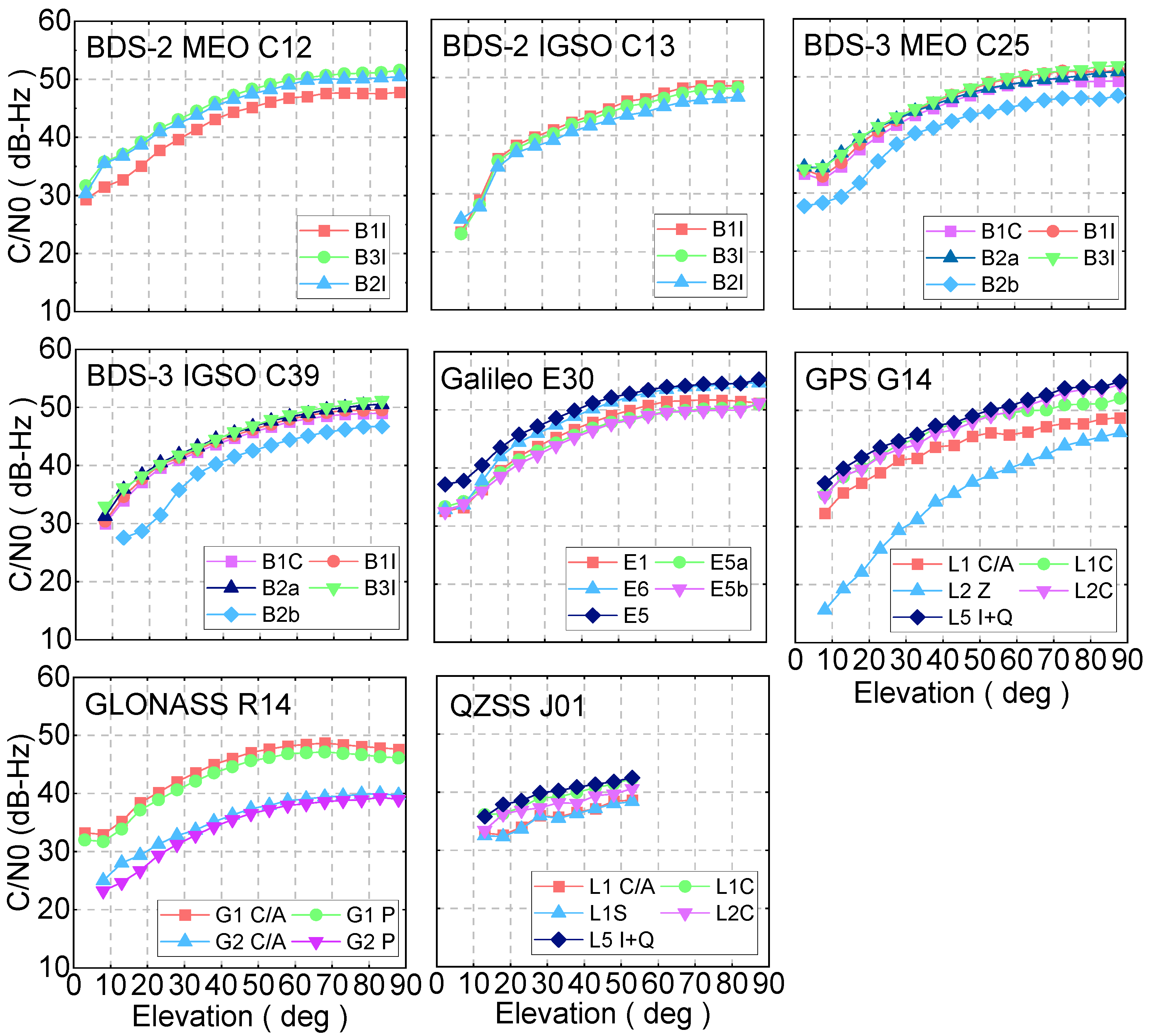
The average C/N0 corresponding to elevation for BDS-2 MEO, BDS-2 IGSO, BDS-3 MEO, BDS-3 IGSO, Galileo, GPS, GLONASS, and QZSS satellite is calculated, and one typical satellite of each system was shown in Figure 2, respectively. For the BDS-2 MEO satellite, the C/N0 of the B1I signal for the C12 satellite is slightly worse than that of B3I and B2I; although the signal strength is different, the C/N0 variation of these three frequencies shows the same variation trend. The C/N0 of B1I, B3I, and B2I signals have comparable performance for all elevation angles in terms of BDS-2 IGSO satellites. If these three signals can be selected for users, the difference in C/N0 does not need to be considered. In terms of the BDS-3 satellites, the C/N0 of the B2b signal is worse than that of B1C, B1I, B2a, and B3I whether for the IGSO or MEO satellites. It can be clearly seen that the C/N0 of BDS-3 satellites is better than that of BDS-2, which may be that the Binary Offset carrier (BOC) and Quadrature Multiplexed Composite Binary Offset Carrier (QMBOC) signal design is applied to BDS-3 satellites. For MEO satellites, the C/N0 of BDS-3 is higher than that of BDS-2 with 1–2 dB-Hz; while these values are 2–3 dB-Hz for IGSO satellites. The C/N0 of the Galileo E5 signal shows the best performance among the five Galileo frequency bands. The C/N0 of the L2 Z-tracking signal channel for GPS satellites is poorer than that of other frequencies. Moreover, the C/N0 for the L1 C/A signal is slightly poorer than that of L1C, L2C, and L5 I + Q. The C/N0 of GLONASS G1 frequency is better than that of G2, which can be attributed to the lower frequency value of the G2 signal. The C/N0 values for five QZSS frequencies present a similar performance at the different elevation angles. In terms of the five systems: the GPS and Galileo satellites show the best performance, and the C/N0 value can reach 55 dB-Hz when the elevation is nearly 90 degrees, both the BDS and GLONASS are poorer than that of GPS and Galileo, and the QZSS presents the worst performance among five GNSS systems.

2.2. Pseudorange Multipath

The combination of the pseudorange and carrier phase observation is used to calculate pseudorange multipath, which can eliminate the effect of tropospheric and ionospheric delays [22], and it can be expressed as follows:

$$M{P}_k=P_k-L_i-\beta \left(L_i-L_j\right)=P_k+\alpha L_i+\beta L_j+\epsilon \cdot \alpha$$

(1)

$$\alpha =f_1^2/f_2^2$$

(2)

$$\beta =-\frac{\left(f_j^2+f_k^2\right)f_j^2}{\left(f_i^2+f_j^2\right)f_k^2}$$

(3)

where $k$, $i$, $j$ are frequency, $M{P}_k$ denotes the pseudorange multipath; $P_k$ represents the pseudorange observation; $L_i$ and $L_j$ are the carrier phase observation on frequency $i$ and $j$, respectively. $f_i$ and $f_j$ are frequencies; $\epsilon$ is the noise.

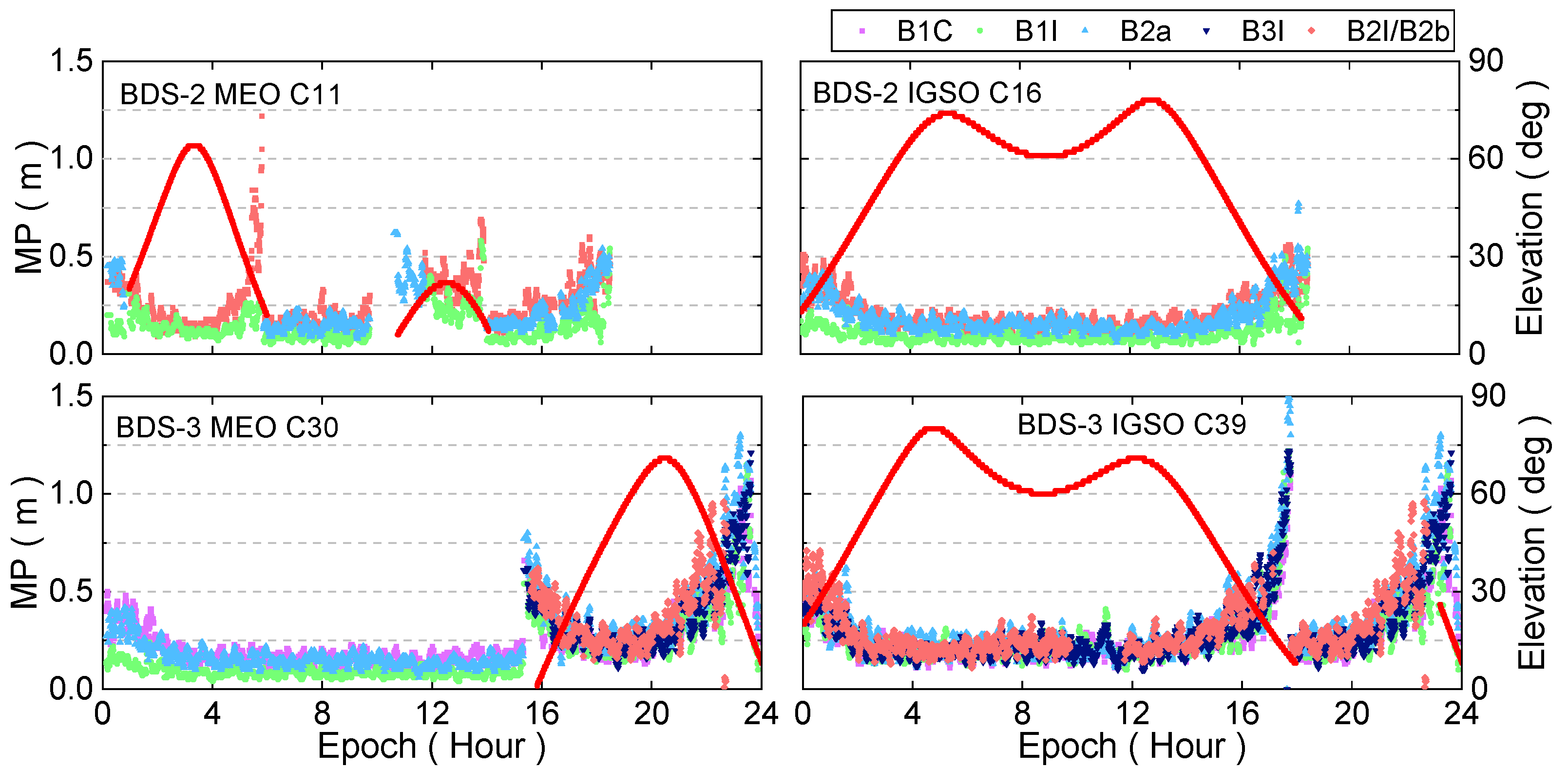
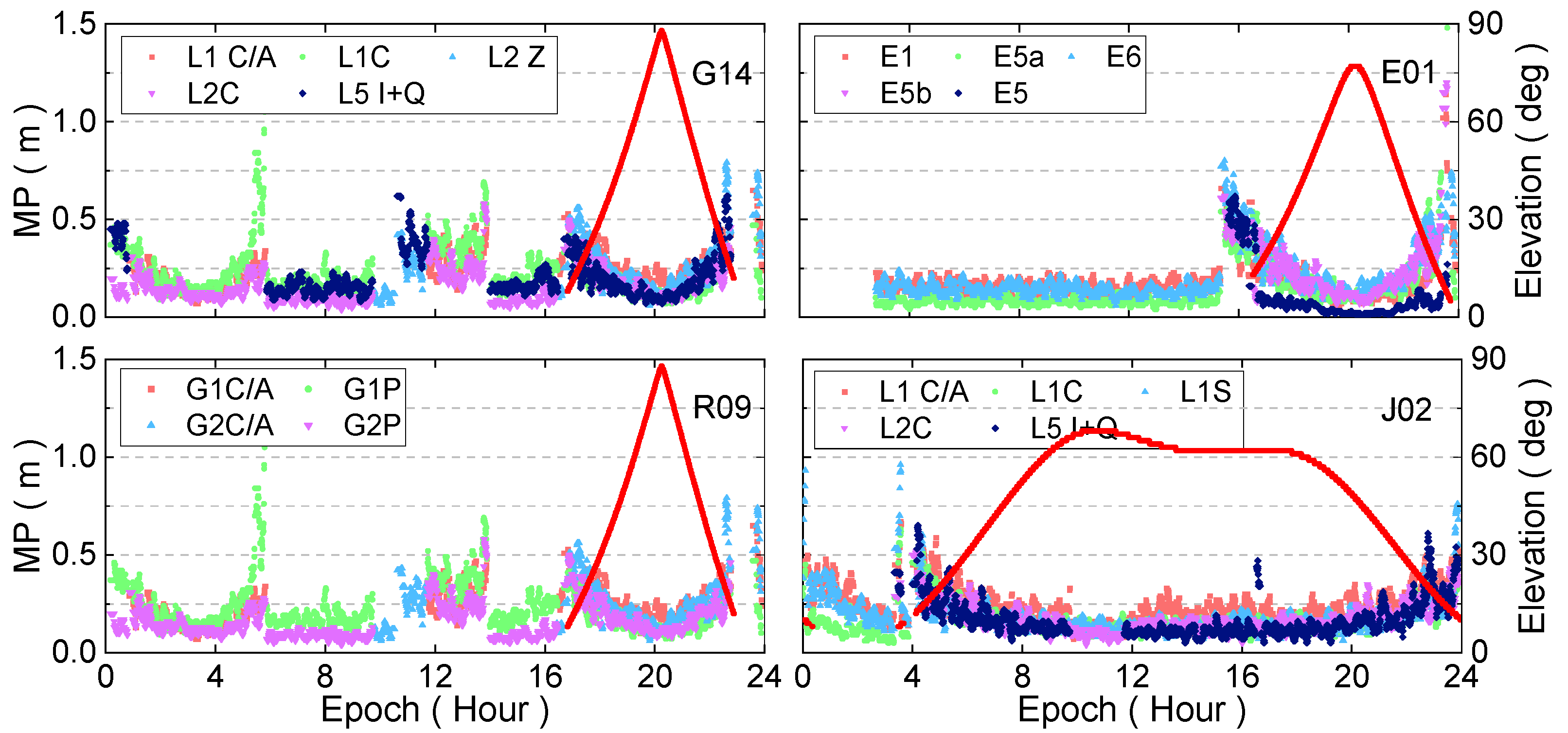
The characteristics of pesudorange multipath for GPS, GLONASS, BDS-2, BDS-3, Galileo, and QZSS satellites are investigated in this study using 10 stations from the Asia-Pacific region. The pesudorange multipath values versus elevation angle for the BDS-2 C11, C16, BDS-3 C30, and C39 on DOY 283 for the JFNG station was shown in Figure 3. It can be seen that there is an opposite relationship between pseudorange multipath and elevation angle, the larger the pseudorange multipath, the smaller the elevation angle, and vice versa. The pseudorange multipath is significantly large when the elevation is extremely small in some cases, which may be caused by the observation noise. For the BDS-2 satellites, the pseudorange multipath of the B3I signal is better than those of B1I and B2I. In terms of the BDS-3 satellites, the B1I frequency band of the MEO satellite presents the best performance, its pseudorange multipath is the smallest. Overall, the BDS-3 pseudorange multipath is around 0.28 m, while it is about 0.3 m for the BDS-2 satellites. The time series of pseudorange multipath with respect to elevation on the JFNG station for GPS, GLONASS, Galileo, and QZSS is shown in Figure 4. Similar to BDS-2 and BDS-3 satellites, the pseudorange multipath shows an opposite relationship with the elevation angle. Among them, the pseudorange multipath value of Galileo is the smallest, and it is around 0.2 m, the GPS and QZSS systems show comparable performance, and its value is around 0.3 m, while the value is about 0.4 m for GLONASS satellites. Since the pseudorange multipath effect is an important error source at the receiver side, it has a negative impact on GNSS precise data processing. In GNSS precise data processing, the following measures can be adopted to eliminate or weaken the effect of it: Firstly, reducing or eliminating the weight of observation with low elevation; secondly, modeling the pseudorange multipath errors.

3. Broadcast Ephemeris Performance

3.1. Broadcast Ephemeris Clock Offset Performance

The broadcast ephemeris clock offset accuracy of GPS, BDS-2, BDS-3, GLONASS, Galileo, and QZSS satellites from DOY 283 to 289 in 2021 are depicted in Figure 5, and the mean clock offset accuracy is listed in

Table 3. Clock offset accuracy of each system (units: ns).

System	Clock Offset STD
GPS	0.65
BDS-2	1.72
BDS-3	1.04
GLONASS	3.10
Galileo	0.61
QZSS	0.75

. The clock offset accuracy assessment method is referred to Huang et al. [23]. For GPS, the clock offset accuracy of the G08 satellite is 2.57 ns, which shows the poorest performance among all GPS satellites since the cesium atomic clock was installed on it. Furthermore, except for the G03, G17, G28, and G29 satellite clock, the clock offset accuracy of other satellites is better than 1 ns. The mean accuracy is 0.65 ns. The broadcast ephemeris clock offset accuracy is 0.98 ns, 1.72 ns, and 2.11 ns for BDS-2 GEO, IGSO, and MEO satellites, respectively. The clock offset accuracy of GEO satellites outperforms that of IGSO and MEO satellites, the reason is that the stations applied to estimate broadcast ephemeris clock offset are mainly located in China. Compared to the IGSO and MEO satellites, the observation arc of GEO satellites is longer, and the data used for predicting clock offset are more, resulting in the clock offset accuracy being higher, whereas the observation data of MEO satellites are few, leading to inferior clock offset accuracy. Moreover, the frequency stability of BDS-2 onboard satellite clocks is poorer, which has a negative impact on broadcast ephemeris clock offset accuracy. The broadcast ephemeris clock offset accuracy of the BDS-3 satellites is about 1 ns apart from the C38, C39, and C40 satellites, the operation period of these three satellites is shorter, and the stations can receive the signal of these three satellites are few. In a word, the mean accuracy is 1.04 ns, its accuracy is improved compared to that of BDS-2 satellites, which can be attributed to the following reasons: Firstly, the improved rubidium atomic clocks and high-performance Passive Hydrogen Masers (PHM) are equipped on BDS-3 satellites, the frequency stability is extremely improved compared to BDS-2 satellites; secondly, since the Inter-Satellite Link (ISL) technology is employed to estimate BDS-3 broadcast ephemeris clock offset [24], the broadcast ephemeris clock offset accuracy can be significantly improved.

The cesium atomic clocks are installed on GLONASS satellites, previous studies have demonstrated that the performance of cesium atomic clocks is poorer than that of rubidium atomic clocks and PHM [25]. Compared to other systems, the broadcast ephemeris clock offset accuracy of GLONASS is worse, and the broadcast ephemeris clock offset accuracy of R13, R16, and R22 satellites is poorer than 4 ns. The mean clock offset accuracy is 3.10 ns. In terms of Galileo satellites, the broadcast ephemeris clock offset accuracy of each satellite is better than 1 ns, and the mean is 0.61 ns, which shows superior performance; the reason may be that the high-precision rubidium atomic clocks and PHM are employed on Galileo satellites [26]. Moreover, the update frequency of Galileo satellites is high, it is updated every 10 min, which also guarantees the high-precision performance of broadcast ephemeris clock offset. Each QZSS satellite clock offset accuracy is better than 1 ns, and the mean is 0.75 ns, the atomic clocks equipped on QZSS satellites are the same as that of GPS, while the clock offset accuracy is poorer than that of GPS, which may be related to the satellite orbit type. The QZSS broadcast ephemeris clock offset difference from DOY 283 to 289 is presented in Figure 6. It can be clearly seen that the clock offset difference time series is rather stable, and the value is between −2 ns and 2 ns, the mean is 0.75 ns, 0.71 ns, 0.88 ns, and 1.64 ns for J01, J02, J03, and J07 satellites, respectively.

3.2. Broadcast Ephemeris Orbit Performance

The broadcast ephemeris orbit accuracy of GPS, BDS-2, BDS-3, GLONASS, Galileo, and QZSS satellites from DOY 283 to 289 in 2021 are presented in Figure 7, and the mean orbit accuracy is listed in

Table 4. Average accuracy of DOY 283–289 broadcast orbit for Multi-GNSS satellites (unit: m).

System	Radial	Along-Track	Cross-Track	3D RMS
GPS	0.24	0.84	0.57	0.60
BDS-2	1.91	1.32	2.56	1.99
BDS-3	0.11	0.25	0.25	0.21
GLONASS	0.46	1.92	0.99	1.27
Galileo	0.69	0.68	0.46	0.62
QZSS	0.56	0.80	1.06	0.83

. For GPS satellites, the radial accuracy of G04, G14, G18, and G23 satellite orbit is worse than that of other satellites, which may be that these four satellites belong to Block III, and the operation period is shorter, and their broadcast ephemeris orbit accuracy still needs to be improved; the orbit accuracy in the radial direction of other satellites is better than 0.25 m. For the along and cross components, the orbit accuracy is between 0.25 m and 1.5 m, and 0.25 m and 1 m, respectively. The mean 3D RMS is 0.60 m. The orbit accuracy is significantly poor for BDS-2 satellites, especially for GEO satellites, which mainly be since the GEO satellites are static relative to the ground stations, resulting in a strong correlation among the observations at different epochs. Compared to BDS-2 satellites, the broadcast ephemeris orbit accuracy of BDS-3 satellites is considerably improved, the satellite orbit accuracy in radial, along, cross, and 3D RMS is 0.11 m, 0.25 m, 0.25 m, and 0.21 m, respectively, and the improvements are 94.24%, 81.06%, 90.23%, 89.29%, respectively. The reasons can be attributed to the following: Firstly, the inter-satellites link technology is employed to determine the satellite orbit. Secondly, the number of BDS-3 satellites is much more than that of BDS-2, and the satellite type is mainly MEO satellites, the redundancy of observation data has been improved. The satellite orbit accuracy after the PRN 38 is slightly inferior, and the operation period of these satellites is shorter, the stations that can receive the signal of these satellites are few. With the increase of stations, satellite orbit accuracy can be improved in the near future.

The satellite orbit accuracy in radial and cross is small for GLONASS satellites, most satellites are better than 1.5 m, whereas the broadcast ephemeris orbit accuracy in along component shows poorer performance, the mean orbit accuracy is 0.46 m, 0.99 m, 1.92 m, and 1.27 m for radial, cross, along, and 3D direction, respectively. The orbit difference of each Galileo satellite is small, and the orbit accuracy for most satellites is better than 1.0 m in along, cross, and radial directions, and the mean 3D RMS is 0.62 m, which is comparable to that of GPS. The orbit accuracy of QZSS satellites is similar to that of BDS-2, the orbit accuracy of three IGSO satellites is tremendously better than that of GEO satellites. The mean 3D RMS is 0.83 m, which is poorer than that of BDS-3, GPS, and Galileo satellites.

3.3. Signal-in-Space Ranging Errors

To comprehensively assess the accuracy of GNSS broadcast ephemeris orbits and clock offset, the SISRE of all systems was investigated [27]. The SISRE for GPS/BDS-2/BDS-3/GLONASS/Galileo/QZSS satellites from 283 to 289 days in 2021 is given in Figure 8. The mean and RMS of SISRE are given in

Table 5. The average accuracy and RMS of DOY 283–289 SISRE for Multi-GNSS satellites (unit: m).

System	Average	RMS
GPS	0.62	0.21
BDS-2(MEO)	2.19	0.65
BDS-2(IGSO)	3.73	0.90
BDS-3(MEO)	1.97	0.71
BDS-3(IGSO)	2.01	0.35
Galileo	0.62	0.79
GLONASS	2.48	1.04
QZSS	0.98	1.18

. It can be found that the SISRE of GPS and Galileo show the best performance among the five systems, and its fluctuation is between 0 m and 2 m. However, the SISRE of Galileo is larger at some epochs. The rank of SISRE from best to poorest is QZSS, BDS-3, GLONASS, and BDS-2. For the BDS MEO satellites, the SISRE value of the BDS-2 MEO satellites (C11, C12) and the BDS-3 MEO satellites (C25, C30) are from 0 m to 7 m and 0 m to 4 m, respectively. In terms of BDS IGSO satellites, the fluctuation of BDS-2 IGSO satellites (C13, C16) and BDS-3 IGSO satellites (C39, C40) are between 0 m and 6 m, and 0 m and 4 m, respectively. The SISRE of BDS-3 is better than BDS-2 for both MEO and IGSO satellites. Since SISRE can reflect the combined error of orbit and clock offset, and the accuracy of broadcast ephemeris orbit and clock offset are calculated using the observations from ground stations, there is a certain relationship between the observation data quality and SISRE. By comparing the observation data quality and SISRE, it can be found that when the observation data quality is better, the broadcast ephemeris SISRE is also better, and vice versa.

4. PPP Accuracy Evaluation

To investigate the positioning performance of multi-GNSS in the Asia-Pacific region, 10 MGEX stations were selected to conduct static and kinematic PPP experiments. For the data processing strategies, the sampling interval of observation data is 30 s, and the period is from DOY 283 to 289 in 2021. At present, several MGEX analysis centers can provide precise satellite orbit and clock offset products for the five systems, and the consistency between WUM orbit and clock offset products and other MGEX analysis centers is about 3–10 cm and 0.1–0.3 ns, respectively, showing better consistency with the products from other analysis centers. The positioning performance in the Asia-Pacific region can be reflected using the WUM orbit and clock offset products [28,29]. Therefore, the multi-GNSS final satellite orbit, clock offset, and earth rotation parameter (ERP) products generated from Wuhan University are applied in this study [30]. The satellite antenna phase center variation (PCV) and phase center deviation (PCO) values are used from igs14.atx [31]. The dual-frequency ionosphere-free is employed to eliminate the effect of the first-order ionosphere and the higher-order ionosphere is ignored [32]. The zenith hydrostatic delay of the troposphere is corrected using the Saastamoinen model [33], while the zenith wet delay is estimated as the parameter. The carrier phase ambiguities are estimated as float solutions [34]. The station coordinates of the static PPP are estimated as a constant, while it is estimated as white noise in the kinematic model. The receiver clock offset is estimated as white noise. In addition, the relativistic effects, satellite antenna phase wind-up, and station tides are weakened or eliminated using existing models [35,36,37]. To compare the positioning performance differences between single-system and multi-GNSS combinations in the Asia-Pacific region, six mode combinations in the static and kinematic PPP experiments were conducted, which is: GPS(G), GPS/QZSS combination (GJ), BDS (C), BDS/QZSS combination (CJ), GLONASS (R), and Galileo (E), respectively. The convergence time and positioning accuracy are used to evaluate the positioning performance. The convergence time is that the current epoch with 20 consecutive epochs is better than 10 cm, and the positioning accuracy is the RMS of the positioning error after convergence [38]. It is noted that the positioning error is the positioning difference between the PPP solutions and IGS weekly solution [39].

4.1. Static PPP Performance

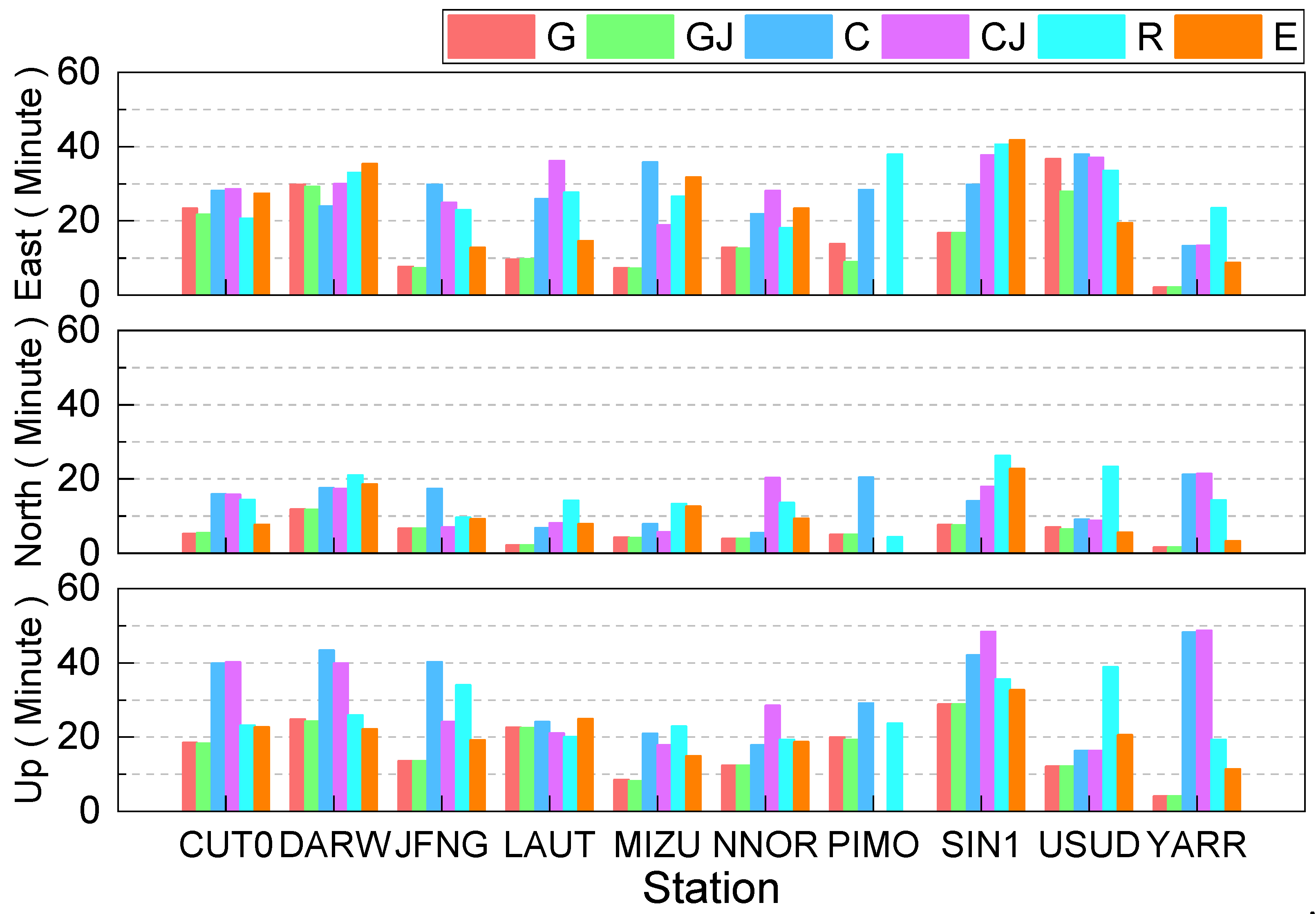
The mean convergence time for static PPP of six combinations for each station in the east, north, and up directions is presented in Figure 9, and the mean convergence time of each combination is listed in

Table 6. Convergence time and positioning accuracy of different combination static PPP.

System	Convergence Time (min)			Positioning Accuracy (cm)
	E	N	U	E	N	U
G	16.01	5.53	16.52	1.09	0.78	1.68
GJ	14.35	5.48	16.33	1.08	0.77	1.66
C	27.47	13.58	32.17	1.40	1.03	2.08
CJ	28.29	13.59	31.64	1.38	1.01	2.04
R	28.44	15.44	26.26	1.93	1.32	3.07
E	23.93	10.78	20.79	2.24	1.12	2.65

. It can be seen from Figure 9 and Table 6 that the convergence time of GPS is the shortest among six combinations, which are 6.01 min, 5.53 min, and 16.52 min for the east, north, and up directions, respectively. For the east and north directions, the convergence time of Galileo is faster than that of BDS, and the GLONASS show the longest convergence time, which may be that all selected stations are located in the region with low latitudes, and better positioning performance can be achieved at high latitudes than low latitudes for GLONASS [38]. In terms of up component, the convergence time of Galileo is shorter than that of GLONASS, while the BDS presents the poorest convergence performance in the up component among the six combinations, and its convergence time is 32.17 min. Furthermore, compared to the GPS-only solution, the convergence time of the GPS/QZSS combination can be shorted, and the improvements are 10.37%, 0.90%, and 1.15% in the east, north, and up directions, respectively. While compared to the BDS-only solution, the BDS/QZSS solutions only short the convergence time in the up direction, the improvement is 1.65%. The reason may be that the number of BDS satellites in Asia-Pacific is larger than 20, when conducting PPP, by adding QZSS satellites, the improvements in convergence time for static PPP are limited.

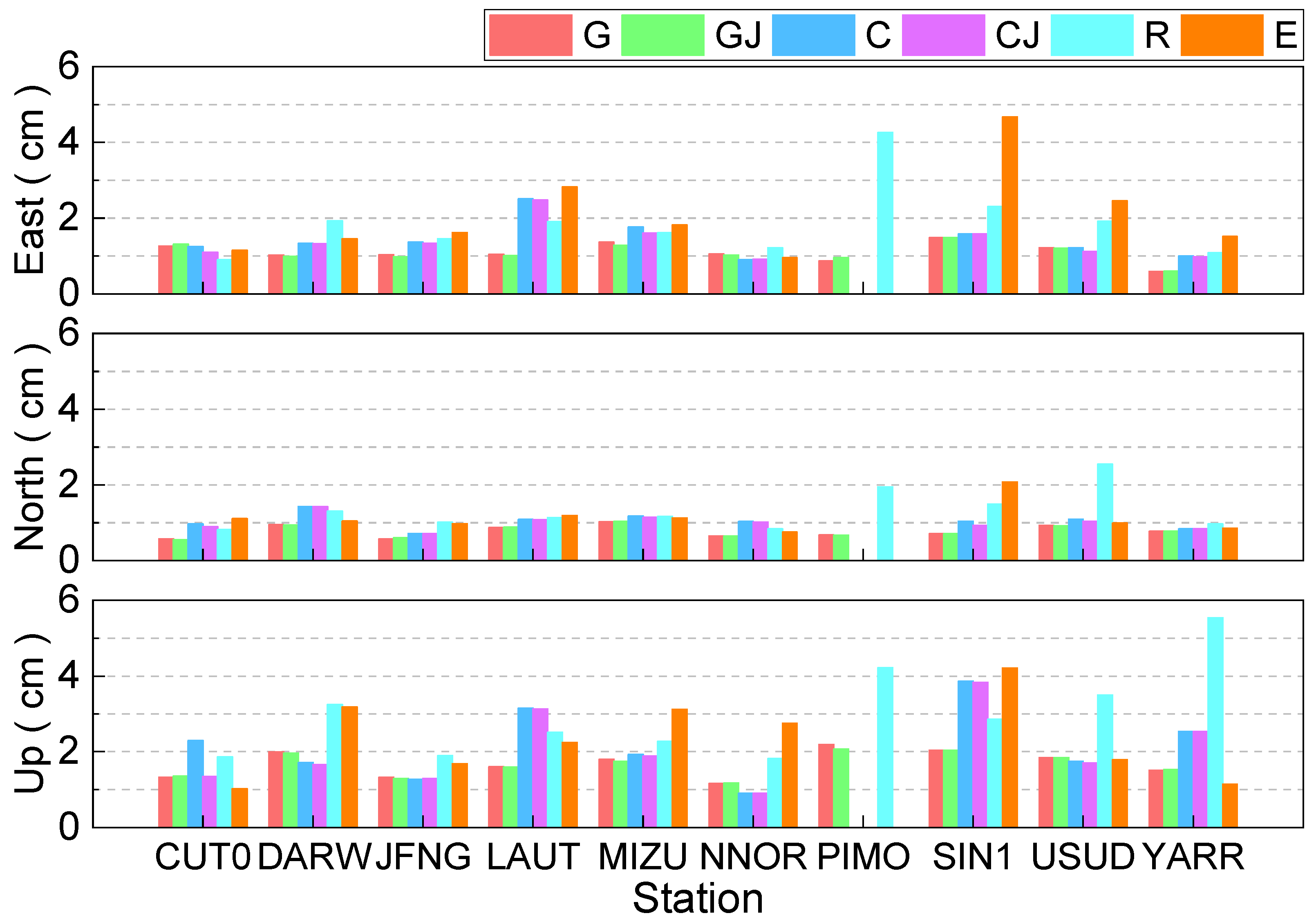
The mean positioning accuracy for static PPP of six combinations for each station in the east, north, and up directions are presented in Figure 10, and the mean positioning accuracy of each combination is listed in Table 6. It can be clearly seen that the positioning accuracy is better than 3 cm in the east direction except for PIMO and SIN1 stations. Apart from the USUD station, the positioning accuracy of other stations is better than 2 cm in the north component. The positioning accuracy is outperformed 5 cm in the up direction except for YARR station. The positioning accuracy of GPS is the best, and it is 1.09 cm, 0.78 cm, and 1.68 cm in east, north, and up directions, respectively. For three components, the positioning accuracy using BDS is better than that of GLONASS, while Galileo shows the worst performance. Compared to the GPS-only solution, the positioning accuracy of GPS/QZSS solutions can be improved, and the improvement is 0.92%, 1.28%, and 1.19% in the east, north, and up directions, respectively. The few improvements may be caused by the limited number of QZSS satellites. The improvement of the BDS/QZSS solution in terms of positioning accuracy is 1.43%, 1.94%, and 1.92% in east, north, and up directions compared to the single BDS-only solution. Totally, the positioning accuracy of six combinations is better than 3 cm, 2 cm, and 4 cm in the east, north, and up directions, respectively.

4.2. Kinematic PPP Performance

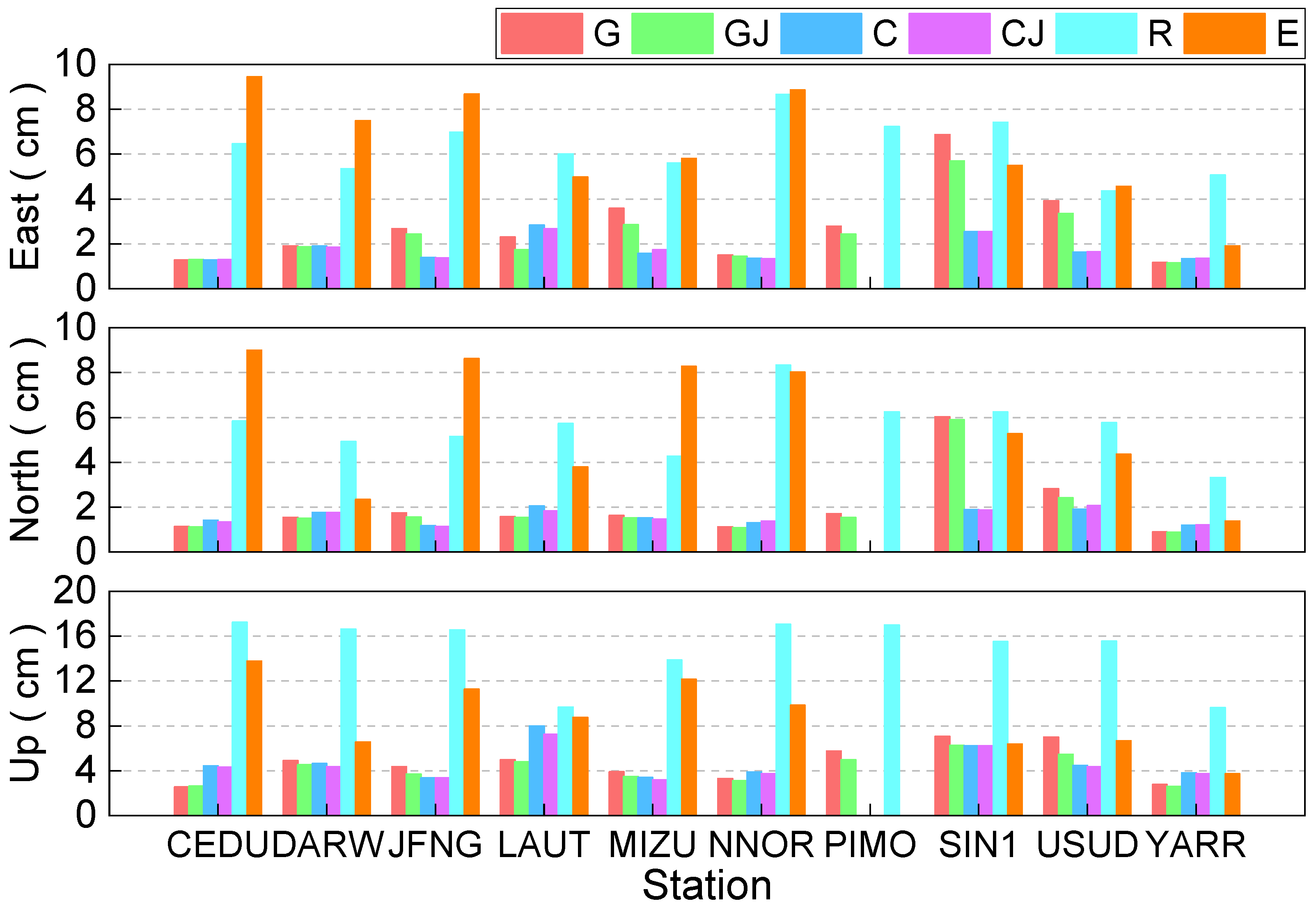
The mean convergence time for kinematic PPP of six combinations for each station in the east, north, and up directions is presented in Figure 11, and the mean convergence time of each combination is listed in

Table 7. Convergence time and positioning accuracy of different combination kinematic PPP.

System	Convergence Time (min)			Positioning Accuracy (cm)
	E	N	U	E	N	U
G	24.78	8.49	24.40	2.80	2.03	4.65
GJ	18.63	7.84	21.74	2.43	1.91	4.15
C	55.62	31.09	45.37	1.77	1.59	4.69
CJ	49.47	24.89	42.35	1.76	1.57	4.50
R	43.39	47.68	50.98	6.32	5.59	14.87
E	23.82	17.80	34.02	6.36	5.68	8.79

. It can be seen that the convergence time of the Galileo solution is the shortest in the east direction, it is 23.82 min, while the shortest convergence time is the GPS-only solution in the north and up directions, with convergence times being 8.49 min and 24.4 min, respectively. For the east direction, the convergence time of the GPS-only solution is faster than that of the GLONASS-only solution, and the BDS-only solution is the longest, nearly one hour is still needed to obtain the centimeter-level position accuracy in kinematic PPP mode, whereas it is about 20 min for the GPS/QZSS solutions. Compared to the GPS-only and BDS-only solutions, the improvement of convergence time for the GPS/QZSS and BDS/QZSS solutions is 24.82%, 7.66%, 10.90%, and 11.06%, 19.94%, and 6.66% in the east, north, and up components, respectively. Compared to the static PPP, the improvement rate of convergence time for the GPS/QZSS and BDS/QZSS solutions is larger, which may be that the increased number of satellites and better geometry distribution of satellites are beneficial to the convergence of kinematic PPP.

The kinematic PPP mean positioning accuracy of six combinations for each station in the east, north, and up directions are presented in Figure 12, and the mean positioning accuracy of each combination is listed in Table 7. One can see that the GPS-only, GPS/QZSS, BDS-only, and BDS/QZSS solutions show similar positioning accuracy in three directions except for the LAUT and MIZU station, which is better than 3 cm in the three directions. The positioning performance of GLONASS and Galileo in the Asia-Pacific region is relatively poorer. The positioning accuracy of BDS presents the best performance in the east and north component, and the positioning accuracy is 1.77 cm and 1.59 cm, respectively. This is due to the launch of BDS-3 satellites, the number of BDS satellites is more than other satellite systems in the Asia-Pacific region. The positioning accuracy in the up direction of GPS shows the best performance, and it is 4.65 cm. For the east and north directions, the positioning accuracy of GPS is better than that of Galileo, whereas the GLONASS is the worst. In terms of the up direction, the positioning accuracy of BDS is better than that of Galileo, while the GLONASS is still the worst. Moreover, compared to the GPS-only solution and BDS-only solutions, the positioning accuracy of the GPS/QZSS and BDS/QZSS solutions can be improved from 2.80 cm, 2.03 cm and 4.65 cm to 2.43 cm, 1.91 cm and 4.15 cm, with the improvement being 13.21%, 5.91%, and 10.75%, from 1.77 cm, 1.59 cm, and 4.69 cm to 1.76 cm, 1.57 cm, and 4.50 cm for the east, north, and up directions, with the improvement being 0.56%, 1.26%, and 4.05%, respectively. Except for the GLONASS-only and Galileo-only solutions, the positioning accuracy of 3 cm, 3 cm, and 5 cm in the east, north, and up components for kinematic PPP can be achieved.

The consistency of performance improvement among systems based on multi-GNSS data quality, broadcast ephemeris accuracy, and precision positioning performance is analyzed. It can be found that the observation data quality of GPS is improved by 28.11%, and the improvement for SISRE, static PPP, and kinematic PPP is 75%, 44.31%, and 69.24% compared to GLONASS, respectively. Compared to GLONASS, the improvement of data quality, SISRE, static PPP, and kinematic PPP of Galileo is improved by 32.71%, 75%, 5.52%, and 28.37%, respectively. The improvement of BDS-3 is 33% and 32.78% compared to BDS-2 in terms of observation data quality and SISRE, respectively. These results show that there is a consistency between data quality, SISRE, and PPP.

5. Conclusions

This paper focused on the performance of multi-GNSS in the Asia-Pacific region. One-week period observation data from 10 MGEX stations, precise satellite orbit and clock offset products, and broadcast ephemeris were used to investigate the performance of C/N0, pseudorange multipath, broadcast ephemeris clock offset accuracy, broadcast ephemeris orbit accuracy, SISRE, static PPP, and kinematic PPP in the Asia-Pacific region, and the conclusions are as follows:

(1) The C/N0 and pseudorange multipath among GPS, BDS-2, BDS-3, QZSS, GLONASS, and Galileo were investigated and compared; the C/N0 of GPS and Galileo shows the best performance, and the C/N0 for BDS and GLONASS are worse, and the C/N0 of QZSS is the poorest. The pseudorange multipath error of Galileo has the smallest, about 0.2 m, GPS and QZSS are comparable at about 0.3 m, and GLONASS is around 0.4 m.

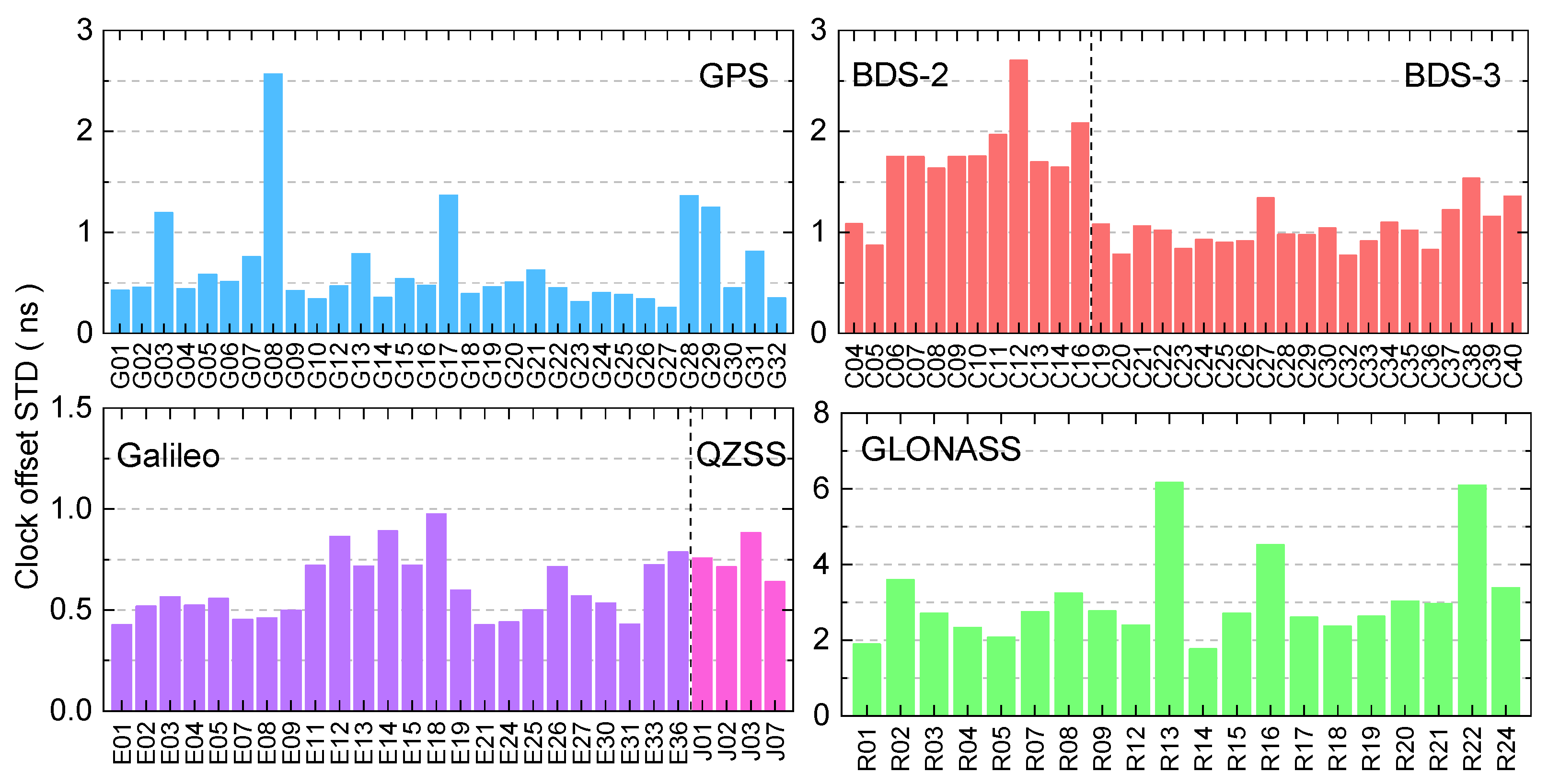
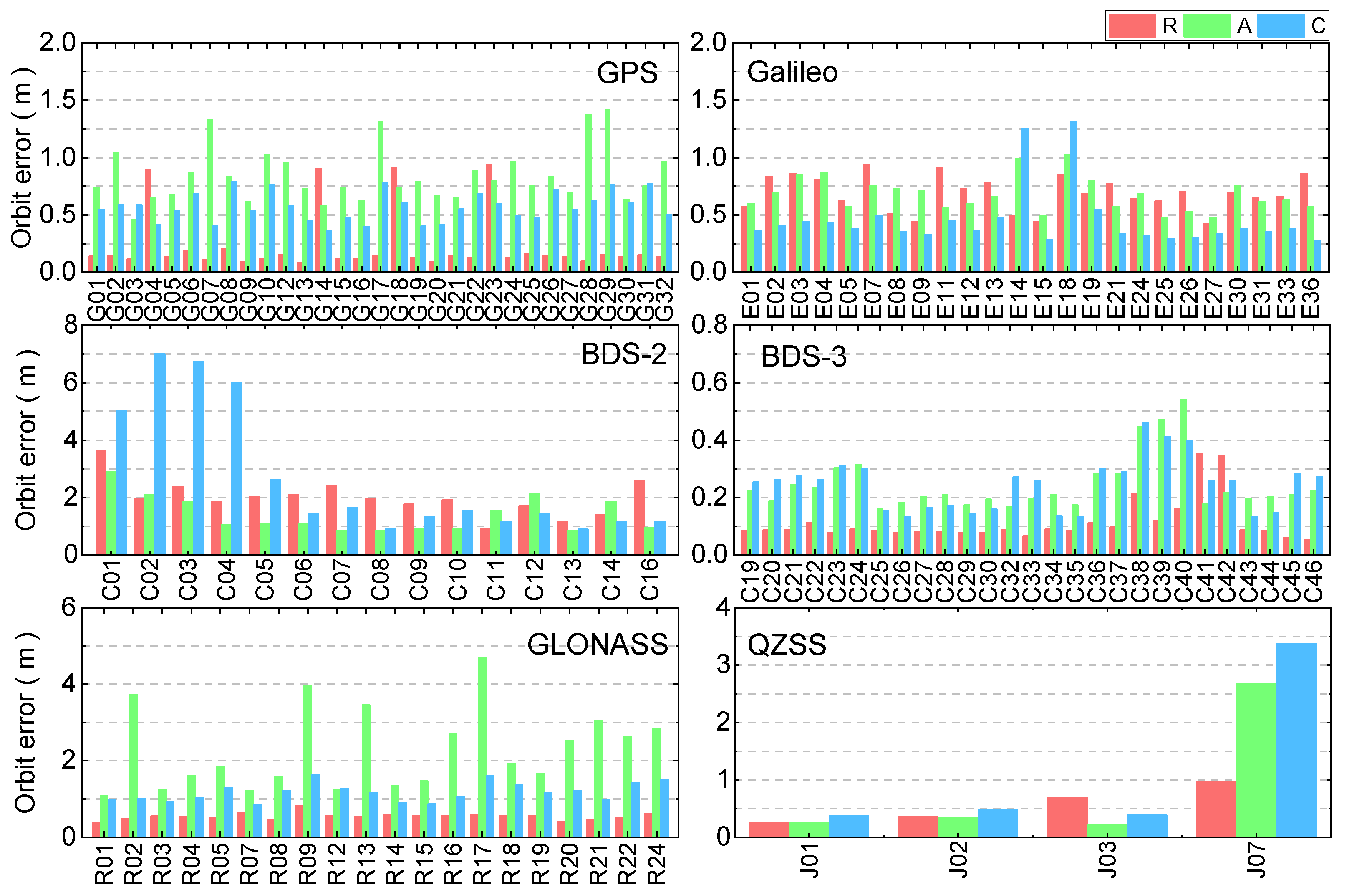
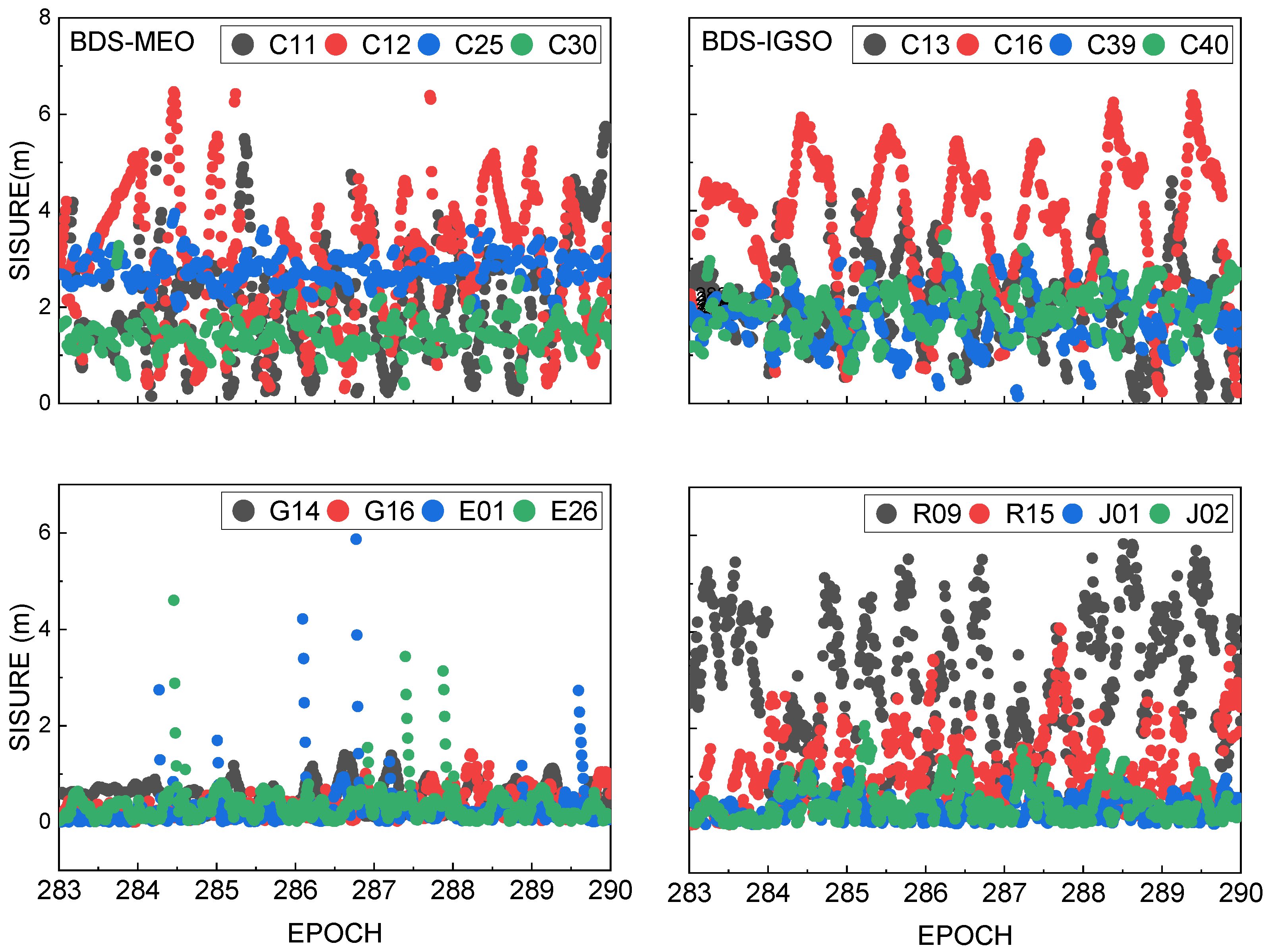
(2) The broadcast ephemeris orbit and broadcast ephemeris clock offset of GPS, BDS-2, BDS-3, QZSS, GLONASS, and Galileo were analyzed, and the results show that the broadcast ephemeris clock offset accuracy of Galileo is the best, followed by GPS, QZSS, BDS-3, BDS-2, and GLONASS, respectively. For the broadcast ephemeris orbit, the accuracy of BDS-3 is the best, followed by GPS, Galileo, QZSS, GLONASS, and BDS-2, respectively. The SISRE of BDS-3 is better than BDS-2 for both MEO and IGSO satellites, and by comparing the observation data quality and SISRE, it can be found that when the observation data quality is better, the broadcast ephemeris SISRE is also better, and vice versa, indicating that the magnitude of SISRE has a certain correlation with the observation data quality results.

(3) The static PPP and kinematic PPP performance were analyzed in terms of GPS, GPS/QZSS combination, BDS, BDS/QZSS combination, GLONASS, and Galileo. For static PPP, the positioning accuracy of GPS and GLONASS present the best and worst performance, respectively. In terms of kinematic PPP, the positioning accuracy in the east and north direction of GPS is better than that of Galileo. For up direction, the positioning accuracy of BDS is better than that of Galileo, the GLONASS shows the worst positioning performance in the east, north, and up component. Compared to the GPS-only and BDS-only solutions, the positioning accuracy of GPS/QZSS and BDS/QZSS solutions is improved, and the improvement rate of kinematic is larger than static PPP.